|
Не могу дома найти транспортир, а надо сделать домашнее задание. Можно проверить, если угол прямой, 45, 30 или 60 градусов. Взять обычный лист бумаги. У него углы по 90 градусов. Свернуть пополам – получим 45 градусов. Поделить на три равные части – получим 30 или 60. Поделим 30 пополам, получим угол в 15 градусов. Можно получить 90 или 180 плюс(минус) любой из этих углов Ну а для других углов точно нужен транспортир. система выбрала этот ответ лучшим Ксарфакс 5 лет назад Если у вас нет транспортира, то измерить угол можно с помощью бумаги в клеточку – нужно на ней построить “стандартные” углы (30, 60 градусов и другие). Существует несколько способов, с помощью которых можно строить углы без транспортира. После построения углов нужно соотнести заданный угол с углами, которые были сделаны на клетчатой бумаге. Понятно, что угол 90 градусов построить очень просто – строим квадрат любого размера на листе в клетку и всё. Угол 45 градусов можно построить, если провести диагональ у данного квадрата. Градусную меру, равную 30 и 60, можно построить с помощью прямоугольника, у которого длина 5 клеток, высота 3 клетки (отношение длины и высоты должно быть 5:3). Проводим диагональ и получаем искомые 30 и 60 градусов. Потом угол 30 градусов делим с помощью луча на 2 части и получаем 15 градусов. Теперь вырезаем углы 15, 30, 45, 60 и 90 градусов и сравниваем их с заданным углом. Если угол тупой, то разделяем его на прямой + острый угол и измеряем таким же образом. В принципе, вряд ли придётся строить каждый угол – обычно уже на глаз становится примерно понятно, какая градусная мера у угла. Трудно спутать, например, 20 градусов и 70 градусов. Как измерить углы без транспортира, линейки, циркуля, интернета и нет под рукой таблицы тангенсов, в которых приведены значения углов? – на мой взгляд очень просто, достаточно иметь под рукой обычные механические часы с циферблатом. Возможно будет небольшая погрешность, но не лететь же нам в космос, а для домашнего задания еще как пойдет. А теперь к делу – обычные механические часы разделены делениями на 60 частей, одно деление равно 6 градусам, половина деления 3 градусам, треть 2 градусам. Если сумеете центр часов установить точно на точку, с которой начинается угол, который нам нужно измерить, то погрешность будет очень небольшая. Пример измерений разных углов с помощью циферблата обычных часов: Chromer 11 лет назад Элементарно. Достраиваем угол до прямоугольного треугольника. Тангенс нужного угла – соотношение ВС к АС. А уж по таблице определить угол не проблема. Ninaarc 5 лет назад Если у вас имеется бумага в клетку, то можно самостоятельно смастерить транспортир, который пригодится для измерения углов. Вырезаем из клетчатой бумаги квадрат, в котором все углы прямые. Теперь соединяем противоположные стороны линией, разделив угол на две части. Каждая часть будет равна углу в 45 градусов. Получить углы в 30 и 60 градусов можно делением прямого угла на три части. Одна часть составит угол 30 градусов, а две части – 60 градусов. Поделив угол в 30 градусов пополам, можно получить угол в 15 градусов, и такие деления можно продолжать. Понятно, что точные определения малых углов с помощью самодельного транспортира сделать невозможно, придется распечатывать транспортир на принтере, предварительно найдя его в интернете. дольфаника 8 лет назад Ориентируйтесь по прямому углу, это 90 градусов. Когда Вы разделите его пополам, это будет ровно 45 градусов. если его разделить на три ровные части, то получится 30 градусов. Его поделить на два раза будет 15 градусов, поделить на три части будет 5 градусов. Можно заранее вырезать на бумаге прямой угол, а потом его разрезать по указанным долям, можно делить на десять частей и прибавлять, а можно поделить так, чтобы получился 1 градус и прибавлять полоску угла к другим бумажным углам. Легко измерить углы в 45, 30 и 60 градусов. Тут даже объяснять ничего не надо. Угол в 45 градусов имеет у основния равносторонний треугольник, а треугольник с углами в 30 и 60 градусов отличается тем, что его гипотенуза равна удвоенному катету при большем угле. То есть построить эти углы можно взяв большим катетом прямую, опустить на нее перпендикуляр, меньший катет, определенной длинны – скажем 5 см, тогда гипотенуза треугольника с заданными углами будет равна 10. Построить ее можно с помощью циркуля, найдя пересечение окружности радиуса 10 см с нижним катетом и центром на вершине перпендикуляра к нему. Другие углы находятся построением прямоугольных трейгольников и вычеслением через тригонометрические функции. Конечно понадобится калькулятор или таблицы. Света 78 8 лет назад Если у вас нет под рукой транспортира, а нужно измерить угол, то можно использовать обычный лист бумаги. На него нужно положить часы и про помощи авторучки перенести основные углы. Дальше вы можете продлить эти линии при помощи любой линейки или просто прямолинейного предмете (например, доски для резки хлеба) до конца листа бумаги. Таким образом, у вас получится достаточно большой транспортир. Обычные наручные часы позволят вам на основании часовых засечек определить угол я точностью до 30 градусов (360 разделить на 12), а на основании минутных засечек даже с точностью в 6 градусов (360 разделить на 60) Каждый человек из школьного курса знает способы определения углов 30, 45, 60 и 90 градусов, знает способы деления углов, дуг и линий на несколько равных частей. Этих знаний достаточно для измерения практически любых углов подручными средствами. Можно использовать циферблат часов. Солнце за один час смещается примерно на 15 градусов. Можно измерять углы с помощью пальцев, ладони, как это делают военные. Odessitka 8 лет назад Без транспортира углы замерить сложно, но нет ничего невозможного. Можно померить углы без транспортира приблизительно. Для этого можно распечатать вот этот рисунок и наложить его на нужный угол либо взять циркуль, приложить к углу рисунка, а потом к тому, что нужно замерить. Кирилл132 11 лет назад Никак ты без транспортира углы не измеришь! Если есть принтер, скачай фотку градусной мера, напечатай, вырежи, может получится. ИринаШ 8 лет назад Советую распечатать транспортир на бумаге, вырезать его, можно наклеить на картон, чтобы удобнее было пользоваться. Но можно и бумажный временно использовать. Вот вам картинка в помощь. Можно и по картинке примерно посчитать угол. Если такой вариант не подходит, то примерно можно прикинуть угол с помощью клетки, угол 180 градусов и 90 градусов делите на 2 , 45 градусов еще на 2 равные части и так далее. Точный результат не получится, но примерно можно прикинуть. Знаете ответ? |
Download Article
Download Article
The easiest way to measure an angle is to use a protractor. However, if you don’t have a protractor handy, you can determine the size of an angle using the basic geometric principles of triangles. You’ll need a scientific calculator to solve the equations. Most smartphones are equipped with them, but you can also download a free app or access a free calculator online. The calculations you need to make depend on whether you’re measuring an acute (less than 90 degrees), obtuse (more than 90 degrees but less than 180), or reflex angle (more than 180 degrees but less than 360).[1]
-
1
Draw a vertical line connecting the 2 rays of the angle. To determine the number of degrees in an acute angle, connect the 2 rays to form a triangle. Line up the short end of your ruler with the bottom ray, then draw a vertical line intersecting the other ray using the long side of your ruler.[2]
- The vertical line creates a right triangle. The angle formed by the adjacent side (the bottom ray of the angle) of the triangle and the opposite side (the vertical line) measures 90 degrees.
-
2
Measure the length of the adjacent side to find the run. Place the end of your ruler at the vertex of the angle. Measure the length of the adjacent side from the vertex to the point where it intersects with the opposite side.[3]
- This amount is the run value in your slope equation, where slope = rise/run. If you measured 7, your equation at this point would be “slope = rise/7.”
Advertisement
-
3
Measure the length of the opposite side to find the rise. Set the short end of your ruler flush against the adjacent side of the triangle. Measure the length of the vertical line from the point where it meets the adjacent side to the point where it meets the upper ray of the angle (the hypotenuse of your triangle).[4]
- This amount is the rise value in your slope equation. If you measured 5, you would fill in your equation so that “slope = 5/7.”
-
4
Divide rise by run to find the slope of the angle. The slope is the steepness of the diagonal line, or hypotenuse, of your triangle. Once you know this number, you can calculate the degrees of your acute angle.[5]
- To continue the example, the equation “slope = 5/7” would yield “slope = 0.71428571.”
Tip: Don’t round the number before calculating the degrees in the angle – it could decrease the accuracy of the result.
-
5
Use your calculator to determine the degrees of the angle. Type the value for slope into your scientific calculator, then press the inverse tan button (tan-1). This will give you the degrees of the angle.[6]
- To continue the example, with a slope of 0.71428571, the angle is 35.5 degrees.
Advertisement
-
1
Extend the bottom ray of the angle in a straight line. Mark your vertex with a dot, then use the long side of your ruler to draw a straight line to the left of the vertex. The bottom ray of the angle should be a single long line that extends below the open top ray of the angle.[7]
- Make sure your line is perfectly straight. If it is angled up or down, it will ruin the accuracy of your equation.
Tip: if you’re working on unlined paper, you can line up the short end of your ruler with the side of the paper to make sure your line extension is straight.
-
2
Draw a vertical line connecting the top ray and the line. Line up the short end of your ruler with the bottom ray at a point where the long side crosses the top ray. Follow the long side to draw a line straight up from the bottom ray that connects the two.[8]
- Effectively, you have created a small right angle underneath the obtuse angle you want to measure, turning the top ray of the obtuse angle into the hypotenuse of your right angle.
-
3
Measure the length of the bottom line from the vertex. Place your ruler below the bottom line, with the beginning at the vertical line creating the right angle. Measure the length from that point of intersection to the vertex of the original angle.[9]
- You’re determining the slope for the angle of the acute triangle, which you can use to calculate the degrees in the acute angle. The bottom line is the run value in the equation “slope = rise/run.”
-
4
Measure the length of the vertical line. Line up the short end of your ruler with the bottom line of the small acute triangle. Read up the ruler to the point where the vertical line meets the open ray of your obtuse angle. This is the length of your vertical line.[10]
- The length of your vertical line is the rise value in the equation “slope = rise/run.” Once you know the values for both rise and run, you can calculate the slope of the acute angle.
-
5
Find the slope of the acute angle. Divide the rise value by the run value to determine the slope of the acute angle. You’ll use this value to calculate the degrees of the acute angle.[11]
- For example, the equation “slope = 2/4” would yield “slope = 0.5.”
-
6
Calculate the degrees of the acute angle. Enter your slope value in your scientific calculator, then press the inverse tan button (tan-1). The value displayed is the number of degrees in the acute angle.[12]
- To continue the example, if your slope is 0.5, the acute angle is a 26.565-degree angle.
-
7
Subtract the degrees of the acute angle from 180. A flat line is a straight angle with 180 degrees. Since you drew a straight line, the sum of the acute angle you calculated and the obtuse angle will be 180 degrees. Subtracting the degrees of the acute angle from 180 will give you the degrees of your obtuse angle.[13]
- To continue the example, if you have an acute angle of 26.565 degrees, you have an obtuse angle of 153.435 degrees (180 – 26.565 = 153.435).
Advertisement
-
1
Identify the smaller acute angle associated with the reflex angle. A reflex angle has more than 180 degrees but fewer than 360. This means that if you look at the reflex angle, you’ll also see an acute angle inside the rays of the reflex angle.[14]
- By determining the degrees of the acute angle, you can calculate the degrees in the reflex angle. You can use the basic slope equation and the inverse tangent function on your scientific calculator to find the degrees in the acute angle.
Tip: If you get confused because the angle is upside down, turn your paper and ignore the reflex angle until the last step.
-
2
Draw a vertical line connecting the rays of the acute angle. Line up the short end of your ruler with the ray of the angle that is horizontal rather than diagonal. Then draw a vertical line that meets the horizontal ray of the angle.[15]
- The horizontal line becomes the adjacent side of your triangle, and the vertical line becomes the opposite side of the acute angle you want to measure.
-
3
Measure the rise and the run of the acute angle. In the equation “slope = rise/run,” the rise is the length of the vertical line, or opposite side of your triangle. The run is the length of the horizontal line, or adjacent side of your triangle.[16]
- Measure the horizontal line from the vertex to the point where it meets the vertical line. Measure the vertical line from the point where it meets the horizontal line to the point where it meets the diagonal line.
-
4
Divide rise by run to find the slope of the acute angle. Plug the values you found for the length of the vertical and horizontal lines into your slope equation. When you divide the length of the vertical line by the length of the horizontal line, you’ll get the slope for the angle.[17]
- For example, if your horizontal line measured 8 and your vertical line measured 4, your equation would be “slope = 4/8.” The slope of your angle would be 0.5.
-
5
Use your calculator to find the degrees of the acute angle. Type the value you got for the slope of the angle into your scientific calculator, then press the inverse tangent button (tan-1). The value displayed is the degrees of the smaller acute angle.[18]
- To continue the example, if your slope is 0.5, the acute angle would measure 26.565 degrees.
-
6
Subtract the degrees of the acute angle from 360. A circle has 360 degrees. Since a reflex angle is an angle of more than 180 degrees, you relate it as a portion of a circle. The degrees of the reflex angle and the degrees of the smaller acute angle would add up to 360.[19]
- To continue the example, if the smaller acute angle measures 26.565 degrees, the reflex angle would measure 333.435 degrees.
Advertisement
Add New Question
-
Question
What if the line is curvy?
If there is no straight line, there’s no angle to measure. (An angle is defined as a figure formed by two “rays,” which are straight line segments.)
-
Question
How do I construct a vertical line?
Use a protractor to draw a line perpendicular to the top or bottom edge of the paper, or measuring with a ruler, draw a line parallel to the sides of the paper.
-
Question
How how accurate are the results for each method?
Those methods can usually yield more precise angles than a protractor can.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Make sure the trig functions of your scientific calculator are set to measure in degrees, not radians.
-
Slope is the relationship between rise and run. The unit of measurement you use to quantify the lengths of the 2 lines is irrelevant – just make sure you’re using the same unit for both lines. In other words, if you measure the length of one line in centimeters, you should also measure the other in centimeters.
Thanks for submitting a tip for review!
Advertisement
Things You’ll Need
- Scientific calculator
- Ruler
References
About This Article
Article SummaryX
To measure an acute angle without a protractor, start by drawing a vertical line connecting the 2 rays of the angle to form a right triangle. Note that the angle formed by the adjacent side of the triangle and the opposite side measures 90 degrees. Next, measure the length of the adjacent side to find the run. Then, measure the length of the opposite side to find the rise. Once you have these measurements, divide rise by run to find the slope, or the steepness, of the diagonal line. When you have this number, you can calculate the degrees of your acute angle by typing the value for slope into a scientific calculator. Finally, press the inverse tan button to get the degrees of the angle. To learn how to measure an obtuse angle without a protractor, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 270,790 times.
Did this article help you?
Добрый день, уважаемые гости!
Сегодня, я хотел бы описать полезный совет, как очень быстро построить или измерить любой угол с помощью обычного строительного угольника, когда других инструментов попросту нет под рукой.
Нам сейчас совершенно не потребуются ни угломеры, ни транспортиры и построение угла будет произведено угольником всего лишь в три шага.
1. Построение
Шаг №1
Как мы знаем, угол — это место на плоскости между двумя пересекающимися линиями (или сторонами какого-либо предмета), которые выходят из одной точки, называемой вершиной угла.
Итак, при построении угла, ставим угольник делением “0” (ноль) см. в вершину будущего угла и от этой точки проводим прямую в нужном вам направлении, от которой необходимо построить угол (эта прямая может являться одной из граней или сторон детали, заготовки или фигуры).
После чего, на этой прямой откладываем 10 см и ставим точку (штрих).
Отметив 10 см, из этой точки проводим к прямой перпендикуляр:
Шаг №2
Для примера, мне нужно построить угол 26°! В вашем же случае он может быть любым: 13°, 25°, 49°, 74° и пр.
Берем смартфон, заходим в приложение “калькулятор”, переводим его в инженерный режим и вводим нужный вам угол. Я ввел “26″.
Далее, нажимаем кнопку “tan” или “tg”, которая обозначает “вычислить тангенс угла”.
Машина мне вывела число 0,487. Из школы мы знаем, что тангенс угла — это отношение противолежащего нашему углу катета к прилежащему. И, зная один катет 10 см и отношение катетов 0,487, мы за одну секунду вычисляем второй катет, который равен 4,87 см.
Скорее, вы теперь поняли, для чего я взял первый катет именно 10 единиц.
Для простоты вычислений! На 10 проще всего умножать, переставив запятую на один разряд вправо.
Шаг №3
Я округляю 4,87 до десятых и на перпендикуляре отмечаю 4,9 см.
Чертим гипотенузу и получаем искомый угол!
Я решил перепроверить построенный угол и приложил угольник Свенсона:
Всё верно! Получил 26°.
2. Измерение
Сейчас мы построили угол, а при измерении угла — производим все то же самое, только в обратном порядке. Измеряя угол, мы будем знать оба катета, а соответственно и их отношение. Вводим в калькуляторе значение отношения противолежащего катета к прилежащему и нажимаем кнопку “arctg”, “atg” или “tan -1”, которая обозначает обратную тангенсу функцию — арктангенс.
На дисплее калькулятора мы увидим значение нашего угла!
…написано много, а на деле все занимает не более одной минуты…
Спасибо за внимание!
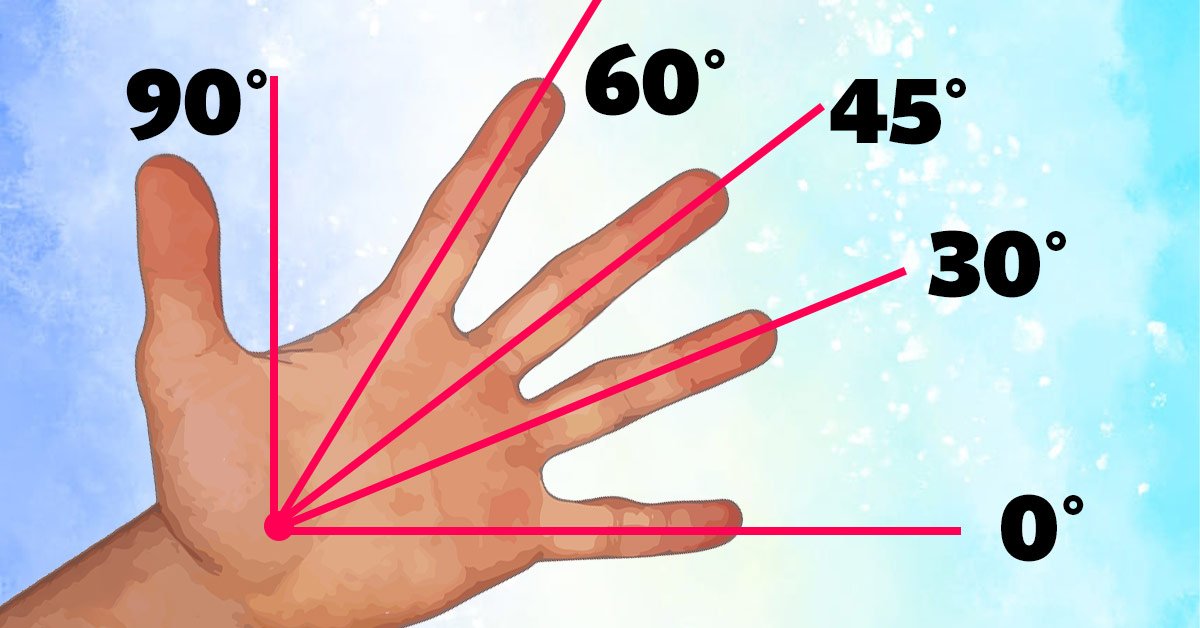
Объясняем ребенку на пальцах одной руки, сколько градусов в угле
Метки
Как хотя бы примерно определить, сколько градусов в угле, если под рукой нет ни транспортира, ни угольника? «Так Просто!» знает остроумный способ и просто не может не поделиться им с читателями.
Сколько градусов в угле
Общепринятой единицей измерения плоских углов является градус. Почему математики древности выбрали именно такую единицу и почему в окружности 360 градусов, а не, скажем, 1000, точно неизвестно.
Одна из гипотез усматривает тут связь с тем, что в году приблизительно 360 дней. Другая гласит, что шумеры выбрали число 360, основываясь на своей шестидесятеричной системе счисления.
Так или иначе, а углы присутствуют не только на страницах учебников, но и повсеместно окружают нас в реальной жизни. Прямой угол легко найти в очертаниях зданий, изгибах мебели и каждом печатном листе.
Без угла в 45 градусов ни один столяр не смастерит простейшую рамку. Угол в 60 градусов требуется для построения равносторонних треугольников. Угол 30 градусов используется редко, но помогает получить угол в 120 градусов, необходимый для построения правильного шестиугольника.
Измеряем угол без транспортира
При наличии транспортира всё просто. Размести его центр в вершине угла, а основание совмести с одной из сторон. Проследи за второй стороной угла. В том месте, где она пересечет дугу транспортира, и будет указана величина угла в градусах.
Без транспортира под рукой, как обычно и бывает, задача усложняется. Но смекалка выручит нас и здесь. Вытяни руку ладонью вверх и максимально расставь пальцы.
Следи за тем, чтобы большой палец находился перпендикулярно мизинцу. Тогда, если мизинец указывает на 0 градусов, то безымянный будет указывать на 30, средний на 45, указательный на 60, а большой на 90 градусов.
Способ, конечно, не очень точный, но всегда поможет приблизительно понять, с каким углом ты имеешь дело. Раньше мы рассказывали о полезном для каждого домашнего мастера угле в 22,5 градуса, который позволяет правильно заточить ножи. Выдержать его поможет сложенный вчетверо лист бумаги.
Строим углы в 90, 60 и 30 градусов без транспортира
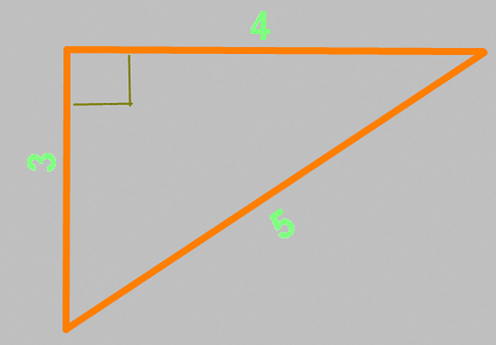
Если нужен угол в 30, 60, 90 градусов, а транспортира или шаблона под рукой нет, помогут эти простые способы. Чтобы получить точный угол в 90 градусов, построй Пифагоров треугольник со сторонами, кратными 3,4,5.
Для этого, например, начерти отрезок длиной 5 см и проведи из его концов дуги с радиусами 3 и 4 см. Теперь соедини точку их пересечения с концами отрезка. Получится прямоугольный треугольник и угол, расположенный напротив гипотенузы, будет составлять ровно 90 градусов.
Когда уже есть прямой угол, легко получить углы в 30 и 60 градусов поможет магическое число 173 (его хорошо бы запомнить). Отложи по одной стороне прямого угла отрезок в 100 мм, а по другой — 173. Соедини их концы. Ты получишь шаблон с углами 90, 60 и 30 градусов!
Точный угол 90 градусов с помощью рулетки
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов – длинна сторон не ограничена. Основной инструмент для измерений – рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:
Стороны a и b – катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c – гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием “египетский треугольник”. Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 – ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 – все сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого – проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены – это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 – это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 – 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали – проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Извлечение квадратного корня никогда меня не привлекало – простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. – диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике – это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем – в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе “египетского треугольника”. Однако это только в теории линии просто чертятся на бумаге, “ловить” же все выбранные размеры растянутыми шнурами или линиями на полу – задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!


Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами – дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера – непрофессионально.
Как с помощью «жёлтого» угольника быстро размечать любые углы
На днях, знакомый профессиональный плотник показал мастерское применение угольника в качестве транспортира. Теперь я знаю, что обычным угольником можно построить не только углы 45° и 90°, а даже 10°, 20°, 30°, 40°, 50°, 60°, 70° и 80°.
Признаюсь, что перед написанием статьи я кучу времени уделил поиску этой темы в интернете — такого способа никто не предлагает, так что, эта статья является первоисточником.
Называется метод: «Правило одиннадцати».
Почему именно «одиннадцати»? В построении любого из углов, нам всегда требуется в первую очередь отложить 11 сантиметров. По данной технологии, угол будет строиться по прямоугольному треугольнику, а точнее — по двум его катетам, один из которых равен 11 см.
Самым первым делом, с помощью угольника — проводим перпендикуляр, удаленный от края заготовки на 11 см. На фото — перпендикуляр выделен красным цветом:
Теперь мы имеем отмеченный отрезок в 11 см. и перпендикуляр. Если любую точку этого перпендикуляра соединить с углом заготовки, то мы получим прямоугольный треугольник. А дальше, немного теории :-)))
Из школьного курса геометрии мы знаем, что именно отношение двух катетов прямоугольного треугольника и определяет тригонометрические функции угла (тангенса и котангенса)
Построение 20° и 70°
Смотрите! Откладывая 11 см. по горизонтали и 4 см. по вертикали мы получаем острый угол в 20°:
На фото, на построенном перпендикуляре отмечаю 4 см. и соединяю концы отрезков:
[spoiler title=”источники:”]
http://yserogo.ru/remont/pryamoi-ugol.html
[/spoiler]
Измерение углов без транспортира является одним из фундаментальных аспектов геометрии. Синус, косинус и тангенс – это три понятия, которые позволят вам рассчитать угол, основанный исключительно на длине двух сторон прямоугольного треугольника. Вы можете сформировать прямоугольный треугольник под любым углом с помощью линейки и карандаша. Запоминание термина «сох-ка-тоа» поможет вам вспомнить, как правильно соотносятся функции синуса, косинуса и тангенса.
1. Изучите угол
Определите, с каким углом вы имеете дело. Если два отрезка линии широко открыты, образуя угол, больший, чем прямой угол, образованный перпендикулярными отрезками линии, то у вас тупой угол. Если они образуют узкое отверстие, то это острый угол. Если линии идеально перпендикулярны друг другу, то это прямой угол, который составляет 90 градусов.
2. Нарисуй крест
Переместите перпендикулярный крест поперек бумаги. Расположите точку пересечения креста ниже и слева от точки пересечения между двумя отрезками линии и вытяните каждый отрезок, чтобы пересечь обе оси пересечения, если это необходимо.
3. Осмотрите склоны
Определите уклоны двух линий, измерив подъем сегмента линии или его вертикальный аспект и разделив его на пробег или горизонтальный аспект. Возьмите 2 точки в каждой линии, измерьте разницу между их вертикальными компонентами и разделите ее на разницу в горизонтальной компоненте Это отношение – наклон линии.
4. Рассчитайте угол
Подставьте наклоны в уравнение tan (phi) = (m2 – m1) / (1 + (m2) (m1)), где m1 и m2 – наклоны линий соответственно.
Найдите арктан этого уравнения, чтобы получить угол между двумя линиями. В своем научном калькуляторе нажмите кнопку tan ^ -1 и введите значение (м2 – м1) / (1 + (м2) (м1)). Например, пара линий с наклоном 3 и 1/4 приведет к углу tan ^ -1 ((3-1 / 4) / (1+ (3) (1/4)) = tan ^ – 1 (2, 75 / 1, 75) = загар ^ -1 (1, 5714) = 57, 5 градуса.