Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов

Серединный перпендикуляр к отрезку
Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .

Докажем, что отрезок AE длиннее отрезка EB . Действительно,


Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,


Полученное противоречие и завершает доказательство теоремы 2
Окружность, описанная около треугольника
Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .

Свойства описанной около треугольника окружности. Теорема синусов
Для любого треугольника справедливы равенства (теорема синусов):
 ,
,
где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.
Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.
Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
| Фигура | Рисунок | Свойство |
| Серединные перпендикуляры к сторонам треугольника |
 |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство |
| Окружность, описанная около треугольника |  |
Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности |  |
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности |  |
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |  |
|
| Площадь треугольника |  |
|
| Радиус описанной окружности |  |
| Серединные перпендикуляры к сторонам треугольника |
 |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
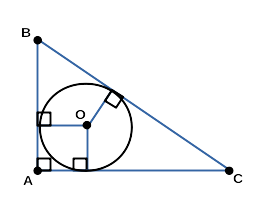
Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.
Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):
 ,
,
где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.
Площадь треугольника

Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.
Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
Доказательства теорем о свойствах описанной около треугольника окружности
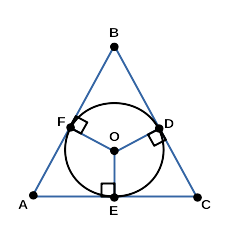
Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).

Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.
Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

 .
.
Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
Формула (1) доказана.
Из формулы (1) для вписанного треугольника ABC получаем (рис.7):
Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.

Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.
Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.
Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
— радиус окружности, вписанной в треугольник.
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника, — радиус описанной окружности.
Для любого треугольника верна теорема синусов:

Ты нашел то, что искал? Поделись с друзьями!
. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .
В ответ запишем .
. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,
Получаем, что . Угол — тупой. Значит, он равен .
. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
Теорема синусов

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, синусы переносим в знаменатели:
bc sinα = ca sinβ
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° – α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° – α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° – α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° – 60°) = sin60° = 3/√2;
- sin150° = sin(180° – 30°) = sin30° = 1/2;
- sin135° = sin(180° – 45°) = sin45° = 2/√2.
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° – α)
Так как sin(180° – α) = sinα, то sinγ = sin(180° – α) = sinα
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
-
Согласно теореме о сумме углов треугольника:
∠B = 180° – 45° – 15° = 120°
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/vpisannyj-i-opisannyj-treugolnik-vpisannaya-i-opisannaya-okruzhnost/
http://skysmart.ru/articles/mathematic/teorema-sinusov
[/spoiler]
Содержание
- Определение
- Формулы
- Радиус вписанной окружности в треугольник
- Радиус описанной окружности около треугольника
- Площадь треугольника
- Периметр треугольника
- Сторона треугольника
- Средняя линия треугольника
- Высота треугольника
- Свойства
- Признаки существования
- Признаки равенства
- Виды
- Термины
Определение
Треугольник, описанный около окружности — это треугольник,
который находится около окружности и соприкасается
с ней всеми тремя сторонами.
На рисунке ниже изображена окружность, вписанная в треугольник;
и треугольник, описанный около окружности.
△ABC — треугольник, описанный около окружности;
A, B, C — вершины треугольника, описанного около окружности;
F, D, E — точки касания треугольника, описанного около окружности;
O — центр окружности, вписанной в треугольник;
OD = OF = OE — радиусы треугольника, описанного около окружности;
AB, BC, CA — касательные;
FA = AE, EC = CD, FB = BD — отрезки касательных;
OF ⟂ AB, OD ⟂ BC, OE ⟂ AC;
Треугольник ABC имеет три точки, где соприкасаются
стороны и сама окружность, эти точки называют точками
касания. У данного треугольника их всего три.
В любой треугольник можно вписать окружность, причем
только одну. Треугольник, в который вписана окружность
называется треугольником описанным около окружности.
Треугольники, описанные около окружности, обладают рядом
рядом отличительных свойств, характерных признаков, уникальными
терминами, а также формулам, по которым можно найти разные величины.
Формулы радиуса вписанной окружности, радиуса описанной окружности,
диаметра, средней линии, периметра, площади стороны позволяют выразить
одни величины через другие, рассчитать длину величины, узнать во сколько
раз одна величина отличается от другой, какая прослеживается взаимосвязь.
Длина любой величины произвольного
треугольника может измеряется в мм, см, м, км.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности треугольника, описанного около окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
[ r = frac{S}{(a+b+c)/2} ]
- Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
[ r = frac{S}{frac{1}{2}P} ]
- Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
[ r = sqrt{frac{(p-a)(p-b)(p-c)}{p}} ]
Радиус описанной окружности около треугольника
R — радиус описанной окружности треугольника, описанного около окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
[ R = frac{AC}{2 sin angle B} ]
- Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
[ R = frac{abc}{4S} ]
- Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:[ R = frac{abc}{4sqrt{p(p-a)(p-b)(p-c)}} ]
Площадь треугольника
S — площадь треугольника, описанного около окружности.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:[ S = pr ]
- Площадь треугольника вписанного в окружность,
если известен полупериметр:[ S = sqrt{p(p-a)(p-b)(p-c)} ]
- Площадь треугольника вписанного в окружность,
если известен высота и основание:[ S = frac{1}2 ah ]
- Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:[ S = frac{a^2}{2cdot (sin(α)⋅sin(β)) : sin(180 — (α + β))} ]
- Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:[ S = frac{1}{2}ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника, описанного около окружности.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
[ P = a + b + c ]
- Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
[ P = frac{2S}{r} ]
- Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:[ P = sqrt{ b2 + с2 — 2 * b * с * cosα} + (b + с) ]
Сторона треугольника
a — сторона треугольника, описанного около окружности.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:[ a = sqrt{b^2+c^2 -2bc cdot cos alpha} ]
- Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
[ a = frac{b · sin alpha }{sin β} ]
Средняя линия треугольника
l — средняя линия треугольника, описанного около окружности.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
[ l = frac{AB}{2} ]
- Средняя линия треугольника вписанного в окружность,
если известны две стороны, ни одна из них не является
основанием, и косинус угла между ними:
[ l = frac{sqrt{b^2+c^2-2bc cdot cos alpha}}{2} ]
Высота треугольника
h — высота треугольника, описанного около окружности.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:[ h = frac{2S}{a} ]
- Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:[ h = b cdot sin alpha ]
- Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:[ h = frac{bc}{2R} ]
Свойства
Свойства треугольника, описанного около окружности,
а также окружности, вписанной в треугольник, медиан,
высот, биссектрис, радиусов-перпендикуляров.
Свойство 1. Окружность, можно вписать
в любой треугольник, только один раз.
Свойство 2. Центр окружности, вписанной в треугольник —
точка пересечения биссектрис, центр окружности.
Свойство 3. Центр окружности, описанной около треугольника —
точка пересечения серединных перпендикуляров.
Свойство 4. Центры вписанной и описанной окружностей
равностороннего треугольника, описанного около
окружности совпадают, имеют одну общую точку.
Свойство 5. Отрезок, проведенный из центра треугольника,
описанного около окружности, к любой из сторон,
является радиусом.
Свойство 6. У любого треугольника центр
вписанной окружности находится только внутри.
Свойство 7. Окружность находящаяся внутри
треугольника, описанного около окружности,
касается всех его сторон.
Свойство 8. Вписанная окружность и треугольник,
описанный около окружности, имеют три общие точки,
которые лежат на трех сторонах треугольника.
Свойство 9. Формула радиуса вписанной окружности
у треугольника, описанного около окружности, и четырехугольника,
у которого суммы противоположных равны, совпадает.
Свойство 10. Радиус описанной около треугольника окружности,
можно выразить и рассчитать через Теорему Синусов.
Свойство 11. У треугольника, описанного около
окружности, радиус вписанной окружности, можно
рассчитать через площадь и полупериметр.
Свойство 12. Радиус в точку касания есть перпендикуляр.
Свойство 13. Окружность, вписанная в треугольник, разделяет
стороны треугольника на 3 пары равных отрезков.
Свойство 14. Стороны треугольника, описанного около
окружности, можно также называть касательными.
Свойство 15. Отрезки, которые проведены из центра вписанной
окружности, к точкам касания, перпендикулярны сторонам.
Свойство 16. Сумма углов треугольника, описанного
около окружности, равна 180 градусам.
Свойство 17. Центр вписанной окружности
равноудален от всех сторон треугольника.
Свойство 18. Центр вписанной в треугольник окружности в научных
кругах называется замечательной точкой треугольника, либо инцентром.
Свойство 19. Правильный треугольник, описанный около
окружности, имеет точки касания с окружность, в серединах сторон.
Свойство 20. Равнобедренный, прямоугольный, равносторонний
треугольники, описанные около окружности, в точке пересечения
биссектрис и центре окружности, имеют одну общую точку.
Признаки существования
Признак 1. Центр вписанной окружности —
это точка пересечения биссектрис.
Признак 2. На сторонах треугольника лежат
три точки касания вписанной окружности.
Признак 3. Вписанная окружность делит смежные
стороны треугольника на равные отрезки касательных.
Признак 4. У вписанной окружности три радиуса в точку касания быть перпендикулярами.
Исходя из вышеперечисленных признаков, исходных
данных, внешнего вида, можно определить является ли
треугольник описанным около окружности или же нет.
Признаки равенства
Признак 1. По двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника, описанного
около окружности, равны двум сторонам и углу между ними другого
треугольника, описанного около окружности, то такие треугольники равны.
Признак 2. По стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника, описанного
около окружности, равны стороне и двум прилежащим к ней углам другого
треугольника, описанного около окружности, то такие треугольники равны.
Признак 3. По трем сторонам.
Если три стороны одного треугольника, описанного
около окружности, равны трем сторонам другого
треугольника, описанного около окружности.
Виды
Как мы знаем, любой треугольник может быть описан около
окружности, исходя из этого можно сказать, что около
окружности, могут быть описаны следующие виды треугольников:
- Разносторонний треугольник
- Равносторонний / правильный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равнобедренный прямоугольный треугольник
- Прямоугольный треугольник, описанный около окружности
Характерные признаки: один из углов прямой,
длину сторон можно найти через Теорему
Пифагора, сумма острых углов 90 градусов.
Основные формулы:
[ r = frac{a+b-c}{2} ]
[ S = pr ]
[ BC^2 = BA^2 + AC^2 ]
- Равнобедренный треугольник, описанный около окружности
Характерные признаки: два угла равны,
две стороны равны, третий угол можно
найти зная два других.
Основные формулы:
[ S = frac{b}{4} cdot sqrt{4a^2-b^2} ]
[ P = 2a + b ]
[ h = frac{2S}{b} ]
- Равносторонний треугольник, описанный около треугольника
Основные формулы:
[ S = frac{a^2sqrt{3}}{4} ]
[ r = frac{a}{2 sqrt 3} ]
[ R = 2r ]
Термины
Точка касания — это точка, где соприкасается вписанная
окружность с треугольником; это общая точка, для окружности
и треугольника, которая лежит на любой из сторон треугольника.
Инцентр — это точка, где пересекаются три биссектрисы
треугольника; это центр вписанной окружности в треугольник;
это одна из замечательных точек в геометрии.
Касательная — это сторона треугольника, которая имеет с
вписанной окружностью одну общую точку — точку касания.
Ортоцентр — точка, где пересекаются высоты треугольника.
Ось симметрии — это прямая, которая делит
треугольник на равные половины.
Замечательная точка — это точка пересечения медиан,
высот, биссектрис, серединных перпендикуляров.
Отрезок касательной — это отрезок, который берет начало
у одной из вершин треугольника, и имеет конец в точке касания.
Здравствуйте, уважаемые читатели. Продолжаем разбор заданий с окружностью. В этой статье рассмотрим третью тему.
1. Центральные и вписанные углы.
2.Касательная, хорда, секущая.
3.Вписанная и описанная окружность (треугольник)
Окружность называется вписанной в треугольник, если она касается всех его сторон. Радиус вписанной окружности обозначается маленькой буквой r
При решении задач, будем вспоминать необходимую теорию непосредственно в решении.
Задача №1
Площадь треугольника, в который вписана окружность, равна произведению полупериметра треугольника на радиус окружности.
Полупериметр – это периметр треугольника, деленный пополам.
В некоторых задачах, даны лишние данные. В этой задаче лишним является длина стороны, которая равна 18. Полупериметр равен 48:2=24, радиус равен 3. Подставим все в формулу, получим:
Задача №2
Решим задачу двумя способами:
Способ №1
Для решения этой задачи, воспользуемся формулой площади треугольника через радиус вписанной окружности
В этой формуле нам известен радиус. Нужно найти полупериметр. Поскольку треугольник равносторонний, то пусть стороны треугольника равны а
Подставим все в нашу формулу:
С другой стороны, площадь треугольника равна половина произведения высоты на сторону, к которой проведена эта высота
Не важно по какой формуле вычислять площадь треугольника, она будет одинаковой, поэтому приравняем эти формулы и найдем высоту треугольника:
Способ №2
Формулу радиуса окружности, вписанной в равносторонний или правильный треугольник, вы можете взять в справочных материалах, которые выдаются на экзамене, и по этой формуле вычислить сторону равностороннего треугольника:
Так как треугольник по условию задачи равносторонний, то высота является медианой.
Поскольку треугольник ВНС – прямоугольный, то ВН найдем по теореме Пифагора.
Задание №3
Окружность называется описанной около треугольника, если все вершины треугольника лежат на окружности. Радиус описанной окружности обозначается большой буквой R
Найдем сторону равностороннего треугольника, через формулу радиуса описанной около равностороннего треугольника окружности. Возьмем эту формулу из справочного материала, выдаваемый на экзамене:
Так как треугольник, вписанный в окружность, равносторонний, то высота треугольника является и медианой. Значит АН=НС
По теореме Пифагора найдем высоту треугольника:
Высоту равностороннего треугольника, можно найти и по формуле:
Но этой формулы в справочнике на экзамене нет, поэтому теорема Пифагора – универсальный способ.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
![]()
Вписанный угол, теория задачи. Друзья! В этой статье речь пойдёт о заданиях, для решения которых необходимо знать свойства вписанного угла. Это целая группа задач, они включены в ЕГЭ. Большинство из них решаются очень просто, в одно действие.
Есть задачи посложнее, но и они большой трудности для вас не представят, необходимо знать свойства вписанного угла. Постепенно мы разберём все прототипы задач, приглашаю вас на блог!
Теперь необходимая теория. Вспомним, что такое центральный и вписанный угол, хорда, дуга, на которые опираются эти углы:
Центральным углом в окружности называется плоский угол с вершиной в ее центре.
Часть окружности, расположенная внутри плоского угла, называется дугой окружности.
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Угол, называется вписанным в окружность, если вершина угла лежит на окружности, а стороны угла пересекают эту окружность.

Отрезок соединяющий две точки окружности называется хордой. Самая большая хорда проходит через центр окружности и называется диаметр.

Для решения задач на вписанные в окружность углы, вам необходимо знать следующие свойства:
1. Вписанный угол равен половине центрального, опирающегося на ту же дугу.


2. Все вписанные углы, опирающиеся на одну и ту же дугу, равны.

3. Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны.

4. Любая пара углов, опирающихся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°.

Следствие: противолежащие углы четырёхугольника вписанного в окружность в сумме составляют 180 градусов.
5. Все вписанные углы, опирающиеся на диаметр, прямые.

Вообще, это свойство является следствием из свойства (1), это его частный случай. Посмотрите – центральный угол равен 180 градусам (и этот развёрнутый угол есть не что иное, как диаметр), значит по первому свойству вписанный угол С равен его половине, то есть 90 градусам.
Знание данного свойства помогает в решении многих задач и часто позволяет избежать лишних расчётов. Хорошо усвоив его — вы более половины задач такого типа сможете решать устно. Два следствие, которые можно сделать:
Следствие 1: если в окружность вписан треугольник и одна его сторона совпадает с диаметром этой окружности, то треугольник является прямоугольным (вершина прямого угла лежит на окружности).
Следствие 2: центр описанной около прямоугольного треугольника окружности совпадает с серединой его гипотенузы.
Многие прототипы стереометрических задач также решаются благодаря использованию этого свойства и данных следствий. Запомните сам факт: если диаметр окружности является стороной вписанного треугольника, то этот треугольник прямоугольный (угол лежащий против диаметра равен 90 градусов). Все остальные выводы и следствия вы сможете сделать сами, учить их не надо.
Как правило, половина задач на вписанный угол даётся с эскизом, но без обозначений. Для понимания процесса рассуждения при решении задач (ниже в статье) введены обозначения вершин (углов). На ЕГЭ вы можете этого не делать. Рассмотрим задачи:

Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Построим центральный угол для заданного вписанного угла, обозначим вершины:

По свойству вписанного в окружность угла:
![]()
Угол АОВ равен 600, так как треугольник АОВ равносторонний, а в равностороннем треугольнике все углы равны по 600. Стороны треугольника равны, так как в условии сказано, что хорда равна радиусу.
Таким образом, вписанный угол АСВ равен 300.
Ответ: 30

Найдите хорду, на которую опирается угол 300, вписанный в окружность радиуса 3.

Это по сути обратная задача (предыдущей). Построим центральный угол.

Он в два раза больше вписанного, то есть угол АОВ равен 600. От сюда можно сделать вывод, что треугольник АОВ равносторонний. Таким образом, хорда равна радиусу, то есть трём.
Ответ: 3

Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную корню из двух. Ответ дайте в градусах.

Построим центральный угол:

Зная радиус и хорду мы можем найти центральный угол АСВ. Это можно сделать по теореме косинусов. Зная центральный угол мы без труда найдём вписанный угол АСВ.
Теорема косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.

Следовательно, второй центральный угол равен 3600 – 900 = 2700.
Угол АСВ по свойству вписанного угла равен его половине, то есть 135 градусам.
Ответ: 135

Найдите хорду, на которую опирается угол 120 градусов, вписанный в окружность радиуса корень из трёх.

Соединим точки А и В с центром окружности. Обозначим её как О:

Нам известен радиус и вписанный угол АСВ. Мы можем найти центральный угол АОВ (больший 180 градусов), затем найти угол АОВ в треугольнике АОВ. А далее по теореме косинусов вычислить АВ.
По свойству вписанного угла центральный угол АОВ (который больше 180 градусов) будет равен вдвое больше вписанного, то есть 240 градусам. Значит, угол АОВ в треугольнике АОВ равен 3600 – 2400 = 1200.
По теореме косинусов:

Ответ:3

Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности. Ответ дайте в градусах.

По свойству вписанного угла он вдвое меньше центрального угла, опирающегося на ту же дугу, в данном случае речь идёт о дуге АВ.
Сказано, дуга АВ составляет 20 процентов от окружности. Это означает, что центральный угол АОВ составляет так же 20 процентов от 3600. *Окружность это угол в 360 градусов. Значит,

Таким образом, вписанный угол АСВ равен 36 градусам.
Ответ: 36

Дуга окружности AC, не содержащая точки B, составляет 200 градусов. А дуга окружности BC, не содержащая точки A, составляет 80 градусов. Найдите вписанный угол ACB. Ответ дайте в градусах.

Обозначим для наглядности дуги, угловые меры которых даны. Дуга соответствующая 200 градусам – синий цвет, дуга соответствующая 80 градусам – красный цвет, оставшаяся часть окружности – жёлтый цвет.

Таким образом, градусная мера дуги АВ (жёлтый цвет), а значит и центральный угол АОВ составляет: 3600 – 2000 – 800 = 800.
Вписанный угол АСВ вдвое меньше центрального угла АОВ,то есть равен 40 градусам.
Ответ: 40
![]()
Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.
Посмотреть решение
Найдите хорду, на которую опирается угол 900, вписанный в окружность радиуса 1.
Посмотреть решение
Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Посмотреть решение
Радиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную корню из двух. Ответ дайте в градусах.

Посмотреть решение
Центральный угол на 360 больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.

Посмотреть решение
Найдите вписанный угол, опирающийся на дугу АВ, которая составляет 0,2 окружности. Ответ дайте в градусах.

Посмотреть решение
Хорда делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

Посмотреть решение
Точки А, В, С, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1:3:5. Найдите больший угол треугольника АВС. Ответ дайте в градусах.

Посмотреть решение
На что обратить внимание при решении подобных задач?
Необходимо знать свойство вписанного угла; понимать, когда и как необходимо использовать теорему косинусов, подробнее о ней посмотрите здесь.
На этом всё! Успехов Вам!
С уважением, Александр Крутицких
Учительница математики в школе в третьем классе:
— Дети, а скажите мне, сколько будет 6*6?
Дети дружно хором отвечают:
— Семьдесят шесть!
— Ну, что вы, такое говорите детки! Шесть на шесть будет тридцать шесть… ну может быть еще 37, 38, 39… ну максимум 40… но никак не семьдесят шесть!
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Окружность, описанная около треугольника
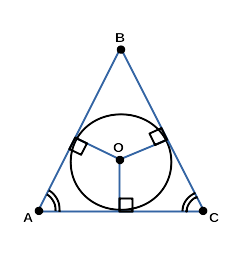
Окружность называют описанной около треугольника, если все вершины треугольника расположены на окружности.
Её центр равноудалён от всех вершин, то есть должен находиться в точке пересечения серединных перпендикуляров к сторонам треугольника.
Следовательно, около любого треугольника можно описать окружность, так как серединные перпендикуляры к сторонам пересекаются в одной точке.

Для остроугольного треугольника центр окружности находится в треугольнике.
Другая ситуация с прямоугольным и тупоугольным треугольниками.


Окружность, вписанная в треугольник
Окружность называют вписанной в треугольник, если все стороны треугольника касаются окружности.
Её центр равноудалён от всех сторон, то есть должен находиться в точке пересечения биссектрис треугольника.
Следовательно, в любой треугольник можно вписать окружность, так как биссектрисы треугольника пересекаются в одной точке.

Так как биссектрисы углов треугольника всегда пересекаются внутри треугольника, то для всех треугольников центр вписанной окружности находится в треугольниках.
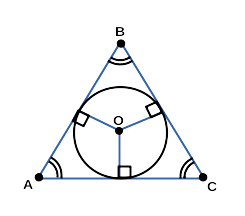
Равносторонний треугольник
Обрати внимание!
У равностороннего треугольника совпадают биссектрисы, медианы и высоты, то есть, эти отрезки являются также серединными перпендикулярами. Это значит, что центры описанной и вписанной окружности совпадают.
Радиус описанной окружности
Радиус вписанной окружности
, где (h) — высота треугольника.
Если дана сторона треугольника (a), то
h=a32
.
Поэтому
r=a36
.
Прямоугольный треугольник
Радиус описанной окружности
, где (c) — гипотенуза.
Радиус вписанной окружности
, где (p) — полупериметр.
Произвольный треугольник
Радиус описанной окружности
, где
α
— угол, противолежащий стороне (a);
.
Радиус вписанной окружности
, где (p) — полупериметр.
