«Треугольник, вписанный в квадрат с их одной общей вершиной, угол при которой равен 45°» — данная конструкция обязательно должна разбираться при подготовке к профильному ОГЭ или ЕГЭ.
В этой конструкции так много любопытных и потрясающих фактов, что считаю знакомство с «треугольником в квадрате» непременным шагом при совершенствовании своих навыков в планиметрии.
Задача 24 ОГЭ (услож. 262 вар. Ларина)
На сторонах BC и CD квадрата ABCD взяты точки E и F, причём ∠EAF = 45°. Отрезки AE и AF пересекают диагональ BD в точках P и Q. Докажите, что площадь △AEF в два раза большие площади △APQ.
https://alexlarin.net/gia/trvar262_1_oge.html
Указания к решению (дополнено 16.11.2020)
См. ранее опубликованные статьи статьи:
1. Удивительный треугольник в квадрате
2. Удивительный треугольник в квадрате
Поворот квадрата

Firstly We can write
(1) Oklid relation from $triangle CNB$
$h^2=m(k+x)$
(2) Pisagor relation from $triangle DPN$
$a^2=(x+k)^2+(x+k+m-h)^2$
(3) Pisagor relation from $triangle FRN$
$b^2=h^2+k^2$
(4) Pisagor relation from $triangle DCF$
$c^2=x^2+(x+k+m)^2$
if DNF triange is a right triangle,It must satisfy $a^2+b^2=c^2$.
$(x+k)^2+(x+k+m-h)^2+h^2+k^2=x^2+(x+k+m)^2$
$(x+k)^2+(x+k+m)^2-2h(x+k+m)+h^2+h^2+k^2=x^2+(x+k+m)^2$
$(x+k)^2-2h(x+k+m)+2h^2+k^2=x^2$
$xk+k^2-h(x+k+m)+h^2=0$
$xk+k^2-h(x+k+m)+m(k+x)=0$
$-h(x+k+m)+(k+m)(k+x)=0$
$frac{x+k}{x+k+m}=frac{h}{k+m}$
This result is equal to the rates of thales formula for similar triangles $triangle CRN sim triangle CBE$
Thus $a^2+b^2=c^2$ is correct for $triangle DNF$ .
Проверьте свою логику с этой интересной геометрической задачей: Найдите длину стороны квадрата
Тесты
Вам предлагается решить логическую задачу, используя приёмы элементарной геометрии, и, возможно, некоторые алгебраические трюки.
Задача на логику
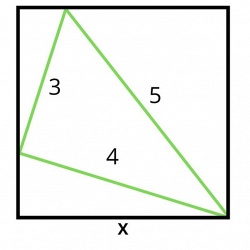
Внутри квадрата вписан треугольник со сторонами 3, 4 и 5.
Найдите длину стороны этого квадрата (Х).
Одно из решений данной задачи появиться чуть позже.
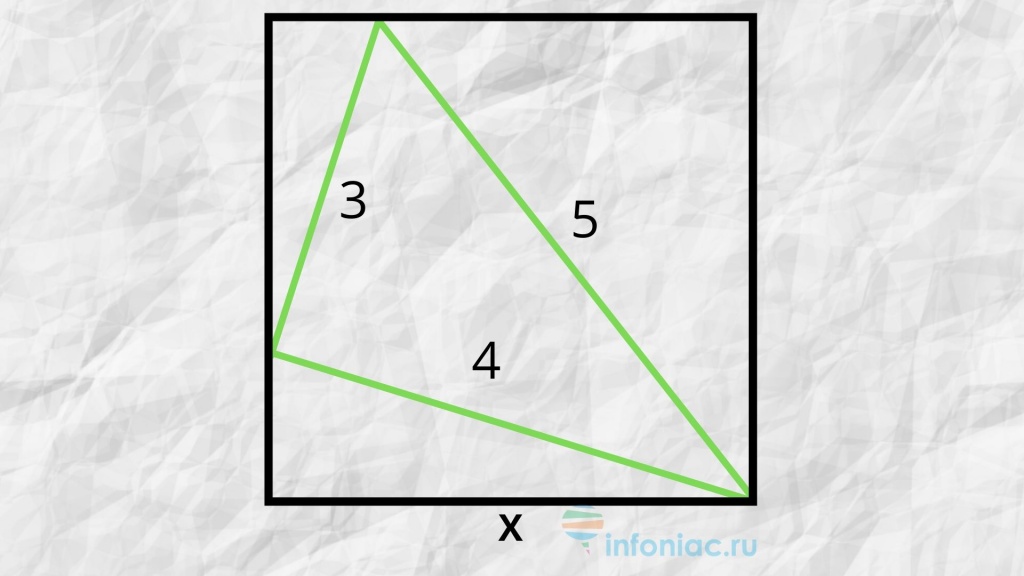
Решили? Делитесь своим решением и ответом в комментариях.
Заметьте, что треугольник имеет стороны 3, 4 и 5, а это значит, что перед вами египетский треугольник. Особенность такого треугольника в том, что все три стороны его целочисленны, то есть длины всех его сторон выражаются целыми числами. Согласно теореме, обратной теореме Пифагора, такой треугольник прямоуголен. Угол между сторонами 3 и 4 равен 90 градусов.
Теперь давайте обратим внимание на другие два треугольника. Они подобны, но это нужно доказать. Это можно сделать доказав, что у них все три угла одинаковые.
Один угол имеет «а» градусов, значит другой угол будет равен 90-а градусов.



Теперь давайте посчитаем угол в другом треугольнике. Отметим, что этот угол имеет «b» градусов. d = 180 — 90 — (90-а) => b = а. А раз и в одном, и в другом треугольники два угла равны, то и оставшиеся также равны
Как это нам поможет?
Давайте сначала обозначим один катет вот этого треугольника «y», а другой катет «x«.
Так как один их катетов равен стороне квадрата, вот это расстояние будет равно x-y.
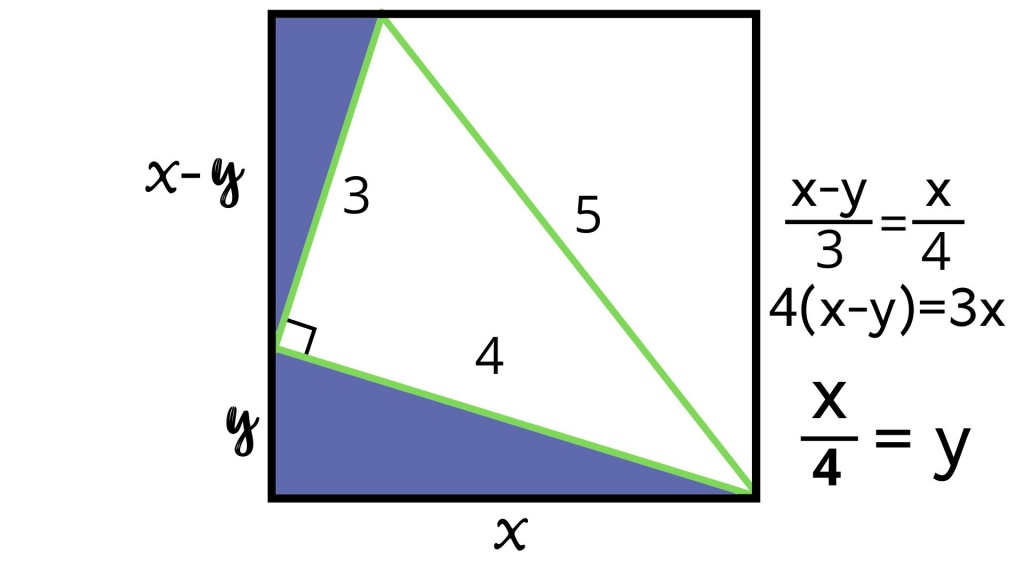
Теперь используем тот факт, что эти треугольники подобны. Соотношение длинного катета и гипотенузы у них равны. То есть (x-y)/3 = x/4. Узнаем, чему равен y (используем метод перекрестного умножения): 4(x-y)=3x => y=x/4.
Заменим это значение в этом треугольнике.
Мы в соцсетях






Теперь мы можем узнать, чему равен x, так как у нас прямоугольный треугольник. По теореме Пифагора получаем: x 2 +(x/4) 2 =16, то есть 17/16x 2 =16 и для x>0 мы имеем x=16/√17 и это наш ответ.
Сколько углов у треугольника
Сколько углов у треугольника? Ответ на этот вопрос заложен в самом названии фигуры.
Тре угольник — фигура, имеющая три угла. У треугольника любого вида есть ровно три угла.
 Например, углы треугольника ABC —
Например, углы треугольника ABC —
угол A, угол B и угол C.
Для обозначения угла используют специальный знак: ∠.
Запись ∠A читают как «угол A».
Угол можно назвать также тремя буквами.
При этом название вершины угла обязательно должно стоять посередине:
Сколько тупых углов у треугольника?
В треугольнике может быть только один тупой или один прямой угол.
 Например, в тупоугольном треугольнике MNP
Например, в тупоугольном треугольнике MNP
один тупой угол — угол M
и два острых — угол N и угол P.
Сколько прямых углов у треугольника?
 В прямоугольном треугольнике KFT
В прямоугольном треугольнике KFT
Треугольник вписанный в окружность

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — не диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.

Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Площадь треугольника
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
[ S = fracab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Сторона треугольника
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Высота треугольника
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
[ h = b cdot sin alpha ]
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Нужно найти углы вписанных в квадрат треугольников.
Ms. Outsider
Знаток
(498),
на голосовании
6 лет назад
ABCD — квадрат. ∆OBC — равносторонний.
1) Чему равен угол BAO?
2) ~ AOD?
Дополнен 7 лет назад
Прошу писать не только готовый ответ, но и само решение. Прошу.
Голосование за лучший ответ
esmeralda
Искусственный Интеллект
(293042)
7 лет назад
угол ВАО=75 град
АОД=150 град
Ms. OutsiderЗнаток (498)
7 лет назад
Можно решение, пожалуйста?
esmeralda
Искусственный Интеллект
(293042)
ВОС равносторонний треуг., значит все углы = 60 град.
угол В=90, тогда угол АВО=90-60=30 град. ,АВ=ВО по условию, тогда треуг. ВОА – равнобедренный и углы у основания =(180-30) :2=75 град
если угол ВАО =75 град, то угол ОАД=90-75=15
треуг. ОАД – равнобедренный, углы при основании равны, тогда угол АОД=180-15-15=150 град
Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.
- Угол треугольника через три стороны
- Угол прямоугольного треугольника через две стороны
- Угол треугольника через высоту и катет
- Угол при основании равнобедренного треугольника через
биссектрису и боковую сторону - Угол при основании равнобедренного треугольника через
биссектрису и основание - Угол между боковыми сторонами равнобедренного треугольника
через биссектрису и боковую сторону - Острый угол прямоугольного треугольника через катет и
площадь - Острый угол между боковыми сторонами равнобедренного
треугольника через площадь и боковую сторону
Угол треугольника через три стороны
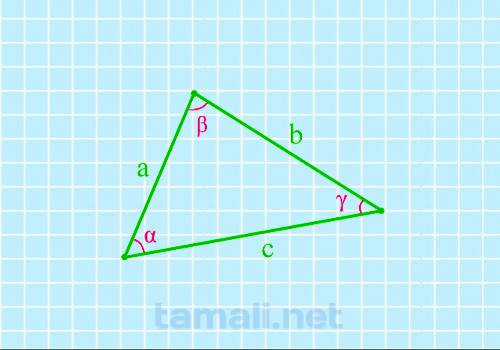
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить
cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb
где a, b, c — стороны треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.
Угол прямоугольного треугольника через две стороны
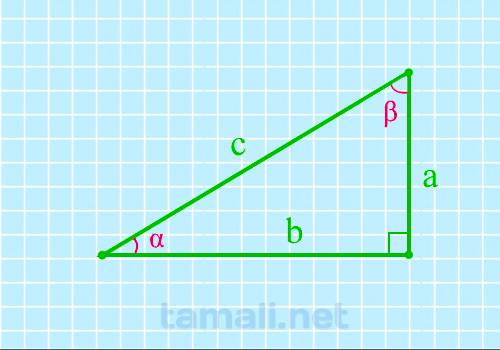
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.
sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a
где a, b — катеты, c — гипотенуза.
Цифр после запятой:
Результат в:
Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.
Острый угол прямоугольного треугольника через катет и площадь
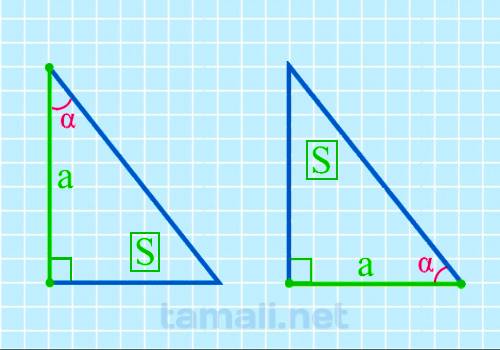
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:
tg(α) = a² / 2S
где a — катет, S — площадь прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.
Угол треугольника через высоту и катет
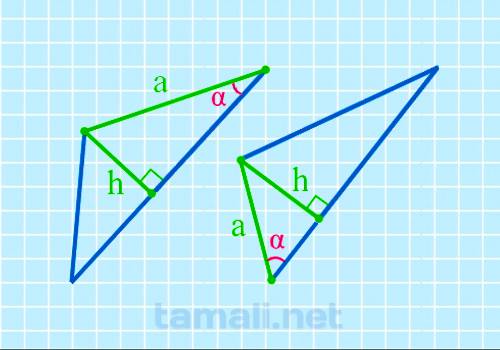
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.
sin α = h / a
где h — высота, a — катет.
Цифр после запятой:
Результат в:
Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°
Угол при основании равнобедренного треугольника через биссектрису и основание
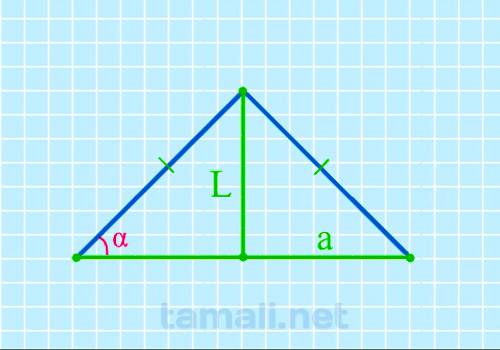
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:
tg α = L / (a/2)
где L — биссектриса, a — основание.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º
Угол при основании равнобедренного треугольника через биссектрису и боковую сторону
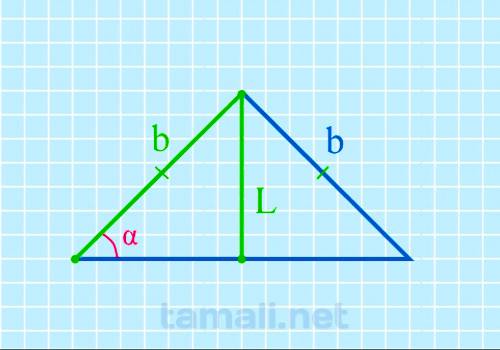
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:
sin α = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.
Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону
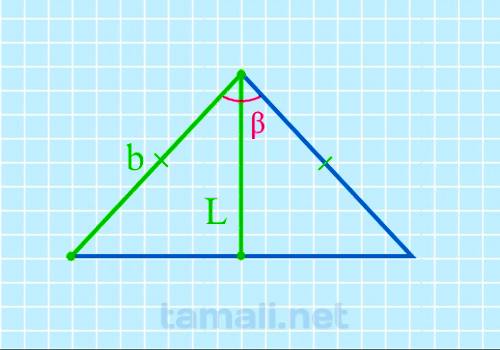
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).
2cos(β) = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º
Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону
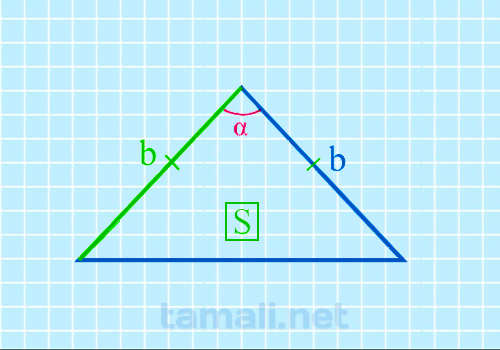
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:
sin(α) = 2S / b²
где b — боковая сторона равнобедренного треугольника, S — площадь.
Цифр после
запятой:
Результат в:
Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º
Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.
Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.
