Как найти угол треугольника зная его координаты

Как найти угол треугольника зная его координаты

eigenbasis

Гуру

(3250)


1 год назад

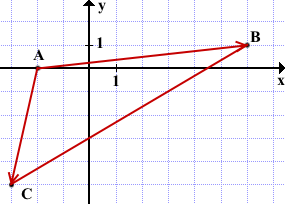
1. находим вектора, образующие угол (BA и BC):
BA = A – B = (-1, 1)
BC = C – B = (-1, -1)

2. находим скалярное произведение этих векторов
⟨BA, BC⟩ = (-1)*(-1) + 1*(-1) = 0

3. находим длины этих векторов (конкретно здесь уже ясно, что угол 90 градусов, но для других координат точек этот шаг надо было бы сделать)
|BA| = √((-1)² + (1)²) = √2
|BC| = √((-1)² + (-1)²) = √2

4. косинус угла между векторами равен их скалярному произведению, делённому на произведение длин этих векторов, то есть
cos(ABC) = ⟨BA, BC⟩ / (|BA| * |BC|) = 0 / 2 = 0
Поэтому угол ABC = 90 градусов

Альтернативный способ (если вы знаете, что такое определитель матрицы 2х2).

1. опять находим координаты образующих векторов
BA = (-1, 1) и BC = (-1, -1)

2. составляем из них матрицу и находим её определитель
| -1 -1 |
| 1 -1 | = (-1)*(-1) – (-1)*1 = 2
из геометрического смысла определителя он равен удвоенной площади треугольника, то есть 2*S(ABC) = 2

3. делим определитель на произведение длин векторов и из формулы площади треугольника через синус получаем синус нашего угла
sin(ABC) = 2 / (√2 * √2) = 2 / 2 = 1
отсюда аналогично заключаем, что угол 90 градусов

eigenbasisГуру (3250)

1 год назад

Из ответа ниже правда стоило бы считать не определитель, а его модуль (ориентация площади нам правда здесь не очень инетесна)

Тадасана

Просветленный

(32144)


1 год назад

Применяем оба способа 1 и 2
Площадь параллелограмма-то ориентированная, это ж симплектическое скалярное пргизведение, согласованное с евклидовым скалярыным произведением в E2, оно называется псевдокакое-то.
Зная синус и косинус угла, найдем и угол с т. до 2пи, если считать, что он гткладывается против часовй

Источник

Как найти угол треугольника по его координатам

Если известны координаты всех трех вершин треугольника, можно найти и его углы. Координаты точки в трехмерном пространстве – x,y и z. Однако через три точки, которые являются вершинами треугольника, всегда можно провести плоскость, поэтому в этой задаче удобнее рассматривать только две координаты точек – x и y, считая координату z для всех точек одинаковой.

Как найти угол треугольника по его координатам

Вам понадобится

  • Координаты треугольника

Инструкция

Пусть точка A треугольника ABC имеет координаты x1, y1, точка B этого треугольника – координаты x2, y2, а точка C – координаты x3, y3. Что представляют из себя координаты x и y вершин треугольника. В декартовой системе координат с перпендикулярными друг другу осями X и Y от начала координат можно провести радиус-векторы ко всем трем точкам. Проекции радиус-векторов на координатные оси и будут давать координаты точек.

Пусть тогда r1 – радиус вектор точки A, r2 – радиус-вектор точки B, а r3 – радиус-вектор точки C.
Очевидно, что длина стороны AB будет равна |r1-r2|, длина стороны AC = |r1-r3|, a BC = |r2-r3|.
Следовательно, AB = sqrt(((x1-x2)^2)+((y1-y2)^2)), AC = sqrt(((x1-x3)^2)+((y1-y3)^2)), BC = sqrt(((x2-x3)^2)+((y2-y3)^2)).

Углы треугольника ABC можно найти из теоремы косинусов. Теорему косинусов можно записать в следующем виде: BC^2 = (AB^2)+(AC^2) – 2AB*AC*cos(BAC). Отсюда, cos(BAC) = ((AB^2)+(AC^2)-(BC^2))/2*AB*AC. После подстановки в это выражения координаты, получится: сos(BAC) = (((x1-x2)^2)+((y1-y2)^2)+((x1-x3)^2)+((y1-y3)^2)-((x2-x3)^2)-((y2-y3)^2))/(2*sqrt(((x1-x2)^2)+((y1-y2)^2))*sqrt(((x1-x3)^2)+((y1-y3)^2)))

Источники:

  • как найти координаты третьей вершины
  • Медианы, биссектрисы и высоты треугольника

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Найти угол треугольника зная координаты

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Стороны треугольника заданы уравнениями:

Найти координаты вершин треугольника.

Координаты вершины A найдем, решая систему, составленную из уравнений сторон AB и AC:

Систему двух линейных уравнений с двумя неизвестными решаем способами, известными из элементарной алгебры, и получаем

Вершина A имеет координаты

Координаты вершины B найдем, решая систему из уравнений сторон AB и BC:

получаем .

Координаты вершины C получим, решая систему из уравнений сторон BC и AC:

Вершина C имеет координаты .

[spoiler title=”источники:”]

http://kalk.top/sz/corners-pr-triangle

http://planshet-info.ru/kompjutery/kak-najti-ugol-treugolnika-znaja-koordinaty

[/spoiler]

A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Углы прямоугольного треугольника

Калькулятор расчёта углов прямоугольного треугольника

Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).

Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.

Формула тангенса

  • tg α – тангенс угла α
  • a – противолежащий катет
  • b – прилежащий катет

Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x . Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.

Углы треугольника

Сумма углов треугольника всегда равна 180 градусов:

Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.

Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:

Острый угол — угол, значение которого меньше 90°.

У прямоугольного треугольника один угол прямой, а два других угла – острые.

Как найти угол треугольника зная координаты вершин

Ответ

Проверено экспертом

Длина сторон треугольника

Найдем угол между векторами AB(-3;3) и AC(1;-3)

Найдем угол между векторами BA(3;-3) и BC(4;-6)

Тогда третий угол, если А=153°, В=11°, С=180°-(153°+11°)=16°

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

 A ( ; ), B ( ; ), C ( ; )

Источник

Примеры решений по аналитической геометрии на плоскости

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.

Найти косинусы углов треугольника

Мы уже находили косинусы углов треугольника по его сторонам в произвольном треугольнике и косинус острого угла прямоугольного треугольника.

Рассмотрим, как найти косинусы углов треугольника по его вершинам.

1) Найти косинусы углов треугольника ABC;

2) Определить вид треугольника.

kosinusy-uglov-treugolnika

1) Угол A образован векторами

[overrightarrow {AB} uoverrightarrow {AC} .]

(Чертёж не обязательно делать на координатной плоскости. Достаточно выполнить его схематически, для упрощения понимания, какой угол какими векторами образован).

[cos A = frac{{overrightarrow {AB} cdot overrightarrow {AC} }}{{left| {overrightarrow {AB} } right| cdot left| {overrightarrow {AC} } right|}}.]

[overrightarrow {AB} (x_B - x_A ;y_B - y_A ),]

[overrightarrow {AB} (6 - ( - 2);1 - 0),]

[overrightarrow {AB} (8;1).]

[overrightarrow {AC} (x_C - x_A ;y_C - y_A ),]

[overrightarrow {AC} ( - 3 - ( - 2); - 5 - 0),]

[overrightarrow {AC} ( - 1; - 5).]

[overrightarrow {AB} cdot overrightarrow {AC} = 8 cdot ( - 1) + 1 cdot ( - 5) = - 13.]

Поскольку скалярное произведение меньше нуля, угол, образованный данными векторами, тупой. Значит треугольник ABC — тупоугольный.

[left| {overrightarrow {AB} } right| = sqrt {8^2 + 1^2 } = sqrt {65} ,]

[left| {overrightarrow {AC} } right| = sqrt {( - 1)^2 + ( - 5)^2 } = sqrt {26} .]

[cos A = frac{{ - 13}}{{sqrt {65} cdot sqrt {26} }} = frac{{ - 13}}{{sqrt {5 cdot 13 cdot 2 cdot 13} }} = ]

[= frac{{ - 13}}{{13sqrt {10} }} = - frac{1}{{sqrt {10} }} = - frac{{sqrt {10} }}{{10}}.]

2) Угол B образован векторами

[overrightarrow {BA} uoverrightarrow {BC} .]

[cos B = frac{{overrightarrow {BA} cdot overrightarrow {BC} }}{{left| {overrightarrow {BA} } right| cdot left| {overrightarrow {BC} } right|}}.]

[overrightarrow {BA} uoverrightarrow {AB} ]

— противоположные векторы, то их координаты отличаются только знаками и векторы имеют одинаковую длину:

Как найти косинус внутреннего угла при вершине В?

Вычислим стороны треугольника АВС, используя формулу определения расстояния между точками в прямоугольной декартовой системе координат в пространстве.

Затем, применив теорему косинусов, найдем искомый угол.

Вот таким образом у меня получилось, если не ошибся в арифметике

Найти косинус угла АВС можно по формуле для расчёта угла между двумя векторами.

Зная координаты вершин А(2;-2;-2), В(2;2;-1) и С(3;1;-2), находим вектора АВ = , СВ = . Для этого мы использовали формулу вида:

Источник

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Добавить комментарий