|
Как построить угол 30 градусов с помощью циркуля и линейки ? На мой взгляд самый быстрый способ построить угол 30 градусов с помощью линейки и циркуля состоит в следующем: проводим горизонтальную линию, ставим на нее в произвольной точке циркуль и проводим окружность. В точке, где окружность пересекла линию (например справа) опять ставим циркуль и проводим еще одну такую же окружность. Проводим линию через центр первой окружности и точку пересечения окружностей (красная линия) и проводим линию через точки пересечения окружностей (зеленая линия). Острый угол между красной и зеленой линиями равен 30 градусам. Чтобы построить нужный нам угол, понадобилось всего пять движений. система выбрала этот ответ лучшим Limitless 6 лет назад Построить угол в 30 градусов можно достаточно быстро, используя, согласно условию, циркуль и линейку. Для начала рисуем две перпендикулярные прямые а и b, которые пересекаются в точке А. Отмечаем в любом месте на прямой b точку B. Строим окружность, где В – центр, а 2АВ – радиус. О – точка пересечения построенной окружности с прямой a. Угол ВОА как раз и будет составлять тридцать градусов. Galina7v7 7 лет назад Что угол в 30 градусов , что в 60 градусов строится в прямоугольном треугольнике с углами 30 и 60 градусов. 1) Начинаем с окружности : из т.О проведём окружность произвольного радиуса ОА = ОВ . 2) Далее , пусть из точки А радиусом , равным ОА , сделаем засечку радиусом , равным ОА на окружности , и получим точку О. 3) Соединив точки А , С , В , получим искомый треугольник АВС с углами : < CAB = 60 гр. , < CBA = 30 гр. Данное построение основано на свойстве катета АС ,равного половине гипотенузы АВ , лежащего против угла < CBA = 30 градусов , соответственно , второй угол < САВ = 60 гр. Метод построения тоже простой. 88SkyWalker88 6 лет назад Чертим окружность любого радиуса. Затем выбираем точку на окружности и проводим еще окружность такого же радиуса. обозначим точки. где пересекаются две окружности как C и D. Теперь соединяем точки с помощью прямой. Теперь построим равносторонний треугольник, у которого все углы будут равняться 60 градусов. Теперь делим этот угол пополам, и у нас получается угол 30 градусов. Zolotynka 6 лет назад Для построения угла в 30 градусов с помощью линейки и циркуля предлагаю воспользоваться таким вариантом: сначала чертим ромб, а затем – его диагонали. Используя свойства ромба, можно утверждать, что угол ромба будет 30 градусов. Итак:
Искатель приключений 6 лет назад Построит угол в тридцать градусов, можно следующим способом. Инструкция простая: 1) Сначала рисуете круг любого диаметра; 2) Рисуете еще один круг, точно такого же диаметра, а сторона второго круга, должна проходить через центр первого круга. 3) Строите треугольник FCD, как показано на рисунке вверху. 4) И теперь у вас есть два угла по тридцать градусов, это CFO и DFO. Как вы видите это достаточно простой способ построения угла в тридцать градусов используя только линейку и циркуль. Научиться так строить углы может любой человек, причем ему не придется очень долго мучится, так как все просто. Удачи. Грустный Роджер 9 лет назад 30 градусов – это половина от 60. Деление угла пополам знаете? Ну вот. А 60 градусов строится на раз. Отметьте точку и проведите окружность с центром в этой точке. Потом, не меняя раствор циркуля, проведите ещё такую же окружность, но с центром на первой окружности. Вот угол между радиусом, проведённым в “новый” центр, и точкой пересечения двух окружностей будет точнёхонько 60 градусов. Alen4uk 6 лет назад Очень часто на уроках геометрии у нас дается задание – нарисовать угол 30 градусов с помощью циркуля и линейки. Сделать это можно несколькими способами. Рассмотрим один из них. С помощью линейки рисуем отрезок АВ. Дальше следуем схеме. При удалении помогших нам в постройке угла линий, получается долгожданный угол 30 градусов. tana76 6 лет назад
moreljuba 7 лет назад Итак, я предлагаю поступить для построения угла 30 градусов при помощи циркуля и линейки следующим образом: 1) Сначала нам необходимо построить равносторонний треугольник, а именно он будет CFD Перед этим мы циркулем строим две окружности одинакового диаметра, вторая окружность строится из точки В. 2) Теперь, CD делится пополам отрезком FО. 3) Значит угол CFD у нас получается равным 60 градусам 4) А в соответствии с этим наши углы CFO и DFO будут равны 30 градусам Наш угол построен. Знаете ответ? |
Добрый день, уважаемые гости и подписчики моего канала!
На днях, знакомый профессиональный плотник показал мастерское применение угольника в качестве транспортира. Теперь я знаю, что обычным угольником можно построить не только углы 45° и 90°, а даже 10°, 20°, 30°, 40°, 50°, 60°, 70° и 80°.
Называется правило: “Правило одиннадцати”.
Почему именно “одиннадцати”? В построении любого из углов, нам всегда требуется в первую очередь отложить 11 сантиметров. По данной технологии, угол будет строиться по прямоугольному треугольнику, а точнее — по двум его катетам, один из которых равен 11 см.
Самым первым делом, с помощью угольника — проводим перпендикуляр, удаленный от края заготовки на 11 см. На фото — перпендикуляр выделен красным цветом:
Теперь мы имеем отмеченный отрезок в 11 см. и перпендикуляр. Если любую точку этого перпендикуляра соединить с углом заготовки, то мы получим прямоугольный треугольник. А дальше, немного теории 🙂
Из школьного курса геометрии мы знаем, что именно отношение двух катетов прямоугольного треугольника и определяет тригонометрические функции угла (тангенса и котангенса)
Построение 20° и 70°
Смотрите! Откладывая 11 см. по горизонтали и 4 см. по вертикали мы получаем острый угол в 20°:
На фото, на построенном перпендикуляре отмечаю 4 см. и соединяю концы отрезков:
Доказываю: Ниже, под каждой иллюстрацией, для проверки значения угла, я специально в качестве доказательства рассчитываю обратную тригонометрическую функцию — арктангенс (arctg).
Арктангенс отношения катетов 4 и 11 дает нам угол 19,98°. Погрешностью в две сотые определенно можно пренебречь. Соответственно, смежный угол будет равняться 70,02° или ~70°.
Построение 40° и 50°
Следующие углы 40° и 50° получаются от двух катетов: 11 см. по горизонтали и 13 см. по вертикали. Доказываю:
Построение: На этом же перпендикуляре ставим отметку в 13 см. и соединяем концы. Получаем угол в 49,76°. — погрешность мизерна и составляет не больше острия гвоздя, поэтому можно считать это углом в ~50°.
Построение 30° и 60°
Откладывая 19 см. по вертикали, мы получаем угол в 60°.
Удивительно, но именно катет 11 см. дает нам целочисленное значение второго катета, что и положено в основу этого правила.
Не имея под рукой угломера, мы легко можем построить нужные нам углы!
Теперь остается только наклеить на угольник бирку, чтобы первое время об этом не забывать 🙂
P.S.
Конечно… забыл про 10°, но этот угол очень редко применяется у плотников. Достаточно отложить на перпендикуляре 2 см. при длине второго катета в 11 см., тогда угол будет равен ~10°, а смежный с ним — 80°.
Подведем итоги:
Не имея под рукой угломера/транспортира, нам достаточно запомнить 5 чисел: 2,4,13,19 и основное 11, чтобы построить любой из углов с шагом в 10°. При этом, нам требуется только линейка!
Удачи Вам!
|
В строительстве часто требуется отмерить угол в 90*, реже 45* и 30*. Не всегда есть под рукой необходимые инструменты. А углы-то нужны. Так как плотники народ изобретательный, появились способы построения углов при помощи метра или рулетки, которая всегда в наличии. Начнём с построения прямого угла, от него проще построить все остальные. Способ 3-4-5. Если соединить эти отрезки в треугольник, то угол образованный меж 3,4 будет прямым. Квадрат гипотенузы равен сумме квадратов катетов. 3*3 + 4*4= 25= 5*5. Отрезок можно брать какой удобно: в см, в метрах или 5 см, 20 см. Просто потом умножаем его на 3,4,5. При отложении на катетах равных отрезков и соединяя гипотенузой точки, получаем 45*. При отложении отрезков в соотношении 1/2 получаем 30* и 60*. P.S. При расчётах стропил, чтоб на коньке получился прямой угол, берётся длина подстропильной балки делится на 7 и умножается на 5, получается угол максимально приближенный к прямому. 7*7=49 почти ровно 5*5+5*5=50. автор вопроса выбрал этот ответ лучшим Rashitgaray 5 лет назад Для этого берем гвоздик, рейку и карандашик. Проводим прямую линию, на чертеже штрих пунктирная линия, пробиваем рейку с гвоздем и фанерой по штрих пунктирной линии в любой его точке и используя рейку как циркуль чертим окружность любого диаметра, но этот же диаметр пригодится еще для одного круга который мя начертим на месте пересечения окружности и штрих пунктирной линии. После этого проводим две линии – первая линия это вертикальную линию от центра окружности с любого из кругов, а вторую от центра окружности к линии пересечения двух окружностей и получим угол равный 30 градусам при аккуратном выполнении своей задачи как на чертеже. postscriptum 2 года назад Есть разные способы, лучше всего использовать то, что найти можно без особых проблем. Тетрадь в клетку имеется у каждого, по крайней мере, ее можно купить без проблем. Нам понадобится один лист, в нем следует построить треугольник (прямоугольный), у которого один из катетов будет составлять одиннадцать клеток. От длины второго катета будет зависеть величина углов (острых) между гипотенузой и катетами. Рисуем горизонтальную линию (наш искомый 11-ти клеточный катет): Второй катет на 1 летку даст прирост угла (справа, внизу) от 0 до 5 градусов и уменьшение угла (слева, вверху) с 90 до 85 градусов. 2 клетки дадут, соответственно, 10/80, 3 клетки – 15/75, 4 клетки – 20/70, 5 клеток – 25/65, 6 клеток – 30/60. На рисунке это угол у треугольника с гипотенузой черного цвета. Погрешность есть, но она практически отсутствует. Есть еще показатели измерений по клеткам, если один катет будет на 4 клетки, а второй на 7 клеток (в сумме 11, кстати, клеток), то один из острых углов (меньший) будет те самые искомые 30 градусов равен, причем погрешность тут куда меньше 1/2 градуса. Есть и такое математическое утверждение, что катет, который равен 1/2 гипотенузы, лежать будет напротив как-раз 30-ти градусного угла. Мстислав 3 года назад Будем исходить из условий задачи. Специального инструмента для измерения углов у нас нет. Вполне реальная ситуация. Возможно, подобная необходимость появилась внезапно. однако выйти из неё не так уж и сложно. Поочерёдно рассмотрю несколько способов, позволяющих с минимальной погрешностью отмерить угол в 30 градусов. Материал при этом (фанера или ДВП, или картон и пр.) не имеет значения. Поскольку задавшийся целью измерения человек находится не в лесу в пасмурную погоду, то какие-то из нижеперечисленных вспомогательных предметов у него найдутся.
Elden 3 года назад Из личного опыта могу сказать, что всё гораздо проще меряется, а именно 30 градусов и получается даже более точнее, чем вымерять маленьким транспортиром, так как разбежка больше. Итак, есть лист фанеры, главное, чтобы у него был прямой угол, а если его нет, тогда надо нарисовать. От точки, где находится прямой угол (90 градусов) по сторонам надо отложить два одинаковых отрезка, чем длиннее они будут, тем точнее угол получится, главное, чтобы линейки или рулетки хватило. Смотрите на рисунке отрезок “а” должен равняться отрезку “в” Далее измеряем расстояние от одной точки до другой и делим значение на три равных части, отмечаем в одном месте точку отрезка. Остаётся соединить две точки и получиться угол в 30 градусов. Всё достаточно просто, угол 90 градусов содержит в себе 3 угла по 30 градусов, за счёт этого равенства, просто находим один из углов. Также можно сделать и с любыми углами, которые делятся на целое число, например 45 градусов, 22,5 градуса, 18 градусов, 15 градусов. Просто надо делить отрезок на равные части. Ким Чен Ын 4 года назад На мой взгляд вообще не совсем правильно приступать к разметочным работам без специальных инструментов, тем более если нужен угол точно в 30-ь градусов, а не 31-н, 29-ь и.т.д. Но если так получилось (нет инструмента) то мой вариант следующий. Возьмите кафельную плитку, или любой плитный материал (ДСП, МДФ, ГКЛ, да тот же кусок фанеры). Если кафель, то не важно прямоугольный он или квадратный, важно что угол в 90-о градусов есть в заводском исполнении. Прикладываем кафель к фанере, очерчиваем угол в 90-о градусов, можно простым карандашом, его проще будет стереть. Далее растопыриваем максимально возможно пальцы рук. Прикладываем руку к углу с таким расчётом что бы мизинец соприкасался с нижней стороной угла (линией). Расстояние между мизинцем и безымянными пальцами и будет тот самый угол в 30-ь градусов. Отмечаем его на фанере. Можно и по часам циферблата найти нужный угол, сделать солнечные часы и.т.п. Или купите уголок (колено) канализационный в 30-ь градусов и просто очертите его контур (внутренний) на фанере. Знаете ответ? |
-
1
Draw a ray AB. Let A be the vertex of the angle we’re going to construct.[2]
-
2
Place the tip of the compass on A and draw an arc which cuts AB at some point (say X). Let’s call this arc as Arc One. Retain this width of the compass for the remaining steps.[3]
Advertisement
-
3
Place the tip of the compass on X and draw another arc (call it Arc Two) which cuts Arc One at some point (say Y).[4]
-
4
Place the tip of the compass on Y and draw another arc (Arc Three) so as to cut Arc Two at a point (say Z) which is on that side of Arc Two which does not contain the point A.
-
5
Connect the points A and Z with a straight line and extend it to form a ray AC.[5]
- The measure of the angle CAB is 30o. Erase any extraneous constructions if you so wish.[6]
- The measure of the angle CAB is 30o. Erase any extraneous constructions if you so wish.[6]
Advertisement
-
1
Construct a 60o angle as described [7]
here. -
2
Bisect the 60o angle as described here.[8]
- Upon bisection, you’ll have two angles measuring 30o each.
- Upon bisection, you’ll have two angles measuring 30o each.
Advertisement
Add New Question
-
Question
Can I construct a 30-degree angle from a 60-degree angle?
Let’s assume you want to bisect a 60° angle using a compass and straightedge. Place the point of the compass at the 60° angle’s vertex. Strike an arc through the angle at a convenient distance. Label as A and B the points where the arc intersects the angle’s two rays. Place the compass point at A, and strike an arc within the angle’s rays. Place the compass point at B, and using the same radius, strike another arc within the rays. Label as C the point of intersection of the two arcs. Draw a straight line from the angle’s vertex to point C. That line bisects the 60° angle, forming two 30° angles.
-
Question
How to construct 15 degree angle?
Construct a 30° angle and bisect it.
-
Question
How do I construct an angle of 60 degrees?
Draw a horizontal line segment of any convenient length. Use a compass to measure the length of the line segment. Put the compass point at one end of the line segment and strike an arc with a radius the length of the line segment. Do the same from the other end of the line segment so that the second arc intersects the first arc. From the intersection of the two arcs, draw straight lines to both ends of the line segment. The triangle thus drawn will consist of three 60-degree angles.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
Things You’ll Need
- Paper
- Pen or Pencil
- Compass
- Straightedge
References
About This Article
Article SummaryX
To construct a 30-degree angle, you’ll need a compass, a straightedge, such as a ruler, and a pencil. Start by drawing a horizontal line and marking the left end “A” and the right end “B” to serve as the vertex of the angle. Then, place the tip of the compass on “A” and draw an arc through the vertex line. Mark the spot the arc crosses the vertex as “X.” Now place the tip of the compass on “X” and draw a second arc through the first arc. Mark the point they intersect as “Z” To make the 30-degree angle, simply use your ruler to draw a line connecting “A” and “Z.” To learn how to measure out a 60-degree angle, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 200,678 times.
Did this article help you?
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы.
Углы 0°,30°,45°,60°,90°,180°270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Sin, Cos, tg, ctg.
Раздел: Таблицы численных значений + Таблицы Брадиса:
Центральные и вписанные углы
О чем эта статья:
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую опирается.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?
Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°
Углы 30, 45, 60, 90 градусов: наглядные, стихотворные, боевые, электрические, драматические, музыкальные
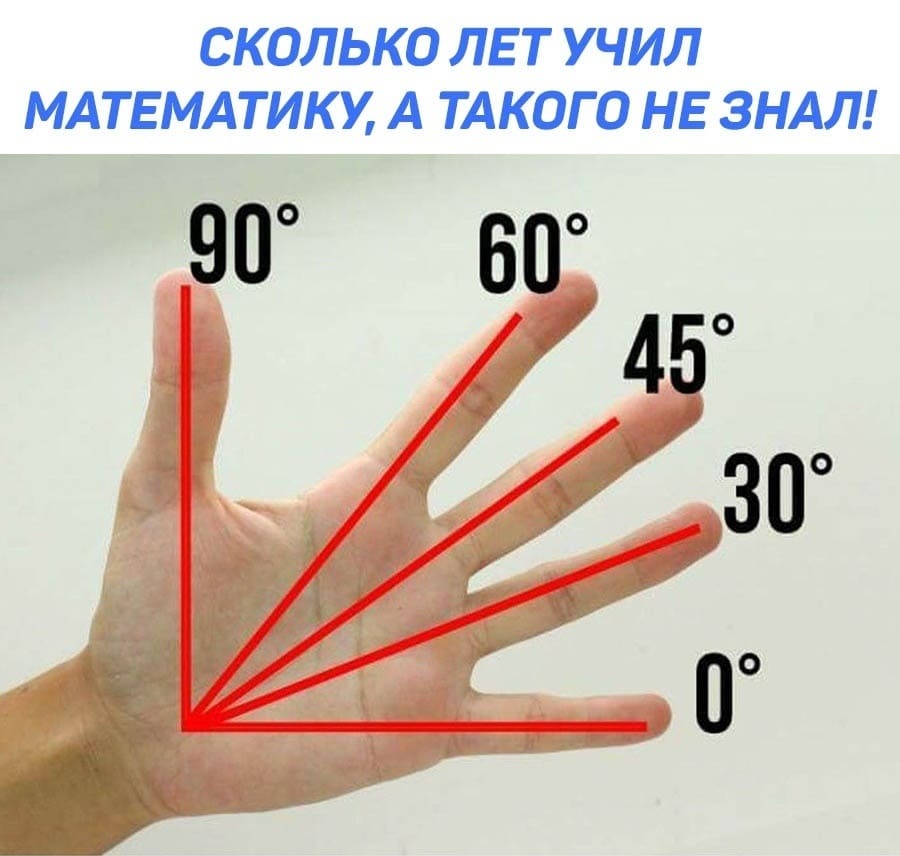
Можно определить углы 30, 45, 60, 90 градусов с помощью своей ладони.
Градусы наглядные: как их определить с помощью своей ладони
Наша рука, оказывается, очень даже может помочь с величинами углов, с градусами. Если посмотреть на нее под определенным углом зрения (см. рис. 1), то вот они, родимые: 0 градусов, 30, 45, 60 и даже 90 градусов!
Почему нам так важны именно эти величины? Почему нас могут интересовать углы 0, 30, 60 и 90 градусов, а также 45? Нет бы поинтересоваться, скажем, углами 15, 20, 75 или 80 градусов…
Оказывается, все дело в синусах и косинусах! Ибо синус нуля градусов есть ноль, а косинус 90 градусов — тоже равен нулю. Синус 30 градусов равен половинке единицы. Такое же значение 0,5 дает косинус 60 градусов.
А вот 45 градусов интересны тем, что синус и косинус 45 градусов равны между собой. Это значит, что тангенс 45 градусов будет равен единице. Ведь мы помним, что тангенс угла есть частное от деления синуса угла на косинус угла.
Но не только об этом хотелось сказать, глядя на рисунок…
Градусы стихотворные и число «пи»
Есть такое число – «пи». Оно почему-то равно 3,14. Хотя не совсем так. Это число с бесконечным количеством цифр после запятой. После запятой стоят не только цифры 1 и 4, но и множество других цифр.
Первый десяток цифр числа «пи» легко написать, если запомнить необычное стихотворение. Правда, стихи про «пи» нужно писать со старинной буквой «ять» — ведь и число «пи» очень старое, и стихотворение совсем не молодое:
Кто и шутя, и скоро пожелаетъ
Пи узнать число — ужъ знаетъ
Зачем в стихотворении стоит «ять» на конце? И при чем тут «пи»? Все очень просто: считаем буквы в словах стихотворения и подставляем цифры в число «пи».
Получается, кто=3, и=1, шутя=4, и=1, скоро=5 и так далее: 3,1415926536… Многоточие на конце — это значит, что есть продолжение цифрам, бесконечное продолжение.
Причем тут градусы? При том, что «пи» — это величина развернутого угла, но не в градусах, а в радианах (другая единица измерения величины угла). «Пи» радиан есть угол величиной 180 градусов.
Как говорят математики, отсюда нетрудно догадаться, что 0 градусов есть ноль радиан. 90 градусов есть «пи пополам» радиан. Нам этот термин «пи пополам» еще пригодится далее. Все остальные градусы таким же образом можно свести к разным частям числа «пи».
Получается, что мы теперь знаем стишок про 180 градусов — стишок про «пи»! Что это дает?
Градусы боевые: почему наши деды победили
Плывет боевой корабль. Вернее, идет боевой корабль, ибо корабли не плавают, а ходят. Штурман прокладывает курс на карте. И вдруг появляется супостат. Тревога!
Штурман откладывает карту в сторону. Достает маневренный планшет. Теперь он отслеживает на нем положение корабля относительно одного противника или сразу нескольких противников.
Тут — сплошные градусы. Кто из супостатов виден под каким углом? Угол есть решающая величина. Приходится учитывать как углы, так и их синусы, и косинусы.
Кто в школе учился, тот помнит, что синус и косинус угла не может быть больше единицы. Хоть что делай, больше единицы не получается.
А вот в годы войны у штурмана боевого корабля косинусы углов доходили порой до четырех! Потому и победили, что делали невозможное! Даже с косинусами, ограниченными правильной математикой!
Так что запомним вопреки математике: в годы войны косинусы углов могут доходить до «четырех». В том числе, поэтому наши деды победили!
Градусы электрические: отклонение между напряжением и током
Ну, синус? Ну, косинус? И что тут такого? Спросим любого человека, например, возле пивного ларька, что такое синус и как давно он пользовался косинусом после школы. Что услышим в ответ?! Во, именно «это» и услышим.
Вместе с тем мы постоянно живем, можно сказать, под градусом, точнее, под косинусом! Ежедневно мы пользуемся электричеством: нажимаем кнопки и выключатели, и дело с концом — все светится, крутится, работает.
Чтобы электричество выполняло свое предназначение, нужно электрическое напряжение и электрический ток. Обе «субстанции» должны быть вместе и одновременно. Но эти две величины могут иметь между собой угол отклонения, измеряемый «косинусом фи», как выражаются энергетики на своем профессиональном языке.
Если отклонение напряжения от тока есть ноль градусов, то электрическая мощность будет получена умножением величины напряжения на величину тока.
Допустим, подключаем электрообогреватель. Он начинает излучать тепло, равное по мощности этой самой величине: напряжение 220В (двести двадцать вольт) умножить на ток, скажем, 5А (пять ампер) равно 1КВт (1 киловатт) мощности. Становится тепло!
Если между напряжением и током есть отклонение, хотя бы на 1 градус, то придется перемножать не только напряжение и ток, но и полученный результат дополнительно умножать на косинус угла отклонения. Ноль градусов отклонения — косинус равен единице, умножение на единицу ничего не меняет. А вот косинус всего лишь 1-го градуса возможного отклонения уже меньше единицы. Не намного, но меньше. Это значит, что греть наша батарея будет уже слабее.
Чем больше отклонение электрического напряжения от электрического тока, чем будет больше между ними градусов так называемого угла «фи». Тем слабее будут греть батареи, хуже станет накал лампочек, и вообще будет меньше электричества.
И не говорите теперь, что косинус — это абстракция, которую мы оставили в школе навсегда…
Градусы драматические: косинус 90 градусов равен нулю
А что как напряжение и ток отклоняются друг от друга на 90 градусов?! Ведь косинус такого угла равен нулю. Умножение на ноль есть ноль. Это, что называется, страшный сон энергетиков — ужасная апокалиптическая драма!
Представьте себе, газ сжигается на тепловых электростанциях, вода крутит турбины на гидроэлектростанциях, нейтроны делятся в реакторах атомных электростанций. Ток «бежит» по проводам в дома. А там — косинус угла «фи» равен нулю — полный швах! Батареи не греют, лампочки не светятся, холодильники не работают.
Чтобы мысленный эксперимент с отклонением напряжения и тока на 90 градусов не стал реальностью, энергетики по всему миру постоянно следят за «косинусом фи». Денно и нощно, без устали, без перерывов.
Почему отклоняются напряжение и ток? Из-за потребителей электричества! Нет, не из-за домашних электрических обогревателей. И не из-за домашних лампочек накаливания. Но из-за оборудования заводов и фабрик.
Везде, где крутятся электромоторы, их «кручение» приводит как бы к обратному закручиванию электричества. Работающее оборудование возвращает энергетикам в электрические сети сдвинутое между собой напряжение и ток.
Образно говоря, чтобы крутить моторы, электричество должно «упираться» во что-то. И из-за этого понемногу «проворачивается» в обратную сторону. Что и приводит к возникновению угла сдвига между напряжением и током.
Если не следить за последствиями такого «сдвига», то угол между напряжением и током будет постоянно расти. Косинус фи начнет уменьшаться. Электростанции начнут работать сначала чуть-чуть вхолостую, потом все больше и больше, потом еще больше…
Градусы из радиоточки
Если напряжение и ток встанут друг относительно друга на 90 градусов — это будет недопустимое отклонение или «сдвиг по фазе на пи пополам»! Тогда электричество останется в проводах, но оно ничего не будет греть, освещать, двигать.
«Сдвиг по фазе на пи пополам» есть расхожее выражение, которое означает абсолютную неприемлемость того или иного действия, поступка.
Пришло оно к нам из того самого электротехнического «косинуса фи».
Про сдвиг между напряжением и током можно написать не одну драму с яркими событиями и участниками. Но мы не будем это делать, ибо наши энергетики не допустят подобного хода событий…
Кстати, кто помнит еще советское радио, что звучало практически в каждом доме? Там по утрам во многих городах сообщали не только про погоду. Погода — это тоже градусы, но другие.
Из радиоточки строго так говорили, обычно после прогноза погоды: «на сегодня режим энергопотребления установлен два тире два» или «. два тире один». Это про «наши» градусы, про «косинус фи»!
Что это за режимы такие: 2-2, 2-1 и другое? То были прямые указания предприятиям, как они должны именно сегодня компенсировать возникающие сдвиги между напряжением и током.
Энергетики шли к компенсирующим установкам и включали озвученные по радио режимы. Вот ведь насколько важны углы! Про них даже по центральному радио (с местным уклоном, разумеется) вещали ежедневно.
А вы говорите градусы, синусы, косинусы! И зачем мы их в школе «проходили», если вокруг нас их как не было, так и нет? Оказывается, были, есть и будут. Даже в обычной электрической розетке, в лампочке, в утюге.
Градусы музыкальные
Для тех, кто «добрался» до конца — маленький сюрприз: музыкальные «градусы». Вот как, оказывается, можно сыграть на фортепиано про число «пи» с точностью аж до 122 знаков после запятой. Музыка «развернутого угла 180 градусов»!
Словами добавить нечего, достаточно послушать. И все это про «пи» и про градусы, которые в школе «прошли» и забыли:
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/centralnye-i-vpisannye-ugly
http://prostoznat.ru/ugly-30-45-60-90-gradusov/
[/spoiler]