Углы – это геометрические фигуры, образованные двумя лучами, которые выходят из одной точки. Обозначения углов регламентированы ГОСТ 2.307-2011 «Нанесение размеров и предельных отклонений».
Как обозначается угол на чертеже
Угол на чертеже обозначается с помощью универсального и общепринятого символа, на котором показаны два луча, выходящие из одной точки. За символом указывается размер угла в градусах, минутах и секундах. Острый угол символа направлен в сторону уклона.
Обозначение углов на чертеже по ГОСТу
Согласно ГОСТ 2.307 размеры делятся на линейные и угловые. И если в линейных размерах не ставят единицы измерения, т. к. всегда подразумевается, что значения приведены в миллиметрах, то для угловых размеров обязательно указывается значок градуса, минуты и секунды, в зависимости от того, в каких величинах измеряется угол.
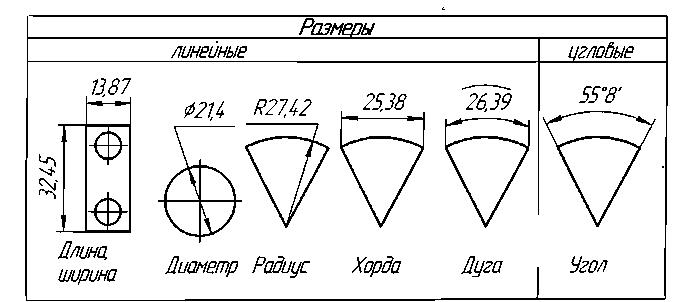
Рисунок 1. Линейные и угловые размеры
Как показать угол на чертеже
Чтобы показать размер используются сплошные тонкие линии, они могут быть выносные или размерные. Любой угол имеет вершину и две стороны. Градусами или минутами обычно обозначается внутренняя сторона угла. В качестве условного обозначения используется символ в виде острого угла, далее указывается числовое значение и единицы измерения. Следует помнить о том, что минута — это одна шестидесятая часть градуса, а секунда одна шестидесятая часть минуты. Градусы обозначаются с помощью маленького круга в верхнем правом углу возле значения, минуты обозначаются одной надстрочной запятой, а секунды двумя надстрочными запятыми.
Допуск угла
В ГОСТ 8908-81 приведены стандарты на допуски углов, применяемые в машиностроении, при меньшей стороне угла до 2,5 м. Значения уклона и угла уклона приведены в таблице (рис. 1). Стандартом установлено 17 степеней точности допусков, которые зависят от длин сторон и размера угла.
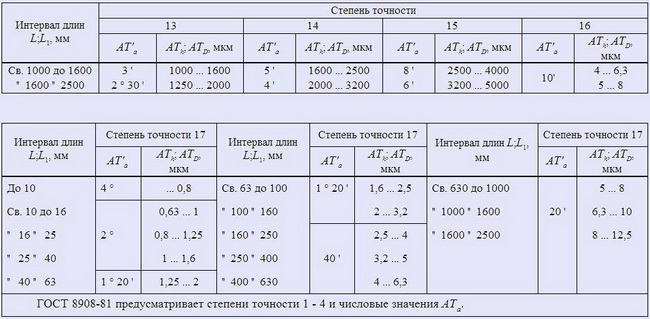
Рисунок 2. Степень точности допуска угла
Виды углов на чертеже
На чертежах могут быть обозначены следующие виды углов:
- острый – менее 90 градусов;
- прямой – равен 90 градусам;
- тупой – более 90 и менее 180 градусов;
- развернутый – равен 180 градусам.
Обозначение у прямого и развернутого угла ставится при необходимости.
Углы наклона
Угол уклона часто встречается как на машиностроительных, так и на строительных чертежах. Он показывает, под каким углом к базовой линии расположен наклонный элемент. Для обозначения наклона используется универсальный символ, который ставится перед размерным числом. К примеру, на строительном чертеже отмостка всегда имеет уклон, для обозначения этого уклона ставится символ и значение в 5 промилле.
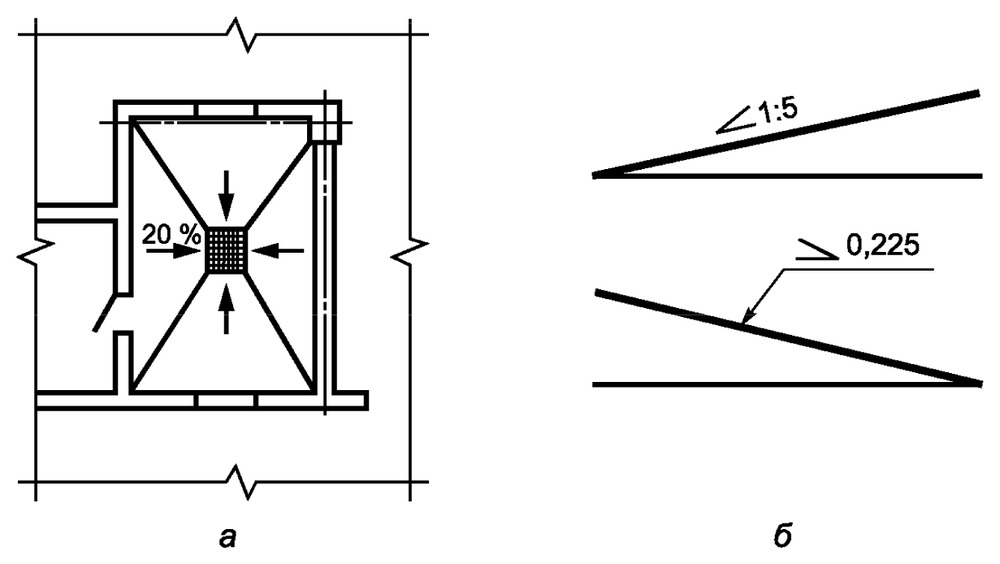
Рисунок 3. Обозначение уклона на плане кровли
Промилле — это одна тысячная или десятая часть процента, поэтому к знаку промилле добавлен еще один нолик. Через промилле в строительных чертежах указывается уклон пандусов и других наклонных поверхностей.
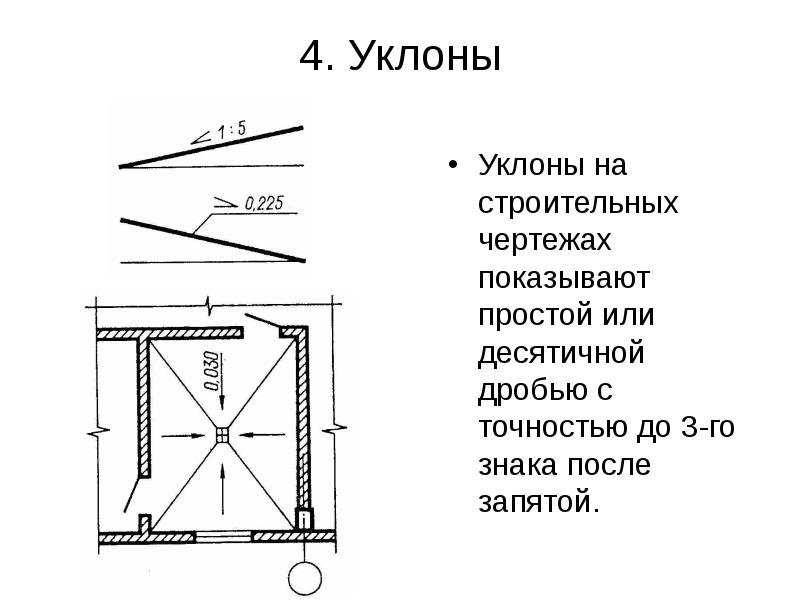
Рисунок 4. Уклон на чертеже
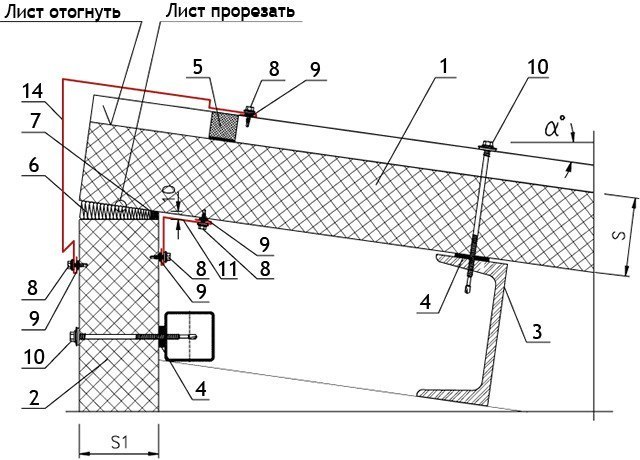
Рисунок 5. На узле сопряжения сендвич панелей указывается угол под которым конструкции крпятся друг к другу
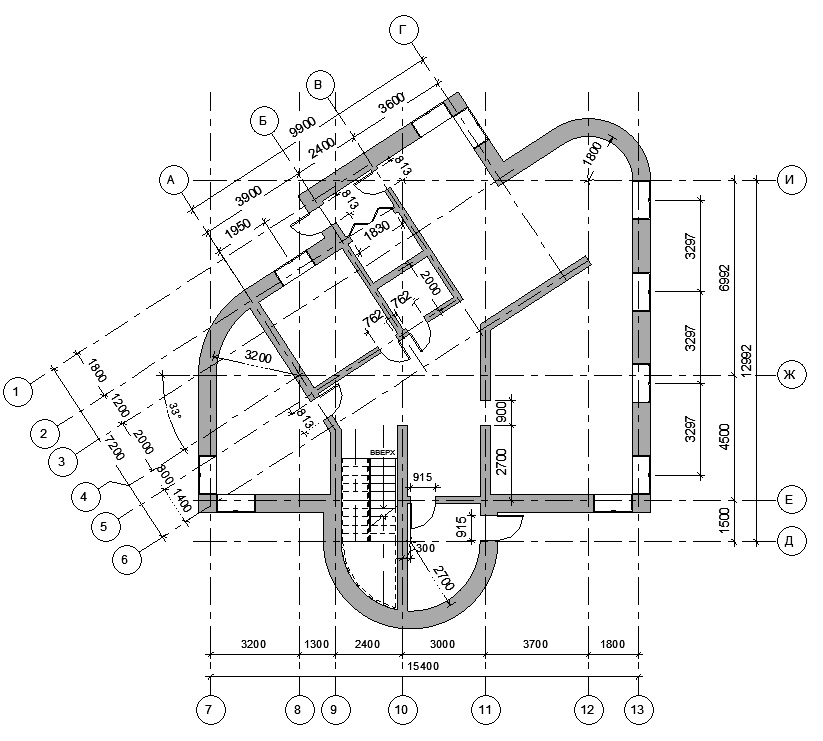
Рисунок 6. Углы. На строительном чертеже обозначен угол в 33 градуса
Угол преломления
Преломление возникает на границе двух сред, при этом угол падения равен углу отражения. Падающий и отраженный лучи показывают на чертеже, а значение угла наносят относительно вертикали, прямого угла.
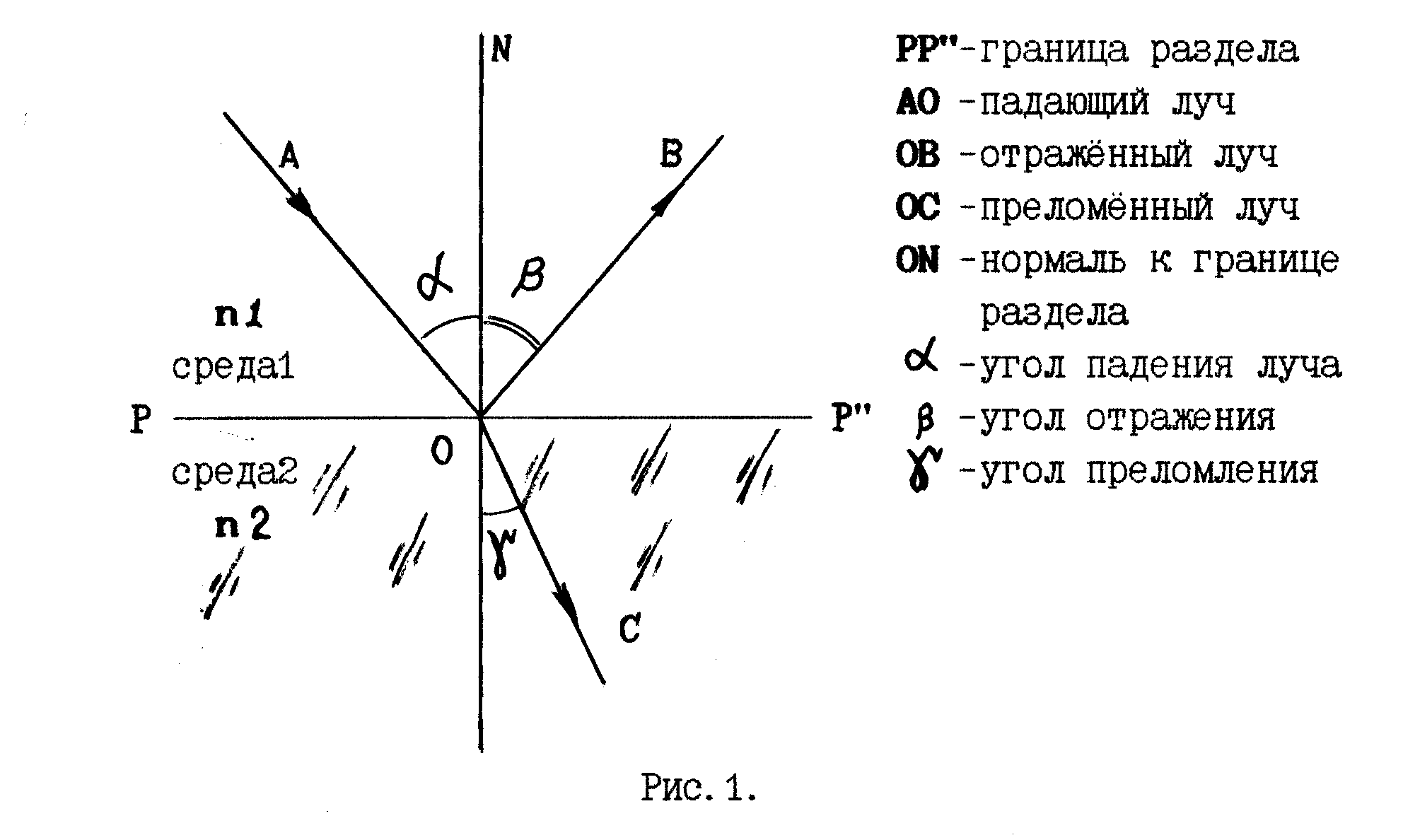
Рисунок 7. Угол преломления
Вертикальные углы
Согласно определению вертикальными называют два угла, в том случае, если стороны одного угла являются продолжением сторон другого. Такие углы будут попарно равны. Обычно на чертеже их обозначают с помощью полукруга или двойного полукруга.
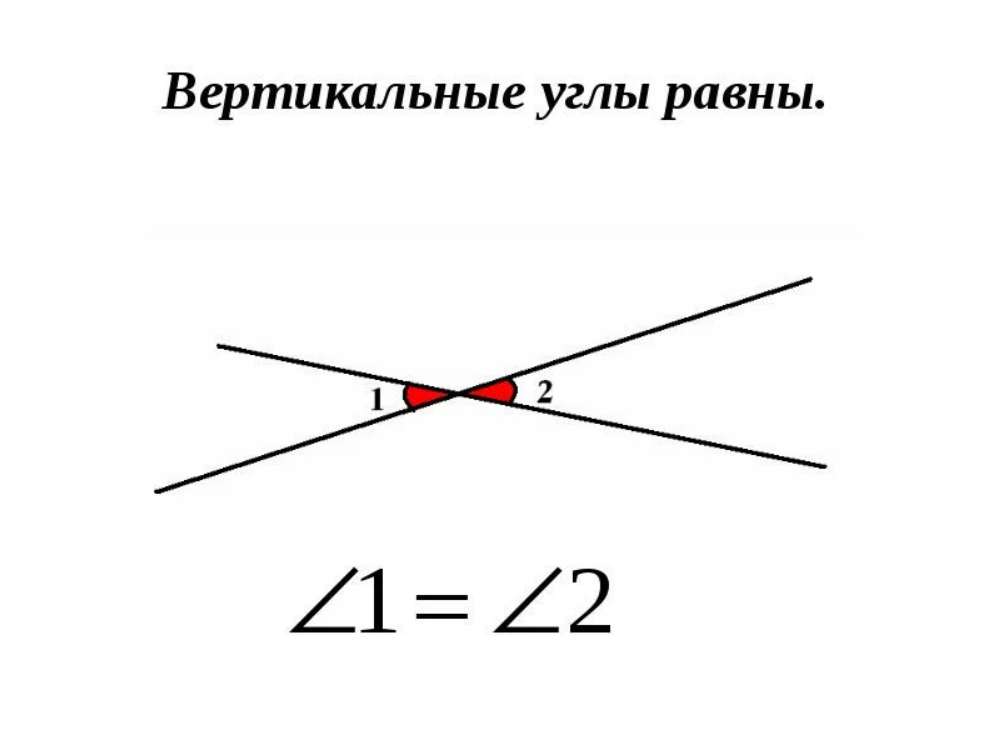
Рисунок 8. Вертикальные углы, пример обозначения
Многогранные углы
Понятие многогранного угла относится к трехмерному пространству, такой угол состоит из плоских углов, которые его образуют, имея общую точку. При этом они не должны лежать в одной плоскости.
У многогранного угла есть два свойства:
- сумма плоских углов многогранного угла превышает 360 градусов;
- существует плоскость, пересекающая все ребра многогранного угла.
По количеству граней многогранные углы делят на трехгранные, четырехгранные, пятигранные и так далее.
Самым показательным примером многогранного угла является вершина четырехугольной пирамида. Многогранный угол может быть невыпуклым и выпуклым.
Смежные углы
Смежными называются углы, которые имеют одну общую сторону, а две другие их стороны являются продолжением друг друга. Сумма смежных углов равна 180 градусам. Поэтому, если известно значение одного угла, то найти значение второго не составляет труда.
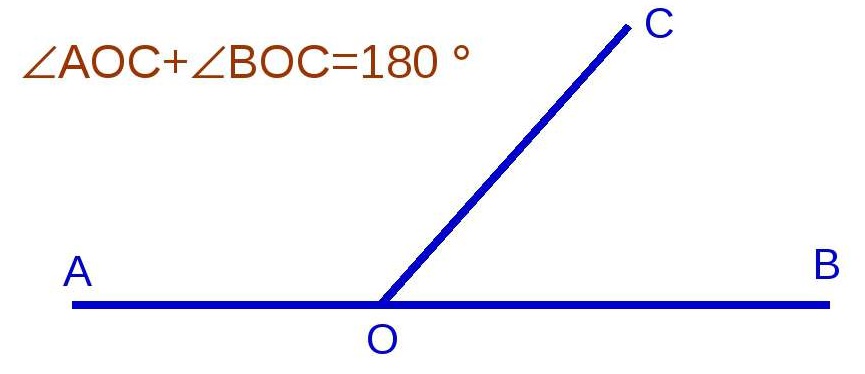
Рисунок 9. Пример смежных углов
Углы фаски
Деталь может иметь скос или скругление, которое называется фаской. Обозначение фаски установлено в ГОСТ 2.307-2011, обычно ее показывают размерными линиями. Запрещено использовать осевые и контурные линии для обозначения фаски. На чертеже обязательно указывают ширину, размер скоса и угол относительно главной оси элемента или механизма. Если на чертеже показана фаска, но не указан угол, то подразумевается ее стандартное значение 45 градусов. Обозначение выполняется с помощью выносной линии или с помощью линейных размеров.
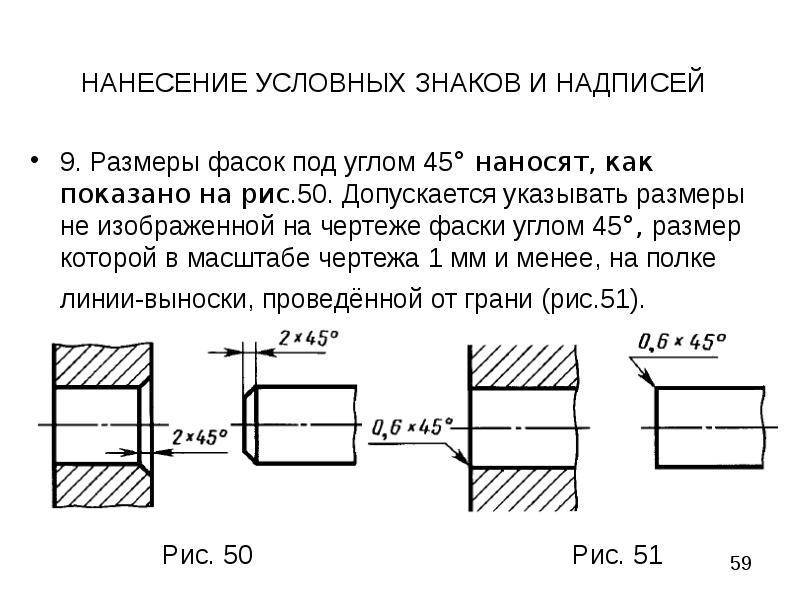
Рисунок 10. Обозначение фаски по ГОСТ
Внешние углы на чертеже
На чертежах может потребоваться указать внешний угол треугольника, это угол смежный с любым из внутренних углов. Следовательно, у каждой вершины можно построить два равных внешних угла. Также существует теорема, доказывающая что внешний угол равен сумме двух внутренних углов, которые не смежны с ним.
Центральные углы на чертеже
Центральным называется угол, который равен градусной мере дуги, на которую он опирается. Центральный угол отличается от вписанного тем, что вершин вписанного угла лежит на окружности, и он равен половине дуги, на которую опирается. Вписанные и центральные углы имеют зависимость, например, если нарисовать их на одной окружности, то вписанный угол будет равен половине центрального, если они опираются на одну дугу. Таким образом, зная один угол, можно определить другой.
Ответы на вопросы
Как обозначается радиус окружности на чертеже?
Для обозначения радиуса используется значок R, после которого указывается значение в миллиметрах и сплошная тонкая линия со стрелкой на конце. Радиус проводят от центра окружности к обозначаемому отрезку. Обычно указывают только радиус, диаметр при необходимости можно найти путем удвоения радиуса.
Как указать прямой угол?
При обозначении острого или тупого угла в основании между лучами проводят полукруг, если угол прямой в его основании рисуют квадрат.
Как отсчитывают угол на чертеже?
Угол образовывается двумя лучами, чтобы найти его значение используют транспортир.

В каждой сфере деятельности, где требуется создание технических чертежей и схем, важным элементом является обозначение углов на чертеже. Это необходимо для точного производства. В данной статье мы рассмотрим основные понятия и правила, которые нужно знать для правильного обозначения угла на чертеже.
Что такое угол на чертеже?
Угол на чертеже представляет собой две линии, которые пересекаются в определенной точке. Он может быть обозначен несколькими способами, включая градусы, радианы, грады и милы.
Для каждого способа обозначения существуют свои формулы расчета и обозначения на чертеже.
Уклон в процентах и промилле
Угол уклона относительно горизонта используется для определения наклона поверхности.
Угловые размеры уклона на чертежах обычно указываются в виде градусов, минут и секунд. В соответствии со стандартами ГОСТ 2.307-2011 и ГОСТ Р 21.1101-2013, на планах и схемах направление уклона указывается стрелкой, с числовым значением в процентах. Допустимо использовать указание уклона в промилле или в виде десятичной дроби с точностью до третьего знака.
Часто на чертежах для обозначения уклона используют знак угла, который направлен в сторону уклона. На чертежах также можно встретить буквенное обозначение уклона (i). В процентах обычно обозначают уклон крыш, пандусов, лестничных маршей и других поверхностей. Эти данные необходимы для правильного и точного выполнения проекта.
Виды углов на чертеже
Существует несколько видов углов на чертежах. К ним относятся:
- Прямой угол — угол в 90 градусов;
- Острый угол— угол меньше 90 градусов;
- Тупой угол — угол больше 90 градусов, но меньше 180 градусов;
- Равный угол — угол в 180 градусов;
- Смежный угол — угол, смежный с другим углом и имеющий общую сторону;
- Вертикальный угол — угол между двумя вертикальными плоскостями;
- Горизонтальный угол — угол между двумя горизонтальными плоскостями.
Кроме того, на чертежах могут быть указаны углы скоса, наклона и поворота, которые могут быть важными для определения размеров и расположения объектов на чертеже. От обозначения углов зависит понимание и правильное выполнение чертежа.
Углы наклона
На чертежах, как машиностроительных, так и строительных, часто встречается угол уклона. Этот параметр показывает, под каким углом к базовой линии расположен наклонный элемент. Чтобы обозначить наклон, используется универсальный символ, который ставится перед размерным числом. Например, на строительных чертежах отмостка всегда имеет уклон, который обозначается символом и числом в 5 промилле (рис. 1).
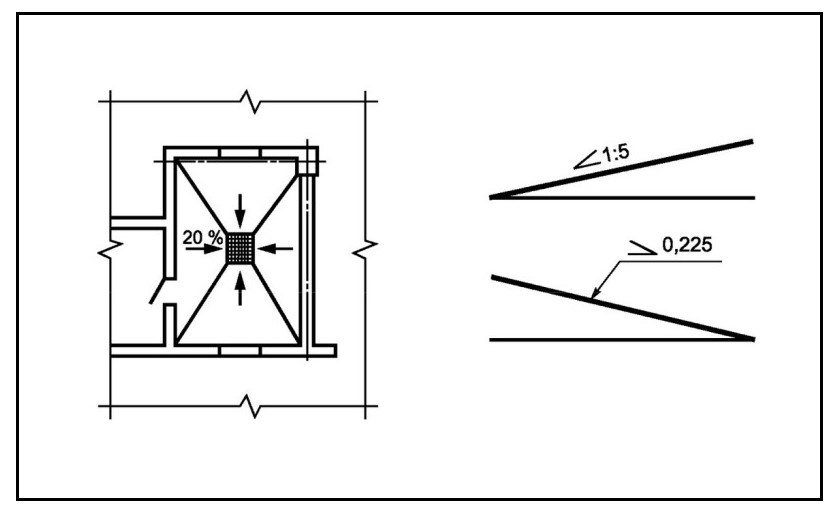
рисунок 1
Угол преломления
Это угол между лучом, преломленным внутри оптической среды, и нормалью к поверхности раздела сред (рис. 2).
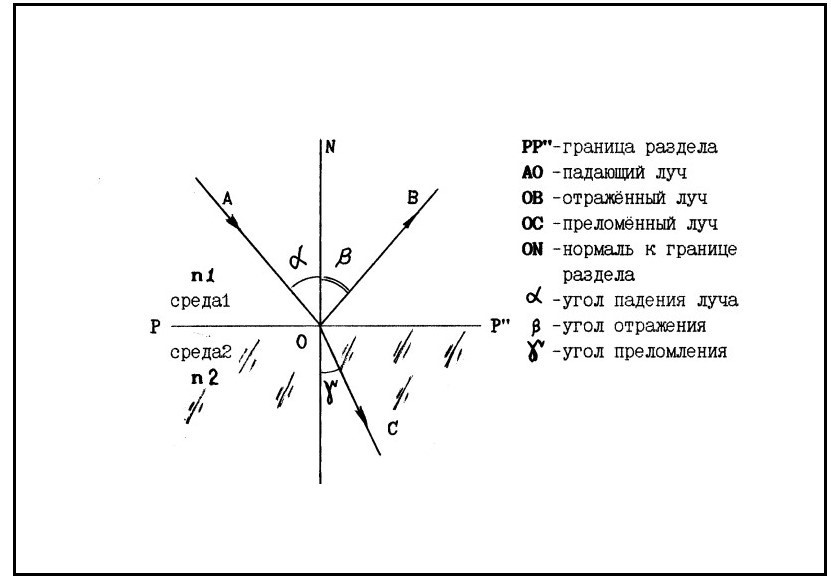
рисунок 2
Нормалью называется линия, перпендикулярная к границе раздела двух сред.
Обычно угол преломления указывается в градусах. Он может быть обозначен специальной стрелкой или символом, указывающим направление преломленного луча.
Вертикальные углы
Вертикальными углами на чертеже называют пару углов, основания которых являются продолжением сторон друг друга. По определению, вертикальные углы равны между собой, что важно для создания точных и понятных технических схем и чертежей. Обычно вертикальные углы на чертеже обозначаются полукругами или двойными полукругами (рис. 3).
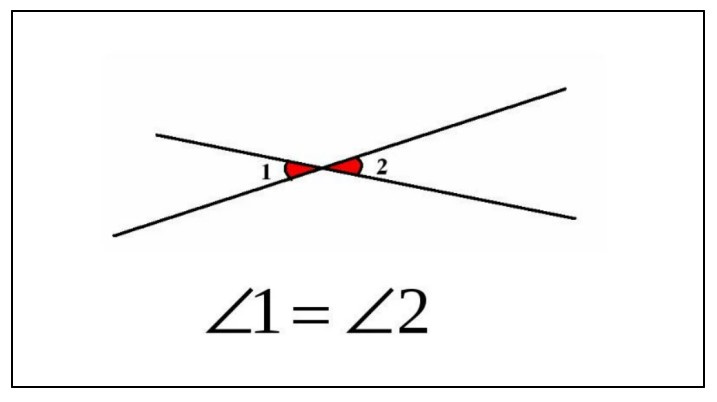
рисунок 3
Многогранные углы
Это углы, которые имеют более двух сторон и образуются пересечением линий на плоскости. Такие углы могут быть обозначены различными способами на чертеже в зависимости от их типа. Например, наиболее распространенными видами многогранных углов на чертеже являются прямоугольники, треугольники и пятиугольники, которые обычно обозначаются соответствующими символами и линиями на чертежной плоскости (рис. 4).
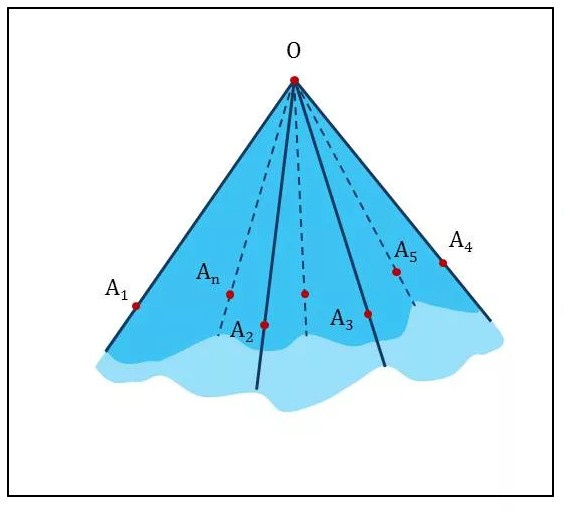
рисунок 4
Многогранный угол обладает двумя основными свойствами:
- Общая сумма плоских углов этого угла больше 360 градусов;
- Существует такая плоскость, которая проходит через все ребра многогранного угла.
Смежные углы
Это пара углов, у которых общая сторона лежит на одной прямой. Такие углы обычно располагаются рядом друг с другом и могут иметь различные значения в зависимости от их величины. Для обозначения смежных углов на чертеже обычно используются специальные символы, например, знаки «∠» или «∡», а также цифры, которые указывают на величину угла в градусах или радианах (рис. 5).
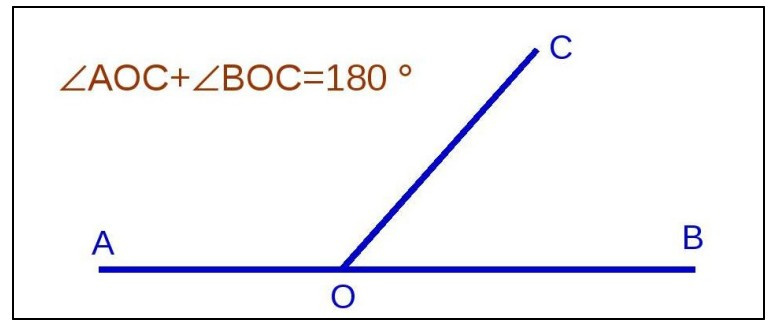
рис. 5
Углы фаски
Углы фаски на чертеже — это углы, образующиеся на гранях детали, которые должны иметь скругление или скос. Фаски на чертеже обычно указываются с помощью специальных символов, которые показывают величину и форму фаски, а также местоположение на чертеже. Они могут быть различных форм и величин (рис. 6).
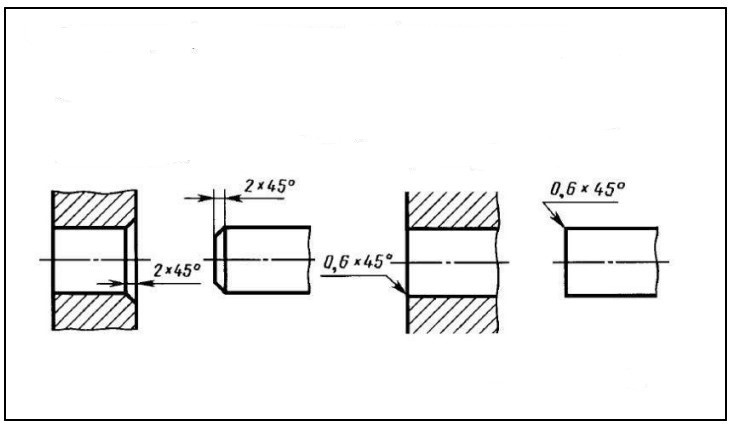
рисунок 6
Для обозначения фасок на чертеже запрещено использовать осевые и контурные линии. Вместо этого обязательно нужно указывать ширину, размер скоса и угол фаски относительно главной оси элемента или механизма. Если угол фаски не указан явно на чертеже, то подразумевается его стандартное значение в 45 градусов. Обозначение фасок может быть выполнено с помощью выносной линии или линейных размеров, которые показывают все необходимые параметры фаски.
Внешние углы на чертеже
Углы, образованные объединением двух прямых линий, которые встречаются в точке наружной грани детали, называются внешними. Они обозначаются на чертеже с помощью специальных символов, например, знака «∠» и цифровых значений, показывающих величину угла в градусах или радианах. Внешние углы могут иметь различные значения в зависимости от формы детали и условий ее использования.
Центральные углы на чертеже
Центральный угол — это угол, опирающийся на дугу окружности и равный ее градусной мере. В отличие от него, вписанный угол имеет вершину на окружности и равен половине градусной меры соответствующей дуги. Тем не менее, между вписанными и центральными углами существует связь: например, на одной окружности вписанный угол будет вдвое меньше центрального, если они опираются на одну и ту же дугу. Зная значение одного угла, можно определить значение другого.
Определение угла на чертеже
Угол на чертеже можно определить по следующим признакам:
- Угол имеет общую вершину;
- Угол образован двумя отрезками, лучами или прямыми;
- Лучи угла могут быть обозначены буквами, цифрами или специальными символами;
- Угол может иметь разные размеры, которые указываются в градусах, минутах и секундах;
- Угол может быть острый, тупой или прямой.
Для определения размеров угла на конструкторских документах используют специальный градусный инструмент. При помощи этого инструмента можно узнать значение угла в градусах, минутах и секундах, а также проверить его соответствие заданным требованиям допусков.
Как обозначается угол на чертеже
Угол на чертеже обычно обозначается символом «∠», за которым следует наименование точек. Например, ∠ABC означает угол, образованный линиями AB и BC. Также некоторые инженеры и архитекторы могут использовать другие символы, такие как латинские буквы «A», «BAC» или «∡A», но общеиспользуемым является символ «∠».
Условное обозначение угла содержит информацию о его размере, выраженном в градусах, минутах и секундах. Направление символа свидетельствует об остроте или тупости угла, а также указывает на его уклон.
Обозначение углов на чертеже по ГОСТу
Обозначения углов определены стандартом ГОСТ 2.307-2011 «Нанесение размеров и предельных отклонений». Согласно стандарту, размеры бывают двух видов: линейные и угловые. Обычно линейные размеры не сопровождаются единицами измерения, потому что предполагается, что они задаются в миллиметрах. Угловые — обязательно должны содержать символ измерения (рис.7).
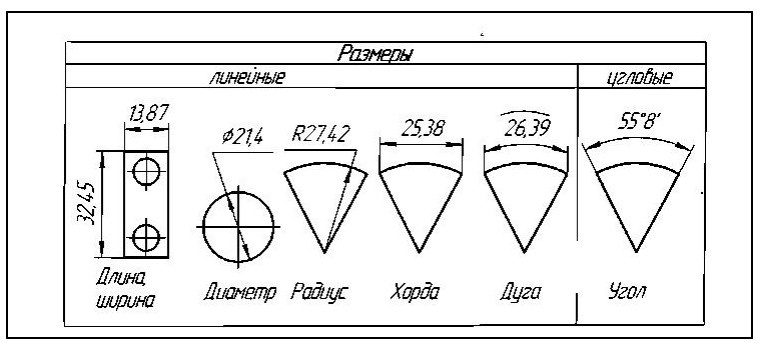
рисунок 7
Допуск угла
ГОСТ регулирует допуски углов на чертежах. Согласно стандарту, при указании размеров углов на чертеже следует учитывать их допуски. Допуски угла можно представить в виде отклонения от заданного размера угла в градусах, минутах или секундах (рис. 8).
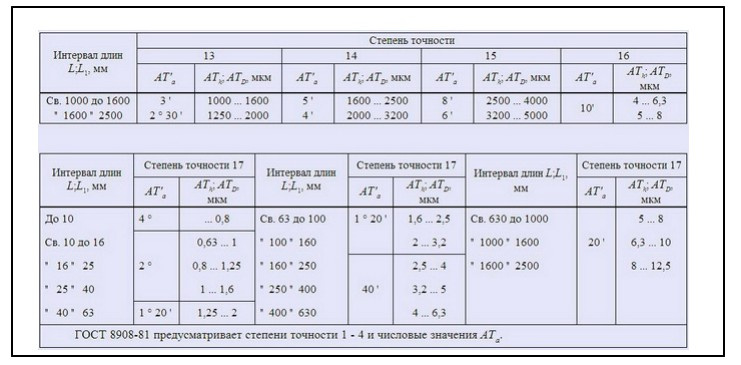
рисунок 8
Допуски угла на чертеже зависят от класса точности, который выбирается в зависимости от требований детали. Выделяются три класса точности: высокий, средний и низкий. Чем выше класс точности, тем меньше допуски углов.
Допуски могут быть двух видов: по форме и по расположению.
Допуски по форме определяются отклонением фактической формы угла от его идеальной формы (например, отклонение угла от равенства). Допуски по расположению учитывают расположение угла на детали и могут быть связаны с требованиями к точности сборки, необходимостью установки других элементов и т. д.
Сравнение углов на чертеже
Корректное сравнение углов на чертеже является важным условием для создания точной и понятной технической документации и предотвращения ошибок в процессе производства.
На чертеже углы обычно обозначаются специальными символами, которые позволяют определить их величину и форму. Для сравнения углов на чертеже важно учитывать их тип, направление и величину, а также знать правила и формулы, которые позволят вычислить значение угла и его разность.
Не знаете как выполнить работу? Обратитесь за помощью к нашим экспертам. Сделайте заказ чертежа на сайте Студворк!
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
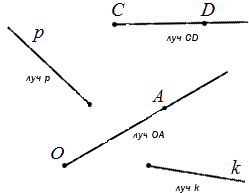
Перейдем к понятию определения угла.
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
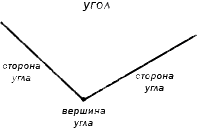
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.

Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
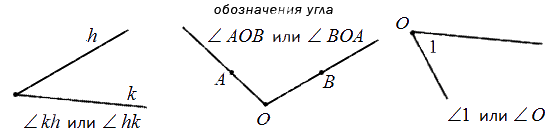
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной – ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
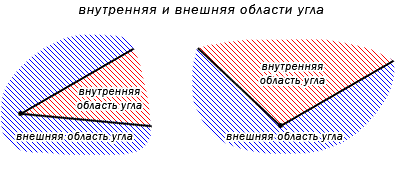
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
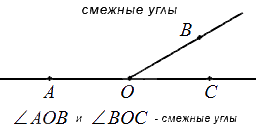
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
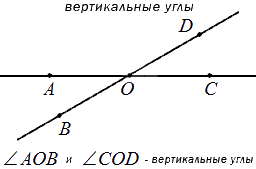
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
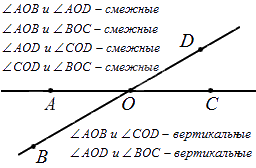
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
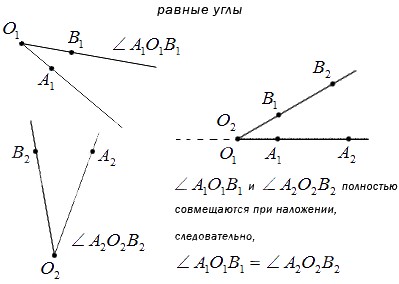
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
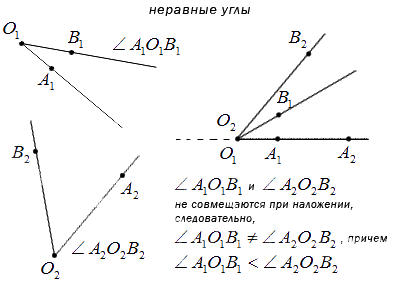
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
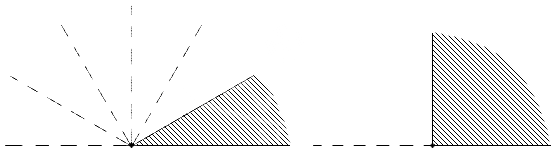
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Минутой называют одну шестидесятую часть градуса.
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «”». Имеет место обозначение:
1°=60’=3600”, 1’=(160)°, 1’=60”, 1”=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59” .
Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17°3’59” . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
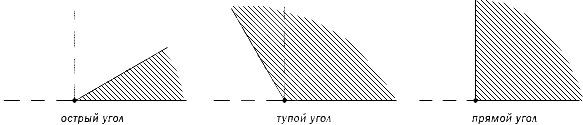
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
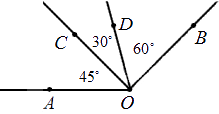
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
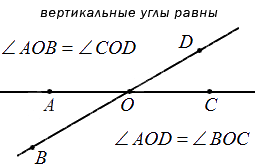
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
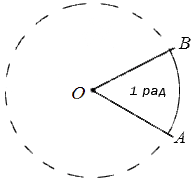
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
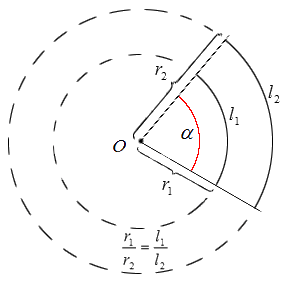
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
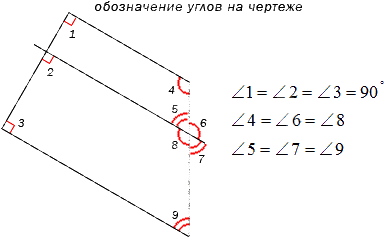
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
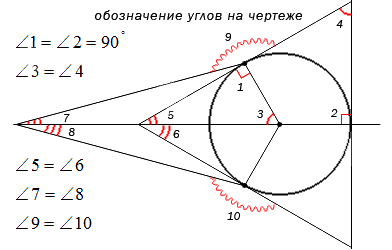
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Угловые размеры

Угловые размеры на чертеже
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Наиболее распространенный способ измерения угловых величин – градусная мера.
Градус – «gradus», в переводе с латинского языка, означает – шаг, ступень.
При обозначении угловых размеров используется единицы измерения – градусы, минуты и секунды. После числового значения угловых размеров ставится специальные знаки:
- Градус – «
°» - Минута – «
′» - Секунда – «
″»
Размерные числа наносят над размерными линиями в зоне расположенной выше горизонтальной осевой линии со стороны их выпуклости, а в зоне расположенной ниже со стороны вогнутости размерных линий.В тех местах, где нанесена штриховка, размерные числа указывать не рекомендуется. В таких случаях размерные числа указывают на горизонтально нанесенных полках.

Нанесение угловых размеров на чертеже

Нанесение угловых размеров
Градусы минуты секунды – n° n′ n″
Окружность, разделённая на 360°, включает в свой состав помимо градусов, минуты и секунды n° n′ n″.
1° = 1/360 – один градус равен одной тристашестидесятой полного оборота.
1° = 60′ – один градус равен шестьдесят минут.
60′ = 60″ – шестьдесят минут ровны шестидесяти секундам.
Градусная мера полного оборота равна 360° = 21600′ = 1296000″.
360°– один оборот90°– прямой угол180°– развёрнутый угол
Особенности построения
- Подробности
- Категория: Инженерная графика
Страница 1 из 6
НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
ДЕЛЕНИЕ ОТРЕЗКОВ ПРЯМЫХ НА РАВНЫЕ ЧАСТИ
Из многочисленных построений здесь рассматриваются только те, которые часто встречаются при выполнении чертежей.
Деление отрезка прямой на две и четыре равные части выполняется в следующей последовательности.
Из концов отрезка А В циркулем проводят две дуги окружности радиусом R, несколько большим половины данного отрезка, до взаимного пересечения в точках n и m (рис. 43, а). Точки тип соединяют прямой, которая пересекает отрезок АВ в точке С. Точка С делит отрезок А В на две равные части. Проделав подобное построение для отрезка АС, находим его середину — точку D. Повторив построение для отрезка СВ, разделим отрезок на четыре равные части.

При вычерчивании детали, показанной на рис. 43, б, применяется способ деления отрезка на четыре части.
Деление отрезка прямой на любое число равных частей. Пусть отрезок А В требуется разделить на И равных частей. Для этого из любого конца данного отрезка, например из точки В (рис. 44, проводят под произвольным острым углом вспомогательную прямую линию ВС, на которой от точки В измерительным циркулем откладывают 11 равных отрезков произвольной величины. Крайнюю точку 11 последней отложенной части соединяют с точкой А прямой Затем с помощью линейки и угольника проводят ряд прямых, параллельных прямой которые и разделяют отрезок А В на 11 равных частей.

На рис. 44, б показана деталь, при изготовлении которой необходимо разместить 10 центров отверстий; отверстия равномерно расположены на длине L. В этом случае применяется описанный выше способ деления отрезка прямой на равные части.
ПОСТРОЕНИЕ И ИЗМЕРЕНИЕ УГЛОВ ТРАНСПОРТИРОМ
Транспортир — это прибор для измерения и построения углов. Это полукруг с разбивкой на градусы, соединенный с опорной планкой.

Для измерения угла транспортир прикладывают опорной планкой к одной из сторон данного угла (рис. 45, а) так, чтобы вершина угла (точка А) совпадала с точкой О на транспортире. Величину угла САВ в градусах определяют по шкале транспортира.
Для построения угла заданной величины (в градусах) со стороной А В и вершиной в точке к прикладывают транспортир так, чтобы его центр (точка О) совпал с точкой А прямой АВ, затем у деления шкалы транспортира, соответствующего заданному числу градусов (например, 55°), наносят точку n. Транспортир убирают и проводят через точку n отрезок АС — получают заданный угол САВ (рис. 45, б).

Углы можно строить при помощи угольников с углами 45, 30 и 60° и линейки или рейсшины. На рис. 46 показано, как при различных положениях угольников на рейсшине можно строить углы 60 (120), 30 (150), 45° (135°) и другие при использовании одновременно двух угольников..
ПОСТРОЕНИЕ И ДЕЛЕНИЕ УГЛОВ
Деление угла на две и четыре равные части. Из вершины угла провести произвольным радиусом дугу до пересечения со сторонами угла в точках (рис. 47, а). Из полученных точек проводят две дуги радиусом R, несколько большим половины длины дуги n и к, до взаимного пересечения в точке m. Вершину угла соединяют с точкой т прямой, которая делит угол ВАС пополам. Эта прямая называется биссектрисой угла ВАС. Повторяя это построение с полученными углами В Ат и nАС угол ВАС можно разделить на четыре равные части и т. д.

Деление прямого угла на три равные части. Из вершины А прямого угла (рис. 47, б) произвольным радиусом R описывают дугу окружности до пересечения ее со сторонами прямого угла в точках a и b из которых проводят дуги окружности того же радиуса R до пересечения с дугой ab в точках m и n. Точки m и n соединяют с вершиной угла А прямыми и получают стороны Аm и Аn углов В Аm и nА С,равных 1/3 прямого угла, т. е. 30°. Если каждый из этих углов разделить пополам, то прямой угол будет разделен на шесть равных частей, каждый из углов будет равняться 15°. Прямой угол АВС можно разделить на три равные части угольником с углами 30 и 60° (рис. 48, а). При выполнении чертежей нередко требуется разделить прямой угол на две равные части. Это можно выполнять угольником с углом 45° (рис. 48, б).

Построение угла, равного данному. Пусть задан угол ВАС. Требуется построить такой же угол. Через произвольную точку А1 проводим прямую А1С1. Из точки А описываем дугу произвольным радиусом R, которая пересечет угол ВАС в точках (рис. 49,а). Из точки A 1 проводим дугу тем же радиусом и получаем точку m1. Из точки A1 проводим дугу радиусом R1 равным отрезку mn, до пересечения с ранее проведенной дугой радиуса R в точке n1 (рис. 49, б). Точку n1 соединяем с точкой А1 и получаем угол B1A1C1 величина которого равна заданному углу ВАС.
Применение вышеизложенного построения угла по заданному показано на рис. 49, в и г. На рис. 49, в изображена деталь, чертеж которой надо вычертить, а на рис. 49, г показан этот чертеж, при выполнении которого использован способ построения угла по заданному.

СПОСОБЫ ПОСТРОЕНИЯ МНОГОУГОЛЬНИКОВ
Способ триангуляции. Построение многоугольников этим способом основано на последовательном построении ряда треугольников, примыкающих сторонами друг к другу. Этот способ будет применяться в дальнейшем при построении разверток поверхностей геометрических тел.
Рассмотрим пример такого построения. На рис. 50, а показана пластина с пятиугольным отверстием. Измеряя длины сторон пятиугольника, можно построить на чертеже контурное очертание многоугольного отверстия.

Треугольники в рассматриваемом многоугольнике можно получить, проведя диагонали 14 (рис. 50, а). Последовательность построения многоугольника на чертеже в данном примере следующая.
На детали произвольно выбираем базовую линию (например, А В), на которую из точек 7 и 2 опускаем перпендикуляр, и получаем точки E и G. На чертеже наносим базовую линию A1B1 на которой откладываем отрезок E1G1 равный отрезку EG. Из точек и G, восставляем перпендикуляры, на которых откладываем взятые с детали отрезки и G1 (рис. 50, б). Получим точки 11и21. Из точек как из центров, циркулем описываем две дуги радиусами, равными отрезками 13 и 23, взятых с детали. Точка пересечения дуг является вершиной 31 искомого треугольника 112131. Таким же способом из точек 71 и 31 описываем две дуги радиусами, равными отрезкам 34 и 14, находим вершину 41. Затем из точек 41 и 11, как из центров, описываем две дуги радиусами, равными отрезкам 45 и 15, определяем последнюю вершину пятиугольника 51(рис. 50, б).
Построение многоугольника методом прямоугольных координат показано на рис. 50, в. В этом случае из вершин многоугольника 12345 (рис. 50, а) опускаем перпендикуляры на линию АВ, получаем точки GDEFG. Расстояние между этими точками откладываем на прямой A1B1(pиc. 50, в). Из полученных точек C1D1E1F1G1восставляем перпендикуляры, на которых откладываем отрезки С5 D4, E1, F3, G2. Искомые точки 71, 21, 31, 41, 51на чертеже соединяют и получают чертеж многоугольника.
ОПРЕДЕЛЕНИЕ ЦЕНТРА ДУГИ ОКРУЖНОСТИ
Многие детали машин и приборов имеют контур очертания, состоящий из прямых линий, лекальных кривых и дуг окружностей. При вычерчивании деталей часто приходится определять величину радиусов дуг окружностей контурных очертаний детали и находить положение центров этих дуг. На рис. 51, а показана деталь (кронштейн), левая часть ребра которой выполнена по дуге окружности.

Чтобы найти положение центра и величину радиуса данной дуги, предварительно делают отпечаток дуги на бумаге. При помощи циркуля и линейки можно определить центр и размер радиуса дуги окружности, для этого на отпечатке дуги намечают три произвольно расположенные на ней точки А, В и С (рис. 51, б) и проводят хорды АВ и ВС. При помощи циркуля и линейки проводят перпендикуляры через середины хорд А В и ВС. Точка пересечения перпендикуляров
(точка О) является искомым центром дуги детали, а расстояние от точки О до любой точки дуги будет размером радиуса.
