Как найти угол в четырехугольнике онлайн

Геометрический калькулятор представляет собой собрание формул и он-лайн калькуляторов, которые не только считают все возможные параметры геометрической фигуры или тела, но и выводят новые отношения и взаимосвязи между теми измерениями, которые напрямую между собой не связаны.

В данном разделе можно рассчитать стороны, углы, площади, периметры и объемы всех геометрических фигур, а также вычислить определенные величины, свойственные конкретному ряду фигур. Здесь вы найдете наиболее полный список возможных вариантов расчета в задачах по геометрии и сможете он-лайн получить моментальный результат из любого расклада данных. Все калькуляторы для удобства распределены по разделам с разными фигурами, внутри которых можно найти категории типов расчетных формул.

Угол А четырехугольника Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Угол C четырехугольника: 85 степень –> 1.4835298641949 Радиан (Проверьте преобразование здесь)

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

1.65806278939489 Радиан –>95.0000000000339 степень (Проверьте преобразование здесь)

У параллелограмма 4 угла, это частный случай четырехугольника, у которого противоположные стороны
попарно параллельны. Из этого свойства вытекает равенство противоположных сторон, равенство
противоположных углов и равенство суммы смежных углов двум прямым. Свойства параллелограмма широко
используются в быту и технике.

Острый угол параллелограмма через боковую сторону и высоту

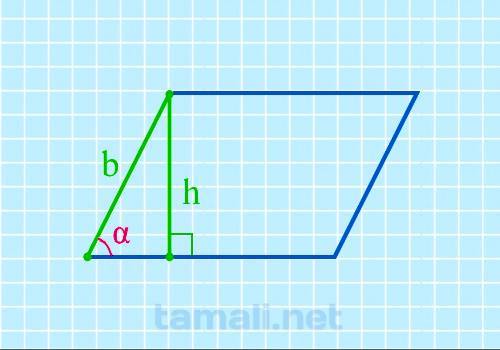
Если известна боковая сторона и высота, то можно найти острый угол параллелограмма по формуле:

sin α = h / b

где α – острый угол, h – высота, b – боковая сторона.

Пример. Пусть h = 4 см, b = 8 см. sin α = h / b = 8 / 4 = 2. α = 90°.

Острый угол параллелограмма через площадь и две стороны

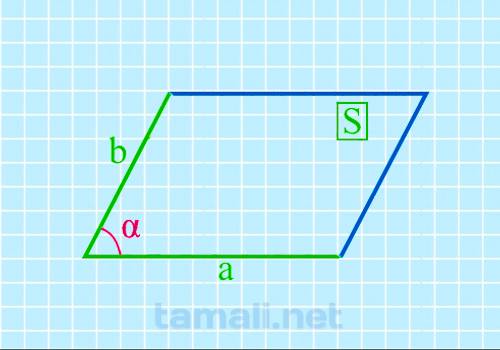
Если известна площадь и две стороны, то можно найти острый угол параллелограмма по формуле:

sin α= S / ab

где α – острый угол, S — площадь параллелограмма, a и b – его стороны.

Пример.  Пусть S=50 м², a=10 м, b=5 м. sin α= S / ab = 50 / (10 * 5) = 1. α = 90°.
Угол прямой, смежные стороны не равны, имеем дело с прямоугольником.

Острый угол параллелограмма через высоту, сторону и периметр

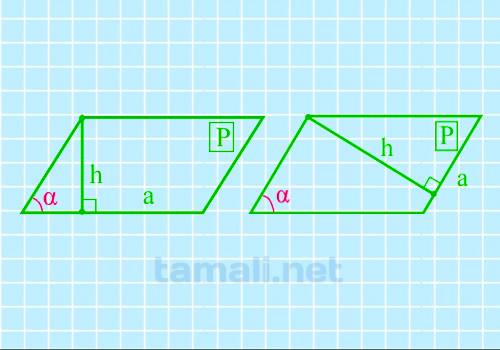
Если известна высота, сторона и периметр, то можно найти острый угол параллелограмма по формуле:

sin α = (2h + a) / P

где α – острый угол, h — высота, a — сторона, P — периметр.

Высота опускается на известную и подставляемую в формулу сторону a. Параллелограмм с заданным
периметром приходится строить, если, например, периметр определен длиной веревки, которую требуется
растянуть на местности в форме параллелограмма.

Пример. Пусть h=10 м, a=15 м, P=70 м. sin α=(2h + a) / P= (2 * 10 + 15) / 70 = 0,5. α = 30°.

Острый угол параллелограмма через две стороны и короткую диагональ

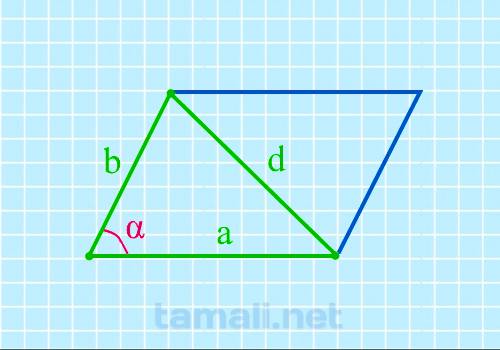
Если известны две стороны и короткая диагональ, то можно найти острый угол параллелограмма по
формуле:

cos α = (a² + b² — d²) / 2ab

где α – острый угол, a и b – стороны параллелограмма, d – его короткая диагональ.

Пример расчета: в данном частном случае 2 прилежащие стороны и короткая диагональ
равны, а именно: a = b = d = 26 мм. cos α=(a² + b² — d²) / 2ab = (26² + 26² — 26²) / (2 * 26 * 26) = 0,5. α=60°.

Из равенства прилежащих сторон следует, что это ромб, а результат расчета показывает, что острый угол
в ромбе равен 60°. Знаете, что это за ромб с подобными размерами? Это нагрудный академический знак
для лиц, окончивших советские высшие учебные заведения, установленный с 1961 года.

Тупой угол параллелограмма через две стороны и длинную диагональ

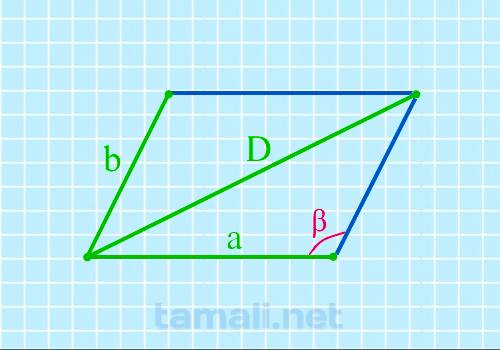
Если известны две стороны и длинная диагональ, то можно найти тупой угол параллелограмма по
формуле:

cos β = (a² + b² — D²) / 2ab

где α – тупой угол, a и b – стороны параллелограмма, D – его длинная диагональ.

Пример расчета: вновь ромб со сторонами a = b = 26 мм и длинной диагональю D=43 мм.
cos β = (a² + b² — D²) / 2ab = (26² + 26² — 43²) / (2 * 26 * 26) = -0,368. α = 112°.
Это опять-таки нагрудный академический знак из предыдущего примера, небольшое отличие полученного
результата от 120° (при остром угле 60° по предыдущему примеру) объясняется округлением исходных
данных до целого числа миллиметров.

Свойства параллелограмма

У любого выпуклого четырехугольника сумма всех внутренних углов равна 360°, исходя из общей формулы
суммы внутренних углов выпуклого многоугольника в градусах s = 180 (n — 2), где n – количество
сторон. Следовательно, если хотя-бы 1 угол параллелограмма равен прямому (90°), остальные 3 угла
также являются прямыми, и параллелограмм вырождается в свой частный вид – прямоугольник.

Если 2 смежные стороны параллелограмма равны, то равны все его 4 стороны, и параллелограмм
вырождается в ромб. И, наконец, если у параллелограмма равны 2 смежные стороны, а угол между ними
прямой, параллелограмм является одновременно и прямоугольником, и ромбом, и вырождается в квадрат.
Зачастую возникает необходимость определения неизвестных характеристик параллелограмма через
известные. Выше ряд примеров подобного рода.

Самый наглядный пример параллелограмма – пантограф электропоезда. При подключении опущенного
пантографа к контактной сети железной дороги изменяется конфигурация пантографа при сохранении длин
сторон, в результате изменяется вертикальная диагональ и происходит касание с подачей электрического
тока.
Форму параллелограмма имеет автомобильный реечный домкрат, велосипедная рама (с
диагональю для увеличения жесткости). Ведь параллелограмм — фигура нежесткая, в отличие от
треугольника. Из нежесткости параллелограмма следует, что знания одних длин сторон недостаточно для
вычисления площади фигуры. Так, пантограф электропоезда можно «сложить» до нулевой площади.
Стеклоочиститель лобового стекла автобуса также представляет собой параллелограмм, и именно
нежесткость фигуры позволяет стеклоочистителю «ометать» при движении стекло.