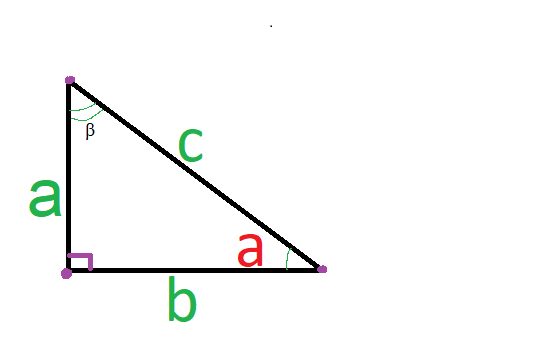Загрузить PDF
Загрузить PDF
В геометрии угол — это фигура, которая образована двумя лучами, которые выходят из одной точки (она называется вершиной угла). В большинстве случаев единицей измерения угла является градус (°) — помните, что полный угол или один оборот равен 360°. Найти значение угла многоугольника можно по его типу и значениям других углов, а если дан прямоугольный треугольник, угол можно вычислить по двум сторонам. Более того, угол можно измерить с помощью транспортира или вычислить с помощью графического калькулятора.
-
1
Сосчитайте число сторон многоугольника. Чтобы вычислить внутренние углы многоугольника, сначала нужно определить, сколько у многоугольника сторон. Обратите внимание, что число сторон многоугольника равно числу его углов.[1]
- Например, у треугольника 3 стороны и 3 внутренних углов, а у квадрата 4 стороны и 4 внутренних углов.
-
2
Вычислите сумму всех внутренних углов многоугольника. Для этого воспользуйтесь следующей формулой: (n – 2) x 180. В этой формуле n — это количество сторон многоугольника. Далее приведены суммы углов часто встречающихся многоугольников:[2]
- Сумма углов треугольника (многоугольника с 3-мя сторонами) равна 180°.
- Сумма углов четырехугольника (многоугольника с 4-мя сторонами) равна 360°.
- Сумма углов пятиугольника (многоугольника с 5-ю сторонами) равна 540°.
- Сумма углов шестиугольника (многоугольника с 6-ю сторонами) равна 720°.
- Сумма углов восьмиугольника (многоугольника с 8-ю сторонами) равна 1080°.
-
3
Разделите сумму всех углов правильного многоугольника на число углов. Правильный многоугольник это многоугольник с равными сторонами и равными углами. Например, каждый угол равностороннего треугольника вычисляется так: 180 ÷ 3 = 60°, а каждый угол квадрата находится так: 360 ÷ 4 = 90°.[3]
- Равносторонний треугольник и квадрат — это правильные многоугольники. А у здания Пентагона (Вашингтон, США) и дорожного знака «Стоп» форма правильного восьмиугольника.
-
4
Вычтите сумму всех известных углов из общей суммы углов неправильного многоугольника. Если стороны многоугольника не равны друг другу, и его углы также не равны друг другу, сначала сложите известные углы многоугольника. Теперь полученное значение вычтите из суммы всех углов многоугольника — так вы найдете неизвестный угол.[4]
- Например, если дано, что 4 угла пятиугольника равны 80°, 100°, 120° и 140°, сложите эти числа: 80 + 100 + 120 + 140 = 440. Теперь вычтите это значение из суммы всех углов пятиугольника; эта сумма равна 540°: 540 – 440 = 100°. Таким образом, неизвестный угол равен 100°.
Совет: неизвестный угол некоторых многоугольников можно вычислить, если знать свойства фигуры. К примеру, в равнобедренном треугольнике две стороны равны и два угла равны; в параллелограмме (это четырехугольник) противоположные стороны равны и противоположные углы равны.
Реклама
-
1
Помните, что в любом прямоугольном треугольнике один угол всегда равен 90°. Это так, даже если прямой угол никак не отмечен или его значение не указано. Таким образом, один угол прямоугольного треугольника всегда известен, а другие углы можно вычислить с помощью тригонометрии.[5]
-
2
Измерьте длину двух сторон треугольника. Самая длинная сторона прямоугольного треугольника называется гипотенузой. Прилежащая сторона это сторона, которая находится возле неизвестного угла. Противолежащая сторона — это сторона, которая находится напротив неизвестного угла. Измерьте две стороны, чтобы вычислить неизвестные углы треугольника.[6]
Совет: воспользуйтесь графическим калькулятором, чтобы решить уравнения, или найдите онлайн-таблицу со значениями синусов, косинусов и тангенсов.
-
3
Вычислите синус угла, если вам известны противолежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: sin(x) = противолежащая сторона ÷ гипотенуза. Например, противолежащая сторона равна 5 см, а гипотенуза равна 10 см. Разделите 5/10 = 0,5. Таким образом, sin(x) = 0,5, то есть x = sin-1 (0,5).[7]
- Если у вас есть графический калькулятор, введите 0,5 и нажмите клавишу sin-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 30°.
-
4
Вычислите косинус угла, если вам известны прилежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: cos(x) = прилежащая сторона ÷ гипотенуза. Например, прилежащая сторона равна 1,67 см, а гипотенуза равна 2 см. Разделите 1,67/2 = 0,83. Таким образом, cos(x) = 0,83, то есть x = cos-1 (0,83).[8]
- Если у вас есть графический калькулятор, введите 0,83 и нажмите клавишу cos-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 33,6°.
-
5
Вычислите тангенс угла, если вам известны противолежащая и прилежащая стороны. Для этого подставьте значения в уравнение: tg(x) = противолежащая сторона ÷ прилежащая сторона. Например, противолежащая сторона равна 75 см, а прилежащая сторона равна 75 см. Разделите 75/100 = 0,75. Таким образом, tg(x) = 0,75, то есть x = tg-1 (0,75).[9]
- Если у вас есть графический калькулятор, введите 0,75 и нажмите клавишу tg-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 36,9°.
Реклама
Советы
- Названия углов соответствуют их значениям. Угол в 90° — это прямой угол. Угол в 180° — это развернутый угол. Угол, который лежит между 0° и 90° — это острый угол. Угол, который лежит между 90° и 180° — это тупой угол. Угол, который лежит между 180° и 360° — это невыпуклый угол.
- Если сумма двух углов равна 90°, они называются дополнительными. Запомните: два острых угла прямоугольного треугольника всегда являются дополнительными. Если же сумма двух углов равна 180°, они называются смежными.
Реклама
Об этой статье
Эту страницу просматривали 235 886 раз.
Была ли эта статья полезной?
Download Article
Download Article
In geometry, an angle is the space between 2 rays (or line segments) with the same endpoint (or vertex). The most common way to measure angles is in degrees, with a full circle measuring 360 degrees. You can calculate the measure of an angle in a polygon if you know the shape of the polygon and the measure of its other angles or, in the case of a right triangle, if you know the measures of two of its sides. Additionally, you can measure angles using a protractor or calculate an angle without a protractor using a graphing calculator. This is to allow you to calculate angles
-
1
Count the number of sides in the polygon. In order to calculate the interior angles of a polygon, you need to first determine how many sides the polygon has. Note that a polygon has the same number of sides as it has angles.[1]
- For instance, a triangle has 3 sides and 3 interior angles while a square has 4 sides and 4 interior angles.
-
2
Find the total measure of all of the interior angles in the polygon. The formula for finding the total measure of all interior angles in a polygon is: (n – 2) x 180. In this case, n is the number of sides the polygon has. Some common polygon total angle measures are as follows:[2]
- The angles in a triangle (a 3-sided polygon) total 180 degrees.
- The angles in a quadrilateral (a 4-sided polygon) total 360 degrees.
- The angles in a pentagon (a 5-sided polygon) total 540 degrees.
- The angles in a hexagon (a 6-sided polygon) total 720 degrees.
- The angles in an octagon (an 8-sided polygon) total 1080 degrees.
Advertisement
-
3
Divide the total measure of all of a regular polygon’s angles by the number of its angles. A regular polygon is a polygon whose sides are all the same length and whose angles all have the same measure. For instance, the measure of each angle in an equilateral triangle is 180 ÷ 3, or 60 degrees, and the measure of each angle in a square is 360 ÷ 4, or 90 degrees.[3]
- Equilateral triangles and squares are examples of regular polygons, while the Pentagon in Washington, D.C. is an example of a regular pentagon and a stop sign is an example of a regular octagon.
-
4
Subtract the sum of the known angles from the total measure of the angles for an irregular polygon. If your polygon doesn’t have sides of the same length and angles of the same measure, all you need to do is add up all of the known angles in the polygon. Then, subtract that number from the total measure of all of the angles to find the missing angle.[4]
- For example, if you know that 4 of the angles in a pentagon measure 80, 100, 120, and 140 degrees, add the numbers together to get a sum of 440. Then, subtract this sum from the total angle measure for a pentagon, which is 540 degrees: 540 – 440 = 100 degrees. So, the missing angle is 100 degrees.
Tip: Some polygons offer “cheats” to help you figure out the measure of the unknown angle. An isosceles triangle is a triangle with 2 sides of equal length and 2 angles of equal measure. A parallelogram is a quadrilateral with opposite sides of equal lengths and angles diagonally opposite each other of equal measure.
Advertisement
-
1
Remember that every right triangle has one angle equal to 90 degrees. By definition, a right triangle will always have one angle that’s 90 degrees, even if it’s not labeled as such. So, you will always know at least one angle and can use trigonometry to find out the other 2 angles.[5]
-
2
Measure the length of 2 of the triangle’s sides. The longest side of a triangle is called the “hypotenuse.” The “adjacent” side is adjacent (or next to) to the angle you’re trying to determine.[6]
The “opposite” side is opposite to the angle you’re trying to determine. Measure 2 of the sides so you can determine the measure of the remaining angles in the triangle.[7]
Tip: You can use a graphing calculator to solve your equations or find a table online that lists the values for various sine, cosine, and tangent functions.
-
3
Use the sine function if you know the length of the opposite side and the hypotenuse. Plug your values into the equation: sine (x) = opposite ÷ hypotenuse. Say that the length of the opposite side is 5 and the length of the hypotenuse is 10. Divide 5 by 10, which is equal to 0.5. Now you know that sine (x) = 0.5 which is the same as x = sine-1 (0.5).[8]
- If you have a graphing calculator, simply type 0.5 and press sine-1. If you don’t have a graphing calculator, use an online chart to find the value. Both will show that x = 30 degrees.
-
4
Use the cosine function if you know the length of the adjacent side and the hypotenuse. For this type of problem, use the equation: cosine (x) = adjacent ÷ hypotenuse. If the length of the adjacent side is 1.666 and the length of the hypotenuse is 2.0, divide 1.666 by 2, which is equal to 0.833. So, cosine (x) = 0.833 or x = cosine-1 (0.833).[9]
- Plug 0.833 into your graphing calculator and press cosine-1. Alternatively, look up the value in a cosine chart. The answer is 33.6 degrees.
-
5
Use the tangent function if you know the length of the opposite side and the adjacent side. The equation for tangent functions is tangent (x) = opposite ÷ adjacent. Say you know the length of the opposite side is 75 and the length of the adjacent side is 100. Divide 75 by 100, which is 0.75. This means that tangent (x) = 0.75, which is the same as x = tangent-1 (0.75).[10]
- Find the value in a tangent chart or press 0.75 on your graphing calculator, then tangent-1. This is equal to 36.9 degrees.
Advertisement
Calculator, Practice Problems, and Answers
Add New Question
-
Question
How do you find an angle?
Mario Banuelos is an Assistant Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels.
Assistant Professor of Mathematics
Expert Answer
-
Question
How do I create a 90 degree corner by swinging an arch?
Pick a convenient point on a line to be the vertex of your 90° angle. Choose two points on the line, one on each side of the vertex and equidistant from the vertex. Use a compass to draw two arcs of the same diameter, each centered on one of those latter points. Draw a line connecting the vertex point with the intersecting point(s) of the arcs. That line describes a 90° angle with the first line.
-
Question
How do I find the interior angles of a hexagon without base or height or anything?
The sum of the six interior angles of a regular polygon is (n-2)(180°), where n is the number of sides. Therefore, in a hexagon the sum of the angles is (4)(180°) = 720°. All the angles are equal, so divide 720° by 6 to get 120°, the size of each interior angle.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Angles are given names according to how many degrees they measure. As noted above, a right angle measures 90 degrees. An angle measuring more than 0 but less than 90 degrees is an acute angle. An angle measuring more than 90 but less than 180 degrees is an obtuse angle. An angle measuring 180 degrees is a straight angle, while an angle measuring more than 180 degrees is a reflex angle.
-
Two angles whose measures add up to 90 degrees are called complementary angles. (The two angles other than the right angle in a right triangle are complementary angles.) Two angles whose measures add up to 180 degrees are called supplementary angles.
Advertisement
References
About This Article
Article SummaryX
To calculate the angles inside a polygon, first count the number of interior angles. A polygon has the same number of interior angles as sides. For example, a triangle always has 3 angles, while a square or rectangle always has 4, and so on. Next, use the formula (n – 2) x 180 to find the total number of degrees of all the interior angles combined. In this formula, n is equal to the number of interior angles. So, a triangle would have (3 – 2) x 180 degrees, or 180 degrees total. On the other hand, a quadrilateral, such as a square or a rectangle, would have (4 – 2) x 180 degrees, or a total of 360 degrees. If the polygon is regular—that is, if all the sides are the same length—then all you have to do is divide the total number of degrees of all the interior angles by the number of sides in the polygon. For instance, to calculate the angles in a regular pentagon, divide 540 degrees by 5 to get 108. Each angle in the pentagon is 108 degrees. If the polygon has irregular sides, your job is a little trickier. If you know all the angles in the polygon but one, you can add the known angles up and subtract the sum from the total number of degrees of all the interior angles. This will give you the number of degrees in the missing angle. In other cases, you may need to look up a formula or function that’s specific to the type of polygon you’re working with. For instance, you can use a sine, cosine, or tan function to find the angles in a right triangle depending on which angle you’re calculating and which side lengths you know. To find out how to calculate angle measure in a right triangle, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 688,033 times.
Reader Success Stories
-
Cynthia Trent
Dec 29, 2022
“I was doing my homework and I didn’t understand something, so now it helped me.”
Did this article help you?
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Понятие угла
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Стороны угла – лучи, которые образуют угол.
Вершина угла – точка, из которой выходят лучи.
Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.
Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠ A O B или ∠ B O A , но ни в коем случае не ∠ O A B , ∠ O B A , ∠ A B O , ∠ B A O .
Величину угла измеряют в градусах. ∠ A O B = 24 ° .
Виды углов:
Биссектриса угла
Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.
Или
Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.
O D – биссектриса угла ∠ A O B . Она делит этот угол на два равных угла.
∠ A O D = ∠ B O D = ∠ A O B 2
Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон O A и O B угла ∠ A O B .
Углы, образованные при пересечении двух прямых
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.
Свойство: сумма смежных углов равна 180 ° .
Пример:
Пары углов
( 1 ) и ( 3 )
( 2 ) и ( 4 )
называются вертикальными.
По свойству вертикальных углов:
∠ C O D = ∠ A O B
∠ B O D = ∠ A O C
Пары углов
( 1 ) и ( 2 )
( 2 ) и ( 3 )
( 3 ) и ( 4 )
( 4 ) и ( 1 )
называются смежными.
По свойству смежных углов:
∠ C O D + ∠ D O B = 180 ° ∠ D O B + ∠ B O A = 180 ° ∠ B O A + ∠ A O C = 180 ° ∠ A O C + ∠ C O D = 180 °
Углы, образованные при пересечении двух прямых секущей
Прямая, пересекающая две заданные прямые, называется секущей этих прямых.
Существует пять видов углов, которые образуются при пересечении двух прямых секущей.
Пары углов:
( 1 ) и ( 5 )
( 2 ) и ( 6 )
( 3 ) и ( 7 )
( 4 ) и ( 8 )
называются соответственными.
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).
Пары углов:
( 3 ) и ( 5 )
( 4 ) и ( 6 )
называются внутренними односторонними.
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).
Пары углов:
( 1 ) и ( 7 )
( 2 ) и ( 8 )
называются внешними односторонними.
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).
Пары углов:
( 3 ) и ( 6 )
( 4 ) и ( 5 )
называются внутренними накрест лежащими.
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).
Пары углов:
( 1 ) и ( 8 )
( 2 ) и ( 7 )
называются внешними накрест лежащими.
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).
Если прямые, которые пересекает секущая, параллельны, то углы имеют следующие свойства:
- Соответственные углы равны.
- Внутренние накрест лежащие углы равны.
- Внешние накрест лежащие углы равны.
- Сумма внутренних односторонних углов равна 180 ° .
- Сумма внешних односторонних углов равна 180 ° .
Сумма углов многоугольника
Сумма углов произвольного n -угольника вычисляется по формуле:
S n = 180 ° ⋅ ( n − 2 )
где n – это количество углов в n -угольнике.
Пользуясь этой формулой, можно вычислить сумму углов для произвольного n -угольника.
Сумма углов треугольника: S 3 = 180 ° ⋅ ( 3 − 2 ) = 180 °
Сумма углов четырехугольника: S 4 = 180 ° ⋅ ( 4 − 2 ) = 360 °
Сумма углов пятиугольника: S 5 = 180 ° ⋅ ( 5 − 2 ) = 540 °
Так можно продолжать до бесконечности.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.
На рисунках изображены примеры правильных многоугольников:
Чтобы найти величину угла правильного n -угольника, необходимо сумму углов этого многоугольника разделить на количество углов.
α n = 180 ° ⋅ ( n − 2 ) n
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с углами
Скачать домашнее задание к уроку 2.
При рассмотрении основных составляющих измерения углов, следует изучить исходные геометрические сведения:
- Угол.
- Развернутый угол, неразвернутый угол.
- Градус, секунда и минута.
- Градусная мера.
- Острый, прямой или тупой.
Геометрическая фигура, которая представляет собой точку — называется вершиной. А исходящие из этой вершины два луча, являются ее сторонами.
Измерение углов производится с помощью градусной меры угла. Углы измеряются таким же способом, как и отрезки, при помощи специальных единиц измерения – градусов.
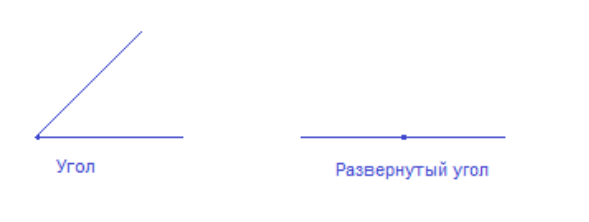
Определение
Градус — геометрическая единица измерения, представляющая собой угол, который сравнивается с другими углами.
Равенство градуса таково: [frac{1}{180}] от развернутого угла. Исходя из этого, можно понять, что развернутый угол равен 180 градусам, а неразвернутый угол любой меньше 180 градусов.
Чему равна градусная мера угла
Определение
Градусная мера угла – это положительное число, которое показывает сколько раз градус и его части укладываются в данном углу.
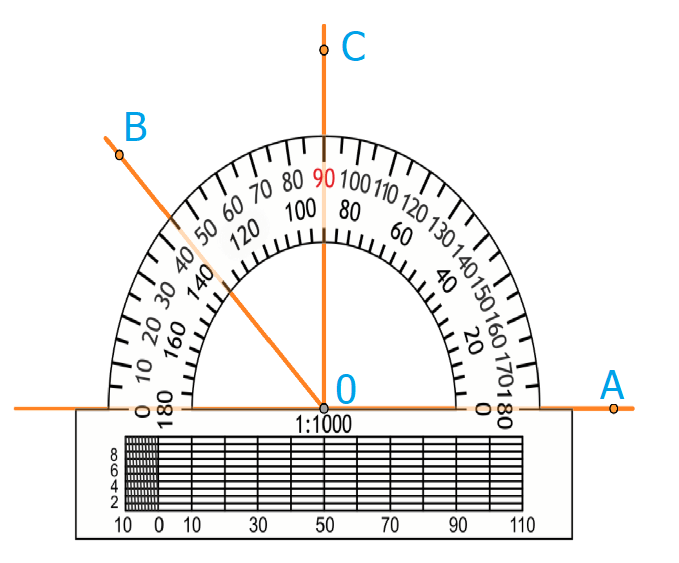
А для их измерения используется инструмент – транспортир.
Транспортир используется следующим образом:
- Совместить вершину угла с центром транспортира, при этом одна сторона угла должна пройти по линейке.
- Штрих на шкале транспортира, через который пройдет 2-я сторона, покажет его градусную меру.
Как найти градусную меру угла
На рисунке угол АОВ = 135 градусов. Угол АОС = 90 градусов, угол ВОС = 45 градусов. Градусная мера углов равна сумме углов, на которые он разбит лучом, который проходит между его сторонами.
Отсюда следует, что величина угла AOB на рисунке 1 равна сумме величин углов AOC и [B O C: angle A O B=angle A O C+angle B O C].
Какие бывают названия углов можно понять, разобравшись со следующими обозначениями.
- Минута – 1/60 часть градуса. Обозначается знаком ‘
- Секунда – 1/60 часть минуты. Обозначают знаком»
Например: угол в 65 градусов, 35 минут,18 секунд записывается так: 75°45’28». Если градусная мера у нескольких углов одинаковая, эти углы считаются равными. Сравнить их можно по размерам – больше или меньше. Развернутый и неразвернутый углы.
Нет времени решать самому?
Наши эксперты помогут!
Градусная мера вписанного угла
Градусная мера вписанного угла равняется половине градусной меры дуги, опирающуюся на нее, и половине градусной меры угла, находящегося по центру, которая опирается на эту же дугу.
Вписанный угол равняется половине градусной меры дуги, на которую он опирается.
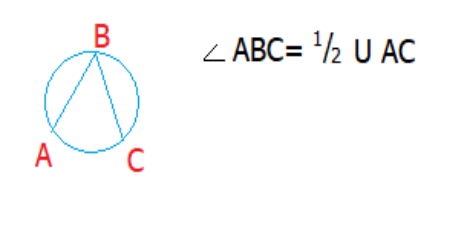
АВ-хорда
ВС-хорда
В-точка окружности.
Углы также различаются несколькими типами:
- Прямыми
- Острыми
- Тупыми
Равность прямого угла составляет — 90 градусов. Острый равен цифре меньше 90 градусов. А тупой же – больше 90 и меньше 180 градусов. В чем же заключается важность умения измерения углов и градусной меры в жизни? Оно пригодится в исследованиях, таких как: астрономия. Например, чтобы вычислить положение различных тел в космосе. Чтобы попрактиковаться, необходимо прочертить несколько неразвернутых углов, отличающихся друг от друга. Также важно потренироваться чертить развернутые. А еще, можно при помощи транспортира поупражняться, задавая случайные цифры, в правильности воспроизведения углов.
Существует еще такое понятие, как, биссектриса.
Определение
Биссектриса— луч, который исходит из вершины этого угла и делит его пополам.
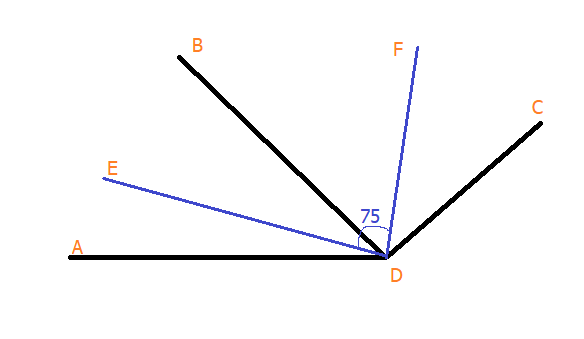
Пример 1. Задача с биссектрисой и развернутым углом.
Рис.3 Лучи DЕ и DF – это биссектрисы, которые соответствуют углам ADB и BDC.
Теперь нужно найти угол ADC, при этом угол EDF = 75°
Ответ. Угол EDF имеет по половинке от углов ADB и BDC, это значит, что EDF – это половина самого угла ADC. Теперь получили вычисление угол ADC = 75 умножить на 2 = 150°.
Ответ: 150°
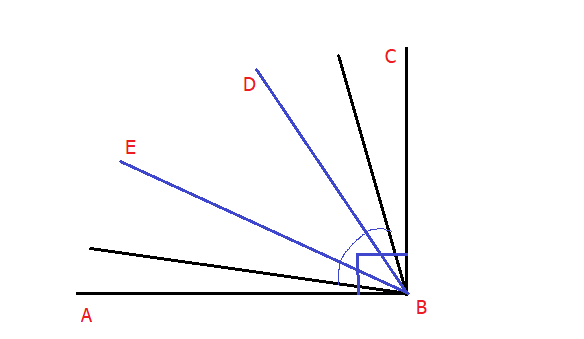
Пример 2. Задача с биссектрисой и прямым углом.
Рисунок 4. По рисунку 4 видно, что угол АВС прямой, а углы ABE EBD DBC равны. Нужно найти угол, который образовали биссектрисы — ABE и DBC.
Решение будет таким: угол АВС прямой, и исходя из этого, можно понять что он равен 90°. Угол ЕВD=90/3=30°. Согласно правилу, углы ABE EBD DBC равны и поэтому каждый из них будет = 30°. Далее видно, что биссектриса любого из трех углов делит любой из этих углов на 2 угла, которые будут равны 15°. Обе половины углов ABE и DBC относятся к углу, который необходимо найти, то можно смело утверждать, что угол, который мы вычисляем, равен 30+15+15=60°.
Решение: 60°
Градусная мера углов треугольника
У любой геометрической фигуры, кроме округлой, имеются углы. При рассмотрении углов треугольника можно увидеть следующее: Сумма углов треугольника всегда равняется 180°. Если рассматривать прямоугольный треугольник, то можно увидеть, что один из углов равен 90°. А сумма двух других углов тоже равняется 90°.
Поэтому, если известно сколько градусов составляет один из острых углов треугольника, второй угол можно найти по формуле:
[angle a=90^{circ}-angle beta]
У прямоугольного треугольника один из углов прямой, соответственно, два других – острые.
Разъяснение острого угла таково: острым углом называется угол, значение которого составляет менее 90 градусов.
Исходя из вышесказанного, можно отметить, что прямоугольный треугольник — это геометрическая фигура, которая образовалась из трех отрезков. Эти отрезки соединяются между собой тремя точками. Углы у нее все внутренние, а один из них — прямой и равняется 90°. Пример — рисунок 5.
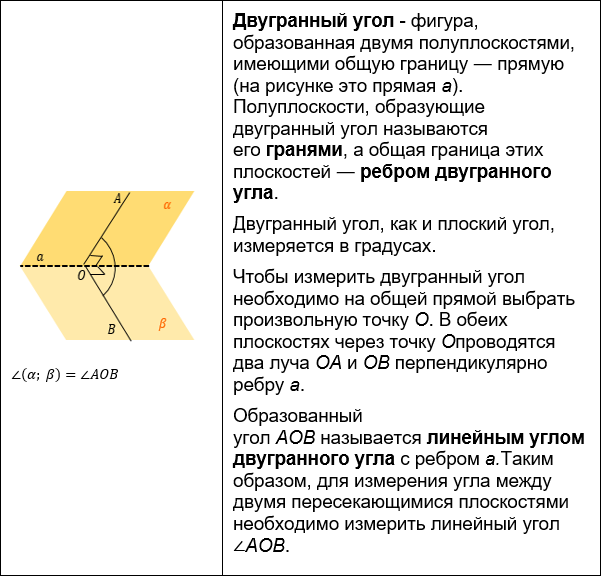
Углы
Классическим заданием с развернутым ответом на стереометрию является задача на нахождение угла. В стереометрии найти угол могут предложить между следующими комбинациями фигур:
Рассмотрим каждую комбинацию, чтобы понять, как искать разные виды углов и какие методы можно применять.
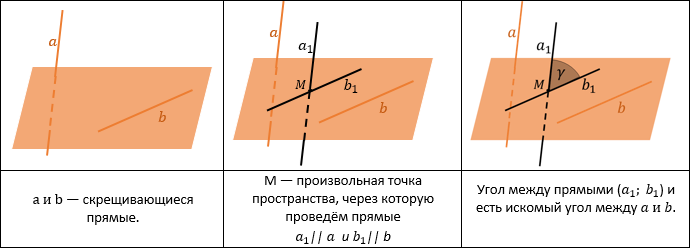
УГОЛ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Угол между скрещивающимися прямыми ― это угол между параллельными им прямыми, лежащими в одной плоскости.
Это значит, что никогда не пересекающиеся прямые в пространстве мы делаем «пересекающимися»: для этого нужно построить пересекающиеся прямые, параллельные данным. Угол между ними будет искомым.
Часто достаточно только к одной из скрещивающихся прямых построить параллельную прямую.
Например, если бы мы отметили точку M на прямой b и через точку M провели прямую $ a_1 parallel a $.
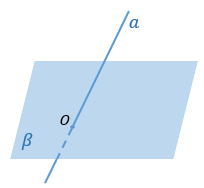
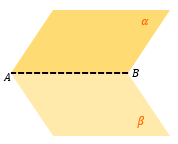
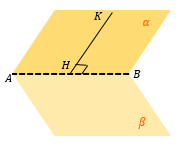
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Угол между прямой и плоскостью – угол между прямой и ее проекцией на эту плоскость.
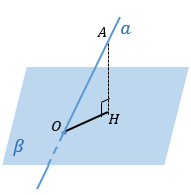
Для того, чтобы найти угол между прямой и плоскостью, нужно сначала получить проекцию этой прямой на плоскость, а потом найти угол.
|
|
|
|
|
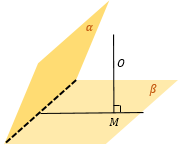
Прямая, пересекающая плоскость β в точке O |
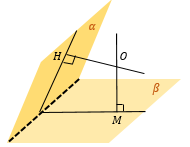
Из произвольной точки А на прямой опустим перпендикуляр AH на плоскость β. Тогда OH – проекция прямой на плоскость β. |
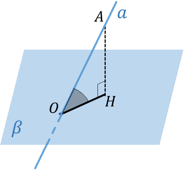
Угол между прямой и наклонной, то есть ∠ AOH и есть искомый угол между . |
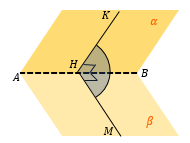
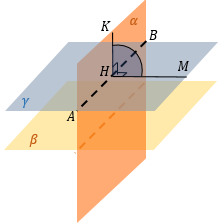
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Для начала вспомним пару определений:
Метод перпендикуляров к линии пересечения.Нахождения угла между плоскостями – одна из самых сложных задач на углы, поэтому тут мы можем воспользоваться несколькими методами.
Угол между плоскостями вычисляется как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения. Это основной способ нахождения угла между плоскостями.
|
|
|
|
|
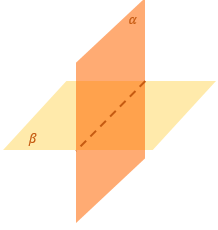
Находим линию пересечения плоскостей α и β – AB. |
Из «удобной» точки К в плоскости α (это может быть вершина многогранника, середина ребра и т.д.) опускаем перпендикуляр KH на AB. |
В точку H опустим перпендикуляр из точки M в плоскости β. ∠ KHM – искомый угол между плоскостями α и β |
- Метод перпендикуляров к плоскостям.
Угол между плоскостями вычисляется как угол между перпендикулярами к данным плоскостям. Этот способ удобен, если перпендикуляр к плоскости построить удобнее, чем построить перпендикуляры к линии пересечения плоскостей (или перпендикуляр к плоскости уже есть по условию задачи).
|
|
|
|
|
Из произвольной точки O пространства опустим перпендикуляр OM на плоскость β. |
Из точки O опустим так же перпендикуляр OH на плоскость α. |
Любой из двух смежных углов между OM и OH может считать искомым, но так как угол между плоскостями измеряется от 0 до 90°, то берем острый. ∠ MOK – искомый угол между плоскостями α и β |
- Метод параллельных плоскостей.
Угол между плоскостями вычисляется как угол между плоскостями, параллельными данным плоскостям. Этот способ применим, когда угол между данными плоскостями по каким-то причинам искать неудобно, а удобнее найти угол между плоскостями, параллельными данным.
|
|
|
|
|
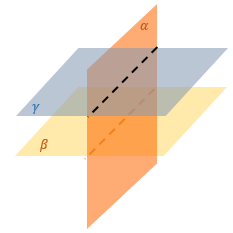
Угол между плоскостями α и β затруднительно искать (например, нет «удобных точек» или тяжело построить взаимные перпендикуляры). |
Построим плоскость γ, параллельную β (или в стереометрической фигуре она уже есть) |
По методу перпендикуляров к линии пересечения найдем угол между плоскостями α и γ. ∠ MНK – искомый угол между плоскостями α и β |
