Математика
5 класс
Урок № 27
Углы. Измерение углов
Перечень рассматриваемых вопросов:
– понятие «угол», «величина угла»;
– виды углов;
– построение углов;
– измерение величины угла.
Тезаурус
Угол – геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки, которая называется вершиной угла.
Градус – единица измерения углов, составляющая часть развёрнутого угла.
Градусная мера угла – число, которое показывает, сколько единиц измерения (градусов) содержится между сторонами этого угла.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О.Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия», – сказал в своё время французский архитектор Ле Корбюзье, и трудно с ним не согласиться. Геометрические фигуры постоянно встречаются в творениях природы и человека.
Сегодня мы рассмотрим ещё одну геометрическую фигуру – угол, разберём его виды и опишем процесс построения и измерения углов.
Для начала определим, что называют углом.
Углом называют геометрическую фигуру, образованную двумя лучами, выходящими из одной точки.
Построим угол. Для этого отметим на плоскости точку О и проведём два луча – ОК и ОМ. Получим геометрическую фигуру, образованную точкой О и двумя лучами, исходящими из этой точки. Такую геометрическую фигуру и называют углом.
Лучи ОК и ОМ называют сторонами угла, точку О – общее начало этих лучей – называют вершиной угла.
Обозначается угол чаще всего тремя буквами. Например, ∠КОМ или ∠МОК. В середине пишется буква, которой обозначена вершина угла. Также угол можно обозначать и одной буквой, поставленной у вершины угла. Например, ∠О.
Начертим два луча, исходящих из точки О и принадлежащих одной прямой.
Лучи ОС и OК вместе с точкой О дополняют друг друга до прямой – это дополнительные лучи. Угол называют развёрнутым, если его стороны являются дополнительными лучами.
Угол СОК – развёрнутый.
Построим развёрнутый угол АОВ и полуокружность с центром в точке О. Полуокружность разделим на 180 равных частей. Если построим углы с вершиной в точке О, стороны которых проходят через точки деления полуокружности, то таких углов будет 180. Один такой угол будет составлять часть развёрнутого угла.
рисунок
Меру угла, составляющего часть развёрнутого угла, принимают за единицу измерения углов и называют градусом. Обозначают: 1º.
Градусной мерой угла называют число, которое показывает, сколько единиц измерения (градусов) содержится между сторонами этого угла.
Например, градусная мера угла КOВ равна 25 градусам, так как в нём единица измерения градус содержится двадцать пять раз. Записывают: ∠КОВ = 25º.
рисунок
Стоит отметить, что для более точного измерения угла используют доли градуса:
– минуты, которые обозначают одной чёрточкой сверху над цифрой справа,
– секунды, которые обозначаются двумя чёрточками над цифрой справа.
В одном градусе содержится 60 минут, а в одной минуте – 60 секунд.
Например, если угол А равен 10 градусам 5 минутам, записывают: ∠А = 10º5′.
Градусная мера развёрнутого угла равна 180º.
Для измерения углов в градусах пользуются прибором, который называется транспортиром. На транспортире имеется шкала – полуокружность, разделённая на 180 равных частей. На линейке транспортира чёрточкой отмечен центр полуокружности транспортира.
Чтобы найти градусную меру угла, например, угла АВС, нужно совместить центр транспортира с вершиной угла, в данном случае точкой В; расположить линейку транспортира так, чтобы одна из сторон угла прошла через начало отсчёта шкалы транспортира – ноль градусов (в данном случае сторона АВ), и найти на шкале транспортира деление, через которое проходит другая сторона угла – в данном случае сторона ВС.
Это деление шкалы покажет градусную меру угла. В нашем случае – это 120º.
Транспортир применяется также для построения угла, мера которого известна. Построим, например, угол KNM, равный 60º. Для этого:
– проведём луч NM;
– совместим центр транспортира с точкой N;
– расположим линейку транспортира так, чтобы луч NM прошёл через начало отсчёта шкалы транспортира;
– найдём на шкале транспортира деление, соответствующее шестидесяти градусам, и отметим напротив него точку К;
– проведём луч NK. Мы построили угол KNM, равный 60º.
Ответить на вопрос, равны ли углы, и, если не равны, то какой из них больше или меньше, можно, сравнивая их градусные меры. Углы с равными градусными мерами равны. Из двух углов больше тот, который имеет большую градусную меру; а меньше тот, который имеет меньшую градусную меру.
Углы можно сравнить также наложением. Если при этом они совпадают, то равны.
Помимо развёрнутого, углы можно разделить на следующие виды: прямой, острый и тупой.
Угол называют прямым, если его градусная мера равна 90º.
Острым – если его градусная мера меньше 90º.
Тупым – если его градусная мера больше 90º и меньше 180º.
Рассмотрим ещё два вида углов, которые встречаются в геометрических задачах: это вертикальные углы, то есть пара углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого. Например, угол один и два.
И смежные углы – это два угла, у которых одна сторона общая, а две другие являются дополнительными полупрямыми.
Например, угол САВ и угол САD.
Вместе смежные углы составляют развёрнутый угол. Следовательно, сумма величин смежных углов составляет 180º.
Итак, сегодня мы познакомились с разными видами углов и научились строить их с помощью транспортира.
Для определения величины углов используется прибор, который называют транспортир. Но существуют и более высокоточные приборы.
Так, гониометр использовался для определения положения судна в море или океане.
Теодолит – прибор для измерения горизонтальных и вертикальных углов при геодезических работах, в строительстве и т. п.
Секстант применялся для измерения высоты Солнца над горизонтом с целью определения географических координат той местности, в которой производится измерение, и на судах.
Посох Якова, служащий для измерения углов, – один из первых инструментов для астрономических наблюдений.
Геометрическая фигура угол образуется из двух лучей с общей начальной точкой.
Общая точка называется вершиной угла, а лучи — сторонами угла.
Для названия угла часто используют три большие латинские буквы, название вершины угла пишется посередине.
Иногда угол можно назвать только одной буквой, которая находится у вершины.
Можно также познакомиться с греческим алфавитом и использовать маленькие буквы для названий углов.
Чаще используют:
α,β,γ,δ,ϵ,η,ϕ,ω
— и другие.
Попытаемся представить точку как что-то бесконечно маленькое, а прямую — как что-то бесконечно простирающееся в обе стороны.
Рис. (1). Угол
∡ABC
,
∡B
или
∡α
.
Если угол образован дополнительными (или противоположными) лучами, то он называется развёрнутым.
Рис. (2). Развёрнутый угол
∡KLM
.
Так же как каждый отрезок имеет длину, которую можно измерить линейкой и выразить в единицах измерения, так и каждый угол имеет величину.
За единицу измерения углов принимают градус, что является
1180
частью развёрнутого угла.
Величина развёрнутого угла — (180°).
Углы измеряют транспортиром.
Рис. (3). Транспортир.
Особый угол, половина развёрнутого угла — прямой угол.
Прямой угол обозначают маленьким квадратиком внутри угла.
Величина прямого угла равна (90°).

Рис. (4). Прямой угол.
Углы, величина которых меньше (90°), называются острыми.
Углы, величина которых больше (90°), называются тупыми.
Источники:
Рис. 1. Угол, © ЯКласс.
Рис. 2. Развёрнутый угол, © ЯКласс.
Рис. 3. Транспортир. © ЯКласс.
Рис. 4. Прямой угол, © ЯКласс.
На этом уроке мы познакомимся с прибором для
измерения углов – транспортиром. Научимся с помощью транспортира измерять и
строить углы.
Коснёмся истории, чтобы узнать, как появился транспортир.
Понятие «градуса» и появление первых инструментов для
измерения углов связывают с развитием цивилизации в древнем Вавилоне. Хотя само
слово градус имеет латинское происхождение (градус
– от лат. gradus – “шаг, ступень”). Предполагают, что создание
транспортира было связано с созданием первого календаря.
Древние вавилонские математики и астрономы полный
оборот (окружность) разделили на столько частей, сколько дней в году. Они
думали, что в году 360 дней. Поэтому круг,
обозначающий год, они разделили на 360
равных частей. Такое изображение было очень удобным. На нём можно было отмечать
каждый прошедший день, и видеть, сколько дней осталось до конца года. Каждой
части дали название – градус.
Каждый градус разделили на 60 минут,
а минуту – на 60 секунд.
Градусная мера сохранилась и до наших дней.
Итак, для измерения углов применяют транспортир.
Транспортир
состоит из линейки (прямолинейной шкалы) и полуокружности
(угломерной шкалы). Центр этой полуокружности отмечен на транспортире
или штрихом, или отверстием. Штрихи шкалы транспортира делят полуокружность на 180 долей. В некоторых моделях – на 360 долей – это круглые транспортиры.
Если из центра этой полуокружности провести лучи
через каждый штрих, то получится 180 углов.
Каждый, из которых равен доле
развернутого угла.
Определение
Такие углы принято называть градусами.
Градусы обозначают вот таким знаком °.
Каждое деление шкалы транспортира равно 1°. Кроме делений по 1°
на шкале транспортира есть ещё деления по 5°
и по 10°.
А
теперь давайте разберёмся, как с помощью транспортира измерить угол. Запомните алгоритм
измерения углов:
1)
Совместить вершину угла с центром транспортира.
2)
Расположить транспортир так, чтобы одна из сторон угла проходила через
начало отсчёта на шкале транспортира; 0 –
начало отсчёта.
3)
Найдём штрих на шкале, через который пройдёт вторая сторона угла; (заметьте,
используем ту шкалу для определения градусной меры угла, где располагается
нулевой градус).
4)
Смотрим, через какой штрих проходит вторая сторона и какой градус
соответствует этому штриху.
На нашем слайде угол АОВ
равен 50°. Пишут так:
Развёрнутый угол равен 180°.
Так как мы с вами выяснили, что прямой угол равен половине развёрнутого угла,
то он равен
Прямой угол
равен 90°.
Так как равные углы полностью совмещаются при наложении,
то равные углы имеют равные градусные меры. Следовательно, больший
угол имеет большую градусную меру, меньший угол имеет меньшую
градусную меру.
Транспортир применяют и не только для измерения углов, а
также и для их построения.
Запомним алгоритм построения углов.
Алгоритм будем исследовать на конкретном примере:
построить угол МКN
равный 110°.
1.
Отметим
произвольную точку и обозначим её буквой К.
2.
Начертим
луч с началом в точке А и на нём отметим произвольную точку М. Получили луч КМ.
3.
Наложим
транспортир так, чтобы центр его совпал с точкой К, а луч КМ прошёл через
начало отсчёта на шкале.
4.
На
этой же шкале транспортира найдём штрих, который соответствует 110°. Отметим на
чертеже точку N
против штриха с отметкой 110°.
5.
Проведём
луч КN.
Построенный нами угол МКN и есть искомый.
6.
Не
забудем записать МКN = 110°.
Такой же угол можно построить и по другую сторону от луча КМ.
Повсюду есть углы
любые:
Прямые, острые, тупые,
Есть смежные, развёрнутые есть,
Их много, всех не перечесть.
Определение
Если угол меньше 90°,
то его называют острым углом.
Если угол больше 90°,
но меньше 180°, то его называют тупым
углом.
На экране изображены угол АОС
– острый и угол МКN – тупой. Градусная мера угла АОС
равна 30°,
т.е. меньше 90°, следовательно, он острый.
Градусная мера угла МКN
равна 120°, т.е. больше 90°, но меньше 180°,
следовательно, он тупой.
Итоги
Итак, сегодня на уроке мы познакомились с прибором для
измерения углов – транспортиром. Научились с помощью него измерять и строить
углы.
Как построить современный урок?
Современные требования, предъявляемые к
организации учебной деятельности и проведению
уроков, предполагают не только активную
деятельность учащихся, носящую
поисково-исследовательский характер, но и
непременное развитие самоконтроля, самоанализа
и самооценки. Учителю необходимо не только
донести знания и заинтересовать своим предметом,
но научить ребенка ставить цели, разрабатывать
планы достижения этих целей, анализировать свои
поступки и действия. То есть ребенок должен
научиться ставить перед собой учебную задачу
самостоятельно и решать ее.
Формированию такого умения и средств контроля
и оценки помогает особый тип урока –
урок-рефлексия по ФГОС.
В качестве примера привожу урок математики в 5
классе по теме “Виды углов. Измерение углов”.
УМК: Математика: 5 класс: учебник для
учащихся общеобразовательных организаций / А.Г.
Мерзляк, В.Б. Полонский, М.С. Якир. – 2-е изд.,
перераб. – М.: Вентана – Граф, 2016.
Тема урока. Виды углов. Измерение углов.
Тип урока. Урок рефлексии.
Вид урока. Комбинированный урок.
Цели:
- Содержательная: повторение понятий
“угол”, “виды углов”, закрепление навыка
измерения углов с помощью транспортира,
исследование техники построения угла в 30° с
помощью квадратного листа бумаги. - Деятельностная: развитие умения
контролировать процесс и результат учебной и
математической деятельности, развитие навыков
оценки своей деятельности
Основные понятия: градус, транспортир,
измерение углов, развернутый угол, острый,
прямой, тупой угол.
Оборудование и материалы: транспортиры,
видеопроектор, кроссворд, раздаточный материал
(макеты углов трех цветов: красный – 90°, зеленый –
45°, синий – 30° по количеству парт в классе,
квадратный лист бумаги, инструкция по выполнению
исследования), презентация.
Оформление доски.
| Я знаю:
Я умею: |
Классная работа
31.10.16 |
Я узнал:
Я научился: |
Ход урока
1. Организационный момент. (слайд 1)
– Здравствуйте, ребята, садитесь. Я рада видеть
всех вас на занятии. На нашем уроке присутствуют
гости, давайте порадуем их хорошими знаниями.
Презентация.
2. Мотивация урока. (слайд 2)
– Все вы, наверняка, любите решать кроссворды?…
Поэтому я хочу предложить вам решить небольшой
кроссворд.
– В выделенном столбце получится ключевое слово
урока.
1. Угол, стороны которого образуют прямую?
(развернутый)
2. Единица измерения угла? (градус)
3. Угол, градусная мера которого меньше 90°?
(острый)
4. Геометрическая фигура, образующая сторону
угла? (луч)
Рисунок 1
– Теперь прочтем слово, которое получилось в
первом вертикальном столбце? (угол)
– Какую фигуру называют углом? (фигуру,
образованную двумя лучами, имеющими общее
начало)
– Какие виды углов вы знаете? (развернутый,
прямой, острый, тупой)
(учитель предлагает одному, двум учащемся
записать на доске, что дети уже знают по теме
урока, продолжив выражения: Я ЗНАЮ)
3. Актуализация и фиксация затруднений в
индивидуальной деятельности.
1) Постановка целей.
– Итак, сформулируйте цели урока. (применение
полученных знаний для построения, измерения и
определения вида углов)
– На предыдущих уроках вы познакомились с
геометрической фигурой, которая называется
“Угол”, научились измерять и строить углы с
помощью – измерительного прибора (как он
называется – транспортир).
(учитель предлагает одному, двум учащемся
записать на доске, что дети уже знают по теме
урока, продолжив выражения: Я УМЕЮ)
– Сегодня на уроке мы продолжим работу по
измерению и построению углов. Вы покажите свои
знания, выполняя разнообразные задания. (слайд
3)
– Запишите тему урока. “Виды углов. Измерение
углов”.
2) Упражнение 1.
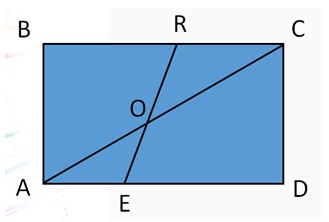
– Запишите острые, тупые и прямые углы,
изображенные на рисунке. (слайд 4)
Рисунок 2
– У доски будут работать 3 учащихся (первый
учащийся выписывает названия острых углов,
второй учащийся – прямых углов, третий учащийся –
тупых углов). Остальные ученики записывают в
тетради.
- Острые углы:
АОЕ,
ROC,
BAC,
ACD,
DCA,
CAD,
BRE,
RED,
BAO
- Прямые углы:
АВС,
ВСD,
CDA,
BAD
- Тупые углы:
AOR,
COE,
ERC,
REA
3) Упражнение 2. (самостоятельная работа
учащихся)
– У вас на парте три макета углов трех
цветов: красный – 90o, зеленый – 45o, синий
– 30o.
– Развернитесь друг к другу, поработайте в паре.
Я прошу вас составить из макетов углы: 135o,
75o, 15o.
Проверка (слайд 5)
4. Выполнение мини-проекта.
Проблемный вопрос
– С помощью макетов у вас получились углы с
заданными градусными мерами. Макеты я построила
с помощью транспортира. А как без транспортира
строить углы? Решим задачу, внимательно слушайте
ее условие.
Исследовательская работа (слайд 6)
– Основным показателем при расчете лестничного
марша является его уклон (крутизна). Идеальный
уклон 30 градусов, он создается с помощью Тетивы.
Тетива – это основа лестницы, несущая опорная
конструкция, в виде наклонных балок. Папа на даче
строит лестницу и хочет установить угол наклона
балок в 30 градусов. Для этого ему нужен макет угла
из фанеры. Он просит своего сына помочь ему
сделать бумажный шаблон угла, который он затем
приложит к фанере и выпилит нужный макет.
– При наличии транспортира отложить любой угол
можно! Но транспортира на даче нет, и данный угол
нужно получить здесь и сейчас!!!
– Можно ли построить угол без транспортира? (слайд
7)
– На каком этапе работы мы сейчас находимся? (1.
этап постановки проблемы)
– В чём проблема? Сформулируйте проблему.
(как без транспортира построить угол в 30°, как
изготовить шаблон угла в 30° без транспортира)
– Хватает имеющихся знаний для решения
проблемы? У вас есть только квадратный лист
бумаги! Предположим, что с помощью него можно
отложить угол в 30 градусов!
– Какой этап работы сейчас? (происходит
выдвижение гипотезы – предположение)
– Сформулируйте гипотезу. (гипотеза: можно
отложить угол, равный 30 градусам, без
транспортира с помощью квадратного листа бумаги)
– Как? Ваши предположения, как это можно сделать?
(дать время подумать)
– Что происходит сейчас, какой этап работы?
Поиск и предложение возможных вариантов решения
– Проведем эксперимент – это некоторое
количество опытов, которые показывают
одинаковый результат.
– К какому этапу мы подошли? (исследование)
– Приглашаю присоединиться ко мне.
(демонстрация учителя)
– Воспользуйтесь инструкцией, на вашем столе.
Эксперимент:
| Инструкция | ||
| № | Действия | Рисунок |
| 1 | Берем обыкновенный квадратный лист бумаги и сворачиваем его пополам. |
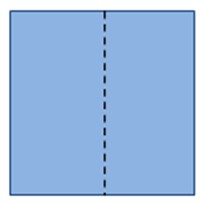
Рисунок |
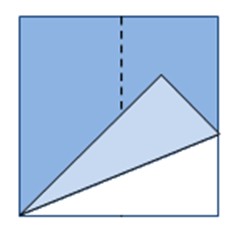
| 2 | Затем, делаем второй сгиб, посмотрите на рисунок, мы загибаем угол квадрата таким образом, чтобы вершина квадрата, она обозначена точкой совпала с линией первого сгиба. |
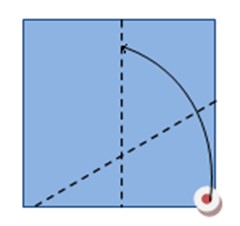
Рисунок
Рисунок 5 |
| 3 | Измерить получившийся угол. | 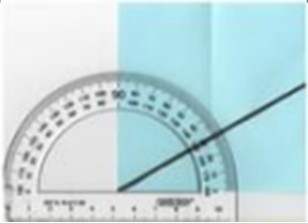
Рисунок |
– Берем обыкновенный квадратный лист бумаги и
сворачиваем его пополам. Затем, делаем второй
сгиб, посмотрите в инструкцию, мы загибаем угол
квадрата таким образом, чтобы вершина квадрата
совпала с линией первого сгиба.
– Как проверить градусную меру получившегося
угла? (взять транспортир и измерить)
– Сколько градусов получился угол?
– Подтвердился эксперимент?
– Какой этап работы сейчас? (анализ)
– Что нам нужно было получить? (шаблон угла)
– Ребята прогладьте хорошо сгиб несколько раз и
сделайте отрыв угла.
– Получился шаблон?
– Какой этап работы сейчас? (продукт)
– Какой вид угла мы получили? (острый)
– Что нового вы узнали? (ответы учащихся) – запись
на доске Я УЗНАЛ:
– Чему научились? (без транспортира строить угол
в 30°) – запись на доске Я НАУЧИЛСЯ:
5. Физкультминутка (учитель читает
утверждения, учащиеся выполняют определенные
движения)
“Верно или ложно?”
– Внимание! Если я читаю верное утверждение, то
вы хлопаете в ладошки; если неверное, то
поднимаете вверх руки.
- Единицы измерения углов: миллиметры,
сантиметры? - Единицы измерения углов: миллиграммы,
килограммы? - Единицы измерения углов: градусы, минуты?
- Развёрнутый угол имеет градусную меру 100°?
- Развёрнутый угол имеет градусную меру 90°?
- Развёрнутый угол равен 180°?
- Прямой угол равен 160°?
- Прямой угол равен 90?
- Острый угол больше прямого?
- Острый угол равен прямому?
- Острый угол меньше прямого?
- Тупой угол меньше прямого?
- Тупой угол всегда больше прямого и меньше
развёрнутого? - Угол, меньше 90° называется острым?
- Угол, больше 90°, но меньший 180°, называется тупым
углом?
6. Оценочный этап.
Самостоятельная работа.
– Мы отдохнули и готовы работать дальше.
Запишите на листочке свою фамилию, имя, класс.
| Вариант 1 | ||||
| Работу выполнил(а) | ||||
| Задание:
– назвать угол – измерить этот угол – записать результат измерения – записать вид угла |
||||
|
1) |
2) |
3) |
4) |
5) |
| Вариант 2 | ||||
| Работу выполнил(а) | ||||
| Задание:
– назвать угол – измерить этот угол – записать результат измерения – записать вид угла |
||||
| 1)
|
2)
|
3)
|
4)
|
5)
|
7. Домашнее задание.
Найдите углы, обозначьте их градусную меру.
Рисунок 7
8. Рефлексия (качественная оценка работы
класса и отдельных учащихся)
– Ребята заполните БИЛЕТИК на выход, продолжив
предложение “Сегодня на уроке я повторил….,
научился…, узнал…., закрепил…”, отметив то
высказывание, которое больше всего подходит к
работе на уроке.
| БИЛЕТИК на выход | БИЛЕТИК на выход |
| Сегодня на уроке я:
повторил________________________, научился________________________, узнал___________________________, закрепил________________________” |
Сегодня на уроке я:
повторил_______________________, научился_______________________, узнал___________________________, закрепил________________________” |
|
|
Список использованной литературы.
- А.Г.Мерзляк, В.Б. Полонский, М.С.Якир, Е.В. Буцко,
Математика 5 класс, Москва “Вентана-Граф”, 2016 - Интернет ресурс “Геометрия бумажного
листа”.
http://komarovana.ucoz.ru/load/tvorcheskie_raboty_moikh_detej/geometrija_bumazhnogo_lista/6-
1-0-195
Тема: Углы. Измерение
углов.
Угол
— это фигура, образованная двумя лучами, имеющими общее начало.
Обозначение:
∟АВС или ∟В
Точка В –
вершина угла.
Лучи АВ и ВС –
стороны угла
|
Вид |
Изображение |
Градусная |
|
Прямой |
|
900 |
|
Развернутый |
|
1800 |
|
Острый |
|
Меньше |
|
Тупой |
|
Больше |
Если
прямые пересекаются под прямым углом, то они называются перпендикулярными.

диктант
1. Геометрическая
фигура, образованная двумя лучами, исходящими из одной точки – это……………………………………………….
2.
Лучи,
исходящие из одной точки – это……………………………….
3.
Угол,
который меньше прямого угла – это……………………………
4.
Угол,
который больше прямого угла – это……………………………..
5.
Равные
углы – это углы, у которых………………………………….
6.
Угол,
равный 900 –это……………………………………………………
7.
Угол,
равный 1800 –это…………………………………………………
8.
Подпишите
названия углов
Алгоритм измерения углов:
1. Совместим вершину угла с центром транспортира.
2. Расположим транспортир так, чтобы сторона угла проходила через
начало отсчета на шкале транспортира; 0 – начало отсчета
3. Находим штрих на шкале, через который проходит вторая сторона
угла; используем ту шкалу для определения градусной меры угла, где
располагается нулевой градус.
4. Смотрим, через какой штрих проходит вторая сторона и какой
градус соответствует этому штриху.
Алгоритм построения углов:
Построить,например, угол ВАС=500
1.
Отметьте произвольную точку и обозначьте ее буквой А.
2. Начертите луч с началом в точке А и на нем отметьте произвольную
точку В. Получили луч АВ.
3. Наложите транспортир так, чтобы центр его совпал с точкой А, а
луч АВ прошел через начало отсчета на шкале.
4. На этой же шкале транспортира найдите штрих, который
соответствует 50°. Отметьте на чертеже точку С против штриха с отметкой 50°.
5. Проведи луч АС. Построенный угол ВАС есть искомый.
6. Запиши ВАС = 50°.
Смежные углы Вертикальные углы
Тема: Углы. Измерение
углов.
Угол
— это фигура, образованная двумя лучами, имеющими общее начало.
Обозначение:
∟АВС или ∟В
Точка В –
вершина угла.
Лучи АВ и ВС –
стороны угла
|
Вид |
Изображение |
Градусная |
|
Прямой |
|
900 |
|
Развернутый |
|
1800 |
|
Острый |
|
Меньше |
|
Тупой |
|
Больше |
Если
прямые пересекаются под прямым углом, то они называются перпендикулярными.

диктант
9. Геометрическая
фигура, образованная двумя лучами, исходящими из одной точки – это……………………………………………….
10.
Лучи,
исходящие из одной точки – это……………………………….
11.
Угол,
который меньше прямого угла – это……………………………
12.
Угол,
который больше прямого угла – это……………………………..
13.
Равные
углы – это углы, у которых………………………………….
14.
Угол,
равный 900 –это……………………………………………………
15.
Угол,
равный 1800 –это…………………………………………………
16.
Подпишите
названия углов
Алгоритм измерения углов:
1.
Совместим вершину угла с центром транспортира.
2. Расположим транспортир так, чтобы сторона угла проходила через начало
отсчета на шкале транспортира; 0 – начало отсчета
3. Находим штрих на шкале, через который проходит вторая сторона
угла; используем ту шкалу для определения градусной меры угла, где
располагается нулевой градус.
4. Смотрим, через какой штрих проходит вторая сторона и какой
градус соответствует этому штриху.
Алгоритм построения углов:
Построить,например, угол ВАС=500
- Отметьте произвольную точку и обозначьте ее
буквой А. - Начертите луч с началом в точке А и на нем
отметьте произвольную точку В. Получили луч АВ. - Наложите транспортир так, чтобы центр его
совпал с точкой А, а луч АВ прошел через начало отсчета на шкале. - На этой же шкале транспортира найдите штрих,
который соответствует 50°. Отметьте на чертеже точку С против штриха с
отметкой 50°. - Проведи луч АС. Построенный угол ВАС есть
искомый. - Запиши
ВАС =
50°.
Смежные
углы Вертикальные углы