| Главная » Файлы » Сканави_ Сборник задач по математике » Задачи по Геометрии с применением Тригонометрии |
12.126_Найти угол при вершине в осевом сечении конуса
| 28.11.2013, 18:32 | |
Найти угол в осевом сечении конуса если сфера с центром в вершине конуса, касающаяся его основания,делит объем конуса пополам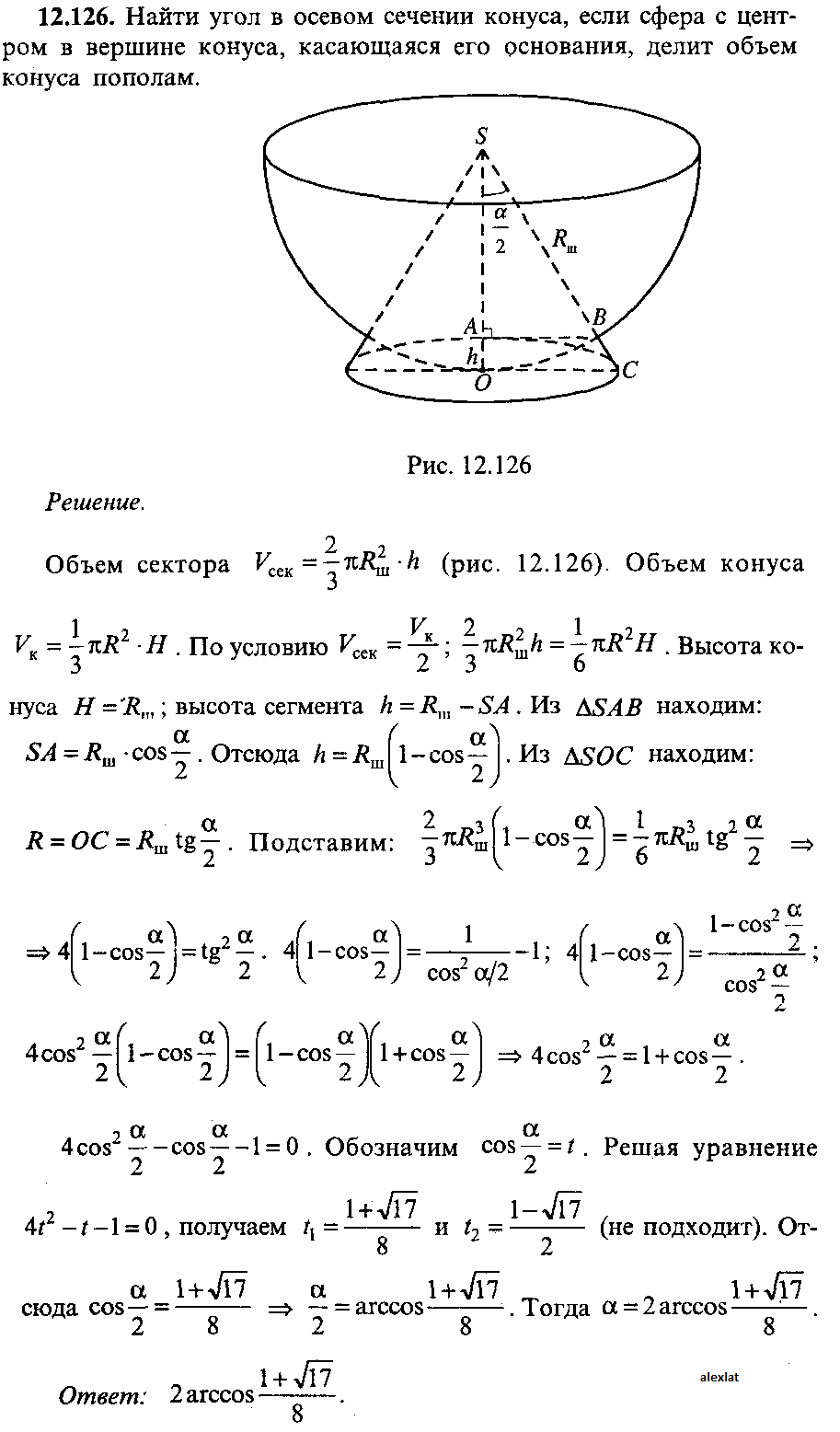
|
|
Категория: Задачи по Геометрии с применением Тригонометрии | Добавил: alexlat |
|
| Просмотров: 602 | Загрузок: 0
| Рейтинг: 0.0/0 |
| Всего комментариев: 0 | |
Добавлять комментарии могут только зарегистрированные пользователи.
[
Регистрация
|
Вход
]
Категории раздела
|
Алгебра [52] |
|
Тождество [503] |
|
Прогрессии [53] |
|
Координаты и Вектороы [35] |
|
Алгебраические уравнения [250] |
|
Логарифмы [348] |
|
Тригонометрические уравнения [499] |
|
Неравенства [305] |
|
Задачи по планиметрии [433] |
|
Задачи стереометрии [234] |
|
Задачи по Геометрии с применением Тригонометрии [450] |
|
Применение уравнений к решению задач [453] |
|
Математический Анализ [60] |
|
Комбинаторика,Бином Ньютона и Комплексные числа [80] |
|
Элементарная математика [112] |
Друзья сайта
Статистика
Copyright MyCorp © 2023Сайт управляется системой uCoz
�������
���� � ���ף���� ������� ����������� ������ ����� 120o .
������� ���� ��� ������� ������� ������� ������.
�������
����� α – ���� � ������ ������� ������, l – ����������
������, r – ������ ��������� ������. ���ף���� ������� �����������
������ ���� ������ ���������� ������� l (���.1). �� ������� ������ ���� �����
��������� ����� ������� ����� 120o , ������� ����� ���� �������
���������� ������ ����� ����� ���������� ������� l , �.�. .
� ������ �������, ����� ���� ������� ����� ����� ���������� ���������
������, �.�. 2π r (���.2). �� ��������� = 2π r �������, ���
sin =
=
.
�����
2 arcsin .
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ������ | |
| ����� | 8059 |
Ученик
(110),
на голосовании
10 лет назад
Голосование за лучший ответ
Boris Fedorchuk
Мудрец
(10795)
10 лет назад
Боковая развертка конуса — это часть круга радиусом R (длина образующей конуса) . При центральном угле 180° развертка равна половине круга. Длина полуокружности равна пи*R и равна длине окружности основания — пи*D (диаметр основания) . Осевое сечение конуса — треугольник: основание — диаметр основания D, стороны — образующие конуса R. Т. к. диаметр основания и образующая конуса равны, получается равносторонний треугольник. Все углы в равностороннем треугольнике равны 60°.
Ivan Kunin
Мудрец
(14242)
10 лет назад
зачем тебе, Кусочек, эта стереометрия?
пусть л, р — образующая и радиус основания соответственно
угол развертке равен 360*р/л=180
откуда л=2*р
полугла при вершине сечения имеют синус р/л=1/2
значит это 30 градусов, а весь искомый угол в2 раза больше. Умножиш?
