В прямоугольном треугольнике один из углов равен 90°, соответственно два других угла дают в сумме тоже 90°. Поэтому зная один из острых углов, можно определить и второй:
α=90°-β
Используя отношения синусов, косинусов, тангенсов и котангенсов можно найти угол в прямоугольном треугольнике, зная любые две стороны:
Зная два катета: 
Зная катет и гипотенузу:  или
или 
Как найти угол прямоугольного треугольника, зная его катеты? Как?
Ученик
(31),
на голосовании
12 лет назад
Голосование за лучший ответ
Бессердечная скотина
Профи
(939)
12 лет назад
Зная катеты, мы можем найти гипотенузу. А из соотношений гипотенузы и катетов мы можем найти синусы и косинусы нужных углов. А потом перевести через инженерный калькулятор. Можно, кажется, как-то проще, без гипотенузы обойтись, но я уже не помню.
Алексей Бараев
Гений
(69534)
12 лет назад
Один угол – точно прямой.
Любой треугольник можно “решить”, зная один угол и две стороны.
Третья сторона (гипотенуза) в прямоугольном треугольнике находится из теоремы Пифагора с^2 = a^2 + b^2
Осталось найти углы через соотношения:
Синус угла есть отношение отношение противолежащего катета к гипотенузе, косинус угла есть отношение прилежащего катета к гипотенузе.
Углы находим через арксинус/арккосинус.
Triangles are three-sided closed polygons formed by the intersection of three lines. It is encountered a lot in everyday life. It is one of the basic shapes of geometry. It has three sides, three angles, and three vertices. A Right Angled Triangle is one where one of the angles is always equal to 90°. Pythagoras Theorem is derived for Right-angled triangles, Which states that the square of the hypotenuse (the longest side) is equal to the sum of the squares of base and perpendicular.
Given the length of at least two sides of a Right-Angled triangle, we can find the value of any angle of the right-angled triangle. For this, we use various trigonometric functions like sine, cosine, tangent, cotangent, sec, and cosec. These help us to relate the angles of a right-angled triangle with its sides.
Properties
- There is a right-angle vertex among the three vertices
- The side opposite to the right-angled vertex is called the hypotenuse.
- The length of the sides follows the Pythagoras theorem, which states
hypotenuse2 = base2 + altitude2
- The hypotenuse is the longest side of a right-angled triangle.
- The angles other than the right angle are acute angles since the value is less than 90o
Trigonometric functions
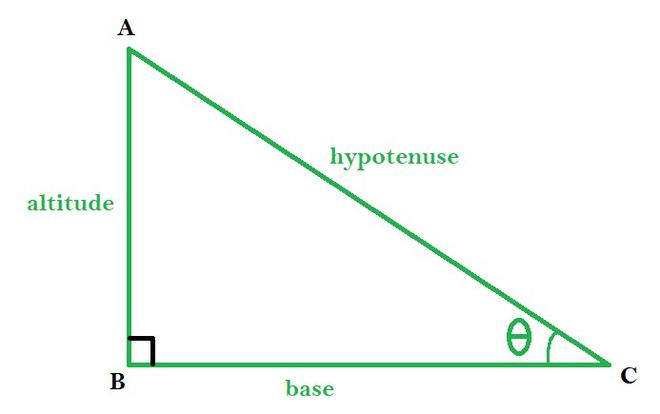
ABC is a right-angled triangle with ∠B as right-angle
- cosθ: This gives the ratio of the base by the hypotenuse of a right-angled triangle.
cosθ = base / hypotenuse
- sinθ: This gives the ratio of altitude by the hypotenuse of a right-angled triangle.
sinθ = altitude / hypotenuse
- tanθ: It is the ratio of altitude by the base of a right-angled triangle.
tanθ = altitude / base
- cotθ: It is the inverse of tanθ
- secθ: It is the inverse of cosθ
- cosecθ: It is the inverse of sinθ
To find the angles of a right-angled triangle, we can take the trigonometric inverse of the ratio of given sides of the triangle.
Example:
If sinθ = x, then we can write
θ = sin-1x.
This returns the angle for which the sine value of the angle is x.
Similarly, there exists cos-1θ, tan-1θ, cot-1θ, sec-1θ, and cosec-1θ
Sample Problems
Question 1. Given a right-angled triangle, with base equals 10cm and hypotenuse equals 20cm. Find the value of the base angle.
Solution:
Given, Base = 10cm
Hypotenuse = 20cm
Let, the value of the base angle be θ. We can write
cosθ = base / hypotenuse = 10/20 = 1/2
θ = cos-1(1/2) = 60o
Thus, the value of base angle is 60o.
Question 2. Find the value of angles of a right angles triangle, given that one of the acute angles is twice the other.
Solution:
Since we know the sum of all the three angles in a triangle is 180o.
Since one of the angles is 90o and one of the acute angles is twice the other, we can consider them as θ and 2θ.
So, we can write
90o + θ + 2θ = 180o
3θ = 180o – 90o
3θ = 90o
θ = 90o/3 = 30o
2θ = 2 × 30o = 60o
So, the angles are 30o, 60o, and 90o.
Question 3. Find the value of the angle of elevation of a ladder of length 5m, given that base of the ladder is at a distance of 3m from the wall.
Solution:
Since the ladder acts as a hypotenuse of a right angles triangle and base distance equals 3m, we can write
Hypotenuse = 5m
Base = 3m
Let the angle of elevation be θ. So, we can write
cosθ = Base / Hypotenuse = 3/5
θ = cos-1(3/5)
θ = 53o
Thus, the value of the angle of elevation is 53o.
Question 4. Find the value of hypotenuse, given the length of the altitude is 8m and the base angle equals 30o.
Solution:
Given, the base angle is equal to 30o and altitude equals 8m, we can apply the sine function to find the length of the hypotenuse.
sin30o = altitude / hypotenuse
hypotenuse = altitude / sin30o
Since the value of sin30o equals 1/2, we can write
hypotenuse = altitude / (1/2) = 2 × altitude
Thus, hypotenuse = 2 × 8 = 16m
Thus, the length of the hypotenuse is equal to 16m.
Last Updated :
18 Aug, 2022
Like Article
Save Article
Как найти углы прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти углы прямоугольного треугольника
Чтобы найти углы прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для угла α:
- угол β
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
- для угла β:
- угол α
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
Введите их в соответствующие поля и получите результат.
Найти угол α зная угол β и наоборот
Если ∠β = , то ∠α =
0
Если ∠α = , то ∠β =
0
Формула
α = 90° – β
β = 90° – α
Найти углы прямоугольного треугольника зная катеты
Катет a =
Катет b =
∠α =
0
∠β =
0
Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?
Формулы
или так:
α = arctg(a/b)
β = arctg(b/a)
Пример
Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:
∠α = arctg(5/2) = arctg(2.5) ≈ 68.2°
∠β = arctg(2/5) = arctg(0.4) ≈ 21.8°
Найти углы прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет =
∠α =
0
∠β =
0
Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?
Формулы
sin(α) = a/c
sin(β) = b/c
cos(α) = b/c
cos(β) = a/c
или так:
α = arcsin(a/c) = arccos(b/c)
β = arcsin(b/c) = arccos(a/c)
Пример
Для примера определим чему равны углы α и β в градусах если гипотенуза c = 6 см, а катет b = 3 см:
∠α = arccos(3/6) = arccos(0.5) = 60°
∠β = arcsin(3/6) = arcsin(0.5) = 30°
См. также
Как найти углы прямоугольного треугольника
Онлайн калькулятор

Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для угла α:
- угол β
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
- для угла β:
- угол α
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
Введите их в соответствующие поля и получите результат.
Найти угол α зная угол β и наоборот
Формула
Найти углы прямоугольного треугольника зная катеты
Катет a =
Катет b =
Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?
Формулы
Пример
Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:
Найти углы прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет =
Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?
Все формулы прямоугольного треугольника – примеры расчетов
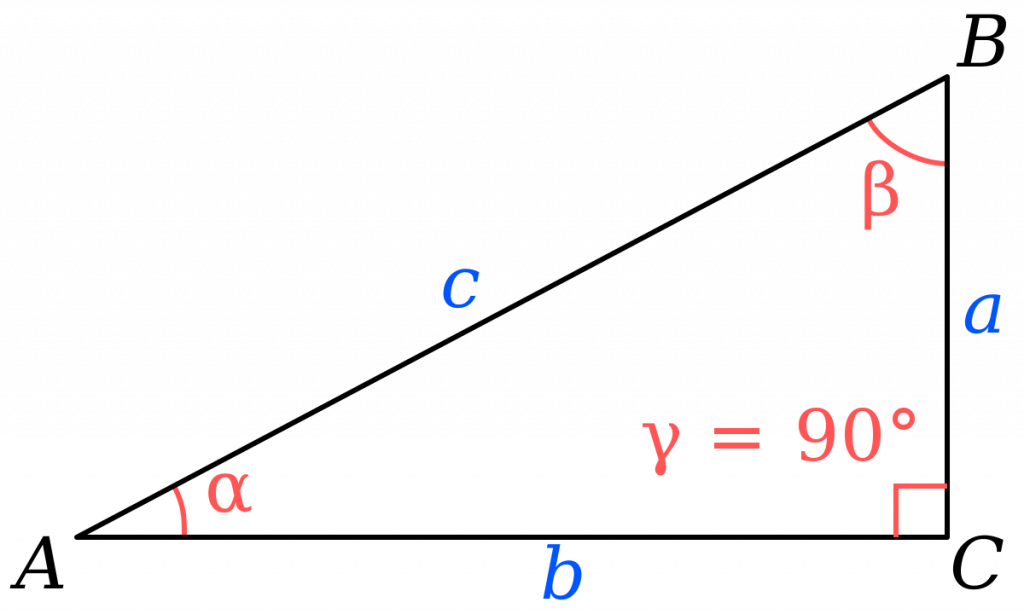
Формулы
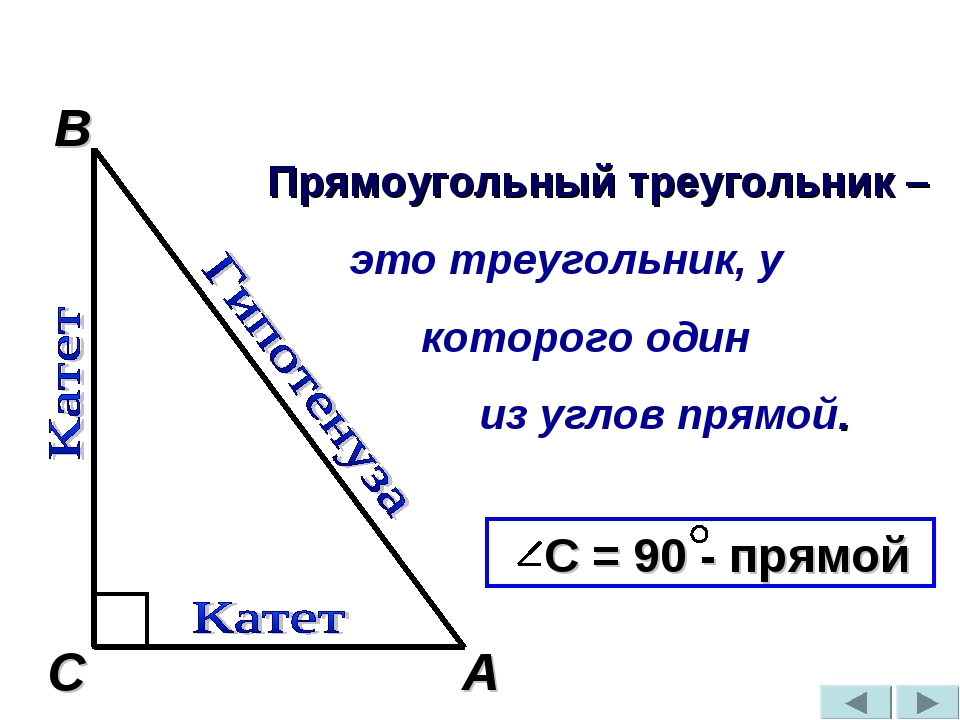
1. Сумма острых углов прямоугольного треугольника равна 90 0 :
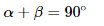
2. Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе:
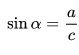
3. Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе:
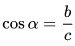
4. Тангенс острого угла равен отношению противолежащего катета к прилежащему катету:
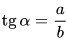
5. Котангенс острого угла равен отношению прилежащего катета к противолежащему катету:
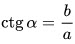
6. Секанс острого угла равен отношению гипотенузы к прилежащему катету:
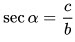
7. Косеканс острого угла равен отношению гипотенузы к противолежащему:
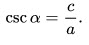
8. Катет, противолежащий углу, равен произведению гипотенузы на синус этого угла:
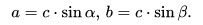
9. Катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла:
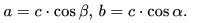
10. Катет, противолежащий углу, равен произведению второго катета на тангенс угла:
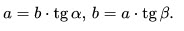
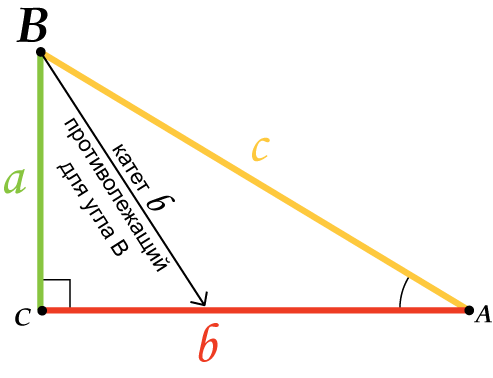
11. Катет, прилежащий углу, равен произведению второго катета на котангенс угла:
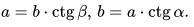
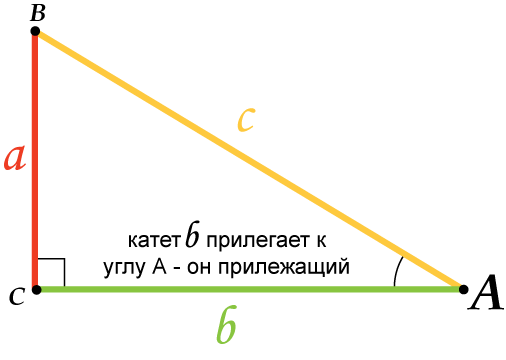
12. Гипотенуза равна отношению катета к синусу противолежащего угла, и/или частному отношению катета и косинуса прилежащего угла (угла между ними):
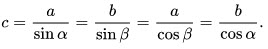
13. Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
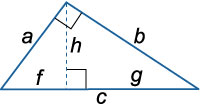


14. Медианы, проведенные к катетам прямоугольного треугольника:
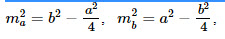
15. Медиана, проведенная к гипотенузе:
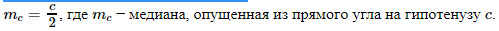
16. Радиус окружности, описанной около прямоугольного треугольника:
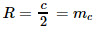
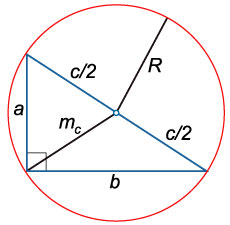
17. Радиус окружности, вписанной в прямоугольный треугольник:
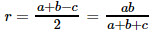
18. Площадь прямоугольного треугольника равна половине произведения катетов треугольника:
Углы прямоугольного треугольника
Калькулятор расчёта углов прямоугольного треугольника
Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).
Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.
Формула тангенса
- tg α – тангенс угла α
- a – противолежащий катет
- b – прилежащий катет
Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x . Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.
Углы треугольника
Сумма углов треугольника всегда равна 180 градусов:
Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.
Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:
Острый угол — угол, значение которого меньше 90°.
У прямоугольного треугольника один угол прямой, а два других угла – острые.
[spoiler title=”источники:”]
http://nauka.club/matematika/geometriya/formuly-pryamougolnogo-treugolnika.html
http://kalk.top/sz/corners-pr-triangle
[/spoiler]
