Главная » Геометрия » Биссектриса трапеции – свойства биссектрис углов трапеции
Биссектриса трапеции – свойства биссектрис углов трапеции
Опубликовано 21.04.2021
Биссектрисы трапеции обладают рядом интересных свойств, которые часто используются в задачах экзамена по математике. Давайте рассмотрим все замечательные свойства биссектрис трапеции здесь. Сначала дадим определение биссектрисы трапеции.
Биссектриса трапеции
Биссектриса трапеции – это биссектриса угла трапеции, то есть это луч, исходящий из вершины трапеции и делящий угол трапеции пополам. Рассмотрим теперь разные варианты пересечения биссектрис в трапеции и узнаем какими свойствами обладают биссектрисы в трапеции.

Свойства пересечения биссектрис в трапеции
1 Свойство – биссектрисы углов при боковой стороне пересекаются под прямым углом.
Давайте докажем это свойство. Рассмотрим трапецию . Проведем в этой трапеции биссектрисы углов
и
. Получим биссектрисы
и
. Докажем, что угол K – прямой.

Сумма углов при боковой стороне трапеции равна 1800. То есть ![]() .
.
Так как и
биссектрисы углов
и
соответственно, то они делят эти углы пополам. А это значит, что
![]() или
или ![]() .
.
Делим левую и правую части этого равенства на 2, получим: ![]() . Что и требовалось доказать.
. Что и требовалось доказать.
2 Свойство биссектрис трапеции – точка пересечения биссектрис углов трапеции при одной боковой стороне лежит на средней линии трапеции.
Доказательство. Нарисуем трапецию и биссектрисы
и
. Докажем, что точка
пересечения биссектрис трапеции лежит на средней линии MN трапеции.

Продолжим биссектрису до пересечения со стороной
трапеции
. Точку пересечения биссектрисы и основания трапеции обозначим
.
Рассмотрим треугольник . Этот треугольник равнобедренный. Так как
, поскольку
, поскольку
– биссектриса, а
как накрест лежащие углы при параллельных
и
и секущей
.
В равнобедренном треугольнике биссектриса
также является медианой, то есть делит основание
пополам, а значит, точка
лежит на средней линии трапеции MN согласно теореме Фалеса: если прямая отсекает равные отрезки на одной стороне угла, то она отсекает равные отрезки и на другой стороне угла. Таким образом если
, то и
и MN – средняя линия трапеции. Вот мы и доказали второе свойство биссектрис в трапеции.
Из доказательства второго свойства вытекает важное свойство биссектрисы трапеции:
Биссектриса тупого угла трапеции отсекает от нее равнобедренный треугольник.
Эти свойства биссектрис трапеции важно знать, поскольку они помогают в решении задач на трапецию в ОГЭ и в ЕГЭ.
( 3 оценки, среднее 5 из 5 )
 Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.
Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.
При этом трапеция обладает всеми свойствами четырехугольника. Поэтому запоминать надо свойства, которые характерны для трапеции.
Определения для трапеции:
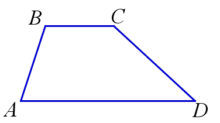 Параллельные стороны называются основаниями трапеции (BC и AD), непараллельные – боковыми сторонами (AB и CD).
Параллельные стороны называются основаниями трапеции (BC и AD), непараллельные – боковыми сторонами (AB и CD).
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
Средняя линия трапеции — отрезок, который соединяет середины боковых сторон данной трапеции (на рис. MN). Средняя линия трапеции параллельна её основаниям и равна их полусумме. Средняя линия параллельна основаниям. Её длина находится по формуле: MN=(AD+BC)/2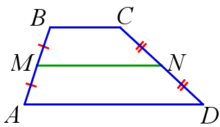 M – середина AB, N – середина CD,
M – середина AB, N – середина CD,
AD||BC, MN||AD, MN||BC,
Равнобедренная (равнобокая) трапеция – трапеция, у которой боковые стороны равны (AB=CD).
В равнобедренной трапеции:
— углы при основании равны,
— проекции боковых сторон на основание равны: AE=FD,
— диагонали равны.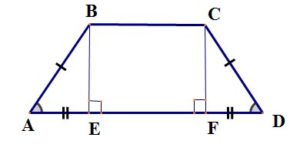
Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.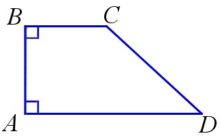
Свойства углов трапеции
- Свойства углов четырехугольника
- Сумма углов трапеции равна 360°
- Сумма внешних углов трапеции , взятых по одному при каждой вершине, равна 360°.
- Каждый угол трапеции всегда меньше суммы трёх остальных углов.
- Свойства углов трапеции
1. Сумма углов, прилежащих к боковой стороне, равна 180°: ∠A+∠B=180°, ∠C+∠D=180°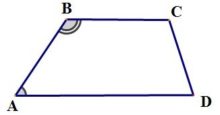
2. Каждая диагональ трапеции образует с её основаниями равные углы.
3. Биссектриса любого угла трапеции отсекает на ее основании отрезок, равный боковой стороне: AB=BE.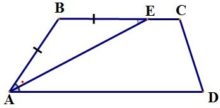
4. Биссектрисы смежных углов трапеции пересекаются под прямым углом.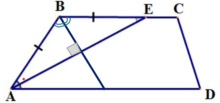
Свойства сторон трапеции
- Свойства сторон трапеции (как у четырехугольника)
- Каждая сторона четырехугольника меньше суммы всех его других сторон.
- Сумма диагоналей меньше его периметра.
- Диагонали трапеции (как у четырехугольника)
- Диагонали пересекаются в одной точке.
- Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
При пересечении диагоналей трапеции и продолжений её боковых сторон образуются подобные треугольники, прилежащие к основаниям. 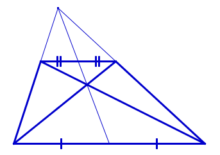
Трапеция и окружность
В трапецию можно вписать окружность, если сумма её оснований равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.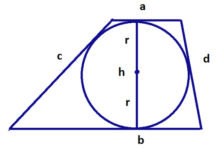 Радиус вписанной окружности:
Радиус вписанной окружности: ![]()
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной. Центр описанной около трапеции окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон.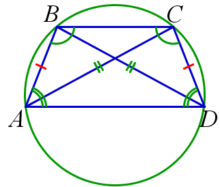 AB=CD ⇒ ∠ABC=∠DCB, ∠BAD=∠CDA;
AB=CD ⇒ ∠ABC=∠DCB, ∠BAD=∠CDA;
AB=CD ⇒ AC=BD;
AB=CD ⇒ ABCD вписанная
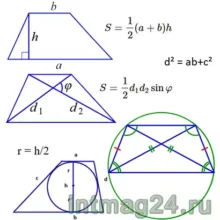
Основные формулы:
Периметр трапеции равен сумме длин всех его сторон:![]()
Площадь трапеции можно найти по двум формулам:
1. Половине произведения суммы её оснований на высоту трапеции.
2. Половине произведения её диагоналей на синус угла между ними.
Стороны и диагональ равнобокой трапеции: ![]()
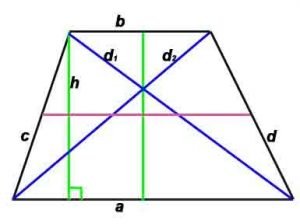 Расшифровка:
Расшифровка:
a,b — основания,
c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая),
d1, d2 –диагонали,
P-периметр,
S-площадь,
h -высота, проведенная к противоположной стороне
Свойства трапеции, описанной около окружности: формулы и теоремы

Трапеция – это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как “трапедзион”, что означало “столик”, “обеденный столик”.
Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.
Элементы, виды и признаки геометрической фигуры трапеция
Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны – боковыми сторонами. При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:
- Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
- При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
- Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
- При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
- При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
- Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°. Отрезок, соединяющий основания, будет равен 1/2 их разности.
Свойства трапеции, описанной около окружности
Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.
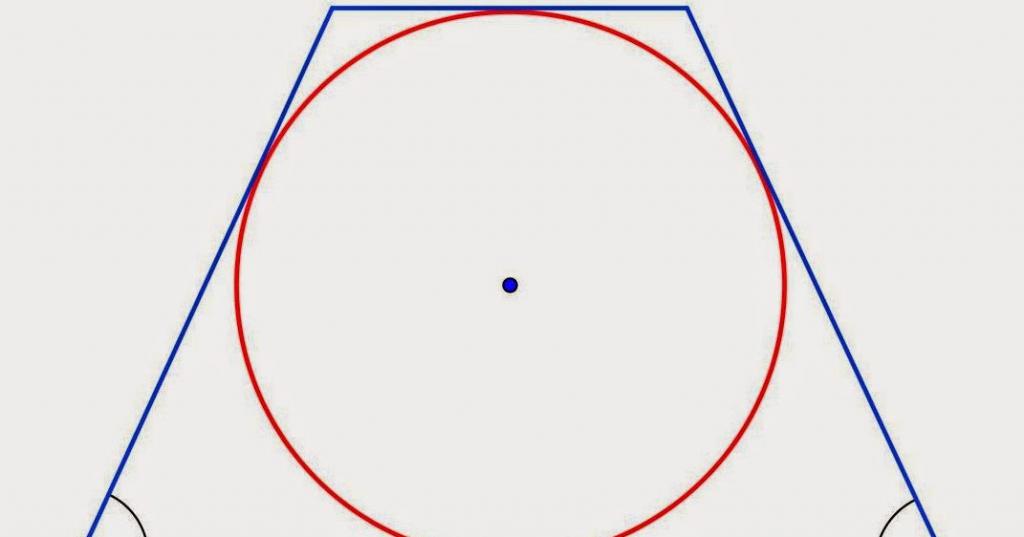
Итак, подробнее о свойствах трапеции, описанной около окружности:
- Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
- При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
- Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.
Еще немного о свойствах трапеции, заключенной в окружность
Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.
Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.
На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться – не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.
Как найти угол трапеции в описанной окружности
Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.
$$ 4.<1>^<○>$$. Диагонали трапеции разбивают её на четыре треугольника с общей вершиной (рис. 20). Площади треугольников, прилежащих к боковым сторонам, равны, а треугольники прилежащие к основаниям – подобны.
$$ 4.<2>^<○>$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).
$$ 4.<3>^<○>$$. В равнобокой трапеции углы при основании равны (рис. 22).
$$ 4.<4>^<○>$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).
$$ 4.<5>^<○>$$. В равнобокой трапеции диагонали равны (рис. 24).
$$ 4.<6>^<○>$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме
(рис. 25, основания равны `a` и `b`, `a>b`).
$$ 4.<7>^<○>$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).
$$ 4.<8>^<○>$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).
$$ 4.<9>^<○>$$.В равнобокой трапеции `d^2=c^2+ab`, где `d` – диагональ, `c` – боковая сторона, `a` и `b` основания.
Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.
$$ 4.<10>^<○>$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).
$$ 4.<11>^<○>$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
Докажем, например, утверждение $$ 4.<9>^<○>$$ .
Применяем теорему косинусов (см. рис. 29а и б):
`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,
`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).
Проводим `CK“||“BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:
`d_1^2+d_2^2=c_1^2+c_2^2+2ab`.
В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем
Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.
`AC=6`, `BM=MC`, `AN=ND`, `MN=5` (рис. 30а). Во всякой трапеции середины оснований и точка пересечения диагоналей лежат на од-ной прямой (свойство $$ 4.<2>^<○>$$). Треугольник `BOC` прямоугольный (по условию `AC_|_BD`), `OM` – его медиана, проведённая из вершины прямого угла, она равна половине гипотенузы: `OM=1/2BC`. Аналогично устанавливается `ON=1/2AD`, поэтому `MN=1/2(BC+AD)`. Через точку `D` проведём прямую, параллельную диагонали `AC`, пусть `K` – её точка пересечения с прямой `BC` (рис. 30б).
По построению `ACKD` – параллелограмм, `DK=AC`, `CK=AD` и `/_BDK=90^@`
(т. к. угол `BDK` – это угол между диагоналями трапеции).
Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то
Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.
Пусть `BC=a`, `AD=b`, и пусть `h` – высота трапеции (рис. 31). По свойству $$ 4.<1>^<○>$$ `S_(ABO)=S_(CDO)`, обозначим эту площадь `S_0` (действительно, `S_(ABD)=S_(ACD)`, т. к. у них общие основания и равные высоты, т. е. `S_(AOB)+S_(AOD)=S_(COD)+S_(AOD)`, откуда следует `S_(AOB)=S_(COD)`). Так как `S_(ABC)=S_0 + S_1=1/2ah` и `S_(ACD)=S_0+S_2=1/2bh`, то `(S_0+S_1)/(S_0 + S_2)=a/b`.
Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна
Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).
Найти радиус окружности, описанной около этой трапеции.
Трапеция равнобокая, по свойству $$ 4.<11>^<○>$$ около этой трапеции можно описать окружность. Пусть `BK_|_AD`, по свойству $$ 4.<6>^<○>$$
Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда
$$ 4.<12>^<○>$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.
$$ 4.<13>^<○>$$. Если `S_1` и `S_2` – площади треугольников, прилежащих к основаниям, то площади треугольников, прилежащих к боковым сторонам равны `sqrt(S_1S_2)`, а площадь всей трапеции равна `(sqrt(S_1) +sqrt(S_2))^2`.
$$ 4.<14>^<○>$$. Радиус окружности, описанной около трапеции, находится по формуле `R+a/(2sin alpha)`, где `a` – какая-то сторона (или диагональ трапеции), `alpha` – смотрящий на неё вписанный угол.
Как найти угол трапеции в окружности
Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) |
| a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
a — большее основание
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Узнать ещё
Знание — сила. Познавательная информация
Трапеция вписана в окружность
Рассмотрим несколько направлений решения задач, в которых трапеция вписана в окружность.
Когда трапецию можно вписать в окружность? Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию.
Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции лежит внутри трапеции.
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
Радиус описанной около трапеции окружности можно найти по следствию из теоремы синусов. Из треугольника ACD
Из треугольника ABC
Другой вариант найти радиус описанной окружности —
Синусы угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и ACF:
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. Например,
Кстати, использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали
В равнобедренном треугольнике AMD углы при основании равны. Внешний угол CMD равен сумме внутренних углов, не смежных с ним:
[spoiler title=”источники:”]
http://zftsh.online/articles/5259
http://b4.cooksy.ru/articles/kak-nayti-ugol-trapetsii-v-okruzhnosti
[/spoiler]
Рассмотрим некоторые задачи, в которых биссектрисы углов трапеции пересекаются.
I. Биссектрисы углов при боковой стороне трапеции пересекаются.
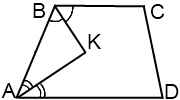 1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB).
1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB).
2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам).
3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º.
Вывод:
Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
Это утверждение, в частности, применяется при решении базовой задачи на трапецию, в которую вписана окружность.
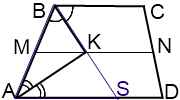 Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS (доказательство можно посмотреть здесь). Значит, его биссектриса AK является также медианой, то есть точка K — середина BS.
Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS (доказательство можно посмотреть здесь). Значит, его биссектриса AK является также медианой, то есть точка K — середина BS.
Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD.
Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS.
Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
Вывод:
Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.
II. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию.
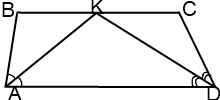 В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно.
В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно.
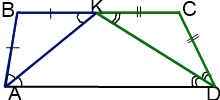 Таким образом, BC=BK+KC=AB+CD.
Таким образом, BC=BK+KC=AB+CD.
Вывод:
Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции.
В частности, у равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.
III.Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.
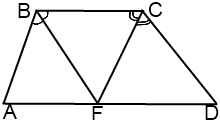 В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно.
В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно.
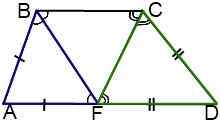 Отсюда AD=AF+FD=AB+CD.
Отсюда AD=AF+FD=AB+CD.
Вывод:
Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции.
У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.
