Угловое перемещение (угол поворота) – это угол, на который переместился радиус-вектор при перемещении тела из точки 1 в точку 2.
Δφ=φ-φ0
Угловое Δφ перемещения при движении тела по окружности.
Единица измерения угла поворота – 1 радиан [1 рад]. Радиан – это угол, опирающийся на дугу окружности, равную ее радиусу.
Длина дуги связана с углом поворота соотношением Δl = RΔφ.
Считая, что в начальный момент времени φ0=0, угловое перемещение (угол поворота) часто обозначают φ.
Зная угловую скорость и время, за которое был совершен поворот, можно определить угол поворота:
φ=ωt
Обозначения:
Δφ, φ– угловое перемещение (угол поворота)
Δl – длина дуги
R – радиус окружности
ω – угловая скорость
t – время, за которое был совершен поворот
Движение тела по криволинейной траектории
можно приближенно представить как
движение по дугам некоторых окружностей
см. рис.1.
Пусть произвольная точка М сначала
находилась в неподвижной плоскости Q(рис. 2). Затем переместилась в подвижной
плоскостиPна угол
поворота.
Угол поворота (угловое перемещение)
будим отсчитывать от неподвижной
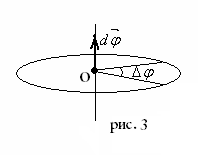
плоскости Qпо часовой
стрелке (см. рис. 3).
Направление углового
перемещения
совпадает с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения точки
по окружности, т.е. подчиняется правилу
правого винта.
Модуль углового
перемещениязапишется по аналогии
с координатой:
|
|
|
|
7. Модуль и направление угловой скорости
При малом угловом перемещении
равен (1)
(2)
Разделим обе части последнего выражения
на
:
или(3)
(4)
где выражение
– есть средняя угловая скорость,т.е
,(5)
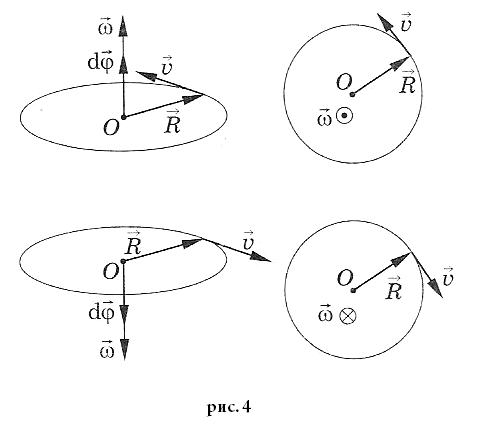
Вектор угловой
скорости
направлен вдоль
оси вращения по правилу
правого винта,
т.е. также как и вектор
Модуль угловой
скорости запишется по аналогии с
линейной скоростью:
|
|
|
|
8. Мгновенная угловая скорость.
Мгновенная угловая скорость равна
первой производной углового перемещения
по времени:
(6)
При равномерном вращении
,
тогда
(7)
9. Связь линейной и угловой скоростей.
Если продолжить (3), то получим:
или
(8)
(9)
Вектор линейной
скорости
совпадает по
направлению
с векторным произведением
.
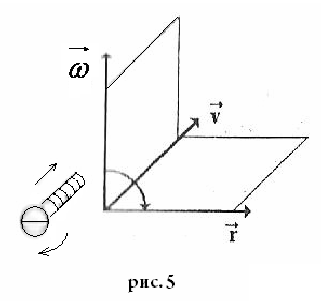
Векторное произведение всегда связано
справилом
правого винта:
вращая головку винта по направлению
вектора
,
стоящего на первом месте в (9), к вектору,
стоящему на втором месте, определяем
по поступательному движению винта
направление третьего вектора,
см. рис. 5.
Модуль векторного произведения:
(10)
10. Модуль и направление углового ускорения.
При
вращении за время
угловая скорость получит приращение
,
тогда (8) примет вид:
(11)
Разделим обе части
на
,
получим:
,
(12)
где отношение
– есть среднее угловое ускорение.
(13)
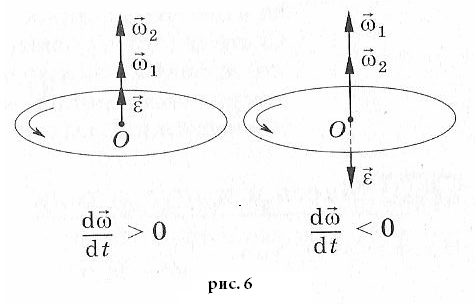
Вектор
углового ускорения
сонаправлен с вектором угловой скости
прии противоположен ему при
,
см. рис 6.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вращательное движение (Движение тела по окружности)
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
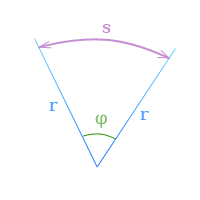
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
[
φ = frac{s}{r}
]
Соотношение между единицами угла
[ frac{φ_{рад}}{φ_{°}} = frac{π}{180°} ]
|
$ 1 enspace рад = 57.3° $ |
$ 1° = 17.45 enspace мрад $ |
$ 1´ = 291 enspace мкрад $ |
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
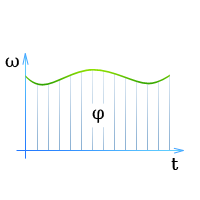
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t).
Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
[ [n] = [f] = frac{Обороты}{Секунда} = frac{(об)}{с} = frac{1}{c} = Герц ]
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
[
T = frac{1}{f} = frac{1}{n}
]
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
[
φ = 2 π N
]
Угловая скорость
Из формулы для одного оборота следует:
[
ω = 2 π f = frac{2π}{T}
]
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
Вращательное движение (движение тела по окружности) |
стр. 422 |
|---|
Векторное описание движения является полезным, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения. Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами – проекциями векторов.
Проекцией вектора на ось называют скалярную величину, равную произведению модуля проектируемого вектора на косинус угла между направлениями вектора и выбранной координатной оси.
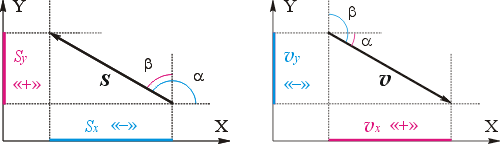
На левом чертеже показан вектор перемещения, модуль которого 50 км, а его направление образует тупой угол 150° с направлением оси X. Пользуясь определением, найдём проекцию перемещения на ось X:
sx = s · cos(α) = 50 км · cos( 150°) = –43 км
Поскольку угол между осями 90°, легко подсчитать, что направление перемещения образует с направлением оси Y острый угол 60°. Пользуясь определением, найдём проекцию перемещения на ось Y:
sy = s · cos(β) = 50 км · cos( 60°) = +25 км
Как видите, если направление вектора образует с направлением оси острый угол, проекция положительна; если направление вектора образует с направлением оси тупой угол, проекция отрицательна.
На правом чертеже показан вектор скорости, модуль которого 5 м/с, а направление образует угол 30° с направлением оси X. Найдём проекции:
υx = υ · cos(α) = 5 м/c · cos( 30°) = +4,3 м/с
υy = υ · cos(β) = 5 м/с · cos( 120°) = –2,5 м/c
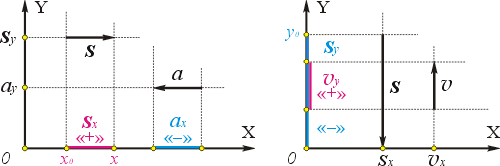
Гораздо проще находить проекции векторов на оси, если проецируемые векторы параллельны или перпендикулярны выбранным осям. Обратим внимание, что для случая параллельности возможны два варианта: вектор сонаправлен оси и вектор противонаправлен оси, а для случая перпендикулярности есть только один вариант.
Проекция вектора, перпендикулярного оси, всегда равна нулю (см. sy и ay на левом чертеже, а также sx и υx на правом чертеже). Действительно, для вектора, перпендикулярного оси, угол между ним и осью равен 90°, поэтому косинус равен нулю, значит, и проекция равна нулю.
Проекция вектора, сонаправленного с осью, положительна и равна его модулю, например, sx = +s (см. левый чертёж). Действительно, для вектора, сонаправленного с осью, угол между ним и осью равен нулю, и его косинус «+1», то есть проекция равна длине вектора: sx = x – xo = +s .
Проекция вектора, противонаправленного оси, отрицательна и равна его модулю, взятому со знаком «минус», например, sy = –s (см. правый чертёж). Действительно, для вектора, противонаправленного оси, угол между ним и осью равен 180°, и его косинус «–1», то есть проекция равна длине вектора, взятой с отрицательным знаком: sy = y – yo = –s .
На правых частях обоих чертежей показаны другие случаи, когда векторы параллельны одной из координатных осей и перпендикулярны другой. Предлагаем вам убедиться самостоятельно, что и в этих случаях тоже выполняются правила, сформулированные в предыдущих абзацах.