Как найти угол ветта

Вертикальные углы в геометрии

19 июня 2022

В двух словах: вертикальные углы возникают при пересечении двух прямых, не имеют общих сторон и всегда равны друг другу.

Содержание

1. Определение и примеры
2. Основная теорема
3. Комбинированные задачи

1. Определение и примеры

Определение. Два угла называются вертикальными, если стороны одного из них являются продолжениями сторон другого.

На рисунке ниже пересекаются две прямые: $AB$ и $MN$:

В результате образуются две пары вертикальных углов: $angle ASM$ и $angle BSN$, а также $angle ASN$ $angle BSM$.

Обратите внимание: вертикальные углы образуются только в точке пересечении прямых. Например, углы $ASM$ и $BSN$ на картинке ниже — не вертикальные, даже если они равны:

Если в одной точке пересекается более двух прямых, то вертикальных углов становится очень много:

Я не случайно пометил вертикальные углы одинаковыми дугами. Дело в том, что верна следующая теорема.

2. Основная теорема

Теорема 1. Вертикальные углы всегда равны друг другу.

Доказательство. Рассмотрим «синие» вертикальные $ASN$ и $BSM$. Каждый из них является смежным с углом $BSN$:

Но сумма смежных углов равна 180°, и если $angle BSN=color{red}{x}$, то

[begin{align}angle ASN&={180}^circ -color{red}{x} \ angle BSM&={180}^circ -color{red}{x} end{align}]

Итак, вертикальные углы равны одной и той же величине. Т.е. они равны между собой.

Эта теорема позволяет решать огромное количество задач — от самых простых до весьма нетривиальных. Начнём с простых.

Задача 1. Найдите углы 2, 3 и 4, если $angle 1={134}^circ $.

Решение.

Углы 1 и 3 вертикальные, поэтому они равны: $angle 3=angle 1={134}^circ $.

Углы 1 и 2 смежные, поэтому их сумма равна 180°:

[begin{align}angle 1+angle 2&={180}^circ \ angle 2&={180}^circ -angle 2= \ &={180}^circ -{134}^circ ={46}^circ end{align}]

Углы 2 и 4 вертикальные, поэтому они равны: $angle 4=angle 2={46}^circ $.

Из всех чертежей видно, что при пересечении двух прямых обычно возникает два острых угла и два тупых. Причём острый и тупой угол всегда будут смежными.

Если предположить, что острый угол равен $color{red}{x}$ градусов, то тупой равен $180-color{red}{x}$ градусов.

Задача 2. Найдите углы, образованные при пересечении двух прямых, если разность двух из них равна 68°.

Решение. Пусть острые углы содержат $color{red}{x}$ градусов. Тогда смежные с ними тупые углы содержат по ${180}^circ -color{red}{x}$ градусов.

По условию задачи, разность двух углов равна 68°. Очевидно, речь идёт о смежных углах. Потому что разность вертикальных углов была бы равна нулю. Вычитаем из тупого угла острый и получаем:

[begin{align}{180}^circ -color{red}{x} -color{red}{x} &={68}^circ\ 2color{red}{x}&={112}^circ\ color{red}{x}&={56}^circend{align}]

Итак, острые углы содержат по 56°. Тогда тупые углы содержат по 124°.

Единственный случай, когда все вертикальные углы равны — это когда прямые перпендикулярны, т.е. пересекаются под углом 90°.

Задача 3. На рисунке прямые $a$ и $b$ перпендикулярны, $angle color{red}{1}={36}^circ $. Найдите углы 2, 3 и 4.

Решение.

Углы 1 и 3 вертикальные, поэтому они равны: $angle color{red}{3}=angle color{red}{1}={36}^circ $.

Углы 1 и 2 смежные, поэтому их сумма равна 180°:

[begin{align}angle color{red}{1}+angle color{blue}{2}&={180}^circ \ angle color{blue}{2}&={180}^circ -angle color{red}{1}= \ &={180}^circ -{36}^circ ={144}^circ end{align}]

Углы 3 и 4 вместе образуют прямой угол, поэтому их сумма равна 90°:

[begin{align}angle color{red}{3}+angle color{green}{4}&={90}^circ \ angle color{green}{4}&={90}^circ -angle color{red}{3}= \ &={90}^circ -{36}^circ ={54}^circ end{align}]

Перед тем как переходить к более сложным задачам, рассмотрим ещё одно интересное свойство вертикальных углов.

Теорема 2. Биссектрисы вертикальных углов лежат на одной прямой.

Доказательство. В самом деле, пусть $SC$ и $SD$ — биссектрисы вертикальных углов $ASM$ и $BSN$ соответственно.

Допустим, градусные меры углов $ASM$ и $BSN$ равны $2color{red}{x}$. Тогда градусные меры всех маленьких углов $ASC$, $BSD$ и т.д. равны $color{red}{x}$. Но тогда

[begin{align}angle CSD&=angle CSA+angle ASN+angle NSD= \ &=2color{red}{x}+angle ASN end{align}]

С другой стороны, углы $ASN$ и $ASM=2color{red}{x}$ смежные, поэтому

[2color{red}{x}+angle ASN={180}^circ ]

Итак, угол $angle CSD={180}^circ $, т.е. является развёрнутым. А это как раз и означает, что лучи $SC$ и $SD$ являются дополнительными друг другу и образуют прямую.

3. Комбинированные задачи

Рассмотрим несколько более сложных задач. Тут встречаются вертикальные углы, смежные углы, а также перпендикуляры.

Задача 4. Найдите углы, образованные при пересечении двух прямых, если:

1. Сумма двух из них равна 110°.
2. Сумма трёх из них равна 308°.

Решение. Для обоих пунктов будем использовать один и тот же чертёж. Пусть острые вертикальные углы содержат по $color{red}{x}$ градусов, тогда два других угла содержат по ${180}^circ -color{red}{x}$ градусов:

1. Если сумма двух углов равна 110°, то, очевидно, речь идёт о вертикальных углах. Потому что сумма смежных углов всегда равна 180°, а не 110°.

Кроме того, это явно острые углы, иначе их сумма была бы больше 180°. Поэтому

[begin{align}color{red}{x}+color{red}{x}&={110}^circ\ 2color{red}{x}&={110}^circ\ color{red}{x}&={55}^circend{align}]

Итак, острые вертикальные углы содержат по 55°. Следовательно, смежные с ними тупые вертикальные углы содержат по 125°.

2. Сумма трёх углов всегда содержит два вертикальных и один смежный с ними. Например, так:

Зелёным пунктиром обозначены три угла, участвующие в сумме. Следовательно, эта сумма равна

[begin{align}left( {180}^circ -color{red}{x} right)+color{red}{x}+left( {180}^circ -color{red}{x} right)&={308}^circ \ {360}^circ -color{red}{x}&={308}^circ\ color{red}{x}&={52}^circend{align}]

Итак, углы равны 52° и 128°.

Эту задачу можно решить по-разному. Взгляните ещё раз на чертёж:

Мы знаем, что «большой зелёный угол» содержит 308°. А «полный оборот» содержит 360°. Но чтобы получить полный оборот, нужно добавить к зелёному сектору небольшой угол $color{red}{x}$. Поэтому

[begin{align}{308}^circ +color{red}{x}&={360}^circ\ color{red}{x}&={52}^circend{align}]

Возможно, такой подход покажется вам более простым и «очевидным».

Заметьте: благодаря введённым обозначениям нам даже не потребовались буквы для обозначения углов.:)

Задача 5. Сумма двух углов, образованных при пересечении двух прямых, равна 250°. Докажите, что эти углы вертикальные.

Решение. Пусть тупой угол $ACN$ содержит $color{blue}{x}$ градусов. Тогда смежный с ним угол $BCN$ содержит ${180}^circ -color{blue}{x}$ градусов, а вертикальный угол $BCM$ тоже равен $color{blue}{x}$ градусов:

Но тогда

[angle ACN+angle BCN={180}^circ ne {250}^circ ]

И это вполне логично, поскольку сумма смежных углов всегда равна 180°. То же самое можно сказать, например, про углы $ACN$ и $ACM$ — они тоже смежные.

Остаётся лишь вариант вертикальных углов $ACN$ и $BCM$. Но эти углы вертикальные, что и требовалось доказать.

В последнем задании мы построили чертёж исходя из следующих соображений. Если искомые углы вертикальные (а именно это мы и пытаемся доказать), то они равны, и каждый из них будет равен 125°. Следовательно, речь идёт о тупых углах, поэтому именно тупые углы мы обозначили за $x$.

Помните: в геометрии важно построить правильный чертёж. И чем сложнее задачи, тем выше требования к качеству чертежей. Иначе на можно просто «не увидеть» алгоритм решения задачи.

Кроме того, в следующих уроках мы будем всё чаще отождествлять углы и их градусные меры. Абсолютно нормально писать и говорить «угол $ABC$ равен $x$» вместо «угол $ABC$ содержит $x$ градусов» — все прекрасно поймут, о чём речь.

Смотрите также:

1. Перпендикулярные прямые — определение и свойства
2. Что такое смежные углы
3. Тест к уроку «Площади многоугольников без координатной сетки» (средний)
4. Метод координат в пространстве
5. Интегрирование по частям
6. Как формулы приведения работают в задаче B11

Вертикальные углы. Свойства вертикальных углов

Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.

На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.

Свойства вертикальных углов

1. Вертикальные углы равны.

2. Две пересекающие прямые образуют две пары вертикальных углов.

Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем

Тогда

Следовательно 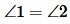. Аналогично доказывается, что .

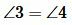Задачи и решения

Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).

Решение. Так как углы 1 и 2 вертикальны, то 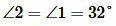. Углы 1 и 4 смежные. Следовательно 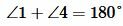. Тогда

Углы 3 и 4 вертикальные. Тогда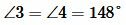

Ответ. .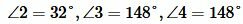

Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.

Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:

Ответ. .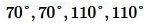

Какие углы называются вертикальными: определение и свойства

Содержание:

• Вертикальные углы — что это такое в геометрии, определение
• Свойства вертикальных углов
• Равны или нет, доказательство теоремы
• Примеры решения задач
  • Задача 1
  • Задача 2

Вертикальные углы — что это такое в геометрии, определение

Определение

Вертикальные углы – пара углов с общей вершиной, которые образованы при пересечении двух прямых таким образом, что стороны одного из них являются продолжением сторон другого. Иными словами – они противоположны.

Свойства вертикальных углов

1. Когда две прямые пересекаются, то образуется две пары вертикальных углов.
2. Синусы, косинусы и тангенсы их равны.
3. В сумме два вертикальных угла создают полный угол. Его градус равняется 360^circ.

Равны или нет, доказательство теоремы

Особенность вертикальных углов в том, что они абсолютно идентичны.

Убедимся в справедливости этого свойства. Докажем его: на чертеже 1 и 2, 2 и 3, 3 и 4, 4 и 1 являются смежными, 1 и 3, 2 и 4 – вертикальные.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

По свойству смежных углов, в сумме они дают (180^circ). Используем этот признак и получаем:

(angle1+angle2=180^circ и angle2+angle3=180^circ)

Отсюда выведем, что:

(angle1=180^circ-angle2, angle3=180^circ-angle2)

Уравнение доказало равенство углов 1 и 3.

Примеры решения задач

Задача 1

Дано

(angle1=45^circ)

Найти: значения (angle2, angle3, angle4)

Решение

(angle1) и (angle3) вертикальные. Значит (angle1=angle3=45^circ.)

(angle1) и (angle4) смежные. По правилу о смежных углах:

(angle1+angle4=180^circ)

(angle4=180^circ-angle1=180^circ-45^circ=135^circ)

Так как (angle4) и (angle2) вертикальные, то (angle4=angle2=135^circ.)

Ответ: величина (angle3=45^circ,) величина (angle2) и (angle4=135^circ.)

Задача 2

Дано

Две прямые пересеклись и сформировали четыре угла. Сумма двух из них составляет (140^circ.)

Найти: значения всех углов, образовавшихся при пересечении прямых.

Решение

Поскольку по условию пара углов образует (140^circ), это дает право сделать вывод – они вертикальные, так как смежные в сумме должны достигать (180^circ).

Так как вертикальные углы равны, то значение каждого из них соответствует:

(140/2=70=70^circ)

Оставшиеся углы – смежные к вертикальным и вертикальные по отношению друг к другу. Для того, чтобы их вычислить, выполним следующее действие:

(180-70=110=110^circ)

Ответ: (70^circ), (110^circ), (70^circ), (110^circ).

Текст с ошибкой:

Расскажите, что не так

Содержание:

• Определение вертикальных углов
• Примеры решения задач с вертикальными углами

Определение вертикальных углов

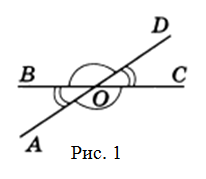
На приведенном рисунке вертикальными есть углы
$AOB$ и
$COD$, а также
$AOC$ и
$BOD$ .

Вертикальные углы образуются при пересечении двух прямых.

Примеры решения задач с вертикальными углами

Читать дальше: что такое синус угла.

Вертикальные углы. Свойства вертикальных углов

Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.

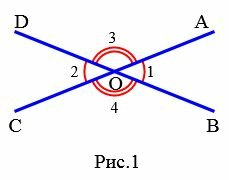
На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.

Свойства вертикальных углов

1. Вертикальные углы равны.

2. Две пересекающие прямые образуют две пары вертикальных углов.

Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем

Следовательно 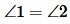. Аналогично доказывается, что .

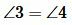Задачи и решения

Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).

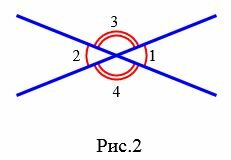
Решение. Так как углы 1 и 2 вертикальны, то 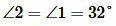. Углы 1 и 4 смежные. Следовательно 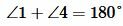. Тогда

Углы 3 и 4 вертикальные. Тогда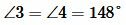

Ответ. .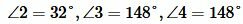

Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.

Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:

.

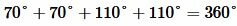Ответ. .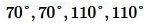

Вертикальные углы

Какие углы вертикальные? Каким свойством обладают вертикальные углы?

Рассмотрим определение вертикальных углов и их свойство, а также применим свойство вертикальных углов для решения задач.

Определение.

Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.

При пересечении двух прямых образуется две пары вертикальных углов:

∠1 и ∠2 — вертикальные углы

∠3 и ∠4 — вертикальные углы

Свойство вертикальных углов.

Вертикальные углы равны.

Таким образом, при пересечении двух прямых образуется две пары равных межу собой углов.

1) Сумма вертикальных углов равна 140º. Найти эти углы.

Так как вертикальные углы равны, а в условии сказано, что их сумма равна 140º, то каждый из них равен по 140:2=70º.

2) Сумма двух углов, образованных при пересечении двух прямых, равна 100º. Найти эти углы.

При пересечении двух прямых образуются углы двух видов — вертикальные и смежные.

Так как сумма смежных углов равна 180º, а по условию, сумма углов равна 100º, то эти углы — вертикальные.

А так как вертикальные углы равны, то каждый из них равен по 100:2=50º.

Вертикальные углы во многих задачах — важный элемент при доказательстве равенства треугольников и подобия треугольников.

Смежные и вертикальные углы. Треугольник. Равнобедренный треугольник. Медиана, биссектриса, высота, средняя линия

Готовиться с нами – ЛЕГКО!

Эффективное решение существует!

Вы ищете теорию и формулы для ЕГЭ по математике ? Образовательный проект «Школково» предлагает вам заглянуть в раздел «Теоретическая справка». Здесь представлено пособие по подготовке к ЕГЭ по математике, которое фактически является авторским. Оно разработано в соответствии с программой школьного курса и включает такие разделы, как арифметика, алгебра, начала анализа и геометрия (планиметрия и стереометрия). Каждое теоретическое положение, содержащееся в пособии по подготовке к ЕГЭ по математике, сопровождается методически подобранными задачами с подробными разъяснениями.

Таким образом, вы не только приобретете определенные знания. Полный справочник для ЕГЭ по математике поможет вам научиться логически и нестандартно мыслить , выполнять самые разнообразные задачи и грамотно объяснять свои решения. А это уже половина успеха при сдаче единого государственного экзамена.

После того, как вы нашли необходимые формулы и теорию для ЕГЭ по математике, рекомендуем вам перейти в раздел «Каталоги» и закрепить полученные знания на практике. Для этого достаточно выбрать задачу по данной теме и решить ее. Кроме того, справочные материалы по математике для ЕГЭ пригодятся вам и для других естественнонаучных дисциплин, таких как физика, химия и т. д.

Факт 1.
(bullet) Смежные углы – два угла, имеющие общую сторону, а две другие стороны являются продолжениями одна другой.

Смежные углы: (angle AOB) и (angle BOC) .
Теорема: Сумма смежных углов равна (180^circ) : (angle AOB+angle BOC=180^circ) .

Факт 2.
(bullet) Вертикальные углы – два угла, у которых стороны одного угла являются продолжениями сторон другого (образуются, например, при пересечении двух прямых).

Вертикальные углы: (angle 1) и (angle 2) , (angle 3) и (angle 4) .
Теорема: Вертикальные углы равны: (angle 1=angle 2) и (angle 3=angle 4) .

Факт 3.
(bullet) Сумма углов (angle A, angle B, angle C) треугольника (ABC) равна (180^circ) .
(bullet) Внешний угол (angle BCD) треугольника (ABC) равен сумме двух углов треугольника, не смежных с ним.

Факт 4.
(bullet) Биссектрисы смежных углов взаимно перпендикулярны.
(bullet) Биссектрисы односторонних углов при параллельных прямых взаимно перпендикулярны.

Факт 5.
(bullet) Прямая теорема: каждая точка биссектрисы угла равноудалена от сторон угла.
(bullet) Обратная теорема: если точка равноудалена от сторон угла, то она лежит на его биссектрисе.

Факт 6.
(bullet) Равнобедренный треугольник – треугольник, у которого две стороны равны. Третья сторона треугольника называется основанием.
Первое свойство равнобедренного треугольника:

Второе свойство равнобедренного треугольника: углы при основании равны.

Первый признак равнобедренного треугольника: если у треугольника два угла равны, то он равнобедренный.
Второй признак равнобедренного треугольника: если у треугольника совпадают высота и медиана (высота и биссектриса или медиана и биссектриса), проведенные к одной и той же стороне, то этот треугольник является равнобедренным.

Факт 7.
(bullet) Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.

Факт 8.
(bullet) Медианы в треугольнике точкой пересечения делятся в отношении (2:1) , считая от вершины.

Факт 9.
(bullet) Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.

Факт 10.
(bullet) Высота, проведенная из вершины прямого угла треугольника, делит его на два треугольника, подобных исходному.
(bullet) Квадрат этой высоты равен произведению отрезков, на которые она делит гипотенузу.

Факт 11.
(bullet) Средняя линия треугольника – отрезок, соединяющий середины двух его сторон.
(bullet) 1. Средняя линия треугольника параллельна третьей стороне.
(bullet) 2. Средняя линия треугольника равна половине третьей стороны.
(bullet) 3. Средняя линия отсекает от треугольника подобный ему треугольник.

Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, – на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.

Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?

1. Потому что это расширяет кругозор . Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.
2. Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.

Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.

[spoiler title=”источники:”]

http://shkolkovo.net/theory/smezhnye_i_vertikalnye_ugly_treugolnik_ravnobedrennyj_treugolnik_mediana_bissektrisa_vysota_srednyaya_liniya

[/spoiler]