|
falconav Пользователь Сообщений: 2 Инженер |
Прошу помочь по формуле – как получить значение угла в градусах /минутах от числового значения его косинуса? |
|
Сергей Пользователь Сообщений: 11251 |
зайдите в эксель нажмите F1 почитайте справку по функциям там кажись в разделе математические функции что то подобное есть Лень двигатель прогресса, доказано!!! |
|
Jack Famous Пользователь Сообщений: 11000 OS: Win 8.1 Корп. x64 | Excel 2016 x64: | Browser: Chrome |
falconav, интересный вопрос. =ГРАДУСЫ(ACOS(A1)) Изменено: Jack Famous – 16.09.2016 12:51:36 Во всех делах очень полезно периодически ставить знак вопроса к тому, что вы с давних пор считали не требующим доказательств (Бертран Рассел) ►Благодарности сюда◄ |
|
falconav Пользователь Сообщений: 2 Инженер |
#4 08.06.2018 07:32:36 Спасибо, Jack Famous , очень Вам благодарен. |
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Таблица данных:
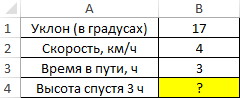
Для решения используем формулу:
=B2*B3*SIN(РАДИАНЫ(B1))
Описание аргументов:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
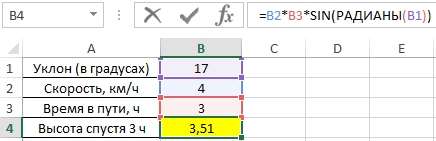
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
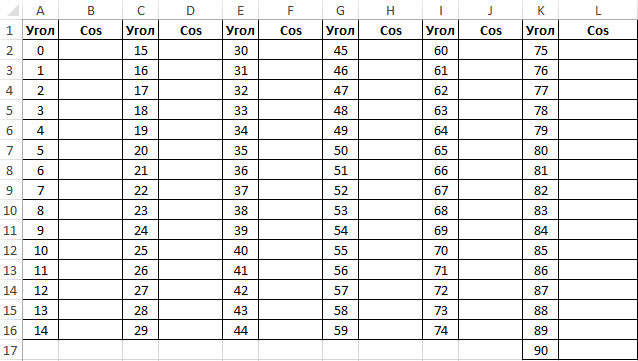
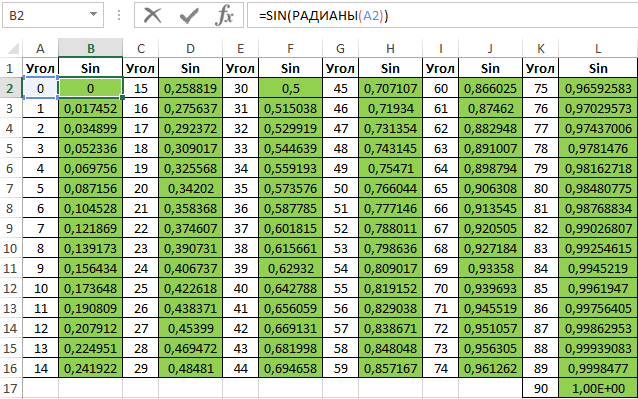
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
=COS(РАДИАНЫ(A2:A16))
Вычислим значения для всех значений углов. Полученный результат:

Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.
Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Исходные данные:
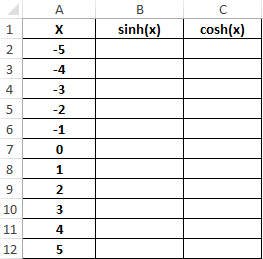
Формула для нахождения синусов гиперболических:
=SINH(A2:A12)
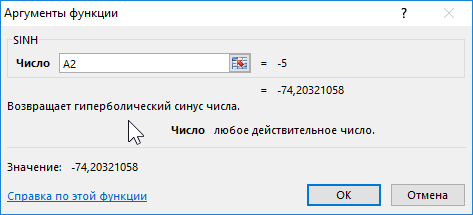
Формула для нахождения косинусов гиперболических:
=COSH(A2:A12)
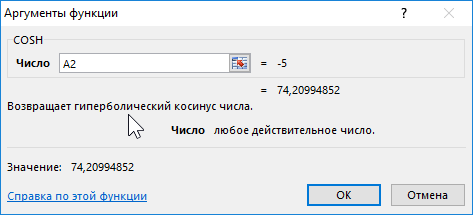
Таблица полученных значений:
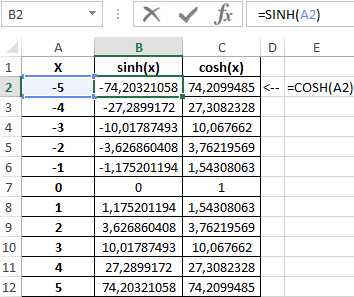
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
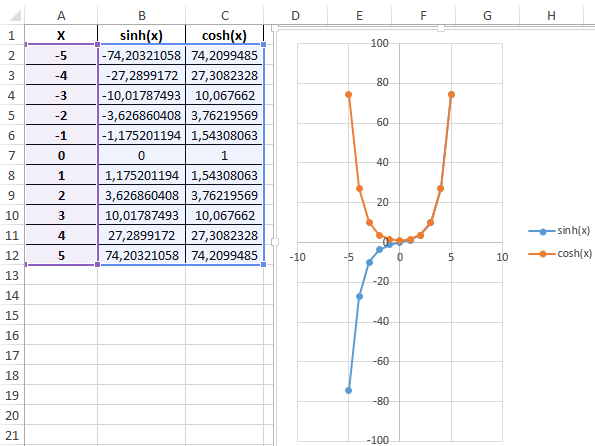
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
=SIN(число)
Синтаксис функции SINH:
=SINH(число)
Синтаксис функции COS:
=COS(число)
Синтаксис функции COSH:
>=COSH(число)
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
Примечания 1:
- Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
- В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
- Все рассматриваемые функции могут быть использованы в качестве формул массива.
Примечения 2:
- Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
- Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
- При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:
Скачать примеры тригонометрических функций SIN и COS
- Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
- Выражение ПИ()*угол_в_градусах/180.
|
К примеру cos = 0,5 Допустим, что число 0,5 записано в ячейке А1. В ячейке А2 набираете формулу =ACOS(А1). Затем в ячейке А3 набираете формулу =TAN(А2), и в ней получаете значение тангенса. Можно конечно сделать и в одной ячейке, например так =TAN(ACOS(А1)). Но удобнее делать поэтапно, особенно когда цепочка вычислений довольно большая. При наборе формул в наименованиях ячеек обязательно должны быть латинские символы (не кириллица). автор вопроса выбрал этот ответ лучшим Знаете ответ? |
Смотрите также: Почему в русском тангенс — tg, а в английском tan? А как в других языках? Чему равен tg 1 (тангенс единицы)? Как оставить первый комментарий под постом в телеграмм? Что случилось с MMG и TG? Вычислите tg 1065 градусов? Как применить в жизни sin, cos, tg? Как быстро запомнить таблицу значений sin, cos, tg, ctg? Как найти тангенс тупого угла? Что такое тангенс, катангенс, синус, косинус, секанс, касеканс? Как выучить таблицу значений синуса, косинуса, тангенса разных углов? |
Перейти к содержимому
Добрый день.
Очень часто работая с тригонометрическими функциями в программе «Эксель» приходится их переводить из одной в другую для проведения расчетов. Казалось бы нет ничего сложного в этих тригонометрических преобразованиях изученных нами еще в курсе алгебры школьной программы, но когда голова забита рабочими процессами и планами на ближайшие выходные, вспомнить формулу перевода косинуса в тангенс достаточно сложно и хочется иметь под рукой небольшую шпаргалку.
Она поможет Вам быстро без лишних затрат времени на поиск в интернете рассчитать cos и sin двойных и тройных углов, произвести перевод синуса в косинус, косинуса в тангенс, синуса в котангенс и наоборот.
Такую шпаргалку мы для Вас подготовили и приводим ниже в тексте.

Надеемся, что данная шпаргалка будет полезна для Вас.
Простые тригонометрические функции в программе «Excel» выглядят следующим образом:
- Косинус (cos) – COS()
- Синус (sin) – SIN()
- Тангенс (tg) – TAN()
- Котангенс (ctg) – 1/TAN()
- Угол следует указывать в радианах .
- Перевод градусов в радианы по формуле — угол°*Пи/180
Вопросы можно задавать в комментариях и на форуме.
На чтение 5 мин. Просмотров 49 Опубликовано 15.12.2019
В этой статье описаны синтаксис формулы и использование функции COS в Microsoft Excel.
Содержание
- Описание
- Синтаксис
- Замечания
- Пример
Описание
Возвращает косинус заданного угла.
Синтаксис
Аргументы функции COS описаны ниже.
Число — обязательный аргумент. Угол в радианах, для которого определяется косинус.
Замечания
Если угол задан в градусах, умножьте его на ПИ()/180 или воспользуйтесь функцией РАДИАНЫ, чтобы преобразовать его в радианы.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формулы тригонометрии – редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т.д. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна.
Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel. Так, функция КОРЕНЬ извлечет квадратный корень из заданного числа. Например, запишем: =КОРЕНЬ(121) , и получим результат «11». Хотя правильным решением будет «11» и «-11», программа возвращает только положительный результат в таких случаях.
Еще одна функция – ПИ() , не нуждается в аргументах и является зарезервированной константой. Ее результатом будет известное число 3,1415, описывающее соотношение длины окружности к ее диаметру. Эту функцию-константу можно активно применять в расчетах.
Тригонометрические функции Excel, до которых мы еще доберемся, используют запись угла в радианах. Эта общепринятая практика часто бывает ненаглядной, ведь нам привычнее выражать угол в градусах. Чтобы устранить эту проблему, есть две функции преобразования величин:
- ГРУДУСЫ(Угол в радианах) – преобразует радиальные величины в градусы
- РАДИАНЫ(Угол вградусах) – наоборот, преобразует градусы в радианы.
Пользуясь этими функциями, Вы обеспечиваете совместимость и наглядность вычислений.
Конечно, Вы знаете эти функции:
- COS(Угол в радианах) – косинус угла, соотношение между прилежащим катетом и гипотенузой прямоугольного треугольника
- SIN(Угол в радианах) – синус угла, отношение противолежащего катета к гипотенузе
Для удобства чтения формул, можно использовать вложенную функцию РАДИАНЫ и задать угол в градусах. Например, формула =COS(РАДИАНЫ(180)) вернет результат «-1».
Еще две функции Вам так же знакомы – это тангенс и котангенс:
- TAN(Угол в радианах) – отношение длины противолежащего катета к прилежащему
- COT(Угол в радианах) – обратная величина – соотношение прилежащего угла к противолежащему.
Здесь так же рекомендую использовать функции преобразования величин РАДИАНЫ и ГРАДУСЫ.
Среди прочих тригонометрических функций можно выделить секанс и косеканс:
- SEC(Угол в радианах) – отношение гипотенузы к прилежащему катету
- CSC(Угол в радианах) – отношение гипотенузы к противолежащему катету
Легко заметить, что секанс – обратно-пропорциональная величина к косинусу, косеканс – к синусу.
Такие функции выполняют обратный расчет по отношению к перечисленным выше:
- Арккосинус – это угол, который образуют прилежащий катет и гипотенуза с определенным косинусом. Чтобы посчитать эту величину, используйте функцию ACOS(Значение косинуса) .
- Арксинус – угол между противолежащим катетом и гипотенузой с определенным синусом, вычисляется так: ASIN(Значение синуса) .
- Арктангенс – угол между противолежащим и прилежащим катетами для заданного тангенса: ATAN(Значение тангенса) .
- Арккотангенс – угол, для которого справедливо заданное значение котангенса: ACOT(Значение котангенса).
Все перечисленные функции вернут угол в радианах. Естественно, для перевода его в градусы, используем функцию ГРАДУСЫ .
Знание и умелое применение перечисленных функций, конечно, не сделает Вас богом в тригонометрии, но все же позволит выполнить сложные расчеты, «стоимость» которых часто довольно высока. Научитесь комбинировать их с другими функциями, построением графиков, чтобы получить максимальный эффект от полученных знаний.
Это все о тригонометрических функциях, спасибо, что читаете мой блог и развиваетесь в своих знаниях. Следующую статью я напишу об округлении чисел и очень Вам рекомендую ее не пропустить!
В этой практической задаче я покажу вам как при помощи возможностей Excel 2010 найти значение косинуса угла в 136 градусов. Задачка из школьной программы, так что этот практический урок будет полезен не только родителям, но и школьникам. Заодно вы узнаете какими тригонометрическими функциями обладает Excel 2010.
Обратите внимание на то, что в тригонометрических функциях программы Excel углы измеряются не в градусах, а в радианах. Поэтому, прежде чем вычислить косинус угла 136°, его нужно перевести в радианы. Это можно сделать двумя способами.
Первый: умножить 136 на число пи и разделить произведение на 180.
Второй: воспользоваться специальной функцией, которая переводит градусы в радианы.
Как видите, на рис. 10.2 результат в обоих случаях одинаков.

Рис. 10.2. Вычисление косинуса: формулы (а) и результат (б)
Рассмотрим некоторые математические функции программы.
- Пи() — возвращает число 3,14159265358979, математическую константу пи с точностью до 15 цифр. Аргументы отсутствуют.
- РАДИАНЫ(угол) — возвращает значение угла в радианах. Аргумент угол — обязательный. Это величина угла в градусах.
- ГРАДУСЫ(угол) — возвращает значение угла в градусах. Аргумент угол — обязательный. Это угол в радианах, который необходимо преобразовать в градусы.
- SIN(число) — возвращает значение синуса угла. Аргумент число — обязательный. Это угол в радианах, для которого вычисляется синус.
- COS(число) — возвращает значение косинуса угла. Аргумент число — обязательный. Это угол в радианах, для которого вычисляется косинус.
- TAN(число) — возвращает значение тангенса угла. Аргумент число — обязательный. Это угол в радианах, для которого вычисляется тангенс.
