Вот сильно я сомневаюсь, что, не посчитавши прежде на калькуляторе, можно будет рыть преобразования в нужном направлении, особенно от синуса к углу. От угла к синусу проще, но вопрос по другому сформулирован. На мой взгляд подтасовка преобразований.
Первые два слагаемых √(2+√3) * (√5 -1). Восьмёрку из дроби распределяем между ними
(√(2+√3))/2) * ((√5 -1)/4)
Задний радикал: группируем чётные и нечётные слагаемые
√(10(2 – √3) + 2√5(2 – √3)) = √(10+2√5) (2-√3))
И распределяем восьмёрку (√(2-√3))/2) * √(10+2√5)/4
Из предположения, что sin a = sin(x – y) = sin x cos y – cos x sin y
Выписываем
sin y = √(2-√3))/2 ; cos y = √(2+√3))/2 ; sin 2y = 2 sin y cos y = 1/2; 2y = pi/6; y = pi/12
sin x = (√5 -1)/4 ; cos x = √(10+2√5)/4
sin 2x = 2 sin x cos x = ((√5 -1)√(10+2√5))/8
cos 2x = cos^2 x – sin^2 x = (10 + 2√5 – 5 + 2√5 – 1)/16 = (1+√5)/4
sin 4x = 2 sin 2x cos 2x = 2 * (((√5 -1)√(10+2√5))/8) * (1+√5)/4 = √(10+2√5) / 4
Получилось sin 4x = cos x или cos (pi/2 – 4x) = cos x, pi/2 – 4x = x; x = pi/10
a = x – y = pi/10 – pi/12= pi/60
известен синус угла, как определить угол
Мыслитель
(6934),
закрыт
14 лет назад
Дополнен 14 лет назад
Дополнение:
И где в виндовом куркуляторе кнопка арксинус? Пусть даже в инженерном?
Алексей Сикоренко
Мастер
(1399)
14 лет назад
открыть программу калькулятор на компе, привести к виду Инженерный, он встроен во все системы, и вычислить. не понимаю, в чем собственно проблема. набираешь значение синуса, ставишь там галочку, где INV и жмешь SIN. Не забыть при этом указать единицы измерения угла, это можно видеть под строкой Градусы, Радианы, Грады.
Косинус острого угла прямоугольного треугольника

Cos (α) острого угла прямоугольного треугольника — это отношение прилежащего катета(AC) к гипотенузе(AB).Пимер:α = 40°; AC = 6,98см; AB = 9см. cos (40°) = 6,989 = 0,776
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
| 0° | 1 | |
| 1° | 0.0174524064 | 0.9998476952 |
| 2° | 0.0348994967 | 0.9993908270 |
| 3° | 0.0523359562 | 0.9986295348 |
| 4° | 0.0697564737 | 0.9975640503 |
| 5° | 0.0871557427 | 0.9961946981 |
| 6° | 0.1045284633 | 0.9945218954 |
| 7° | 0.1218693434 | 0.9925461516 |
| 8° | 0.1391731010 | 0.9902680687 |
| 9° | 0.1564344650 | 0.9876883406 |
| 10° | 0.1736481777 | 0.9848077530 |
| 11° | 0.1908089954 | 0.9816271834 |
| 12° | 0.2079116908 | 0.9781476007 |
| 13° | 0.2249510543 | 0.9743700648 |
| 14° | 0.2419218956 | 0.9702957263 |
| 15° | 0.2588190451 | 0.9659258263 |
| 16° | 0.2756373558 | 0.9612616959 |
| 17° | 0.2923717047 | 0.9563047560 |
| 18° | 0.3090169944 | 0.9510565163 |
| 19° | 0.3255681545 | 0.9455185756 |
| 20° | 0.3420201433 | 0.9396926208 |
| 21° | 0.3583679495 | 0.9335804265 |
| 22° | 0.3746065934 | 0.9271838546 |
| 23° | 0.3907311285 | 0.9205048535 |
| 24° | 0.4067366431 | 0.9135454576 |
| 25° | 0.4226182617 | 0.9063077870 |
| 26° | 0.4383711468 | 0.8987940463 |
| 27° | 0.4539904997 | 0.8910065242 |
| 28° | 0.4694715628 | 0.8829475929 |
| 29° | 0.4848096202 | 0.8746197071 |
| 30° | 0.5 | 0.8660254038 |
| 31° | 0.5150380749 | 0.8571673007 |
| 32° | 0.5299192642 | 0.8480480962 |
| 33° | 0.5446390350 | 0.8386705679 |
| 34° | 0.5591929035 | 0.8290375726 |
| 35° | 0.5735764364 | 0.8191520443 |
| 36° | 0.5877852523 | 0.8090169944 |
| 37° | 0.6018150232 | 0.7986355100 |
| 38° | 0.6156614753 | 0.7880107536 |
| 39° | 0.6293203910 | 0.7771459615 |
| 40° | 0.6427876097 | 0.7660444431 |
| 41° | 0.6560590290 | 0.7547095802 |
| 42° | 0.6691306064 | 0.7431448255 |
| 43° | 0.6819983601 | 0.7313537016 |
| 44° | 0.6946583705 | 0.7193398003 |
| 45° | 0.7071067812 | 0.7071067812 |
| 46° | 0.7193398003 | 0.6946583705 |
| 47° | 0.7313537016 | 0.6819983601 |
| 48° | 0.7431448255 | 0.6691306064 |
| 49° | 0.7547095802 | 0.6560590290 |
| 50° | 0.7660444431 | 0.6427876097 |
| 51° | 0.7771459615 | 0.6293203910 |
| 52° | 0.7880107536 | 0.6156614753 |
| 53° | 0.7986355100 | 0.6018150232 |
| 54° | 0.8090169944 | 0.5877852523 |
| 55° | 0.8191520443 | 0.5735764364 |
| 56° | 0.8290375726 | 0.5591929035 |
| 57° | 0.8386705679 | 0.5446390350 |
| 58° | 0.8480480962 | 0.5299192642 |
| 59° | 0.8571673007 | 0.5150380749 |
| 60° | 0.8660254038 | 0.5 |
| 61° | 0.8746197071 | 0.4848096202 |
| 62° | 0.8829475929 | 0.4694715628 |
| 63° | 0.8910065242 | 0.4539904997 |
| 64° | 0.8987940463 | 0.4383711468 |
| 65° | 0.9063077870 | 0.4226182617 |
| 66° | 0.9135454576 | 0.4067366431 |
| 67° | 0.9205048535 | 0.3907311285 |
| 68° | 0.9271838546 | 0.3746065934 |
| 69° | 0.9335804265 | 0.3583679495 |
| 70° | 0.9396926208 | 0.3420201433 |
| 71° | 0.9455185756 | 0.3255681545 |
| 72° | 0.9510565163 | 0.3090169944 |
| 73° | 0.9563047560 | 0.2923717047 |
| 74° | 0.9612616959 | 0.2756373558 |
| 75° | 0.9659258263 | 0.2588190451 |
| 76° | 0.9702957263 | 0.2419218956 |
| 77° | 0.9743700648 | 0.2249510543 |
| 78° | 0.9781476007 | 0.2079116908 |
| 79° | 0.9816271834 | 0.1908089954 |
| 80° | 0.9848077530 | 0.1736481777 |
| 81° | 0.9876883406 | 0.1564344650 |
| 82° | 0.9902680687 | 0.1391731010 |
| 83° | 0.9925461516 | 0.1218693434 |
| 84° | 0.9945218954 | 0.1045284633 |
| 85° | 0.9961946981 | 0.0871557427 |
| 86° | 0.9975640503 | 0.0697564737 |
| 87° | 0.9986295348 | 0.0523359562 |
| 88° | 0.9993908270 | 0.0348994967 |
| 89° | 0.9998476952 | 0.0174524064 |
| 90° | 1 | |
| 91° | 0.9998476952 | -0.0174524064 |
| 92° | 0.9993908270 | -0.0348994967 |
| 93° | 0.9986295348 | -0.0523359562 |
| 94° | 0.9975640503 | -0.0697564737 |
| 95° | 0.9961946981 | -0.0871557427 |
| 96° | 0.9945218954 | -0.1045284633 |
| 97° | 0.9925461516 | -0.1218693434 |
| 98° | 0.9902680687 | -0.1391731010 |
| 99° | 0.9876883406 | -0.1564344650 |
| 100° | 0.9848077530 | -0.1736481777 |
| 101° | 0.9816271834 | -0.1908089954 |
| 102° | 0.9781476007 | -0.2079116908 |
| 103° | 0.9743700648 | -0.2249510543 |
| 104° | 0.9702957263 | -0.2419218956 |
| 105° | 0.9659258263 | -0.2588190451 |
| 106° | 0.9612616959 | -0.2756373558 |
| 107° | 0.9563047560 | -0.2923717047 |
| 108° | 0.9510565163 | -0.3090169944 |
| 109° | 0.9455185756 | -0.3255681545 |
| 110° | 0.9396926208 | -0.3420201433 |
| 111° | 0.9335804265 | -0.3583679495 |
| 112° | 0.9271838546 | -0.3746065934 |
| 113° | 0.9205048535 | -0.3907311285 |
| 114° | 0.9135454576 | -0.4067366431 |
| 115° | 0.9063077870 | -0.4226182617 |
| 116° | 0.8987940463 | -0.4383711468 |
| 117° | 0.8910065242 | -0.4539904997 |
| 118° | 0.8829475929 | -0.4694715628 |
| 119° | 0.8746197071 | -0.4848096202 |
| 120° | 0.8660254038 | -0.5 |
| 121° | 0.8571673007 | -0.5150380749 |
| 122° | 0.8480480962 | -0.5299192642 |
| 123° | 0.8386705679 | -0.5446390350 |
| 124° | 0.8290375726 | -0.5591929035 |
| 125° | 0.8191520443 | -0.5735764364 |
| 126° | 0.8090169944 | -0.5877852523 |
| 127° | 0.7986355100 | -0.6018150232 |
| 128° | 0.7880107536 | -0.6156614753 |
| 129° | 0.7771459615 | -0.6293203910 |
| 130° | 0.7660444431 | -0.6427876097 |
| 131° | 0.7547095802 | -0.6560590290 |
| 132° | 0.7431448255 | -0.6691306064 |
| 133° | 0.7313537016 | -0.6819983601 |
| 134° | 0.7193398003 | -0.6946583705 |
| 135° | 0.7071067812 | -0.7071067812 |
| 136° | 0.6946583705 | -0.7193398003 |
| 137° | 0.6819983601 | -0.7313537016 |
| 138° | 0.6691306064 | -0.7431448255 |
| 139° | 0.6560590290 | -0.7547095802 |
| 140° | 0.6427876097 | -0.7660444431 |
| 141° | 0.6293203910 | -0.7771459615 |
| 142° | 0.6156614753 | -0.7880107536 |
| 143° | 0.6018150232 | -0.7986355100 |
| 144° | 0.5877852523 | -0.8090169944 |
| 145° | 0.5735764364 | -0.8191520443 |
| 146° | 0.5591929035 | -0.8290375726 |
| 147° | 0.5446390350 | -0.8386705679 |
| 148° | 0.5299192642 | -0.8480480962 |
| 149° | 0.5150380749 | -0.8571673007 |
| 150° | 0.5 | -0.8660254038 |
| 151° | 0.4848096202 | -0.8746197071 |
| 152° | 0.4694715628 | -0.8829475929 |
| 153° | 0.4539904997 | -0.8910065242 |
| 154° | 0.4383711468 | -0.8987940463 |
| 155° | 0.4226182617 | -0.9063077870 |
| 156° | 0.4067366431 | -0.9135454576 |
| 157° | 0.3907311285 | -0.9205048535 |
| 158° | 0.3746065934 | -0.9271838546 |
| 159° | 0.3583679495 | -0.9335804265 |
| 160° | 0.3420201433 | -0.9396926208 |
| 161° | 0.3255681545 | -0.9455185756 |
| 162° | 0.3090169944 | -0.9510565163 |
| 163° | 0.2923717047 | -0.9563047560 |
| 164° | 0.2756373558 | -0.9612616959 |
| 165° | 0.2588190451 | -0.9659258263 |
| 166° | 0.2419218956 | -0.9702957263 |
| 167° | 0.2249510543 | -0.9743700648 |
| 168° | 0.2079116908 | -0.9781476007 |
| 169° | 0.1908089954 | -0.9816271834 |
| 170° | 0.1736481777 | -0.9848077530 |
| 171° | 0.1564344650 | -0.9876883406 |
| 172° | 0.1391731010 | -0.9902680687 |
| 173° | 0.1218693434 | -0.9925461516 |
| 174° | 0.1045284633 | -0.9945218954 |
| 175° | 0.0871557427 | -0.9961946981 |
| 176° | 0.0697564737 | -0.9975640503 |
| 177° | 0.0523359562 | -0.9986295348 |
| 178° | 0.0348994967 | -0.9993908270 |
| 179° | 0.0174524064 | -0.9998476952 |
| 180° | -1 | |
| 181° | -0.0174524064 | -0.9998476952 |
| 182° | -0.0348994967 | -0.9993908270 |
| 183° | -0.0523359562 | -0.9986295348 |
| 184° | -0.0697564737 | -0.9975640503 |
| 185° | -0.0871557427 | -0.9961946981 |
| 186° | -0.1045284633 | -0.9945218954 |
| 187° | -0.1218693434 | -0.9925461516 |
| 188° | -0.1391731010 | -0.9902680687 |
| 189° | -0.1564344650 | -0.9876883406 |
| 190° | -0.1736481777 | -0.9848077530 |
| 191° | -0.1908089954 | -0.9816271834 |
| 192° | -0.2079116908 | -0.9781476007 |
| 193° | -0.2249510543 | -0.9743700648 |
| 194° | -0.2419218956 | -0.9702957263 |
| 195° | -0.2588190451 | -0.9659258263 |
| 196° | -0.2756373558 | -0.9612616959 |
| 197° | -0.2923717047 | -0.9563047560 |
| 198° | -0.3090169944 | -0.9510565163 |
| 199° | -0.3255681545 | -0.9455185756 |
| 200° | -0.3420201433 | -0.9396926208 |
| 201° | -0.3583679495 | -0.9335804265 |
| 202° | -0.3746065934 | -0.9271838546 |
| 203° | -0.3907311285 | -0.9205048535 |
| 204° | -0.4067366431 | -0.9135454576 |
| 205° | -0.4226182617 | -0.9063077870 |
| 206° | -0.4383711468 | -0.8987940463 |
| 207° | -0.4539904997 | -0.8910065242 |
| 208° | -0.4694715628 | -0.8829475929 |
| 209° | -0.4848096202 | -0.8746197071 |
| 210° | -0.5 | -0.8660254038 |
| 211° | -0.5150380749 | -0.8571673007 |
| 212° | -0.5299192642 | -0.8480480962 |
| 213° | -0.5446390350 | -0.8386705679 |
| 214° | -0.5591929035 | -0.8290375726 |
| 215° | -0.5735764364 | -0.8191520443 |
| 216° | -0.5877852523 | -0.8090169944 |
| 217° | -0.6018150232 | -0.7986355100 |
| 218° | -0.6156614753 | -0.7880107536 |
| 219° | -0.6293203910 | -0.7771459615 |
| 220° | -0.6427876097 | -0.7660444431 |
| 221° | -0.6560590290 | -0.7547095802 |
| 222° | -0.6691306064 | -0.7431448255 |
| 223° | -0.6819983601 | -0.7313537016 |
| 224° | -0.6946583705 | -0.7193398003 |
| 225° | -0.7071067812 | -0.7071067812 |
| 226° | -0.7193398003 | -0.6946583705 |
| 227° | -0.7313537016 | -0.6819983601 |
| 228° | -0.7431448255 | -0.6691306064 |
| 229° | -0.7547095802 | -0.6560590290 |
| 230° | -0.7660444431 | -0.6427876097 |
| 231° | -0.7771459615 | -0.6293203910 |
| 232° | -0.7880107536 | -0.6156614753 |
| 233° | -0.7986355100 | -0.6018150232 |
| 234° | -0.8090169944 | -0.5877852523 |
| 235° | -0.8191520443 | -0.5735764364 |
| 236° | -0.8290375726 | -0.5591929035 |
| 237° | -0.8386705679 | -0.5446390350 |
| 238° | -0.8480480962 | -0.5299192642 |
| 239° | -0.8571673007 | -0.5150380749 |
| 240° | -0.8660254038 | -0.5 |
| 241° | -0.8746197071 | -0.4848096202 |
| 242° | -0.8829475929 | -0.4694715628 |
| 243° | -0.8910065242 | -0.4539904997 |
| 244° | -0.8987940463 | -0.4383711468 |
| 245° | -0.9063077870 | -0.4226182617 |
| 246° | -0.9135454576 | -0.4067366431 |
| 247° | -0.9205048535 | -0.3907311285 |
| 248° | -0.9271838546 | -0.3746065934 |
| 249° | -0.9335804265 | -0.3583679495 |
| 250° | -0.9396926208 | -0.3420201433 |
| 251° | -0.9455185756 | -0.3255681545 |
| 252° | -0.9510565163 | -0.3090169944 |
| 253° | -0.9563047560 | -0.2923717047 |
| 254° | -0.9612616959 | -0.2756373558 |
| 255° | -0.9659258263 | -0.2588190451 |
| 256° | -0.9702957263 | -0.2419218956 |
| 257° | -0.9743700648 | -0.2249510543 |
| 258° | -0.9781476007 | -0.2079116908 |
| 259° | -0.9816271834 | -0.1908089954 |
| 260° | -0.9848077530 | -0.1736481777 |
| 261° | -0.9876883406 | -0.1564344650 |
| 262° | -0.9902680687 | -0.1391731010 |
| 263° | -0.9925461516 | -0.1218693434 |
| 264° | -0.9945218954 | -0.1045284633 |
| 265° | -0.9961946981 | -0.0871557427 |
| 266° | -0.9975640503 | -0.0697564737 |
| 267° | -0.9986295348 | -0.0523359562 |
| 268° | -0.9993908270 | -0.0348994967 |
| 269° | -0.9998476952 | -0.0174524064 |
| 270° | -1. | |
| 271° | -0.9998476952 | 0.0174524064 |
| 272° | -0.9993908270 | 0.0348994967 |
| 273° | -0.9986295348 | 0.0523359562 |
| 274° | -0.9975640503 | 0.0697564737 |
| 275° | -0.9961946981 | 0.0871557427 |
| 276° | -0.9945218954 | 0.1045284633 |
| 277° | -0.9925461516 | 0.1218693434 |
| 278° | -0.9902680687 | 0.1391731010 |
| 279° | -0.9876883406 | 0.1564344650 |
| 280° | -0.9848077530 | 0.1736481777 |
| 281° | -0.9816271834 | 0.1908089954 |
| 282° | -0.9781476007 | 0.2079116908 |
| 283° | -0.9743700648 | 0.2249510543 |
| 284° | -0.9702957263 | 0.2419218956 |
| 285° | -0.9659258263 | 0.2588190451 |
| 286° | -0.9612616959 | 0.2756373558 |
| 287° | -0.9563047560 | 0.2923717047 |
| 288° | -0.9510565163 | 0.3090169944 |
| 289° | -0.9455185756 | 0.3255681545 |
| 290° | -0.9396926208 | 0.3420201433 |
| 291° | -0.9335804265 | 0.3583679495 |
| 292° | -0.9271838546 | 0.3746065934 |
| 293° | -0.9205048535 | 0.3907311285 |
| 294° | -0.9135454576 | 0.4067366431 |
| 295° | -0.9063077870 | 0.4226182617 |
| 296° | -0.8987940463 | 0.4383711468 |
| 297° | -0.8910065242 | 0.4539904997 |
| 298° | -0.8829475929 | 0.4694715628 |
| 299° | -0.8746197071 | 0.4848096202 |
| 300° | -0.8660254038 | 0.5 |
| 301° | -0.8571673007 | 0.5150380749 |
| 302° | -0.8480480962 | 0.5299192642 |
| 303° | -0.8386705679 | 0.5446390350 |
| 304° | -0.8290375726 | 0.5591929035 |
| 305° | -0.8191520443 | 0.5735764364 |
| 306° | -0.8090169944 | 0.5877852523 |
| 307° | -0.7986355100 | 0.6018150232 |
| 308° | -0.7880107536 | 0.6156614753 |
| 309° | -0.7771459615 | 0.6293203910 |
| 310° | -0.7660444431 | 0.6427876097 |
| 311° | -0.7547095802 | 0.6560590290 |
| 312° | -0.7431448255 | 0.6691306064 |
| 313° | -0.7313537016 | 0.6819983601 |
| 314° | -0.7193398003 | 0.6946583705 |
| 315° | -0.7071067812 | 0.7071067812 |
| 316° | -0.6946583705 | 0.7193398003 |
| 317° | -0.6819983601 | 0.7313537016 |
| 318° | -0.6691306064 | 0.7431448255 |
| 319° | -0.6560590290 | 0.7547095802 |
| 320° | -0.6427876097 | 0.7660444431 |
| 321° | -0.6293203910 | 0.7771459615 |
| 322° | -0.6156614753 | 0.7880107536 |
| 323° | -0.6018150232 | 0.7986355100 |
| 324° | -0.5877852523 | 0.8090169944 |
| 325° | -0.5735764364 | 0.8191520443 |
| 326° | -0.5591929035 | 0.8290375726 |
| 327° | -0.5446390350 | 0.8386705679 |
| 328° | -0.5299192642 | 0.8480480962 |
| 329° | -0.5150380749 | 0.8571673007 |
| 330° | -0.5 | 0.8660254038 |
| 331° | -0.4848096202 | 0.8746197071 |
| 332° | -0.4694715628 | 0.8829475929 |
| 333° | -0.4539904997 | 0.8910065242 |
| 334° | -0.4383711468 | 0.8987940463 |
| 335° | -0.4226182617 | 0.9063077870 |
| 336° | -0.4067366431 | 0.9135454576 |
| 337° | -0.3907311285 | 0.9205048535 |
| 338° | -0.3746065934 | 0.9271838546 |
| 339° | -0.3583679495 | 0.9335804265 |
| 340° | -0.3420201433 | 0.9396926208 |
| 341° | -0.3255681545 | 0.9455185756 |
| 342° | -0.3090169944 | 0.9510565163 |
| 343° | -0.2923717047 | 0.9563047560 |
| 344° | -0.2756373558 | 0.9612616959 |
| 345° | -0.2588190451 | 0.9659258263 |
| 346° | -0.2419218956 | 0.9702957263 |
| 347° | -0.2249510543 | 0.9743700648 |
| 348° | -0.2079116908 | 0.9781476007 |
| 349° | -0.1908089954 | 0.9816271834 |
| 350° | -0.1736481777 | 0.9848077530 |
| 351° | -0.1564344650 | 0.9876883406 |
| 352° | -0.1391731010 | 0.9902680687 |
| 353° | -0.1218693434 | 0.9925461516 |
| 354° | -0.1045284633 | 0.9945218954 |
| 355° | -0.0871557427 | 0.9961946981 |
| 356° | -0.0697564737 | 0.9975640503 |
| 357° | -0.0523359562 | 0.9986295348 |
| 358° | -0.0348994967 | 0.9993908270 |
| 359° | -0.0174524064 | 0.9998476952 |
| 360° | 1 |
Как найти синус определенного угла в градусах? Нужна сама формула, а не таблица Брадиса
Во-первых, переведите угол из градусов в радианы по формуле x = alpha * pi / 180 а потом воспользуйтесь разложением в ряд Тейлора. С достаточно хорощей степенью точности можно ограничиться формулой sin(x) = x — x^3 / 3
такой формулы нет. только брадис или инженерный калькулятор ой!
Константин! Sin x = x — x^3/6
Синус угла A минут B = (3.14/180) + B * (3.14/(180*60))) Так будет точнее. В некоторых случаях минуты (B) равны нулю, тогда остается только первая часть. В интернете есть готовые калькуляторы, например: <a rel=»nofollow» href=»http:///bradis/tablica-sinusov/» target=»_blank»>http:///bradis/tablica-sinusov/</a> или что-нибудь подобное
Видео
Навигация по записям
Предыдущая статьяРешение слау при помощи обратной матрицы – Решение систем линейных алгебраических уравнений с помощью обратной матрицы.
Следующая статья Тесты по математике с 1 11 класс – Тест по математике 1 — 11 классы
Теги
Как найти угол, если известен синус
Синус и косинус – пара основных тригонометрических функций, которые косвенно выражают величину угла в градусах. Всего таких функций существует больше десятка и среди них есть те, что позволяют по значению, например, синуса восстановить величину угла в градусах. Для практической работы с ними можно использовать программный калькулятор или сетевые сервисы.

Инструкция
Используйте функцию арксинус для вычисления величины угла в градусах, если известно значение синуса этого угла. Если угол обозначить буквой α, в общем виде такое решение можно записать так: α = arcsin(sin(α)).
Если у вас есть возможность пользоваться компьютером, для практических расчетов проще всего использовать встроенный калькулятор операционной системы. В последних двух версиях ОС Windows его можно запустить так: нажмите клавишу Win, наберите буквы «ка» и надавите Enter. В более ранних выпусках этой ОС ссылку «Калькулятор» ищите в подразделе «Стандартные» раздела «Все программы» главного меню системы.
После запуска приложения переключите его в режим, позволяющий работать с тригонометрическими функциями. Сделать это можно выбором строки «Инженерный» в разделе «Вид» меню калькулятора или нажатием клавиш Alt + 2.
Введите значение синуса. По умолчанию в интерфейсе калькулятора нет кнопки для вычисления арксинуса. Чтобы получить возможность использовать эту функцию, вам нужно инвертировать значения кнопок по умолчанию – кликните по клавише Inv в окне программы. В более ранних версиях эту кнопку заменяет чекбокс с таким же обозначением – поставьте в нем отметку.
Кликните по кнопке вычисления синуса – после инвертирования функций ее обозначение сменится на sin⁻¹. Калькулятор рассчитает угол и отобразит его величину.
Можно использовать в расчетах и различные онлайн-сервисы, которых более чем достаточно в интернете. Например, перейдите на страницу http://planetcalc.com/326/, прокрутите ее немного вниз и в поле Input введите значение синуса. Для запуска процедуры вычисления здесь предназначена оранжевая кнопка с надписью Calculate – кликните по ней. Результат вычислений вы найдете в первой строке таблицы под этой кнопкой. Кроме арксинуса в ней отображаются и величины арккосинуса, арктангенса и арккотангенса введенного значения.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Теорема синусов

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, синусы переносим в знаменатели:
bc sinα = ca sinβ
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° – α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° – α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° – α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° – 60°) = sin60° = 3/√2;
- sin150° = sin(180° – 30°) = sin30° = 1/2;
- sin135° = sin(180° – 45°) = sin45° = 2/√2.
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° – α)
Так как sin(180° – α) = sinα, то sinγ = sin(180° – α) = sinα
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
-
Согласно теореме о сумме углов треугольника:
∠B = 180° – 45° – 15° = 120°
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
Синус угла. Таблица синусов.
Синус угла через градусы, минуты и секунды
Синус угла через десятичную запись угла
Как найти угол зная синус этого угла
У синуса есть обратная тригонометрическая функция – arcsin(y)=x
Пример sin(30°) = 1/2; arcsin(1/2) = 30°
Определение синуса
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.

Периодичность синуса
Функция y = sin(x) периодична, с периодом 2π
Площадь треугольника через синус

Определение
Площадь треугольника через синус — это площадь треугольника,
выраженная через две любые стороны треугольника и синус угла между ними.
Синус угла — это число, которое используется для нахождения
разных величин в треугольниках, его можно найти в специальных таблицах.
Введение
Площадь треугольника кроме половины произведения высоты
на основания, можно также найти и другим способом.
Мало кто знает, но через синусы углов можно найти обычно
не только стороны, но и площадь любого треугольника!
Площадь треугольника выраженная без синуса численно равна
половине произведения двух сторон друг на друга
на синус угла между ними.
Площадь треугольника через синус ищется только в том случае,
если по другой формуле площадь треугольника найти нельзя.
Теорема
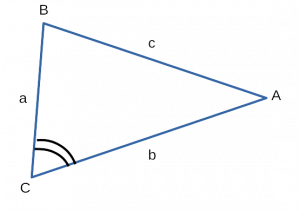
( S = frac<1>2 * BC * AC * sin angle BCA )
Площадь произвольного треугольника равна полусумме
произведения двух любых сторон треугольника друг на друга,
и на синус угла между этими сторонами.
Формула
[ S = frac<1>2 * a * b * sin α ]
Где a, b — две стороны треугольника, синус α — синус угла α.
Пример
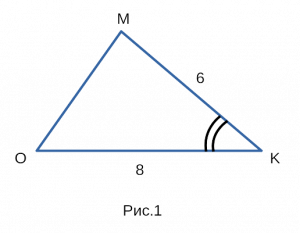
Для примера, возьмем треугольник omk, изображенный на рисунке 1, со сторонами om, mk, ok.
Известно, что mk равен 6, ok равен 8, синус угла okm равен 1/4.
Нужно найти площадь треугольника omk.
Дано: △omk, mk = 6, ok = 8, sin okm = 1/4.
Найти: S △omk — ?
Решение:
1) ( S = frac<1>2*a*b*sin α ) ( implies ) ( S = frac<1>2*mk*ok*sin okm )
2) S = 1/2 * 6 * 8 * 1/4 = 1/2 * 6 * 8 * 0.25 = 1/2 * 48 * 0.25 = 1/2 * 12 = 6
Ответ: Площадь треугольника omk равна 6.
Доказательство
Докажем, что площадь произвольного треугольника
равна полусумме произведения двух любых сторон
друг на друга, и на синус угла между этими сторонами.
Чтобы вам наглядно было видно, как мы доказываем,
используем один из известнейших треугольников — египетский треугольник.
Высота в египетском треугольнике равна длине одного из катетов.
Построим прямоугольный треугольник, изображенный на рисунке 2,
со сторонами 3,4,5 с одним из углов 90 градусов.
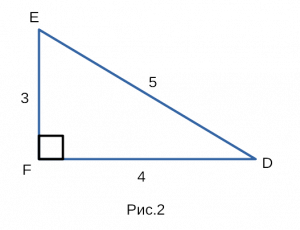
Первым делом найдем площадь обычной формулой,
затем с помощью синуса. Площадь равна половине
основания на высоту — ½3*4 = 6. Теперь найдем с
помощью синуса: ½3*4*sin90 = 6 * 1 = 6. Как видим,
полученные значения площадей сходятся, соответственно
через синус можно найти площадь треугольника ч.т.д.
Теперь, чтобы найти площадь треугольника нам не нужно
знать основание и высоту, можно знать только
две стороны и синус угла между ними.
Заключение
В заключение, можно сказать, что площадь
треугольника можно найти разными способами.
Например, в прямоугольном треугольнике площадь
рассчитать легче чем в любом другом треугольнике,
так как высота уже известна. Именно поэтому,
в школьном курсе, отчасти так подробно изучаются
прямоугольные треугольники. В Древнем Египте были
распространены прямоугольные треугольники со
сторонами 3,4,5; 6,8,10; 5,12,13. Длины этих прямоугольных
треугольников треугольников целые, что значительно,
упрощало разного рода вычисления.
Формулу площади треугольника делает универсальной то,
что она может применена к абсолютно любым треугольникам.
Главное, чтобы были известные две стороны,
и угол или синус угла между ними.
Формула площади треугольника через синус — универсальна,
поэтому может быть применена к любым видам треугольников.
[spoiler title=”источники:”]
http://calc-best.ru/matematicheskie/trigonometriya/sinus-ugla?n1=3
http://colibrus.ru/ploschad-treugolnika-cherez-sinus-ugla-i-dve-storony/
[/spoiler]
