Как найти уклон треугольника

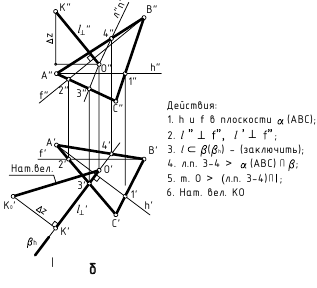
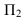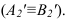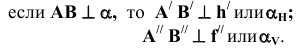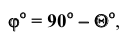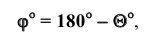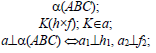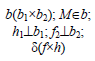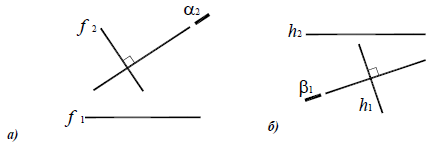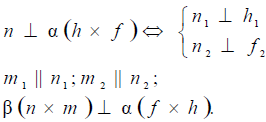Начертательная геометрия, решение задачи №7 ОмГУПС

>>>Назад к решению задач №6 и 8

З а д а ч а 7.

Определить угол наклона плоскости треугольника ABC к плоскостям проекций П₁ и П₂

Порядок решения задачи: проводим линии наибольшего наклона плоскости и способом прямоугольного треугольника определяем углы наклона этих прямых к плоскостям П₁ и П₂.

Линии наибольшего наклона – это линии, лежащие в заданной плоскости и перпендикулярные линиям уровня (горизонтали или фронтали) или следам плоскости.

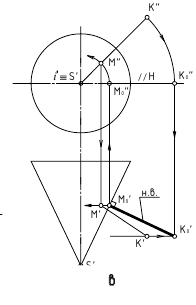
П р и м е р. Дана плоскость треугольника АВС. Определить угол наклона треугольника АВС к плоскости П₁

В плоскости треугольника ABC проводим горизонталь h и из точки A опускаем перпендикуляр к горизонтали C₁D₁, т. е. линию наибольшего наклона к плоскости П₁.

Способом прямоугольного треугольника определяем натуральную величину отрезка |СD| (C₁D 0 ).

Угол между натуральной величиной отрезка СD и его горизонтальной проекцией C₁D₁ является углом наклона АВС к плоскости П₁ (alfa).

Угол между натуральной величиной отрезка и его фронтальной проекцией линии наибольшего наклона к плоскости П₂ является углом наклона АВС к плоскости П₂ (beta).

Чертежи высылаются, сразу после оплаты на карту Сбербанка, Яндекс.Деньги или Киви кошелек, в формате *.cdw (Компас)+рисунки jpeg в цвете в хорошем разрешении 300dpi. По желанию, могу заполнить штампы. Выполнение карандашом таких чертежей на заказ — от 1300 руб. в зависимости от варианта.

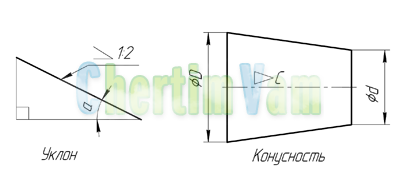
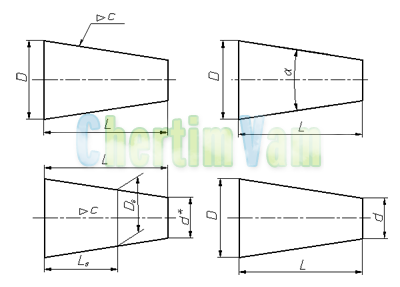
Уклон и Конусность

Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

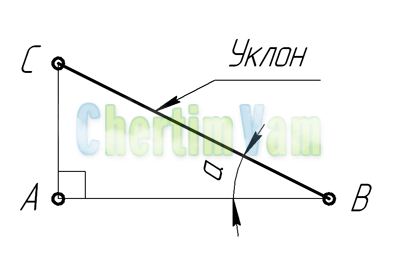
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.

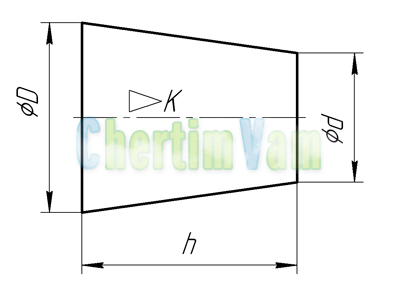
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.

Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.

Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.

Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.

Решение метрических задач в начертательной геометрии с примерами

Содержание:

К метрическим задачам относятся задачи на определение натуральной величины отрезков, расстояний углов, площадей плоских фигур.

Определение натуральной величины отрезка и углов наклона к плоскостям проекций методом прямоугольною треугольника Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка, а вторым – разность расстояний концов отрезка от той плоскости, на которой ведется построение. При этом угол между гипотенузой и катетом проекций является углом наклона отрезка к той плоскости, ряльной величины выполнено на горизонтальной проекции. Поэтому одним катетом прямоугольного треугольника, является горизонтальная проекция

Если необходимо определить угол наклона отрезка АВ к плоскости 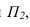то построение прямоугольного треугольника ведется на фронтальной проекции.

Решение метрических задач методами преобразовании проекций

Положении геометрических образов, при которых расстоянии и углы не искажаются на плоскостях проекций

Метрические характеристики объектов на чертежах не искажаются, если геометрические образы занимают частное положение относительно плоскостей проекций.

Приведем некоторые из них.

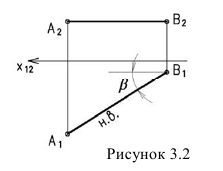
1. Прямая проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.2).

– угол наклона к плоскости

2. Расстояние от точки до прямой проецируется в натуральную величину, если прямая проецирующая (рисунок 3.3).

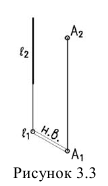
3. Расстояние между параллельными прямыми проецируется в натуральную величину, если прямые проецирующие (рисунок 3.4).

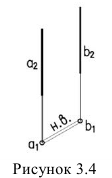
4. Расстояние между скрещивающимися прямыми проецируется в натуральную величину, если одна из прямых проецирующая (рисунок 3.5).

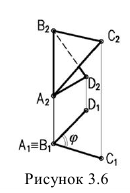
5. Угол между плоскостями (двугранный угол) проецируется в натуральную величину, если ребро угла проецирующее (рисунок 3.6).

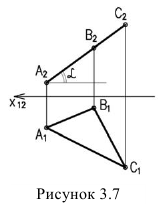
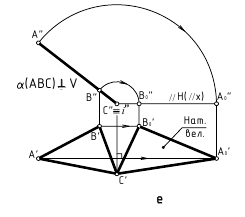
6. Угол наклона плоскости к плоскости проекций проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.7)

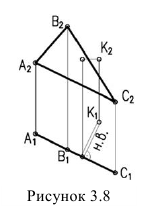
7. Расстояние от точки до плоскости проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.8)

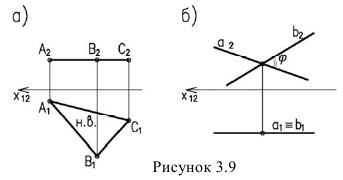
8. Любая плоская фигура проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.9а,б)

Таким образом, для решения метрических задач целесообразно данный объект привести в частное положение с тем, чтобы на одной из новых проекций получить более простое решение задачи.

Для такого перехода и служат способы преобразования проекций.

Существует несколько способов преобразовании проекций: способ вращения вокруг осей перпендикулярных плоскостям проекций, способ плоскопараллельного перемещения, способ замены плоскостей проекций и др.

Четыре основных задачи преобразовании проекций

Этими способами решаются четыре основные задачи:

• Задача 1. Прямую общего положения преобразуем в линию уровня (одно преобразование).
• Задача 2. Прямую общего положения преобразуем в проецирующую (два преобразования)
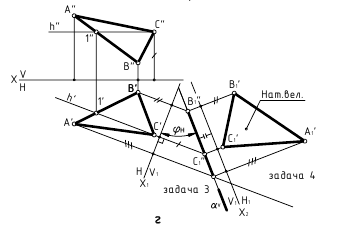
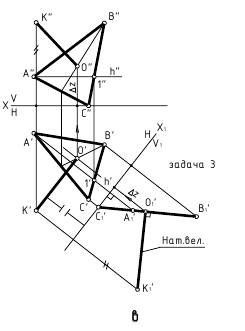
• Задача 3. Плоскость общего положения преобразуем в проецирующую (одно преобразование)
• Задача 4. Плоскость общего положения преобразуем в плоскость уровня (два преобразования)

Решение 1-ой и 2-ой задачи преобразовании проекций методом вращении, плоскопараллельного перемещении и замены плоскостей проекций

Способ вращения

Способ вращения заключается в том, что геометрические образы вращаются вокруг осей перпендикулярных плоскостям проекций до занятия ими какого-либо частного положения относительно плоскостей проекций. При этом одна проекция точки перемещается по окружности, вторая – но прямой параллельной оси проекций.

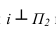
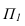
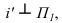
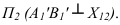
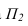
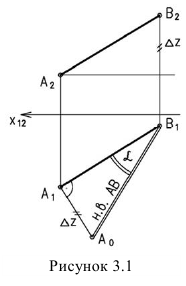
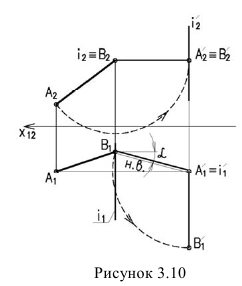
На рисунке 3.10 вокруг осивращаем отрезок ЛВ до положения параллельного плоскости(1 задача). Далее вращением вокруг осиполученный отрезок до положения перпендикулярного плоскости На отрезок с проецируется в точку

Способ плоскопараллельного перемещения

Способ плоскопараллельного перемещения является разновидностью способа вращения (вращение без закрепленных осей), т.е. положение объекта можно преобразовывать путем перемещения его параллельно одной плоскости проекций, одновременно изменяя его положение относительно другой плоскости проекций до занятия им какого-либо частного положения.

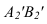
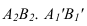
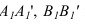
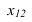
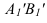
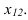
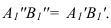
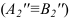
На рисунке 3.11 сначала АВ переводим из общего положения в положение горизонтальное. При этом должно быть равно по величина находим в пересечении вертикальных линий связи и линий параллельных оси (1 задача). Далее отрезок перемещаем до положения перпендикулярного оси При этом На фронтальной проекции отрезок с проецируется в точку (2 задача).

Способ замены плоскостей проекций

Сущность способа замены плоскостей проекций заключается в том, что старая система плоскостей проекций заменяется на новую, с таким расчетом, чтобы относительно новой системы плоскостей, геометрический образ занял какое-то частное положение. При этом нужно помнить, что линии связи будут перпендикулярны относительно новой оси проекций и расстояния от новой оси проекций до новой проекции точки равно расстоянию от старой проекции точки до старой оси.

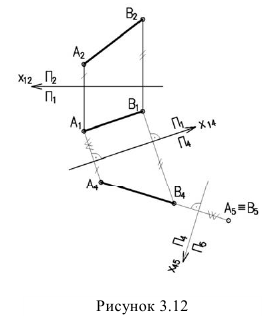
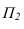
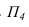
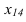
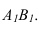
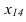
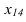
На рисунке 3.12 произведена первая замена плоскость заменена на новую фронтальную плоскость параллельную прямой АВ. При этом новая ось проводится параллельно проекции Линии связи проводятся перпендикулярно оси и на них от откладываются координаты z точек А и В (1 задача).

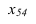
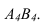
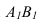
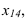
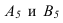
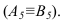
Далее прямую АВ преобразуем в проецирующую. Для этого проводим новую ось перпендикулярно проекции. Т.к. параллельна оси , расстояние до проекций будет одинаковое и прямая спроецируется в точку (2 задача)

Решение 3-ой и 4-ой задачи преобразовании проекций методом плоскопараллельного перемещения и замены плоскостей проекций

Так как метод вращения является более громоздким, рассмотрим решение 3-ей и 4-ой задачи преобразования методом плоскопараллельного перемещения и методом замены плоскостей проекций.

Способ плоскопараллельного перемещения

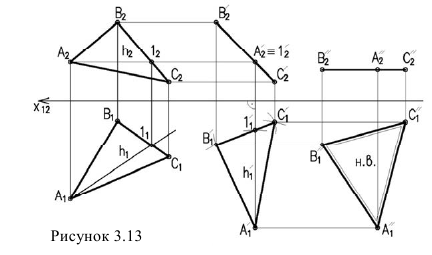
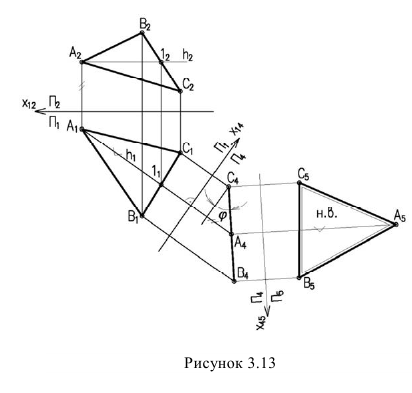
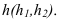
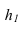
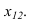
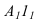
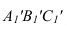
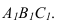
Для того чтобы плоскость из общего положения перевести в проецирующее, нужно иметь ввиду, что при этом ее горизонталь или фронталь должна быть перпендикулярна плоскости проекций. Поэтому на рисунке 3.13 проведена горизонталь Далее располагаем перпендикулярно оси Откладываем на ней отрезок и циркулем строим треугольник равный по величине На фронтальной проекции треугольник проецируется в линию (3 задача).

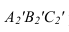
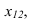
Чтобы плоскость треугольника перевести в положение плоскости уровня, достаточно полученную фронтальную проекцию расположить параллельно оси при этом на горизонтальной проекции треугольник проецируется в натуральную величину (4-я задача)

Способ замены плоскостей проекций

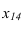
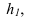
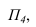
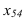
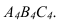
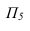
При решении задачи методом замены (рисунок 3.14) новую ось проводим перпендикулярно горизонтали тогда на новую фронтальную плоскость треугольник спроецируется в линию, т.е. станет перпендикулярным (3-я задача). Чтобы плоскость перевести в положение плоскости уровня, необходимо новую ось провести параллельно плоскости На новую плоскость треугольник спроецируется в натуральную величину.

Для того, чтобы методами преобразования решить любую метрическую задачу, необходимо определить какую из четырех основных задач преобразования необходимо решать в каждом конкретном случае.

Метрические задачи

Метрические задачи – это задачи на определение линейных или угловых размеров геометрических объектов, а также расстояний и углов между ними.

Главным вопросом метрических задач является вопрос о построении перпендикуляра к прямой или плоскости. Построение взаимно перпендикулярных прямых было рассмотрено ранее.

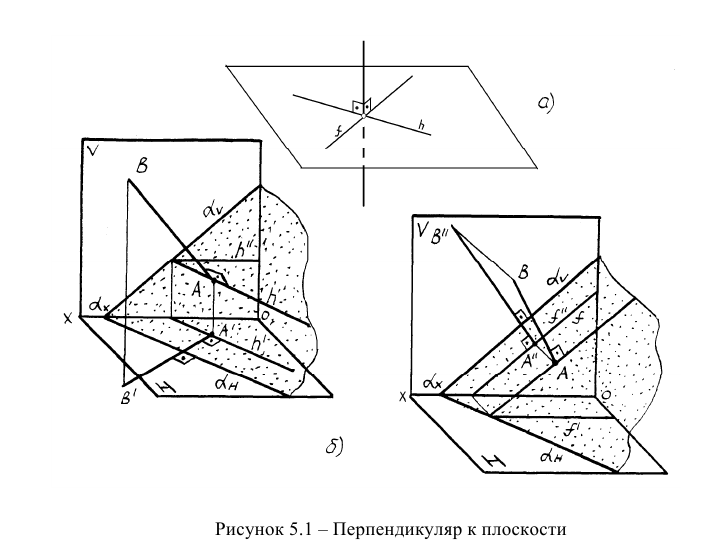
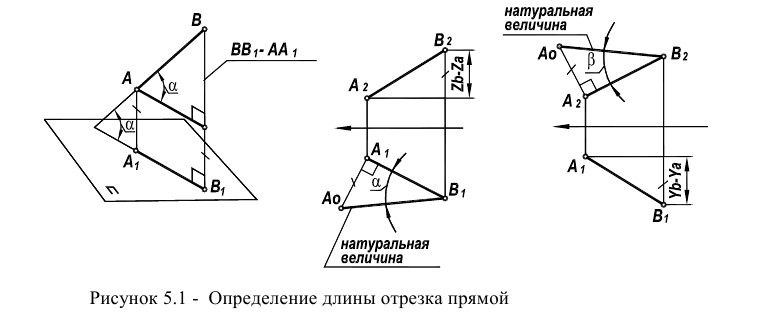
Из элементарной геометрии известно, что прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. В качестве этих пересекающихся прямых наиболее целесообразно использовать горизонталь и фронталь плоскости. Это объясняется тем, что только в этом случае прямой угол будет проецироваться в натуральную величину на соответствующие плоскости проекций. На рисунке 5.1 приведен пространственный чертеж, на котором из плоскости а (из точки А) восстановлен перпендикуляр АВ. Из приведенного изображения можно выяснить методику построения проекций перпендикуляра к плоскости: горизонтальная проекция перпендикуляра к плоскости проводится перпендикулярно горизонтальной проекции горизонтали или горизонтальному следу плоскости, а фронтальная проекция перпендикуляра проводится перпендикулярно фронтальной проекции фронтали или фронтальному следу плоскости. Таким образом, необходимо выполнить следующий алгоритм проведения проекций перпендикуляра к плоскости:

Построение перпендикуляра к плоскость и восстановление перпендикуляра из плоскости называется прямой задачей, а построение плоскости, перпендикулярной к прямой – обратной задачей. Обе задачи решаются по одному и тому же вышеописанному алгоритму. При этом плоскость, перпендикулярную заданной прямой, можно задать следами или пересекающимися горизонталью и фронталью.

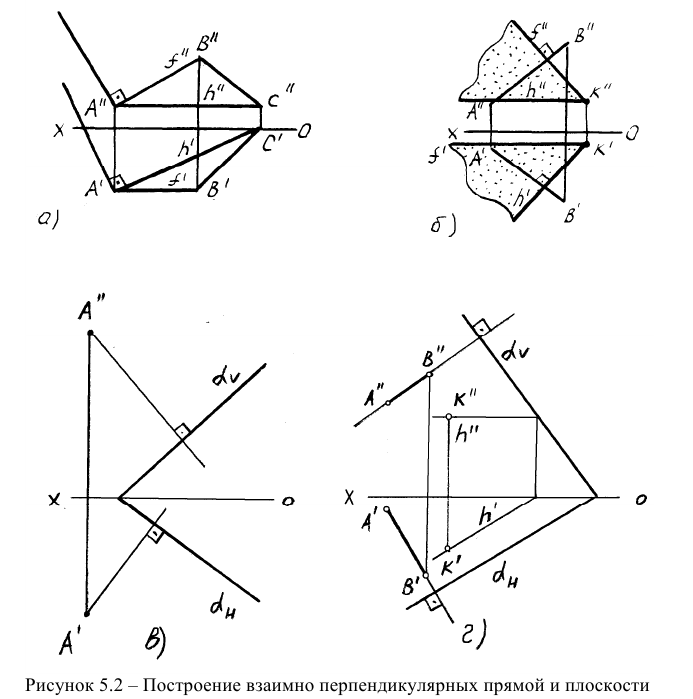
На рисунке 5.2 показано решение прямой (а) и обратной (б) задач. В прямой задаче из точки A треугольника AВС восстановлен перпендикуляр, в обратной задаче через точку К проведена плоскость, перпендикулярная прямой АВ. Плоскость задана пересекающимися горизонталью и фронталью.

Здесь же приведены примеры прямой и обратной задач, если плоскость задана следами. В прямой задаче (в) из точки Л построен перпендикуляр на плоскость, в обратной (г) – через точку К проведена плоскость перпендикулярно прямой АВ.

Определение расстояний между геометрическими объектами

Среди этих задач можно выделить следующие задачи: расстояние от точки до плоскости, расстояние от точки до прямой, расстояние между двумя параллельными прямыми, расстояние между двумя скрещивающимися прямыми, расстояние между двумя параллельными плоскостями и другие. В общем случае все задачи сводятся к определению расстояний между двумя точками.

Чтобы определить расстояние от точки до плоскости, необходимо выполнить ряд логических действий:

1. Из точки опустить перпендикуляр на заданную плоскость;
2. Найти точку встречи перпендикуляра с плоскостью;
3. Определить НВ расстояния между заданной и найденной точками.

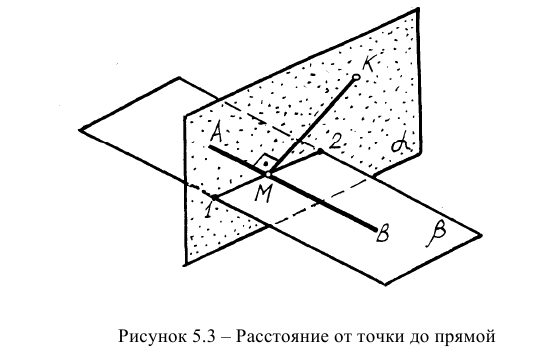
Задача на определение расстояния от точки до прямой решается по следующему плану:

1. Через точку к провести плоскость, перпендикулярную заданной прямой;
2. Найти точку встречи М заданной прямой с проведенной плоскостью;
3. Соединить полученные точки (это будет перпендикуляр из точки на прямую);
4. Определить НВ перпендикуляра.

Пространственная модель решения второй задачи представлена на рисунке 5.3. Рассмотренная задача относится также к задачам на перпендикулярность двух прямых.

Другие упомянутые задачи на определение расстояний легче решаются методами преобразования эпюра, которые будут рассмотрены в последующих разделах.

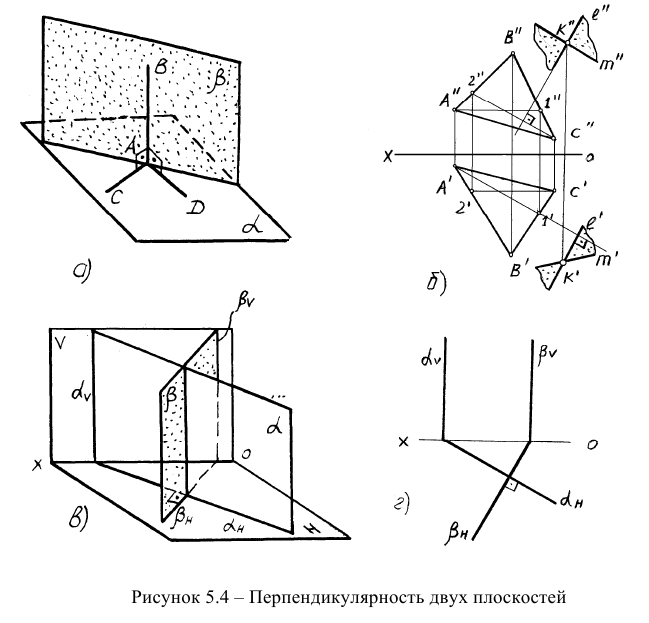
Перпендикулярность плоскостей

Плоскость перпендикулярна другой плоскости, если она содержит прямую, перпендикулярную другой плоскости (рисунок 5.4а). Таким образом, для того, чтобы провести плоскость, перпендикулярную другой, необходимо сначала провести перпендикуляр к заданной плоскости, а затем через него провести искомую плоскость. На рисунке 5.46 представлена задача: через точку К провести плоскость, перпендикулярную плоскости треугольника AВС. Искомая плоскость задана двумя пересекающимися прямыми, одна из которых перпендикулярна заданной плоскости.

Если две плоскости являются одноименными плоскостями частного положения (например, горизонтально- или фронтально-проецирующими), то при перпендикулярности плоскостей их собирательные следы будут перпендикулярны друг другу (рисунок 5.4в,г).

Если плоскости являются плоскостями общего положения, то при их перпендикулярности одноименные следы не будут взаимно перпендикулярны. Другими словами, перпендикулярность одноименных следов плоскостей общего положения не является достаточным условием для перпендикулярности самих плоскостей.

Определение углов между прямой и плоскостью и между двумя плоскостями

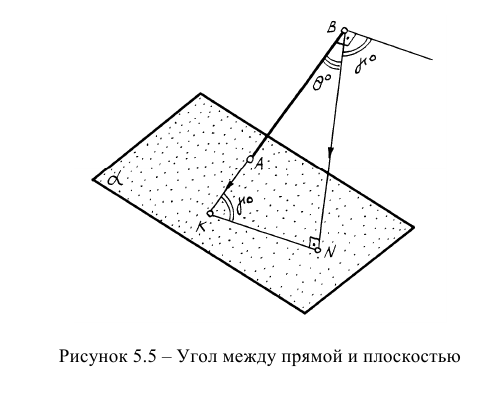
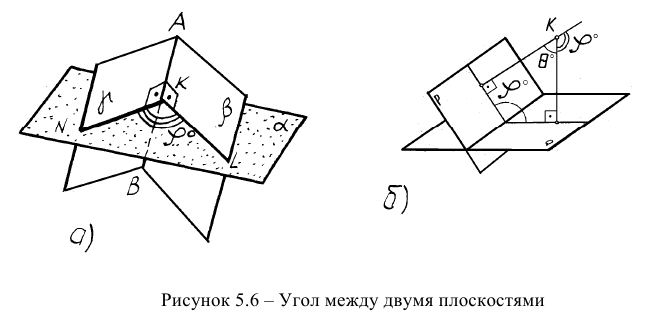
Определение углов между геометрическими объектами является трудоемкой задачей, если её решать традиционными геометрическими способами. Так, например, задачу на определение угла между прямой и плоскостью (рисунок 5.5) можно решить способом, алгоритм которого содержит следующие операции:

1. Определить точку встречи прямой АВ с плоскостью а;
2. Из точки В построить перпендикуляр на плоскость;
3. Найти точку встречи перпендикуляра с плоскостью;
4. Точки К и N соединить и определить НВ угла BKN.

Однако задача может быть значительно упрощена, если использовать способ решения задачи с помощью дополнительного угла. Дополнительным углом назовем угол между заданной прямой АВ и перпендикуляром BN, обозначенный через Из приведенного рисунка видно, что, если из точки В прямой построить на плоскость перпендикуляр, определить НВ дополнительного угла то искомый угол определится по формуле:

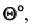
которую можно решить графически, достроив угол 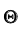до 90°.

То же самое можно сказать о задаче на определение двугранного угла, то есть угла между двумя плоскостями (рисунок 5.66). Первый способ (геометрический) достаточно трудоемок. Он заключается в пересечении угла вспомогательной плоскостью а, перпендикулярной ребру АВ, построении линий пересечения KN и KL и определении натуральной величины угла NKL.

С помощью дополнительного угла задача решается следующим образом. В растворе двугранного угла (рисунок 5.6в) берут любую точку К и строят из неё перпендикуляры на обе плоскости двугранного угла, которые образуют дополнительный угол 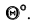Далее определяют НВ дополнительного угла и дополняют его (графически) до 180 градусов, исходя из формулы:

Дополненный угол будет искомым.

Натуральную величину дополнительного угла в обеих задачах наиболее целесообразно определять методом вращения вокруг горизонтали или фронтали, который будет изложен в последующих темах.

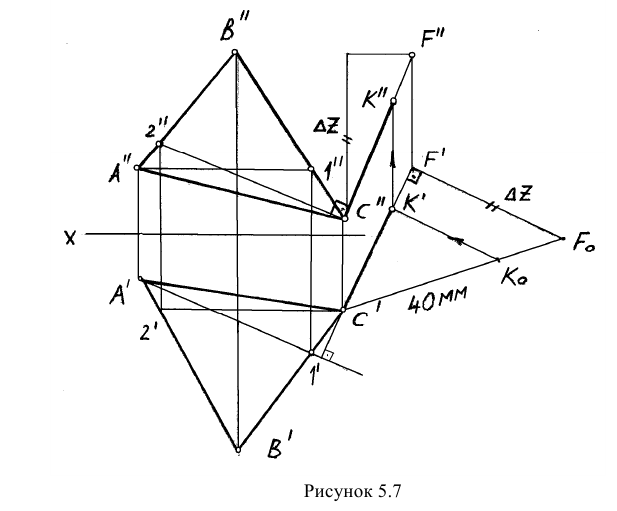
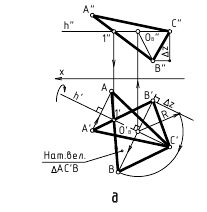
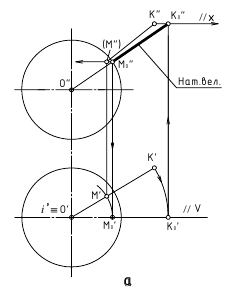
Пример: Из любой вершины треугольника АВС восстановить перпендикуляр длиной 40 мм.

Решение: Сначала необходимо в плоскости треугольника АВС провести горизонталь и фронталь для того, чтобы построить проекции восстановленного перпендикуляра. Далее из точки С проводим проекции перпендикуляра согласно рассмотренному выше алгоритму о перпендикуляре к плоскости. Для того, чтобы отложить 40 мм, необходимо определить НВ ограниченного отрезка перпендикуляра CF (точку F берем произвольно). НВ отрезка CF определяем методом прямоугольного треугольника на горизонтальной проекции CF. Полученную точку К возвращаем на проекции по теореме Фалеса. Получаем проекции перпендикуляра длиной 40 мм (рисунок. 5.7).

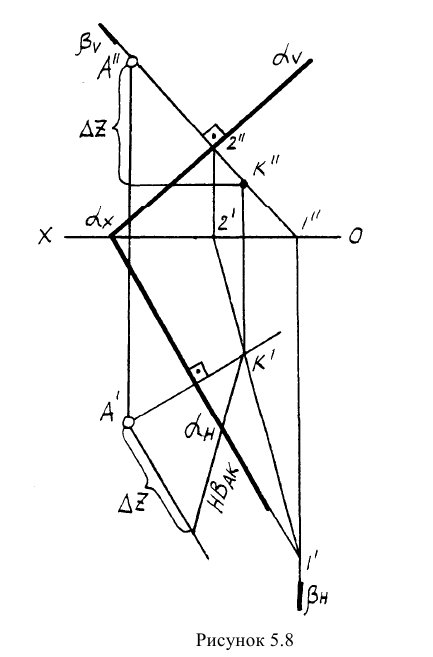
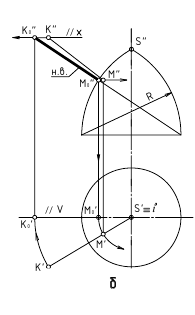
Пример: Найти расстояние от точки А до плоскости, заданной следами

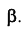
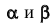
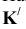
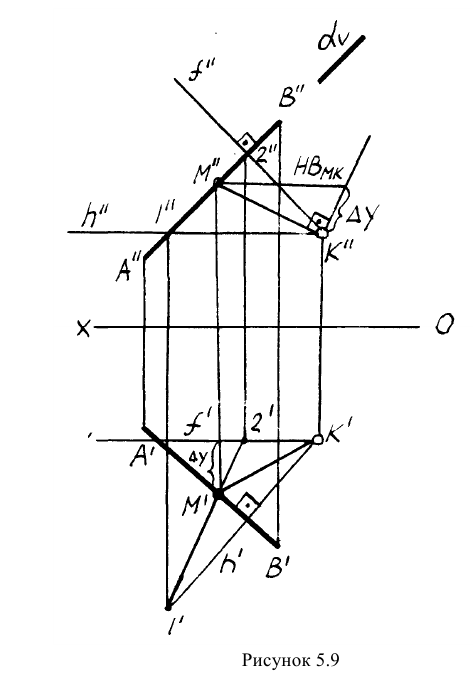
Решение: Из точки А строим перпендикуляр на заданную плоскость. Проекции перпендикуляра проводим перпендикулярно следам. Далее находим точку встречи перпендикуляра с заданной плоскостью с помощью вспомогательной фронтально-проецирующей плоскости Находим линию пересечения плоскостей (линия 1-2) и точку встречи в месте пересечения горизонтальной проекции перпендикуляра с линией 1-2. Методом прямоугольного треугольника определяем НВ расстояния АК (рисунок 5.8).

Пример: Определить расстояние от точки К до прямой AВ.

Решение: Через точку К проводим плоскость, перпендикулярную заданной прямой. Плоскость задаем пересекающимися горизонталью и фронталью. Их проекции проводим согласно алгоритму о перпендикуляре к плоскости (обратная задача). Далее находим точку встречи прямой AВ с проведенной плоскостью (точка М). Определяем натуральную величину КМ методом прямоугольного треугольника (рисунок 5.9).

Примеры метрических задач

Задачи, в которых определяются различные геометрические величины -расстояния между объектами, длины отрезков, углы, площади и т.д. называются метрическими. Решение многих метрических задач, например задач на определение кратчайших расстояний, требует построения перпендикулярных прямых и плоскостей.

Перпендикулярность является частным случаем пересечения прямых, прямой и плоскости или двух плоскостей. Необходимо установить соотношения, по которым строятся проекции перпендикулярных прямых и плоскостей.

Теорема о проекциях прямого угла

Прямой угол проецируется на плоскость без искажения, если одна из его сторон параллельна этой плоскости (рис. 10.1).

Рис. 10.1. Теорема о проекциях прямого угла

Дано :BAC = 90°; AB || П’

Доказать, что C’A’A’B’

Доказательство: если AB||П’, то A’B’||AB, но AA’П’^AA’A’B’ значит ABAA,AB плоскости CAA’C’, тогда и A’B’ CAA’C’. Следовательно,CA’A’B’.

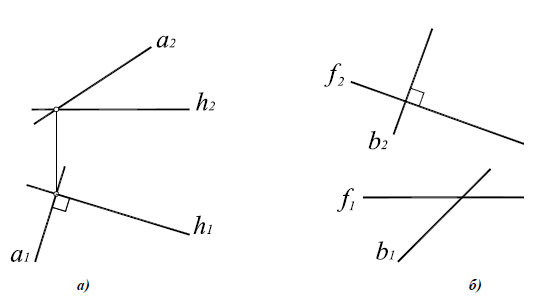
На основании этой теоремы две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся) проецируются на П₁ в виде взаимно перпендикулярных прямых, если одна из них горизонталь, на П₂ – если одна из них фронталь (рис. 10.2,а).

Условие перпендикулярности скрещивающихся прямых (рис. 10.2,б) сводятся к условиям перпендикулярности пересекающихся прямых, поведенных через произвольную точку и соответственно параллельных скрещивающимся прямым. Таким образом, понятие перпендикулярности можно отнести как к пересекающимся, так и к скрещивающимся прямым.

Рис. 10.2. Перпендикулярные прямые:
а -пересекающиеся a₁ h₁ a h ;
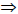
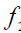
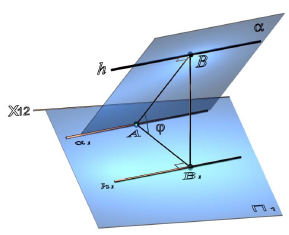
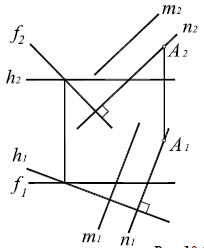
б -скрещивающиеся b2 ₂ b

Линии наибольшего наклона плоскости

Прямые, лежащие в плоскости и перпендикулярные линиям уровня этой плоскости, называются линиями наибольшего наклона к соответствующей плоскости проекций (рис. 10.3). Так, прямая, лежащая в плоскости и перпендикулярная горизонтали плоскости, называется линией наибольшего наклона к горизонтальной плоскости проекций, а прямая, перпендикулярная фронтали – линией наибольшего наклона к фронтальной плоскости проекций.

Угол между линией наибольшего наклона и ее проекцией на соответствующую плоскость равен углу наклона плоскости к плоскости проекций (см. рис. 9.15).

Рис. 10.3. Линия наибольшего наклона плоскости а к П₁:
а – плоскость общего положения; h ∈α – горизонталь плоскости а; AB h – линия наибольшего наклона;
φ = AB, AB ₁ – угол наклона плоскости а к П₁

Перпендикулярность прямой и плоскости

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. На основании теоремы о проекциях прямого угла можно получить условие перпендикулярности прямой общего положения и плоскости общего положения:
Если прямая а перпендикулярна плоскости α(ABC), то ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости.

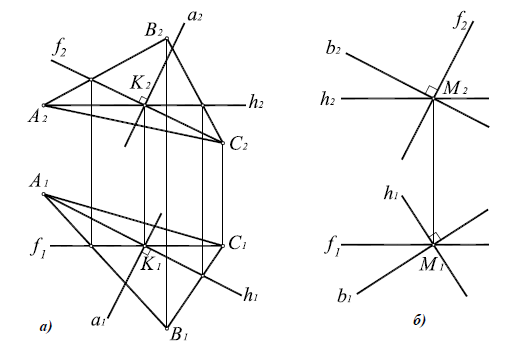
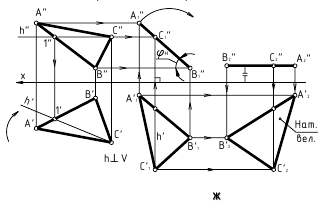
Например, при построении прямой а, перпендикулярной плоскости α(ABC) (рис. 10.4,а), в плоскости строятся линии уровня – горизонталь и фронталь, затем через произвольную точку в плоскости, в данном случае точку K(h×), строится прямая, горизонтальная проекция которой перпендикулярна горизонтальной проекции горизонтали плоскости α(ABC), а фронтальная проекция – фронтальной проекции фронтали плоскости.

Рис. 10.4. Перпендикулярность прямой и плоскости:

а -построение прямой, перпендикулярной плоскости:

б -построение плоскости, перпендикулярной прямой:

Аналогично решается задача о построении плоскости, перпендикулярной прямой общего положения (рис. 10.4,б)

Если плоскость проецирующая, проекции линий уровня совпадают со следом плоскости, перпендикулярность устанавливается по отношению к следу плоскости. Горизонтальная проекция перпендикуляра к горизонтально-проецирующей плоскости строится перпендикулярно горизонтальному следу плоскости (рис. 10.5,а). Прямая, перпендикулярная горизонтально-проецирующей плоскости, занимает положение горизонтальной линии уровня.
Аналогично, фронтальная проекция перпендикуляра к фронтально-проецирующей плоскости строится перпендикулярно фронтальному следу плоскости (рис. 10.5,б). Прямая, перпендикулярная фронтально-проецирующей плоскости, занимает положение фронтали.

Рис. 10.5. Перпендикулярность прямой и проецирующей плоскости:
а -построение прямой, перпендикулярной плоскости;
б -построение плоскости, перпендикулярной прямой

Взаимная перпендикулярность плоскостей

Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Таким образом, построение взаимно перпендикулярных плоскостей сводится к построению перпендикулярных прямой и плоскости. Например, чтобы через произвольную точку А провести плоскость, перпендикулярную плоскости a(× h) (рис. 10.6), достаточно построить прямую n,перпендикулярную плоскости α(×h): n₁h₁; n₂₂. Вторая прямая m, определяющая искомую плоскость, может быть задана произвольно – как пересекающая прямую n или параллельная ей.

Рис. 10.6. Перпендикулярность двух плоскостей

Дано: α(h × ) ; A (A₁, A₂).

Построить: A ∈ β α .

Определение метрических задач

Традиционно задачи, связанные с измерением длин, углов, площадей и объемов относят к метрическим. В основе решения этих задач лежит определение длины отрезка и, как производной от этого, площади плоской фигуры.

Определение длины отрезка

Одним из наиболее распространенных методов (рисунок 5.1) является метод прямоугольного треугольника (так его называют в начертательной геометрии) или метод ортогональных дополнений (название, принятое в линейной алгебре).

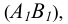
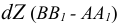
Идея метода базируется на следующем. Истинная величина отрезка AВ является гипотенузой прямоугольного треугольника, один из катетов которого, является проекцией отрезка AВ на плоскость проекции а второй катет -разница координат концов отрезка для оси, отсутствующей в рассматриваемой плоскости проекции (ортогональное дополнение). Угол между проекцией и гипотенузой этого треугольника (а) определяет наклон прямой к соответствующей плоскости проекции.

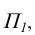
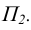
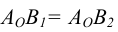
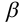
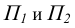
На комплексном чертеже возможно решение как на плоскости так и на плоскости При правильных построениях . Углы а и -углы наклона отрезка прямой АВ к плоскости соответственно.

Определение площади треугольника

Определение площади треугольника и величины плоского угла можно свести к известной задаче построения треугольника по трем сторонам.

Для этого достаточно, используя рассмотренный выше способ прямоугольного треугольника, найти по порядку истинные величины сторон (в соответствии с рисунком 5.2), а затем на свободном месте построить треугольник по трем сторонам.

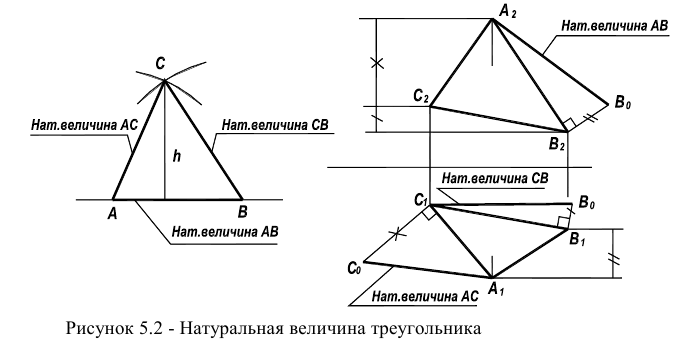
Величина плоского угла между двумя любыми сторонами этой фигуры может быть измерена на истинной величине треугольника.

Проецирование прямого угла

Решение многих задач Начертательной геометрии связано с необходимостью построения на чертеже взаимно перпендикулярных прямых и плоскостей. Базой для этого служит умение строить прямые углы на комплексном чертеже.

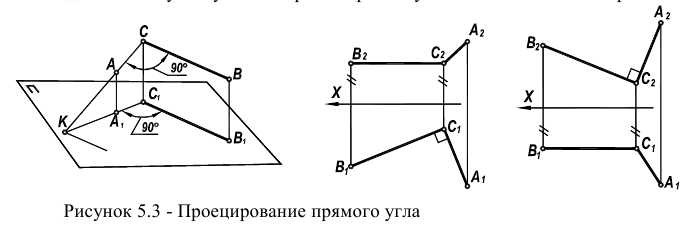
Известная в теории чертежа теорема (приведем ее без доказательства) утверждает, что прямой угол (в соответствии с рисунком 5.3) проецируется на

соответствующую плоскость проекций вез искажения, если одна из его сторон параллельна этой плоскости проекций, а вторая – ей не перпендикулярна.

Перпендикулярность прямых и плоскостей

Выше уже отмечалось, что в трехмерном Евклидовом пространстве отсутствует полная параллельность, то же самое можно сказать и о перпендикулярности. Понятие перпендикулярности так же, как и параллельности, вводится через определение.

Перпендикулярность прямой и плоскости

Считают, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся (любым) прямым этой плоскости.

При решении задачи возможны два варианта: проведение перпендикулярной прямой к плоскости из внешней точки и из точки, лежащей в плоскости.
Рассмотрим возможность проведения перпендикуляра из точки К, лежащей в плоскости общего положения Р, заданной следами (рисунок 5.4).

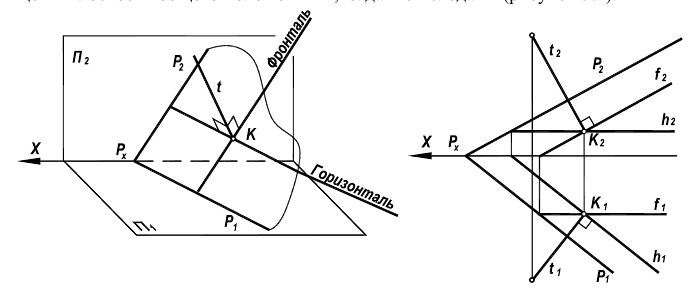
Рисунок 5.4 – Перпендикулярность прямой и плоскости

В плоскости Р (через точку К) проводятся горизонталь h и фронталь f. Прямые, перпендикулярные соответствующим проекциям линий уровня в соответствии с теоремой о проецировании прямого угла и данным выше определением, могут быть приняты за проекции прямой .

В том случае, когда точка К не лежит в плоскости Р, решение задачи аналогично (рисунок 5.5).

Поскольку положение точки пересечения искомого перпендикуляра не определено, решение соответствует следующей схеме:

а) в плоскости проводятся горизонталь h (через точку В) и фронталь f (через точку A), в случае задания плоскости следами за фронталь и горизонталь принимаются соответствующие следы плоскости

Рисунок 5.5 – Перпендикуляр к плоскости

б) из внешней точки К к соответствующим проекциям линий уровня (следам) проводятся перпендикулярные прямые– Линия t принимается за перпендикуляр, опущенный из точки К к плоскости Р;

в) определяется точка S пересечения этого перпендикуляра t и плоскости.

Расстояние от точки до плоскости

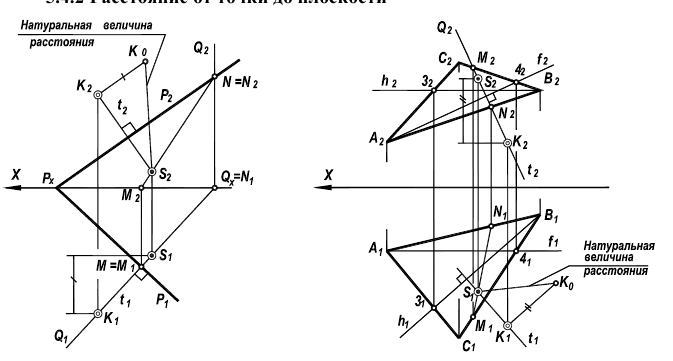
Рисунок 5.6 – Расстояние от точки до плоскости

Задачу на определение расстояние от точки до плоскости (рисунок 5.6) можно свести к решению уже известных задач на построение перпендикуляра к плоскости (рисунок 5.5) и определения натуральной величины отрезка прямой (рисунок 5.1)

Перпендикулярность плоскостей

Считают, что две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную другой плоскости.

Задача может ставиться, как проведение плоскости, перпендикулярной заданной, проходящей через точку или прямую.

При проведении искомой плоскости через точку, как и в предыдущем случае, возможны два варианта проведения плоскости перпендикулярной заданной: через точку, лежащую в плоскости и через точку вне ее (рисунок 5.7).

Точно такой же вариант возникает и при проведении перпендикулярной плоскости через прямую (лежащую в исходной плоскости или не лежащую).

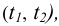
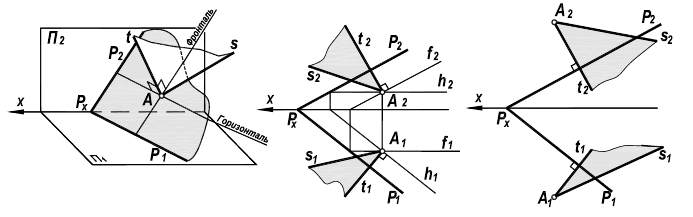
Рассмотрим вариант построения плоскости, проходящей через точку. Пусть точка А лежит в плоскости Р. Линии перпендикулярные соответствующим проекциям линий уровня (следам), определят перпендикуляр t к плоскости Р.

Рисунок 5.7 – Перпендикулярность плоскостей
Проведение через точку А произвольной прямой s позволяет определить плоскость Q, которая будет перпендикулярна плоскости Р.

Если точка А лежит вне плоскости Р, то решение аналогично. Проведение через точку А перпендикуляра t и произвольной прямой s определит плоскость Q, которая также, по определению, будет перпендикулярна плоскости Р.

Решение задачи на проведение плоскости через прямую аналогично решению задачи по проведению плоскости через точку. Достаточно вместо произвольной прямой s использовать заданную прямую АВ. И тогда, в соответствии с рисунком 5.8, задача сведется к проведению перпендикуляра t к плоскости Р (из точки, лежащей в плоскости или лежащей вне ее).

Рисунок 5.8 – Перпендикулярность плоскостей

Определение натуральных величин геометрических элементов

1. Определить натуральную величину отрезка общего положения:

• способом прямоугольного треугольника;
• способом замены плоскостей проекций преобразовать в прямую уровня;
• способом вращения вокруг проецирующей оси преобразовать в прямую уровня.

2. Определить натуральную величину плоскости общего положения (замкнутого отсека):

• способом замены плоскостей проекций преобразовать в плоскость уровня;
• способом вращения вокруг линии уровня преобразовать в плоскость уровня;
• способом плоскопараллельного перемещения преобразовать в плоскость уровня.

Определение расстояния между геометрическими элементами (образами)

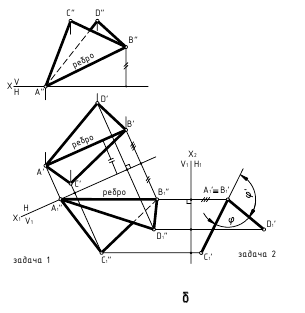
1. Определить расстояние от точки до прямой общего положения:

• способом замены плоскостей проекций преобразовать плоскость, заданную прямой и точкой, в плоскость уровня (задачи 3 и 4 преобразования; прямую и точку рассматривать как плоскость);
• способом замены плоскостей проекций преобразовать прямую общего положения в проецирующую прямую (задачи 1 и 2 преобразования);
• способом вращения вокруг линии уровня преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
• способом плоскопараллельного перемещения преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
• способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить через заданную точку плоскость, перпендикулярную к прямой, и определить точку пересечения последней с плоскостью.

2. Определить расстояние между параллельными прямыми:

• способом замены плоскостей проекций преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня (задачи 3 и 4 преобразования);
• способом замены плоскостей проекций преобразовать две параллельные общего положения в проецирующие прямые (задачи 1 и 2 преобразования);
• способом вращения вокруг линии уровня преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня, ограничив ее замкнутым отсеком;
• способом плоскопараллельного перемещения преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня;
• способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить плоскость через любую точку, принадлежащую одной из прямых, перпендикулярную ко второй прямой, и определить точку пересечения этой плоскости со второй прямой.

3. Определить расстояние между скрещивающимися прямыми, преобразовав одну из прямых в проецирующую (задачи 1 и 2 преобразования).

4. Определить расстояние от точки до плоскости:

• по теме «Перпендикулярность» – провести перпендикуляр к плоскости, построить точку пересечения этого перпендикуляра с заданной плоскостью и найти любым способом натуральную величину построенного отрезка (см. пункт 1);
• способом замены плоскостей проекций преобразовать плоскость общего положения в плоскость проецирующую.

5. Определить расстояние от точки до поверхности вращения:

• способом замены плоскостей проекций преобразовать плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня (задача 4 преобразования);
• способом вращения вокруг проецирующей оси повернуть плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня.

Определение углов наклона геометрических элементов к плоскостям проекций H и V

1. Определить углы наклона прямой общего положения к плоскостям проекций H и V:

• способом прямоугольного треугольника построить на двух проекциях натуральные величины отрезка и определить углы наклона прямой;
• способом замены плоскостей проекций преобразовать прямую общего положения в горизонтальную, а затем во фронтальную прямую (задача 1 преобразования);
• способом вращения вокруг соответствующей проецирующей оси преобразовать прямую общего положения в горизонтальную и во фронтальную прямые.

2. Определить угол наклона прямой к заданной плоскости общего положения:

• из любой точки прямой опустить перпендикуляр к плоскости;
• способом вращения вокруг линии уровня преобразовать построенную плоскость, заданную прямой и перпендикуляром, в плоскость уровня;
• искомый угол будет дополнять построенный угол до 90°.

3. Определить величину двухгранного угла, если на чертеже есть линии пересечения плоскостей, образующих двухгранный угол (ребро):

• способом замены плоскостей проекций преобразовать ребро двухгранного угла в проецирующую прямую (задачи 1 и 2 преобразования).

4. Определить угол между двумя плоскостями общего положения, если на чертеже нет линии пересечения заданных плоскостей (ребра):

• задача решается косвенным путем, для чего из любой точки пространства следует опустить перпендикуляры к заданным плоскостям, которые, в свою очередь, задают вспомогательную плоскость, перпендикулярную к этим плоскостям;
• эту вспомогательную плоскость способом вращения вокруг линии уровня следует преобразовать в плоскость уровня, определив угол между перпендикулярами (преобразование вспомогательной плоскости в плоскость уровня возможно и другими способами – ее плоскопараллельным перемещением или заменой плоскостей проекций);
• искомый угол будет дополнять построенный угол до 180° (углом между плоскостями считают угол острый).

Структуризация материала тринадцатой лекции в рассмотренном объеме схематически представлена на рис. 13.1 (лист 1). На последующих листах 2–7 компактно приведены иллюстрации к этой схеме для визуального повторения изученного материала при его повторении (рис. 13.2–13.7).

Метрические задачи:

Определение натуральной величины геометрических элементов:

1. Определение длины отрезка

Способ прямоугольного треугольника

Способ замены плоскостей проекций (задача 1)

Способ вращения вокруг проецирующей оси

2. Определение площади замкнутого отсека

Способ замены плоскостей проекций (задачи 3 и 4)

Способ вращения вокруг прямой уровня (горизонтали)

Способ вращения вокруг проецирующей оси i(i V)

Способ плоско-параллельного перемещения (переноса)

Определение расстояний:

1. Расстояние между точками – определяется величиной отрезка, соединяющего эти точки

2. Расстояние от точки до прямой – определяется величиной перпендикуляра, опущенного из точки к прямой

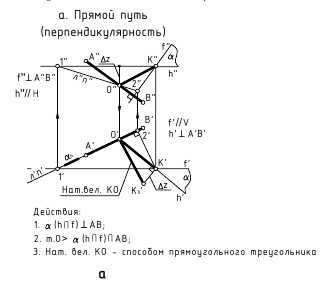
а. Прямой путь (перпендикулярность)

б. Способ замены плоскостей проекций: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис. 13.2, г)

в. Способ вращения вокруг прямой уровня: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, д)

г. Способ плоскопараллельного переноса: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, ж)

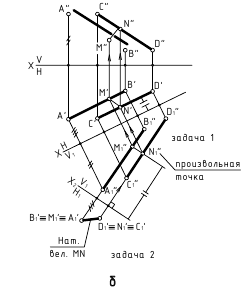
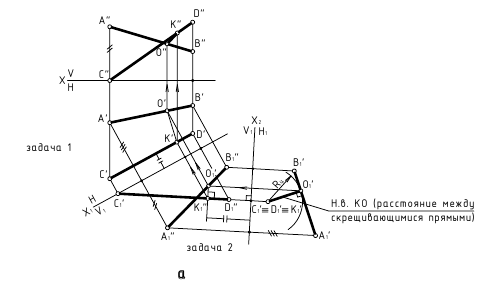
3. Расстояние между параллельными прямыми – определяется величиной перпендикуляра, проведённого из произвольной точки одной прямой к другой прямой

а. Способ замены плоскостей проекции (рассматриваем две прямые) – задачи 1 и 2 (преобразовать прямые общего положения AB и CD в проецирующие)

б. Способ замены плоскостей проекции (рассматриваем плоскость, которую определяют параллельные прямые) – задачи 3 и 4 (определить натуральную величину плоскости ? (AB//СВ))

4. Расстояние между скрещивающимися прямыми – определяется величиной перпендикуляра, проведённого от одной из прямых, преобразованной в точку, к другой прямой (задачи 1 и 2 замены плоскостей проекции).

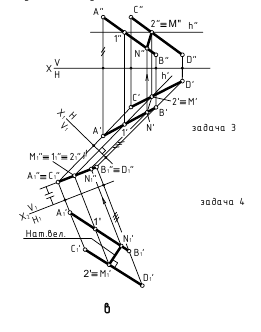
Способ замены плоскостей проекций – задачи 1 и 2

5. Расстояние от точки до плоскости – определяется величиной перпендикуляра, проведённого из точки на плоскость до точки его пересечения с этой плоскостью.

а. Прямой путь (перпендикулярность)

б. Способ замены плоскостей проекций (плоскость преобразовать в проецирующую – задача 3)

6. Расстояние между прямой и параллельной ей плоскостью – определяется величиной перпендикуляра, проведённого из произвольной точки на прямой к плоскости.

7. Расстояние между параллельными плоскостями – определяется величиной отрезка перпендикуляра, опущенного из точки одной плоскости на другую плоскость (до точки пересечения с другой плоскостью).

8. Расстояние от точки до поверхности

a. Cпособ вращения вокруг проецирующей оси

б. Способ замены плоскостей проекции

Определение величин углов:

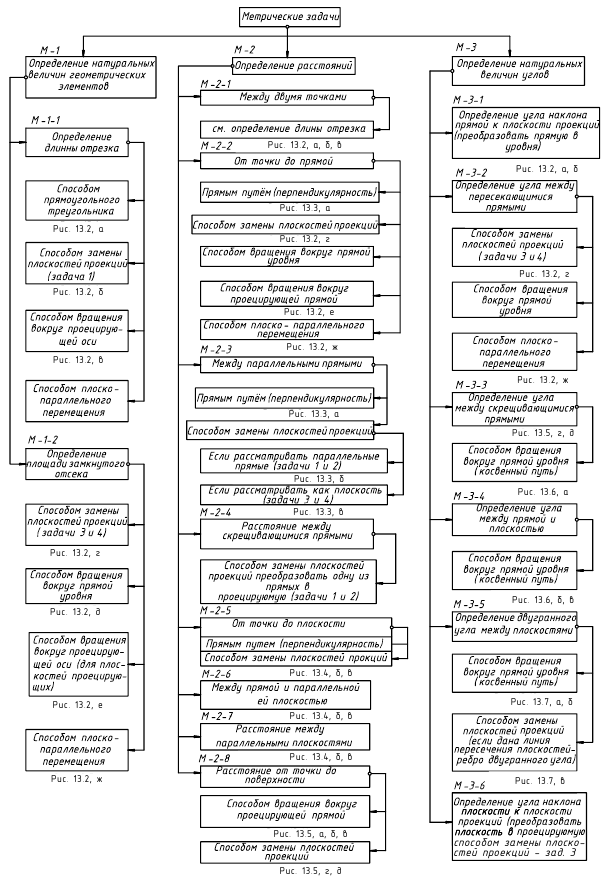
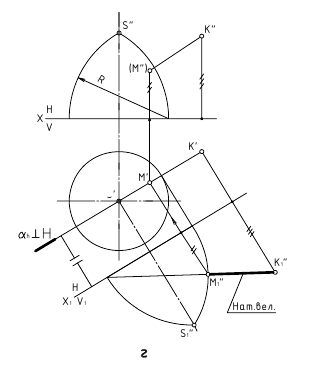
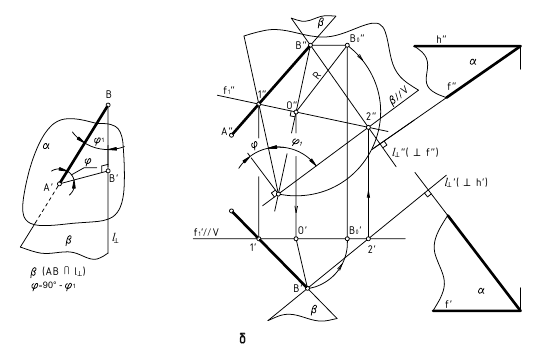
1. Угол φ между скрещивающимися прямыми – определяется плоским углом, образованным двумя пересекающимися прямыми, проведёнными из произвольной точки пространства параллельно скрещивающимся прямым (рис. 13.6, а)

Способ вращения вокруг линии уровня

Дано:
а и b – скрещивающиеся прямые
Требуется:
∠φ – ?

Решение:
1.
2. ∠φ – вращением вокруг фронтали, проведённой в построенной плоскости α(d ∩с)

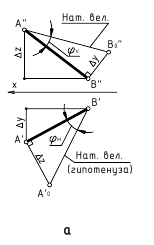
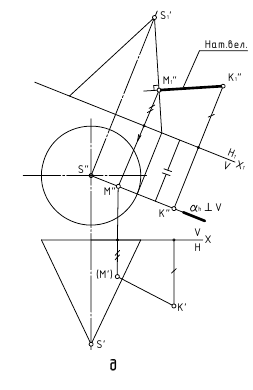
2. Угол φ между прямой и плоскостью – определяется углом между прямой и её проекцией на эту плоскость.

Дано:
α(h ∩ f);
AB – прямая общего положения
Требуется:
∠φ – ?

Решение:
1. l α(h ∩ f);
l” f”;
l‘ h’;
2. ∠φ – вращением вокруг фронтали, проведённой в построенной плоскости β(AB∩l)

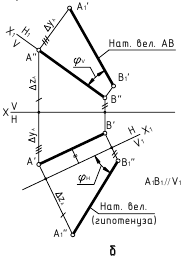
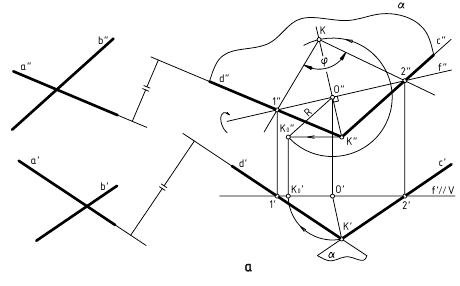
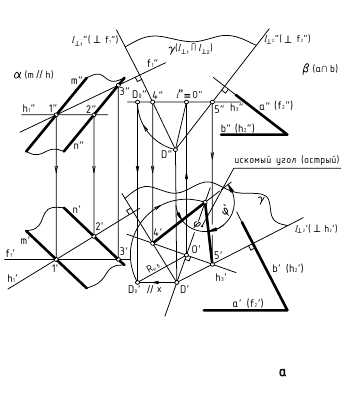
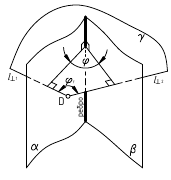
3. Угол φ между плоскостями α и β – определяется линейным углом, образованным двумя прямыми, по которым некоторая плоскость γ, перпендикулярная плоскостям (или их ребру), пересекает эти плоскости (углом между плоскостями считают острый угол).

а. Если на чертеже нет ребра (линии пересечения заданных плоскостей) – угол φ определяется способом вращения вокруг линии уровня (рис. а)

Дано:
(m // h); (а ∩ b).
Требуется:
∠φ – ?
Решение:
1. провести в заданной плоскости фронтали и горизонтали;

2. из произвольной точки пространства D (D’, D”) провести перпендикуляры l₁ и l₂ к заданными плоскостям, которые определяют плоскость γ(l₁ ∩ l₂);
3. ∠φ – вращением вокруг горизонтали h₃, проведённой в построенной плоскости γ(l₁ ∩ l₂).

б. Если на чертеже есть ребро (линия пересечения заданных плоскостей) – угол φ определяется способом замены плоскостей проекций (задачи 1 и 2, рис. б)

ребро АВ двугранного угла преобразовать двумя заменами в проецирующую прямую.

Рекомендую подробно изучить предметы:

Инженерная графика Начертательная геометрия Компас Автокад Черчение Проекционное черчение Аксонометрическое черчение Строительное черчение Техническое черчение Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

• Тени в ортогональных проекциях
• Кривые поверхности
• Пересечения криволинейных поверхностей
• Пересечения поверхностей с прямой и плоскостью
• Пересечение поверхности плоскостью и прямой
• Развертки поверхностей
• Способы преобразования проекций
• Взаимное положение прямой и плоскости

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

[spoiler title=”источники:”]

http://www.evkova.org/reshenie-metricheskih-zadach

[/spoiler]

Наклон под любым углом – это подъем над трассой. Наклон треугольника измеряет его «крутизну». Представьте себе вертикальный прямоугольный треугольник. По мере того, как его гипотенуза достигает соседнего – также называемого основания или бега – наклон уменьшается. Если вы сгладите его достаточно, треугольник станет прямой линией с гипотенузой, смежной и противоположной – также называемой возвышением или перпендикуляром – падающей в прямую линию. И наоборот, если вы вытащили треугольник из его вершины или подтолкнули гипотенузу ближе к противоположному, наклон увеличивается. Когда гипотенуза бесконечно близко к противоположному, наклон треугольника стремится достичь бесконечности. Следовательно, наклон треугольника может варьироваться между двумя крайностями – нулем и бесконечностью. Формула для нахождения наклона треугольника имеет вид: Slope = противоположный / соседний

Измерьте длину противоположной стороны. Допустим, это 5 сантиметров.

Измерьте длину соседней стороны. Допустим, это 2 сантиметра.

Разделите противоположное на соседний, чтобы получить уклон. В этом примере наклон составляет 5 сантиметров, разделенных на 2 сантиметра. Это делит на 2, 5. Это число означает, что для каждого изменения юнита в соседних – или пробегах – противоположное изменение или увеличение в 2, 5 раза, что меняется.

Математическая продлёнка. Про углы и тригонометрию

Продолжаю знакомить вас с наработками к занятиям математического кружка. В этой статье собраны два сюжета, связанные друг с другом одной темой: математика углов и тригонометрия. Каким образом обосновываются угловые меры? Какие из них для чего более пригодны? Почему значения тригонометрических функций от рациональных долей окружности почти все иррациональны и, наоборот, почему в рациональной тригонометрии только восемь рациональных углов и те, по большей части тривиальны? Материал рассчитан на школьников, но он приоткрывает двери в большую математику, поэтому здесь появятся элементы теории чисел, теории алгебраических полей и полиномы Чебышёва.

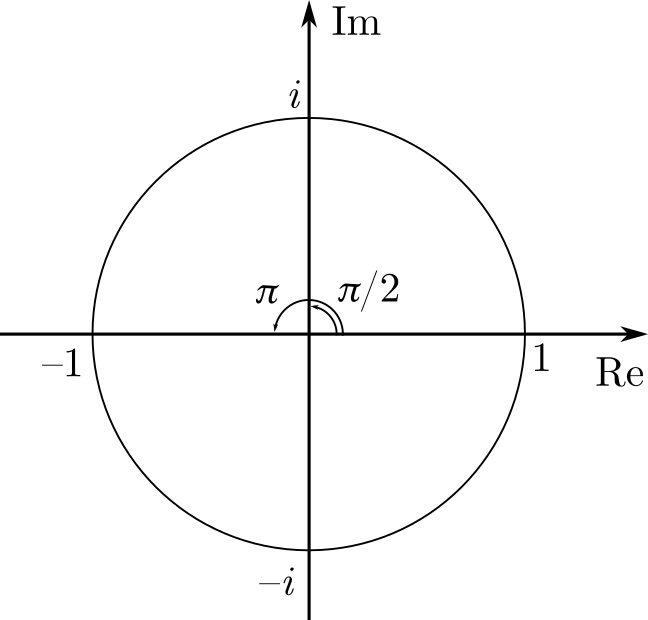
В чём лучше измерять углы?

— А вам зачем? Определить направление в море, или, может быть, узнать уклон дороги? Хотите найти расстояние на сфере, либо угловое расстояние между звёздами? Или вам для геометрических нужд, треугольничек построить или звезду пятиконечную? Может, вас тригонометрия интересует, синус вычислить, координату какую отыскать, или фигуру Лиссажу нарисовать даме к 8 марта? Или вы больше по физике: вращения, колебания, гармонические функции, спектры, дифференциальные уравнения. А топологию окружности или группу поворотов изучить не желаете?

Для разных задач годятся разные меры, и какую попало выбирать не стоит. Во-первых, надо, что бы углы выражались числами (желательно, удобными — целыми или рациональными) и были пригодны для бытового использования. Во-вторых, они должны быть удобны для геометрических построений, имели внятные значения для часто встречающихся геометрических фигур. И, в-третьих, помогали нам дружить с тригонометрией и алгеброй — не одними же только циркулем и линейкой вычислять!

Обороты

Для длины абсолютной единицы не существует, выбирай, хоть аршин, хоть астрономическую единицу, хоть планковскую. А вот с оборотами не так. Полный оборот — сам себе единица. Вещь в себе, так сказать. Раз такое дело, самым естественным решением будет измерять углы оборотами и его долями. Нормальный способ, именно его мы используем для измерения частоты вращения, когда пишем об/минуту или когда просим кого нибудь повернуться на четверть-оборота для фотографии.

Однако, для геометрических нужд имеет смысл оборот представить, не как единицу, а как двойку, точнее, как два развернутых угла. Преимущества этого способа могут быть заметны при измерении углов правильных многоугольников, все они будут выражаться понятными говорящими дробями. Сумма углов в треугольнике тогда будет равна 1, в правильном многоугольнике с вершинами — Углы в квадрате: 1/4, в равностороннем треугольнике — 1/3, в пятиугольной звезде — 1/10, в пятиугольнике — 3/5. Удобно.

Грады и градусы

Но правильные дроби нравятся не всем. Так вышло, что законодателями мод в измерении углов были моряки и астрономы, и именно им принадлежат основные практичные угловые меры.

Мореходы и землемеры, в своё время, решили, что разделить угол между Севером и Востоком на 100 частей будет в самый раз! Так получились грады. Прямой угол — 100 град, развёрнутый — 200 град, полный оборот — 400. Кстати, при таком способе 1 град это 1% от прямого угла, можно было бы записывать углы в процентах.

Есть у град один конструктивный недостаток: у числа 400 сравнительно немного делителей: 2, 4, 5, 8, 10, 16, 20, 25, 40, 50, 80, 100, 200 и среди них нет чисел, кратных трём. Так что у равностороннего треугольника получится угол в 133⅓ града, которые в десятичной дроби представляются лишь периодичной дробью. Давайте поищем что-нибудь получше. Взглянем на то, как растёт количество делителей у чисел в первой тысяче:

Как видите, есть такие числа, которые имеют наибольшее число делителей, среди всех предыдущих. Среди них значится знакомое число 360. Так что, если вам хочется рисовать правильные многоугольники, у которых 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 24, 30, 36, 40, 45, 60, 72, 90, 120 и 180 вершин, имеющие целые значения углов, или заниматься астрономией, в которой угловые размеры Солнца и Луны составляют половину деления, то 360° — ваш выбор!

Ну, а если вам до зарезу нужны семиугольники, то вместо 360 делений выбирайте, например, 420. Делителей у этого числа столько же, что и у трёхсот шестидесяти, но среди них есть кратные 7. Если полный оборот принять за 420 единиц, то прямой угол будет равен 105, углы в правильном треугольнике — 70, в пятиугольнике — 127, в шестиугольнике — 140, семиугольнике — 150. Красота!

Часы

А ещё мне по душе штурманский способ измерять угол в часах и минутах. Разделив оборот на 24 часа, а час — на 60 минут, мы получим привычное бытовое деление суточного периода. К тому же, число 24 относится к числам с наибольшим числом делителей в своей весовой категории. Более того, 24×60 = 1440 имеет целых 34 делителя!

Так что углы во всех привычных правильных многоугольниках будут иметь вполне аккуратное выражение: треугольник — 4ʰ, квадрат — 6ʰ, пятиугольная звезда — 2ʰ24ᵐ, а пятиугольник — 7ʰ12ᵐ. Это менее привычно, чем десятичная запись, но легко ложится на визуальный образ циферблата. Вместо 24 делений можно использовать и 12 часов, но тогда половина прямого угла будет выражаться как 1ʰ 30ᵐ. Зато транспортир превратится в хорошо знакомый и привычный для нас часовой циферблат.

Но особенно мне нравится, как выглядит таблица тригонометрических функций, в которой аргумент выражен в часах:

Кроме привычных значений, в этой таблице можно разместить две дополнительные величины в 1 час и в 5 часов, соответствующие 15° и 75°. Значения синусов и косинусов для них громоздковаты, конечно, но во второй части статьи мы с вами убедимся в том, что это хорошие величины: они имеют алгебраическую степень равную четырём, но при этом выражаются в виде внятного сочетания корней. Таким образом, все целые часы имеют относительно неплохие значения тригонометрических функций.

Румбы

Углы это не только части оборота, это ещё и способ обозначать направления. В отличие от оборотов, направления образуют модулярную арифметику, то есть, не бывает направления соответствующего 25 часам. Так что 25ʰ = 1ʰ и 20ʰ + 6ʰ = 2ʰ. Ещё более явно эту особенность алгебры направлений демонстрируют румбы и азимуты.

К любому углу можно подобраться с помощью дихотомии или методом деления пополам. Сначала выясняем в какой полуплоскости лежит нужное нам направление, потом — в какой четверти, потом — в какой из половинок четвертей и так далее. Так с незапамятных времён делили горизонт моряки, измеряя углы в румбах, разделив окружность на 2⁵ = 32 части, и дав им звучные имена, типа вест-зюйд-вест, норд-ост-тень-ост или даже стрик встока к обеднику, которые очень прикольно выкрикивать хриплым голосом, стоя на мостике.

Наконец, углы можно измерять даже в пальцах, как это делают бывалые морские и речные волки, идя “на два пальца левее Алголя“.

Однако, степени двойки, не могут похвастаться большим числом делителей, у числа 32 их всего 5 и все… степени двойки. Так что, поскольку 1/6 выражается только в виде бесконечной двоичной дроби:

используя номенклатуру румбов, угол в равностороннем треугольнике придётся выражать бесконечным символом. И о тригонометрии на языке румбов говорить будет нелегко, поскольку косинусы углов, являющихся степенями двойки, кроме четверти и восьмой части оборота, вычисляются не особо изящно:

Ну, а для других румбов тригонометрические дела обстоят и того хуже!

Радианы

Все описанные выше способы деления окружности, более или менее, подходят для базовой тригонометрии и бытового использования. Но если вы решите вычислить производную от какого-нибудь синуса, то она не будет равна косинусу, покуда аргумент будет измеряться в оборотах, градах, часах или румбах. Однако, при равномерном вращении, скорости изменения прямоугольных координат точки выражаются именно так:

Если в качестве угловой меры взять расстояние, на которое прокатится колесо единичного радиуса, при известном повороте, то угол поворота будет измеряться в радианах, то есть, в отношениях длины дуги, стягиваемой углом, к её радиусу. При этом появится иррациональное число , но этот значок не хуже значка ° или, например, ₽. Если вместо “пи” произносить “развёрнутый угол”, то смысл угла, выраженного в радианах станет яснее. Например, угол в правильном треугольнике равен π/3, то есть трети развёрнутого угла, а у квадрата — π/2, сиречь половина развёрнутого угла. А формула Эйлера гласит, что число −1, если рассматривать его, как комплексное , имеет аргумент, равный развёрнутому углу.

Несомненные выгоды от использования радиан начинаются при занятиях серьёзной тригонометрией и матанализом. В радианах синусы и косинусы решают дифференциальное уравнение: их можно раскладывать в ряды, и использовать методы приближённых вычислений, типа для малых углов. С аргументом, выраженным в радианах, тригонометрия позволяет решать задачи на движение, строить теорию функций комплексного переменного и методы разложения в ряды Фурье для решения задач матфизики. Начиная с первого курса физфака или мехмата, про градусы можно забыть.

Уклоны

Наконец, можно отказаться от равномерных делений и сразу измерять углы в тангенсах. Именно этот способ используется на дорожных знаках, где уклон дороги, то есть тангенс угла, образуемого дорогой к горизонту, выражен в процентах. Этот подход полезен в геодезии и в дорожном строительстве. И даже позволяет кое-где упростить тригонометрию.

Например, если величина угла выражается через его тангенс рациональной дробью, то нетрудно точно посчитать его синус и косинус, не используя калькулятор:

Но есть и существенные проблемы. Уклон в равностороннем треугольнике будет равен 1/√3 ≈57.73%, а вот угол квадрата, простите, будет неопределён, ибо тангенс для прямого угла терпит разрыв. Но самое главное: углы, измеряемые таким образом, перестают быть аддитивными. Это значит, что сумма двух уклонов или, скажем, удвоение уклона будут вычисляться весьма нетривиально, особенно, с учётом разрывов.

От геометрии к алгебре

Эти ограничения можно обойти, если использовать не дробь для выражения тангенса, а пару чисел: (числитель, знаменатель). Тогда прямой угол примет безопасное “значение” (1,0), а его половина может быть выражена, как (1,1) или (√2,√2) — это одно и тоже. Последовательно развивая такое представление, можно прийти к теоретикогрупповому представлению об угле, как о повороте, то есть, действии на множестве точек пространства или элементов поля.

Если разглядеть в упомянутых выше парах чисел комплексные числа, то алгебру углов можно определить, как мультипликативную группу комплексных чисел, факторизованную по норме (модулю). Тогда аддитивная абелева группа поворотов становится изоморфна мультипликативной группе комплексных чисел. Сложению углов (композиции поворотов) соответствует умножение соответствующих комплексных чисел, а вычитанию — умножение на сопряжённое число.

Ограничившись только такими парами чисел , что , получим полноценную алгебру, в которой повороты можно складывать таким образом: . Если все числа в парах будут рациональными, то результаты тоже окажутся парами рациональных чисел. Так можно построить группу рациональных точек окружности и рациональную тригонометрию, в которой нет корней, зато полно дробей с пугающими числами.

Наконец, окончательно абстрагировавшись от угловых мер, градусов, румбов и даже радиан, можно рассматривать углы, как топологическое пространство и унитарную группу первого порядка изоморфную группе вращений двумерного вещественного пространства SO(2). Впрочем, этот подход, необходимый для определения базовых понятий в геометрии, для решения прикладных геометрических и инженерных задач, всё-таки, не очень удобен. Даже тот фундаментальный для евклидовой геометрии факт, что сумма углов в треугольнике равна развёрнутому углу, будет непросто выразить и доказать, оперируя комплексными числами или рациональными точками на окружности. Но в следующей части статьи именно такой взгляд на углы станет нашим основным инструментом.

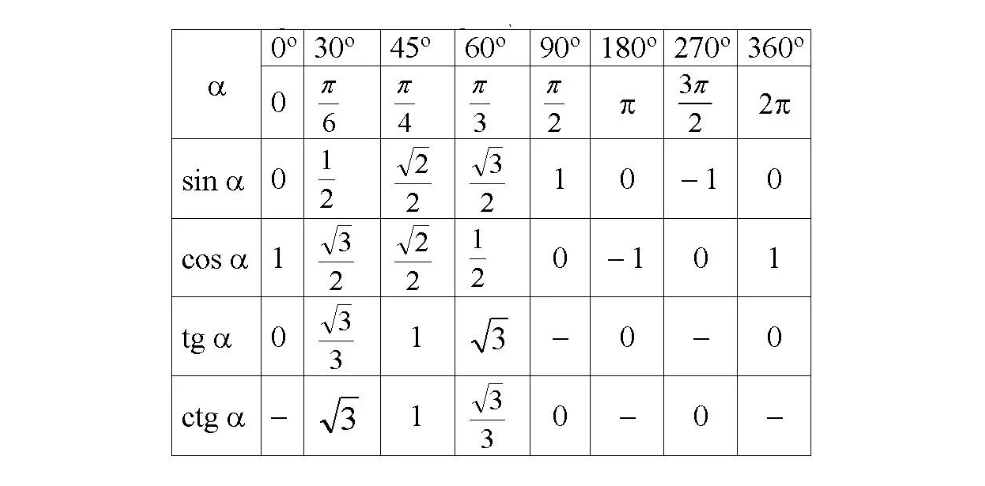
Эй, тригонометрия, ты почему такая иррациональная?!

Вернёмся к таблице тригонометрических функций, заучиваемой в школе. Почему в школьной таблице синусов и косинусов так мало чисел, которые легко запомнить? Почему тангенсы, синусы и косинусы от “хороших” углов имеют “нехорошие” значения?

Взгляните ещё раз на привычную таблицу тригонометрических функций:

Вся эта красота врывается в жизнь восьмиклассника и способна здорово отравить её неинтуитивными иррациональными значениями, содержащими корни не то из 2 не то из 3, которые как-то надо запоминать. Рациональные значения представлены в этой таблице только четырьмя числами: 0,1/2 и ±1, все же остальные содержат квадратные корни. Наконец, в таблице кроме нулевого и прямого, нет таких углов, для которых все тригонометрические функции принимали бы рациональные значения одновременно.

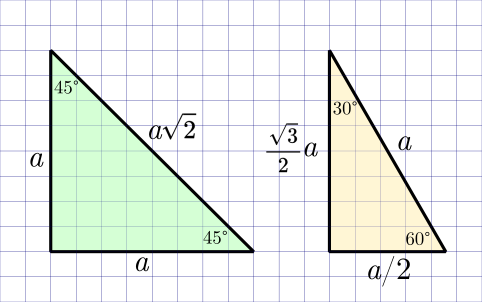
Из-за этой сплошной иррациональности полностью решить прямоугольный треугольник, то есть узнать все точные значения углов, сторон и их отношений, возможно лишь в двух особых случаях: в треугольнике с углами (45°, 45°, 90°) и с углами (30°, 60°, 90°). Этим треугольникам в школьной программе можно смело ставить памятник!

Что же делает перечисленные углы “хорошими”, и почему именно их мы заучиваем в школе? Они выражаются целыми числами в угловой мере, то есть, являются делителями 360°, или полного оборота. Может быть, мы не те углы выбрали для таблицы? Давайте взглянем на некоторые другие рациональные доли полного оборота:

Жуть! Ещё хуже стало. Получается, что в школьную таблицу попали те углы, для которых тригонометрия ещё терпимо иррациональна. У других шансов получить звание “хороших” очень невелики.

В то же самое время, все тригонометрические функции, это ведь просто отношения длин сторон в прямоугольном треугольнике. В обыкновенной тетрадке в клеточку мы можем нарисовать сколько угодно прямоугольных треугольников с целочисленными сторонами, для которых все тригонометрические функции будут принимать внятные рациональные значения:

Почему же эти значения не оказываются в таблицах тригонометрических функций? Дело в том, что для этих чудесных треугольников невозможно точно вычислить углы: они не будут рациональными долями 360° или полного оборота.

Получается, что либо углы рациональны, но тогда тригонометрия превращается в нагромождение корней, либо тригонометрия рациональна, а углы — нет. Одновременно всё становится рациональным только в самых примитивных случаях для 0°, 90°, 180° и 270°. Это значит, что углы и тригонометрические функции почти всегда несоизмеримы друг с другом. И дело тут не в выборе конкретной угловой меры, а в более фундаментальном свойстве евклидова пространства, в котором мы работаем.

А почему не вместе?

Все прямоугольные треугольники с рациональной тригонометрией имеют стороны, образующие, так называемые, пифагоровы тройки: целые числа  и , такие что . И все они могут быть построены на регулярной прямоугольной решётке. Но увы, кажется, на этой же решётке невозможно построить никакой угол, выражающийся через рациональную долю полного оборота, кроме тех, что кратны 45°.

Для того, чтобы убедиться в этом, нужно представить точки на регулярной квадратной решётке, как комплексные числа с целыми вещественной и мнимой частями. Они называются гауссовыми числами. Они образуют алгебраическое кольцо и для этих чисел действует основная теорема арифметики и любое гауссово число раскладывается на простые множители не единственным, но вполне определённым способом. Эти разложения имеют некоторые особенности, существенно отличающие их от разложения вещественных целых чисел и из этих особенностей можно вывести следующее утверждение:

Если гауссово число при возведении в степень становится вещественным, то либо , либо , либо .

Схема доказательства

Из этого свойства вытекает следующее:

Углы, которые опираются на узлы регулярной квадратной решётки либо кратны 45°, либо несоизмеримы с 360°.

Доказательство

Осталось показать, что это свойство относится не только к углам, отсчитываемым от горизонтальной оси, но справедливо для любого угла, опирающегося на узлы решётки. Это легко продемонстрировать на рисунке, который показывает, что переходя к регулярным подрешёткам, легко можно свести любой угол к доказанному случаю.

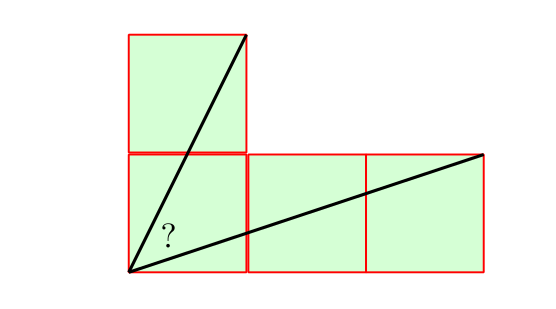
Таким образом, школьные задачи, подразумевающие внятный ответ, в которых нужно найти углы, опирающиеся на узлы квадратной сетки, скорее всего, имеют решение 45°, 90° или 135°. Либо задача формулируется на поиск тангенса угла.

В этой популярной задаче нужно найти точное значение угла, а значит, это может быть только 45°. Её можно решить разными способами, с привлечением геометрии, векторов, вычисляя арктангенсы, но если вас спрашивают про угол, то единственный возможный точный ответ, в принципе, вы уже знаете.

В сети легко найти множество рекомендаций по построению приближений к углам, кратным 10° или даже 5°. Однако, очень мало где говорится, то это только приближения, причём, удобно работающие только для построения углов, отсчитываемых от горизонтали. Впрочем, для быстрых построений они, действительно, могут быть полезны.

Копаемся в тригонометрическом лайфхаке

На многих ресурсах, созданных для облегчения жизни школьникам, то и дело появляются разнообразные лайфхаки: приёмы, существенно облегчающие запоминание чего-либо или упрощающие вычисления. Отношение у педагогов к таким приёмам неоднозначное. Одни с удовольствием их пропагандируют, продвигая мысль, что “Математика — это просто!”. Другие возражают: “Ученик — не попка, заученное, но не понятое бесполезно”, и считают лайфхаки, шпаргалки и линейки с формулами вредными.

Мне не нравится считать математику простой. Она сложна, но невероятно интересна, а главное, она познаваема! Это же относится и к жизни. Не уверен, что хочу прожить “простую” жизнь, в которой “всё понятно”, потому что есть “правильные ответы”, найденные кем-то для меня и выученные мною до автоматизмов. Это не вопрос “свободы выбора” или “права на самовыражение”. Это про удовольствие, про красоту, про интерес, про мастерство, как в математике, так и в жизни. Так что, мне кажется очень полезным и интересным рассмотреть ответы, найденные другими, и самостоятельно постараться понять, что они означают и откуда взялись.

Выходит, я отношусь тем, кто любит лайфхаки, и с удовольствием о них рассказывает, но использует их, как повод заглянуть “под капот”, и разобраться с тем почему, как и при каких условиях они работают. Многие “простые приёмы” имеют под собой интереснейшие и глубокие основания, открывающие двери в разделы серьёзной математики.

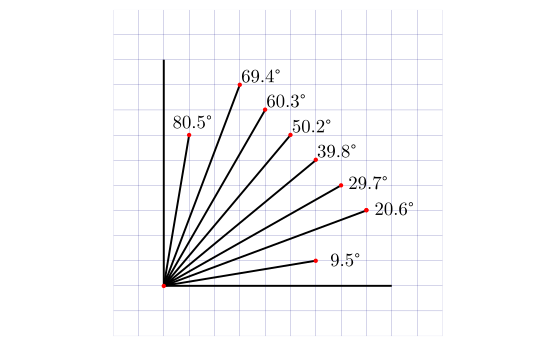
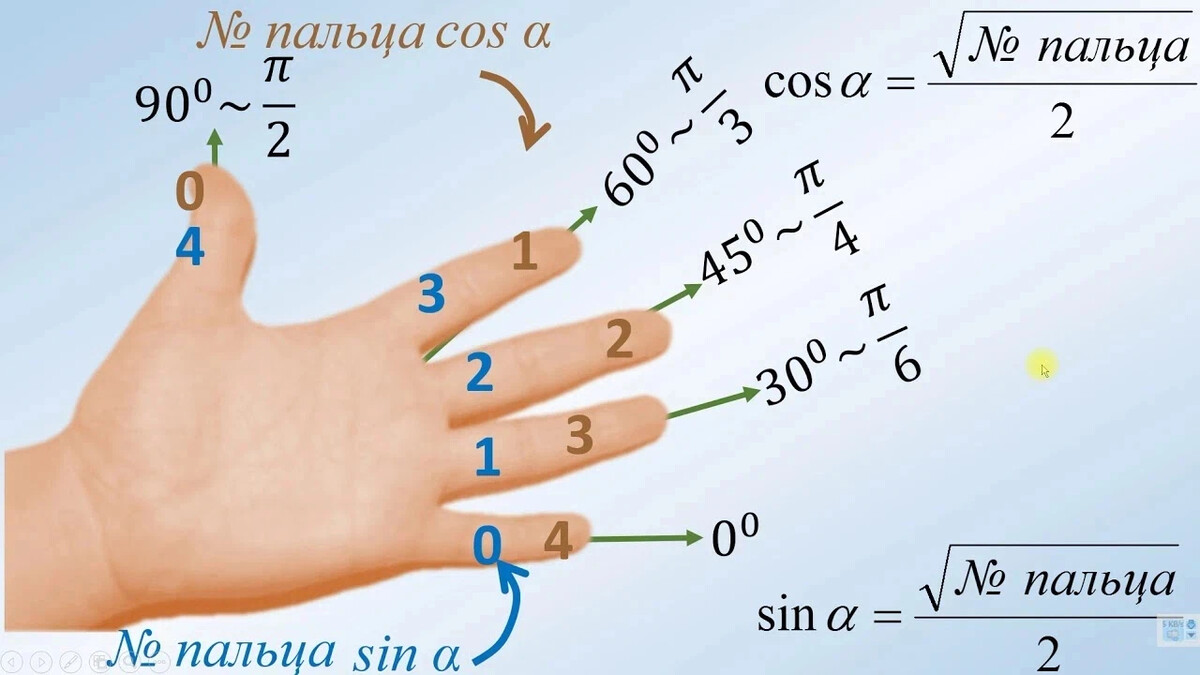
Уверен, многие из вас встречали этот симпатичный способ запомнить табличные значения тригометрических функций, синуса и косинуса, в первой четверти, который столь же часто рекомендуют, сколько поругивают:

Польза от этого способа есть, он позволяет не только запомнить значения синуса и косинуса, но и усвоить кто из них растёт, а кто убывает в первой четверти. Но есть в нём кое-что любопытное. Аргумент меняется неравномерно, а под корнями при этом наблюдаются линейные зависимости. Но мы же прекрасно понимаем, что тригонометрия не ограничивается квадратными корнями. О чём говорит нам эта линейная зависимость? Почему значений именно пять, а не больше? И почему под корнями равномерно перебираются четверти?

Откуда взялась линейность

Давайте сначала посмотрим на то, как этот способ выглядит графически. Нанесём значения синуса и косинуса из таблицы, как точки на координатной плоскости.

Ожидаемо получим пять точек, лежащих на окружности с единичным радиусом. Точки, соответствующие подкоренным выражениям (зелёные), при этом выстраиваются в аккуратную линию. В этом тоже нет ничего неожиданного, если вспомнить, что , а значит, квадраты синуса и косинуса, действительно, связаны линейным соотношением.

Почему значений только пять?

В теории полей, есть такой термин степень алгебраического числа. Им обозначается минимальная степень многочлена, корнем которого может быть число.

Например, целые и рациональные числа имеют алгебраическую степень, равную единице, потому что они могут быть решением уравнения для целых коэффициентов  и . Числа , или золотое сечение имеют степень равную двум, потому что являются корнями квадратных уравнений, так же как и гауссовы числа, не являющиеся вещественными. А вот кубический корень, решая квадратное уравнение с рациональными коэффициентами получить не выйдет, тут требуется уравнение третьей степени. Так что имеет алгебраическую степень, равную трём.

Методами теории полей можно показать, что алгебраическая степень значений тригонометрических функций от угла вида  зависит от числа :

В приведённой выше формуле используется функция Эйлера , которая играет очень важную роль в теории чисел. Она определена на множестве натуральных чисел и равна количеству чисел, не превышающих n и взаимно с ним простых.

Взгляните на первые двенадцать значений функции Эйлера, а также на соответствующие доли круга и алгебраические степени косинуса и синуса для этих долей:

Эту таблицу можно продолжить и дальше, но чем больше оказывается число n, тем больше можно отыскать чисел с ним взаимно простых. Вот как растёт функция Эйлера:

Более или менее удобоваримыми можно считать числа с алгебраической степенью 1 и 2. Но становится больше 2, для всех , а если , то уже не опустится ниже четырёх. Это значит, что в табличке мы перечислили все возможные рациональные доли окружности, в которых косинус и синус имеют шанс попасть на страницы школьного учебника. Таких углов в первой четверти оказывается всего пять, и это ровно те углы, что оказались в таблице, с которой начался наш разговор.

Вот как выглядит распределение по углам максимального значения алгебраических степеней для тригонометрических функций.

Табличные значения углов попадают внутрь радиуса, ограничивающего алгебраические степени меньше 3.

А причём тут четвёрки?

Итак, почему чисел в таблице всего пять, мы разобрались. Понятно также почему они образуют линейную зависимость под корнем. Но каким образом они оказались расположены на одинаковом расстоянии друг от друга, и отчего во всех подкоренных выражениях в знаменателях четвёрки?

Пора нам взглянуть на те самые алгебраические уравнения, о решениях которых мы говорили, когда рассуждали об алгебраических степенях.

В школьном курсе значения тригонометрических функций от примечательных углов выводятся геометрически. Однако эти вычисления можно свести к решению чисто алгебраических задач.

Из формул косинуса суммы несложно получить полезное соотношение:

Подставляя натуральные числа , можно вывести следующие равенства:

Если теперь заменить на формальную переменную  и ввести обозначение то мы получим последовательность многочленов:

для которых выполняется общее правило:

Мы получили семейство многочленов Чебышёва (первого рода), которые используются в широком ряде задач от приближённых вычислений и численного интегрирования, до теории сигналов и радиосвязи.

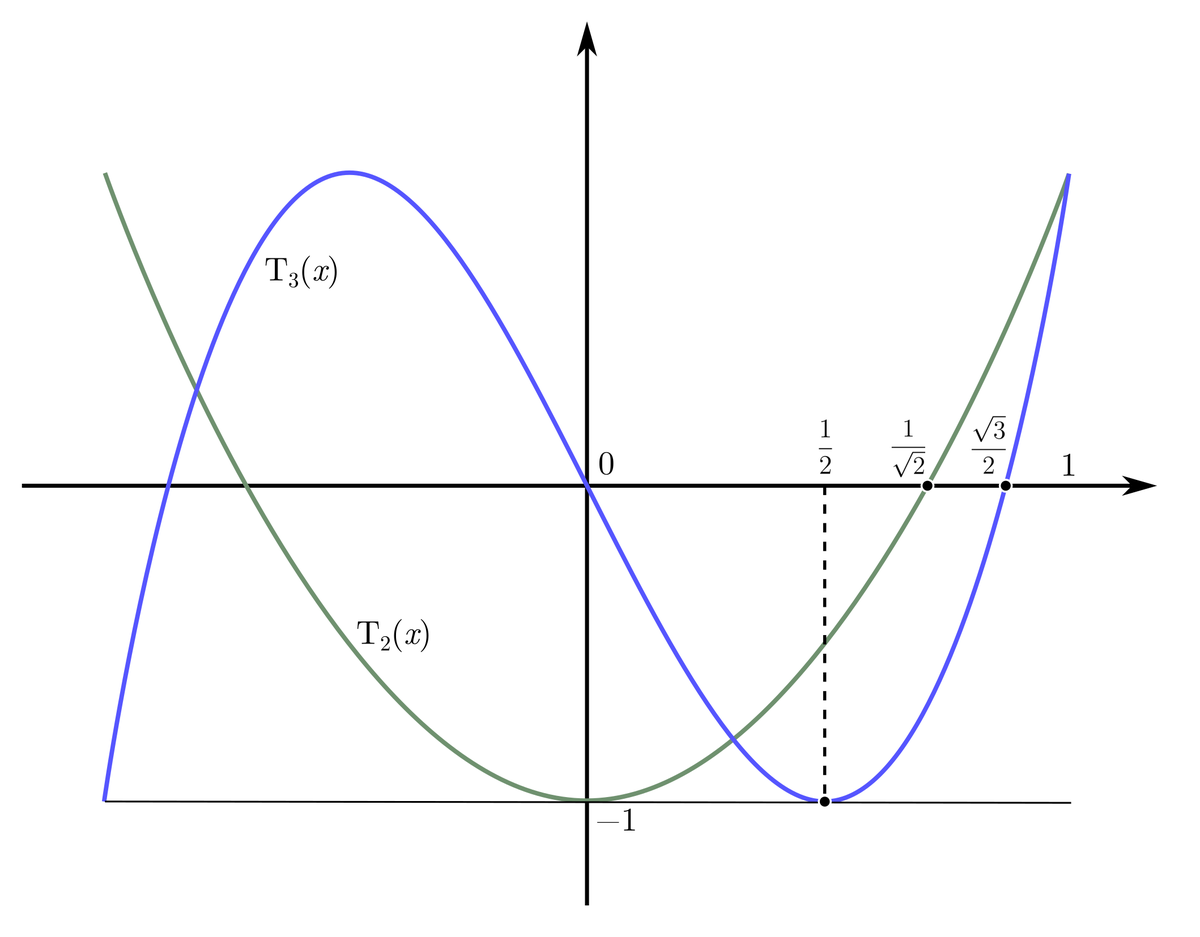
Приравнивая многочлен к значениям косинуса какого-нибудь угла, можно вычислить косинус от -ной доли этого угла. Например, решив уравнение , мы найдём .

Так можно найти все значения из обсуждаемой нами волшебной таблицы. Например, для мы получаем:

вы можете найти сами алгебраические значения и , и чтобы почувствовать себя крутым математиком, косинусы румбов NNE и NbE.

Имея общий вид для многочленов Чебышёва, можно увидеть откуда берутся четвёрки в таблице-лайфхаке. Обратите внимание на то, что все многочлены имеют коэффициент при старшей степени вида , который появляется из-за двойки в рекуррентном определении многочленов. В то же время, все пять значений из мнемонической таблицы получаются из уравнений, вытекающих из и . А в них старшие коэффициенты равны 2 или 4. В результате, все квадраты значений с алгебраической степенью не превышающей 2, можно записать так, чтобы старший коэффициент был равен 4. Для других долей окружности порядки уравнений становятся выше, и либо их решения будут выражаться через нагромождение корней и дробей, либо не решаются в конечной форме вовсе.

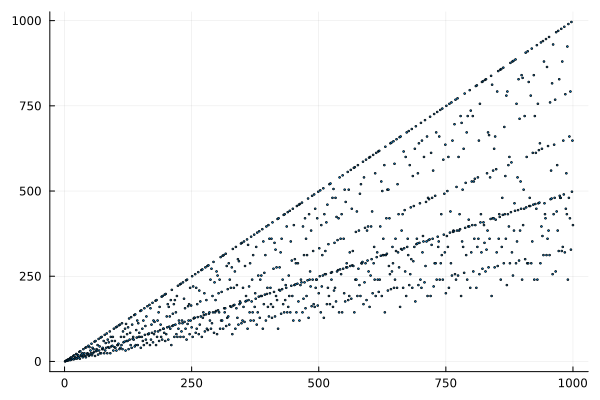
Подведём итог нашей вылазки. Мы выяснили, что среди углов, являющихся рациональной долей полного круга, есть только пять, для которых значения синуса и косинуса имеют алгебраическую степень 1 или 2. Для всех этих углов уравнения, выводимые из многочленов Чебышёва имеют старший коэффициент 2 или 4, таким образом, все эти значения будут квадратными корнями из рациональных чисел со знаменателем 4. Так как все они должны оказаться в интервале [0, 1], то в нашем распоряжении оказывается ровно пять таких рациональных чисел: 0/4, 1/4, 2/4, 3/4 и 4/4. Иные значения возможны, но будут иметь более сложную структуру и более высокую алгебраическую степень.

Используя теорию чисел, можно составить исчерпывающий список значений уклонов, имеющих алгебраическую степень 2, соответствующих углам, соизмеримым с 2π. И убедиться в том, что все они выражаются целыми значениями, если измерять углы в часах.

По-моему, теория чисел и теория полей — это круто! Здорово иметь возможность не просто вычислять какие-то значения, а ещё до начала вычислений знать, в какой мере эти значения вычислимы. Именно благодаря таким рассуждениям удалось дать исчерпывающий ответ на давний вопрос: какие задачи можно решить с помощью циркуля и линейки, а какие нельзя.

Благодарю за храбрость тех, кто пробрался вместе со мной сквозь дебри теории! Вместе не так страшно. А тех, кому интересно, приглашаю на Дзен-канал Онлайн-кружок математики, в котором занимательно-математические статьи появляются в облегчённом варианте.

Предыдущие статьи в серии Математическая продлëнка:

Квадратные уравнения во всей красе

Теория чисел на пальцах

Калькулятор уклонов

Чтобы посчитать уклон кровли, крыши, трубопровода, пандуса, лестницы, дороги, реки и т.п. воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Посчитать уклон

Посчитать превышение

Посчитать расстояние

Просто введите значения и выберите единицы измерения уклона.

Теория

Как посчитать уклон

Как посчитать превышение

Как посчитать расстояние

См. также

Содержание

• – Как посчитать угол зная длину и высоту?
• – Как высчитать угол наклона?
• – Как правильно рассчитать градус?
• – Как рассчитать угол наклона трубы?
• – Как найти угол зная длину катетов?
• – Как найти cos?
• – Как рассчитать угол наклона пандуса?
• – Как измерить угол наклона лестницы?
• – Как узнать угол запила?
• – Как определить правильный угол наклона крыши?
• – Как рассчитать угол наклона в градусах формула?
• – Как посчитать уклон в промилле?
• – Как определить уклон канализации?
• – Какой уклон у канализационных труб?
• – Какой уклон канализации на метр?

Чтобы определить угол наклона крыши, нужно воспользоваться таблицей Брадиса и простой методикой: высота кровельной конструкции делится на длину фронтона, разделенную на два, после чего остается найти таблице угол, который соответствует полученному результату.

Как посчитать угол зная длину и высоту?

α = 180°-β-γ

Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.

Как высчитать угол наклона?

sin α = H/S, где «S» – это длина ската. Соответственно высота конька будет равна: Н=S x sin α. Точно также можно определить длину ската, или, зная оба параметра, можно рассчитать угол наклона крыши.

Как правильно рассчитать градус?

Разделите сумму всех углов правильного многоугольника на число углов. Правильный многоугольник это многоугольник с равными сторонами и равными углами. Например, каждый угол равностороннего треугольника вычисляется так: 180 ÷ 3 = 60°, а каждый угол квадрата находится так: 360 ÷ 4 = 90°.

Как рассчитать угол наклона трубы?

Рассмотрим, как действует правило: Предположим, нужно рассчитать оптимальный уклон для трубы 110 мм, согласно ГОСТ он составляет 0,02 мм. Чтобы рассчитать общий угол, нужно длину трубы умножить на уклон, указанный в СНиП или ГОСТ. Получится: 10 м (длина канализационной системы) * 0,02 = 0,2 м или 20 см.

Как найти угол зная длину катетов?

Углы прямоугольного треугольника

1. α = 90°-β Если известна величина двух катетов прямоугольного треугольника (а, b), находим угол, используя отношения тангенсов.
2. tg (α) = a/b. Т. …
3. β = 180° — 90° — α …
4. sin (α) = a/c.

Как найти cos?

Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.

Как рассчитать угол наклона пандуса?

Вычисляется уклон пандуса с помощью формулы: наклон пандуса = H / L, где: H — перепад высот, который необходимо оборудовать пандусом, а L — длина горизонтальной проекции наклонного участка пандуса (нажмите для увеличения).

Как измерить угол наклона лестницы?

Как рассчитать угол наклона лестницы

Высота ступеней будет идеальной при значении 150 – 180 мм, ширина – 280 – 300 мм. Придерживаясь таких стандартов, угол наклона можно рассчитать по формуле: 2х + у = 580/660 мм, где х – это высота ступеней, а у – ширина.

Как узнать угол запила?

КАК ОПРЕДЕЛИТЬ УГОЛ ЗАПИЛА

Для каждого соединения необходимо замерить и определить стыковочный угол, а затем, чтобы определить угол косого запила, разделить результат замера пополам. на необрезанном конце заготовки и в этой точке начинают косой запил. Повторяют эту операцию по всему периметру изделия.

Как определить правильный угол наклона крыши?

В основном угол выбирают от 9 до 20 градусов. Среднегодовые объемы осадков: Однако на практике в разных регионах возникают как сильные порывы ветра, так и обильные осадки, и выбор угла должен учитывать этот факт. Поэтому наиболее оптимальным является уклон крыши, в средних значениях, то есть от 20 до 45 градусов.

Как рассчитать угол наклона в градусах формула?

Найти его несложно по следующей формуле: i = H / L, где i — уклон кровли, H — высота конька, L — половина пролета (ширины здания). Если нужно произвести расчет в процентах, то применяем формулу: i = H / L * 100%. Из таблицы преобразования “градусы в проценты” для 44,5% находим величину 24 — градусная мера.

Как посчитать уклон в промилле?

Перевод уклона из промилле в мм на м длины онлайн

Чтобы узнать сколько составляет уклон в промилле, необходимо ознакомиться с определением: Промилле (‰) — это одна десятая процента или 1/1000 доля. 1‰=1мм/м.

Как определить уклон канализации?

«Наибольший уклон трубопроводов не должен превышать 0,15 (за исключением ответвлений от приборов длиной до 1,5 м)». То есть уклон 15 сантиметров на метре. Если превысить данный угол при прокладке, то возможно заиливание трубопровода канализации. Или, проще говоря, вода быстро уйдет, а все остальное останется.

Какой уклон у канализационных труб?

Итак нормы уклона канализационных труб по СНиП: Уклон канализационной трубы 110 – 2 см на 1 метр Уклон канализационной трубы 50 – 3 см на 1 метр

Какой уклон канализации на метр?

минимально допустимый показатель уклонения канализационного трубопровода составляет 3 см на 1 м. п., при условии, что диаметр магистрали не превышает 50 мм; рекомендуемый уклон трубопровода с размером сечения 1600 мм составляет 8 мм на 1 м.

Интересные материалы:

Какую функцию в луковице выполняют листья?
Какую функцию в луковице выполняют сочные чешуи листья )?
Какую функцию выполняют сочные чешуи листья?
Когда краснеют листья клена?
Когда листья меняют окраску?
Когда лучше бросать в суп лавровый лист?
Когда лучше положить в суп лавровый лист?
Когда надо собирать листья лещины?
Когда надо собирать листья мать и мачехи?
Когда нужно добавлять лавровый лист в суп?