Сегодня мы с вами будем изучать умножение целого числа на дробь. Эта тема очень актуальна в наши дни для любых людей: от биолога до математика. Но для начала давайте познакомимся поближе с этим «чудо-зверем» — дробью.
Что такое дробь
Дробью называется число, которое состоит из нескольких долей единицы.
Если говорить простым языком, есть у вас торт. Он один, он является одним целым. Но вот вы отрезали от него половину. Это его доля. Всего один целый торт сейчас состоит из двух частей. Одну вы съели (очень уж вкусный был). То есть получается, что вы съели одну часть из двух, на которые вы его разделили. Значит, вы съели ½ торта. В подобном виде можно представить любую вещь, разделив ее на части.
Для того чтобы овладеть умением умножения числа на дробь, не нужно много мудрости или знаний. Достаточно уметь перемножать целые числа. Это довольно похожие понятия и имеют одинаковый смысл.
Умножение целых чисел можно представить в виде сложения равных слагаемых. То есть: 5*2 = 5+5= 10. В принципе, умножать дробь на число – почти такое же занятие. Мы просто находим сумму этих самых слагаемых, которые, кстати, являются одинаковыми.
Как вы могли заметить, подразумевающийся смысл у обоих действий один и тот же — сложение слагаемых.
Теперь же мы можем подняться на новую ступень и попробуем перемножить целое и дробь. Наши примеры будут выглядеть так: 5 • 2/4. Однако прежнее определение для умножения чисел не подходит для этого случая, потому что вы не сможете заменить такое умножение сложением.
Поэтому давайте дадим новое определение для умножения, как же нам теперь нужно понимать это действие.
Как происходит умножение
Для проникновения в тайный смысл хитрого умножения дадим определение, что же все-таки это значит: чтобы совершить умножение числа на дробь, нужно найти дробь этого целого числа.
Поэтому что мы получаем? Для того чтобы умножить 5 на 2/3, нам нужно найти 2/3 от пяти.
Возникает естественный и значимый вопрос: почему же действия, которые с первого взгляда кажутся нам различными, такие, как поиск дроби и суммы равных чисел, в математике получили объяснение только одним словом — «умножение»?
Все это объясняется достаточно просто. Оба действия помогают нам решать очень похожие вопросы. Поэтому логичнее всего здесь будет понимать и принимать тот факт, что похожие задачи решаются одними и теми же действиями, и это в реальной жизни вполне оправдано.
Задача
Чтобы понять все это на живом примере, давайте рассмотрим такую задачу: «1 кг яблок стоит 40 р. Сколько тогда будут стоить 3 кг этих яблок?»
И ежику понятно, что подобная задача решается умножением количества килограммов на стоимость за 1 кг, т. е. 40*3 = 120 рублей.
Теперь попробуем понять и решить похожую задачу, но с дробями. Посчитаем: «1 кг яблок стоит 40 рублей. Какова будет стоимость 3/4 кг таких яблок?»
Эта задача, как и предыдущая, тоже решается перемножением стоимости яблок за 1 кг на требуемый нам вес.
В данную задачу можно подставить любую другую дробь, будь то 2/3 или же 3/7, не меняя при этом концепции и условий самой задачи.
Как мы выяснили ранее, если не трогать основной смысл задач и не менять ничего, кроме чисел, то мы можем применять одинаковое действие при решении заданий, которое называется умножением. Все гениальное просто, не так ли?
Все-таки давайте вернемся к нашему главному вопросу: умножение целого на части. Как это сделать?
Для примера возьмем опять нам всем полюбившуюся задачу про яблоки. Разберем числа, которые там встречаются:
40 * 3/4 =?
Если снова взглянуть на определение, то найти нам нужно 3/4 от 40. Давайте начнем с более простого и попробуем найти четверть от 40, а только потом уже 3/4.
Четверть (т. е. 1/4) от 40 это 40/4;
3/4 от 40 является значение (3*40)/4.
Что мы имеем:
40*3/4 = (40*3)/4 = 10*3 = 30.
Давайте посмотрим другой случай: 40 * 5/8 равно чему?
- 1/8 от 40 это 40/8;
- 5/8 от 40 составляют (5*8)/40;
- В итоге получается: 40 * 5/8 = (40*5)/8 = 5*5 = 25.
Правило умножения
Давайте теперь попробуем понять правило, применяемое для умножения:
- Для того чтобы умножить целое число на дробь, мы должны умножить числитель этой дроби на нужное нам значение целого числа, а потом получившийся результат поставить числителем новой дроби, а знаменатель новой дроби оставить прежним.
Если понимать это правило с помощью букв, то выглядеть оно будет так:
Но также нам важно помнить об одном очень важном моменте. Перед тем как выполнять умножение, следует сократить все, что сокращается, чтобы облегчить себе жизнь. Например: умножим 15*2/3 = (15*2)/3. Но 15 и 3 можно сократить на 3, остается (5*2)/1. Но мы знаем, что любая дробь, знаменателем которой является 1 — это целое число, которое стоит в числителе. Вот и получается, что (5*2)/1 = 5*2 = 10. Поэтому для упрощения своей же работы рекомендуется сокращать числа.
Итак, вот мы с вами и научились умножать целое число на дробь. Надеюсь, что эта статья очень поможет вам в ваших продвижениях в математике. Широких вам горизонтов!
Видео
Это видео поможет вам лучше понять и запомнить, как умножается целое число на дробь.
Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.
Как умножить одну обыкновенную дробь на другую
Запишем сначала основное правило:
Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей a/b и c/d это можно выразить как ab·cd=a·cb·d.
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 14 и 18 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8·4=32). Соответственно, площадь каждого из них будет равна 132 от площади всей фигуры, т.е. 132 кв. единицы.
Далее нам надо выделить цветом часть исходного квадрата так, как это сделано на рисунке:
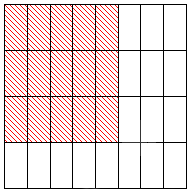
У нас получился закрашенный фрагмент со сторонами, равными 58 числовой единицы и 34 числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна 58·34 кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их 15, значит, общая площадь составляет 1532 квадратных единиц.
Поскольку 5·3=15 и 8·4=32, мы можем записать следующее равенство:
58·34=5·38·4=1532
Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как ab·cd=a·cb·d. Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Разберем решения нескольких задач на умножение обыкновенных дробей.
Умножьте 711 на 98.
Решение
Для начала подсчитаем произведение числителей указанных дробей, умножив 7 на 9. У нас получилось 63. Затем вычислим произведение знаменателей и получим: 11·8=88. Составим их двух чисел ответ: 6388.
Все решение можно записать так:
711·98=7·911·8=6388
Ответ: 711·98=6388.
Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.
Вычислите произведение дробей 415 и 556.
Решение
Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:
415·556=4·5515·6=22090
Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на 10.
Выполним сокращение дроби: 22090 НОД (220, 90)=10, 22090=220:1090:10=229. В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 229=249.
Ответ: 415·556=249.
Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду a·cb·d. Разложим значения переменных на простые множители и одинаковые из них сократим.
Поясним, как это выглядит, используя данные конкретной задачи.
Вычислите произведение 415·556.
Решение
Запишем вычисления, исходя из правила умножения. У нас получится:
415·556=4·5515·6
Поскольку как 4=2·2, 55=5·11, 15=3·5 и 6=2·3, значит,4·5515·6=2·2·5·113·5·2·3.
Далее мы можем просто сократить некоторые множители и получить следующее: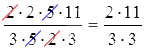 
.
Нам осталось подсчитать несложные произведения в числителе и знаменателе и выделить целую часть из получившейся в итоге неправильной дроби:
2·113·3=229=249
Ответ: 415·556=249.
Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:
ab·cd=cd·ab=a·cb·d
Как перемножить обыкновенную дробь с натуральным числом
Запишем сразу основное правило, а потом попробуем объяснить его на практике.
Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби ab на натуральное число n можно записать в виде формулы ab·n=a·nb.
Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:
ab·n=ab·n1=a·nb·1=a·nb
Поясним нашу мысль конкретными примерами.
Вычислите произведение 227 на 5.
Решение
В результате умножения числителя исходной дроби на второй множитель получим 10. В силу правила, указанного выше, мы получим в результате 1027. Все решение приведено в этой записи:
227·5=2·527=1027
Ответ: 227·5=1027
Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.
Условие: вычислите произведение 8 на 512.
Решение
По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что 512·8=5·812=4012. Итоговая дробь имеет признаки делимости на 2, поэтому нам нужно выполнить ее сокращение:
НОК(40, 12)=4, значит, 4012=40:412:4=103
Теперь нам осталось только выделить целую часть и записать готовый ответ: 103=313.
В этой записи можно видеть все решение целиком: 512·8=5·812=4012=103=313.
Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.
Ответ: 512·8=313.
Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:
ab·n=n·ab=a·nb
Как выполнить умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.
Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Покажем на примере, как это делается.
Умножьте четыре обыкновенные дроби 120, 125, 37 и 58.
Решение: для начала сделаем запись произведения. У нас получится 120·125·37·58. Нам надо перемножить между собой все числители и все знаменатели: 120·125·37·58=1·12·3·520·5·7·8.
Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.
1·12·3·520·5·7·8=1·(2·2·3)·3·52·2·5·5·7(2·2·2)=3·35·7·2·2·2=9280
Ответ: 1·12·3·520·5·7·8=9280.
Перемножьте 5 чисел 78·12·8·536·10.
Решение
Для удобства мы можем сгруппировать дробь 78 с числом 8, а число 12 с дробью 536, поскольку при этом нам будут очевидны будущие сокращения. В итоге у нас получится:
78·12·8·536·10=78·8·12·536·10=7·88·12·536·10=71·2·2·3·52·2·3·3·10==7·53·10=7·5·103=3503=11623
Ответ: 78·12·8·536·10=11623.
Математика
5 класс
Урок № 62
Умножение натурального числа на дробь
Перечень рассматриваемых вопросов:
– произведение двух дробей;
– взаимно обратные дроби;
– умножение натурального числа на дробь.
Тезаурус
Произведение двух дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Взаимно обратные дроби – это дроби, произведение которых равно единице.
Обязательная литература
1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. ФГОС./ С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др.– М.: Просвещение, 2017, стр. 272.
Теоретический материал для самостоятельного изучения
Произведение двух дробей есть дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Например,
Можно ли умножить дробь на натуральное число n? Конечно, да! Натуральное число n можно представить в виде обыкновенной дроби n/1 и применить правило умножения дробей. Итак, чтобы умножить натуральное число на дробь, можно числитель дроби умножить на это натуральное число, а знаменатель оставить тот же.
Например:
Вычислим произведение четырёх пятых и трёх. Умножение можно заменить сложением, то есть три раза сложить дробь четыре пятых. Применяем правило сложения обыкновенных дробей и получаем:
Если произведение дробей равно единице, то такие дроби называют взаимно обратными.
Например,
Дроби ¼ и 4/1 называются взаимно обратными.
Чтобы умножить простую и смешанную дробь, можно записать последнюю в виде неправильной дроби и выполнить умножение обыкновенных дробей.
Например,
Перед возведением в степень смешанную дробь записывают в виде неправильной, и эту дробь возводят в степень.
Решим задачу: в равностороннем треугольнике длина стороны равна 4/7 м. Найдите периметр треугольника.
Решение. Как мы знаем, периметр – это сумма длин всех сторон. В треугольнике три стороны, а т. к. треугольник равносторонний – стороны равны. Получается, что сумму длин всех сторон можно представить как произведение натурального числа 3 на обыкновенную дробь
Разбор решения заданий тренировочного модуля
№ 1. Вычислите значение выражения, результат запишите в виде смешанной дроби.
Переведём смешанные дроби в неправильные, после чего перемножим числители и знаменатели, а результат запишем в виде смешанной дроби. Получим:
№ 2. Вычислите значение произведения, результат сократите.
Умножим числитель первой дроби на числитель второй дроби, знаменатели тоже перемножим. Получим:
Ответ:
В данной публикации мы рассмотрим, каким образом можно обыкновенную (простую) дробь умножить на число или другую дробь, и как найти произведение смешанных дробей. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
-
Умножение дроби
-
На число
- На другую дробь
-
На число
- Произведение смешанных дробей
- Примеры задач
Умножение дроби
На число
Умножение обыкновенной дроби на число n равно сумме, слагаемыми которой является данная дробь n-ое количество раз.
Другими словами, числитель дроби умножается на данное число n, а знаменатель остается тем же.
Примечание: дробь, полученную в результате умножения, следует проверить на предмет того, можно ли ее сократить.
На другую дробь
В результате умножения одной дроби на другую получается новая дробь, числитель которой равняется произведению числителей исходных дробей, а знаменатель – произведению знаменателей.
Произведение смешанных дробей
Чтобы умножить смешанные дроби, необходимо их сперва представить в виде неправильных дробей, и только после этого выполнить умножение.
X
a/b
⋅ Y
c/d
=
X ⋅ b + a/b
⋅
Y ⋅ d + c/d
Примеры задач
Задание 1
Умножьте дробь
3/15
на число 5.
Решение
3/15
⋅ 5 =
3⋅5/15
=
15/15
=1
Задание 2
Найдите произведение дробей
9/17
и
4/7
.
Решение
9/17
⋅
4/7
=
9⋅4/17⋅7
=
36/119
Задание 3
Найдите произведение дробей 3
3/8
и 7
1/9
.
Решение
Т.к. мы имеем дело со смешанными дробями, сперва представим их в виде неправильных, затем выполним умножение.
3
3/8
⋅ 7
1/9
=
3⋅8+3/8
⋅
7⋅9+1/9
=
27/8
⋅
64/9
=
27⋅64/8⋅9
=
1728/72
=24
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Умножение обыкновенных дробей
Примеры:
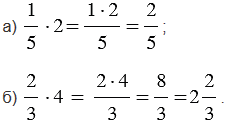
Обратите внимание, если в ответе получается неправильная дробь, то из нее выделяют целую часть.
Если мы умножаем на натуральное число, которое можно сократить с числом, стоящим в знаменателе, то сначала выполняют сокращение, а затем умножение (такой ход действий облегчает вычисления).
Пример:
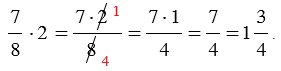
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
Пример:
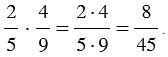
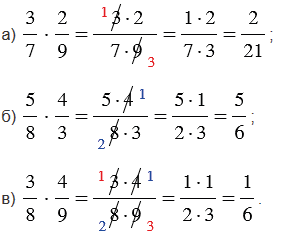
Если мы перемножаем дроби, у которых можно сократить числитель первой и знаменатель второй дроби и (или) знаменатель первой и числитель второй дроби, то сначала выполняют сокращение, а затем умножение (такой ход действий облегчает вычисления).
Примеры:
Умножение смешанных чисел
Чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Примеры:
Для обыкновенных дробей, как и для натуральных чисел, выполняются свойства умножения (переместительное свойство умножения, сочетательное свойство умножения, распределительные свойства умножения относительно сложения и относительно вычитания). Также при умножении дроби на ноль (или нуля на дробь) получаем ноль, и при умножении дроби на единицу (или единицы на дробь) получим равную ей дробь.
Примеры:
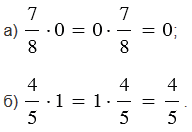
Пример:
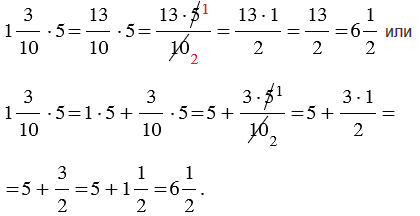
Нахождение дроби от числа
Чтобы найти дробь от числа, нужно умножить число на эту дробь.
Примеры:
а) Найти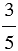 
от числа 20.
Решение:
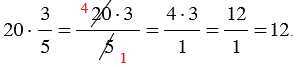
б) Найти 0,6 от числа 9.
Решение:
9·0,6 = 5,4.
в) Найти 30 % от числа 500.
Решение:
1) 30% = 30 : 100 = 0,30 = 0,3
2) 500·0,3 = 150.
Взаимно обратные числа
Два числа, произведение которых равно 1, называют взаимно обратными.
Примеры:
1) 
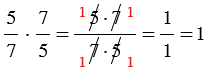, значит, числа 
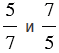– взаимно обратные;
2) 
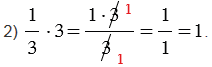
Чтобы определить число обратное смешанному числу, нужно представить это смешанное число в виде неправильной дроби.
Пример:
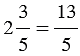, значит, числу 
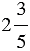обратно число 
.
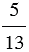Запомните:
Советуем посмотреть:
Доли. Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Деление и дроби
Сложение и вычитание дробей с одинаковыми знаменателями
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
5 класс
Задание 567,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1348,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1751,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
6 класс
Номер 375,
Мерзляк, Полонский, Якир, Учебник
Номер 480,
Мерзляк, Полонский, Якир, Учебник
Номер 504,
Мерзляк, Полонский, Якир, Учебник
Номер 1086,
Мерзляк, Полонский, Якир, Учебник
Задание 536,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 543,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 659,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1155,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1430,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1557,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 155,
Мерзляк, Полонский, Якир, Учебник
Номер 430,
Мерзляк, Полонский, Якир, Учебник
Номер 652,
Мерзляк, Полонский, Якир, Учебник
Номер 763,
Мерзляк, Полонский, Якир, Учебник
Номер 796,
Мерзляк, Полонский, Якир, Учебник
Номер 845,
Мерзляк, Полонский, Якир, Учебник
Номер 858,
Мерзляк, Полонский, Якир, Учебник
Номер 1035,
Мерзляк, Полонский, Якир, Учебник
Номер 1101,
Мерзляк, Полонский, Якир, Учебник
Номер 1118,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 140,
Мерзляк, Полонский, Якир, Учебник
Номер 197,
Мерзляк, Полонский, Якир, Учебник
Номер 225,
Мерзляк, Полонский, Якир, Учебник
Номер 242,
Мерзляк, Полонский, Якир, Учебник
Номер 245,
Мерзляк, Полонский, Якир, Учебник
Номер 251,
Мерзляк, Полонский, Якир, Учебник
Номер 276,
Мерзляк, Полонский, Якир, Учебник
Номер 347,
Мерзляк, Полонский, Якир, Учебник
Номер 379,
Мерзляк, Полонский, Якир, Учебник
Номер 462,
Мерзляк, Полонский, Якир, Учебник
