Unitary Matrices are defined as square matrices of complex numbers such that the product of the conjugate transpose of a unitary matrix, with unitary matrix itself, gives an identity matrix. Matrices are defined as rectangular arrays in which numbers are arranged in rows and columns. Number of rows and columns determined the size of the matrix. We have different types of matrices, such as rectangular matrices, square matrices, triangular matrices, symmetric matrices, singular matrices, etc. In this article, we learn about a unitary matrix in detail.
What is Unitary Matrix?
A square matrix of complex numbers is said to be a unitary matrix if its inverse is equal to the conjugate transpose. In other words, the product of a unitary matrix and its conjugate transpose is equal to the identity matrix. As the determinant of a unitary matrix is not equal to zero, it is a non-singular matrix. The rows and columns of a unitary matrix are orthonormal. If “U” is a unitary matrix and “UH” is its conjugate transpose, then the following condition must be satisfied:
- UUH = UHU = I
- UH = U-1
Examples of a Unitary Matrix
- Matrix given below is a unitary matrix of order “2 × 2.”
- Matrix given below is a unitary matrix of order “3 × 3.”
Properties of a Unitary Matrix
Following are some important properties of a unitary matrix:
- Every unitary matrix is a square matrix.
- A unitary matrix is a non-singular matrix.
- Every unitary matrix is an invertible matrix.
- Every unitary matrix is diagonalizable.
- When two unitary matrices of the same order are multiplied, the resultant matrix is also unitary.
- When two unitary matrices of the same order are added or subtracted, the resultant matrix is also unitary.
- Absolute value of the determinant of a unitary matrix is one, i.e., |det(U)| = 1.
- An identity matrix is also a unitary matrix.
- In a unitary matrix, the modulus of every eigenvalue is always one, i.e., |λ| = 1.
Read More,
- Minors and Cofactors of Determinants
- Determinant of a Matrix
- Adjoint of a Matrix
Solved Examples on Unitary Matrix
Example 1: Prove that the matrix given below is unitary.
Solution:
To prove that the given matrix is unitary, we need to prove that UUH = I
Hence the given matrix is unitary.
Example 2: Is the matrix given below a unitary matrix?
Solution:
To prove that the given matrix is unitary, we need to prove that AAH = I
Hence the given matrix is unitary.
Example 3: Prove that the absolute value of the determinant of a unitary matrix is one.
Solution:
Hence proved.
FAQs on Unitary Matrix
Question 1: Define a matrix.
Answer:
A matrix is defined as a rectangular array of numbers that are arranged in rows and columns.
Question 2: What is a unitary matrix?
Answer:
A square matrix of complex numbers is said to be a unitary matrix if its inverse is equal to the conjugate transpose. In other words, the product of a unitary matrix and its conjugate transpose is equal to the identity matrix.
Question 3: How to determine whether a matrix is unitary or not?
Answer:
A matrix can be determined to be unitary if the product of the given matrix and its conjugate transpose is equal to the identity matrix. If “U” is a unitary matrix and “UH” is its conjugate transpose, then the following condition must be satisfied:
- UUH = UHU = I
- UH = U-1
Question 4: How to find the complex conjugate transpose matrix?
Answer:
Follow the steps given below to find a complex conjugate transpose matrix:
- First, replace every element in the matrix with its complex conjugate.
- Now, find the transpose of the resultant matrix.
Last Updated :
26 Mar, 2023
Like Article
Save Article
Ортогональные и унитарные матрицы
Ортогональная матрица и её свойства
Действительная квадратная невырожденная матрица называется ортогональной, если
. Из определения следуют основные свойства ортогональной матрицы
.
1. .
2. — модуль определителя ортогональной матрицы равен единице.
3. Матрица (или, что то же самое
) является ортогональной.
4. Произведение ортогональных матриц одного и того же порядка является ортогональной матрицей.
Докажем последнее свойство. Пусть и
— ортогональные матрицы одного и того же порядка. Тогда по свойствам операций обращения и транспонирования матриц имеем
Следовательно, произведение есть ортогональная матрица.
Пример 4.1. Доказать, что матрица является ортогональной.
Решение. Найдем произведения
Следовательно, по определению . Вычислим определитель матрицы
(см. свойство 2).
Унитарная матрица и её свойства
Комплексная квадратная невырожденная матрица называется унитарной, если
. Следующие свойства унитарной матрицы
аналогичны свойствам ортогональной матрицы.
1. .
2. — модуль определителя унитарной матрицы равен единице.
3. Матрица является унитарной.
4. Произведение двух унитарных матриц одного и того же порядка является унитарной матрицей.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Унита́рная ма́трица — квадратная матрица с комплексными элементами, результат умножения которой на эрмитово сопряжённую равен единичной матрице: 
Другими словами, матрица унитарна тогда и только тогда, когда существует обратная к ней матрица, удовлетворяющая условию 
Унитарные матрицы обобщают понятие ортогональных матриц, элементы которых — только действительные числа, на матрицы с компле́ксными числами.
Следующие утверждения относительно данной квадратной матрицы 
— унитарна.
— унитарна.
- Столбцы матрицы
образуют ортонормированный базис в унитарном пространстве.
- Строки матрицы
образуют ортонормированный базис в унитарном пространстве.
Интерпретация[править | править код]
Унитарная матрица представляет преобразование, переводящее ортонормированный базис комплексного векторного пространства размерности, соответствующей её размеру, в ортонормированный базис. (Это верно для любого ортонормированного базиса).
Это эквивалентно утверждению, что преобразование, представляемое унитарной матрицей, сохраняет скалярное произведение (а потому и длины всех векторов).
Свойства[править | править код]
Если определитель унитарной матрицы 
Множество всех специальных унитарных матриц порядка 



См. также[править | править код]
- Эрмитова матрица
- Унитарный оператор
- Унитарная группа
- Специальная унитарная группа
- Группа Ли
- Ортонормированный базис
- Гильбертово пространство
- Группа вращений
Литература[править | править код]
- Унитарная матрица // Ужи — Фидель. — М. : Советская энциклопедия, 1956. — С. 242. — (Большая советская энциклопедия : [в 51 т.] / гл. ред. Б. А. Введенский ; 1949—1958, т. 44).
|
|
Макеты страниц
Пусть 

и

Задача. Требуется найти матрицу преобразования 


Решение. Умножим это равенство справа на

Суммируя по 

Здесь обнаруживается аналогия с преобразованиями координат. Преобразованию векторов при переходе от одной системы координат к другой можно придать матричную форму. Как станет ясно в дальнейшем, при таких преобразованиях особенно важную роль играют преобразования, описываемые унитарными матрицами.
Определение. Матрицу 

Теорема. Матрица 

Доказательство.
Производя эрмитово сопряжение, получаем:

а на основании (15.20) и (15.23) находим окончательно:

Теорема. Если матрица 

Доказательство.

Теорема. Если матрица 



Доказательство очевидным образом следует из теоремы (16.7). Вывод. Унитарные преобразования переводят один ортонормированный базис в другой.
Пример 1. Преобразование ортонормированной системы функций-«векторов» 

с помощью унитарной матрицы 


Пример 2. Преобразование координат «вектора» 

к новым «осям» 

где 



Зная, таким образом, связь между базисами, найдем теперь связь между «старыми» и «новыми» координатами:

[где в последнем шаге использована формула (16.9)]. В матричной
записи для вертикальных столбцов,

это соотношение принимает вид

Вывод. Преобразование координат описывается той же матрицей, что и обратное преобразование базисных векторов.
Преобразование, индуцируемое матрицей-оператором А.
Вопрос. Если матричный оператор А определяет некоторое линейное преобразование координат х некоторого вектора, то какое соответствующее линейное преобразование А действует на координаты х этого же вектора в другой координатной системе?
Ответ. Пользуясь преобразованием (16.116), заметим, что

Отсюда

для произвольных значений х. Следовательно,

и наоборот,

Таким образом, матрица 
Свойства преобразований. Рассмотрим ряд свойств матриц-операторов, широко используемых в квантовомеханических расчетах.

Доказательство этих свойств производится путем непосредственной проверки.
2. Алгебра операторов 

3. Оператору А соответствуют те же самые собственные значения, что и оператору А, а их собственные функции связаны между собой следующим образом:

или

Определение. След, или шпур, квадратной матрицы А есть

т.е. равен сумме элементов, стоящих на главной диагонали.
Существенно, что шпур имеет смысл только для квадратных матриц.
Полезно знать следующее свойство шпура: циклическая перестановка матриц в произведении под знаком 

Теорема. Шпуры матриц 


Задача. Определить унитарную матрицу 

Решение (см. (16.9)). 
В самом деле, 

(Здесь использованы равенства 


Теорема. Шпур оператора А равен сумме его собственных значений: 
Доказательство очевидно следует из (16.17) и (16.16). Теперь можно дать новое определение матрицы 
Определение. Первый шаг: приведем матрицу А к диагональному виду А методом (16.17):

Второй шаг: возьмем в качестве 

Третий шаг: вернемся к прежнему базису

С помощью равенства (16.13) легко доказать справедливость этого определения. Определение (16.19) эквивалентно общему определению, данному в лекции 10, во всех случаях, когда последнее имеет смысл. Однако определение (16.19) не накладывает ограничений на функции 
Теорема. Перестановочное соотношение 
Доказательство.
Коммутатор 

Обратная теорема. Если матрицы 

Доказательство.
Приведем А к диагональному виду, следуя методу (16.17):

Сделаем то же с матрицей В:

(при этом заведомо неизвестно, диагональна ли матрица В). Из 


Но поскольку 




Тогда можно записать равенство 


Остается лишь произвести обратное преобразование и использовать определение (16.19). Теорема доказана.
Заметим, что по ходу дела фактически была доказана следующая
Теорема. Если невырожденная матрица В коммутирует с диагональной матрицей А, то матрица В должна быть также диагональна.
Если в теореме (16.22) диагональная матрица А является вырожденной, то В не обязательно должна быть диагональна, но имеет характерный вид, который можно усмотреть из следующего примера, с легкостью поддающегося обобщению:

Важное приложение. Устанавливаемые теоремой (16.22) и обобщением (16.23) факты находят в квантовой механике важное приложение:
Пусть 


Матрицы 
Если же А вырожденная, то В имеет вид, подобный (16.23); тогда ее секулярное уравнение распадается на более простые уравнения, порядок которых равен кратности вырождения собственных значений матрицы А.
Оглавление
- Предисловие к американскому изданию
- Лекция 1. Аналогия между оптикой и механикой
- Лекция 2. Уравнение Шредингера
- Лекция 3. Простейшие одномерные задачи
- Лекция 4. Линейный осциллятор
- Лекция 5. Метод Вентцеля-Крамерса-Бриллюэна
- Лекция 6. Сферические функции
- Лекция 7. Случай центральных сил
- Лекция 8. Атом водорода
- Лекция 9. Ортогональность волновых функций
- Лекция 10. Линейные операторы
- Лекция 11. Собственные функции и собственные значения
- Лекция 12. Операторы материальной точки
- Лекция 13. Принцип неопределенности
- Лекция 14. Матрицы
- Лекция 15. Эрмитовы матрицы. Задача на собственные значения
- Лекция 16. Унитарные матрицы и преобразования
- Лекция 17. Наблюдаемые
- Лекция 18. Момент импульса
- Лекция 19. Зависимость наблюдаемых от времени. Гейзенберговское представление
- Лекция 20. Законы сохранения и сохраняющиеся величины
- Лекция 21. Стационарная теория возмущений. Метод Ритца
- Лекция 22. Случай вырождения и квазивырождения. Эффект Штарка на водороде
- Лекция 23. Нестационарная теория возмущений. Борновское приближение
- Лекция 24. Испускание и поглощение излучения
- Лекция 25. Теория спина Паули
- Лекция 26. Электрон в центральном поле
- Лекция 27. Аномальный эффект Зеемана
- Лекция 28. Сложение векторов момента
- Лекция 29. Атомные мультиплеты
- Лекция 30. Системы тождественных частиц
- Лекция 31. Двухэлектронная система (атом гелия)
- Лекция 32. Молекула водорода
- Лекция 33. Теория столкновений
- Лекция 34. Теория свободного электрона Дирака
- Лекция 33. Теория столкновений
- Лекция 35. Электрон Дирака в электромагнитном поле
- Лекция 36. Электрон Дирака в центральном поле. Водородоподобный атом
- Лекция 37. Преобразование дираковских спиноров
- Комментарии
В линейной алгебре, complex квадратная матрица U является унитарной, если ее сопряженное транспонирование U также является его обратным, то есть если
- U ∗ U = UU ∗ = I, { displaystyle U ^ {*} U = UU ^ {*} = I,}
где I – единичная матрица.
В физике, особенно в квантовой механике, эрмитово сопряженное матрицы обозначается кинжалом (†), и приведенное выше уравнение принимает вид
- U † U = UU † = I. { displaystyle U ^ { dagger} U = UU ^ { dagger} = I.}
Реальным аналогом унитарной матрицы является ортогональная матрица. Унитарные матрицы имеют большое значение в квантовой механике, поскольку они сохраняют нормы и, следовательно, амплитуды вероятности.
Содержание
- 1 Свойства
- 2 Эквивалентные условия
- 3 Элементарные конструкции
- 3.1 Унитарная матрица 2 × 2
- 4 См. Также
- 5 Ссылки
- 6 Внешние ссылки
Свойства
Для любой унитарной матрицы U конечного размера выполняется следующее:
- Для двух комплексных векторов x и y умножение на U сохраняет их внутренний продукт ; то есть ⟨Ux, Uy⟩ = ⟨x, y⟩.
- U нормальный (U ∗ U = UU ∗ { displaystyle U ^ {*} U = UU ^ {*}}
).
- U диагонализуем ; то есть U унитарно подобен диагональной матрице, как следствие спектральной теоремы. Таким образом, U имеет разложение вида
-
- U = VDV ∗, { displaystyle U = VDV ^ {*},}
- U = VDV ∗, { displaystyle U = VDV ^ {*},}
- где V – унитарное, а D – диагональное и унитарное.
- | det (U) | = 1 { displaystyle left | operatorname {det} (U) right | = 1}
.
- Его собственные подпространства ортогональны.
- U может быть записывается как U = e, где e обозначает экспоненту матрицы, i – мнимая единица, а H – эрмитова матрица.
. Для любого неотрицательного целого числа n Набор всех унитарных матриц размера n × n с матричным умножением образует группу, называемую унитарной группой U (n).
Любая квадратная матрица с единичной евклидовой нормой является среднее двух унитарных матриц.
Эквивалентные условия
Если U – квадратная комплексная матрица, то Условия понижения эквивалентны:
- U унитарен.
- U унитарен.
- U обратим с U = U.
- Столбцы U образуют ортонормированный базис из C n { displaystyle mathbb {C} ^ {n}}
по отношению к обычному внутреннему произведению. Другими словами, UU = I.
- Строки U образуют ортонормированный базис C n { displaystyle mathbb {C} ^ {n}}
относительно обычный внутренний продукт. Другими словами, U U = I.
- U является изометрией по отношению к обычной норме. То есть ‖ U x ‖ 2 = ‖ x ‖ 2 { displaystyle | Ux | _ {2} = | x | _ {2}}
для всех x ∈ C n { displaystyle x in mathbb {C} ^ {n}}
, где ‖ x ‖ 2 = ∑ i = 1 n | х я | 2 { displaystyle | x | _ {2} = { sqrt { sum _ {i = 1} ^ {n} | x_ {i} | ^ {2}}}}
.
- U – это нормальная матрица (эквивалентно, существует ортонормированный базис, образованный собственными векторами U) с собственными значениями, лежащими на единичной окружности.
Элементарные конструкции
2 × 2 унитарная матрица
Общее выражение унитарной матрицы 2 × 2:
- U = [ab – ei φ b ∗ ei φ a ∗], | а | 2 + | б | 2 = 1, { displaystyle U = { begin {bmatrix} a b \ – e ^ {i varphi} b ^ {*} e ^ {i varphi} a ^ {*} \ end {bmatrix} }, qquad left | a right | ^ {2} + left | b right | ^ {2} = 1,}
, который зависит от 4 реальных параметров (фаза a, фаза b, относительная величина между a и b и угол φ). Определитель такой матрицы равен
- det (U) = e i φ. { displaystyle det (U) = e ^ {i varphi}.}
Подгруппа этих элементов U { displaystyle U}

Матрица U также может быть записана в этой альтернативной форме:
- U = ei φ / 2 [ei φ 1 cos θ ei φ 2 sin θ – e – i φ 2 sin θ e – я φ 1 соз θ], { Displaystyle U = е ^ {я varphi / 2} { begin {bmatrix} e ^ {я varphi _ {1}} cos theta e ^ {я varphi _ {2}} sin theta \ – e ^ {- i varphi _ {2}} sin theta e ^ {- i varphi _ {1}} cos theta \ end {bmatrix }},}
который, вводя φ 1 = ψ + Δ и φ 2 = ψ – Δ, принимает следующую факторизацию:
- U = ei φ / 2 [ei ψ 0 0 e – i ψ] [cos θ sin θ – sin θ cos θ] [ei Δ 0 0 e – i Δ]. { displaystyle U = e ^ {i varphi / 2} { begin {bmatrix} e ^ {i psi} 0 \ 0 e ^ {- i psi} end {bmatrix}} { begin {bmatrix} cos theta sin theta \ – sin theta cos theta \ end {bmatrix}} { begin {bmatrix} e ^ {i Delta} 0 \ 0 e ^ {- i Delta} end {bmatrix}}.}
Это выражение подчеркивает связь между унитарными матрицами 2 × 2 и ортогональными матрицами 2 × 2 угла θ.
Другая факторизация:
- U = [cos α – sin α sin α cos α] [ei ξ 0 0 ei ζ] [cos β sin β – sin β cos β]. { Displaystyle U = { begin {bmatrix} cos alpha – sin alpha \ sin alpha cos alpha \ end {bmatrix}} { begin {bmatrix} e ^ {i xi} 0 \ 0 e ^ {i zeta} end {bmatrix}} { begin {bmatrix} cos beta sin beta \ – sin beta cos beta \ конец {bmatrix}}.}
Возможны многие другие факторизации унитарной матрицы в базовые матрицы.
См. Также
- Эрмитова матрица
- Разложение матрицы
- Ортогональная группа O (n)
- Специальная ортогональная группа SO (n)
- Ортогональная матрица
- Квантовый логический элемент
- Специальная унитарная группа SU (n)
- Симплектическая матрица
- Унитарная группа U (n)
- Унитарный оператор
Ссылки
Внешние ссылки
- Weisstein, Eric W. «Унитарная матрица». MathWorld.
- Иванова, О.А. (2001) [1994], Энциклопедия математики, EMS Press
- “Показать, что собственные значения унитарной матрицы имеют модуль 1”. Обмен стеками. 28 марта 2016 г.
![Rendered by QuickLaTeX.com A_{2times2} = frac{1}{sqrt{2}}left[begin{array}{cc} 1 & 1\ i & -i end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6a10e53d7584c25444fd655a2f968eba_l3.png)
![Rendered by QuickLaTeX.com B_{3times3} = left[begin{array}{ccc} i & 0 & 0\ 0 & i & 0\ 0 & 0 & i end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ba81c9dc39cae0af7e030f9ae44a3aa9_l3.png)
![Rendered by QuickLaTeX.com U = frac{1}{2}left[begin{array}{cc} 1+i & -1+i\ 1+i & 1-i end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2280d553304f386df2c1ed288476defc_l3.png)
![Rendered by QuickLaTeX.com Conjugate matrix of U =frac{1}{2} left[begin{array}{cc} 1-i & -1-i\ 1-i & 1+i end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-382eeffcb2fe6b0bbf0401e9d3710553_l3.png)
![Rendered by QuickLaTeX.com U^{H} = frac{1}{2}left[begin{array}{cc} 1-i & 1-i\ -1-i & 1+i end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d9fb36fb7d63b612e5756c8fc7b70be4_l3.png)
![Rendered by QuickLaTeX.com UU^{H} = frac{1}{2}left[begin{array}{cc} 1+i & -1+i\ 1+i & 1-i end{array}right]timesfrac{1}{2}left[begin{array}{cc} 1-i & 1-i\ -1-i & 1+i end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7f46dbcf619f72ca4524dfc7da30f2e5_l3.png)
![Rendered by QuickLaTeX.com UU^{H} = frac{1}{4} left[begin{array}{cc} [(1+i)(1-i)+(-1+i)(-1-i)] & [(1+i)(1-i)+(-1+i)(1+i)]\{} [(1+i)(1-i)+(1-i)(-1-i)] & [(1+i)(1-i)+(i-i)(1+i)] end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2db1d6dbcae04eb3a38cd349e24120a9_l3.png)
![Rendered by QuickLaTeX.com UU^{H} = frac{1}{4}left[begin{array}{cc} [1+1+1+1] & [1+1-1-1]\{} [1+1-1-1] & [1+1+1+1] end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b5b625bb49f8a9b03461eea404b2e6da_l3.png)
![Rendered by QuickLaTeX.com UU^{H} = frac{1}{4}left[begin{array}{cc} 4 & 0\ 0 & 4 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ccba296c616417c498fab80680c7ff38_l3.png)
![Rendered by QuickLaTeX.com UU^{H} = left[begin{array}{cc} 1 & 0\ 0 & 1 end{array}right] = I](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-91d58bd5a97591fc276c92cdf00bfca1_l3.png)
![Rendered by QuickLaTeX.com A = left[begin{array}{cc} i & 0\ 0 & 1 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e187f3caa6f62c80d80ffe212fabd67b_l3.png)
![Rendered by QuickLaTeX.com The conjugate matrix of U = left[begin{array}{cc} -i & 0\ 0 & 1 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-941888f95aed898cd3270d1fa71970b8_l3.png)
![Rendered by QuickLaTeX.com A^{H} = left[begin{array}{cc} -i & 0\ 0 & 1 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f7dde76b08ad746311588bbd1a44f1de_l3.png)
![Rendered by QuickLaTeX.com AA^{H} = left[begin{array}{cc} i & 0\ 0 & 1 end{array}right]timesleft[begin{array}{cc} -i & 0\ 0 & 1 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-48fa2561f6715d913b122cb7c2aaef4d_l3.png)
![Rendered by QuickLaTeX.com AA^{H} = left[begin{array}{cc} [(itimes-i)+0] & [0+0]\{} [0+0] & [0+1] end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2583f4f45a8910ffbfef3a099243658a_l3.png)
![Rendered by QuickLaTeX.com AA^{H} = left[begin{array}{cc} -i^{2} & 0\ 0 & 1 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-53cb8fbc0697b8f465e5e0dcc58b5fc9_l3.png)
![Rendered by QuickLaTeX.com AA^{H} = left[begin{array}{cc} -(-1) & 0\ 0 & 1 end{array}right] = left[begin{array}{cc} 1 & 0\ 0 & 1 end{array}right] = I](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dedbe76b8f0c9fcd4ea8373f594f2469_l3.png)
![Rendered by QuickLaTeX.com P =frac{1}{3} left[begin{array}{cc} 2-i & 2\ 2 & 2+i end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a57cbbe34ed8129a56c7ff329bebad17_l3.png)
![Rendered by QuickLaTeX.com P = left[begin{array}{cc} frac{2-i}{3} & frac{-2}{3}\ frac{2}{3} & frac{2+i}{3} end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7241a002671062a587a25df43a433325_l3.png)
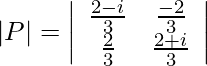




 ).
).
 .
. по отношению к обычному внутреннему произведению. Другими словами, UU = I.
по отношению к обычному внутреннему произведению. Другими словами, UU = I. для всех x ∈ C n { displaystyle x in mathbb {C} ^ {n}}
для всех x ∈ C n { displaystyle x in mathbb {C} ^ {n}} , где ‖ x ‖ 2 = ∑ i = 1 n | х я | 2 { displaystyle | x | _ {2} = { sqrt { sum _ {i = 1} ^ {n} | x_ {i} | ^ {2}}}}
, где ‖ x ‖ 2 = ∑ i = 1 n | х я | 2 { displaystyle | x | _ {2} = { sqrt { sum _ {i = 1} ^ {n} | x_ {i} | ^ {2}}}} .
.




