Как найти универсальную температуру

Как найти температуру газа

Для того чтобы найти абсолютную температуру идеального газа, можно воспользоваться уравнением, которое широко известно, как уравнение Клапейрона-Менделеева. Эта формула позволяет установить зависимость между давлением, температурой газа и его молярным объемом.

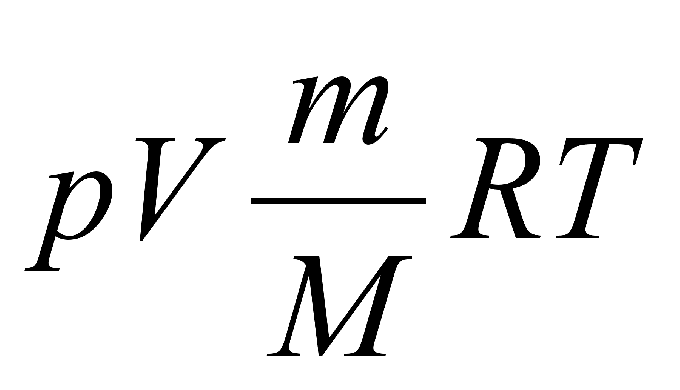
Вам понадобится

• Лист бумаги, ручка.

Инструкция

Формула выглядит следующим образом: p•Vm = R•T, где p — это давление, Vm — молярный объем газа, R — это универсальная газовая постоянная, а Т — абсолютная температура идеального газа.

Выясняем, какие данные нам доступны для того, чтобы использовать формулу, таким образом: Т = (p•Vm)/ R.

В случае если нам не известен молярный объем газа, мы можем найти его по формуле:
Vm = V/?. В этой формуле ? представляет собой количество вещества, Найти эту величину можно разделив массу газа на его молярную массу.

Формула, которая носит название закон Менделеева-Клапейрона, записывается именно в таком виде: p•V = (m/М) • R•T.

Видоизменяем эту формулу, чтобы найти температуру газа: T = (p•V • М)/(R• m).

Находим все величины, которые требуются нам для подстановки в формулу. Выполняем расчеты и находим искомую температуру идеального газа.

Обратите внимание

Внимательно разберитесь в условных обозначениях, чтобы из-за неправильно распознанного символа в формуле не допустить ошибки в расчетах.

Полезный совет

Закон Менделеева-Клапейрона также называют объединенным газовым законом, именно из него выводятся законы Шарля и Гей-Люссака, а также Бойля-Мариотта.

Источники:

• Здесь вы найдете не только информацию, которая касается непосредственно поиска абсолютной температуры идеального газа, но и массу информации о свойствах газов.
• как определить температуру газа
• Температура газовой плиты

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Узнать температуру процессора, видеокарты и дискового носителя

Обновлено: 12.03.2023
Опубликовано: 10.04.2018

Тематические термины: Процессор, Видеокарта, HDD, SSD

Перегрев компонентов компьютерной техники приводит к ее нестабильной работе и непредвиденным сбоям. В случае проблем, необходимо узнать температуру комплектующих, а лучше, постоянно ее мониторить, чтобы не допустить критического состояния.

Примеры, приведенные в данной статье применимы к различным производителям процессоров (Intel, AMD), видеокарт (NVIDIA, AMD, Intel), дисковых носителей. Также, руководство применимо к настольным компьютерам, ноутбукам и моноблокам под управлением Windows, и в некоторых случаях, Linux. Большинство рассматриваемых программ имеют русский перевод или интуитивно понятный интерфейс.

Универсальные программы

Самый простой способ определить температурные показатели — использовать программу, которая может показать термо-датчики всех устройств. Ниже представлены примеры, именно, таких программ.

1. Speccy

Это бесплатная небольшая программа. Скачать можно с официального сайта.

После установки и запуска в первом окне мы увидим всю нужную нам информацию:

* 1) температура процессора. 2) материнской платы (северного моста). 3) видеокарты. 4) дисковых носителей.

2. SpeedFan

Программа предназначена для контроля скорости кулеров, однако, отображение температур — ее неотъемлемая часть. Также, можно настроить автозапуск программы и постоянно видеть температурные показатели в трее.

Запускаем программу – в первом окне увидим показатели с датчиков:

Подробнее, программа описана в статье SpeedFan — изменение скорости вентиляторов.

3. AIDA64 (everest)

Это хорошая программа, но некоторые функции доступны только в платной версии. Поэтому применять ее только для определения температуры не целесообразно. Однако, если AIDA уже стоит в системе, стоит ей воспользоваться.

Запускаем программу – раскрываем пункт Компьютер – кликаем по Датчики. Справа находим Температуры:

Если свернуть программу, в трее мы будем видеть все показатели температур.

Подробнее об AIDA64.

4. HWMonitor

Переходим на официальный сайт и скачиваем утилиту (можно обойтись портативной версией — zip-архив). Устанавливаем или распаковываем программу и запускаем ее — информацию о температурах мы увидим в удобно сгруппированных разделах:

5. MSI Afterburner

С ее помощью можно мониторить температуру комплектующих во время игр. Скачиваем утилиту с официального сайта, устанавливаем ее и запускаем.

Для настройки мониторинга открываем настройки:

Переходим на вкладку Мониторинг, выбираем галочками счетчики и для каждого из них настраиваем Показывать в ОЭД:

6. lm-sensors (Linux)

Утилита позволяет в системах на базе Linux увидеть температуру процессора и других устройств, которые сможет обнаружить утилита.

Установка немного отличается в зависимости от типа Linux.

а) Для Linux DEB (Debian / Ubuntu / Astra Linux):

apt update

apt install lm-sensors

б) Для Linux RPM (Rocky Linux / CentOS / РЕД ОС):

yum install lm_sensors

Установка завершена.

После запускаем команду для обнаружения сенсоров:

sensors-detect –auto

Можно смотреть температуру:

sensors

Температура процессора

Разберем программы для определения температуры процессора.

1. Core Temp

Простая бесплатная утилита с поддержкой русского языка. Скачать можно на официальном сайте. После загрузки, установки и запуска мы увидим основное окно программы со всеми необходимыми показаниями:

2. Команда в Powershell

Открываем Powershell от имени администратора и выполняем команду:

Get-WMIObject msacpi_thermalzonetemperature -namespace “root/wmi” | Select CurrentTemperature | ForEach-Object { ($_.CurrentTemperature/10)-273.15 }

Мы получим что-то на подобие:

27,85
29,85

* результат получиться в градусах по Цельсию.

3. БИОС или UEFI

Без установки дополнительных программ, температуру процессора можно посмотреть в базовой системе ввода вывода. Для начала, заходим в БИОС.

В разных версиях микропрограммы мы увидим разные варианты представления информации:

4. Различные гаджеты

Также можно найти в сети Интернет различные гаджеты для постоянного отображения информации о температуре на рабочем столе Windows, например, IntelCoreSerie.

5. CPU-Z

Казалось бы, программа CPU-Z должна показывать всю информацию о процессоре. Однако, разработчики выпустили отдельную утилиту HWMonitor (описана выше), которая позволяет смотреть температуру комплектующих ПК.
 

Температура видеокарты

Без специальных программ, узнать температуру видеокарты не представляется возможным. Рассмотрим несколько утилит, которые позволят это сделать.

1. GPU-Z

Простая утилита для отображения информации о видеокарте, в частности, температуры. Хороший способ, если не хочется ничего устанавливать — есть возможность запустить программу, не устанавливая. Скачать можно с официального сайта.

После запуска, переходим на вкладку Sensors и в разделе GPU Temperature мы увидим информацию о текущей температуре:

Кликнув по разделу, можно выбрать режим отображения, например, средние температурные показатели за весь период:

2. GPU Temp

Переходим на сайт программы, скачиваем ее и запускаем процесс установки. После запускаем и видим необходимые показатели:

3. Гаджеты

Как и для процессора, для видеокарты тоже можно найти гаджеты. Например, NVIDIA GPU Temp, отображает температуру видеокарты от одноименного производителя.
 

Температура HDD или SSD

Ну и разберем программы, которые позволят узнать температуру жесткого диска.

1. CrystalDiskInfo

Программа полезна, в первую очередь, отображением здоровья диска. Но она также отображает его температуру:

Подробнее о программе читайте статью CrystalDiskInfo — мониторинг жестких дисков.

2. HD Tune

Данная утилита позволяет проводить диагностику диска, смотреть его показатели, в то числе — температурные:

Подробнее о программе и как с ней работать — HD Tune — сканирование жесткого диска.

3. HDD Temperature

Это платная утилита, поэтому не интересна в контексте просмотра температуры. Однако, если такая программа уже есть в системе, можно пользоваться ей:

4. HDDLife

Вариант рабочий, но также — не самый лучший выбор для проверки температуры — во первых, платная, во-вторых, поддерживает не все оборудование.
 

Нормальная температура комплектующих

В каких же пределах должна держаться температура для различных комплектующих.

Процессора

• До 42 ^oC. Процессор в режиме простоя.
• До 65 – 70 ^oC (в зависимости от модели). При нагрузке.
• До 61 – 72 ^oC (в зависимости от модели). Максимально рекомендуемая.

А также:

• 94 – 105 ^oC. Включение троттлинга — снижения производительности.
• Более 105 ^oC. Выключение компьютера с целью предотвращения сгорания.

Обратите внимание, что данные показатели могут постоянно меняться, так как меняются технологии. Если необходимо узнать точную информацию по конкретному процессору, можно воспользоваться подсказками в различных программах, например, в представленной выше Core Temp:

Таким образом, данные цифры условны — норма зависит от производителя (Intel, AMD …) и конкретной модели. Также, норма для процессоров большинства ноутбука ниже. Правильнее всего зайти на страничку конкретного процессора и посмотреть его норму по температуре.

Видеокарты

В большей степени, рабочая температура видеокарты зависит от ее класса — для точного определения стоит изучить документацию. Средние показатели, примерно, следующие:

• До 45 ^oC. В режиме простоя.
• До 85 ^oC. При нагрузке.
• До 100 ^oC. Максимально рекомендуемая.

Свыше 100 ^oC видеокарта запускает процесс троттлинга и, если он не помогает — выключает компьютер.

Диска

• До 45 ^oC. В режиме простоя.
• До 53 ^oC. Максимально рекомендуемая.

При температуре выше 53 градусов значительно увеличивается амортизация диска, что приводит к ускорению его выхода из строя. Максимально допустимый порог SSD дисков чуть выше и может доходить до 70 градусов.

Минимальная рабочая температура диска должна быть в пределах 24-26 градусов. При более низких показателях возможны повреждения. Поэтому, если мы принесли с улицы холодный носитель, не стоит его сразу использовать в работе. Таким образом, комфортная температура для диска — от 25 до 45 градусов по Цельсию.

Данные цифры справедливы как для внутренних дисков, так и внешних, так как, по сути, последние — это те же самые диски, помещенные в отдельные боксы.
 

Последствия перегрева

Как говорилось выше, перегрев комплектующих может вызвать различного рода проблемы. Судить о возможном перегреве можно по следующим симптомам:

1. Замедление работы компьютера. Для предотвращения сгорания и выключения, процессор и видеокарта запускают процесс троттлинга. По сути, они начинают работать с заниженными показателями, что приводит, с одной стороны, к понижению выделения тепла, с другой — уменьшение производительности.
    
2. Излишний шум. Чаще всего, в компьютер устанавливаются управляемые вентиляторы, которые начинают вращаться быстрее при превышении температуры. Само собой, это приводит к повышению уровня шума.
    
3. Самопроизвольное выключение компьютера. Для предотвращения окончательного сгорания, устройство подает сигнал на остановку подачи электропитания, что приводит к резкому выключению ПК. Это крайняя мера.
    
4. Появление на экране цветных фигур (артефактов). Типичный симптом при перегреве видеокарты.
    
5. Проседание FPS в играх. Частный случай замедления работы ПК.
    
6. Горячий корпус. Как правило, это можно заметить только для моноблоков и ноутбуков.
    
7. Синий экран смерти (BSOD). В редких случаях, система выдает стоп ошибку.

Причины перегрева и как снизить температуру

Разберем причины, когда температура комплектующих начинает выходит за рамки допустимой.

1. Пыль. Чаще всего, грязь внутри системного блока или ноутбука является причиной ухудшения теплопроводности и повышения температуры. Для решения проблемы, разбираем компьютер и выдуваем пыль, используя баллончик со сжатым воздухом.
    
2. Скопление горячего воздуха внутри корпуса. Для начала можно попробовать открыть боковую крышку компьютера, если поможет — установить дополнительный вентилятор на боковую стенку. Для ноутбука можно купить охлаждающую подставку.
    
3. Высыхание термопасты. Снимаем кулер процессора, стираем остатки термопасты и наносим новый слой.
    
4. Слабая работа вентиляторов. При слабом их вращении, эффективность охлаждения будет ниже предполагаемой. Замерить скорость вращения вентиляторов можно с помощь вышеупомянутых программ, например, SpeedFan. Вентиляторы можно попробовать почистить от пыли, смазать, заменить.
    
5. Близкое расположение комплектующих друг к другу. Железо может греть друг друга. Если есть место, стоит разместить диски на большом расстоянии друг от друга, то же самое имеет отношение к видеокартам. Внутри корпуса все провода стоит аккуратно загнуть по краям, оставив много пространства в центре для эффективной циркуляции воздуха.
    
6. Высокая температура окружения. Летом требуется больше охлаждать компьютер. Также стоит следить, чтобы компьютер стоял подальше от батарей или иных источников тепла.
    
7. Проблема с электропитанием. При завышенной подаче электропитания, будет наблюдаться перегрев. Измерить напряжение можно вышеописанными утилитами, например, AIDA64 или HWMonitor. При превышении показателей напряжения попробуем подключить компьютер к другому источнику электроэнергии или заменить блок питания.
    
8. Неэффективный режим работы электропитания Windows. Если выставлен режим работы электропитания на максимальную производительность, стоит попробовать выставить сбалансированный.
    
9. Перегрев блока питания. Некоторые модели блоков питания имеют выдувной вентилятор в сторону процессора, что ухудшает эффект от системы охлаждения последнего.

Дополнительно, о снижении температуры читайте статью Перегревается компьютер.

Random converter

• Калькуляторы
• Термодинамика — теплота

Калькулятор закона состояния идеального газа (давление–объем–температура–количество)

Термодинамика — теплота

На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.

Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.

Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!

Канал Конвертера единиц TranslatorsCafe.com на YouTube

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:

Примеры задач на уравнение Менделеева-Клапейрона

В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
Вопрос: сколько молей кислорода содержится в колбе?

Некоторое количество гелия при 78 градусах Цельсия и давлении 45,6 атмосфер занимает объем 16,5 литров.
Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)

В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Теперь немного формул.

где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль

Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также

где n — число молей газа

И как нетрудно заметить, соотношение

есть величина постоянная для одного и того же количества моль газа.

И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.

Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.

Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры

Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры

Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.

Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.

Уравнение Клапейрона-Менделеева

Что такое уравнение Клапейрона-Менделеева

Идеальный газ — это газ, в котором пренебрегают взаимодействием молекул газа между собой.

Идеальными считают разреженные газы. Особенно близкими к идеальным считают гелий и водород.

Идеальный газ — это упрощенная математическая модель, которая широко применяется для описания свойств и поведения реальных газов при атмосферном давлении и комнатной температуре.

Давление, объем и температура — это основные параметры состояния системы, и они связаны друг с другом. Соотношение, при котором определяется данная связь, называется уравнением состояния данного газа.

Существует эквивалентная макроскопическая формулировка идеального газа — это такой газ, который одновременно будет подчиняться закону Бойля-Мариотта и Гей-Люссака, то есть:

p V = c o n s t * T

В представленном выше уравнении состоянии газа под const подразумевается количество молей.

Свойства классического и квазиклассического идеального газа описываются уравнением состояния идеального газа, которое называется уравнением Менделеева-Клапейрона, ниже представлена формула Менделеева-Клапейрона.

p V = m M R T = n R T , где m — масса газа, M — молярная масса газа, R = 8 , 314 Д ж / ( м о л ь * К ) — универсальная газовая постоянная, T — температура (К), n — количество молей газа.

Таким образом давление и объем прямо пропорциональны количеству молей и температуре.

Также уравнение Клапейрона-Менделеева можно записать в ином виде:

p V = N k T , где N — это количество молекул газа массой m , k = 1 , 38 * 10 – 23 Д ж / К — постоянная Больцмана, которая определяет «долю» газовой постоянной, приходящуюся на одну молекулу и определяется по формуле:

N = m N A M , где

N A = 6 . 02 * 10 23 м о л ь – 1 ; — это постоянная Авогадро.

Какое значение имеет универсальная газовая постоянная

Универсальная газовая постоянная (R) — это величина, которая является константой, численно равная работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 K.

Значение данной константы находится как произведение постоянной Больцмана ( k = 1 , 38 * 10 – 23 Д ж / К ) на число Авогадро ( N A = 6 . 02 * 10 23 м о л ь – 1 ) . Таким образом универсальная газовая постоянная принимает следующее значение: R = 8 , 314 Д ж / ( м о л ь * К ) .

Постоянную Больцмана используют в формулах, описывающих изучаемое явление или поведение рассматриваемого объекта с микроскопической точки зрения, тогда как универсальная газовая постоянная более удобна при расчетах, касающихся макроскопических систем, когда число частиц задано в молях.

Связь с другими законами состояния идеального газа

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса и один трех макропараметров (давление, температура или объем) — остаются неизменными.

Количественные зависимости между двумя параметрами газа при фиксированном третьем параметре называют газовыми законами, которые связывают эти параметры.

Изопроцессы — это термодинамические процессы, во время протекания которых количество вещества и один из макропараметров состояния: давление, объем, температура или энтропия — остается неизменным.

В зависимости от того, какой параметр остается неизменным различают разные процессы, которые выражаются законами, являющимися следствием уравнения состояния газа:

• изотермический процесс (T=const);
• изохорный процесс (V=const);
• изобарный процесс (p=const).

Изотермический процесс (T=const)

Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.

Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой — термостатом. Им может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.

Согласно уравнению Клапейрона-Менделеева, в любом состоянии с неизменной температурой произведение давления газа на объем одно и то же, то есть постоянно:

Этот закон был открыт экспериментально английским ученым Бойлем и несколько позднее французским ученым Мариоттом. Именно поэтому он называется закон Бойля-Мариотта.

Закон Бойля-Мариотта справедлив для любых газов, а также для смеси газов (например, для воздуха).

Зависимость давления газа от объема при постоянной температуре изображается графической кривой — изотермой. Изотерма для различных температур представлена в координатах pV на рис.1. и представляет собой гиперболу.

Рис.1. Изотерма в pV — координатах.

Изохорный процесс (V=const)

Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным.

Из уравнения состояния следует, что отношение давлений газа данной массы при постоянно объеме равно отношению его абсолютных температур:

p 1 p 2 = T 1 T 2

Газовый закон был установлен экспериментально в 1787 г. французским физиком Ж. Шарлем и носит название закона Шарля: давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.

Так, если в качестве одного из состояний газа выбрать состояние газа при нормальных условиях, тогда

p = p 0 T T 0 = p 0 γ T

Коэффициент γ называют температурным коэффициентом давления газа. Он одинаков для всех газов.

Зависимость давления газа от температуры при постоянном объеме изображается графически прямой, которая называется изохорой (Рис.2).

Рис.2 Изображение изохоры в pT-координатах.

Изобарный процесс (p=const)

Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным.

Из уравнения Клапейрона-Менделеева вытекает, что отношение объемов газа данной массы при постоянном давлении равно отношению его абсолютных температур.

V 1 V 2 = T 1 T 2

Если в качестве второго состояния газа выбрать состояние при нормальных условиях (нормальном атмосферном давлении, температуре таяния льда) следует:

V = V 0 T T 0 = V 0 α T

Этот газовый закон был установлен экспериментально в 1802 г французским ученым Гей-Люссаком.

Закон Гей-Люссака: объем данной массы газа при постоянном давлении прямо пропорционален абсолютной температуре.

Коэффициент α называют температурным коэффициентом объемного расширения газов.

Зависимость объема газа от температуры при постоянном давлении изображается графической прямой, которая называется изобарой (Рис.3).

Рис. 3. Изобара в VT-координатах.

Использование универсального уравнения для решения задачи

В реальности проводятся различные физико-химические процессы. Рассмотрим каким образом уравнение состояния идеального газа и законы, связанные с ним находят применение для решения физических и химических задач.

Определить давление кислорода в баллоне объемом 1 м 3 при температуре t = 27 C o . Масса кислорода 1 кг.

Так как в уравнении даны объем и температура — два из трех макроскопических параметров, а третий (давление) нужно определить, то мы можем использовать уравнение Клапейрона-Менделеева:

p V = n R T = m M R T

Не забываем перевести температуру в Кельвины:

T = t + 273 = 27 + 273 = 300 K

Молярная масса кислорода известна из таблицы Менделеева:

M ( O 2 ) = 2 * 16 = 32 г / м о л ь = 32 * 10 – 3 к г / м о л ь

Выразим из уравнения состояния давления и поставим все имеющиеся данные:

p = n R T V = m R T M V = 1 * 8 . 31 * 300 32 * 10 – 3 * 1 = 77 . 906 П а = 78 к П а

Ответ: p = 78 кПа.

Каким может быть наименьший объем баллона, содержащего кислород массой 6,4 кг, если его стенки при t = 20 C o выдерживают p = 1568 Н / с м 2 ?

Используем уравнение Менделеева-Клапейрона, из которого выражаем объем кислорода, который нужно найти:

p = n R T V = m R T M V

Молярная масса кислорода предполагается равной:

M ( O 2 ) = 2 * 16 = 32 г / м 3

Не забываем перевести температуру в Кельвины:

T = t + 273 = 20 + 273 = 293 K

Переводим давление: p = 15680000 Па

Выражаем из уравнения Клапейрона-Менделеева объем и подставляем значения, данные в условиях задачи:

V = n R T p = m R T M p = 6 . 4 * 8 . 31 * 293 15680000 * 32 * 10 – 3 = 3 . 1 * 10 – 2 м 3 = 31 л .

Используя уравнение состояния идеального газа, доказать, что плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .

Согласно уравнению Менделеева-Клапейрона:

p = n R T V = m R T M V

Плотность — это величина, характеризующая массу некоторого объема и находится по формуле:

ρ = m V и л и V = m ρ

Тогда p m ρ = n R T = m R T M

Откуда выражаем плотность газа:

Для водорода эта формула запишется следующим образом:

ρ H 2 = p M H 2 R T

По условию задачи водород и любой другой газ находятся при одинаковых условиях, откуда следует, что:

ρ H 2 M H 2 = p R T

Поставим последнее выражение в выражение для плотности любого газа:

ρ = M * ρ H 2 M H 2

Молярная масса водорода, исходя из таблицы Менделеева равна 2 г/моль и тогда. Молекулярная масса численно равная молярной и представляет собой массу молекулы в атомных единицах, поэтому в дальнейшем мы совершили переход к молекулярной массе.

ρ = M r * ρ H 2 2

Вывод: плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .

Рассмотрим несколько задач на законы, связанные с уравнение Клапейрона-Менделеева, то есть на изотермические, изохорные, изобарные процессы.

При уменьшении давления газа в 2,5 раза его объем увеличился на 12 л. Какой объем занимал газ в начальном состоянии, если температура на протяжении всего процесса оставалась постоянной?

По условию задачи температура в ходе всего процесса оставалась постоянной, откуда следует, что у нас изотермический процесс, и мы можем воспользоваться для решения законом Бойля-Мариотта.

p 1 V 1 = p 2 V 2 , г д е p 1 – давление газа в начальном состоянии (до расширения), V 1 — объем газа в начальном состоянии, p 2 = p 1 2 . 5 — давление газа в конечном состоянии (после расширения), V 2 = V 1 + ∆ V — объем газа в конечном состоянии.

Откуда можем найти начальный объем:

p 1 V 1 = p 1 2 . 5 ( V 1 + ∆ V ) = p 1 2 . 5 V 1 + p 1 2 . 5 ∆ V

V 1 ( p 1 – p 1 2 . 5 ) = p 1 2 . 5 ∆ V

p 1 2 . 5 V 1 ( 2 . 5 – 1 ) = p 1 2 . 5 ∆ V

V 1 = ∆ V 1 , 5 = 8 л

Ответ: первоначальный объем газа был равен 8 л.

Газ находится в баллоне при температуре 400 К. До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 1,5 раза?

Так как нагревание газа по условиям данной задачи происходит при постоянном объеме, значит перед нами изохорный процесс.

При изохорном процессе:

p 1 T 1 = p 2 T 2

T 2 = p 2 T 1 p 1

p 2 p 1 = 1 . 5 T 2 = 1 . 5 * T 1 = 1 . 5 * 400 = 600 K

При 27°C объем газа равен 600 мл. Какой объем займет газ при 57°C, если давление будет оставаться постоянным?

Так как давление по условию остается постоянным, то можем использовать закон Гей-Люссака.

V 1 V 2 = T 1 T 2

V_2 – искомый объем

Для правильного расчета необходимо перевести температуры из Цельсий в Кельвины:

T 1 = 273 + 27 = 300 K

T 2 = 273 + 57 = 330 K

T 2 V 1 T 1 = V 2

V 2 = ( 600 * 330 ) / 300 = 660 м л

Газ в трубе плавильной печи охлаждается от температуры t 1 = 1150 ° С д о t 2 = 200 ° С . Во сколько раз увеличивается плотность газа при этом? Давление газа не меняется.

Так как по условию задания давления газа не изменяется, значит перед нами изобарный процесс. Для решения воспользуемся законом Гей-Люссака:

V 1 V 2 = T 1 T 2

Перейдем к абсолютной температуре:

T 1 = 1150 + 273 = 1423 K

T 2 = 200 + 273 = 473 K

Масса газа: m = ρ 1 V 1 = ρ 2 V 2

Использование этих формул приводит к следующему:

Уравнение состояния идеального газа

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:

Уравнение состояния идеального газа

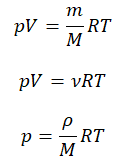
Внимание! При решении задач важно все единицы измерения переводить в СИ.

Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.

Из основного уравнения состояния идеального газа выразим массу:

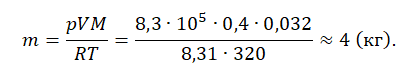
Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.

Подсказки к задачам

Важна только та масса, что осталась в сосуде. Поэтому:

Давление возросло на 15%	p2 = 1,15p1
Объем увеличился на 2%	V2 = 1,02V1
Масса увеличилась в 3 раза	m2 = 3m1
Газ нагрелся до 25 о С	T2 = 25 + 273 = 298 (К)
Температура уменьшилась на 15 К (15 о С)	T2 = T1 – 15
Температура уменьшилась в 2 раза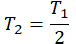
Масса уменьшилась на 20%	m2 = 0,8m1
Выпущено 0,7 начальной массы
Какую массу следует удалить из баллона?	Нужно найти разность начальной и конечной массы:
Газ потерял половину молекул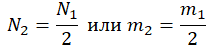
Молекулы двухатомного газа (например, водорода), диссоциируют на атомы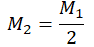
Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ)	M (O3) = 3Ar (O)∙10 –3 кг/моль M (O2) = 2Ar (O)∙10 –3 кг/моль
Открытый сосуд	Объем V и атмосферное давление pатм остаются постоянными
Закрытый сосуд	Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины
Нормальные условия	Температура T0 = 273 К Давление p0 = 10 5 Па
Единицы измерения давления	1 атм = 10 5 Па

Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.

2,8 МПа = 2,8∙10 6 Па

1,5 МПа = 1,5∙10 6 Па

Так как половина молекул была выпущена, m₂ = 0,5m₁. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:

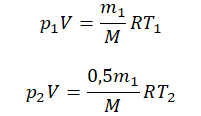
Преобразим уравнения и получим:

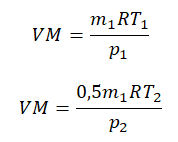
Приравняем правые части и выразим искомую величину:

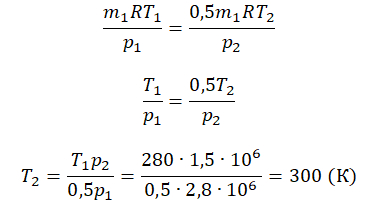
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.

[spoiler title=”источники:”]

http://wika.tutoronline.ru/fizika/class/10/uravnenie-klapejronamendeleeva

[/spoiler]