Как найти упорядоченный столбец в матрице - Сайт, где вы сможете решить свои вопросы

Под отсортированной матрицей будем понимать такую матрицу, строки и столбцы которой отсортированы.

Чтобы найти нужный элемент, можно воспользоваться бинарным поиском по каждой строке. Алгоритм потребует O(M log(N)) времени, так как необходимо обработать М столбцов, на каждый из которых тратится O(log(N)) времени. Также можно обойтись и без сложного бинарного поиска. Мы разберем два метода.

Решение 1: обычный поиск

Прежде чем приступать к разработке алгоритма, давайте рассмотрим простой пример:

15	20	40	85
20	35	80	95
30	55	95	105
40	80	100	120

Допустим, мы ищем элемент 55. Как его найти?

Если мы посмотрим на первые элементы строки и столбца, то можем начать искать расположение искомого элемента. Очевидно, что 55 не может находиться в столбце, который начинается со значения больше 55, так как в начале столбца всегда находится минимальный элемент. Также мы знаем, что 55 не может находиться правее, так как значение первого элемента каждого столбца увеличивается слева направо. Поэтому, если мы обнаружили, что первый элемент столбца больше х, нужно двигаться влево.

Аналогичную проверку можно использовать и для строк. Если мы начали со строки, значение первого элемента которой больше х, нужно двигаться вверх.

Аналогичные рассуждения можно использовать и при анализе последних элементов столбцов или строк. Если последний элемент столбца или строки меньше х, то, чтобы найти х, нужно двигаться вниз (для строк) или направо (для столбцов). Это так, поскольку последний элемент всегда будет максимальным.

Давайте используем все эти наблюдения для построения решения:

Если первый элемент столбца больше х, то х находится в колонке слева.
Если последний элемент столбца меньше х, то х находится в колонке справа.
Если первый элемент строки больше х, то х находится в строке, расположенной выше.
Если последний элемент строки меньше х, то х находится в строке, расположенной ниже.

Давайте начнем со столбцов.

Мы должны начать с правого столбца и двигаться влево. Это означает, что первым элементом для сравнения будет [0][с-1], где с — количество столбцов. Сравнивая первый элемент столбца с х (в нашем случае 55), легко понять, что х может находиться в столбцах 0,1 или 2. Давайте начнем с [0][2].

Данный элемент может не являться последним элементом строки в полной матрице, но это конец строки в подматрице. А подматрица подчиняется тем же условиям. Элемент [0][2] имеет значение 40, то есть он меньше, чем наш элемент, а значит, мы знаем, что нам нужно двигаться вниз.

Теперь подматрица принимает следующий вид (серые ячейки отброшены):

15	20	40	85
20	35	80	95
30	55	95	105
40	80	100	120

Мы можем раз за разом использовать наши правила поиска. Обратите внимание, что мы используем правила 1 и 4.

Следующий код реализует этот алгоритм:

public static boolean findElement(int[][] matrix, int elem) {
	int row = 0;
	int col = matrix[0].length - 1;
	while (row < matrix.length && col >= 0) {
		if (matrix[row][col] == elem) {
			return true;
		} else if (matrix[row][col] > elem) {
			col--;
		} else {
			row++;
		}
	}
	return false;
}

Другой подход к решению задачи — бинарный поиск. Мы получим более сложный код, но построен он будет на тех же правилах.

Решение 2: бинарный поиск

Давайте еще раз обратимся к нашему примеру:

15	20	70	85
20	35	80	95
30	55	95	105
40	80	100	120

Мы хотим повысить эффективность алгоритма. Давайте зададимся вопросом: где может находиться элемент?

Нам сказано, что все строки и столбцы отсортированы. Это означает, что элемент [i][j] больше, чем элементы в строке i, находящиеся между столбцами 0 и j и элементы в строке j между строками 0 и i-1.
Другими словами:

a[i][0] <= a[i][1] <= … <= a[i][j-i] <= a[i][j]
a[0][j] <= a[1][j] <= … <= a[i-1][j] <= a[i][j]

Посмотрите на матрицу: элемент, который находится в темно-серой ячейке, больше, чем другие выделенные элементы.

15	20	70	85
20	35	80	95
30	55	95	105
40	80	100	120

Элементы в белых ячейках упорядочены. Каждый из них больше как левого элемента, так и элемента, находящегося выше. Таким образом, выделенный элемент больше всех элементов, находящихся в квадрате.

15	20	70	85
20	35	80	95
30	55	95	105
40	80	100	120

Можно сформулировать правило: нижний правый угол любого прямоугольника, выделенного в матрице, будет содержать самый большой элемент.

Аналогично, верхний левый угол всегда будет наименьшим. Цвета в приведенной ниже схеме отражают информацию об упорядочивании элементов (светло-серый < белый < темно-серый):

15	20	70	85
20	35	80	95
30	55	95	105
40	80	100	120

Давайте вернемся к исходной задаче. Допустим, что нам нужно найти элемент 85. Если мы посмотрим на диагональ, то увидим элементы 35 и 95. Какую информацию о местонахождении элемента 85 можно из этого извлечь?

15	20	70	85
20	35	80	95
30	55	95	105
40	80	100	120

85 не может находиться в темно-серой области, так как элемент 95 расположен в верхнем левом углу и является наименьшим элементом в этом квадрате.

85 не может принадлежать светло-серой области, так как элемент 35 находится в нижнем правом углу.

85 должен быть в одной из двух белых областей.

Таким образом, мы делим нашу сетку на четыре квадранта и выполняем поиск в нижнем левом и верхнем правом квадрантах. Их также можно разбить на квадранты и продолжить поиск.

Обратите внимание, что диагональ отсортирована, а значит, мы можем эффективно использовать бинарный поиск.

Приведенный ниже код реализует этот алгоритм:

public Coordinate findElement(int[][] matrix, Coordinate origin, Coordinate dest, int x) {
	if (!origin.inbounds(matrix) || !dest.inbounds(matrix)) {
		return null;
	}
	if (matrix[origin.row][origin.column] == x) {
		return origin;
	} else if (!origin.isBefore(dest)) {
		return null;
	}

	/* Установим start на начало диагонали, a end - на конец
	* диагонали. Так как сетка, возможно, не является квадратной, конец
	* диагонали может не равняться dest. */
	Coordinate start = (Coordinate) origin.clone();
	int diagDist = Math.min(dest.row - origin.row, dest.column - origin.column);
	Coordinate end = new Coordinate(start.row + diagDist, start.column + diagDist);
	Coordinate p = new Coordinated(0, 0);

	/* Производим бинарный поиск no диагонали, ищем первый
	* элемент больше х */
	while (start.isBefore(end)) {
		р.setToAverage(start, end);
		if (x > matrix[p.row][p.column]) {
			start.row = p.row + 1;
			start.column = p.column + 1;
		} else {
			end.row = p.row - 1;
			end.column = p.column - 1;
		}
	}

	/* Разделяем сетку на квадранты. Ищем в нижнем левом и верхнем
	 * правом квадранте */
	return partitionAndSearch(matrix, origin, dest, start, x);
}

public Coordinate partitionAndSearch(int[][] matrix,
Coordinate origin. Coordinate dest, Coordinate pivot, int elem) {
	Coordinate lowerLeftOrigin = new Coordinate(pivot.row, origin.column);
	Coordinate lowerLeftDest = new Coordinate(dest.row, pivot.column - 1);
	Coordinate upperRightOrigin = new Coordinate(origin.row, pivot.column);
	Coordinate upperRightDest = new Coordinate(pivot.row - 1, dest.column);
	
	Coordinate lowerLeft = findElement(matrix, lowerLeftOrigin, lowerLeftDest, elem);
	if (lowerLeft == null) {
		return findElement(matrix, upperRightOrigin, upperRightDest, elem);
	}
	return lowerLeft;
}

public static Coordinate findElement(int[][] matrix, int x) {
	Coordinate origin = new Coordinate(0, 0);
	Coordinate dest = new Coordinate(matrix.length - 1, matrix[0].length - 1);
	return findElement(matrix, origin, dest, x);
}
public class Coordinate implements Cloneable {
	public int row;
	public int column;
	public Coordinate(int r, int c) {
		row = r;
		column = c;
	}

	public boolean inbounds(int[][] matrix) {
		return row >= 0 && column >= 0 &&
		row < matrix.length && column < matrix[0].length;
	}

	public boolean isBefore(Coordinate p) {
		return row <= p.row && column <= p.column;
	}

	public Object clone() {
		return new Coordinate(row, column);
	}

	public void setToAverage(Coordinate min, Coordinate max) {
		row = (min.row + max.row) / 2;
		column = (min.column + max.column) / 2;
	}
}

Этот код довольно трудно написать правильно с первого раза.

Запомните, что вы облегчите себе жизнь, выделяя код в методы. При написании программ, концентрируйтесь на ключевых местах. А собрать все воедино вы всегда сможете.

_{Разбор взят из книги Гейл Л. Макдауэлл «Cracking the Coding Interview» (есть в переводе).}

Источник

Задача:

Задана отсортированная двумерная матрица (матрица, для которой выполнено следующее условие: ), состоящая из строк и столбцов. Необходимо найти расположение указанного элемента в матрице или определить, что данный элемент в матрице отсутствует.

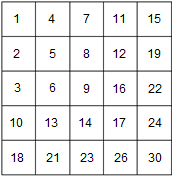
Пример отсортированной матрицы

Содержание

1 Решение за O(n[math]cdot[/math]m)
2 Решение за O(n[math]cdot[/math]log(m))
3 Решение за O(n + m)
- 3.1 Доказательство корректности
- 3.2 Код
- 3.3 Оценка времени работы
4 См. также
5 Источники информации

Решение за O(nm)

Для начала рассмотрим наивный алгоритм поиска элемента. В каждой строке исходной матрицы запускаем линейный поиск, если находим элемент, то возвращаем его координаты . Время работы — .

Решение за O(nlog(m))

Данный способ решения использует наивное решение за , улучшенное с помощью двоичного поиска. Для этого в каждой строке запускается двоичный поиск. Время работы — .

Замечание

Время работы может быть улучшено до . Для этого необходимо модифицировать алгоритм так, чтобы в том случае, если столбцов больше чем строк, он бы запускал двоичный поиск по строкам, если строк больше — наоборот.

Существует еще один способ оптимизации. Рассмотрим случай, когда используется двоичный поиск по строке. Достаточно очевидно, что искомое число может находится только в тех строках, где первый элемент меньше искомого, а последний — больше. Перед началом поиска можно исключить два прямоугольных участка матрицы: первый состоит из строк, у которых последний элемент меньше искомого; второй состоит из строк, у которых первый элемент больше искомого. Используя двоичный поиск, можно найти границы этих участков за для столбцов и за строк.

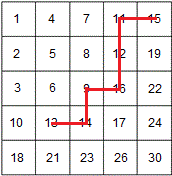
Пример поиска числа 13 в матрице

Решение за O(n + m)

В данном решении мы начинаем поиск из правого верхнего угла и движемся к искомому элементу. Идея алгоритма в том, что если текущий элемент меньше необходимого, то мы сдвигаемся на одну строку вниз. Если он больше, то мы сдвигаемся на одну колонку влево.

Доказательство корректности

Докажем, что каждый ход в соседнюю ячейку отсекает только те столбцы или строки, которые точно не содержат искомый элемент. Назовем ход корректным, если он отсекает только те строки или колонки, в которых точно нет искомого элемента. Пусть первый ход (в правую верхнюю ячейку) корректный (он не отсек ни одной строки или столбца).

Пусть предыдущий ход был корректным. Докажем, что следующий ход, выполненный по правилам, будет корректным.
Если текущий элемент меньше искомого, то все ячейки левее и выше меньше, чем искомый (по определению отсортированной матрицы, все элементы левее в строке меньше текущего, а текущий меньше искомого).
Если текущий элемент больше искомого, то очевидно, что все ячейки правее и ниже больше, чем искомый (по определению отсортированной матрицы, все элементы ниже в столбце больше текущего, а текущий больше искомого). Значит, их можно отсечь.

В определенный момент времени алгоритм либо найдет ячейку с искомым элементом (значит, элемент найден), либо в матрице не останется тех элементов, которые не были отсечены (значит, элемента в матрице нет).

Код

 Pair<int, int> matrixFind(int[N][M] a, int target):
   if (target < a[0][0] or target > a[N-1][M-1]) 
     return (-1, -1)
   row = 0
   col = M - 1
   while (row <= N-1 and col >= 0) 
     if (a[row][col] < target) 
       row++
     else if (a[row][col] > target)
       col--
     else
       return (row, col)
   return (-1, -1)

Оценка времени работы

Очевидно, что во время работы указатель сдвигается максимум на строк и столбцов. В этом случае время работы составляет .

См. также

Целочисленный двоичный поиск

Источники информации

Searching a 2D Sorted Matrix часть 1 на Leetcode
Searching a 2D Sorted Matrix часть 2 на Leetcode

Источник

#include <iostream>
#include <math.h>
#include <stdio.h>
#include <time.h> 
#define n 6
#define m 9
 
int main(int argc, char* argv[])
 
{
    {
        srand(time(0));
        int i, j;
        int X[n][m] = { {46, 2, 3, 4, 5, 51, 7, 8, 9}, {37, 11, 12, 13, 14, 42, 16, 17, 18 }, { 28, 20, 21, 22, 23, 33, 25, 26, 27},
            {19, 29, 30, 31, 32, 24, 34, 35, 36}, {10, 38, 39, 40, 41, 12, 43, 44, 45}, {1, 47, 48, 49, 50, 6, 52, 53, 54 } };
 
 
        for (i = 0; i < n; i++)
        {
            printf("n");
            for (j = 0; j < m; j++)
            {
                printf("%7.d ", X[i][j]);
            }
        }
        printf("n");
 
        int k, s;
        k = 0;
        s = 0;
        for (j = 0; j < m; j++) {
 
            for (i = 0; i < n; i++)
            {
                if (X[i][j] > X[i + 1][j])
                    s++;
                {
                    if (s == n)
                        k = j;
                }
            }
        }
        printf("n %d n", k + 1);
    }
    return 0;
}

Источник

Перейти к содержанию

Сортировка столбцов матрицы по возрастанию элементов первой строки

Просмотров 10к. Обновлено 15 октября 2021

Изменить последовательность столбцов матрицы так, чтобы элементы их первой строки были отсортированы по возрастанию. Например, дана матрица

 3 -2  6  4
 8  1 12  2
 5  4 -8  0

В результате работы программы она должна быть преобразована в следующую:

-2  3  4  6
 1  8  2 12
 4  5  0 -8

Как мы видим, первая строка отсортирована по возрастанию, а элементы столбцов перемещены в те столбцы, где находятся их первые элементы.

При решении данной задачи сортируется первая строка, например сортировкой выбором, когда на каждой итерации находится максимум (или минимум) и перемещается в конец просматриваемого отрезка массива. С каждым проходом по массиву область просмотра сокращается на 1 с конца.

Так как известен номер столбца элемента первой строки, который перемещается в конец области массива, то для перемещения всего столбца надо пройтись по всем строкам и обменять значения найденного столбца с последним на данном отрезке массива.

Pascal



const

    N = 4; M = 6;

var

    arr: array[1..N,1..M] of integer;

    i,j,k,id: byte;

    max: integer;
 
begin

    randomize;

    for i:=1 to N do begin

        for j:=1 to M do begin

            arr[i,j] := random(50) - 25;

            write(arr[i,j]:4);

        end;

        writeln;

    end;

 
    k := M;

    while k > 1 do begin

        id := 1;

        for j:=2 to k do

            if arr[1,j] > arr[1,id] then 

                id := j;

        for i:=1 to N do begin 

            max := arr[i,id];

            arr[i,id] := arr[i,k];

            arr[i,k] := max;

        end;

        k := k - 1;

    end;

 
    writeln;

    for i:=1 to n do begin

        for j:=1 to m do

            write(arr[i,j]:4);

        writeln;

    end;

end.





Пример(ы) выполнения программы на языке Pascal:

   1   6  10 -21 -22   0

 -25  -8   3  -6  11 -23

  12 -17  23  -5   1  -1

  13   4  -6  10 -16 -21

 
 -22 -21   0   1   6  10

  11  -6 -23 -25  -8   3

   1  -5  -1  12 -17  23

 -16  10 -21  13   4  -6

Язык Си

сортировка столбцов матрицы по возрастанию c++



#include < stdio.h>

#define N 5

#define M 6

main() {

    int a[N][M], i, j, k, id, max;

    srand(time(NULL));

    for (i=0; i< N; i++) {

        for (j=0; j< M; j++) {

            a[i][j] = rand()%50 - 25;

            printf("%4d", a[i][j]);

        }

        printf("n");

    }

    printf("n");
 
    k = M-1;

    while (k > 0) {

        id = 0;

        for (j=1; j<=k; j++)

            if (a[0][j] > a[0][id])

                id = j;

        for (i=0; i< N; i++) {

            max = a[i][id];

            a[i][id] = a[i][k];

            a[i][k] = max;

        }

        k -= 1;

    }   

 
    for (i=0; i< N; i++) {

        for (j=0; j< M; j++) {

            printf("%4d", a[i][j]);

        }

        printf("n");

    }

}

Python

отсортировать строки матрицы по возрастанию Python



from random import random

N = 5

M = 6

a = []

for i in range(N):

    z = []

    for j in range(M):

        n = int(random() * 50) - 25

        z.append(n)

        print("%4d" % n, end='')

    print()

    a.append(z)

print()
 
k = M-1

while k > 0:

    ind = 0

    for j in range(k+1):

        if a[0][j] > a[0][ind]:

            ind = j

    for i in range(N):

        m = a[i][ind]

        a[i][ind] = a[i][k]

        a[i][k] = m

    k -= 1



  


                       
  




 
for i in range(N):

    for j in range(M):

        print("%4d" % a[i][j], end='')

    print()

КуМир



алг обмен диагоналей

нач

  цел N=4, M=6

  цел таб a[1:N,1:M]

  цел i, j, k, id, m

  нц для i от 1 до N

    нц для j от 1 до M

      a[i,j] := int(rand(10,50))

      вывод a[i,j], " " 

    кц

    вывод нс

  кц

  вывод нс
 
  k := M

  нц пока k > 1

    id := 1

    нц для j от 2 до k

      если a[1,j] > a[1,id] то 

        id := j

      все 

    кц

    нц для i от 1 до N

      m := a[i,id]

      a[i,id] := a[i,k]

      a[i,k] := m 

    кц

    k := k-1

  кц

 
  нц для i от 1 до N

    нц для j от 1 до M

      вывод a[i,j], " " 

    кц

    вывод нс

  кц

кон

Basic-256



N = 5

M = 6

dim a(N,M)

for i=0 to N-1

	for j=0 to M-1

		a[i,j] = int(rand*50) + 10

		print a[i,j] + "  ";

	next j

	print

next i

print
 
k = M-1

while k > 0

	id = 0

	for j=1 to k

		if a[0,j] > a[0,id] then id = j

	next j

	for i=0 to N-1

		m = a[i,id]

		a[i,id] = a[i,k]

		a[i,k] = m

	next i

	k = k - 1

end while

 
for i=0 to N-1

	for j=0 to M-1

		print a[i,j] + "  ";

	next j

	print

next i

Источник

6.5.2 Работа со строками и столбцами матрицы

Разработать программу на языке С++ для решения следующей задачи.

Задана матрица целых чисел 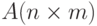. Сформировать массив , в который записать среднее арифметическое элементов каждого столбца заданной матрицы. Вывести номера строк матрицы, в которых находится более
двух простых чисел.
Задана матрица вещественных чисел 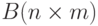. Сформировать массив
, в который записать среднее геометрическое положительных элементов каждой строки заданной матрицы. Определить количество столбцов,
упорядоченных по возрастанию.
Задана матрица целых чисел . Все простые числа, расположенные
на побочной диагонали, заменить суммой цифр максимального элемента
соответствующей строки матрицы. Сформировать массив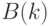 , в который
записать произведения элементов нечётных строк заданной матрицы.
В матрице целых чисел 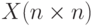поменять местами диагональные элементы,
упорядоченных по убыванию строк. Сформировать массив , в который
записать суммы элементов чётных столбцов заданной матрицы.
Задана матрица целых чисел . Максимальный элемент каждого
столбца заменить суммой цифр максимального элемента матрицы. Сформировать массив , в который записать количество чётных элементов в
каждой строке заданной матрицы.
Задана матрица целых чисел 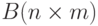. Максимальный элемент каждого
столбца заменить суммой цифр модуля минимального элемента матрицы.
Сформировать массив , в который записать количество нечётных элементов в каждой строке заданной матрицы.
Задана матрица целых чисел . Сформировать массив из максимальных элементов столбцов заданной матрицы. Вывести индексы чиселпалиндромов, которые находятся на диагоналях матрицы.
Задана матрица вещественных чисел . Сформировать массив
из номеров столбцов матрицы, в которых есть хотя бы один ноль. Найти
строку с максимальной суммой элементов и поменять её с первой строкой.
Задана матрица вещественных чисел . Сформировать вектор
из средних арифметических положительных значений строк матрицы, и
вектор из номеров столбцов, которые представляют собой знакочередующийся ряд.
В каждом столбце матрицы вещественных чисел заменить минимальный элемент суммой положительных элементов этого же столбца.
Сформировать вектор из номеров строк, представляющих собой знакочередующийся ряд.
В матрице целых чисел 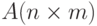обнулить строки, в которых более двух простых чисел. Сформировать массив из минимальных значений столбцов матрицы.
В матрице вещественных чисел найти и вывести номера столбцов, упорядоченных по убыванию элементов. Сформировать массив
из максимальных значений строк матрицы.
В матрице вещественных чисел найти и вывести номера строк,
упорядоченных по возрастанию элементов. Сформировать массив
из номеров минимальных и максимальных значений столбцов матрицы.
В матрице вещественных чисел найти и вывести номера столбцов,
упорядоченных по возрастанию. Сформировать вектор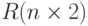 из номеров
минимальных и максимальных значений строк матрицы.
В матрице вещественных чисел найти и вывести номера строк,
упорядоченных по убыванию. Сформировать вектор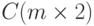 из максимальных и минимальных значений столбцов матрицы.
В матрице вещественных чисел 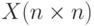найти максимальный и минимальный элементы. Поменять местами элементы строки с максимальным
значением и элементы столбца с минимальным значением.
Задана матрица целых чисел . Сформировать массив , каждый элемент которого равен количеству положительных элементов с чётной суммой цифр в соответствующей строке матрицы. В столбцах матрицы
поменять местами наибольший и наименьший элементы.
Задана матрица целых чисел . Сформировать массив , каждый элемент которого равен количеству положительных чисел с суммой
цифр, кратной трём в соответствующем столбце матрицы. Найти строку с
максимальным произведением элементов.
Задана матрица целых чисел 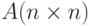. Все числа-палиндромы, расположенные на главной диагонали, заменить суммой цифр модуля минимального
элемента соответствующего столбца матрицы. Сформировать вектор
из произведений абсолютных ненулевых значений соответствующих строк
матрицы.
Задана матрица целых чисел . Поменять местами элементы на
диагоналях в столбцах, упорядоченных по возрастанию модулей. Сформировать вектор , каждый элемент которого равен сумме составных значений в соответствующей строке матрицы.
Задана матрица целых чисел 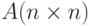. Минимальный элемент каждой строки заменить суммой цифр максимального простого элемента матрицы.
Сформировать вектор , каждый элемент которого — среднее геометрическое ненулевых элементов в соответствующем столбце матрицы.
Задана матрица целых чисел . Максимальный элемент каждого
столбца заменить суммой цифр минимального простого элемента матрицы. Сформировать вектор , каждый элемент которого равен количеству чётных элементов в соответствующей строке матрицы.
Задана матрица целых чисел . Обнулить строки, в которых на
диагоналях нет чисел-палиндромов. Сформировать вектор , каждый
элемент которого равен количеству нечётных элементов в соответствующем
столбце матрицы.
Задана матрица вещественных чисел . Найти столбец с минимальным произведением элементов. Поменять местами элементы этого столбца
и элементы последнего столбца. Сформировать вектор из сумм квадратов соответствующих строк матрицы.
Задана матрица целых чисел . В каждой строке заменить максимальный элемент суммой цифр минимального элемента этой же строки.
Сформировать массив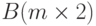 , пара элементов которого равна соответственно количеству чётных и нечётных чисел в соответствующем столбце
матрицы.

6.5.3 Решение задач линейной алгебры

Разработать программу на языке С++ для решения следующей задачи.

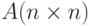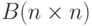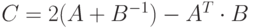Задана матрицы и . Вычислить матрицу $C=2(A+B^{-1})-A^Tcdot B$ .
Задан массив . Сформировать матрицы и 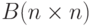по формулам: $A_{ij}=C_icdot C_j, B_{i,j}=frac{A_{i,j}}{max(A)}$ .
Решить матричное уравнение , где — единичная
матрица.
Даны массивы и . Сформировать матрицы и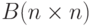
по формулам: $A_{ij}=C_icdot D_j, B_{i,j}=frac{A_{i,j}}{min(A)}$ .

Решить матричное уравнение , где — единичная
матрица.
Квадратная матрица называется ортогональной, если $A^T = A^{-1}$ .
Определить, является ли данная матрица ортогональной:

$left(begin{matrix}1&0.42&0.54&0.66\0.42&1&0.32&0.44\0.54&0.32&1&0.22\0.66&0.44&0.22&1end{matrix}right).$
Для матрицы $H=E-displaystylefrac{vv^T}{left|vright|^2}$ , где — единичная матрица, а $v=left[begin{matrix}1\0\1\1end{matrix}right]$ ,
проверить свойство ортогональности: $H^T=H^{-1}$ .
Проверить, образуют ли базис векторы
$f_1=left[begin{matrix}1\-2\1\1end{matrix}right], f_2=left[begin{matrix}2\-1\1\-1end{matrix}right], f_3=left[begin{matrix}5\-2\-3\1end{matrix}right], f_4=left[begin{matrix}1\-1\1\-1end{matrix}right].$

Если образуют, то найти координаты вектора в
этом базисе. Для решения задачи необходимо показать, что определитель
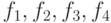матрицы со столбцами отличен от нуля, а затем вычислить
координаты вектора в новом базисе по формуле $y=F^{-1}cdot x$

.
Найти вектор как решение данной системы уравнений
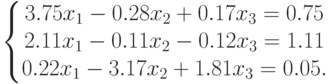
$left{begin{matrix} 3.75x_1-0.28x_2+0.17x_3=0.75\ 2.11x_1-0.11x_2-0.12x_3=1.11\ 0.22x_1-3.17x_2+1.81x_3=0.05. end{matrix}right.$

Вычислить модуль вектора .
Вычислить скалярное произведение векторов и . Вектор ,
а вектор является решением СЛАУ:
_

$left{begin{matrix} 5.7x_1-7.8x_2-5.6x_3-8.3x_4=2.7\ 6.6x_1+13.1x_2-6.3x_3+4.3x_4=-5.5\ 14.7x_1-2.8x_2+5.6x_3-12.1x_4=8.6\ 8.5x_1+12.7x_2-23.7x_3+5.7x_4=14.7. end{matrix}right.$
Вычислить вектор , решив СЛАУ
$left{begin{matrix} 4.4x_1-2.5x_2+19.2x_3-10.8x_4=4.3\ 5.5x_1-9.3x_2-14.2x_3+13.2x_4=6.8\ 7.1x_1-11.5x_2+5.3x_3-6.7x_4=-1.8\ 14.2x_1+23.4x_2-8.8x_3+5.3x_4=7.2. end{matrix}right.$

Найти .
Вычислить вектор , решив СЛАУ
$left{begin{matrix}0.34x_1+0.71x_2+0.63x_3=2.08\0.71x_1-0.65x_2-0.18x_3=0.17\1.17x_1-2.35x_2+0.75x_3=1.28end{matrix}right.$

Найти модуль вектора .
Вычислить угол между векторами и . Вектор является
решением СЛАУ: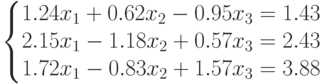

$left{begin{matrix}1.24x_1+0.62x_2-0.95x_3=1.43\2.15x_1-1.18x_2+0.57x_3=2.43\1.72x_1-0.83x_2+1.57x_3=3.88end{matrix}right.$

.
Решив систему уравнений методом Гаусса:
$left{begin{matrix}8.2x_1-3.2x_2+14.2x_3+14.8x_4=-8.4\5.6x_1-12x_2+15x_3-6.4x_4=4.5\5.7x_1+3.6x_2-12.4x_3-2.3x_4=3.3\6.8x_1+13.2x_2-6.3x_3-8.7x_4=14.3end{matrix}right.$

Вычислить .
Решить СЛАУ 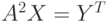, где $A=left[begin{matrix}2&1&5&2\5&2&2&6\2&2&1&2\1&3&3&1end{matrix}right], Y=|3 1 2 1|$ |.
Решить СЛАУ , где $A=left[begin{matrix}2&1&5&2\5&2&2&6\2&2&1&2\1&3&3&1end{matrix}right], Y=left[begin{matrix}3\1\2\1end{matrix}right]$ .
Заданы матрицы и .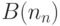
Найти определитель матрицы .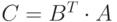
Задан массив . Сформировать матрицы и 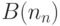по формулам:
$A_{ij}=C_icdot C_j, B_{ij}=frac{A_{ij}}{sumlimits_{i=1}^nA_{ii}}$
. Найти определитель .
Для матрицы, где — единичная матрица, а
$P=left[begin{matrix}-26&-18&-27\21&15&21\12&8&13end{matrix}right]$

проверить свойство . При помощи метода Гаусса решить СЛАУ .
Квадратная матрица является симметричной, если для неё выполняется свойство . Проверить это свойство для матрицы
$left(begin{matrix} 1&0.42&0.54&0.66\ 0.42&1&0.32&0.44\ 0.54&0.32&1&0.22\ 0.66&0.44&0.22&1 end{matrix}right)$

.
Вычислить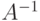 $A^{-1}$
. Убедиться, что $Acdot A^{-1}=E$ .
Ортогональная матрица обладает следующими свойствами:
- модуль определителя ортогональной матрицы равен 1;
- сумма квадратов элементов любого столбца ортогональной матрицы
  равна 1;
- сумма произведений элементов любого столбца ортогональной матрицы на соответствующие элементы другого столбца равна 0.
Проверить эти свойства для матриц:

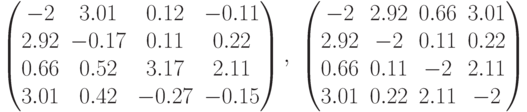
$left(begin{matrix}-2&3.01&0.12&-0.11\2.92&-0.17&0.11&0.22\0.66&0.52&3.17&2.11\3.01&0.42&-0.27&-0.15end{matrix}right) , left(begin{matrix}-2&2.92&0.66&3.01\2.92&-2&0.11&0.22\0.66&0.11&-2&2.11\3.01&0.22&2.11&-2end{matrix}right)$

.
Проверить, образуют ли базис векторы
$f_1=left[begin{matrix}0.25\0.333\0.2\0.1end{matrix}right],f_2=left[begin{matrix}0.33\0.25\0.167\0.143end{matrix}right],f_3=left[begin{matrix}1.25\-0.667\2.2\3.1end{matrix}right],f_4=left[begin{matrix}-0.667\1.333\1.25\-0.75end{matrix}right] .$

Если образуют, то найти координаты вектора в этом базисе. Для решения задачи необходимо показать, что определитель матрицы F
со столбцами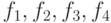 отличен от нуля, а затем вычислить координаты
вектора в новом базисе, решив СЛАУ .
Решить СЛАУ:
$left(begin{matrix} 0.42&0.26&0.33&-0.22\ 0.74&-0.55&0.28&-0.65\ 0.88&0.42&-0.33&0.75\ 0.92&0.82&-0.62&0.75 end{matrix}right)cdot X=left[begin{matrix}1\1\1\0end{matrix}right]$

Для матрицы 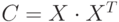проверить условия ортогональности: и .
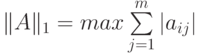Найти $|A|_1=maxsumlimits_{j=1}^m|a_{ij}|$ и $|A|_{11}=maxsumlimits_{i=1}^m|a_{ij}|$ для матрицы
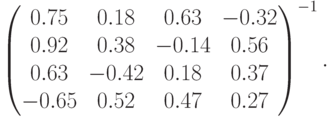
$left(begin{matrix} 0.75&0.18&0.63&-0.32\ 0.92&0.38&-0.14&0.56\ 0.63&-0.42&0.18&0.37\ -0.65&0.52&0.47&0.27 end{matrix}right)^{-1} .$
Найти $|A|_{111}=sqrt{sumlimits_{i,j}a_{i,j}^2}$ для матрицы
$left(begin{matrix} -1.09&7.56&3.45&0.78\ 3.33&4.45&-0.21&3.44\ 2.33&-4.45&0.17&2.21\ 4.03&1&3.05&0.11 end{matrix}right)^{-1}.$
Решить СЛАУ методом Гаусса
$left{begin{matrix} 8.2x_1-3.2x_2+14.2x_3+14.8x_4&=-8.4\ 5.6x_1-12x_2+15x_3-6.4x_4&=4.5\ 5.7x_1+3.6x_2-12.4x_3-2.3x_4&=3.3\ 6.8x_1+13.2x_2-6.3x_3-8.7x_4&=14.3 end{matrix}right.$

Выполнить проверку .
Задан массив . Сформировать матрицы и 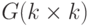по формулам
$B_{ij}=H_icdot H_j), G_{ij}=displaystylefrac{B_{ij}}{min(B)}.$

Решить матричное уравнение , где — единичная
матрица.