Как найти упругую линию

Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

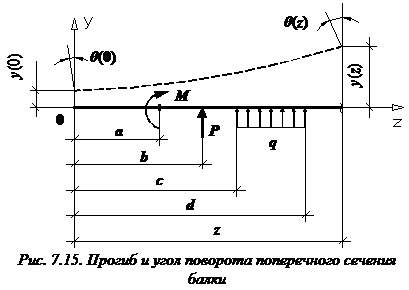
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

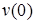
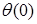
Прогиб и угол поворота балки в начале координат (начальные параметры) определяются из условий закрепления балки.

Уравнение упругой линии балки на примере

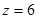
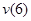
Определим прогиб балки на консоли при м, то есть . Запишем универсальное уравнение упругой линии балки :

Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: .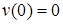

Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.

,

.

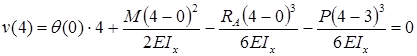
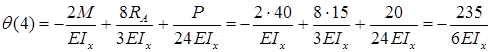
Прогиб консоли при z=6м:

Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).

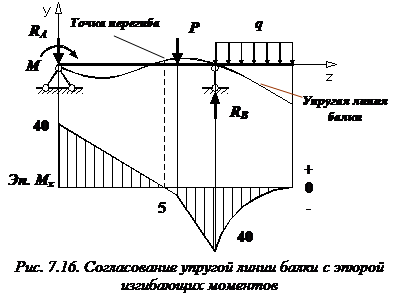
Примерный вид упругой линии балки показан на рис. 7.16.

Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.

Дифференциальное уравнение упругой линии балки и его интегрирование

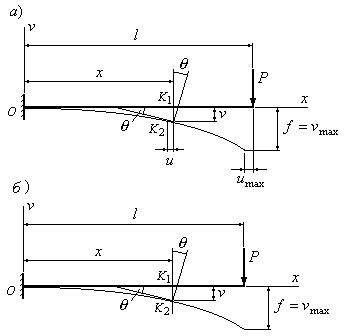
При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией , а поступательные перемещения сечений, равные перемещениям y = y ( x ) их центров тяжести сечений – прогибами балки .

Между прогибами y ( x ) и углами поворота сечений θ ( x ) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии ( θ и φ – углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y / = tg θ . Следовательно, tg θ = tg φ = y / .

В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h , а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y / .

Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M z и жесткости EI z (см. уравнение (8.8)):

.

В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,

.

Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M z и y // были приняты независимо друг от друга, получаем

.

Это равенство называется дифференциальным уравнением упругой линии . При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад ( y / ) 2 =0.01 ) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки

.

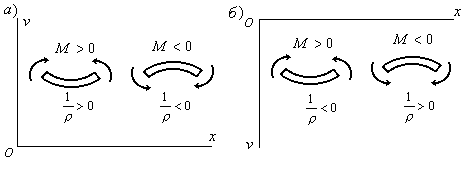
Выбор знака в правой части (8.29) определяется направлением координатной оси y , так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и M z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и M z противоположны, и это заставляет выбрать в правой части знак минус.

Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M z содержит одну из главных осей инерции сечения.

Интегрируя (8.29), находим сначала углы поворота сечений

,

а после второго интегрирования – прогибы балки

.

Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2 n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.

Универсальное уравнение упругой линии балки

Дифференциальные соотношения

Рассмотрим рисунок 5.1. Балка постоянного сечения под воздействием внешней нагрузки Р деформируется так, что ее концевая точка C перемещается в положение С₁. Нейтральная ось балки, называемая в дальнейшем упругой линией, в точке с координатой z имеет кривизну 1/r, прогиб y, угол наклона q =y¢, вторую производную y².

Перечисленные параметры связаны между собой соотношением, доказываемым в дифференциальной геометрии: (5.1)

Для малых перемещений величиной y’ 2 по сравнению с 1 можно пренебречь, тогда: (5.2)

Учитывая (5.2) и (3.7.b) получим:

(5.3)

С учетом соотношений (4.1) и (4.2) можно получить цепочки дифференциальных соотношений для случая бруса переменного сечения:

(5.4)

а также для бруса с постоянным сечением:

(5.5)

В частности, при нагружении бруса постоянного сечения равномерно распределенной нагрузкой q:

(5.6)

Следовательно, эпюры в соответствии с дифференциальными соотношениями (5.5), в зависимости от рассматриваемого параметра, будут иметь следующие формы (рис.5.2): q – горизонтальная прямая, Q – наклонная прямая, М – квадратичная парабола, q – кубическая парабола, у – кривая четвертого порядка. Если q=0, но имеется сосредоточенная сила Р, то ось будет изогнута по кривой третьего порядка. Если балка нагружена только изкибающим моментом М, то ось выразится кривой второго порядка.

Наибольшие удлинения и напряжения в брусе вычисляются по формулам, вытекающим из (4.6) и (4.7):

(5.7)

(5.8)

Пример 5.1

Определим прогибы балки, изображенной на рис.5.1. Изгибающий момент в сечении z равен: M = P (l – z)

После двукратного интегрирования выражения

Постоянную интегрирования С₁ найдем из граничного условия: при z = 0имеем: y¢ = 0. Отсюда С₁ = 0, но для общности решения пока оставим этот член в формуле:

. (5.9)

Постоянную интегрирования С₂ определяем из граничного условия: при z = 0 y = 0. Следовательно, С₂= 0, тогда для произвольной точки:

. (5.10)

Максимальные угол наклона и прогиб имеют место в точке приложения силы Р.

Таким образом,при z=l имеем:

(5.11)

Универсальное уравнение упругой линии балки

Из примера 5.1 видно, что для каждого участка балки после интегрирования уравнения появляются две произвольные постоянные (С₁,С₂ в 5.9). Если балка имеет n участков, то для определения 2n постоянных интегрирования необходимо совместно решить 2n уравнений. Для бруса постоянной жесткости EJ_x этого можно избежать, если при составлении уравнения упругой линии придерживаться определенных правил.

Рассмотрим брус (рис.5.3), нагруженный наиболее часто встречающимися силовыми факторами: сосредоточенным моментом М_а, сосредоточенной силой Р и распределенной нагрузкой интенсивности q. Из этих типов силовых факторов могут быть скомбинированы почти все встречающиеся на практике виды нагрузок. За положительные направления сил при движении от левого конца примем те, которые указаны на рисунке, то есть для Р и q – вверх, а для момента М_а – по часовой стрелке. Система указанных силовых факторов должна удовлетворять условиям равновесия.

Выявим особенности, вносимые в уравнение упругой линии различными типами внешних силовых факторов. Для этого составим выражения изгибающих моментов для каждого из пяти отмеченных на рисунке участков:

(5.12)

Видно, что изгибающий момент для каждого последующего участка целиком включает в себя выражение изгибающего момента предыдущего участка и отличается от него добавкой нового слагаемого. При переходе от четвертого участка к пятому указанная закономерность сохранена специально. При этом равномерно распределенная нагрузка четвертого участка продолжена, как это показано пунктиром, на пятый участок, и одновременно на пятом участке приложена отрицательная (компенсирующая) нагрузка интенсивности q.

Проинтегрируем полученные выражения один раз, не раскрывая скобок. Для того чтобы сохранить однотипность полученных выражений, интеграл от М_а напишем в виде М_а(z-a), что скажется только на величине произвольной постоянной С_i. В итоге, с учетом выражения y² = M / EJ_x получим следующие выражения для угла наклона упругой линии у’ :

(5.13)

Произвольные постоянные С_i, должны быть подобраны так, чтобы при переходе от одного участка к другому величина у’ не претерпевала разрыв. Следовательно, при z=а у’₁=у’₂, при z=b у’₂=у’₃,и так далее.

Так как брус имеет постоянную жесткость, очевидно, что

Угол наклона q₀ упругой линии в начале координат определяется из выражения для первого участка:

Интегрируя полученные выражения второй раз найдем:

(5.14)

Произвольные постоянные D_i, должны быть подобраны из условия непрерывности функции у на границах участков. Следовательно, при z=а у₁=у₂, при z=b у₂=у₃ и т.д. Так как брус имеет постоянную жесткость, очевидно, что

,

где у₀ – ордината упругой линии в начале координат. Уравнения (5.14) удобно записать в виде одного общего, так называемого универсального уравнения упругой линии балки: (5.15)

Для определения координат точек упругой линии первого участка следует пользоваться членами уравнения, расположенными слева от вертикальной черты с индексом I. Для второго участка надо брать слагаемые до черты с индексом II, и т.д. Для определения ординат на пятом участке следует производить вычисления, пользуясь полным уравнением 5.15. Преимущество универсального уравнения заключается в том, что оно позволяет составлять уравнение упругой линии, минуя громоздкое определение произвольных постоянных. Независимо от числа участков, необходимо определить только две постоянные: у₀ и q₀.

Пример 5.2

Написать уравнение упругой линии для консоли с жестко защемленным левым концом и загруженной на среднем участке распределенной нагрузкой q (рис.5.4). Определяем реакцию и момент в заделке:

Теперь можно вместо левой заделки рисовать на схеме эквивалентные ей реакции опор. Таким образом, схема сведена к виду, для которого выписано универсальное уравнение. Начало координат помещаем на левом конце балки. Здесь q₀ = 0 и y₀ = 0.

Далее, из уравнения (5.15) «набираем» члены уравнения, соответствующие рассматриваемой балке.

В первый участок входят слагаемые силы и момента в заделке. На втором участке к ним добавляется слагаемое распределенной нагрузки. На третьем участке перемещения определяются всеми слагаемыми уравнения. Если раскрыть скобки, то для последнего участка получим:

.

Здесь упругая линия представляет собой прямую, поскольку изгибающий момент равен нулю.

[spoiler title=”источники:”]

http://mysopromat.ru/uchebnye_kursy/sopromat/izgib/peremescheniya_pri_izgibe/differentsialnoe_uravnenie_uprugoi_linii_balki/

http://allrefrs.ru/3-44905.html

[/spoiler]

6.1. Понятие об упругой
линии. Прогиб и угол поворота.
Дифференциальное уравнение упругой
линии. Условие жесткости при изгибе

Чтобы судить о работе изгибаемых балок,
недостаточно знать только напряжения,
которые возникают в сечениях балки от
заданной нагрузки. Вычисленные напряжения
позволяют проверить прочность системы.
Однако весьма прочные балки могут
оказаться непригодными к эксплуатации
из-за недостаточной жесткости. Если
балка при нагружении сильно прогибается,
то при эксплуатации сооружения, имеющего
гибкие балки, появятся затруднения и,
кроме того, могут возникнуть колебания
балки с большими амплитудами, а вместе
с тем и значительные дополнительные
напряжения.

Под жесткостью
следует понимать способность
элеменов конструкций и деталей машин
сопротивляться внешним нагрузкам без
видимых деформаций.
Расчет на жесткость заключается в оценке
упругой податливости балки под действием
приложенных нагрузок и подбор таких
размеров поперечного сечения, при
которых перемещения не будут превышать
установленных нормами пределов. Для
выполнения такого расчета необходимо
научиться вычислять перемещения сечений
балки под действием любой внешней
нагрузки.

Рассмотрим деформацию
балки при простом изгибе. Ось балки
(Рис.6.1,а) под действием нагрузки,
расположенной в одной из главных
плоскостей инерции (в плоскости
),
искривляется в той же плоскости, а
поперечные сечения поворачиваются и
одновременно получают поступательные
перемещения. Искривленная ось балки
называетсяизогнутой
осью или упругой
линией. На рис.
6.1 упругая линия изображена тонкой
кривой.

Точка
,
лежащая на оси в сечении, отстоящем не
расстоянииот начала координат, переместится в
точку.
Обозначим перемещение произвольной
точки оси бруса в направлении осичерез,
а перемещение вдоль оси бруса – через.
Если в точкепровести касательную к оси изогнутой
балки, то по отношению к первоначальному
положению оси она будет повернута на
угол.
Одновременно на тот же угол повернется
сечение в точке.
Таким образом, три величины
,иявляются компонентами перемещения
произвольного поперечного сечения
балки. Перемещениецентра тяжести сечения по направлению,
перпендикулярному к оси балки, называетсяпрогибом.
Наибольший прогиб называется стрелой
прогиба и
обозначается буквой
.

Угол
,
на который каждое сечение поворачивается
по отношению к своему первоначальному
положению, называется углом поворота
сечения. Как уже отмечалось, угол поворота
также может быть определен как угол
между касательной к упругой линии и
осью.

Рис.6.1

Проверка жесткости
балок сводится к требованию, в соответствии
с которым наибольший прогиб
не должен превышать определенной доли
пролета:

.

Число
устанавливается нормами проектирования
примерно в пределах от 300 до 1000. Для
ответственных сооружений, например,
для железнодорожных мостов, величинапринимается равной 1000.

Отсюда видно, что
прогибы при изгибе, как правило, малы
по сравнению с пролетом балки. Это
позволяет внести некоторые упрощения.
Во-первых, при малых прогибах
угол наклона касательной к оси изогнутой
балки можно определять с помощью
выражения:

.
(6.1)

Во-вторых, горизонтальными
перемещениями
можно пренебречь, так как они существенно
меньше().
В связи с этим при расчетах будем
пользоваться условной схемой перемещений,
изображенной на рис 6.1,б. Согласно этой
схеме каждая точка перемещается
перпендикулярно продольной оси бруса.

Для определения полной картины деформаций
необходимо получить уравнение упругой
линии

.

Исходя из физической природы изогнутой
оси бруса, можем утверждать, что упругая
линия должна быть непрерывной и гладкой
кривой, следовательно, на протяжении
всей оси бруса должны быть непрерывны
функция и ее первая производная. Прогибы
и углы поворота и являются перемещениями
сечений балок при изгибе. Деформация
того или иного участка балки определяется
его кривизной.

При выводе формулы для нормальных
напряжений при изгибе нами была получена
связь между кривизной и изгибающим
моментом:

.
(6.2)

Из курса высшей математики известно
следующее уравнение кривизны плоской
кривой:

.
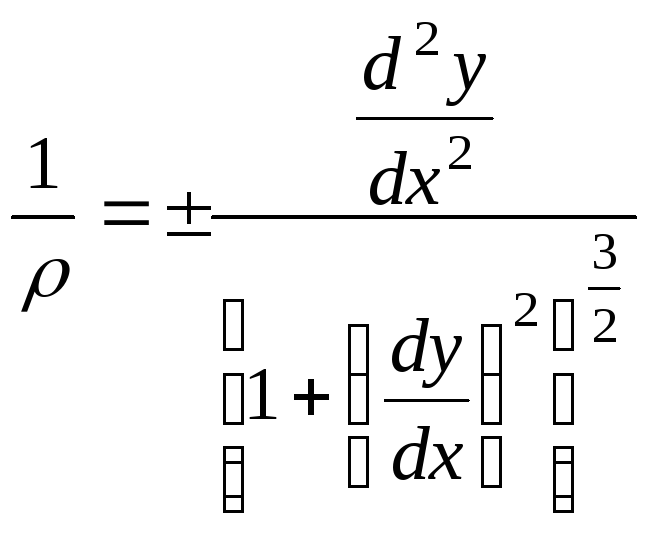
(6.3)

Подставляя значение
кривизны в равенство (6.2) и заменяя
координату
прогибом,
получим точное дифференциальное
уравнение упругой линии балки:

.
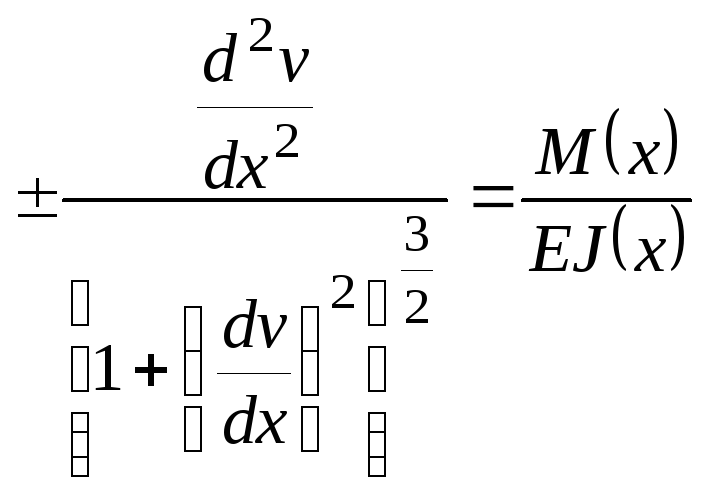
(6.4)

Интегрирование этого
нелинейного дифференциального уравнения
связано с большими трудностями. Учитывая,
что на практике приходится иметь дело
с малыми прогибами и что тангенсы углов
наклона
касательной к оси будут малы, квадратом
первой производнойпо
сравнению с единицей можно пренебречь.
Тогда получим приближенное (основное)
дифференциальное уравнение

(6.5)

Два
знака в уравнении (6.5) поставлены потому,
что знак кривизны
может не совпадать со знаком изгибающего
момента. Знак кривизны зависит от
направления осей координат. Знак
изгибающего момента был выбран в
зависимости от того, где расположены
растянутые волокна. Так, например, для
случая, когда осьнаправлена вверх, положительному моменту
(Рис.6.2,а) соответствует положительная
кривизна, а отрицательному – отрицательная
кривизна.

Рис
6.2

Таким
образом, в случае, когда ось
направлена вверх, знаки кривизны и
изгибающего момента совпадают. Поэтому
в дифференциальном уравнении берется
знак“+”.
Если ось
направлена вниз, то знаки у кривизны и
изгибающего момента будут различны
(Рис.6.2,б). Поэтому в этом случае в правой
части уравнения (6.5) берется знак“”.

6.2. Метод непосредственного
интегрирования приближенного (основного)
дифференциального уравнения упругой
линии

Решая
задачу аналитическим методом, углы
поворота
и прогибывычисляют последовательным интегрированием
приближенного дифференциального
уравнения (6.5). Проинтегрировав уравнение
(6.5) первый раз, получим выражение для
угла поворота:

,
(6.6)

где

постоянная интегрирования.

Интегрируя
второй раз, получим выражение для прогиба
:

,
(6.7)

где
и
постоянные интегрирования.

Для
вычисления интегралов, входящих в (6.6)
и (6.7), необходимо сначала написать
аналитические выражения для изгибающего
момента и жесткости. Постоянные
интегрирования находятся
из граничных условий,
которые зависят от условий перемещения
границ участков балки.

Рассмотрим несколько
примеров применения метода непосредственного
интегрирования приближенного уравнения
упругой линии балки.

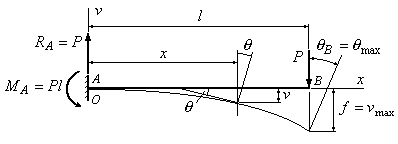
Пример
6.1. Определить
стрелу прогиба и угол поворота сечения
В балки, изображенной на рис.6.3.

Рис.6.3

Решение:

1. Из условий
равновесия определяем опорные реакции:

;
.

2.
Выбираем начало координат
на левом конце балки, совмещая его с
точкой А. Осьнаправляем вверх, ось
вправо.

3.
Составляем уравнение изгибающего
момента в сечении
:

.

4. Предполагая, что
жесткость балки постоянна, записываем
приближенное дифференциальное уравнение
упругой линии балки:

.

Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.

5. Интегрируем
уравнение первый раз. Получаем:

.
(а)

Интегрируя
еще раз, получаем уравнение для прогиба
в сечении
:

.
(б)

Так как в заделке прогиб и угол поворота
равны нулю, то для определения постоянных
интегрирования граничные условия имеют
вид:

при
;
при.

Из
уравнения (а) видно, что постоянная
представляет собой угол поворота в
начале координат (сечении А). Задавая в
уравнении (а),
находим.
Из уравнения (б) следует, что постоянная
прогиб в начале координат. Задавая в
уравнении (б)
,
получаем.

Таким образом,
получаем следующие выражения для прогиба
и угла поворота:

,

.

Подставляя
в первое уравнение
,
найдем стрелу прогиба:

.

Подставляя
во второе уравнение
,
найдем максимальный угол поворота

.

Знак
“”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.
Знак“”
в выражении угла поворота показывает,
что сечение В повернулось не против, а
по часовой стрелке.

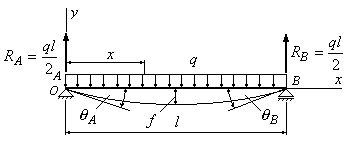
Пример
6.2. Определить
стрелу прогиба двухопорной балки и углы
поворота опорных сечений А и В (рис.6.4).

Рис.6.4

Решение:

1. Из условий
равновесия определяем опорные реакции:

.

2.
Выбираем начало координат
на левом конце балки, совмещая его с
точкой А. Осьнаправляем вверх, ось
вправо.

3.
Составляем уравнение изгибающего
момента в сечении
:

.

4. Предполагая, что
жесткость балки постоянна, записываем
приближенное дифференциальное уравнение
упругой линии балки:

.

Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.

5. Интегрируем
уравнение первый раз. Получим:

.
(в)

Интегрируя
еще раз, получаем уравнение для прогиба
в сечении
:

.
(г)

Постоянные
интегрирования найдем из граничных
условий:

при
;
при.

Подставляя
в уравнение (г)
и приравнивая прогиб нулю, получим;
подставляя в это же уравнение,
находим постоянную интегрирования:

.

Найденные значения
постоянных интегрирования подставим
в уравнения (в) и (г) и получим уравнения
углов поворота и прогибов:

;

.

Подставляя
ив первое уравнение, получим углы поворота
соответственно сечений А и В:

;

.

В
силу симметрии нагрузки максимальный
прогиб
будет посредине балки. Подставляя во
второе уравнение
,
получим:

.

Как
и в предыдущем примере, знак “”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.
Знак“”
в выражении угла поворота
показывает, что сечение А повернулось
не против, а по часовой стрелке, знак“+”
в выражении угла поворота
показывает, что сечение В повернулось
против часовой стрелки.

Пример
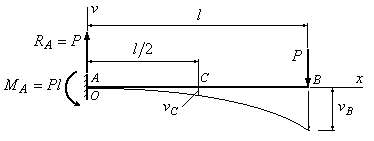
6.3. В сколько
раз прогиб в сечении В на конце изображенной
на рис.6.5 балки, больше, чем прогиб в
сечении С
посредине
балки?

Рис.6.5

Решение:

Воспользуемся
результатами, полученными в примере
6.1. Запишем окончательное выражение для
прогиба:

и подставим в это
уравнение координаты точек С и В. Получим:

при
;

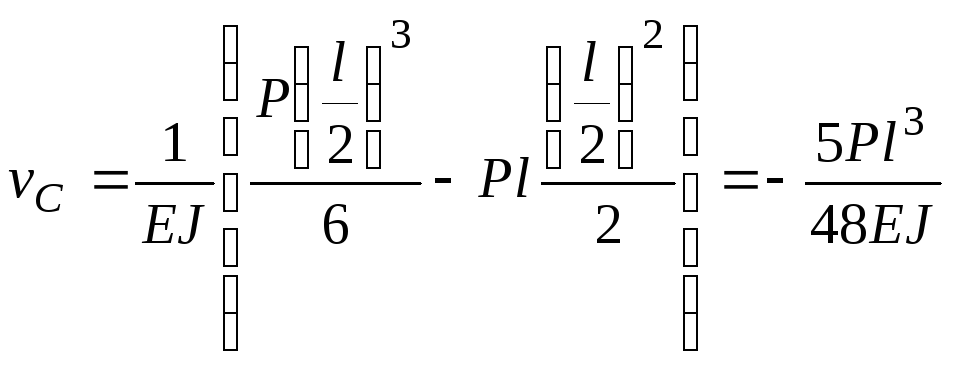
при
.

Сравнивая полученные
величины прогибов, приходим к выводу,
что прогиб в сечении В больше, чем прогиб
в сечении С в 3,2 раза:

.

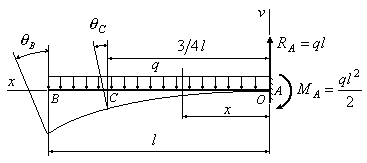
Пример
6.4. В сколько
раз угол
поворота сечения
А
на конце изображенной на рис.6.6 балки
больше, чем угол поворота сечения В на
расстоянии четверти пролета от левого
конца балки?

Решение:

1.
Находим реакции: ;.

2.
Выбираем начало координат
на правом конце балки, совмещая его с
точкой А. Осьнаправляем вверх, ось
влево.

Рис.6.6

3.
Записываем выражение для изгибающего
момента в сечении
:

.

4. Составляем приближенное дифференциальное
уравнение упругой линии балки:

.

Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.

5. Принимаем жесткость балки постоянной.
Интегрируем дифференциальное уравнение.
Получаем:

.(д)

Постоянную интегрирования
в уравнении (д) найдем из условия, что
приугол поворота в сечении А равен нулю.
Подставим в уравнение (д)и приравняем нулю угол поворота сечения
А. Получим.
Тогда окончательно уравнение для угла
поворота принимает вид:

.(е)

6.
Подставляем в уравнение (е) координату
,
получим угол поворота в сечении С:

.

7.
Подставляем в уравнение (е) координату
.
Получим угол поворота в сечении В:

.

8. Сравнивая углы
поворота в сечениях В и С, получим:

.

Таким образом,
угол поворота в сечении В в 1,016 раза
больше, чем угол поворота в сечении С.

Пример
6.5.
Найти
стрелу прогиба (в мм) балки, изображенной
на рис.6.7, если жесткость поперечного
сечения балки равна
кНм².

Рис.6.7

Решение:

Воспользуемся
решение задачи, ход которого изложен в
примере 6.4 и проинтегрируем выражение
(д). Получим уравнение для прогиба в
сечении
:

.
(ж)

Постоянные
интегрирования в уравнении (ж) получим,
воспользовавшись граничными усорвиями
закрепления балки, в соответствии с
которыми прогиб и угол поворота в жесткой
заделке равны нулю:

при
и.

Подставляя
в уравнения (д) и (ж) и приравнивая
последовательно нулю угол поворота и
прогиб нулю, получим:;.
Тогда выражение для прогиба принимает
вид:

.

Подставляя
в это уравнение заданные значения
жесткости сечения, интенсивности
распределенной нагрузки, длину балки,
а также координату сечения В, в котором
определяется стрела прогиба (),
находим:

ммм.

Знак
“”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

Прогиб и угол поворота балки в начале координат (начальные параметры) определяются из условий закрепления балки.

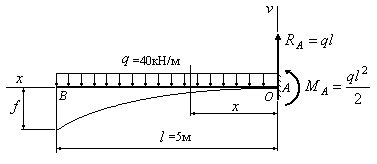
Уравнение упругой линии балки на примере

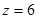
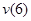
Определим прогиб балки на консоли при м, то есть . Запишем универсальное уравнение упругой линии балки:

Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: .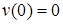

Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.

,

.

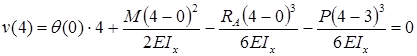
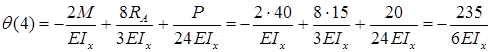
Прогиб консоли при z=6м:

Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).

Примерный вид упругой линии балки показан на рис. 7.16.

Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.

Уравнение упругой линии при изгибе стержней постоянного сечения.

Приведенные примеры определения деформирования оси стержня были относительно просты тем, что изгибающий момент имел одно аналитическое выражение для всего стержня. Но уже для балки, показанной на рис. 8.64, изгибающий момент имеет два выражения:

что делает более громоздким процесс интегрирования в уравнении (239). Можно, однако, существенно упростить использование уравнения (239) для нескольких типичных нагрузок, приведя уравнение упругой линии к «стандартной форме».

Разумеется, такая форма возможна только для стержней постоянного сечеппя. Для приведения уравнения упругой линии к стандартной форме, естественно, потребуется определенная формализация. Начало координат будем всегда помещать в левом конце стержня; направлениям внешних нагрузок в принятой системе координат припишем определенные знаки. На рис. 8.65 показаны положительпые направления внешних нагрузок.

Рис. 8.65. Положительные направления внешних нагрузок для уравнения упругой линии в стандартной форме

Рис. 8.66. Единичная разрывная функция (функция Хевисайда)

К числу внешних сил относятся усилия и моменты в опорах стержня, и потому опоры стержня не показаны. Уравнение упругой линии (239) представим в следующей стандартной форме;

где функция нагрузки

При действии внешнего момвнта в сечении z = а выражение для изгибающего момента принимает вид

Последнее равенство можно записать более кратко, если ввести единичную разрывную функцию (функцию Хевисайда):

График функции Хевисайда приведен на рис. 8.66. Если f(z) — произвольная (интегрируемая) функция, то

Последнее равенство очевидно, так как функция «уничтожает» все значения при . Повторное интегрирование дает (проверьте!)

Равенство (242) представим в виде

Функция нагрузки для внешнего момента на основании формулы (245) будет такой:

Для внешней силы в сечении

или

Функция нагрузки для внешней силы в сечении z имеет вид

На участке (рис. 8.65) к стержню приложена равномерно распределенная нагрузка с постоянной интенсивностью q. Допустим сначала, что распределенная нагрузка приложена на всем протяжении (до конца стержня) при . Тогда изгибающий момент в сечении

или

Функция нагрузки для распределенной нагрузки при имеет вид

Представим теперь, что на участке при приложена такая же нагрузка, по в противоположном направлении. Тогда для нее функция пагрузки представляется в виде

Функция нагрузки для распределенной нагрузки на участке с будет такой:

Рассмотрим теперь общий случай, когда на стержень в сечениях приложены моменты в сечениях усилия и на участках распределена нагрузка Всего таких сечений .

В соответствии с принципом независимости действия сил, справедливым для упругих систем, при одновременном воздействии всех нагрузок уравнение упругой линии будет таким:

Это и есть уравнение упругой линии в стандартной форме (или универсальное уравнение упругой линии). Его, можно дополнить учетом распределенной нагрузки с линейным и квадратным законом изменения по z, но в этом нет необходимости, так как нагрузку всегда можно аппроксимировать участками постоянной интенсивности.

Пример использования уравнения упругой линии стержня в стандартной форме.

Определим уравнение упругой линии стержня на двух шарнирных при действии сосредоточенной силы в середине пролета (см. рис. 8.64). К стержню приложены три внешние силы в сечении в сечении и в сечении

По формулам (240) и (249) находим

Сила (реакция в опоре В) в явном виде не участвует, так как приложена в правом конце стержня . Из краевого условия получаем

тогда уравнение упругой линии стержня примет вид

Наибольший прогиб получается при

Дифференциальное уравнение упругой линии балки и его интегрирование

При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией, а поступательные перемещения сечений, равные перемещениям y=y(x) их центров тяжести сечений – прогибами балки.

Рис. 8.22.

Между прогибами y(x) и углами поворота сечений θ(x) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии (θ и φ – углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y^/=tgθ. Следовательно, tgθ=tgφ=y^/.

В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h, а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ=y^/.

Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M_z и жесткости EI_z (см. уравнение (8.8)):

.

(8.26)

В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,

.

(8.27)

Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M_z и y^// были приняты независимо друг от друга, получаем

.

(8.28)

Это равенство называется дифференциальным уравнением упругой линии. При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ=0.1 рад (y^/)²=0.01) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки

.

(8.29)

Выбор знака в правой части (8.29) определяется направлением координатной оси y, так как от этого направления зависит знак второй производной y^//. Если ось направлена вверх, то, как видно из рис. 8.23, знаки y^// и M_z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y^// и M_z противоположны, и это заставляет выбрать в правой части знак минус.

Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M_z содержит одну из главных осей инерции сечения.

Рис. 8.23.

Интегрируя (8.29), находим сначала углы поворота сечений

,

(8.30)

а после второго интегрирования – прогибы балки

.

(8.31)

Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.

Пример 8.4

Пример 8.5

Пример 8.6

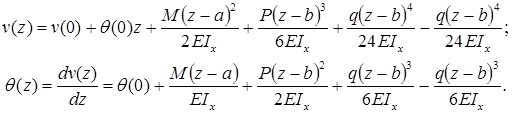
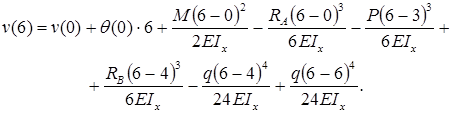
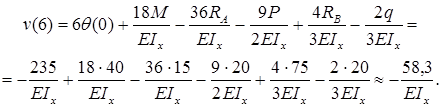
  Следующая