Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей — проводников.
Для начала давайте вспомним, что такое проводник? Проводник — это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:

ρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом

S – площадь поперечного сечения, м2
l – длина проводника, м
Более подробно об этом я писал здесь.
Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.

Последовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

Пример
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Следовательно,
UR1 = IR1 =1×2=2 Вольта
UR2 = IR2 = 1×3=3 Вольта
UR3 = IR3 =1×5=5 Вольт
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Получается
U=UR1+UR2+UR3
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.

Ну что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников
Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.
Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что
I1 = U/R1
I2 = U/R2
I3 = U/R3
Если бы у нас еще были резисторы, соединенные параллельно, то для них
In = U/Rn
В этом случае, сила тока в цепи будет равна:

Задача
Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Решение
Воспользуемся формулами, которые приводили выше.
I1 = U/R1
I2 = U/R2
I3 = U/R3
Если бы у нас еще были резисторы, соединенные параллельно, то для них
In = U/Rn
Следовательно,
I1 = U/R1 = 10/2=5 Ампер
I2 = U/R2 = 10/5=2 Ампера
I3 = U/R3 = 10/10=1 Ампер
Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи
I=I1 + I2 + I3 = 5+2+1=8 Ампер
2-ой способ найти I
I=U/Rобщее
Чтобы найти Rобщее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них — «калькулятор резисторов«. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.
I=U/Rобщее = 10/1,25=8 Ампер.
Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.
Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.
Подробное объяснение на видео:
Прикольный набор радиолюбителя по ссылке <<<
Похожие статьи по теме «последовательное и параллельное соединение»
Закон Ома
Проводник (электрический проводник)
Что такое резистор
Делитель напряжения
Делитель тока
Что такое напряжение
Что такое сила тока
Подскажите формулу для задачи по электротехнике
Ученик
(90),
на голосовании
4 года назад
Голосование за лучший ответ
АЗ
Искусственный Интеллект
(195098)
4 года назад
Z₁=√(R₁²+Xc₁²)=5 Ом;
Z₂=√(R₂²+Xᴌ₂²)=10 Ом;
U=U₁=U₂=20 B;
I₁=U/Z₁=4 A;
I₂=U/Z₂=2 A;
I=√(I₁²+I₂²)=4,5 A;
Ur₁=I₁*R₁=12 B;
Ur₂=I₂*R₂=16 B;
Uᴌ₂=I₂*Xᴌ₂=12 B;
Uc₁=I₁*Xc₁=8 B;
P₁=I₁*Ur₁=48 Вт;
P₂=I₂*Ur₂=32 Вт;
Qᴌ₂=I₂*Uᴌ₂=24 ВАр;
Qc₁=I₁*Uc₁=32 ВАр;
P=P₁+P₂=80 Вт.
Lens LensУченик (90)
4 года назад
Можно написать формулы, не готовые ответы, а формулы, как вы получали ответы, пожалуйста!
Основной целью расчета электрических цепей, является определение токов в ветвях. Если уже нашли токи, то можно найти все остальные величины: напряжения на элементах, мощности, строить диаграммы и т. д.
При расчете электрических цепей заданными считаются источники (ЭДС или источники тока), а также сопротивления резисторов (сопротивления могут быть активными – резисторы и реактивными – катушки и конденсаторы).
Перед тем как переходить к расчету цепи, нужно задать условно положительные направления токов в ветвях.
Цепь считается простой, если она содержит в себе только 1 источник энергии. Это в случае, если цепь разветвленная, имеется несколько ветвей с сопротивлениями. Но также цепь будет считаться простой, если она неразветвленная, но содержит в себе 1 или несколько источников энергии.
На рисунках 1 и 2 изображены простые цепи: одна разветвленная, но содержит в себе только 1 источник энергии, а вторая неразветвленная, хотя содержит в себе более 1 источника энергии. Все остальные цепи считаются сложными.
Если, например, в последнюю ветвь, изображенную на рисунке 1, добавить ЭДС, то эта цепь будет уже сложной. Для расчета сложных электрических цепей существуют такие методы как:
Метод прямого использования законов Кирхгофа;
Метод контурных токов;
Метод узловых потенциалов;
Метод наложения и т. д.
А для простых электрических цепей существуют только два метода расчета:
Метод эквивалентных преобразований;
Метод пропорциональных величин.
Сегодняшняя статья посвящена второму методу.
Имеется схема цепи, изображенная на рисунке 1. Даны сопротивления резисторов и ЭДС. Требуется найти токи ветвей методом пропорциональных величин.
Этот метод состоит в следующем. Считаем, что ток одной ветви, ветви наиболее удаленной от источника Е, известен. Обычно, для удобства расчетов, этот ток принимают равным 1 А.
И уже зная этот ток, находят все остальные токи и напряжения в цепи, а также находят ЭДС. Но найденное ЭДС в общем случае будет отличаться от заданного ЭДС.
Далее нужно найти отношение заданной ЭДС к расчетной при токе, взятому в наиболее удаленной от источника ветви, равным 1 А. Отношение заданного ЭДС к расчетному обозначают, обычно, буквой “к”, где “к” – некоторый постоянный коэффициент.
Зная уже этот коэффициент, находят истинные значения токов и напряжений в цепи путем умножения коэффициента “к” на ранее полученные токи и напряжения при токе в наиболее удаленной от источника ветви (мы возьмем его равным 1 Ампер).
Переходим к решению задачи. Для начала расставим токи ветвей. Но учтем, что это не истинные их значения, поэтому их мы будем обозначать со штрихом.
В данной цепи, наиболее удаленная ветвь от источника, это ветвь с резистором R5. Через эту ветвь протекает ток I5`. Примем его значение равным 1 А.
I5`=1 (A)
Найдем с помощью закона Ома и правил Кирхгофа оставшиеся токи и напряжения, а также ЭДС.
Напряжение на R5:
Ur5`=I5`·R5=1·40=40 (B)
Резистор R4 подключен параллельно резистору R5, а при параллельном соединении элементов, напряжение на них одно и тоже.
Ur4`=Ur5`=40 (В)
Зная напряжение и сопротивление резистора R4, определим ток через R4:
Далее можем найти ток I3` записав первое правило Кирхгофа для узла “с”. Ток втекающий в узел “c” берем со знаком “+”, а вытекающий со знаком “-“
I3`-I4`-I5`=0, от сюда
I3`=I4`+I5`=2+1=3 (A)
Напряжение на R3:
Ur3`=I3`·R3=3·20=60 (B)
Напряжение на резисторах R3 и R4 мы уже знаем. Записав второе правило Кирхгофа для среднего контура, определим напряжение на R2. Обход контура возьмем по часовой стрелке:
Ur3`+Ur4`-Ur2`=0, от сюда
Ur2`=Ur3`+Ur4`=60+40=100 (B)
Зная напряжение и сопротивление резистора R2, определим ток I2`
Записав первое правило Кирхгофа для узла “a”, определим ток I1`:
I1`-I2`-I3`=0, от сюда
I1`=I2`+I3`=10+3=13 (A)
Напряжение на R1:
Ur1`=I1`·R1=13·10=130 (B)
ЭДС найдем, записав второе правило Кирхгофа для левого контура:
I1`·R1+I2`·R2=E`, от сюда
E`=Ur1`+Ur2`=130+100=230 (B)
Теперь определим коэффициент как отношение заданного ЭДС к расчетному:
Далее можем находить истинные значения токов и напряжений в цепи. По заданию, нужно определить токи ветвей, тогда
I1=k·I1`=0.43478·13=5.65 (A)
I2=k·I2`=0.43478·10=4.3478 (A)
I3=k·I3`=0.43478·3=1.304 (A)
I4=k·I4`=0.43478·2=0.849 (A)
I5=k·I5`=0.43478·1=0.43478 (A)
Отличие этого метода от метода эквивалентных преобразований только лишь в том, что в методе пропорциональных величин не нужно искать общее сопротивление цепи.
Подобные цепи, конечно, легче и быстрее рассчитывать методом эквивалентных преобразований.
В качестве проверки правильности найденных токов, соберем схему цепи в программе воркбэнч.
Как видим, амперметры в ветвях показывают те же значения токов, что и расчетные. Задача решена верно.
Вот таким образом решаются задачи методом пропорциональных величин.
Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.
Читайте также:
1. Как электроэнергия передается от электростанций до наших домов;
2. Что такое электрический ток – простыми словами;
В сложных электрических цепях, то есть где имеется несколько разнообразных ответвлений и несколько источников ЭДС имеет место и сложное распределение токов. Однако при известных величинах всех ЭДС и сопротивлений резистивных элементов в цепи мы можем вычистить значения этих токов и их направление в любом контуре цепи с помощью первого и второго закона Кирхгофа. Суть законов Кирхгофа я довольно кратко изложил в своем учебнике по электронике, на страницах сайта http://www.sxemotehnika.ru.
Пример сложной электрической цепи вы можете посмотреть на рисунке 1.

Рисунок 1. Сложная электрическая цепь.
Иногда законы Кирхгофа называют правилами Кирхгофа, особенно в старой литературе.
Итак, для начала напомню все-таки суть первого и второго закона Кирхгофа, а далее рассмотрим примеры расчета токов, напряжений в электрических цепях, с практическими примерами и ответами на вопросы, которые задавались мне в комментариях на сайте.
Первый закон Кирхгофа
Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.
Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.
Поясню первый закон Кирхгофа на примере рисунка 2.

Рисунок 2. Узел электрической цепи.
Здесь ток I1– ток, втекающий в узел , а токи I2 и I3 — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать:
I1 = I2 + I3 (1)
Что бы подтвердить справедливость формулировки №2, перенесем токи I2 и I3 в левую часть выражения (1), тем самым получим:
I1 – I2 – I3 = 0 (2)
Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.
Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).
Можно посмотреть отдельный видеоурок по первому закону Кирхофа в разделе ВИДЕОУРОКИ.
Второй закон Кирхгофа.
Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.
Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:
1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).
2. Произвольно выбираем направление токов через элементы цепи.
3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:
– ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».
– напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».
Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.

Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.
E1– Е2 = -UR1 – UR2 или E1 = Е2 – UR1 – UR2 (3)
Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).
Расчеты электрических цепей с помощью законов Кирхгофа.
Теперь давайте рассмотрим вариант сложной цепи, и я вам расскажу, как на практике применять законы Кирхгофа.
Итак, на рисунке 4 имеется сложная цепь с двумя источниками ЭДС величиной E1=12 в и E2=5 в , с внутренним сопротивлением источников r1=r2=0,1 Ом, работающих на общую нагрузку R = 2 Ома. Как же будут распределены токи в этой цепи, и какие они имеют значения, нам предстоит выяснить.

Рисунок 4. Пример расчета сложной электрической цепи.
Теперь согласно первому закону Кирхгофа для узла А составляем такое выражение:
I = I1 + I2,
так как I1 и I2 втекают в узел А, а ток I вытекает из него.
Используя второй закон Кирхгофа, запишем еще два выражения для внешнего контура и внутреннего левого контура, выбрав направление обхода по часовой стрелке.
Для внешнего контура:
E1-E2 = Ur1 – Ur2 или E1-E2 = I1*r1 – I2*r2
Для внутреннего левого контура:
E1 = Ur1 + UR или E1 = I1*r1 + I*R
Итак, у нас получилась система их трех уравнений с тремя неизвестными:
I = I1 + I2;
E1-E2 = I1*r1 – I2*r2;
E1 = I1*r1 + I*R.
Теперь подставим в эту систему известные нам величины напряжений и сопротивлений:
I = I1 + I2;
7 = 0,1I1 – 0,1I2;
12 = 0,1I1 +2I.
Далее из первого и второго уравнения выразим ток I2
I2=I – I1;
I2 = I1 – 70;
12 = 0,1I1 + 2I.
Следующим шагом приравняем первое и второе уравнение и получим систему из двух уравнений:
I – I1= I1 – 70;
12 = 0,1I1 + 2I.
Выражаем из первого уравнения значение I
I = 2I1– 70;
И подставляем его значение во второе уравнение
12 = 0,1I1 + 2(2I1 – 70).
Решаем полученное уравнение
12 = 0,1I1 + 4I1 – 140.
12 + 140= 4,1I1
I1=152/4,1
I1=37,073 (А)
Теперь в выражение I = 2I1– 70 подставим значение
I1=37,073 (А) и получим:
I = 2*37,073 – 70 = 4,146 А
Ну, а согласно первому закона Кирхгофа ток I2=I – I1
I2=4,146 – 37,073 = -32,927
Знак «минус» для тока I2 означает, то что мы не правильно выбрали направление тока, то есть в нашем случае ток I2 вытекает из узла А.
Теперь полученные данные можно проверить на практике или смоделировать данную схему например в программе Multisim.
Скриншот моделирования схемы для проверки законов Кирхгофа вы можете посмотреть на рисунке 5.
 Рисунок 5. Сравнение результатов расчета и моделирования работы цепи.
Рисунок 5. Сравнение результатов расчета и моделирования работы цепи.
Для закрепления результатата предлагаю посмотреть подготовленное мной видео:

Занятие1
Цели занятия:
1. Ознакомиться с законами коммутации.
2. Научиться использовать классический метод расчета переходных процессов для нахождения мгновенных значений электрических величин, подчиняющихся законам коммутации, в цепях с одним реактивным элементом.
3.Научиться строить графики изменения искомых величин.
4.Научиться определять длительность переходного процесса.
Переходные процессы подчиняются законам коммутации. Согласно первому закону коммутации ток в индуктивной катушке не может измениться скачком. Согласно второму закону коммутации напряжение на емкостном элементе не может измениться скачком.
При рассмотрении переходных процессов продолжительность коммутации принимают равной нулю. Момент, предшествующий коммутации, обозначают t = 0 −, момент завершения – t = 0 +. Тогда законы коммутации можно записать в следующем виде:
iL (0+) =iL (0−) ,
uC (0+) =uC (0−).
Независимыми начальными условиями называют значения тока в индуктивной катушке и напряжения на конденсаторе в момент коммутации
(t =0+).
В классическом методе расчета переходных процессов расчет токов и напряжений производят при помощи уравнений, составленных по законам Кирхгофа для мгновенных значений. В общем случае получают систему неоднородных линейных дифференциальных уравнений. Общий интеграл дифференциального уравнения получают суммированием частного решения этого уравнения и общего решения уравнения без правой части.
Составляющие токов и напряжений, найденные как частное решение неоднородного уравнения, называют принужденными.
Составляющие, найденные как общее решение однородного уравнения, называют свободными. Свободные составляющие обусловлены изменением энергии электрического поля конденсатора и магнитного поля индуктивной катушки. Свободные составляющие стремятся к нулю, так как процессы в цепи, обладающей сопротивлением, при отсутствии источников энергии
|
Теоретические основы электротехники. Практикум |
-238- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
затухают. После переходного процесса остаются только принужденные составляющие, т. е. принужденный режим – это новый установившийся режим после окончания переходного процесса.
В классическом методе токи и напряжения вычисляют как сумму принужденной и свободной составляющих:
i = iпр + iсв, u = uпр + uсв .
Рассмотрим порядок расчета на конкретных задачах.
Задача1
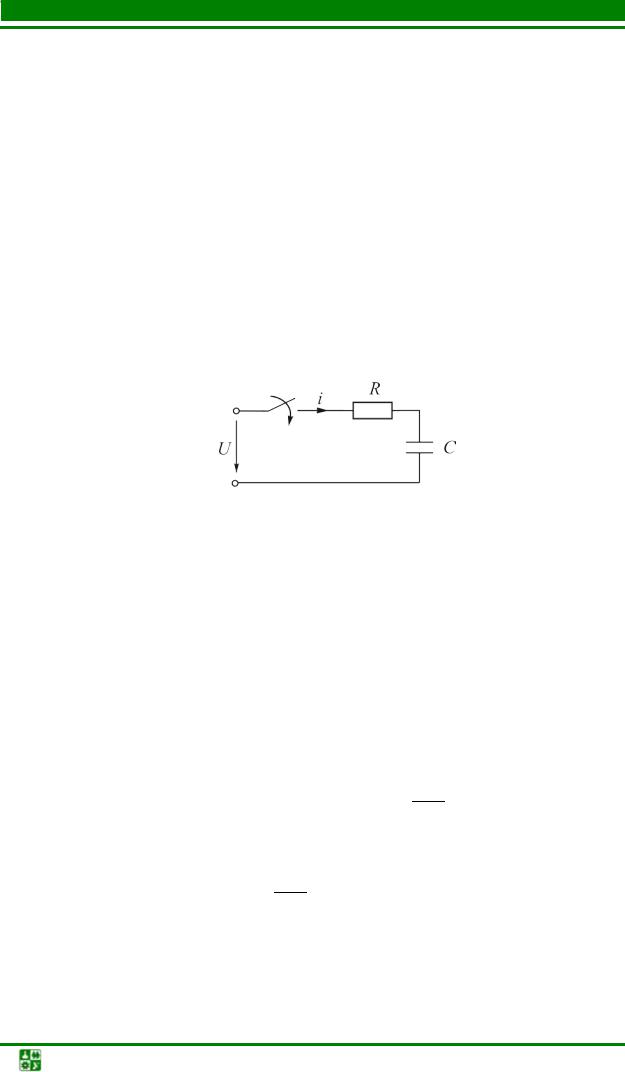
Найти законы изменения напряжения на конденсаторе uC и тока i
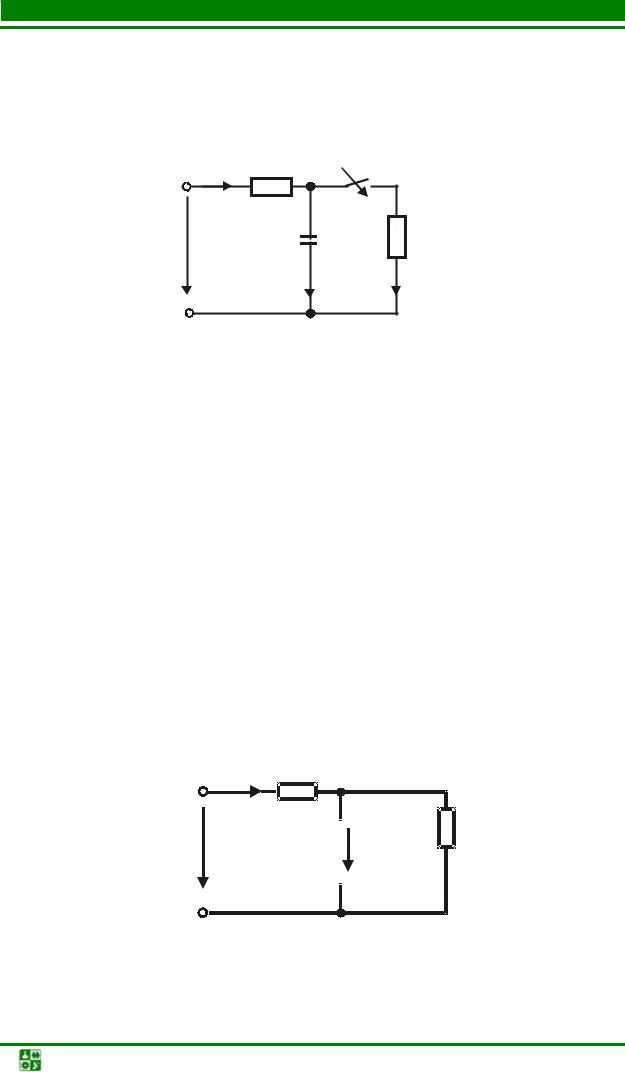
(рис. 5.1), если U =100 В, R =1000 Ом, C =1 мкФ. Определить длительность переходного процесса.
Рис. 5.1
Решение
I. Составим систему уравнений электрического состояния. Так как схема одноконтурная, то можно написать только одно уравнение по второму закону Кирхгофа:
Ri +uС =U.
В этом уравнении во время переходного процесса происходит изменение двух величин: тока i и напряжения на емкостном элементе uС .
Напряжение uС подчиняется второму закону коммутации, поэтому рационально выразить ток по закону Ома i = iС = C ddutС .
Тогда уравнение примет вид
RC ddutС +uС =U.
2. Решение этого уравнения представим как сумму двух слагаемых:
uС = uСпр + uСсв.
|
Теоретические основы электротехники. Практикум |
-239- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
3. Найдем uСпр .
Теоретически переходной процесс длится бесконечно долго, поэтому принужденный режим рассмотрим как новый установившийся режим при t = ∞ . Конденсатор постоянный ток не пропускает (iпр = 0 ), Riпр = 0. Отсюда
uСпр =U =100 В.
4. Вычислим uСсв . Из математики известно, что свободные составляющие меняются по экспоненциальному закону:
uСсв = Аеpt .
4.1. Определим показатель степени р, который является корнем характеристического уравнения.
Для получения характеристического уравнения в уравнении электрического состояния правую часть нужно приравнять к нулю, переменную величину заменить единицей, ее производную – р, вторую производную – р2 и т. д. Получим уравнение RCp +1 = 0.
|
Решение |
характеристического уравнения позволяет определить |
|||||||||
|
1 |
1 |
3 −1 |
||||||||
|
p = − |
= |
= −10с |
. |
|||||||
|
RC |
1000 1 10−6 |
|||||||||
|
Величину |
1 |
= RC обозначают τ и называют постоянной времени; |
||||||||
|
p |
||||||||||
τ=1013 = 0,001 с.
4.2.Определим постоянную интегрирования А.
Постоянные интегрирования определяют из начальных условий с использованием законов коммутации.
Уравнение, по которому проводим решение, справедливо для любого момента времени, следовательно, и для начального:
uС (0+) = uСпр(0+) +uСсв(0+).
По второму закону коммутации uС (0+) =uС(0−) . До коммутации схема не была подключена к источнику энергии, поэтому uС(0−) = 0.
Принужденная составляющая в данной задаче является постоянной величиной, значит, uСпр(0+) =U =100 В.
Свободная составляющая uСсв = Аерt при t = 0+ равна А.
После подстановки получим 0 =U + A. Отсюда A = −U = −100 В.
|
Теоретические основы электротехники. Практикум |
-240- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
|
1 |
t |
||||||||||||||||||||||||||||||
|
Тогда закон изменения напряжения u |
=U −Ue− |
=100 −100e−103 t В. |
|||||||||||||||||||||||||||||
|
RC |
|||||||||||||||||||||||||||||||
|
С |
|||||||||||||||||||||||||||||||
|
Закон изменения тока можно получить как из уравнения по второму |
|||||||||||||||||||||||||||||||
|
закону Кирхгофа, так и из закона Ома. |
|||||||||||||||||||||||||||||||
|
Из уравнения по второму закону Кирхгофа |
|||||||||||||||||||||||||||||||
|
U −U +Ue− |
1 |
t |
1 |
||||||||||||||||||||||||||||
|
U −u |
С |
RC |
U |
− |
t |
= 0,1e−10 |
3 |
t А, |
|||||||||||||||||||||||
|
i = |
= |
= |
e |
RC |
|||||||||||||||||||||||||||
|
R |
R |
R |
|||||||||||||||||||||||||||||
|
либо |
1 |
1 |
|||||||||||||||||||||||||||||
|
d u |
С |
U |
− |
t |
U |
− |
t |
= 0,1e−10 |
3 |
t |
|||||||||||||||||||||
|
i |
= C |
= C |
e |
RC |
= |
e |
RC |
А. |
|||||||||||||||||||||||
|
RC |
R |
||||||||||||||||||||||||||||||
|
d t |
Проиллюстрируем полученные уравнения графиками.
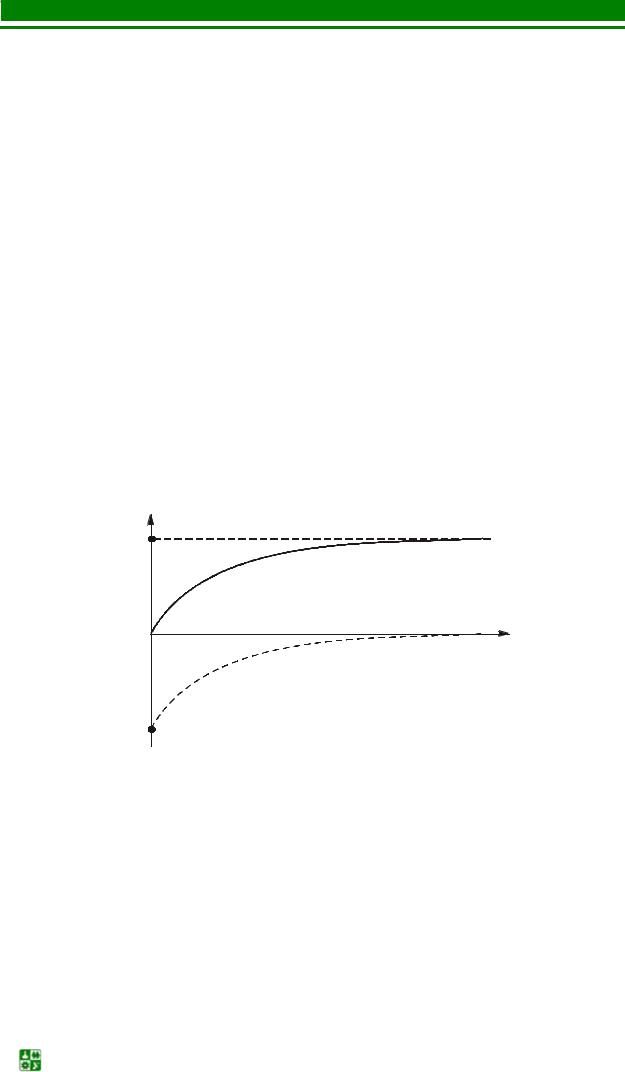
График напряжения uС (рис. 5.2) получаем суммированием графиков uСпр и uСсв. Составляющая uСпр =100 B = const . Свободная составляющая изменяется по закону экспоненты и стремится к нулю. В начальный момент uСсв(0+) = −100 В.
|
uC |
uC пр |
|
|
U |
||
|
uC |
||
|
t |
||
|
uC св |
||
|
–U |
Рис. 5.2 |
|
График подтверждает, что напряжение на конденсаторе меняется плавно и принужденный режим – это новый установившийся режим после переходного процесса.
График изменения тока представлен на рис. 5.3.
При t = 0– тока не было, при t = 0+ ток iС = 0,1 А, далее он стремится к
нулю по закону экспоненты.
5. Вычислим длительность переходного процесса.
Теоретически переходный процесс длится бесконечно долго.
|
Практически переходный процесс заканчивается через (3−5)τ, т. е. |
tпп = = |
|
(0,003 −0,005) с. |
|
|
Теоретические основы электротехники. Практикум |
-241- |

|
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ |
|
iC |
|
U |
|
R |
|
t |
|
Рис. 5.3 |
|
Следующую задачу решите самостоятельно. |
Задача2
Найти законы изменения напряжения на конденсаторе uC и тока i (рис. 5.1), если U = 25 В, R = 20 Ом, C = 5 мкФ, uC (0−) =50 В. Построить графики.
Пояснение к решению
Возможны два варианта решения, так как с резистором могут быть соединены разные обкладки конденсатора.
Ответ: 1) uC = 25 + 25e−104 t В; i = −1,25e−104 t А. 2) uC = 25 −75e−104 t В; i =3,75e−104 t А.
Задача3
Найти законы изменения напряжения на конденсаторе uC и тока i (рис. 5.4), если U = 200 В, R = 80 Ом, R1 = 20 Ом, С =1,25 мкФ. Определить длительность переходного процесса.
i R
|
U |
uС |
СС |
|||||||
R1
Рис. 5.4
|
Теоретические основы электротехники. Практикум |
-242- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
Решение
1. Составим систему уравнений электрического состояния. Коммутация заключается в размыкании рубильника. После коммутации схема становится одноконтурной, поэтому можно написать только одно уравнение по второму закону Кирхгофа: R i +uC =U .
После подстановки выражения тока по закону Ома i =iC =C duС dt
уравнение примет вид
RC ddutC +uC =U .
2. Решение этого уравнения представим как сумму двух слагаемых:
uC = uC пр +uC св .
3. Найдем uC пр.
Принужденный режим – это новый установившийся режим после окончания переходного процесса. Конденсатор постоянный ток не пропускает (iпр = 0) , R iпр = 0 . Отсюда uC пр =U = 200 В.
4. Вычислим uC св .
Свободные составляющие меняются по экспоненциальному закону:
uC св = Aep t .
4.1. Определим показатель степени р, который является корнем характеристического уравнения RC p +1 = 0 .
|
Отсюда p = − |
1 |
= − |
1 |
= − |
106 |
= −10−4 с−1. |
|
|
RC |
80 1,25 10−6 |
100 |
|||||
4.2. Определим постоянную интегрирования А.
Уравнение, по которому проводим решение, справедливо для любого момента времени, следовательно, и для начального:
uC (0+) = uC пр(0+) +uC св(0+) .
По второму закону коммутации uC (0+) = uC (0−) . Схема до
коммутации приведена на рис. 5.5. Ключ замкнут. Конденсатор постоянный ток не пропускает, поэтому вместо него можно изобразить разрыв.
|
Теоретические основы электротехники. Практикум |
-243- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
|
i(0-) |
R |
|||
|
i(0–) |
||||
|
uC(0(0––)) |
R1 |
|||
|
С |
||||
|
1 |
||||
|
Рис. 5.5 |
||||
|
Схема является одноконтурной, ток в ней |
i(0−) = |
U |
= 2 А. |
|
|
R + R |
||||
|
1 |
Напряжение uC (0−) = R1 i(0−) = 20 2 = 40 В.
Принужденная составляющая в рассматриваемой задаче является
|
постоянной величиной, т. е. u |
Cпр |
(0+) =U = 200 В. |
|||||||||
|
Свободная составляющая u |
= Aep t |
при t = 0 + равна А. |
|||||||||
|
C св |
|||||||||||
|
После подстановки получим: 40 = 200 + А. |
|||||||||||
|
Отсюда А= −160 В. |
|||||||||||
|
Тогда закон изменения напряжения u |
= 200 −160e−104 t В. |
||||||||||
|
Закон изменения тока |
C |
||||||||||
|
i = |
U |
−u |
200 − 200 +160e−104 t |
−104 t |
А. |
||||||
|
C |
= |
= 2e |
|||||||||
|
C |
R |
80 |
|||||||||
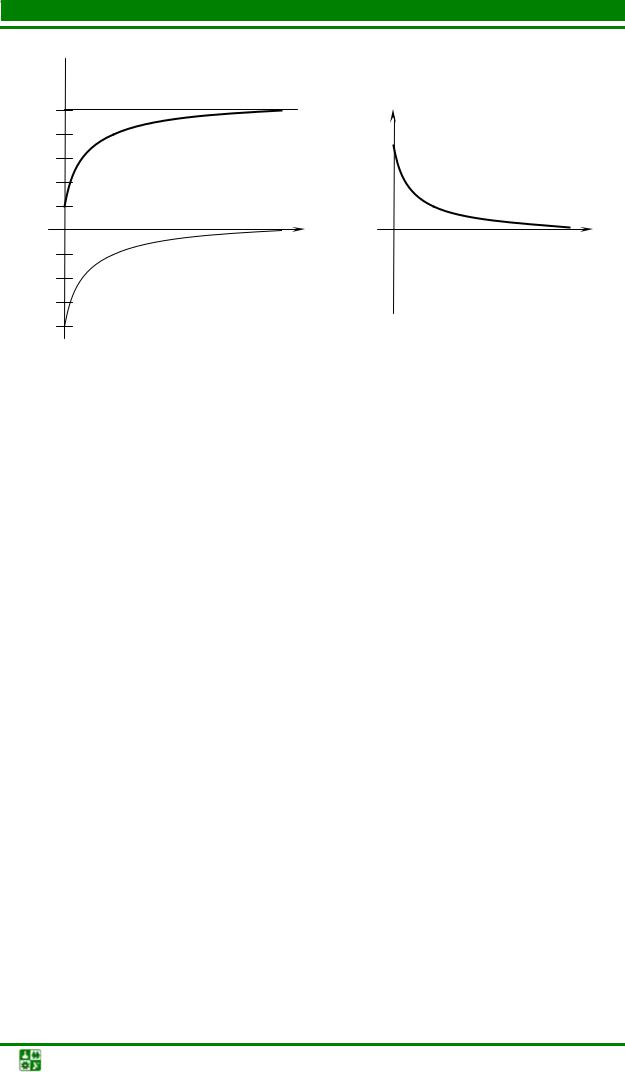
|
Графики напряжения |
uC и тока iC |
представлены соответственно на |
|||||||||
|
рис. 5.6 и 5.7. |
|
Теоретические основы электротехники. Практикум |
-244- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
uC , B 
|
uCпр |
iC , A |
||||||||
|
200 |
|||||||||
|
uC |
2 |
iC |
|||||||
|
40 |
|||||||||
|
t |
t |
||||||||
|
uCсв |
|||||||||
|
– |
|||||||||
|
Рис. 5.6 |
Рис. 5.7 |
||||||||
|
Переходный процесс длится (3 −5) τ = (3 −5) |
1 |
= (0,0003 −0,0005) с. |
|||||||
|
р |
|||||||||
|
Задачи 4 и 5 решите для самоконтроля. |
|||||||||
|
Задача4 |
|||||||||
|
Вычислить начальное значение напряжения |
uC (0+) , принужденную |
составляющую uC пр и длительность переходного процесса в схеме рис. 5.1, если U =50 B , R = 5 Ом, C = 2 мкФ.
Ответ: uC (0+) = 0; uC пр = 50 В; tпп = (3 10−5 − 5 10−5 ) с.
Задача5
Вычислить начальное значение напряжения uC (0+) и принужденную
составляющую uC пр (рис. 5.4), если U = 40 В, R = R1 = 20 Ом, C =1 мкФ. Ответ: uC (0+) = 20 В; uC пр = 40 В.
Задача6
Найти законы изменения тока i , а также напряжений uR и uL (рис. 5.8), если U =100 В, R =10 Ом, L =1 Гн.
|
Теоретические основы электротехники. Практикум |
-245- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
Рис. 5.8
Решение
1. Составим уравнение электрического состояния в дифференциальной форме:
uL + uR =U .
После подстановки uL и uR , выраженных по закону Ома, получим уравнение с одной переменной:
L dditL + RiL =U .
2. Представим решение этого уравнения как сумму двух слагаемых:
iL = iLпр +iLсв.
3. Найдем iLпр в схеме при t = ∞ . Индуктивный элемент не оказывает
сопротивления постоянному току, вместо него будет «закоротка». Тогда
iLпр = UR =10010 =10 А.
4. Вычислим iLсв по закону экспоненты:
iLсв = Аеpt .
4.1. Составим характеристическое уравнение для определения p : Lp +
+ R = 0 .
Отсюда p = − RL = −101 = −10 с−1 .
Постоянная времени τ = 1p = RL = 0,1 с.
4.2.Определим постоянную интегрирования А из начальных условий
сиспользованием законов коммутации.
Вначальный момент времени
|
Теоретические основы электротехники. Практикум |
-246- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
iL (0+) = iLпр(0+) + iLсв(0+) .
По первому закону коммутации iL (0+) =iL (0−) . До коммутации схема не была подключена к источнику энергии, поэтому iL (0−) = 0 .
Принужденная составляющая iLпр =10 А – постоянная величина. Свободная составляющая в начальный момент iLсв(0+) = А.
После подстановки получим: 0 =10 + A. Отсюда A = −10 А.
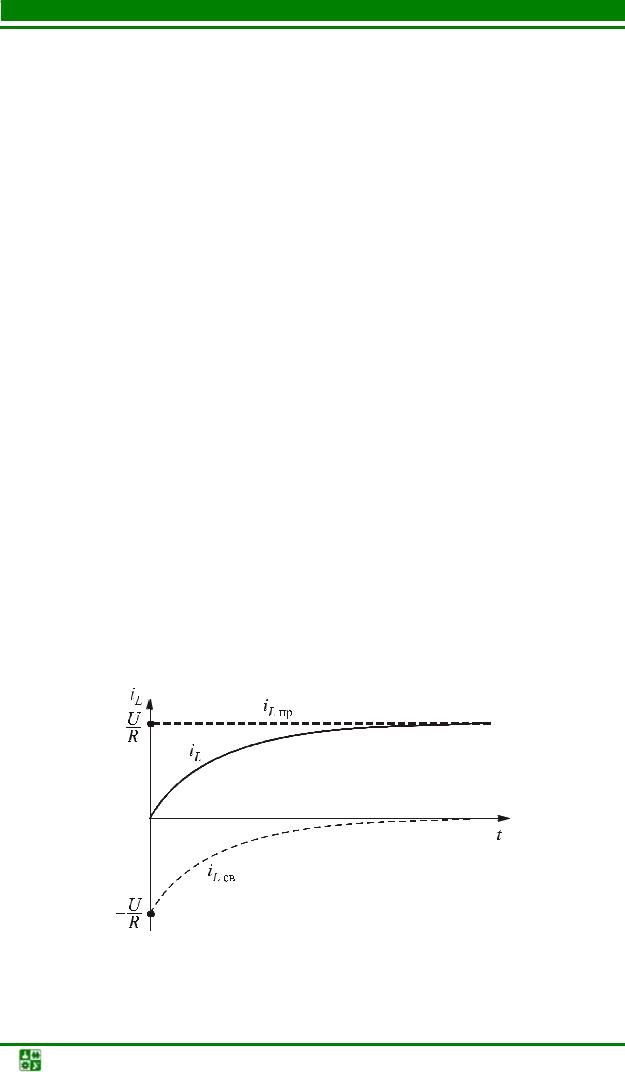
Тогда закон изменения тока iL =10 −10e−10t А.
Закон изменения напряжения uR = RiL =100 −100e−10t В.
Закон изменения напряжения
|
uL = L |
diL |
=1 |
(−10)(−10)e−10t |
=100e−10t В. |
||
|
dt |
||||||
|
В любой момент времени uR +uL =U −Ue |
−Rt |
+Ue |
−Rt |
=U . |
||
|
L |
L |
Проиллюстрируем полученные законы изменения электрических величин графиками.
График тока iL (рис. 5.9) получаем как сумму графиков iLпр и iLсв. Составляющая тока iLпр =10 А = const . Свободная составляющая меняется по закону экспоненты и стремится к нулю. В начальный момент iLсв (0+) = −10 А.
|
Теоретические основы электротехники. Практикум |
-247- |
|
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ |
|
Из графика видно, что ток в индуктивной катушке меняется плавно и |
|
стремится к принужденной составляющей. |
|
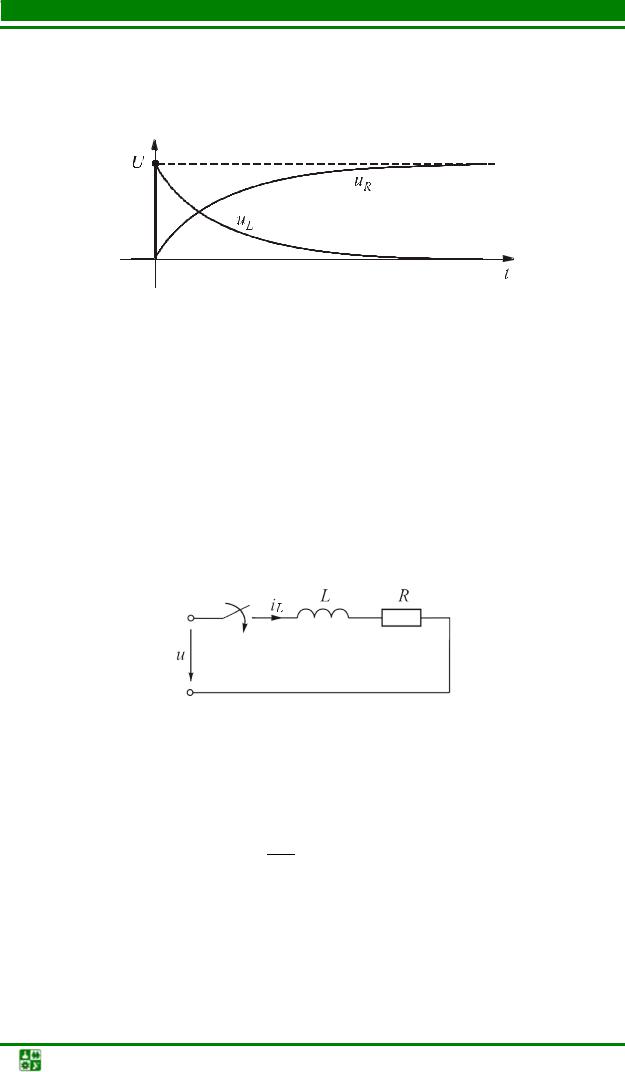
Графики изменения напряжений uR и uL приведены на рис. 5.10. |
|
Рис. 5.10 |
|
График uR аналогичен графику тока iL , так как uR = RiL . |
|
Напряжение uL в начальный момент возрастает скачком до величины |
|
входного напряжения, а затем по экспоненциальному закону уменьшается до |
|
нуля. |
|
Задача7 |
|
Найти закон изменения тока iL (рис. 5.11), если u = 70sin(50t +120o ) В, |
|
R = 20 Ом, L = 3 Гн. Построить график. |
|
Рис. 5.11 |
|
Решение |
|
1. Уравнение электрического состояния в дифференциальной форме: |
L dditL + RiL =u .
2. Закон изменения тока iL ищем как сумму двух слагаемых:
iL = iLпр +iLсв .
|
Теоретические основы электротехники. Практикум |
-248- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
3. Ток iLпр меняется по синусоидальному закону:
iL пр = ILm пр sin(ωt + ψu − φ)= ILm пр sin(ωt + ψi пр).
Проведем расчет для комплексов максимальных значений:
|
Um |
70e j120 |
о |
= 70e j120 |
о |
= 0,46e j 38о |
||||
|
ILm пр = |
= |
о |
А. |
||||||
|
R + jLω |
20 + j3 50 |
||||||||
|
151e j 82 |
Тогда закон изменения принужденной составляющей тока
iL пр = 0,46sin(50t +38о) А.
4.Составляющая тока iLсв меняется по закону экспоненты: iL св = Aept .
4.1.Характеристическое уравнение Lp + R =0 дает решение:
p = − RL = − 203 = −6,67с −1 .
4.2.Определим постоянную интегрирования А.
Вначальный момент времени iL (0+) =iLпр(0+) +iL св(0+).
По первому закону коммутации iL (0+) = iL (0−). До коммутации схема не была подключена к источнику энергии, поэтому iL (0−) = 0. Принужденная
составляющая в начальный момент iL пр (0+) = 0,46sin 38о = 0,28 А. Это конкретное значение тока. Свободная составляющая в начальный момент
iL св(0+) = A .
После подстановки получим
0 = 0,28 + A.
Отсюда А= 0,28 А, т. е. iL пр(0+) и iLсв(0+) равны и противоположны.
Тогда закон изменения тока
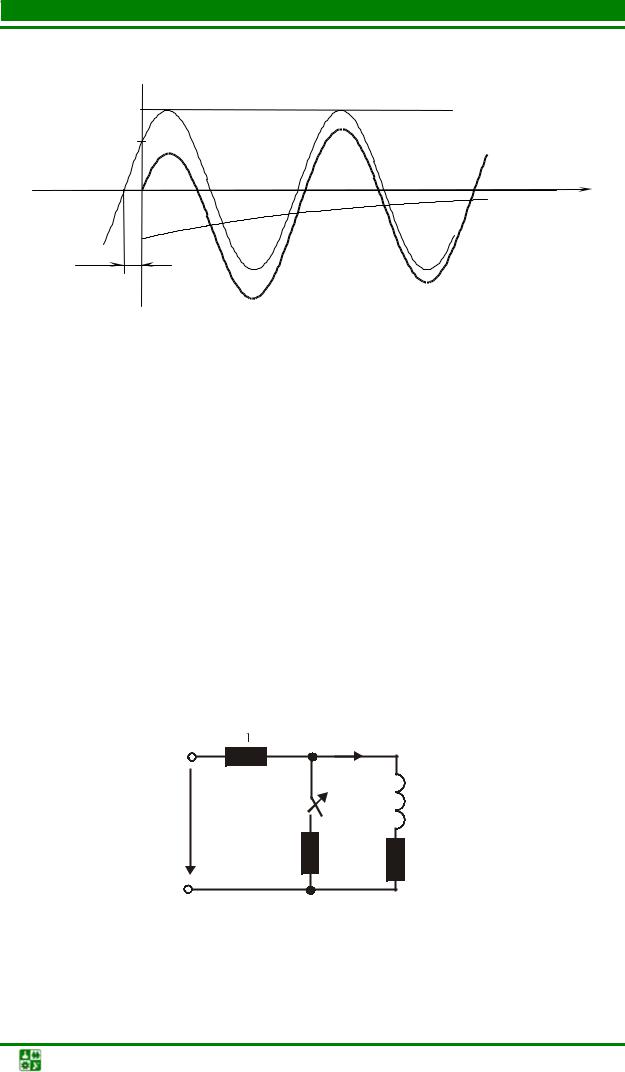
iL = 0,46sin(50t +38о) −0,28e−6,67t А.
График тока iL (рис. 5.12) получаем как сумму графиков iLпр и iLсв. Составляющая тока iLпр меняется по синусоидальному закону. На рис. 5.12 начальная фаза ψi пр > 0, поэтому синусоида смещена влево. Свободная
составляющая меняется по закону экспоненты и стремится к нулю. В начальный момент iL св(0+) = −iL пр(0+) .
|
Теоретические основы электротехники. Практикум |
-249- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
iL , А
0,46
0,28 iL iLпр
t
iLсв
38°
Рис. 5.12
График подтверждает плавное изменение тока в индуктивной катушке. Если ψi пр = 0 , свободная составляющая не возникнет и переходного
процесса не будет.
Следующую задачу решите самостоятельно.
|
Задача8 |
|||
|
Найти закон изменения тока iL (см. рис. 5.11), если u = 200sin (50t + 30о)В, |
|||
|
R = 30 Ом; L = 0,5 Гн. |
|||
|
Ответ: i |
= 5,1sin (50t −9о) |
+ 0,8e−60t А. |
|
|
L |
|||
|
Задача9 |
|||
|
Найти |
закон изменения |
тока iL (рис. |
5.13), если U =100 В, |
|
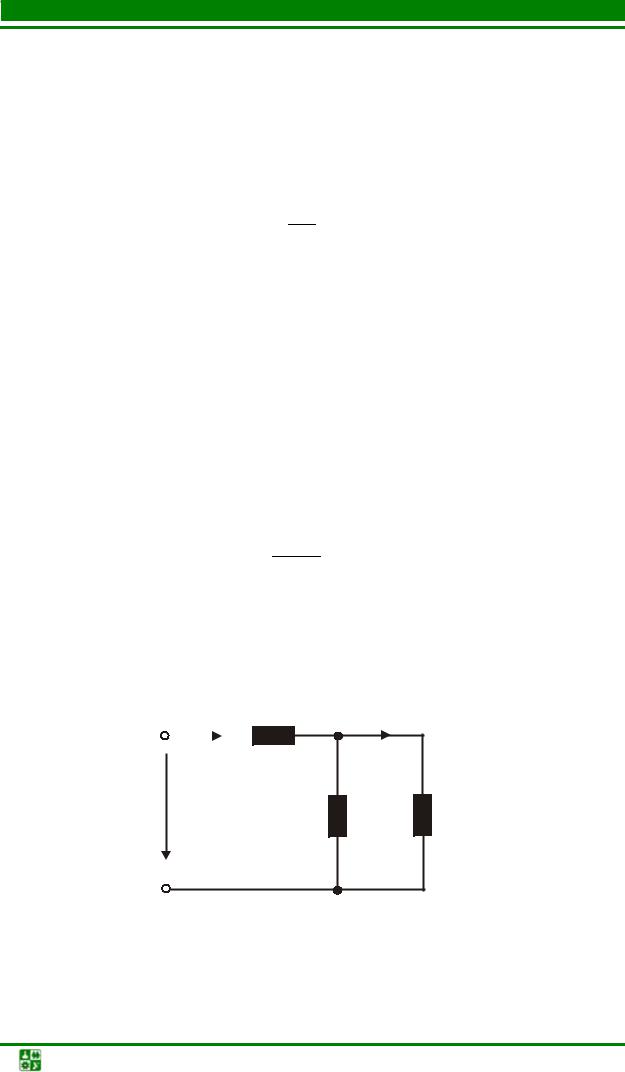
R = R1 = R2 =10 Ом, L = 2 Гн. Построить график. |
|||
|
R |
iL |
||
|
U |
L |
||
|
R 2 |
R |
||
|
Рис. 5.13 |
|
Теоретические основы электротехники. Практикум |
-250- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
Решение
1. Составим систему уравнений электрического состояния. После коммутации, которая заключается в размыкании ключа, схема становится одноконтурной, поэтому можно записать только одно уравнение по второму закону Кирхгофа
R1iL + L dditL + RiL =U .
2. Закон изменения тока iL ищем как сумму двух слагаемых:
iL = iL пр +iL св.
3. Току iL пр оказывают сопротивление два резистора внешнего контура, так как вместо индуктивного элемента – «закоротка». Поэтому
|
принужденная составляющая тока iL пр = |
U |
= |
100 |
=5 А. |
|||
|
R + R |
20 |
||||||
|
4. Составляющая тока i |
1 |
= Aept . |
|||||
|
меняется по закону экспоненты: i |
L св |
||||||
|
L св |
4.1. Характеристическое уравнение R1 + Lp + R = 0 дает решение:
p= − R1 L+ R = −10 c−1 .
4.2.Определим постоянную интегрирования А.
В начальный момент времени iL (0+) = iL пр(0+) + iL св(0+) .
По первому закону коммутации iL (0+) = iL (0−) . Схема до коммутации представлена на рис. 5.14.
|
R1 |
|||||
|
i |
R1 |
i |
|||
|
(0(0––) |
(0–) |
||||
|
L |
L |
– |
|||
Рис. 5.14
Сделаем расчет методом эквивалентных преобразований. Эквивалентное сопротивление
|
Теоретические основы электротехники. Практикум |
-251- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
|
R |
= R |
+ |
R2 R |
=15 Ом. |
|
э |
1 |
R2 + R |
||
|
Ток в свернутой схеме |
i1(0−) = U =100 ≈ 6,67 А. Rэ 15
Сопротивления R2 и R равны по величине, поэтому ток iL (0−) = 12 i1 (0−) = 3,335 A ≈ 3,34 А.
Составляющая тока iL пр(0+) = 5 А. Свободная составляющая в начальный момент iL св(0+) = A .
После подстановки получим
3,34 =5 + A.
Отсюда A = −1,66 A . Тогда закон изменения тока
iL = 5 −1,66e−10t А.
График тока iL получаем как сумму составляющих iLпр и iL св
(рис. 5.15).
|
iL , A |
iLпр |
|
|
5 |
||
|
3,34 |
t
iLсв
–1,66
Рис. 5.15
Задачи 10–12 решите для самоконтроля.
|
Теоретические основы электротехники. Практикум |
-252- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
Задача10
Найти начальные значения тока iL (0+) , напряжений uR (0+) и uL (0+)
(рис. 5.8), если U = 25 В, R =10 Ом, L =1 Гн.
Ответ: iL (0+) = 0 ; uR (0+) = 0 ; uL (0+) = 25 В.
Задача11
Найти принужденные составляющие тока iLпр , напряжений uR пр и
uL пр (рис. 5.8), если U = 30 В; R =10 Ом; L =1 Гн. Ответ: iL пр = 3 А, uR пр = 30 В, uL пр = 0 .
Задача12
За какое время переходный процесс в цепи, схема замещения которой представлена на рис. 5.8, практически закончится, если U =100 В; R =1 Ом; L =1 Гн.
Ответ: tпп = (3 −5) с.
Занятие2
Цели занятия:
1.Ознакомиться с вариантами нахождения мгновенных значений электрических величин, не подчиняющихся законам коммутации.
2.Научиться вычислять корень характеристического уравнения в разветвленных цепях с одним реактивным элементом.
3.Научиться определять зависимые начальные условия (ЗНУ) в схемах, составленных с учетом нулевых независимых начальных условий
(ННУ).
4.Научиться определять ЗНУ в схемах, составленных с учетом ненулевых ННУ.
Возможны два варианта решения.
Вариант 1 Если в условии задачи требуется найти закон изменения величины, не
подчиняющейся законам коммутации, то сначала находим закон изменения величины, подчиняющейся законам коммутации, затем из системы уравнений электрического состояния в дифференциальной форме – требуемую величину. При составлении системы рекомендуется выбирать уравнения, связывающие искомые величины с величинами, подчиняющимися законам коммутации.
|
Теоретические основы электротехники. Практикум |
-253- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
Вариант 2 Сразу ищем закон изменения требуемой по условию величины как
сумму принужденной и свободной составляющих.
Преподавателями курса ТОЭ разработаны приемы, позволяющие упростить нахождение постоянных интегрирования.
Рассмотрим алгоритм нахождения ЗНУ для схемы с одним реактивным элементом.
1.В схеме при t =0– находим ННУ: iL (0−) и uÑ (0−) .
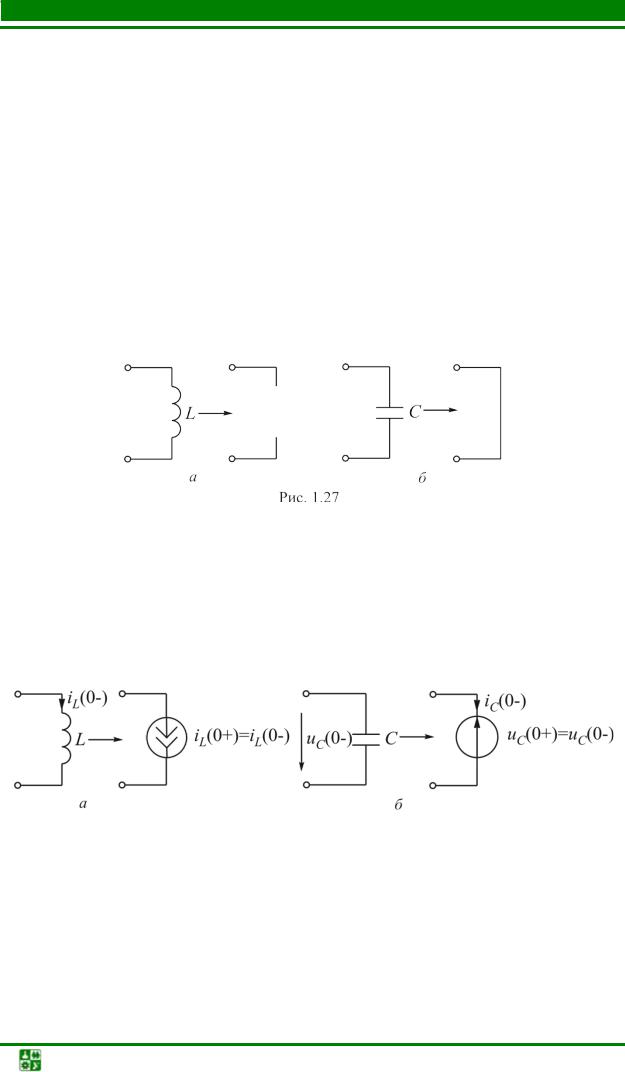
2.В схеме при t =0+ вычисляем ЗНУ. Схему составляем с учетом ННУ, которые могут быть нулевыми и ненулевыми.
|
Если |
iL (0+) = iL (0−) = 0 , то |
вместо |
индуктивного элемента можно |
|
изобразить |
разрыв цепи (рис. |
5.16, а). |
Если uC (0+) = uC (0−) = 0 , то |
емкостный элемент можно заменить «закороткой» (рис. 5.16, б).
|
Рис. 5.16 |
|||||||||||||||||
|
Если |
iL (0+) = iL (0−) ≠ 0 , |
индуктивный |
элемент |
заменяем |
|||||||||||||
|
то |
|||||||||||||||||
|
источником |
тока |
с током iL (0−), |
направления |
которых |
совпадают |
||||||||||||
|
(рис. 5.17, а). |
Если |
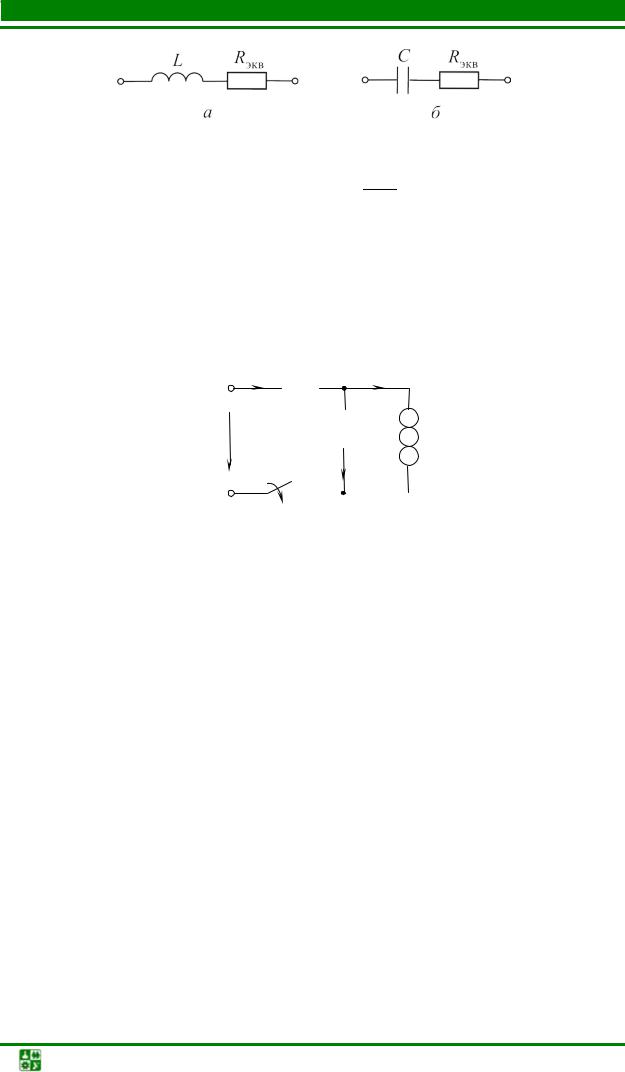
uC (0+) = uC (0−) ≠ 0, |
то емкостный элемент |
заменяют |
|||||||||||||
|
источником ЭДС с ЭДС, равной uC (0−) . |
Направления их противоположны |
||||||||||||||||
|
(рис. 5.17, б). |
|||||||||||||||||
|
Условно-положительные направления uC и iC совпадают. |
|||||||||||||||||
|
(0–) |
|||||||||||||||||
|
(0–) |
|||||||||||||||||
|
(0–) |
(0–) |
||||||||||||||||
|
(0–) |
|||||||||||||||||
Рис. 5.17
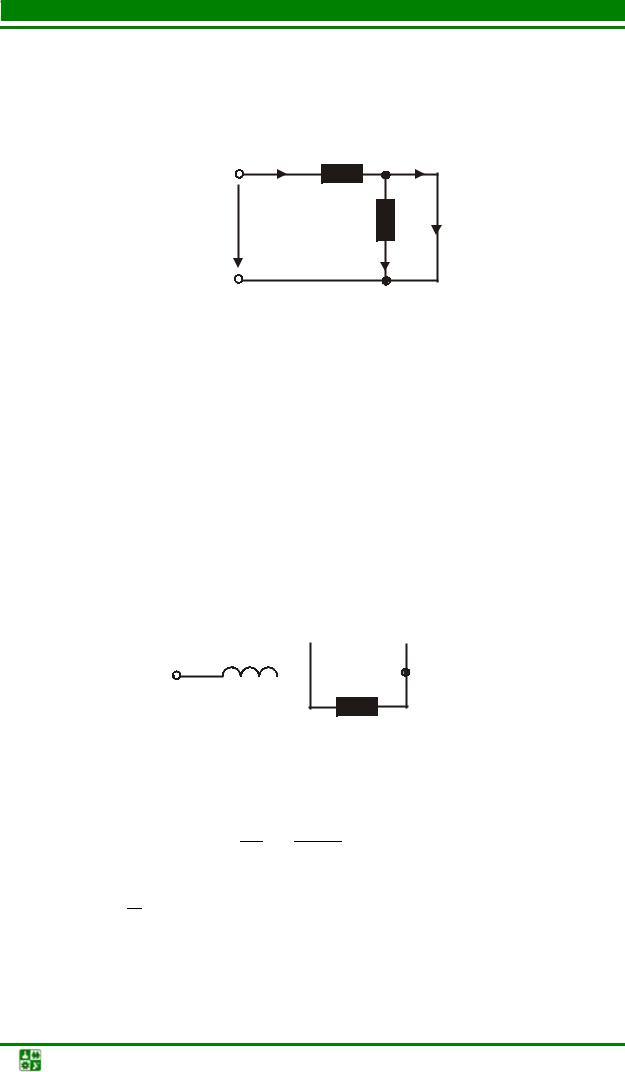
Для вычисления корня характеристического уравнения в схеме с одним реактивным элементом проще всего заменить разветвленную цепь эквивалентной ей одноконтурной. Для этого источники ЭДС закорачиваем, источники тока разрываем, разрываем также ветвь с реактивным элементом и заменяем все резисторы одним с эквивалентным сопротивлением. Схема превращается в последовательное соединение (рис. 5.18, а и б).
|
Теоретические основы электротехники. Практикум |
-254- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
Рис. 5.18
Для схемы рис. 5.18, а корень p = − RLэкв , для схемы рис. 5.18, б –
|
p = − |
1 |
. |
|||||||||||
|
R |
C |
||||||||||||
|
экв |
Задача1 |
||||||||||||
|
Найти закон изменения тока i |
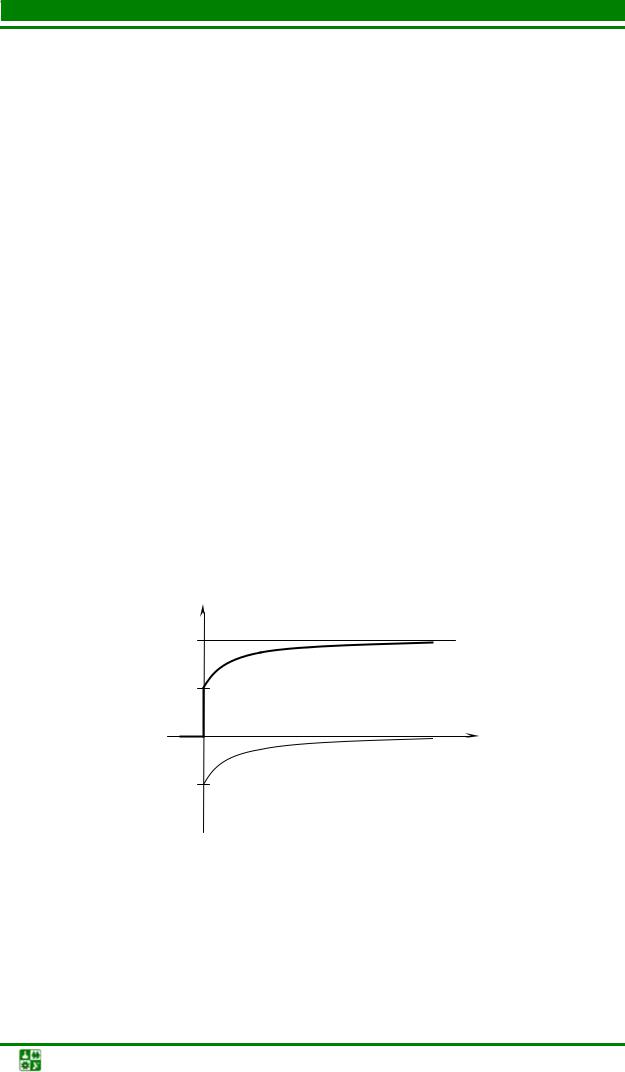
(рис. 5.19), если U =100 В, R = 4 Ом, |
||||||||||||
|
L = 4 мГн. |
|||||||||||||
|
i |
R |
i2 |
|||||||||||
|
R |
|||||||||||||
|
L |
|||||||||||||
|
U |
|||||||||||||
|
i1 |
|||||||||||||
Рис.5.19
Решение
Вариант 1 1. Составим систему уравнений электрического состояния в
дифференциальной форме. При этом рекомендуется выбирать уравнения, связывающие искомые величины с величинами, подчиняющимися законам коммутации:
i −i1 −i2 = 0,
Ri + L ddit2 =U,
Ri + Ri1 =U.
2.Найдем закон изменения тока iL = i2 = i2пп +i2сс .
3.Вычислим принужденную составляющую при t = ∞, так как теоретически переходный процесс длится бесконечно долго. Цепь подключена к источнику постоянного напряжения. Индуктивное
|
Теоретические основы электротехники. Практикум |
-255- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
сопротивление X L = = Lω = 0, поэтому в схеме вместо индуктивного элемента будет «закоротка» (рис. 5.20).
Ток i1пр = 0, ток iпр =i2пр = UR =1004 = 25 А.
iпр R
i1пр
Рис. 5.20
4. Свободные составляющие в схемах с одним реактивным элементом изменяются по закону экспоненты:
i2св = Аept .
4.1. Найдем показатель степени р – корень характеристического
уравнения. Разработаны разные способы составления характеристического уравнения. При наличии одного реактивного элемента проще всего перейти к схеме одноконтурной. Для этого источники ЭДС закорачиваем, источники тока разрываем и разрываем ветвь с реактивным элементом (рис. 5.21). Все
резисторы заменяем одним с эквивалентным сопротивлением Rэ = R2 = 2 Ом.
R
L 

 R
R 

Рис. 5.21
В неразветвленной RL-цепи
р = − RLэ = − 2 104 3 = −500 c−1 .
Cкорость протекания переходного процесса характеризуют постоянной времени τ = − 1p . Через промежуток времени, равный τ, свободные
составляющие уменьшаются в e раз. Практически переходный процесс в цепи можно считать законченным через время (3 −τ4) .
|
Теоретические основы электротехники. Практикум |
-256- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
4.2. Постоянную интегрирования А найдем из начальных условий с использованием законов коммутации.
При t =0+ iL (0+) = i2 (0+) = i2пп(0+) + i2сс (0+).
По первому закону коммутации ток в индуктивной катушке не может измениться скачком. До коммутации цепь была разомкнута. Следовательно,
i2 (0+) = i2 (0−) = 0.
Принужденная составляющая является постоянной величиной, поэтому i2пп(0+) = 25А. Свободная составляющая тока сразу после коммутации
|
i2сс(0+) = A. После подстановки получаем: |
0 = 25 + A, откуда A = −25A. |
||||||||||||
|
Окончательное выражение закона изменения тока i2 |
имеет вид |
||||||||||||
|
i |
= 25 − 25e−500t |
А. |
|||||||||||
|
2 |
|||||||||||||
|
5. Ищем закон изменения тока i |
из уравнения |
Ri + L |
di2 |
=U . Отсюда |
|||||||||
|
dt |
|||||||||||||
|
U − L |
di2 |
100 −4 |
10−3( −500 )( |
− 25e−500t ) |
|||||||||
|
i = |
dt |
= |
= |
||||||||||
|
R |
4 |
||||||||||||
|
=100 − 4 12,5e−500t = 25 − |
12,5e−500 t А. |
||||||||||||
|
4 |
|||||||||||||
|
График изменения тока представлен на рис. 5.22. |
|||||||||||||
|
i, А |
iпр |
||||||||||||
|
25 |
i
12,5
t
iсв
-12,5
Рис. 5.22
Вариант 2
1. Ищем закон изменения тока i как сумму принужденной и свободной составляющих:
i = iпр + iсв.
|
Теоретические основы электротехники. Практикум |
-257- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
2.Найдем iпр (см. вариант 1, п. 3): iпр = 25 А.
3.Свободная составляющая меняется по закону экспоненты:
iсв = Bept .
Вычислим показатель степени p (см. вариант 1, п. 4.1):
p = −500 c−1.
Постоянную интегрирования В найдем из начальных условий с
|
использованием |
законов |
коммутации: i(0+) = iпр(0+) + iсв(0+) . |
Значение |
|
тока i(0+) – зависимое начальное условие, которое ищем в два этапа. |
|||
|
Этап 1. В |
схеме |
при t =0– определяем независимые |
начальные |
|
условия: |
iL (0−) = 0.
Этап 2. В схеме при t =0+, которую составляем с учетом независимых
|
начальных условий, определяем i(0+). Ток |
i2 (0+) = i2 (0−) = 0 . Место, где |
||||
|
нет тока, можно изобразить как разрыв цепи (рис. 5.23). |
|||||
|
i(0+) |
R |
||||
|
U |
R |
||||
|
Рис. 5.23 |
||||
|
Ток |
i( 0 + ) = |
U |
=12,5 А. |
|
|
2R |
||||
|
При |
||||
|
t =0+ составляющие тока iпр(0+) = 25А,iсв(0+) = B . |
После подстановки получаем: 12,5 = 25 + Â , откуда Â = −12,5 . Окончательное выражение закона изменения тока i :
i = 25 −12,5e−500t А.
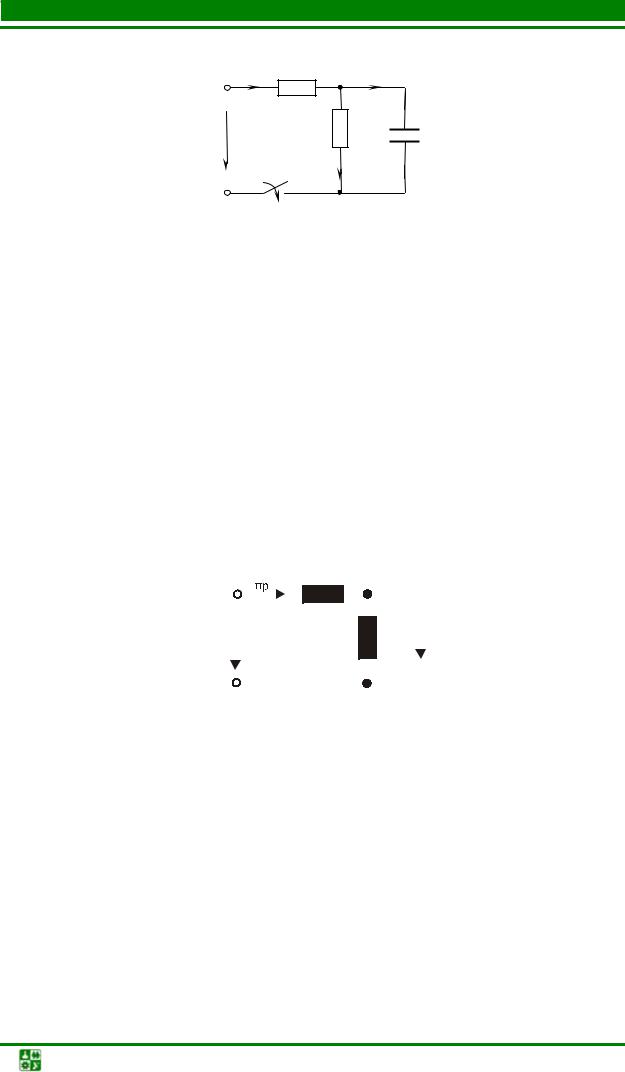
Задача2
Найти закон изменения тока i в схеме (рис. 5.24), если U = 50 В, R = R1 = 2Ом, Ñ = 5 мкФ.
|
Теоретические основы электротехники. Практикум |
-258- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
|
i |
R |
i2 |
|
|
U |
R |
С |
|
|
i1 |
Рис. 5.24
Решение
Вариант 1 1. Система уравнений электрического состояния в дифференциальной
форме:
|
i −i |
−i |
2 |
= 0, |
|||||||
|
1 |
=U, |
|||||||||
|
Ri + uC |
||||||||||
|
=U. |
||||||||||
|
Ri + R1i1 |
||||||||||
|
2. Ищем закон изменения величины, подчиняющейся законам |
||||||||||
|
коммутации: |
||||||||||
|
uC = uC пp + uC св. |
||||||||||
|
3. Вычислим принужденную составляющую uСпр при t = ∞. |
||||||||||
|
i |
R |
|||||||||
|
U |
uС пр |
|||||||||
|
R |
||||||||||
|
1 |
||||||||||
Рис. 5.25
Конденсатор постоянный ток не пропускает, поэтому вместо емкостного элемента в схеме будет разрыв (рис. 5.25).
|
Схема одноконтурная, ток |
в ней |
i = |
U |
= |
50 |
=12,5 |
А. |
|
|
R + R |
4 |
|||||||
|
пр |
||||||||
|
Напряжение uСпр = R1iпр = 2 12,5 = 25 В. |
1 |
|||||||
|
4. Свободная составляющая |
меняется |
по |
закону |
экспоненты: |
uСсв = Aept .
4.1.Ищем корень характеристического уравнения р. Закорачиваем
источник ЭДС, учтенный входным напряжением, разрываем ветвь с емкостным элементом (рис. 5.26).
|
Теоретические основы электротехники. Практикум |
-259- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
R
С
R 1
Рис. 5.26
Резисторы заменяем одним, с эквивалентным сопротивлением
|
R = |
R R1 |
=1 Ом. |
|
|
R + R |
|||
|
э |
|||
|
1 |
В неразветвленной RC-цепи
|
p = − |
1 |
= − |
106 |
= −2 105 с−1. |
|
R С |
5 |
|||
|
э |
Постоянную интегрирования А ищем из начальных условий с использованием второго закона коммутации. При t =0+
uС (0+) = uСпр(0+) + uСсв(0+) ; uС (0+) = uC (0−) .
До коммутации схема не была подключена к источнику энергии, поэтому uС (0−) = 0 . Принужденная составляющая является постоянной
величиной, поэтому uСпр(0+) = 25 В. Свободная составляющая напряжения на конденсаторе сразу после коммутации uС св(0+) = A.
После подстановки получаем: 0 = 25 + А, отсюда А = −25 В.
Тогда закон изменения напряжения uС во время переходного процесса имеет вид
|
u = 25 − 25e−2 105 t В. |
||||
|
С |
||||
|
5. |
Ищем закон изменения тока i |
из уравнения Ri +uС =U . |
||
|
Отсюда |
i = U −uС |
= |
50 − 25 + 25e−2 105 t |
=12,5 −12,5e−2 105 t А. |
|
R |
2 |
График изменения тока представлен на рис. 5.27.
|
Теоретические основы электротехники. Практикум |
-260- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
i, А
25
i
t
Рис. 5.27
Вариант 2
1.Ищем закон изменения тока как сумму принужденной и свободной составляющих:
i= iпр + iсв.
2.Найдем iпр (см. вариант 1, п. 3): iпр =12,5 А.
3.Свободная составляющая меняется по закону экспоненты:
iсв = Be pt .
3.1. Вычислим показатель степени p (см. вариант 1, п. 4.1):
p= −2 105 c−1.
3.2.Постоянную интегрирования ищем из начальных условий с использованием законов коммутации:
i(0+) = iпр(0+) +iсв(0+) .
Значение тока i(0+) – зависимое начальное условие, которое ищут
в два этапа.
Этап 1. В схеме при t =0– определим независимое начальное условие
(см. вариант 1, п. 4.2):
uС (0−) = 0 .
Этап 2. В схеме при t =0+, которую составляем с учетом независимых начальных условий, определяем i(0+). Напряжение uC (0+) = uC (0−) = 0 ,
поэтому вместо емкостного элемента будет «закоротка» (рис. 5.28).
|
Теоретические основы электротехники. Практикум |
-261- |
|
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ |
||||||
|
i(0+) |
R |
|||||
|
U |
R1 |
|||||
|
Рис.5.28 |
||||||
|
Ток от источника будет замыкаться по пути наименьшего |
||||||
|
сопротивления, т. е. по «закоротке», следовательно, ток |
i(0+) = U |
= |
50 |
= 25 |
||
|
R |
2 |
|||||
|
А. При t =0+ составляющие тока iпр(0+) =12,5 А, iсв(0+) = В. |
||||||
|
После подстановки получаем: 25 =12,5 + В, |
отсюда В =12,5 А. |
|||||
|
Ток i меняется по закону: |
i =12,5 +12,5e−2 105 t А.
|
Решите самостоятельно задачу 3. |
||
|
Задача3 |
||
|
Найти закон изменения тока i1 |
в схеме (рис. 5.29), если U = 50 В, |
|
|
R = R1 = 2 Ом, С = 2 мкФ. |
||
|
R |
||
|
U |
R1 |
С |
|
i1 |
Рис. 5.29
Ответ: i1 =12,5 −12,5e−5 105 t А.
Задача4
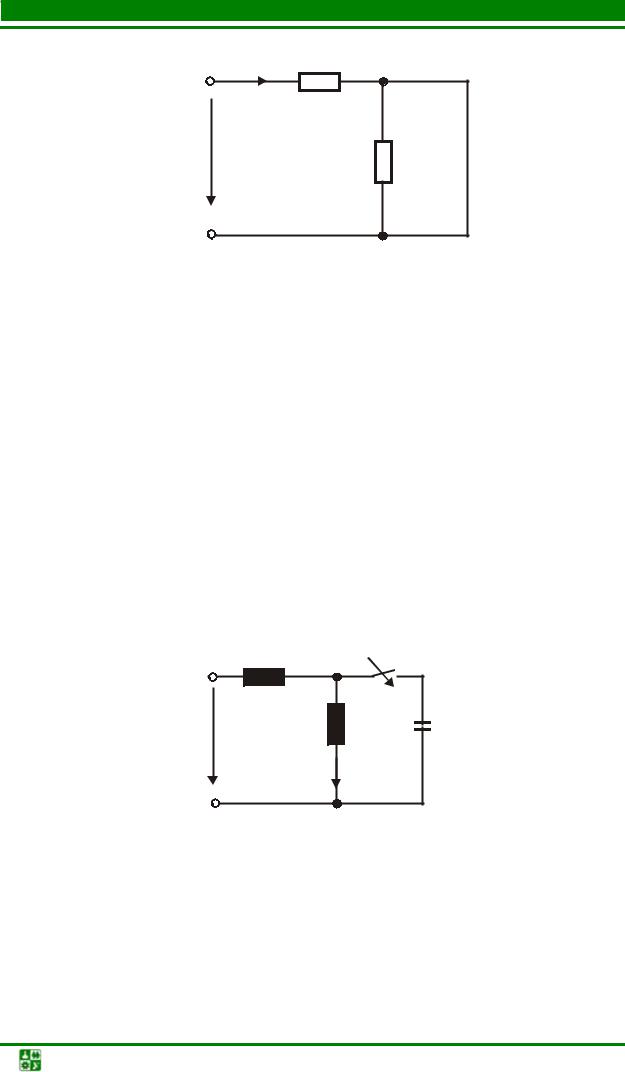
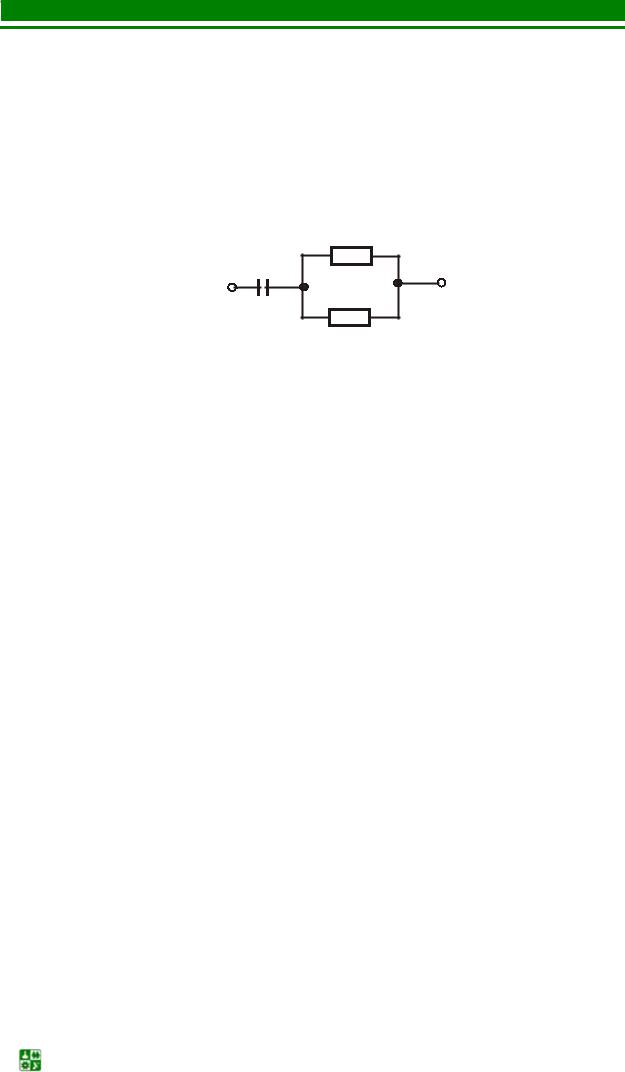
Найти закон изменения тока i в схеме (рис. 5.30), если U = 50 В, R =10 Ом, С =1 мкФ.
|
Теоретические основы электротехники. Практикум |
-262- |
|
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ |
||||
|
Решение |
||||
|
Вариант 1 |
||||
|
1. Система уравнений электрического состояния в дифференциальной |
||||
|
форме: |
R |
|||
|
i |
||||
|
U |
С |
R |
||
|
i1 |
i2 |
|||
|
Рис. 5.30 |
||||
|
i −i |
−i |
= 0, |
||
|
1 |
2 |
|||
|
=U, |
||||
|
Ri +uC |
||||
|
=U. |
||||
|
Ri + Ri2 |
||||
|
2. Ищем закон изменения величины, подчиняющейся законам |
||||
|
коммутации: |
||||
|
uC = uC пp + uC св. |
3. Вычислим принужденную составляющую uСпр при t = ∞.
Конденсатор постоянный ток не пропускает, поэтому вместо емкостного элемента в схеме будет разрыв (рис. 5.31).
Рис. 5.31
|
Теоретические основы электротехники. Практикум |
-263- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
|
Схема одноконтурная, ток в ней |
i |
= |
U |
= |
50 |
= 2,5 А. |
Напряжение |
|
|
2R |
20 |
|||||||
|
uСпр = Riпр =10 2,5 = 25 В. |
пр |
|||||||
|
4. Свободная составляющая |
меняется |
по |
закону |
экспоненты: |
uСсв = Aept .
4.1. Ищем корень характеристического уравнения р. Закорачиваем источник ЭДС, разрываем ветвь с емкостным элементом (рис. 5.32).
R
С
R
Рис. 5.32
|
Резисторы заменяем |
одним |
с |
эквивалентным |
сопротивлением |
|||||
|
R |
= |
R = 5 Ом. |
|||||||
|
э |
2 |
||||||||
|
В неразветвленной RC-цепи |
|||||||||
|
p = − |
1 |
= − |
1 |
= −2 105 |
с−1 . |
||||
|
RэС |
5 10−6 |
||||||||
Постоянная времени τ= RэС .
4.2. Постоянную интегрирования А ищем из начальных условий с использованием второго закона коммутации. При t =0+
uС (0+) = uСпр(0+) +uСсв(0+) .
До коммутации тока в цепи не было, так как конденсатор постоянный
|
ток не пропускает. Из уравнения |
Ri(0−) +uС (0−) =U |
получаем uС (0−) = |
|||||||
|
=U = 50 B. Конденсатор был заряжен до величины входного напряжения. |
|||||||||
|
Принужденная составляющая является постоянной величиной, поэтому |
|||||||||
|
uСпр(0+) = 25 В. |
Свободная составляющая |
напряжения на конденсаторе |
|||||||
|
сразу после коммутации |
uС св(0+) = A. |
||||||||
|
После подстановки получаем: 50 = 25 + А, отсюда А = 25 В. |
|||||||||
|
Тогда закон изменения напряжения uС во время переходного процесса |
|||||||||
|
имеет вид |
uС = 25 + 25e−2 105 t В. |
||||||||
|
5. Ищем закон изменения тока i из уравнения Ri +uС =U . |
|||||||||
|
Отсюда i |
= |
U −uС |
= |
50 |
−25 −25e |
−2 105 t |
−2 105t |
А. |
|
|
R |
10 |
= 2,5 − 2,5e |
|||||||
|
|
Теоретические основы электротехники. Практикум |
-264- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
График изменения тока представлен на рис. 5.33.
|
i, А |
iпр |
|
2,5 |
|
|
i |
|
|
iсв |
|
|
– |
t |
|
Рис. 5.33 |
Вариант 2
1.Ищем закон изменения тока как сумму принужденной и свободной составляющих:
i= iпр + iсв.
2.Найдем iпр (см. вариант 1, п. 3): iпр = 2,5 А.
3.Свободная составляющая меняется по закону экспоненты:
iсв = Be pt .
3.1. Вычислим показатель степени p (см. вариант 1, п. 4.1):
p= −2 105 c−1.
3.2.Постоянную интегрирования ищем из начальных условий с использованием законов коммутации:
i(0+) = iпр(0+) + iсв(0+).
Значение тока i(0+) – зависимое начальное условие, которое ищут в два этапа.
Этап 1. В схеме при t =0– определяем независимые начальные условия
(см. вариант 1, п. 4.2):
uС (0−) =50 В.
Этап 2. В схеме при t =0+, которую составляем с учетом независимых
|
начальных условий, определяем i(0+). Напряжение |
uС(0+) =uС(0−) =50 B . |
|
Теоретические основы электротехники. Практикум |
-265- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
Известное напряжение можно учесть источником ЭДС такого же напряжения, направленным противоположно (рис. 5.34).
|
i(0+) |
R |
a |
||||||||||||||||||||
|
Е |
uC (0+) |
R |
||||||||||||||||||||
|
b |
||||||||||||||||||||||
|
Рис. 5.34 |
||||||||||||||||||||||
|
Напряжение uаb(0+) =uС(0+) = E − Ri(0+) . |
||||||||||||||||||||||
|
Отсюда |
i(0+) = |
E −uС (0+) |
= |
50 −50 |
= 0 . При t = |
0+ составляющие тока |
||||||||||||||||
|
R |
10 |
|||||||||||||||||||||
|
iпр(0+) = 2,5 A, |
iсв(0+) = B . |
|||||||||||||||||||||
|
После подстановки получаем: 0 = 2,5 + В, откуда B = −2,5 А. |
||||||||||||||||||||||
|
Ток i меняется по закону: |
||||||||||||||||||||||
|
i = 2,5 −2,5e−2 105 t А. |
||||||||||||||||||||||
|
Задача5 |
||||||||||||||||||||||
|
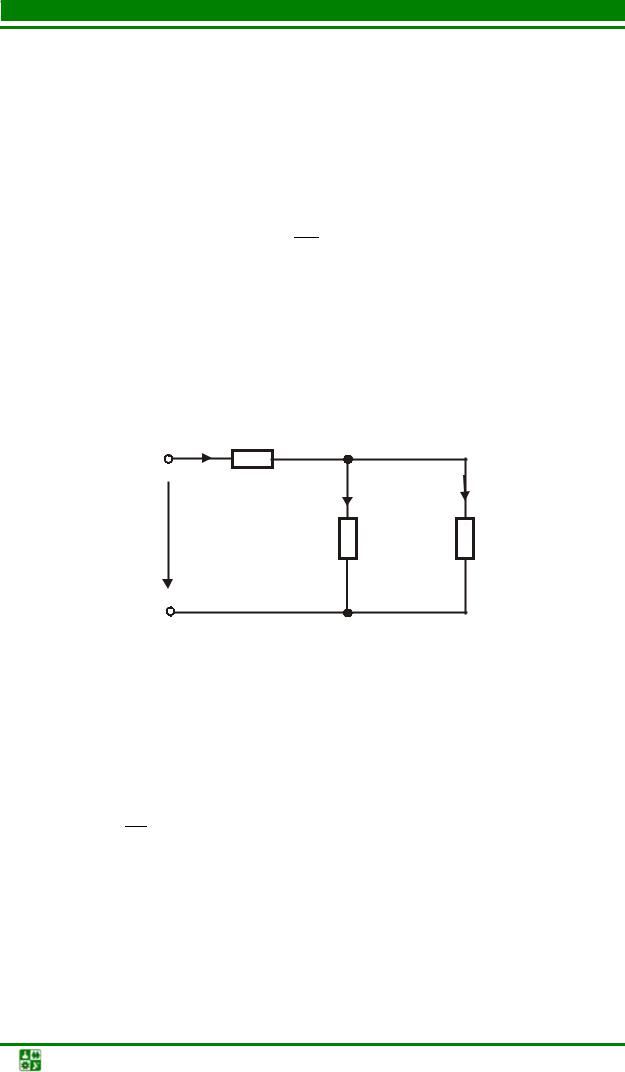
Найти закон изменения тока i2 |
в схеме рис. 5.35, если U =100 В, R = 8 |
|||||||||||||||||||||
|
Ом, R1 = 20 Ом, R2 = 30 Ом, L = 2 Гн.. |
||||||||||||||||||||||
|
R |
i |
i2 |
||||||||||||||||||||
|
i1 |
||||||||||||||||||||||
|
U |
R1 |
R2 |
||||||||||||||||||||
|
L |
||||||||||||||||||||||
Рис. 5.35
Решение
|
Теоретические основы электротехники. Практикум |
-266- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
Вариант 1 1. Составим систему уравнений электрического состояния в
дифференциальной форме, включая в нее уравнение, связывающее искомую величину (ток i2 ) с величиной, подчиняющейся закону
коммутации (током i1):
R1i1
i −i1 −i2 = 0;
+ L ddit1 − R2i2 = 0; Ri + R2i2 =U.
2.Ищем закон изменения тока i1 = i1пр +i1св.
3.Вычислим принужденную составляющую при t = ∞, так как теоретически переходный процесс длится бесконечно долго. Цепь подключена к источнику постоянного напряжения, поэтому вместо индуктивного элемента будет «закоротка» (рис. 5.36).
|
iпр |
R |
|
|
i1пр |
i 2пр |
|
|
U |
R 1 |
R2 |
Рис. 5.36
Воспользуемся методом эквивалентных преобразований. Эквивалентное сопротивление
|
R |
= R + |
R1 R2 |
=8 + |
20 30 |
= 20 Ом. |
|
э |
R1 |
+ R2 |
20 +30 |
||
Ток iпр = U =100 =5 А.
Rэ 20
Ток i1пр можно вычислить по формуле для определения тока в одной из двух пассивных параллельных ветвей:
|
i1пр = |
R2 |
iпр = |
30 |
5 = 3 А. |
|
|
R + R |
50 |
||||
|
1 |
2 |
|
Теоретические основы электротехники. Практикум |
-267- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
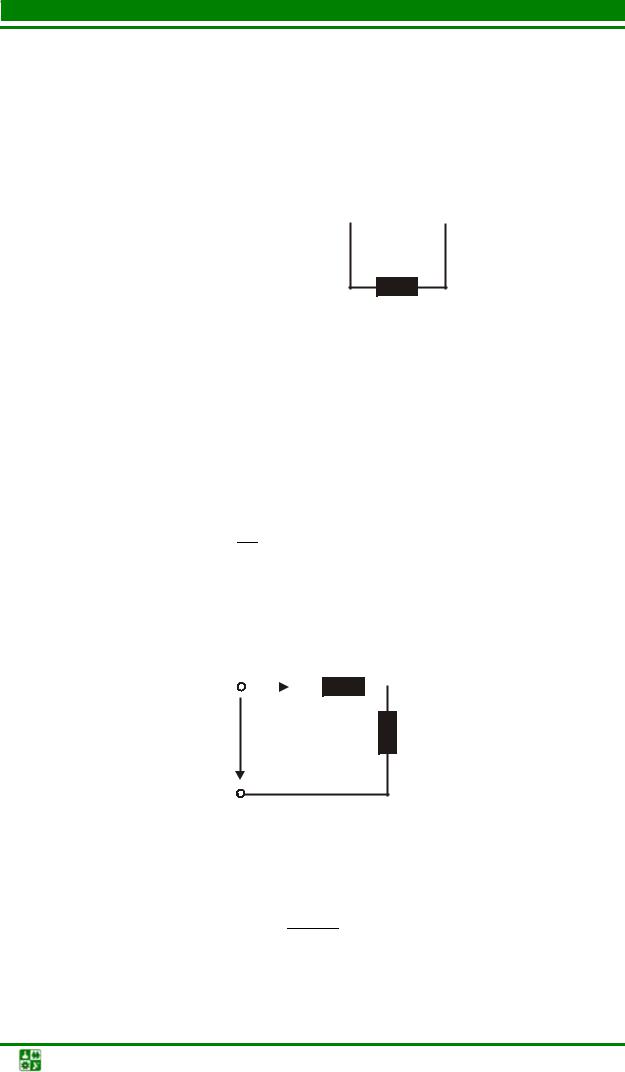
По первому закону Кирхгофа ток i2пр = iпр −i1пр = 5 −3 = 2 А. 4. Свободная составляющая i1св = Аерt .
4.1. Для нахождения показателя степени р перейдем к одноконтурной схеме. Закоротим источник ЭДС, разорвем ветвь с индуктивным элементом
(рис. 5.37).
R
L R 1 


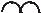




 R2
R2 


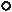
Рис. 5.37
Эквивалентное сопротивление этой схемы
|
R |
= R + |
R1 R2 |
= 20 + |
8 30 |
= 26,32 Ом. |
|
|
8 +30 |
||||||
|
э |
1 |
R |
+ R |
|||
|
1 |
2 |
Внеразветвленной RL-цепи
р= − RLэ = − 26,322 = −13,16 c−1 .
|
4.2. Постоянную интегрирования А |
ищем из начальных условий |
|||
|
с использованием законов коммутации. |
||||
|
При t =0+ i1(0+) = i1пр(0+) +i1св(0+). |
||||
|
i(0-) |
R |
|||
|
U |
R1 |
 i1(0-)
i1(0-)
Рис. 5.38
По первому закону коммутации i1(0+) =iL (0+) =iL (0−) . Найдем ток i1(0−) в схеме при t = 0 − (рис. 5.38). Схема одноконтурная, поэтому
i1(0−) =i(0−) = R U+ R1 =10028 =3,57 А.
|
Теоретические основы электротехники. Практикум |
-268- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
Принужденная составляющая является постоянной величиной, поэтому i1пр(0+) = 3 А. Свободная составляющая тока i1св(0+) = А. После подстановки
получим уравнение
3,57 = 3 + А.
Отсюда А= 0,57 .
Ток i1 меняется по закону:
|
i = 3 + 0,57e−13,16t |
А. |
||||||||
|
1 |
|||||||||
|
5. Ищем закон изменения тока i |
из уравнения |
R i + L |
di1 |
− R i = 0. |
|||||
|
2 |
1 1 |
dt |
2 2 |
||||||
|
R i |
+ L di1 |
||||||||
|
Отсюда i = |
1 1 |
dt |
= 20(3 + 0,57e−13,16t ) + 2(−13,16)0,57e−13,16t |
= |
|||||
|
2 |
R2 |
30 |
|||||||
|
= 60 +11,4e−13,16t −15e−13,16t |
= 2 |
−0,12e−13,16t А. |
|||||||
|
30 |
Вариант 2
1. Ищем закон изменения тока i2 как сумму принужденной и свободной составляющих:
i2 = i2 пр +i2 св .
2.Вычислим i2 пр (см. вариант 1, п. 3): i2 пр = 2 А.
3.Свободная составляющая меняется по закону:
i2св = Веpt .
3.1.Найдем показатель степени р (см. вариант 1, п. 4.1):
р= −13,16с−1 .
3.2.Постоянную интегрирования В найдем из начальных условий с использованием первого закона коммутации:
i2 (0+) = i2 пр(0+) +i2 св(0+).
Значение тока i2 (0+) – зависимое начальное условие, которое ищут в два этапа.
|
Теоретические основы электротехники. Практикум |
-269- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
Этап 1. В схеме при t =0– определим независимое начальное условие ток i1(0−) (см. вариант 1, п. 4.2):
i1(0−) =3,57 А.
Этап 2. В схеме при t =0+, составленной с учетом независимого начального условия, ищем ток i2 (0+) . В индуктивном элементе есть ток,
поэтому вместо него – источник тока, совпадающий по направлению с i1(0−) .
Известное напряжение можно учесть источником ЭДС такого же напряжения, направленным противоположно (рис. 5.39).
 i1(0+)
i1(0+) 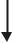 i2(0+)
i2(0+)
b
Рис. 5.39
Наиболее рационально вычислить ток i2 (0+) методом напряжения между двумя узлами. Напряжение
|
Uab (0+) = |
E −i |
(0+) |
100 |
−3,57 |
= |
8,93 = 56,52 В. |
||||||||||||
|
R |
1 |
= |
8 |
|||||||||||||||
|
1 |
+ |
1 |
1 |
1 |
0,158 |
|||||||||||||
|
+ |
||||||||||||||||||
|
R |
R |
8 |
30 |
|||||||||||||||
|
Uab (0+) |
2 |
|||||||||||||||||
|
Ток i |
(0+) = |
= 56,52 = |
1,88 А. |
|||||||||||||||
|
2 |
R2 |
30 |
||||||||||||||||
|
Принужденная |
составляющая |
тока |
i2 пр(0+) = 2А. Свободная |
|||||||||||||||
|
составляющая i2 св(0+) = В. После подстановки получим |
||||||||||||||||||
|
Отсюда В = −0,12 . |
1,88 = 2 + В. |
|||||||||||||||||
|
имеет вид |
||||||||||||||||||
|
Тогда закон изменения тока i2 |
i2 = 2 −0,12е−13,16t .
|
Теоретические основы электротехники. Практикум |
-270- |
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
|
Задачи 6–13 решите для самоконтроля. |
|||
|
Задача6 |
|||
|
Вычислить начальные значения токов iL (0+) , |
i1 (0+) , i2 (0+) |
в схеме |
|
|
рис. 5.41, если U = 40 В, R1 = R2 = 20 Ом, L = 2 Гн. |
|||
|
Ответ: iL (0+) = 2 А, i1 (0+) =1 А, i2 (0+) =1 А. |
|||
|
Задача7 |
|||
|
Вычислить принужденные составляющие токов iL пр , i1пр , i2 пр |
в схеме |
||
|
рис. 5.40, если U = 40 В, R1 = R2 = 20 Ом, L = 2 Гн. |
|||
|
iL |
L |
||
|
U |
R1 |
R |
|
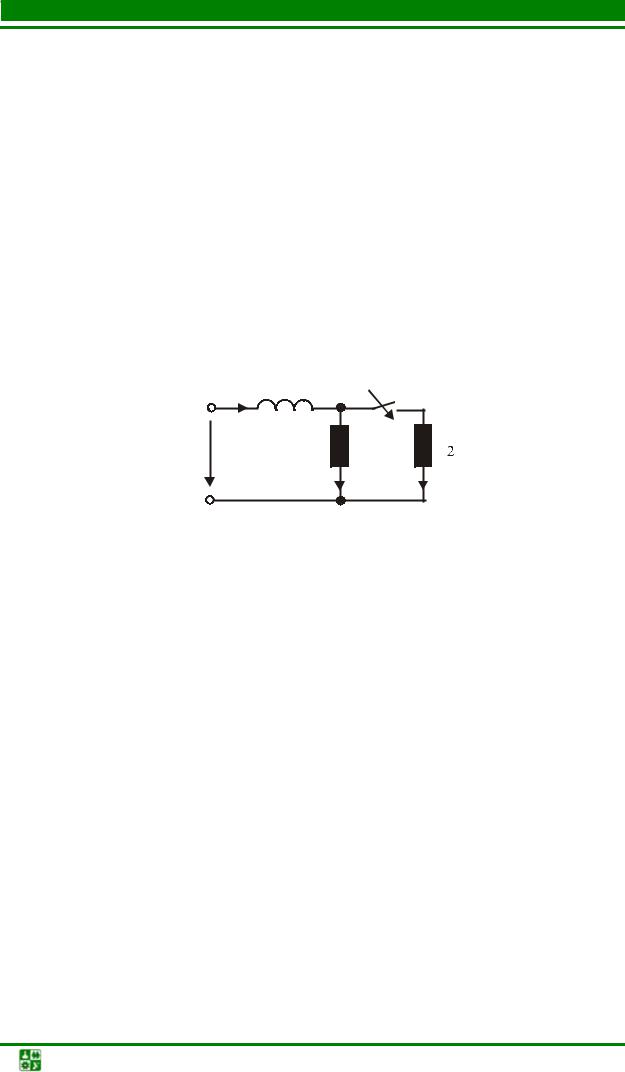
|
i1 |
i2 |
||
|
Рис. 5.40 |
Ответ: iL пр = 4 А, i1пр = 2 А, i2 пр = 2 А.
Задача8
Определить длительность переходного процесса в схеме задачи 6.
Ответ: tпп = (0,6 −1) с.
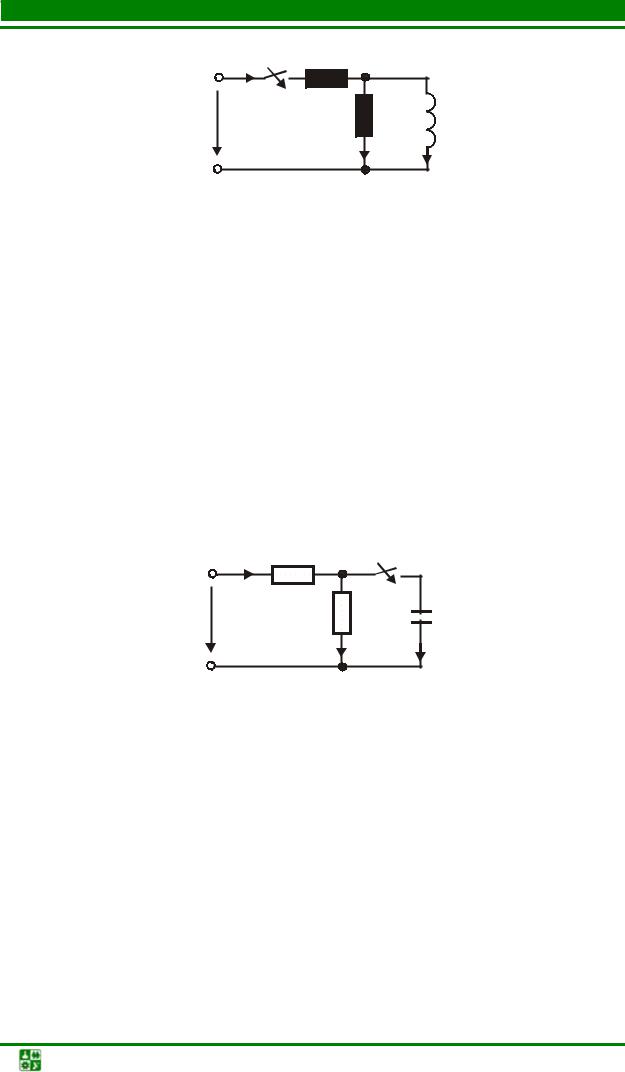
Задача9
Вычислить принужденные составляющие токов i пр , i1пр , iL пр и напряжения uL пр в схеме рис. 5.41, если U = 40 В, R = R1 =10 Ом, L = 5 Гн.
|
Теоретические основы электротехники. Практикум |
-271- |
|
ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ |
||
|
i |
R |
|
|
U |
R1 |
L |
|
i1 |
iL |
|
|
Рис. 5.41 |
||
|
Ответ: i пр = 4 А, i1пр = 0, iL пр = 4 А, uL пр = 0 . |
Задача10
|
Определить |
начальные |
значения |
токов |
i(0+), |
i1(0+) , |
iL (0+) |
и |
|
напряжение uL (0+) для схемы задачи 9. |
|||||||
|
Ответ: i(0+) = 2 А, i1(0+) = 2 А, iL (0+) = 0, |
uL (0+) = 20 В. |
||||||
|
Задача11 |
|||||||
|
Найти принужденные составляющие токов iпр, i1пр , |
iСпр и напряжения |
||||||
|
uC пр в схеме рис. 5.42, если U =100 В, R = R1 = 50 Ом, C = 4 мкФ. |
|||||||
|
i |
R |
||||||
|
U |
R1 |
С |
|||||
|
i1 |
iС |
||||||
|
Рис. 5.42 |
|||||||
|
Ответ: iпр =1 А, i1пр =1 А, iСпр = 0 , uC пр = 50 В. |
|||||||
|
Задача12 |
|||||||
|
Вычислить |
начальные |
значения |
токов |
i(0+), |
iС (0+) , |
i1(0+) |
и |
напряжения uC (0+) в схеме рис. 5.43, если U = 40 В, R = R1 = 20 Ом, C =1 мкФ.
|
Теоретические основы электротехники. Практикум |
-272- |

ГЛАВА 5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
|
i |
R |
|
|
U |
С |
R1 |
|
i |
i1 |
|
|
С |
Рис. 5.43
Ответ: i(0+) = 0 , iС (0+) = −2 А, i1(0+) = 2 А, uC (0+) = 40 В.
Задача13
Определить практическую длительность переходного процесса для схемы на рис. 5.43.
Ответ: tпп = (3 10−5 −5 10−5 ) с.
|
Теоретические основы электротехники. Практикум |
-273- |

ГЛАВА 6 НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ПОСТОЯННОГО ТОКА
Занятие1
Цели занятия:
1.Научиться находить рабочую точку графическим методом в неразветвленной цепи с одним нелинейным элементом.
2.Научиться находить рабочую точку графическим методом в разветвленной цепи с одним нелинейным элементом.
3.Научиться находить рабочую точку графическим методом в разветвленной цепи с несколькими нелинейными элементами.
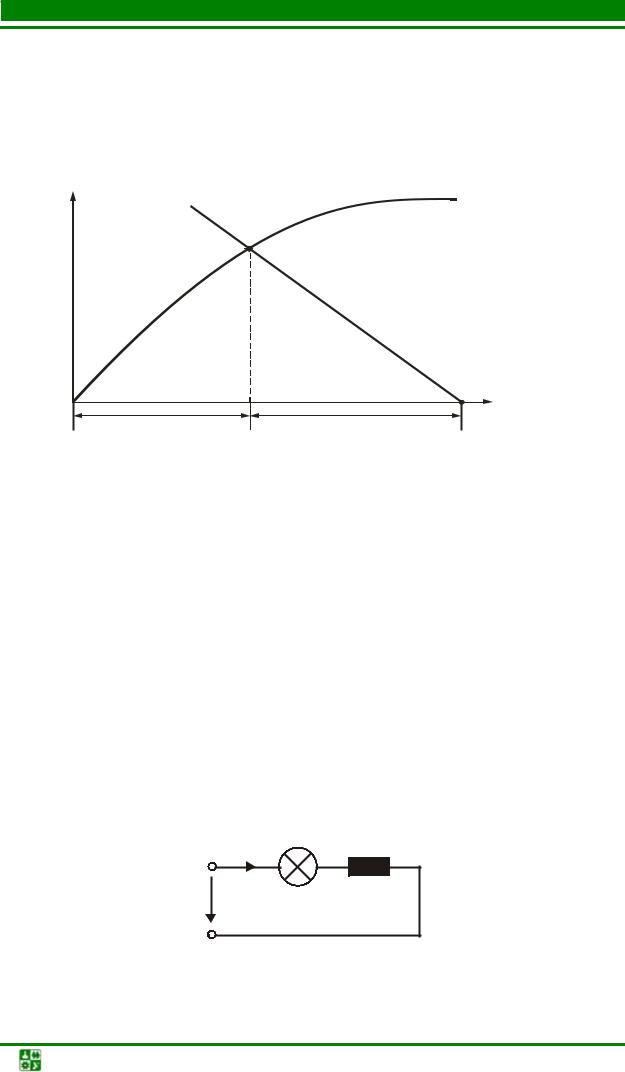
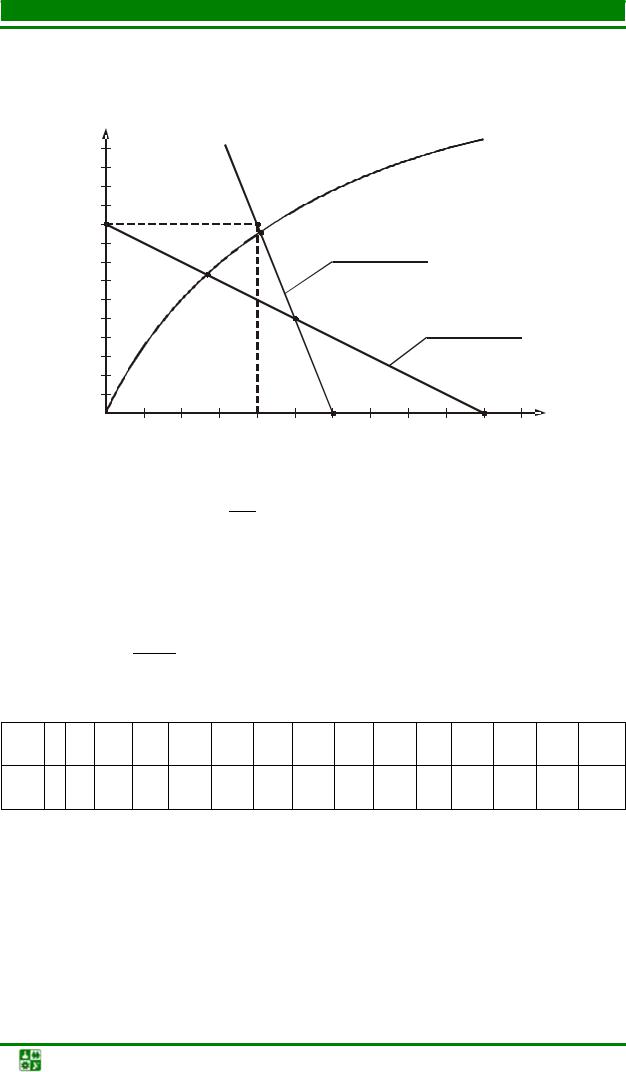
Для цепи с двумя последовательно соединенными элементами, один из которых – линейный (рис. 6.1), рационально отыскание рабочей точки на пересечении вольт-амперной характеристики (ВАХ) нелинейного элемента (НЭ) с зеркальным отображением ВАХ линейного элемента.
|
I |
НЭ1 |
R |
||||||||
|
U |
U 1 |
U 2 |
||||||||
|
Рис. 6.1 |
||||||||||
|
Решение этим методом поясняет рис. |
6.2. Строим ВАХ НЭ I(U1). В |
|||||||||
|
рабочей точке на основании |
второго |
закона Кирхгофа |
напряжение |
|||||||
|
U1 =U −U2 . Построим график |
I(U −U2 ), |
который является |
зеркальным |
отображением графика I(U2 ) , смещенного вправо на величину входного
напряжения U . Так как ВАХ линейного элемента является прямой линией, то для построения графика I(U −UЛЭ) нужны только две точки, одна из
которых с координатами (U,0). Очевидно, что графики пересекаются в рабочей точке А. Находим соответствующие ей значения тока I и напряжений U1 и U2 .
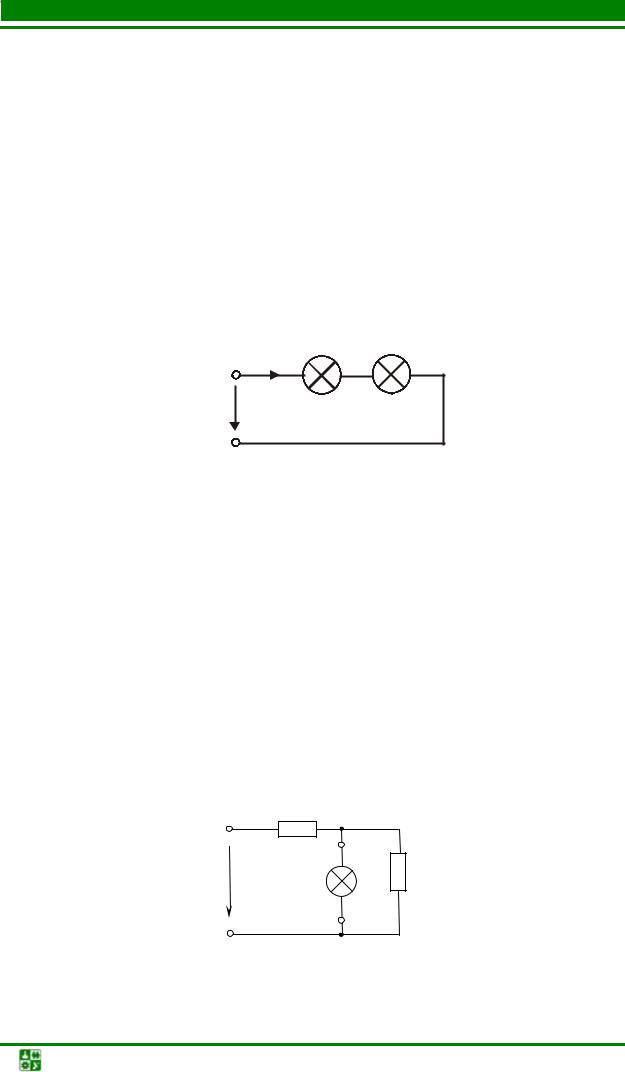
Для разветвленной схемы с одним нелинейным элементом, ток в котором и надо найти, в решении как промежуточный можно использовать метод эквивалентного генератора. Делим схему на две части: НЭ и всю остальную часть схемы, которая является активным двухполюсником.
Активный двухполюсник заменим эквивалентным ему генератором. Активный двухполюсник является линейной цепью, расчет которой намного проще, чем нелинейной. ЭДС генератора Ег равна напряжению холостого
хода на зажимах активного двухполюсника. Сопротивление Rг – это
|
Теоретические основы электротехники. Практикум |
-274- |
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
эквивалентное сопротивление пассивного двухполюсника относительно входных зажимов. Пассивный двухполюсник получаем из активного, закорачивая источники ЭДС и разрывая источники тока. Полученная схема представляет собой последовательное соединение нелинейного и линейного элементов.
|
I |
I(U1 ) |
|
|
I(U–U2) |
||
|
I(U-U2 ) |
I 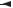
















 A
A
Рабочую точку рационально найти на пересечении ВАХ НЭ и зеркального изображения ВАХ линейного элемента (рис. 6.2). График I(Ег −URг ) является прямой линией, зеркально отображающей график
I (URг ), смещенный вправо на величину Ег. Для его построения нужны две
точки. Одна из них с координатами (Ег,0).
Для построения второй точки можно задаться произвольным значением тока I j . Соответствующее ему напряжение U R j = RгI j отложим от
значения Ег влево. Отыскав рабочую точку А, найдем соответствующее ей значение тока I.
Задача1
Вычислить сопротивление R линейного элемента в схеме рис. 6.3, если входное напряжение U =120 В, напряжение на лампочке Uл = 75 В, ВАХ
лампочки задана табл. 6.1.
I R
U
Рис. 6.3
|
Теоретические основы электротехники. Практикум |
-275- |
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
|
Решение |
||||||||||||||||
|
1. Построим ВАХ лампочки (рис. 6.4). |
||||||||||||||||
|
I, А |
ВАХлампочки |
|||||||||||||||
|
0,7 |
||||||||||||||||
|
0,6 |
||||||||||||||||
|
0,5 |
2 |
2 |
||||||||||||||
|
B |
||||||||||||||||
|
A |
К задаче 5 |
|||||||||||||||
|
0,4 |
||||||||||||||||
|
0,3 |
||||||||||||||||
|
0,2 |
К задаче 2 |
|||||||||||||||
|
0,1 |
||||||||||||||||
|
1 |
1 |
|||||||||||||||
|
40 |
80 |
120 |
160 |
200 U, В |
||||||||||||
|
Рис. 6.4 |
||||||||||||||||
|
2. Сопротивление R = U R . |
||||||||||||||||
|
3. По |
второму |
I |
закону |
Кирхгофа |
напряжение |
|||||||||||
|
U R =U −Uл =120 −75 = 45 В. |
Uл = 75 В |
ток |
||||||||||||||
|
4. Найдем |
ток |
схемы |
по |
ВАХ |
лампочки. При |
|||||||||||
|
I ≈ 0,425 А. |
||||||||||||||||
|
Тогда R = |
45 |
=106 Ом. |
||||||||||||||
|
0,425 |
Таблица 6.1 |
|||||||||||||||
|
U, |
0 |
1 |
20 |
40 |
60 |
80 |
10 |
120 |
14 |
160 |
18 |
200 |
220 |
240 |
260 |
|
|
B |
0 |
0 |
0 |
0 |
||||||||||||
|
I, |
0 |
0, |
0, |
0, |
0,3 |
0,4 |
0,5 |
0,5 |
0,6 |
0,6 |
0, |
0,7 |
0,7 |
0,7 |
0,75 |
|
|
A |
1 |
18 |
3 |
8 |
5 |
5 |
5 |
7 |
2 |
3 |
4 |
Задача2
Найти ток в схеме рис. 6.3, если U = 200 В, R = 400 Ом.
Решение
|
Теоретические основы электротехники. Практикум |
-276- |
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Отыщем рабочую точку на пересечении ВАХ лампочки и зеркального отображения ВАХ линейного элемента, которое можно построить по двум точкам. Первая из них с координатами (200 В; 0). Для построения второй точки зададимся произвольным значением тока, например I j = 0,5 А. Тогда
UR j = R I j = 400 0,5 = 200 В. Отложим напряжение UR j от U = 200 В
влево. Получим вторую точку с координатами (0; 0,5 А). Рабочая точка А находится на пересечении двух графиков (см. рис. 6.4). Ей соответствует значение тока I ≈ 0,38 А.
Задачи 3 и 4 решите самостоятельно.
Задача3
Вычислить входное напряжение в схеме рис. 6.5, если ток I = 0,18 А.
Рис. 6.5
Ответ: U = 40 В.
Задача4
Вычислить мощность, потребляемую лампочкой в схеме рис. 6.3 при входном напряжении U =180 В, если при входном напряжении U = 220 В напряжение на лампочке Uл =127 В.
Ответ: Рл = 50 Вт.
Задача5
Вычислить мощность, потребляемую лампочкой в схеме рис. 6.6, если U =150 В, R1 =100 Ом, R2 = 400 Ом, ВАХ лампочки приведена на рис. 6.4.
Рис. 6.6
Решение
|
Теоретические основы электротехники. Практикум |
-277- |
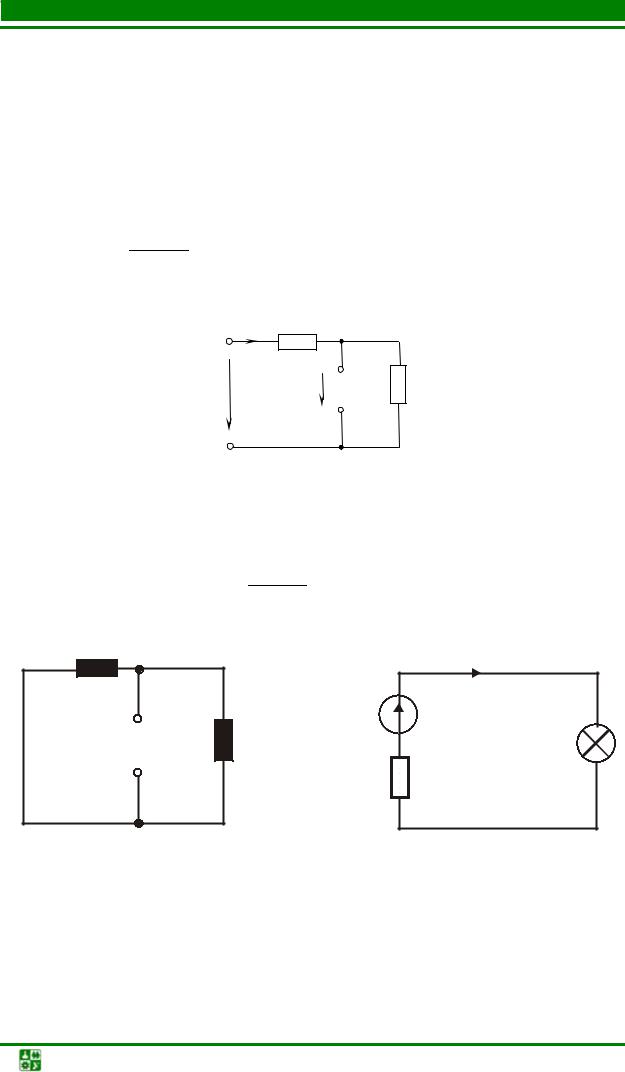
|
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА |
|||||||
|
1. Заменим схему эквивалентной ей одноконтурной с помощью метода |
|||||||
|
эквивалентного генератора. Разделим схему на две части: лампочку и всю |
|||||||
|
остальную схему – активный двухполюсник (рис. 6.7), который заменим |
|||||||
|
эквивалентным ему генератором. ЭДС генератора |
|||||||
|
Eг =Uхх = R2 Iхх . |
|||||||
|
Ток Iхх = |
U |
= 0,3 А. |
|||||
|
R + R |
|||||||
|
Тогда Ег |
1 |
2 |
|||||
|
= 400 0,3 =120 В. |
|||||||
|
Iхх |
R1 |
||||||
|
a |
R2 |
||||||
|
U |
Uхх |
||||||
|
b |
|||||||
|
Рис. 6.7 |
|||||||
|
Схема пассивного двухполюсника приведена на рис. 6.8. |
|||||||
|
Сопротивление |
|||||||
|
R = R |
= R1 R2 |
= 100 400 = 80 Ом. |
|||||
|
г |
ab |
R1 |
+ R2 |
100 + 400 |
|||
|
R1 |
I Л |
||||||
|
а |
R2 |
Ег |
|||||
|
b |
Rг |
||||||
|
Рис. 6.8 |
Рис. 6.9 |
||||||
|
Получившаяся одноконтурная схема изображена на рис. 6.9. |
2. Найдем рабочую точку на пересечении ВАХ лампочки с зеркальным отображением ВАХ линейного резистора. Одна точка для построения графика I (Eг −U Rг ) – с координатами (120 В; 0). Для построения второй
|
Теоретические основы электротехники. Практикум |
-278- |
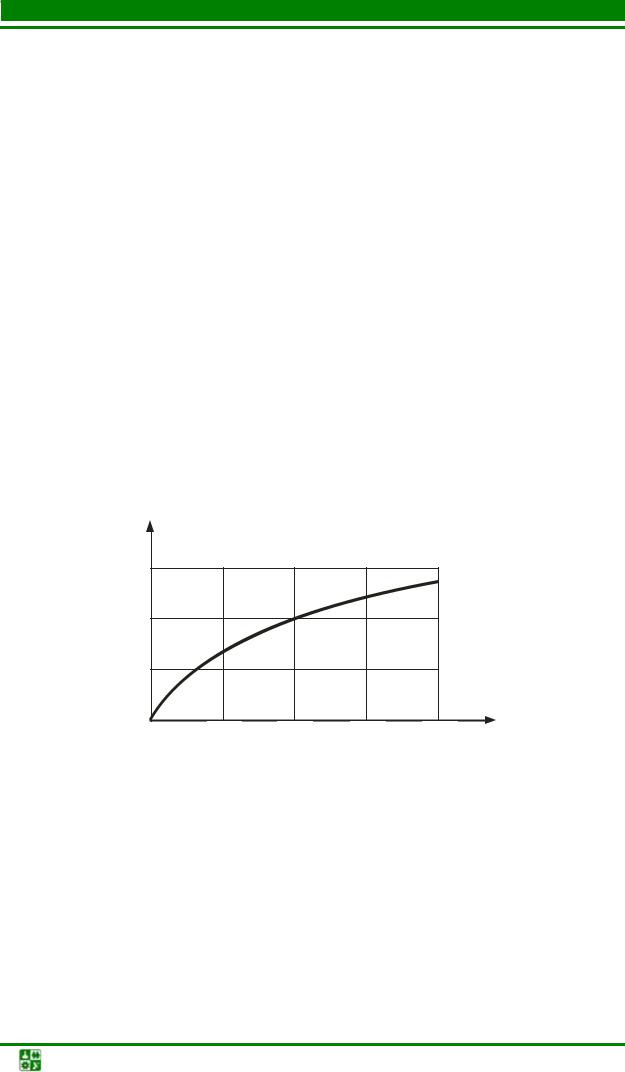
|
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА |
|||||
|
точки зададимся значением тока I j = 0,5 А. Тогда URj |
= Rг I j = 0,5 80 = 40 |
||||
|
В. Отложим 40 В от 120 В влево и получим точку с координатами (80 В; 0,5 |
|||||
|
А). Проведем прямую через эти две точки (см. рис. 6.4). Рабочая точка В |
|||||
|
позволяет определить Uл ≈83 В и Iл ≈ 0,45 А. |
|||||
|
Мощность, потребляемая лампочкой, |
|||||
|
Pл =Uл Iл =83 0,45 ≈ 37,4 Вт. |
|||||
|
Задачу 6 решите самостоятельно. |
|||||
|
Задача6 |
|||||
|
Найти все токи в схеме рис. 6.6, |
если U = 380 В, |
R1 =300 Ом, R2 = 600 |
|||
|
Ом. |
|||||
|
Ответ: I1 = 0,8 А; I2 = 0,22 А; Iл = 0,58 А. |
|||||
|
Задача7 |
|||||
|
Вычислить напряжение на входе схемы рис. |
6.6, |
если R1 =50 Ом, |
|||
|
R2 =100Ом, ток Iл = 0,2 А, ВАХ лампочки приведена на рис. 6.10. |
|||||
|
II,, AА |
|||||
|
0,30,3 |
|||||
|
0,2 |
|||||
|
0,2 |
|||||
|
0,1 |
|||||
|
0,1 |
|||||
|
50 |
100100 |
150150 |
200200 |
U, В |
|
|
U, В |
РисРис. 6..106.10
Решение
1. По ВАХ лампочки найдем напряжение между двумя узлами, равное напряжению на лампочке:
U12 =Uл =100 В.
2. Вычислим ток I2 по закону Ома
|
Теоретические основы электротехники. Практикум |
-279- |
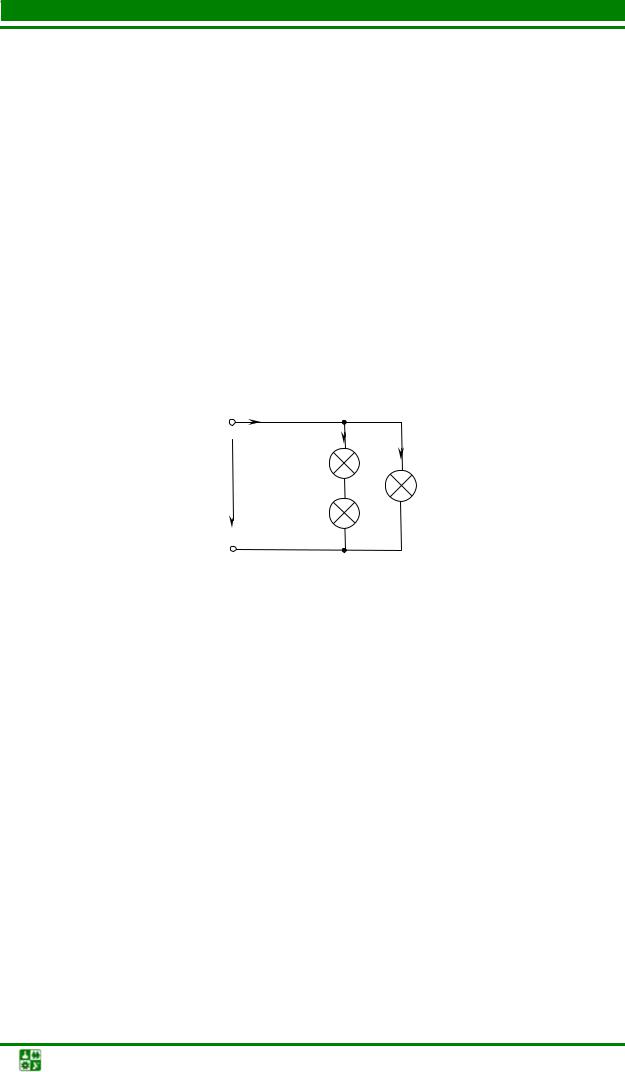
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
I2 = U12 =100 =1 А.
R2 100
3. Вычислим ток I1 по первому закону Кирхгофа
I1 = I2 + Iл =1+ 0,2 =1,2 А.
4. Вычислим входное напряжение по второму закону Кирхгофа
U = R1 I1 +U12 =50 1,2 +100 =160 В.
Задача8
Найти ток в неразветвленной части цепи схемы рис. 6.11, если U =100 В, все лампочки одинаковые. ВАХ лампочки приведена на рис. 6.12.
I
U
Рис. 6.11
Решение
1.По ВАХ лампочки найдем ток I2 = 0,6 А.
2.В ветви с последовательным соединением двух одинаковых
лампочек на каждой лампочке напряжение Uл = U2 = 50 В.
3.По ВАХ лампочки найдем ток I1 = 0,4 А.
4.По первому закону Кирхгофа найдем ток
I = I1 + I2 = 0,4 + 0,6 =1 А.
Задачи 9–11 решите самостоятельно.
|
Теоретические основы электротехники. Практикум |
-280- |
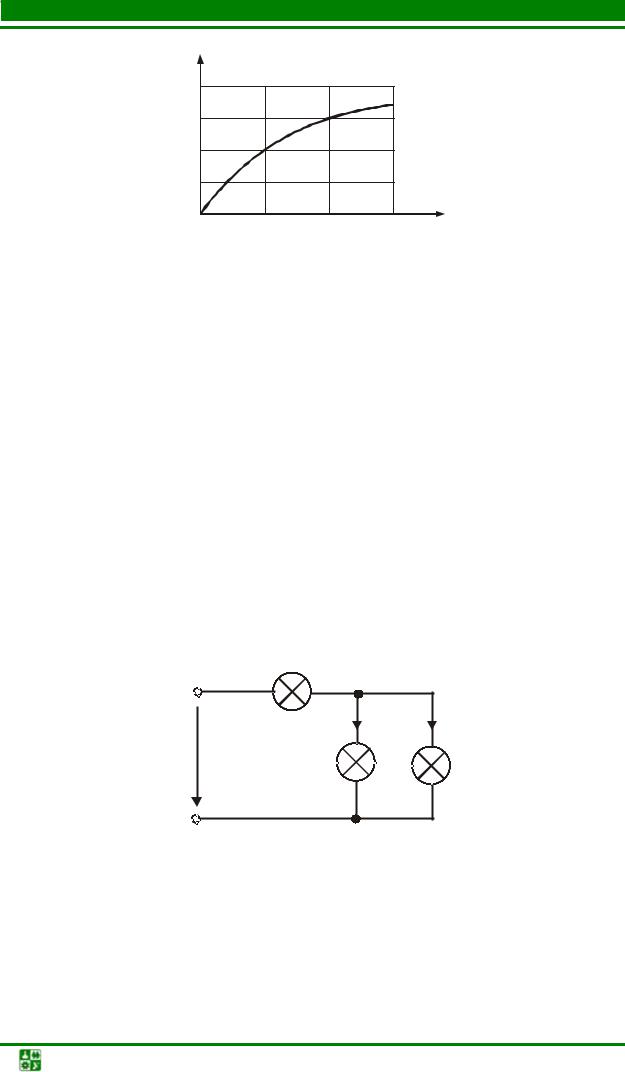
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
|
I, А |
|||
|
0,8 |
|||
|
0,6 |
|||
|
0,4 |
|||
|
0,2 |
|||
|
50 |
100 |
150 |
U, B |
|
Рис. 6.12 |
|||
|
Задача9 |
Найти напряжение на входе схемы рис. 6.11, если ток I1 = 0,4 А и все
лампочки одинаковые. ВАХ лампочки приведена на рис. 6.12. Ответ: U =100 В.
Задача10
Вычислить ток в неразветвленной части схемы рис. 6.11, если ток I1 = 0,4 А и все лампочки одинаковые. ВАХ лампочки приведена нарис. 6.12.
Ответ: I =1 А.
Задача11
Найти напряжение на входе схемы рис. 6.13, если ток I1 = 0,2 А и все лампочки одинаковые. ВАХ лампочки приведена на рис. 6.14.
U
Рис. 6.13
|
Теоретические основы электротехники. Практикум |
-281- |
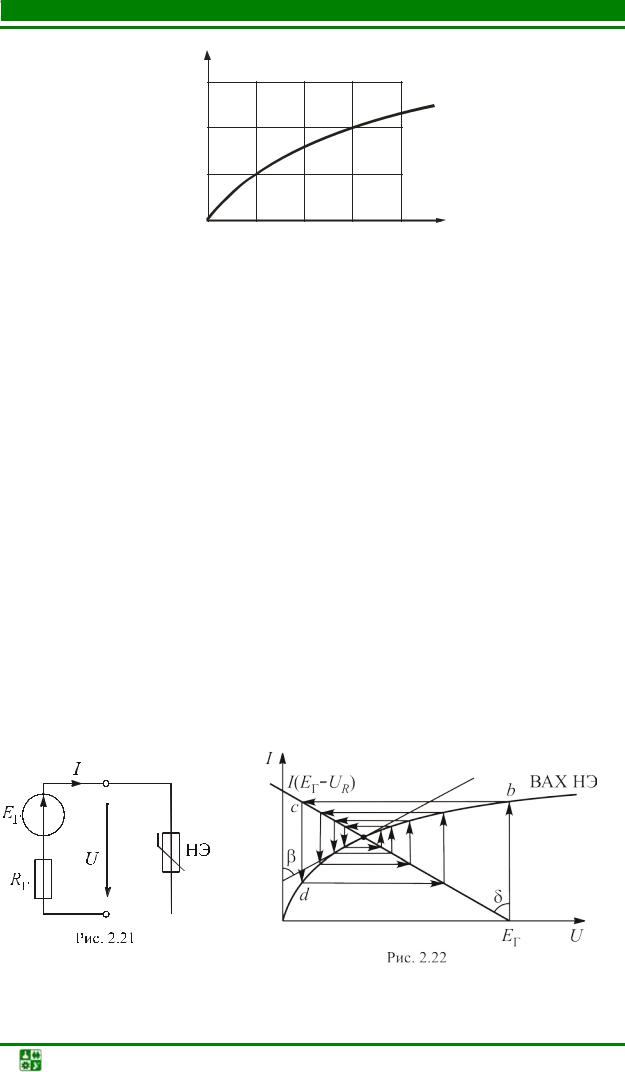
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
|
I, А |
|||
|
0,6 |
|||
|
0,4 |
|||
|
0,2 |
|||
|
50 |
100 |
150 |
200 U, В |
|
Рис. 6.14 |
Ответ: U = 200 В.
Занятие2
Цели занятия:
1.Научиться вычислять ток в нелинейном элементе методом итерации (последовательных приближений).
2.Научиться численному решению нелинейных уравнений методом Ньютона – Рафсона.
Сущность метода итерации (последовательных приближений) заключается в аналитическом решении системы алгебраических нелинейных уравнений. Статическое сопротивление нелинейного элемента должно быть задано в функции от тока или напряжения.
Пусть в схеме один нелинейный элемент (НЭ), ток в котором и надо найти. Остальную часть схемы (активный двухполюсник) заменим эквивалентным ему генератором (рис. 6.15).
Графическая иллюстрация решения методом итерации приведена на рис. 6.16.
Напряжение на нелинейном элементе U = Eг − RгI . Ток зависит от
статического сопротивления НЭ, которое, в свою очередь, зависит от напряжения, поэтому это уравнение является нелинейным: U = F(U ) .
|
Рис. 6.15 |
||||||||
|
Рис. 6.16 |
||||||||
|
Теоретические основы электротехники. Практикум |
-282- |
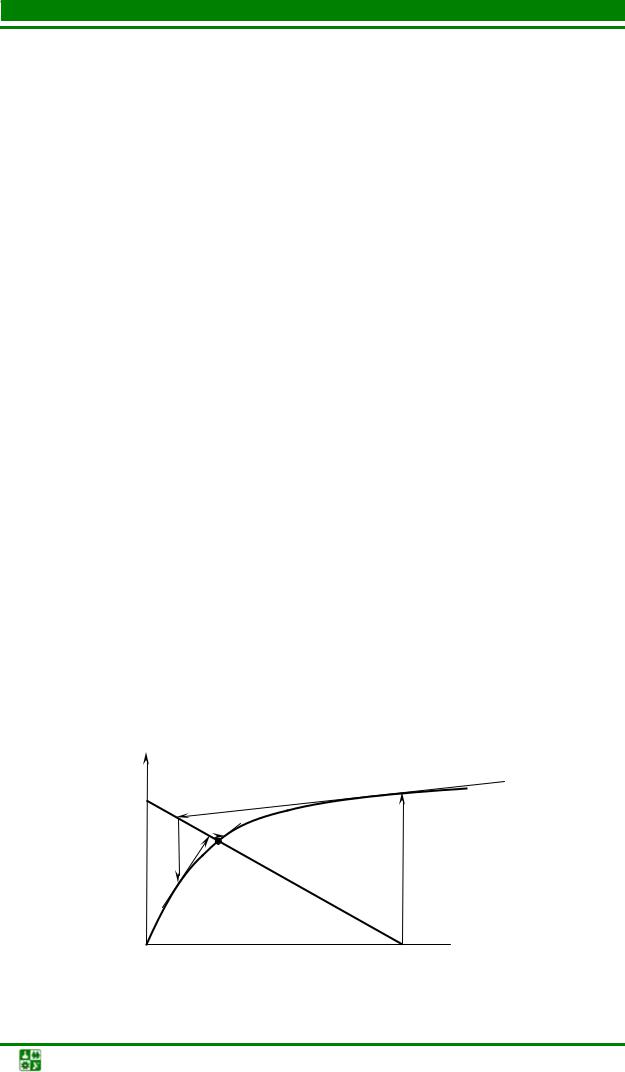
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Пусть напряжение в нулевом приближении U0 = Eг. На ВАХ НЭ
находим соответствующую рабочую точку b. Так как ток в схеме один, то току I0 на графике I(Eг − RгI) соответствует точка с. Напряжение на НЭ
U = Eг − RгI , поэтому переходим из точки с в точку d. Повторяя этот
процесс, получаем рабочую точку А.
Итерационный процесс может быть организован различными методами. Наиболее эффективным считается метод Ньютона – Рафсона. Пусть нелинейное уравнение f (x) = 0 имеет единственный корень x = xk +1.
В окрестности этого корня функция f (xk +1) разлагается в ряд Тейлора: f (xk+1) = f (xk + ∆xk ) ≈ f (x k ) + ∆xk f ′(xk ) = 0
|
Отсюда следует xk +1 = xk + ∆xk , где ∆xk = h = − |
f (xk) |
– поправка |
|
|
f ′(xk ) |
|||
к предыдущему решению. Из приведенных соотношений следует алгоритм метода Ньютона – Рафсона:
1. Задаем начальное приближенное значение искомого решения x0
(k = 0).
2. Определяем поправку h0 . Для ее вычисления по выражению функции находим производную.
3.Определяем уточненное значение корня x1 = x0 + h0 .
4.Повторяем процесс на следующем шаге и уточняем предыдущее решение до необходимой точности.
Геометрическая интерпретация метода приведена на рис. 6.17. В
качестве начального приближения примем U0 = Eг . В точке a проводим касательную к ВАХ НЭ, по касательной переходим на график I(Eг − RгI) в
точку b, далее в точку c на ВАХ НЭ, снова проводим касательную и т. д. Из рисунка видно, что число шагов, необходимых для нахождения решения в случае применения метода Ньютона – Рафсона, значительно меньше, чем при обычном итерационном процессе (рис. 6.16).
|
I |
a |
ВАХ НЭ |
|
|
b |
|||
|
d |
|||
|
c |
A |
I (Eг −U ) |
|
Eг U 
Рис. 6.17
|
Теоретические основы электротехники. Практикум |
-283- |
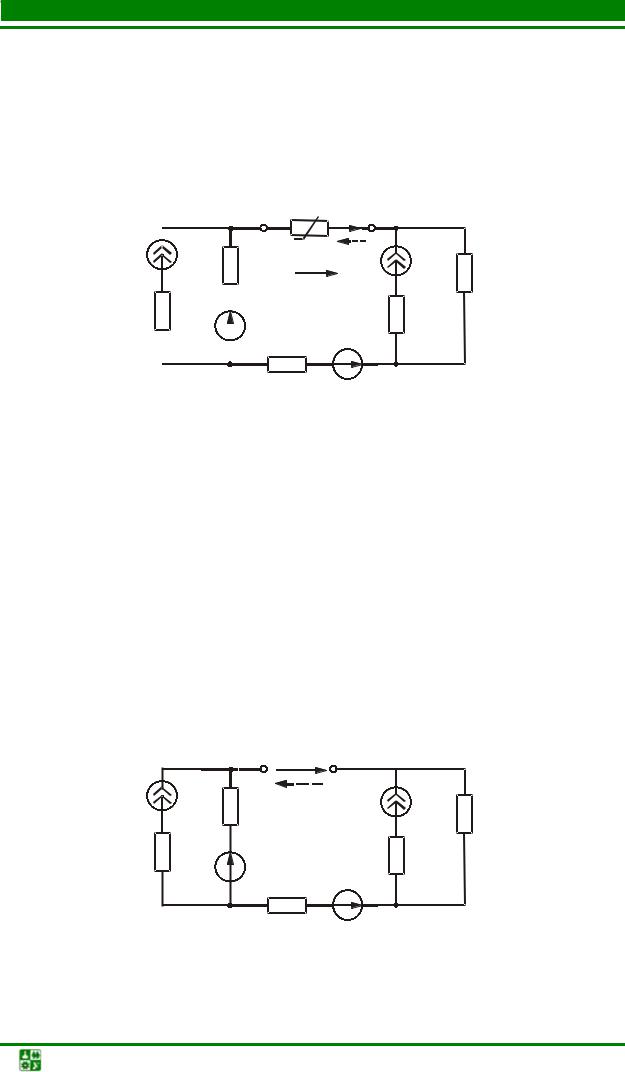
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
|
Задача1 |
||||||||
|
Вычислить ток Iн (рис. 6.18) с точностью до |
пятого знака после |
|||||||
|
запятой, если |
J1 = J4 =1 А, E2 =10 В, |
E3 = 20 В, |
R1 = R2 = R3 = 5 Ом, |
|||||
|
R = R = 4 Ом, U |
н |
= 2 I 2 . |
||||||
|
4 5 |
н |
RН |
||||||
|
а |
IН b |
|||||||
|
J 1 |
R |
2 |
U н |
J 4 |
R 5 |
|||
|
R 1 |
E 2 |
R 3 |
R 4 |
|||||
|
E 3 |
||||||||
|
Рис. 6.18 |
Решение
1. Заменим схему эквивалентной ей одноконтурной с током Iн. Для
этого разделим схему на две части: нелинейный элемент и всю остальную схему, которая является активным двухполюсником (рис. 6.19). Активный двухполюсник заменим эквивалентным ему генератором. Активный двухполюсник содержит две одноконтурные схемы, токи в которых соответственно J1 и J4 . ЭДС эквивалентного генератора равно
Uхх = −R5 J4 − E3 + E2 + R2 J1 = − 4 1 − 20 +10 + 5 1 = −9 В.
Знак минус показывает, что напряжение Uхх , следовательно, и ток Iн направлены противоположно указанным на схемах рис. 6.18 и 6.19.
|
а U хх |
b |
|||
|
J 1 |
R |
2 |
J 4 |
R 5 |
|
R 1 |
E 2 |
R 4 |
||
|
R 3 |
E 3 |
|||
|
Рис. 6.19 |
Пассивный двухполюсник представлен на рис. 6.20. Очевидно, что
|
Теоретические основы электротехники. Практикум |
-284- |
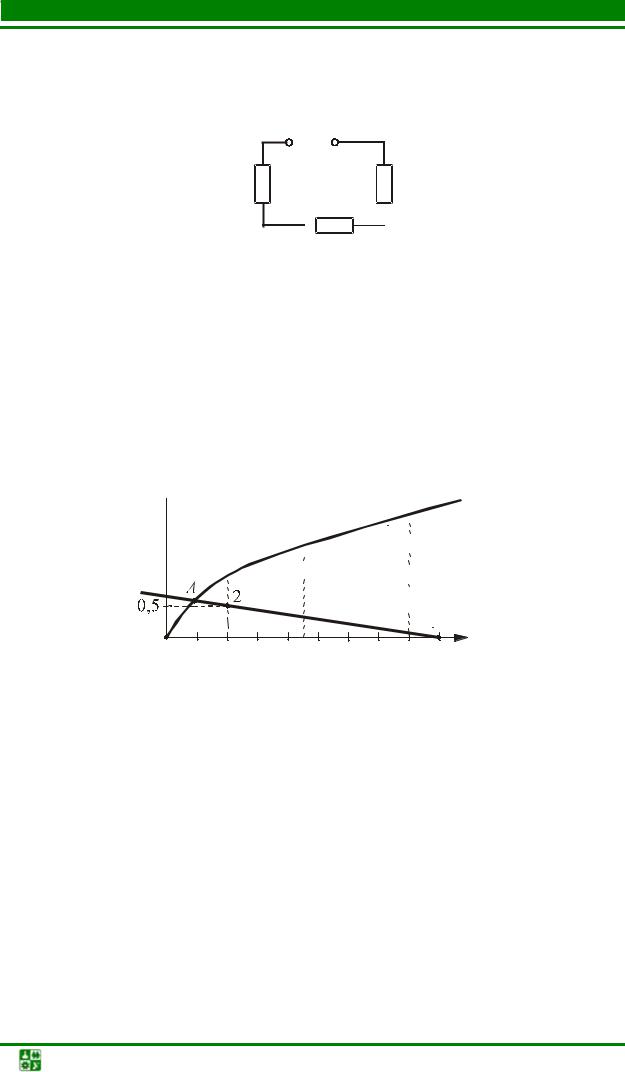
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Rг = R2 + R3 + R5 =5 +5 + 4 =14 Ом.
аb
Рис. 6.20
Схема превратилась в одноконтурную, аналогичную представленной на рис. 6.15.
2. Найдем рабочую точку графическим методом на пересечении ВАХ нелинейного элемента с зеркальным отображением ВАХ линейного
резистора. ВАХ нелинейного элемента задана зависимостью Uн = 2Iн2 . При токе Iн =1 А напряжение Uн = 2 В. При токе Iн =1,5 А напряжение Uн = 4,5 В, при токе Iн = 2 А−Uн =8 В (рис. 6.21).
I, A  ВАХ НЭ
ВАХ НЭ
2 






























 1,5
1,5






















 1
1 








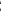

Iн (E Г –UR ) 
1
0 1 2 3 4 5 6 7 8 9 U, В
Рис. 6.21
Зеркальное отображение ВАХ линейного резистора строим по двум точкам. Первая – с координатами (Eг; 0) , т. е. (9; 0). Чтобы получить вторую
|
точку, примем, например, ток I2 = 0,5 |
А. Тогда U R |
= Rг I2 =14 |
0,5 |
= 7 В. |
||
|
2 |
||||||
|
Это напряжение надо отложить влево от точки 1. |
||||||
|
Получаем рабочую точку А. Ток Iн ≈ 0,6 А. |
||||||
|
3. Вычислим ток Iн методом итерации. По закону Ома ток |
||||||
|
Ik +1 = |
Ег |
, |
||||
|
Rг + Rст(Ik ) |
||||||
где k – номер приближения.
|
Теоретические основы электротехники. Практикум |
-285- |

ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
|
Примем |
I |
= 0,6 А. Сопротивление R |
= |
U |
н |
= |
2I 2 |
. |
||||||
|
0 |
н = 2I |
н |
||||||||||||
|
ст |
Iн |
Iн |
||||||||||||
|
Данные расчета сведем в табл. 6.2. |
||||||||||||||
|
Таблица 6.2 |
||||||||||||||
|
k |
Ik, А |
Rст(Ik), Ом |
Ik+1, А |
|||||||||||
|
0 |
0,6 |
1,2 |
0,59210 |
|||||||||||
|
1 |
0,59210 |
1,18421 |
0,59272 |
|||||||||||
|
2 |
0,59272 |
1,18544 |
0,59267 |
|||||||||||
|
3 |
0,59267 |
1,18534 |
0,59268 |
|||||||||||
|
4 |
0,59268 |
1,18535 |
0,59268 |
Ток Iн = 0,59268 А.
|
4. Вычислим ток Iн |
методом Ньютона – Рафсона. |
||||||||||||||||||
|
представленной на рис. 6.15, |
справедливо выражениеRг Iн |
||||||||||||||||||
|
которого получим |
f (I |
н |
) = 2 I 2 |
+ R |
I |
н |
− E |
г |
= 0 , где |
2I 2 |
=U |
н |
. |
||||||
|
н |
г |
н |
|||||||||||||||||
|
Производная |
f ′(Iн) = 4 Iн + Rг . |
Выберем значение тока |
|||||||||||||||||
|
тогда уточненное решение после первого шага будет |
|||||||||||||||||||
|
Iн |
= Iн |
− |
f |
(Iн |
0 |
) |
= 0,6 − |
2 0,62 +14 0,6 − |
9 |
= 0,59268 |
|||||||||
|
f ′(Iн0 ) |
4 0,6 +14 |
||||||||||||||||||
|
1 |
0 |
||||||||||||||||||
Для схемы,
+Uн = Eг , из
Iн0 = 0,6 А,
А.
Верное решение получилось сразу после первой итерации. В качестве
|
исходного приближения возьмем |
ток Iн |
0 |
= 0 |
А, тогда Iн = 0,64286 А, |
|
1 |
||||
|
Iн2 = 0,59298 А, Iн3 = 0,59268 А. |
Мы видим, |
что итерационный процесс |
сходится за три шага. Это дает возможность взять начальное приближение, не строя графически ВАХ.
Задача2
Вычислить ток Iн в схеме рис. 6.21 с точностью до пятого знака после запятой, если Е = 20 В, J = 2 А, R1 = 5 Ом, R2 = R3 = 6 Ом, Rн = 0,8 Iн .
Решение
1. Заменим схему эквивалентной ей одноконтурной. Для этого заменим активный двухполюсник (рис. 6.22) эквивалентным ему генератором.
Выявим узлы (c, d), ветви, направим токи. ЭДС эквивалентного генератора
Ег =Uхх = R1 I1х .
|
Теоретические основы электротехники. Практикум |
-286- |
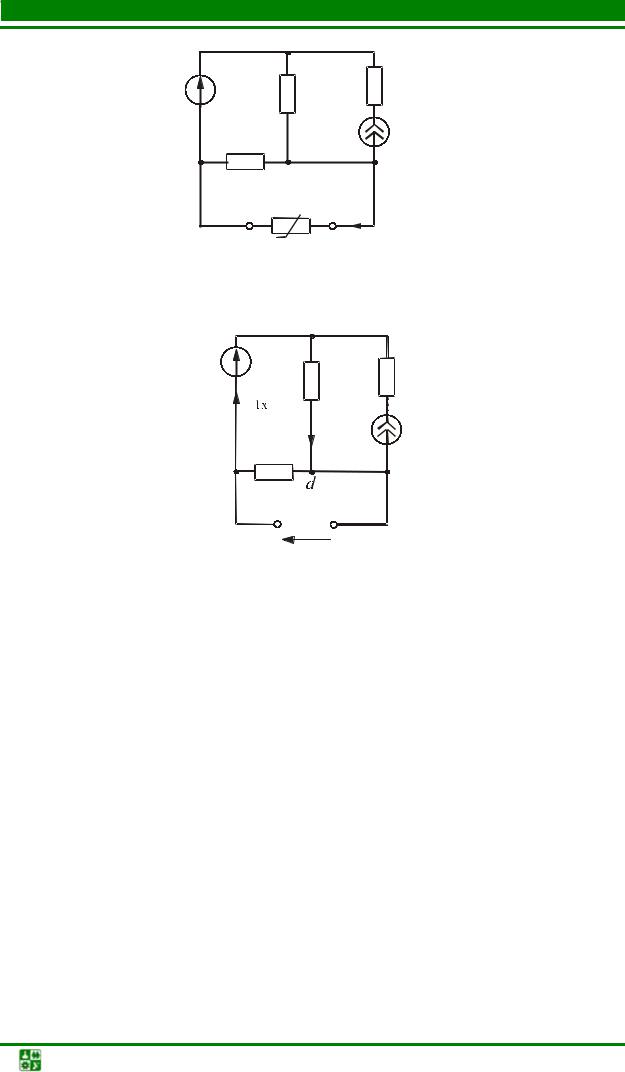
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
|
E |
R 2 |
R 3 |
||
|
R 1 |
J |
|||
|
a |
R н |
b |
||
|
I н |
||||
|
Рис. 6.22 |
||||
|
с |
||||
|
E |
R 3 |
|||
|
I |
R |
2 |
||
|
I 2х |
J |
|||
|
R 1 |
||||
|
а |
b |
U хх
Рис. 6.23
Вычислим ток I1х методом напряжения между двумя узлами. Напряжение
|
E |
+ J |
20 |
+ 2 |
|||||||||||
|
Ucd = |
R1 |
= |
5 |
=16,36 В. |
||||||||||
|
1 |
1 |
|||||||||||||
|
1 |
+ |
+ 1 |
||||||||||||
|
R |
R |
5 |
||||||||||||
|
6 |
||||||||||||||
|
1 |
2 |
|||||||||||||
|
Для ветви с искомым током |
||||||||||||||
|
Ucd = −R1 I1x + E . |
||||||||||||||
|
Отсюда I1x |
= |
E −Ucd |
= 20 −16,36 |
= 0,728 А. |
||||||||||
|
R1 |
5 |
Тогда Uxх =5 0,728 =3,64 B = Eг .
|
Теоретические основы электротехники. Практикум |
-287- |
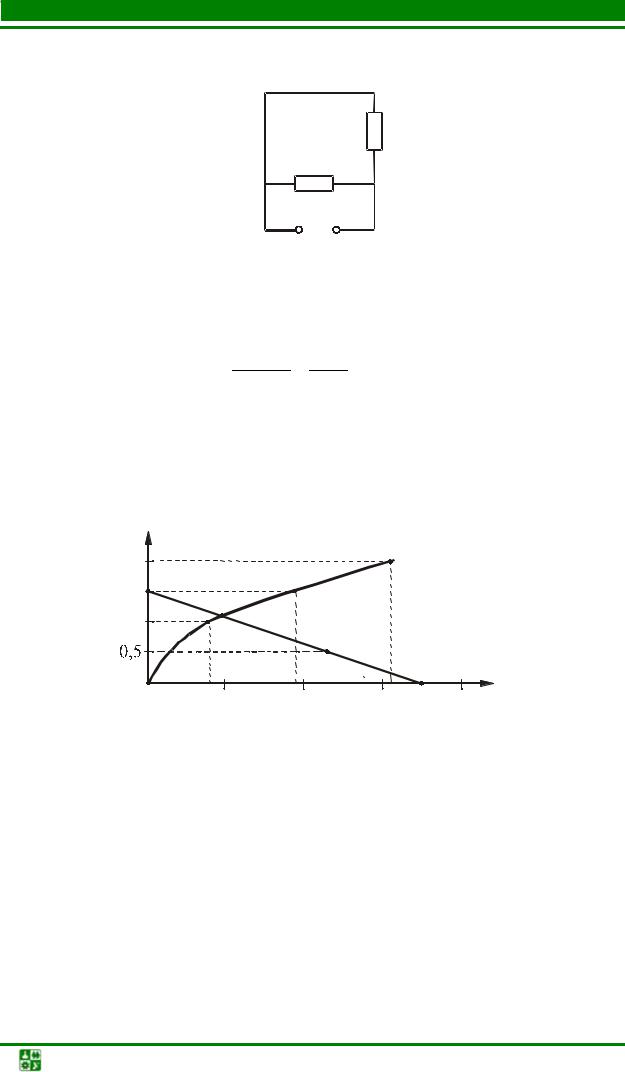
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Пассивный двухполюсник представлен на рис. 6.24.
|
R 2 |
|||||||||||
|
R 1 |
|||||||||||
|
а |
b |
||||||||||
|
Рис. 6.24 |
|||||||||||
|
Очевидно, что |
|||||||||||
|
R = R1 R2 |
= 5 6 = 2,73 Ом. |
||||||||||
|
г |
R1 + R2 |
5 + 6 |
|||||||||
|
2. Найдем рабочую точку графическим методом. ВАХ нелинейного |
|||||||||||
|
элемента U |
н |
= R I |
н |
= 0,8I 2 |
. При токе I |
н |
=1 А напряжение U |
н |
= 0,8 В, при |
||
|
н |
н |
||||||||||
|
токе Iн =1,5 А напряжение Uн =1,8 В, при токе 2 А – Uн = 3,2 В (рис. 6.25). |
|||||||||||
|
I, A |
ВАХ НЭ |
||||||||||
|
2 |
|||||||||||
|
1,5 |
А |
||||||||||
|
1 |
Iн (Eг -UR ) |
||||||||||
|
2 |
|||||||||||
|
1 |
|||||||||||
|
0 |
1 |
2 |
3 |
4 U, В |
|||||||
|
Рис. 6.25 |
Зеркальное отображение ВАХ линейного резистора строим по двум точкам. Точка 1 с координатами (Ег; 0) , т. е. (3,64; 0). Для построения
точки 2 примем I2 = 0,5 А. Тогда U R2 = Rг I2 =1,36 В. Напряжение
Ег −U R2 = 3,64 −1,36 = 2,28 В.
Получаем рабочую точку А. Ток Iн ≈1,1 А.
3. Вычислим ток Iн методом итерации. По закону Ома
|
Ik +1 = |
Ег |
, |
|
|
Rг + Rст(Ik ) |
|||
|
Теоретические основы электротехники. Практикум |
-288- |
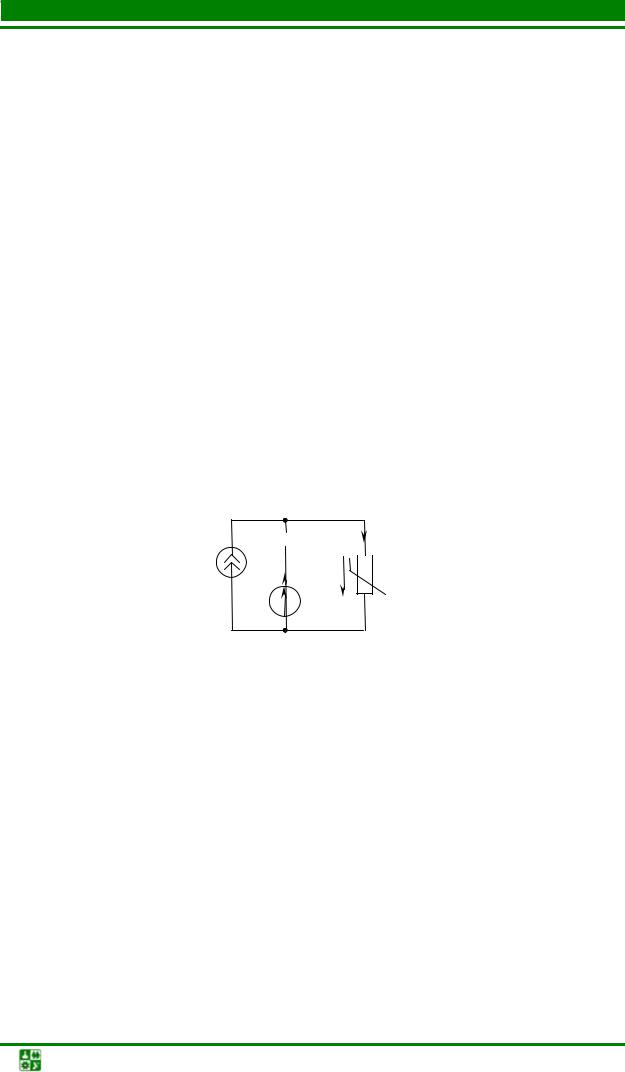
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
где k – номер приближения.
Примем I0 =1 А.
Данные расчета сведем в табл. 6.3
|
Таблица 6.3 |
|||
|
k |
Ik, А |
Rст(Ik), Ом |
Ik+1, А |
|
0 |
1 |
0,8 |
1,03116 |
|
1 |
1,03116 |
0,82493 |
1,02393 |
|
2 |
1,02393 |
0,81914 |
1,02560 |
|
3 |
1,02560 |
0,82048 |
1,02521 |
|
4 |
1,02521 |
0,82017 |
1,02530 |
|
5 |
1,02530 |
0,82024 |
1,02528 |
|
6 |
1,02528 |
0,82023 |
1,02528 |
Ток Iн =1,02528 А.
Задача3
Вычислить ток в нелинейном элементе схемы на рис. 6.26 методом Ньютона – Рафсона, если J = 2 А, E = 10 В, R = 5 Ом, Uн = 2Iн2 +1,2Iн +5 .
|
J |
R |
Uн |
Iн |
|
|
НЭ |
||||
|
I |
||||
E
Рис. 6.26
Решение
1. Запишем уравнение по второму закону Кирхгофа:
R I +Uн = E ,
где I = Iн − J.
2. После подстановки выражений Uн и I получим нелинейное уравнение
f(Iн) = 2Iн2 +1,2Iн +5 + R Iн − R J − E = 2Iн2 +6,2Iн −15 = 0 .
3.Найдем производную
f ′(Iн) = 4 Iн + 6,2.
|
Теоретические основы электротехники. Практикум |
-289- |

ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
4. Выберем начальное приближение Iн0 = 3 А. Тогда значение тока после первого шага будет
|
Iн |
= Iн |
− |
f (Iн |
0 |
) |
= 3 − |
2 32 +6,2 3 −15 |
=1,81319 |
А. |
|
|
f ′(Iн0 ) |
4 3 |
+6,2 |
||||||||
|
1 |
0 |
|||||||||
|
На втором и последующих шагах |
Iн2 =1,60378 А, Iн3 =1,59683 А, |
|||||||||
|
Iн4 =1,59682 А, |
Iн5 |
=1,59682 А. |
Занятие3
Цель занятия: научиться расчету нелинейных цепей методом напряжения между двумя узлами.
Цепи с двумя узлами часто встречаются на практике. Рассмотрим метод на примере конкретной задачи.
Задача1
Вычислить все токи в схеме на рис. 6.27, если Е1 = 4 В, Е2 = 6 В, Е3 =3 В. ВАХ нелинейных элементов НЭ1, НЭ2, НЭ3 для первой четверти
приведены соответственно в табл. 6.4, 6.5, 6.6. ВАХ всех НЭ являются симметричными.
Таблица 6.4
|
I1 |
, |
0 |
0,3 |
0,75 |
1,25 |
1,5 |
2 |
2,25 |
2,5 |
2,7 |
2,75 |
2,85 |
2,9 |
3 |
||||||||||||||||||||||||||||
|
А |
||||||||||||||||||||||||||||||||||||||||||
|
U1 |
, |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
||||||||||||||||||||||||||||
|
В |
||||||||||||||||||||||||||||||||||||||||||
|
Таблица 6.5 |
||||||||||||||||||||||||||||||||||||||||||
|
I2 , А |
0 |
0,5 |
1 |
1,5 |
2 |
2,25 |
3 |
|||||||||||||||||||||||||||||||||||
|
U2 , В |
0 |
2 |
4 |
6 |
6 |
6 |
6 |
|||||||||||||||||||||||||||||||||||
|
Таблица 6.6 |
||||||||||||||||||||||||||||||||||||||||||
|
I3 |
, |
0 |
0,25 |
0,35 |
0,5 |
0,75 |
1 |
1,5 |
2 |
2,25 |
2,5 |
2,75 |
3 |
|||||||||||||||||||||||||||||
|
А |
||||||||||||||||||||||||||||||||||||||||||
|
U2 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
6,5 |
7 |
7,5 |
8 |
8 |
||||||||||||||||||||||||||||||
|
|
Теоретические основы электротехники. Практикум |
-290- |
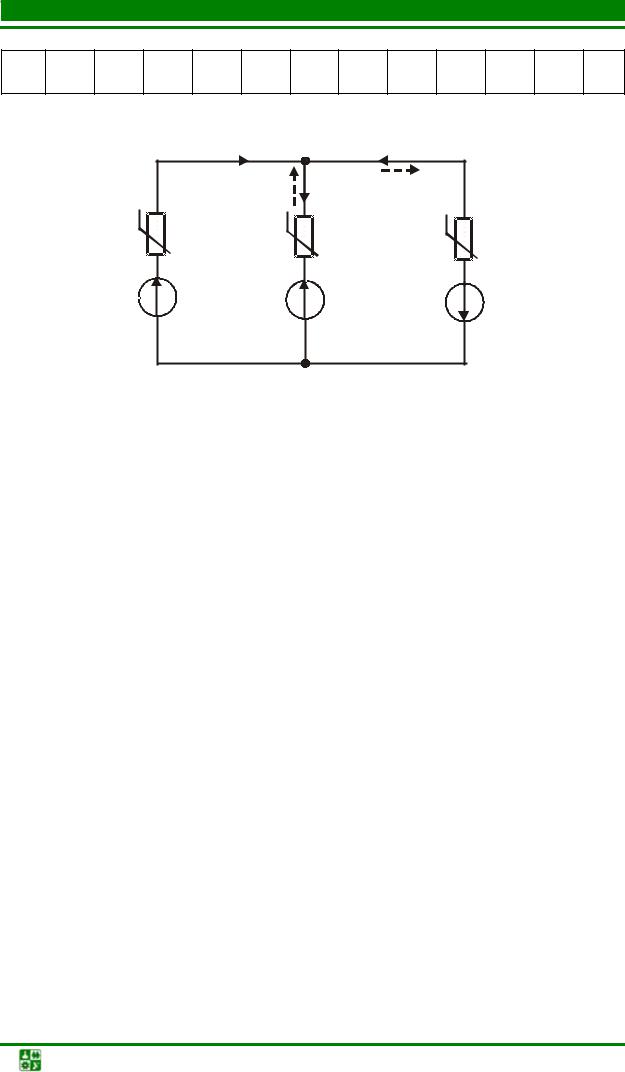
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
,
В
|
I1 |
а |
I3 |
|
I2 |
||
|
НЭ1 |
НЭ2 |
НЭ3 |
|
Е1 |
Е |
Е3 |
|
2 |
b
Рис. 6.27
Решение
1. Запишем уравнение на основании первого закона Кирхгофа:
I1 − I2 + I3 = 0 .
Для решения более удобна запись в виде I2 = I1 + I3 . Это уравнение
является условием для нахождения рабочей точки.
2. Приведем токи к зависимости от одного аргумента. В условии токи ветвей заданы в функции от разных переменных: I1(U1) , I2 (U2 ), I3 (U3 ) .
Общим для всех ветвей является напряжение между двумя узлами Uab . Запишем выражения напряжения Uab для всех трех ветвей схемы:
Uab = Е1 −U1 ; Uab = Е2 +U2 ;
Uab = −Е3 −U3 .
3. Построим графики токов I1(Uab ) , I2 (Uab ), I3 (Uab ) на основании полученных уравнений. График I1(Uab ) является зеркальным отображением
|
графика I1(U1) , |
смещенным по оси абсцисс вправо на величину ЭДС Е1 = 4 |
||
|
В (рис. 6.28). |
График I2 (Uab ) представляет собой |
график |
I2 (U2 ), |
|
смещенный вправо по оси абсцисс на величину ЭДС |
Е2 = 6 В. |
График |
I3 (Uab ) является зеркальным отображением графика I3 (U3 ) , смещенным по оси абсцисс влево на величину ЭДС Е3 =3 В.
|
Теоретические основы электротехники. Практикум |
-291- |
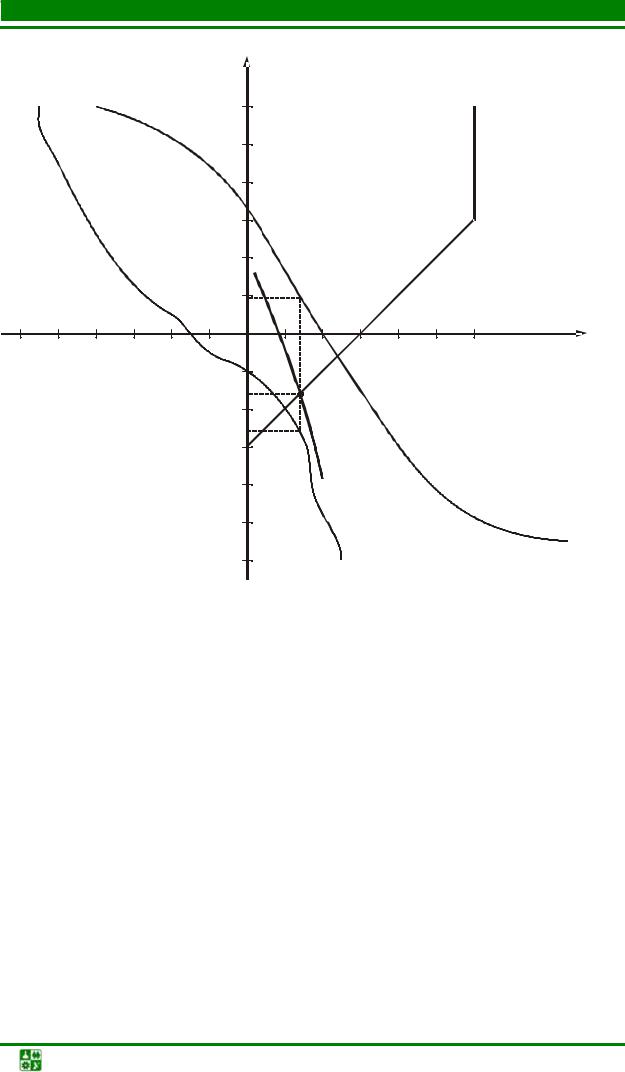
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
I, А
I3(Uab) I1(Uab)
3
2,5
2
1,5
1
0,5
|
–12 –10 |
–8 |
–6 |
–4 |
–2 |
–0,5
–1
–1,5
–2
–2,5
–3
I2(Uab)
А
(I1 + I3)(Uab)
Рис. 6.28
4. Найдем рабочую точку на пересечении графиков (I1 + I3 ) = f (Uab ) и I2 = f (Uab ). Для получения графика (I1 + I3 ) = f (Uab ) при ряде значений напряжения Uab суммируем токи I1 и I3.
5. Определим токи в ветвях и напряжение Uab . Для этого через
рабочую точку А проводим вертикаль. На ее пересечении с осью абсцисс получаем значение напряжения Uab ≈ 2,8 В, на пересечении с графиками
токов – токи I1 ≈ 0,48 А, I2 ≈ −0,8 А, I3 ≈ −1,28 А.
Токи I2 и I3 получились с отрицательными знаками, что
свидетельствует о неправильно выбранных направлениях этих токов. Покажем верные направления токов I2 и I3 на рис. 6.27 пунктирными
стрелками.
Задачи 2 и 3 решите самостоятельно. ВАХ нелинейных элементов такие же, что и в задаче 1.
Задача2
|
Теоретические основы электротехники. Практикум |
-292- |
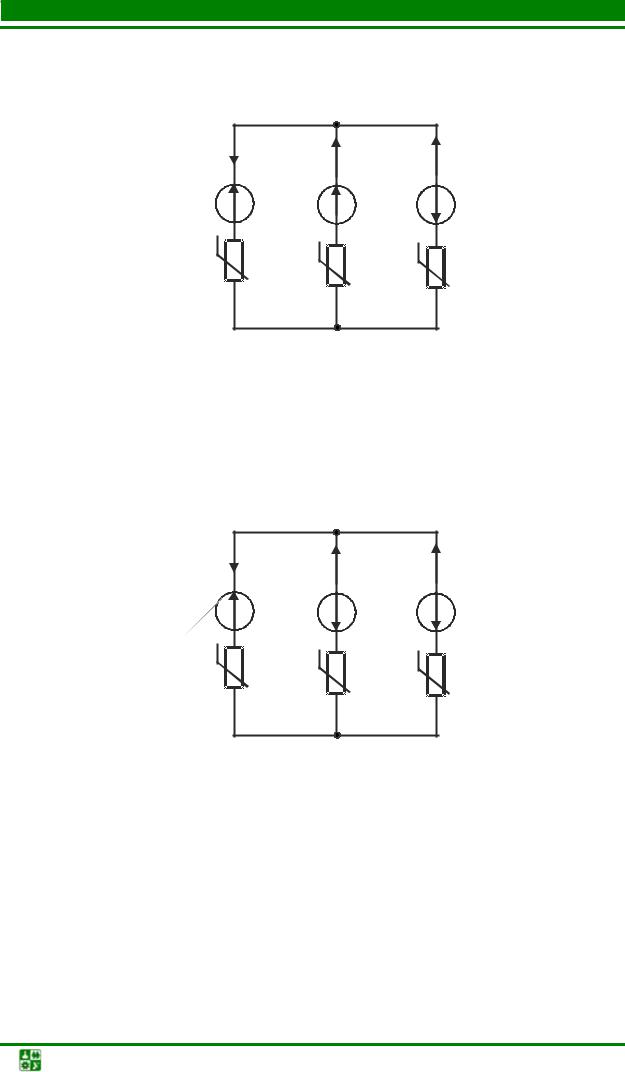
|
ГЛАВА 6. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА |
||||
|
Вычислить все токи в схеме на рис. 6.29, если |
Е1 =5 В, |
Е2 = 2 В, |
||
|
Е3 = 6 В. |
а |
|||
|
I1 |
I |
I3 |
||
|
2 |
||||
|
Е1 |
Е2 |
Е |
||
|
3 |
||||
|
НЭ1 |
НЭ2 |
НЭ3 |
||
|
b |
||||
|
Рис. 6.29 |
||||
|
Ответ: I1 = −1,75 А, I2 = 0,35 А, I3 = −2,1 А. |
||||
|
Задача3 |
||||
|
Вычислить все токи в схемерис. 6.30, если Е1 =5 В, |
Е2 = 2 В, |
Е3 = 6 В. |
||
|
а |
||||
|
I1 |
I |
I3 |
||
|
2 |
||||
|
Е1 |
Е2 |
Е3 |
||
|
НЭ1 |
НЭ2 |
НЭ3 |
||
|
b |
||||
|
Рис. 6.30 |
||||
|
Ответ: I1 = −2 А, I2 = 0,5 А, |
I3 = −1,5 А. |
|||
|
Теоретические основы электротехники. Практикум |
-293- |
