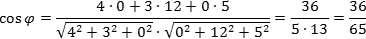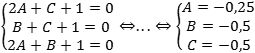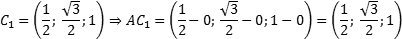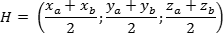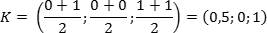Как найти уравнение биссектрисы в пространстве

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте

его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву

, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения

и указать конкретные затруднения.

Обязательно просмотрите тему

Правила данного раздела, иначе Ваша тема может быть удалена

или перемещена в Карантин, а Вы так и не узнаете, почему.

	Биссектриса угла между прямыми в пространстве 22.12.2013, 20:13
22/12/08 155 Москва	Добрый вечер. Мучаюсь с такой задачей: Условие задачи: Написать уравнение биссектрисы острого угла между прямыми и Как решил решать эту задачу? / Т.к. мне даны канонические уравнения прямых, то решил записать выражение для угла между этими прямыми по формуле: . Потом по формуле косинуса двойного угла нашел два таких же выражения для биссектрисы и соседней прямой, и вот тут застрял. Получилась система из двух уравнений, где нужно найти 3 неизвестных. Были мысли найти общую точку двух этих прямых, но формулу для ее нахождения в пространстве так и не нашел. Подскажите пожалуйста, как довести пример до конца.

arseniiv	Re: Биссектриса угла между прямыми в пространстве 22.12.2013, 20:23
Заслуженный участник 27/04/09 28128	Кстати, биссектриса состоит из точек, одинаково удалённых от обоих прямых. Были мысли найти общую точку двух этих прямых, но формулу для ее нахождения в пространстве так и не нашел. А почему бы просто не решить систему из уравнений первой прямой и уравнений второй прямой? Итого 4 уравнения.

svv	Re: Биссектриса угла между прямыми в пространстве 22.12.2013, 20:26
Заслуженный участник 23/07/08 10060 Crna Gora	Найдите точку пересечения прямых. Биссектриса тоже через нее проходит. Найдите направляющие векторы прямых. Приведите их к одной длине (например, единичной). Их сумма (или разность) будет направляющим вектором биссектрисы.

NeBotan	Re: Биссектриса угла между прямыми в пространстве 22.12.2013, 20:41
22/12/08 155 Москва	Цитата: Кстати, биссектриса состоит из точек, одинаково удалённых от обоих прямых. А как в пространстве связать ее с двумя прямыми? По поводу 4 уравнений понял, сейчас найду эту точку. Но тогда у меня остается вопрос, как связать уравнение биссектрисы с тем, что все ее точки равноудалены от прямых, образующих угол? мне останется найти m, n, p – для биссектрисы. — Вс дек 22, 2013 21:43:35 — Решил 4 уравнения. получил точку .

arseniiv	Re: Биссектриса угла между прямыми в пространстве 22.12.2013, 20:44
Заслуженный участник 27/04/09 28128	Почитайте теперь сообщение svv . Может, вам проще будет найти направляющие векторы.

NeBotan	Re: Биссектриса угла между прямыми в пространстве 22.12.2013, 20:56
22/12/08 155 Москва	Получилось так: 1. Направляющие вектора прямых: 2. Длины направляющих векторов: 3. Привожу второй вектор к длине . Получилось 4. Вычитаю вектора и нахожу направляющий вектор биссектрисы: 5. Получаю каноническое уравнение биссектрисы: Правильно? Если да, то у меня только 1 вопрос: как понять, складывать или вычитать нужно направляющие вектора, чтобы найти биссектрису именно острого угла? На сколько я понял, в одном случае будет биссектриса острого, а в другом – тупого углов. Как понять, какую биссектрису нашел я?

_Ivana	Re: Биссектриса угла между прямыми в пространстве 22.12.2013, 21:03
05/09/12 2587	Скалярное произведение должно помочь.

svv	Re: Биссектриса угла между прямыми в пространстве 22.12.2013, 21:03
Заслуженный участник 23/07/08 10060 Crna Gora	3. Привожу второй вектор к длине «Нет, уж лучше вы к нам». Лучше, наоборот, первый вектор привести к длине , потому что , то есть второй вектор в 3 раза длиннее первого, поэтому первый нужно просто умножить на (дробей не будет!)

NeBotan	Re: Биссектриса угла между прямыми в пространстве 22.12.2013, 21:07
22/12/08 155 Москва	Цитата: «Нет, уж лучше вы к нам». Лучше, наоборот, первый вектор привести к длине , потому что , то есть второй вектор в 3 раза длиннее первого, поэтому первый нужно просто умножить на (дробей не будет!) Согласен, неаккуратненько получилось. Цитата: Скалярное произведение должно помочь. А как оно мне поможет? Точнее, какие вектора перемножать?

svv	Re: Биссектриса угла между прямыми в пространстве 22.12.2013, 21:10
Заслуженный участник 23/07/08 10060 Crna Gora	Если скалярное произведение направляющих векторов больше нуля, угол между ними … забыл, не напомните?

arseniiv	Re: Биссектриса угла между прямыми в пространстве 22.12.2013, 21:15
Заслуженный участник 27/04/09 28128	Бабушки говорят, что иногда прямые острого угла не образуют вообще. Надеюсь, тут всё с этим хорошо…

NeBotan	Re: Биссектриса угла между прямыми в пространстве 22.12.2013, 21:16
22/12/08 155 Москва	Острый. Тогда я складываю направляющие вектора прямых, чтобы получить направляющий вектор биссектрисы. Если произведение меньше нуля, то вычитаю. Спасибо вам большое! и с Наступающим всех участников форума Новым Годом!

svv	Re: Биссектриса угла между прямыми в пространстве 22.12.2013, 21:21
Заслуженный участник 23/07/08 10060 Crna Gora	Спасибо за поздравление! Успехов в учебе и всем остальном.

Модераторы: Модераторы Математики, Супермодераторы

Метод координат в пространстве

Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:

Главная формула — косинус угла φ между векторами a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂):

Уравнение плоскости в трехмерном пространстве: Ax + By + Cz + D = 0, где A, B, C и D — действительные числа, причем, если плоскость проходит через начало координат, D = 0. А если не проходит, то D = 1.

Вектор, перпендикулярный к плоскости Ax + By + Cz + D = 0, имеет координаты: n = (A; B; C).

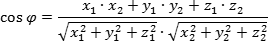
На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.

Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).

Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:

Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.

Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;

Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.

Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.

Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!

Вычисление координат векторов

А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.

Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.

Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:

Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.

Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).

Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).

Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).

Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)

Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!

Вычисление направляющих векторов для прямых

Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.

Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую.

Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый для прямой:

Зачем нужен этот вектор? Дело в том, что — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:

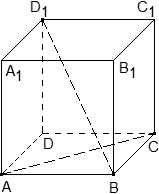
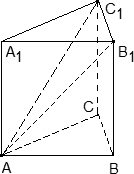
Задача. В кубе ABCDA₁B₁C₁D₁ проведены прямые AC и BD₁. Найдите координаты направляющих векторов этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1.

Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.

Теперь разберемся с прямой BD₁. На ней также есть две точки: B = (1; 0; 0) и D₁ = (0; 1; 1). Получаем направляющий вектор BD₁ = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ: AC = (1; 1; 0); BD₁ = (− 1; 1; 1)

Задача. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, проведены прямые AB₁ и AC₁. Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA₁, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.

Для начала разберемся с прямой AB₁. Тут все просто: у нас есть точки A = (0; 0; 0) и B₁ = (1; 0; 1). Получаем направляющий вектор AB₁ = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор для AC₁. Все то же самое — единственное отличие в том, что у точки C₁ иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:

Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

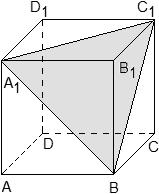
Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение A₁BC₁. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение AA₁C₁C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Координаты середины отрезка

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

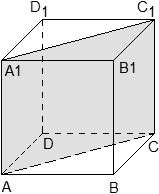
Итак, пусть отрезок задан своими концами — точками A = (x_a; y_a; z_a) и B = (x_b; y_b; z_b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

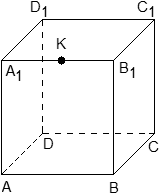
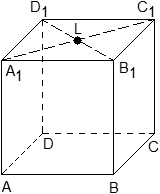
Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A₁B₁. Найдите координаты этой точки.

Поскольку точка K — середина отрезка A₁B₁, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A₁ = (0; 0; 1) и B₁ = (1; 0; 1). Теперь найдем координаты точки K:

Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A₁B₁C₁D₁.

Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A₁L = C₁L, т.е. точка L — это середина отрезка A₁C₁. Но A₁ = (0; 0; 1), C₁ = (1; 1; 1), поэтому имеем:

Уравнение биссектрисы в треугольнике — формула, свойства и решение задач

Треугольник является одной из самых простых фигур, которая часто встречается школьникам в задачах по геометрии. В свою очередь, биссектриса представляет собой важный элемент, характеризующий тот или иной угол. Решение геометрических проблем с участием этих объектов требует наличия определенных знаний. Чтобы уметь составлять по координатам вершин уравнение биссектрисы треугольника, необходимо понимать выражения для прямых линий.

Прямая на плоскости

Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:

На плоскости, где достаточно двух координат для описания любых геометрических объектов.

В трехмерном пространстве, где любая точка имеет три координаты.

Когда рассматривают треугольники и их элементы, то в ряде ситуаций речь идет именно о двумерном пространстве. В нем всякая прямая линия может быть выражена в виде нескольких математических форм или уравнений. Чаще всего используются следующие типы:

Общий. Он также называется универсальным. Прямая представляет собой следующую математическую запись: A*x + B*y + C = 0. Здесь A, B, C — числовые коэффициенты, x и y — переменные, являющиеся координатами. Сразу нужно отметить, что эта форма представления прямой используется для составления уравнения биссектрисы угла. Для удобства геометрического изображения общую форму записи часто представляют в виде y = f (x). Нужно понимать, что указанной форме в пространстве соответствует не прямая, а плоскость.

Канонический или уравнение в отрезках. Имеет оно такой вид: y/p + x/q = 1. Здесь p, q — это координаты, в которых прямая пересекает оси y и x, соответственно, поэтому удобно ее изображать в координатной системе.

Векторный. Это один из важных типов представления прямой как на плоскости, так и в пространстве. По сути, он является исходным представлением, из которого можно получить все остальные. Математически он записывается так: (x, y) = (x0, y0) + α*(v1, v2). Где (x0, y0) — координаты произвольной точки, которая лежит на прямой, (v1, v2) — направляющий вектор, он параллелен заданной прямой, α — произвольное число, параметр.

Параметрический. Этот тип представляет собой систему уравнений, которую удобно использовать во время преобразования одного вида прямой в другой. Представляет он собой следующую математическую запись: x = x0 + α*v1; y = y0 + α*v2. Несложно понять, что, выражая параметр α, можно получить уравнения общего вида и в отрезках. Объединяя же систему уравнений в одно выражение, получается векторная форма записи прямой.

Делящая пополам угол линия

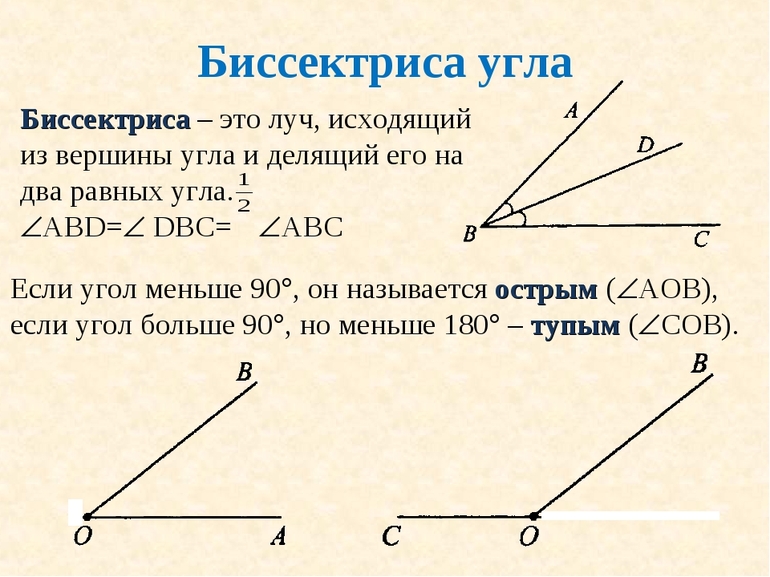
Каждый школьник, который знаком с азами геометрии, знает, что прямая, делящая на две равные части произвольный угол, называется биссектрисой. Этот элемент присутствует для любой фигуры, которая в своем составе содержит какой-либо угол.

Другое определение биссектрисы гласит, что она представляет собой геометрическое расположение точек, которые равноудалены от соответствующих сторон углового объекта. Например, если имеется угол dac, то любая из точек биссектрисы находится на одинаковом расстоянии как от отрезка da, так и от отрезка ac.

Способы построения

В классах общеобразовательных школ рассматривают два основных способа построения биссектрисы. Это следующие:

С помощью транспортира. Для этого следует измерить заданный угол в градусах, разделить его пополам. Полученное значение отметить в виде точки. Затем соединить вершину угла и поставленную точку внутри него. Получится искомый элемент.

С использованием циркуля и линейки. Эти инструменты еще проще применять для построения биссектрисы, чем транспортир. Сначала необходимо установить в вершину угла ножку циркуля и отметить дугами пересечение окружности со сторонами. Затем, в точки пересечения поставить ножку циркуля и провести две окружности. Соединив две точки их пересечения одной прямой, можно получить биссектрису.

Имеется еще один метод, который позволяет просто начертить изучаемый линейный элемент. Для его использования нужна линейка со шкалой. С помощью нее следует от вершины угла отмерить два одинаковых отрезка любой длины. Затем соединить концы этих отрезкой, получится равнобедренный треугольник.

В нем любая биссектриса также является высотой и медианой. Поэтому, разделив его ровно пополам линейкой, и соединив полученную точку с вершиной, можно получить требуемую линию.

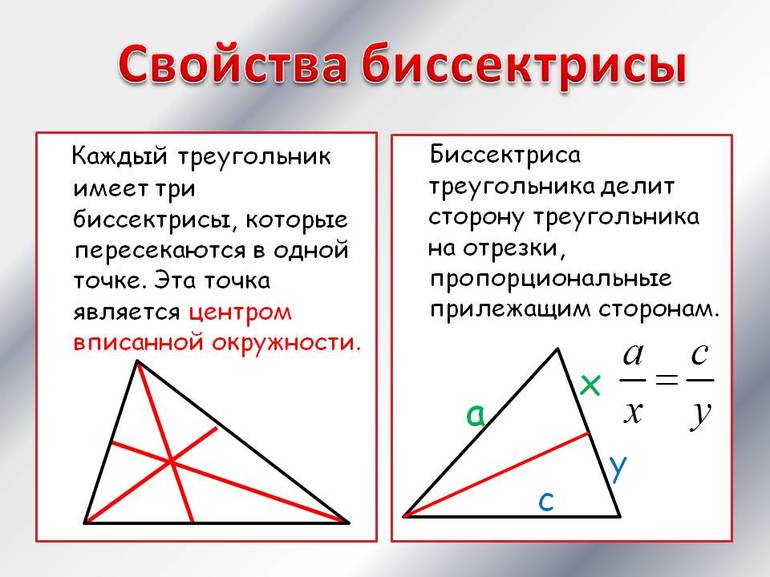
Основные свойства

Чтобы найти по координатам вершин длину биссектрисы треугольника, следует знать некоторые свойства этого геометрического объекта. Главным из них является существование двух линий, которые делят пополам исходный угол. Нужно понимать, что угол бывает не только внутренний, но и внешний. По сути, оба типа образуются при пересечении двух прямых. Нетрудно доказать, что биссектрисы каждого из них пересекаются всегда под углом 90 °.

Еще одним важным свойством является тот факт, что пересекаются в одной точке биссектрисы треугольника. Она представляет собой центр вписанной в фигуру окружности. Чтобы это доказать, следует вспомнить, что каждая точка биссектрисы равноудалена от соответствующих сторон угла.

Пусть имеется треугольник ABC. У него две биссектрисы пересекаются в точке O. Пусть это будут линии для углов A и B. Расстояние от O до AC должно быть равно таковому от O до AB. С другой стороны, расстояния от O до AB и до BC также одинаковые. Поэтому дистанции от O до BC и до AB также равны, а значит, точка O лежит на биссектрисе угла C и центром вписанной окружности является.

В треугольнике рассматриваемый геометрический элемент используется часто для решения задач благодаря применению так называемой теоремы биссектрис. Чтобы ее сформулировать максимально простым языком, следует представить, что имеется треугольник произвольного типа ABC. В нем проведена биссектриса AD, где точка D лежит на прямой BC. Тогда справедливо следующее выражение:

Это равенство не является очевидным, однако, оно было известно еще древнегреческим мыслителям. Эту теорему в несколько иной форме можно встретить в знаменитом труде по геометрии Евклида, который называется «Элементы». Доказательство равенства несложно провести с использованием небольших дополнительных построений и применением признаков подобия треугольников.

Наконец, отрезок биссектрисы, который заключен между вершиной и противоположной стороной треугольника, имеет определенную длину. Вычислить ее можно с использованием следующего равенства:

Это равенство прописано для угла A треугольника ABC, в котором противоположная A сторона имеет длину a. Стороны AB и AC имеют длины c и b, соответственно. Буквой p обозначен полупериметр фигуры.

Важно понимать, если нарисовать прямоугольный параллелепипед (или иную фигуру) в пространстве, и построить биссектрису для его граней, она будет представлять собой не прямую, а плоскость.

Уравнение биссектрисы треугольника

Когда известно, как математически записывать выражения для прямых, и что такое биссектриса, и какими свойствами она обладает, можно переходить к непосредственному нахождению ее уравнения.

В общем случае задача решается в результате применения следующей последовательности действий (существуют онлайн-ресурсы, позволяющие решить данную проблему):

Сначала требуется определить уравнения двух сторон угла по их координатам. Это легко сделать в векторной форме, а затем, преобразовать ее в выражение общего типа.

Далее, необходимо найти уравнение биссектрис первого координатного угла, прировняв расстояния от ее точек до соответствующей стороны. Рабочая формула имеет вид: |A1*x + B1*y + C|/(A1 2 + B1 2 )^0,5 = |A2*x + B2*y + C|/(A2 2 + B2 2 )^0,5. Следует обратить внимание на наличие двух различных решений этого равенства, поскольку в числителе стоит модульное выражение. Два полученных уравнения говорят о наличии взаимно перпендикулярных биссектрис для углов треугольника внутреннего и внешнего.

Для внутреннего угла искомое уравнение можно найти, если определить точку пересечения соответствующей прямой с противоположной исходному углу стороной треугольника. Та точка, сумма расстояний от которой до концов отрезка будет равна длине стороны, принадлежит искомой биссектрисе.

Пример решения задачи

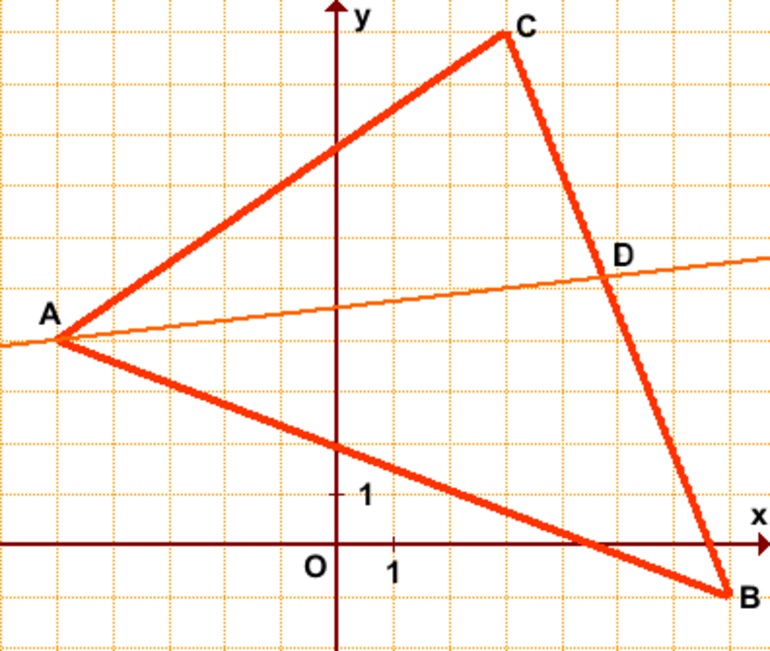
Пусть, треугольник задан координатами A (1, -1), B (0, -2), C (3,0). Следует уравнение биссектрисы найти для угла B и ее длину вычислить.

Сначала нужно написать уравнения прямых для сторон AB и CB, получается:

• AB: (x, y) = (1, -1) + α*(-1, -1) ==> y — x + 2 = 0;
• CB: (x, y) = (3, 0) + α*(-3, -2) ==> 3*y — 2*x + 6 = 0.

Составить уравнения биссектрис можно так:

| y — x + 2 |/(2)^0,5 = | 3*y — 2*x + 6 |/(13)^0,5.

Решение этого уравнения приводит к следующим двум выражениям для взаимно перпендикулярных биссектрис:

Чтобы определить, какая из двух прямых является искомой для треугольника заданного, следует точку пересечения каждой из них со стороной AC найти. Уравнение для AC имеет вид:

Подставляя его в каждое из выражений для биссектрис, можно получить две точки пересечения:

При этом длина основания AC составляет 2,236 единицы через единичный вектор. Расстояние от точек D1 и D2 до A, C равно:

• D1A = 1,4; D1C = 3,635;
• D2A = 0,621; D2C = 1,614.

Видно, что точка пересечения второй прямой D2 лежит между A и C, поэтому соответствующее ей уравнение биссектрисы является ответом на задачу. Ее длину можно вычислить по формуле для модуля вектора BD2:

BD2 = 2,014 единицы.

Таким образом, для определения в треугольнике биссектрисы уравнения по координатам следует уметь находить векторную форму выражений для прямой по координатам двух точек. Также нужно знать свойства делящей пополам угол линии.

Метод координат

Для решения задачи по стереометрии координатным методом нужно выбрать декартову систему координат. Ее можно выбрать как угодно, главное, чтобы она была удобной. Приведем примеры выбора системы координат в кубе, пирамиде и конусе:

Далее необходимо найти координаты основных точек в выбранной системе координат. Это могут быть вершины объемной фигуры, середины ребер или любые другие точки, указанные в условии задачи. Найдем координаты куба и правильной пирамиды (предположим, что все ребра равны (4)):

Куб: Очевидно, что координаты точки (A) в начале координат – ((0;0;0)). т. (B) – ((4;0;0)), т. (G) – ((4;4;4)) и т.д. (Рис. 1).

С кубом все просто, но в других фигурах могут возникнуть трудности с нахождением координат.

Давайте рассмотрим правильную пирамиду (ABCD):

У (т. A) координаты ((0;0;0)), потому что она лежит в начале координат.

Координату (x) точки (С) можно получить, опустив перпендикуляр (CE) из (т.С) на ось (OX). (см. Рис. 2). Получится (т.E), указывающая на искомую координату по (x) – 2.

Координату (y) точки (С) тоже получаем, опустив перпендикуляр (CF) на ось (OY). Координата (y) (т.С) будет равна длине отрезка (AF=CE). Найдем его по теореме Пифагора из треугольника (AFC): $$ ^2=^2+^2,$$ $$ 4^2=2^2+^2,$$ $$ CE=sqrt<12>. $$ Координата (z) точки (C), очевидно, равна (0), потому что (т.С) лежит в плоскости (XOY). $$ C (2;sqrt<12>; 0). $$

И найдем координаты вершины пирамиды ((т.D)). (Рис. 3) Координаты (X) и (Y) у точки (D) совпадают с координатами (X) и (Y) у точки (H). Напомню, что высота правильной треугольной пирамиды падает в точку пересечения медиан, биссектрис и высот. Отрезок (EH=frac<1><3>*CE=frac<1><3>*sqrt<12>) (медианы в треугольнике точкой пересечения делятся в отношении как (frac<1><3>)) и равен координате точки (D) по (Y). Длина отрезка (IH=2) будет равна координате точки (D) по (X). А координата по оси (Z) равна высоте пирамиде: $$ ^2=^2+^2, $$ $$ =sqrt<4^2-<frac<2><3>*AF>^2>, $$ $$ =frac<32><3>. $$ $$ D (2, frac<1><3>*sqrt<12>, frac<32><3>). $$

Координаты вектора

Вектор – отрезок, имеющий длину и указывающий направление.

На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.

Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) : $$ т.А(x_A,y_A,z_A); $$ $$ т.B(x_B,y_B,z_B); $$ Тогда координаты вектора (vec) можно определить по формуле: $$ vec=. $$

Скрещивающиеся прямые

И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора: $$ a=;$$ $$ b=; $$ тогда угол (alpha) между ними находится по формуле: $$ cos<alpha>=frac<sqrt<^2+^2+^2>*sqrt<^2+^2+^2>>. $$

Уравнение плоскости

В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой: $$ A*x+B*y+C*z+D=0,$$ где (A,B,C,D) – какие-то числа.

Если найти (A,B,C,D), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.

Например, пусть даны три точки:

Подставим координаты точек в общее уравнение плоскости:

$$begin A*x_K+B*y_K+C*z_K+D=0,\ A*x_L+B*y_L+C*z_L+D=0, \ A*x_P+B*y_P+C*z_P+D=0.end$$

Получилась система из трех уравнений, но неизвестных 4: (A,B,C,D). Если наша плоскость не проходит через начало координат, то мы можем (D) приравнять (1), если же проходит, то (D=0). Объяснение этому простое: вы можете поделить каждое ваше уравнения на (D), от этого уравнение не изменится, но вместо (D) будет стоять (1), а остальные коэффициенты будут в (D) раз меньше.

Теперь у нас есть три уравнения и три неизвестные – можем решить систему:

Найти уравнение плоскости, проходящей через точки $$ K(1;2;3);,P(0;1;0);,L(1;1;1). $$ Подставим координаты точек в уравнение плоскости (D=1): $$begin A*1+B*2+C*3+1=0,\ A*0+B*1+C*0+1=0, \ A*1+B*1+C*1+1=0.end$$ $$begin A+2*B+3*C+1=0,\ B+1=0, \ A+B+C+1=0.end$$ $$begin A-2+3*C+1=0,\ B=-1, \ A=-C.end$$ $$begin A=-0.5,\ B=-1, \ C=0.5.end$$ Получаем искомое уравнение плоскости: $$ -0.5x-y+0.5z+1=0.$$

Расстояние от точки до плоскости

Зная координаты некоторой точки (M(x_M;y_M;z_M)), легко найти расстояние до плоскости (Ax+By+Cz+D=0:) $$ rho=frac<|A*x_M+B*y_M+C*z_M+D|><sqrt>. $$

Найдите расстояние от т. (H (1;2;0)) до плоскости, заданной уравнением $$ 2*x+3*y-sqrt<2>*z+4=0.$$

Из уравнения плоскости сразу находим коэффициенты: $$ A=2,,B=3,,C=-sqrt<2>,,D=4.$$ Подставим их в формулу для нахождения расстояния от точки до плоскости. $$ rho=frac<|2*1+3*2-sqrt<2>*0+4|><sqrt<2^2+3^2+<-sqrt<2>>^2>>. $$ $$ rho=frac<12><sqrt<16>>=3.$$

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.

Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).

Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.

Дана правильная треугольная призма (ABCFDE), ребра которой равны 2. Точка (G) – середина ребра (CE).

• Докажите, что прямые (AD) и (BG) перпендикулярны.
• Найдите расстояние между прямыми (AD) и (BG).

Решим задачу полностью методом координат.

Нарисуем рисунок и выберем декартову систему координат. (Рис 5).

[spoiler title=”источники:”]

http://kupuk.net/uroki/geometriya/yravnenie-bissektrisy-v-treygolnike-formyla-svoistva-i-reshenie-zadach/

http://sigma-center.ru/method_koordinat

[/spoiler]

Пусть
имеем две прямые:

,
её
вектор нормали
=
и :

,
её
вектор нормали
=.
Будем предполагать, что векторы

и

всегда располагаются внутри одного из
углов, образуемых пересекающимися
прямыми (векторы

и
–
свободные!).
В общем случае прямые при пересечении
образуют один угол острый, а второй
тупой. Возникает классическая
задача:
найти уравнение биссектрисы тупого и
острого углов.

Существует
несколько способов решения задачи. В
каждом из них на первом шаге уста­навливается
факт: векторы

и

располага­ются в области тупого угла
или в области ост­рого. На этот вопрос
достаточно просто отве­чает скалярное
произведение векторов: а)
∙
> 0 – векторы расположены в области
тупого угла; б)
∙
< 0 – векторы расположены в области
острого угла. Далее рассмотрим наиболее
ин­тересные способы решения поставленной
задачи.

Способ–1.
Пусть векторы

и

располагаются в области тупого угла.
Учтём, что для точек, расположенных
внутри тупого угла с векторами

и

отклонения от прямых
и
положи­тельно: >0,
>0.
Это значит, что для точек биссектрисы
тупого угла выполняется равенство:

или: =. ()

Если бы
теперь нужно было построить биссектрису
острого угла, то уравнение нужно за­писать
в виде: =
–. ()

Если бы
векторы

и

располагались в области острого угла,
то биссектриса острого угла определялась
бы выражением ,
а биссектриса тупого –
выражением .

Способ–2.
В этом случае примем схему решения
задачи: а) находим точку

пересече­ния прямых
и ;
б) находим направление биссектрис ;
в) проводим прямую через заданную точку
в заданном направлении.

Для
определения направления биссектрис

построим единичные векторы:

и
,
затем суммы:
=+–определяет
направление биссектрисы угла, содержащего
векторы
,;

=––определяет
направление биссектрисы угла, смежного
первому.

Используя
угловой коэффициент вектора
,
строим биссектрису угла, содержащего
векторы
,;
если использовать угловой коэффициент
век­тора
,
построим биссектрису смежного угла.

Замечание: на
самом деле, достаточно найти толь­ко
один вектор:
для первой биссек­трисы он играет
роль направляющего вектора, а для второй
– роль вектора нормали.

Способ–3.
Воспользуемся уравнением пучка прямых:

и вектором
,
который будет иг­рать роль направляющего
или нормального, в зависимости от
конкретного задания.

Интересно рассмотреть
один и тот же пример, решив его сразу
всеми тремя способами: это позволит
сравнить их трудоёмкости!

☺☺

Пример
3–27:
Составить уравнение биссектрисы тупого
угла, образованного прямыми::;:.

Решение:

Имеем:

=(3,–4)
и
=(12,
5). Вычис­лим:
∙=>0
– векторы рас­по­ло­жены в области
тупого угла. Далее рас­смотрим решения
поставленной задачи тре­мя способами.

Способ–1.
Воспользуемся формулой

при условии равенства отклонений

произвольной точки
биссектрисы от
и :
=,
откуда получаем уравнение биссектрисы
выделенного угла: .

Способ–2.
В этом случае примем схему решения
задачи: а) находим точку
,
в которой пересекаются прямые
и ;
б) находим направление бис­сектрис
;
в) проводим прямую через заданную точку
в заданном направлении.

Координаты
точки
находим из системы урав­нений:
→

=.

Для
определения направления искомой
биссектрисы

построим единичные векторы
=(3,–4)
и
=(12,5),
затем вектор суммы:
=–=–(3,11)
– нормаль биссектрисы угла, содержащего
векторы
,.
Примем:
=(3,11).
Тогда уравнение биссек­трисы запишем
в виде: 3+11=0,
или .

Способ–3.
Воспользуемся уравнением пучка :

+=0,
или в виде:
=0
и направляющим вектором
=(11,–3).
Вектору

соответствует угловой коэффициент

=–.
Тогда:
===–.
Получаем уравнение искомой биссектрисы:
.

Ответ:
искомая
биссектриса: .

Замечание: трудоёмкость
рассмотренных способов различна;
одновременное использование разных
способов полезно наблюдением одинакового
окончательного результата.

☻

Соседние файлы в папке ЛА и АГ пособие

• #
• #
• #
• #
• #
• #

Всем привет, тут такая задача.

Даны координаты вершин треугольника: A = (−3, −3, −1), B = (−5, −4, −2), C = (3, −7, −3)
В треугольнике ABC найти уравнения биссектрис и медиан.

Сначала попробовал найти уравнения по двум точкам, то есть сначала найти точку, в которой биссектриса пересекает противоположную сторону. Это я пытался делать через формулу деления отрезков в заданном отношении, но там отношение получается с корнями, очень некрасивое, и из-за этого потом координаты точки пересечения получаются трёхэтажными дробями, вроде
[math]x_{a} = frac{ -3+frac{ 3sqrt{3} }{ sqrt{37} } }{ 1+sqrt{37} }[/math]

Поэтому нашел второй способ, с помощью уравнения биссектрисы угла, вот такое уравнение нашёл для плоскости:

[math]frac{ a_{1}x+b_{1}x+c_{1} }{ sqrt{a_{1}^{2}+b_{1}^{2} } }= pm frac{ a_{2}x+b_{2}x+c_{2} }{ sqrt{a_{2}^{2}+b_{2}^{2} } }[/math]
Где [math]a_{1}x+b_{1}x+c_{1}[/math] и [math]a_{2}x+b_{2}x+c_{2}[/math] – уравнения сторон, которые образуют наш угол

Так вот, можно ли применять эту формулу для пространства и если да, то как правильно её изменить?

Уравнение биссектрисы в треугольнике — формула, свойства и решение задач

Прямая на плоскости

Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:

1. На плоскости, где достаточно двух координат для описания любых геометрических объектов.
2. В трехмерном пространстве, где любая точка имеет три координаты.

Когда рассматривают треугольники и их элементы, то в ряде ситуаций речь идет именно о двумерном пространстве. В нем всякая прямая линия может быть выражена в виде нескольких математических форм или уравнений. Чаще всего используются следующие типы:

1. Общий. Он также называется универсальным. Прямая представляет собой следующую математическую запись: A*x + B*y + C = 0. Здесь A, B, C — числовые коэффициенты, x и y — переменные, являющиеся координатами. Сразу нужно отметить, что эта форма представления прямой используется для составления уравнения биссектрисы угла. Для удобства геометрического изображения общую форму записи часто представляют в виде y = f (x). Нужно понимать, что указанной форме в пространстве соответствует не прямая, а плоскость.
2. Канонический или уравнение в отрезках. Имеет оно такой вид: y/p + x/q = 1. Здесь p, q — это координаты, в которых прямая пересекает оси y и x, соответственно, поэтому удобно ее изображать в координатной системе.
3. Векторный. Это один из важных типов представления прямой как на плоскости, так и в пространстве. По сути, он является исходным представлением, из которого можно получить все остальные. Математически он записывается так: (x, y) = (x0, y0) + α*(v1, v2). Где (x0, y0) — координаты произвольной точки, которая лежит на прямой, (v1, v2) — направляющий вектор, он параллелен заданной прямой, α — произвольное число, параметр.
4. Параметрический. Этот тип представляет собой систему уравнений, которую удобно использовать во время преобразования одного вида прямой в другой. Представляет он собой следующую математическую запись: x = x0 + α*v1; y = y0 + α*v2. Несложно понять, что, выражая параметр α, можно получить уравнения общего вида и в отрезках. Объединяя же систему уравнений в одно выражение, получается векторная форма записи прямой.

Делящая пополам угол линия

Каждый школьник, который знаком с азами геометрии, знает, что прямая, делящая на две равные части произвольный угол, называется биссектрисой. Этот элемент присутствует для любой фигуры, которая в своем составе содержит какой-либо угол.

Другое определение биссектрисы гласит, что она представляет собой геометрическое расположение точек, которые равноудалены от соответствующих сторон углового объекта. Например, если имеется угол dac, то любая из точек биссектрисы находится на одинаковом расстоянии как от отрезка da, так и от отрезка ac.

Способы построения

В классах общеобразовательных школ рассматривают два основных способа построения биссектрисы. Это следующие:

1. С помощью транспортира. Для этого следует измерить заданный угол в градусах, разделить его пополам. Полученное значение отметить в виде точки. Затем соединить вершину угла и поставленную точку внутри него. Получится искомый элемент.
2. С использованием циркуля и линейки. Эти инструменты еще проще применять для построения биссектрисы, чем транспортир. Сначала необходимо установить в вершину угла ножку циркуля и отметить дугами пересечение окружности со сторонами. Затем, в точки пересечения поставить ножку циркуля и провести две окружности. Соединив две точки их пересечения одной прямой, можно получить биссектрису.

Имеется еще один метод, который позволяет просто начертить изучаемый линейный элемент. Для его использования нужна линейка со шкалой. С помощью нее следует от вершины угла отмерить два одинаковых отрезка любой длины. Затем соединить концы этих отрезкой, получится равнобедренный треугольник.

В нем любая биссектриса также является высотой и медианой. Поэтому, разделив его ровно пополам линейкой, и соединив полученную точку с вершиной, можно получить требуемую линию.

Основные свойства

Чтобы найти по координатам вершин длину биссектрисы треугольника, следует знать некоторые свойства этого геометрического объекта. Главным из них является существование двух линий, которые делят пополам исходный угол. Нужно понимать, что угол бывает не только внутренний, но и внешний. По сути, оба типа образуются при пересечении двух прямых. Нетрудно доказать, что биссектрисы каждого из них пересекаются всегда под углом 90 °.

Еще одним важным свойством является тот факт, что пересекаются в одной точке биссектрисы треугольника. Она представляет собой центр вписанной в фигуру окружности. Чтобы это доказать, следует вспомнить, что каждая точка биссектрисы равноудалена от соответствующих сторон угла.

Пусть имеется треугольник ABC. У него две биссектрисы пересекаются в точке O. Пусть это будут линии для углов A и B. Расстояние от O до AC должно быть равно таковому от O до AB. С другой стороны, расстояния от O до AB и до BC также одинаковые. Поэтому дистанции от O до BC и до AB также равны, а значит, точка O лежит на биссектрисе угла C и центром вписанной окружности является.

В треугольнике рассматриваемый геометрический элемент используется часто для решения задач благодаря применению так называемой теоремы биссектрис. Чтобы ее сформулировать максимально простым языком, следует представить, что имеется треугольник произвольного типа ABC. В нем проведена биссектриса AD, где точка D лежит на прямой BC. Тогда справедливо следующее выражение:

Это равенство не является очевидным, однако, оно было известно еще древнегреческим мыслителям. Эту теорему в несколько иной форме можно встретить в знаменитом труде по геометрии Евклида, который называется «Элементы». Доказательство равенства несложно провести с использованием небольших дополнительных построений и применением признаков подобия треугольников.

Наконец, отрезок биссектрисы, который заключен между вершиной и противоположной стороной треугольника, имеет определенную длину. Вычислить ее можно с использованием следующего равенства:

Это равенство прописано для угла A треугольника ABC, в котором противоположная A сторона имеет длину a. Стороны AB и AC имеют длины c и b, соответственно. Буквой p обозначен полупериметр фигуры.

Важно понимать, если нарисовать прямоугольный параллелепипед (или иную фигуру) в пространстве, и построить биссектрису для его граней, она будет представлять собой не прямую, а плоскость.

Уравнение биссектрисы треугольника

Когда известно, как математически записывать выражения для прямых, и что такое биссектриса, и какими свойствами она обладает, можно переходить к непосредственному нахождению ее уравнения.

В общем случае задача решается в результате применения следующей последовательности действий (существуют онлайн-ресурсы, позволяющие решить данную проблему):

1. Сначала требуется определить уравнения двух сторон угла по их координатам. Это легко сделать в векторной форме, а затем, преобразовать ее в выражение общего типа.
2. Далее, необходимо найти уравнение биссектрис первого координатного угла, прировняв расстояния от ее точек до соответствующей стороны. Рабочая формула имеет вид: |A1*x + B1*y + C|/(A1 2 + B1 2 )^0,5 = |A2*x + B2*y + C|/(A2 2 + B2 2 )^0,5. Следует обратить внимание на наличие двух различных решений этого равенства, поскольку в числителе стоит модульное выражение. Два полученных уравнения говорят о наличии взаимно перпендикулярных биссектрис для углов треугольника внутреннего и внешнего.
3. Для внутреннего угла искомое уравнение можно найти, если определить точку пересечения соответствующей прямой с противоположной исходному углу стороной треугольника. Та точка, сумма расстояний от которой до концов отрезка будет равна длине стороны, принадлежит искомой биссектрисе.

Пример решения задачи

Пусть, треугольник задан координатами A (1, -1), B (0, -2), C (3,0). Следует уравнение биссектрисы найти для угла B и ее длину вычислить.

Сначала нужно написать уравнения прямых для сторон AB и CB, получается:

• AB: (x, y) = (1, -1) + α*(-1, -1) ==> y — x + 2 = 0;
• CB: (x, y) = (3, 0) + α*(-3, -2) ==> 3*y — 2*x + 6 = 0.

Составить уравнения биссектрис можно так:

| y — x + 2 |/(2)^0,5 = | 3*y — 2*x + 6 |/(13)^0,5.

Решение этого уравнения приводит к следующим двум выражениям для взаимно перпендикулярных биссектрис:

• y*(6−3*3 0,5 ) + x*(3*3 0,5 −4)+12−6*3 0,5 = 0;
• y*(3*3 0,5 +6) -x*(4+3*3 0,5 )+12+6*3 0,5 = 0.

Чтобы определить, какая из двух прямых является искомой для треугольника заданного, следует точку пересечения каждой из них со стороной AC найти. Уравнение для AC имеет вид:

Подставляя его в каждое из выражений для биссектрис, можно получить две точки пересечения:

При этом длина основания AC составляет 2,236 единицы через единичный вектор. Расстояние от точек D1 и D2 до A, C равно:

• D1A = 1,4; D1C = 3,635;
• D2A = 0,621; D2C = 1,614.

Видно, что точка пересечения второй прямой D2 лежит между A и C, поэтому соответствующее ей уравнение биссектрисы является ответом на задачу. Ее длину можно вычислить по формуле для модуля вектора BD2:

BD2 = 2,014 единицы.

Таким образом, для определения в треугольнике биссектрисы уравнения по координатам следует уметь находить векторную форму выражений для прямой по координатам двух точек. Также нужно знать свойства делящей пополам угол линии.

Образцы выполнения некоторых заданий

Рассмотрим решения некоторых практических упражнений.

Задание 2(е)

На плоскости даны точки А(11; -5), В(6;7), С(-10; -5). Найти уравнение биссектрисы угла А.

Решение задания 2(е)

Найдем направляющий вектор биссектрисы как сумму ортов векторов и

,

или (умножая на )

.

; ;

; .

.

Таким образом, в качестве направляющего вектора биссектрисы угла А можно взять вектор 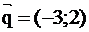и уравнение биссектрисы будет иметь вид

.

Задание 3

Дана точка (0;2) пересечения медиан треугольника и уравнения двух его сторон 5х – 4у + 15 = 0 и 4х + у – 9 = 0. Найти координаты вершин треугольника и уравнение третьей стороны.

Решение Координаты одной вершины найдем как координаты точки пересечения данных сторон, для чего решим систему уравнений

Получаем или

Точка О_ц пересечения медиан треугольника называется его центром. Отметим одно свойство центра треугольника, которое используем для нахождения координат остальных вершин:

; ,

где х_ц, у_ц – координаты центра треугольника;

х_i, y_i – координаты i-ой вершины треугольника,

Для доказательства этих формул рассмотрим треугольник А₁А₂А₃, где А_i(x_i;y_i), i = 1-3 (см.рис.2.1).

Рис.2.1. Вспомогательный чертеж к заданию 3

Пусть В середина стороны А₁А₂. Тогда А₃В – медиана треугольника А₁А₂А₃. По известному из элементарной геометрии свойству медиан треугольника .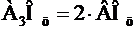

Тогда координаты точки В найдем по формулам

и ,

а координаты центра О_ц из векторного соотношения , которое в координатной форме записывается так

, .

Отсюда, выражая х_ц и у_ц через x_i, y_i, получим требуемые формулы.

Вернемся к решению задания 3. Используя доказанные формулы, полагая в них х₁ = 1 и у₁ = 5, х_ц = 0 и у_ц = 2, получим два уравнения, которым должны удовлетворять координаты остальных двух вершин

; ,

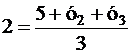
Еще два уравнения получим, если потребуем, чтобы искомые точки, вершины треугольника, принадлежали заданным сторонам, т.е. их координаты удовлетворяли уравнениям этих сторон

Итак, для определения четырех неизвестных х₂, у₂, х₃, у₃, мы имеем четыре независимых (!) условия (уравнения)

Решив эту систему, получим х₂ = -3, у₂ = 0, х₂= 2, у₃ = 1.

Наконец, уравнение третьей стороны запишем как уравнение прямой, проходящей через две заданные точки (-3;0) и (2;1)

или .

Итак, уравнение третьей стороны x – 5у + 3 = 0, а вершины треугольника имеют координаты (1;5), (-3;0), (2;1).

Задание 7

Составить уравнение линии, для каждой точки М которой, отношение расстояний до точки F( ) и до прямой
равно .

Привести уравнение линии к каноническому виду, определить тип линии и построить линию на чертеже. Показать на чертеже фокусы, директрисы, асимптоты (если они имеются у построенной линии).

Замечание. Отметим, что в заданиях этого модуля ; ; .

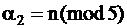
Пусть n = 101. Тогда:

, т.к. ;

, т.к. ;

, т.к. .

Итак, для n = 101 первая часть задания 7 принимает вид:

Составить уравнение линии, для каждой точки М которой, отношение расстояния до точки F(-4;1) и до прямой x = 1
равно .

Решение задания 7 (для n = 101).

Пусть М(х;у) произвольная точка искомой линии, r – расстояние от М до F и d – расстояние от точки М до прямой x = 1. Тогда

и .

По условию , т.е. d = 2r.

— уравнение искомой линии.

Упростим уравнение линии и приведем его к каноническому виду. Для этого возведем обе части уравнения в квадрат и выполним следующие преобразования уравнения

х 2 – 2х +1 = 4х 2 + 32х + 64 + 4(у – 1) 2 ,

3х 2 + 34х + 4(у – 1) 2 + 63 = 0,

,

.

Последнее уравнение – это каноническое уравнение эллипса с полуосями и ( ), центр которого находится в точке с координатами . Координаты вершин эллипса
и , т.е. (-9;1), , ,
. Построим эллипс на чертеже (см.рис.2.2).

Рис.2.2. Эллипс с уравнением

Фокусы эллипса имеют координаты , где .

.

Итак, координаты фокусов F₁(-4;1), F₂( ;1).

Директрисы эллипса имеют уравнения , где е – эксцентриситет эллипса

.

Уравнения директрис , т.е.

D₂: .

Отметим фокусы и директрисы эллипса на рис.2.2.

Обратите внимание на совпадение фокуса F₁ с точкой, данной в условии задания 7, на совпадение директрисы D₁ с прямой х = 1 из условия этого задания, и совпадение эксцентриситета е с параметром е в условии. По этому поводу см. теоретическое упражнение 18.

В пространстве даны точки А(-2; -4;1), В(3;1; -1), С(5;1;1),
S(1;-4;0). Найти координаты центра и радиус вписанной в пирамиду SABC сферы (условие сформулировано для n = 101).

Решение задания 4(м)

Пусть точка О(x₀;y₀;z₀) – центр сферы, вписанной в пирамиду SABC. Найдем точку О как точку, равноудаленную от граней пирамиды. Для этого найдем уравнения всех граней и расстояния от точки О до этих граней (уравнения некоторых граней находятся в предшествующих пункту М пунктах задания 4).

Грань АВС. Уравнение грани

или 5х – 7у – 5z – 13 = 0.

Точки О и S лежат по одну сторону от грани АВС, поэтому отклонения этих точек от грани АВС имеют одинаковые знаки. Отклонение (S) точки S от грани АВС равно

> 0.

.

Аналогично все делается для граней ABS, BCS, CAS.

Грань ABS имеет уравнение 5х + у + 15z – 1 = 0 и
.

Грань BCS имеет уравнение 5х – 3у – 5z – 17 = 0 и
.

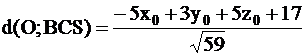
Наконец, грань CAS имеет уравнение 5х – 7у + 15z + 33 = 0 и
.

Так как О – центр сферы, вписанной в пирамиду SABC, то

d(O; ABC) = d(O; ABS) = d(O; BCS) = d(O; CAS) = r,

где r – радиус вписанной сферы.

Тогда координаты точки О должны удовлетворять системе

В отличие от других заданий этого модуля, коэффициенты и решение этой системы найдем приближенно, с помощью микрокалькулятора или ЭВМ. Получим систему

и уравнение вписанной сферы

.

1. Общее уравнение прямой на плоскости. Нормальный вектор прямой. Угол между прямыми. Условия параллельности и перпендикулярности.

2. Уравнение прямой с угловым коэффициентом. Угол между прямыми. Условия параллельности и перпендикулярности.

3. Каноническое и параметрическое уравнения прямой на плоскости. Направляющий вектор прямой. Угол между прямыми. Условия параллельности и перпендикулярности.

4. Уравнение прямой, проходящей через две заданные точки.

5. Уравнения прямых, проходящих через данную точку параллельно и перпендикулярно данной прямой (3 случая задания данной прямой: общим уравнением, каноническим уравнением, уравнением с угловым коэффициентом).

6. Общее уравнение плоскости в пространстве, нормальный вектор плоскости. Угол между плоскостями. Условие параллельности и перпендикулярности.

7. Уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой.

8. Общее, каноническое и параметрическое уравнения прямой в пространстве. Угол между прямыми. Условия параллельности и перпендикулярности.

9. Угол между прямой и плоскостью в пространстве. Условие параллельности и перпендикулярности прямой и плоскости.

10. Уравнение плоскости, проходящей через данную точку, перпендикулярно данной прямой. Уравнение прямой, проходящей через данную точку, перпендикулярно данной плоскости.

11. Расстояние от точки до: прямой на плоскости; прямой в пространстве; плоскости в пространстве.

12. Уравнение линии на плоскости. Общее уравнение кривой второго порядка.

13. Каноническое и параметрическое уравнения окружности.

14. Эллипс (фокусы и директрисы, фокальные радиусы точки, эксцентриситет). Каноническое и параметрическое уравнения эллипса.

15. Гипербола (фокусы, директрисы и асимптоты, фокальные радиусы точки, эксцентриситет). Каноническое и параметрическое уравнения гиперболы.

16. Парабола (фокус и директриса, фокальный радиус точки, эксцентриситет). Каноническое уравнение параболы.

17. Приведение общего уравнения кривой второго порядка к каноническому виду.

18. Полярные координаты на плоскости. Уравнение линии в полярных координатах.

19. Уравнение поверхности в пространстве. Общее уравнение поверхностей второго порядка.

20. Основные типы поверхностей второго порядка и их канонические уравнения.

1. Бугров Н.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1980. 176 с.

2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1: Учебное пособие для студентов втузов. – 3-е изд., перераб. и доп. – М.: Высшая школа, 1980. 320 с.

3. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1981. 232 с.

4. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1980. 240 с.

5. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа/Под ред. А.В. Ефимова, Б.П. Демидович. – М.: Наука, 1981, 464 с.

6. Высшая математика. Методические указания и контрольные задания/Под ред. Ю.С. Арутюнова. – М.: Высшая школа, 1985.

7. Гусак А.А. Пособие к решению задач по высшей математике. – Изд. 3-е. – Минск: Изд-во БГУ, 1973. 532 с.

8. Кузнецов А.А. Сборник заданий по высшей математике (типовые расчеты): Учеб. пособие для втузов. – М.: Высшая школа, 1983. 175 с.

9. Погорелов А.В.Аналитическая геометрия.– М.:Наука, 1968. 176с

Примеры решений по аналитической геометрии на плоскости

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.