Как найти уравнение цилиндра

Содержание:

1. Цилиндры
2. Упражнение
3. Поверхности второго порядка
4. Сфера и ее уравнение
5. Цилиндрические поверхности 
6. Цилиндры второго порядка
7. Эллипсоид 
8. Гиперболоиды
9. Параболоиды
10. Конические поверхности 
11. Поверхность вращения 
12. Понятие о поверхности второго порядка
13. Общее уравнение поверхности второго порядка, основные определения
14. Цилиндрические и конические поверхности
15. Исследование формы поверхностей второго порядка методом сечений

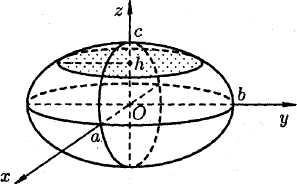
Поверхностью второго порядка в пространстве называется поверхность, определяемая уравнением второй степени относительно текущих координат

Рассмотрим частные виды поверхностей второго порядка. Сфера с центром в точке и радиусом имеет уравнение где — заданные числа (рис. 2.18).

Раскрыв скобки и перенеся в левую часть, получим Нетрудно проверить, что уравнение второй степени относительно в котором коэффициенты при равны, а члены с произведениями координат отсутствуют, представляет собой уравнение сферы (кроме случаев, когда это уравнение не определяет никакой поверхности).

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Цилиндры

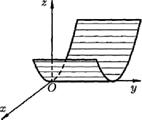
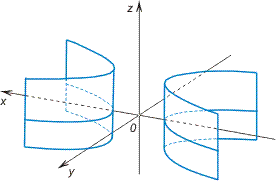
Цилиндрической называется поверхность, описываемая прямой, остающейся параллельной некоторому направлению и пересекающей данную линию. Последняя называется направляющей цилиндрической поверхности, а сама прямая — образующей. Пусть, например, образующие цилиндрической поверхности параллельны оси и направляющей служит эллипс (рис. 2.19)

в плоскости с уравнением Эта поверхность называется эллиптическим цилиндром. Пусть — произвольная точка этого цилиндра, а точка — проекция на плоскость

Ясно, что абсциссы и ординаты точек и совпадают. Так как точка лежит на эллипсе, то ее координаты х и у удовлетворяют уравнению (2.55). Но тогда этому уравнению удовлетворяют координаты х и у точки цилиндра. Значит, (2.55) есть уравнение цилиндра.

Итак, уравнение (2.55) на плоскости определяет эллипс, а в пространстве — эллиптический цилиндр с образующей, параллельной направляющей которого является указанный эллипс.

Возможно вам будут полезны данные страницы:

Упражнение

Изобразите самостоятельно:

1) гиперболический цилиндр с уравнением и образующей, параллельной оси

2) параболический цилиндр с уравнением и образующей, параллельной оси

Поверхности второго порядка

Определение. Поверхности второго порядка называют геометрическое место точек пространства, декартовые координаты которых удовлетворяют уравнению второй степени. 

Сфера и ее уравнение

Сферой называют геометрическое место точек пространства,  равноудаленное от заданной точки – центра сферы. 

Если центром сферы является точка  а радиус  тогда уравнение сферы будет: 

Если центр сферы находится в начале координат  и радиус  тогда уравнение сферы будет: 

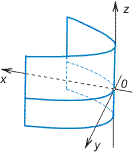
Цилиндрические поверхности 

Поверхность называется цилиндрической, если она образуется прямой (образующая), параллельно к заданной прямой   и которая проходит через заданную линию  (направляющая линия). Пример цилиндрической линии изображен на рис. 2.24

Если образующая цилиндрической поверхности параллельна оси  а образующая  лежит на плоскости  и задана уравнением: 

тогда уравнение цилиндрической поверхности будет: 

Уравнение  обозначает цилиндрическую поверхность с образующей, что параллельна оси  уравнение  – цилиндрическая поверхность с образующей, что параллельна оси  

Цилиндры второго порядка

а) Эллиптичным цилиндром  называется поверхность (рис. 2.25), каноничное уравнение которой имеет вид: 

Если  то получим круговой цилиндр: 

б) Гиперболичным цилиндром называется поверхность, уравнение которой имеет вид (рис. 2.26): 

в) Параболическим цилиндром называется поверхность, каноничное уравнение которой имеет вид (рис. 2.27): 

Эллипсоид 

Эллипсоидом называется поверхность, каноничное уравнение которой имеет вид (рис. 2.28): 

 Отрезки  – называются полуосями эллипсоида. 

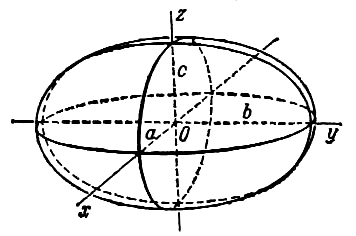
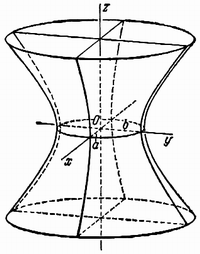
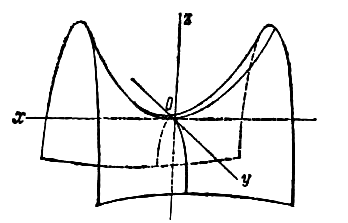
Гиперболоиды

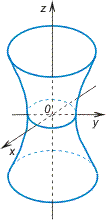
а) однополосный гиперболоид. 

Однополосным гиперболоидом (рис. 2.29) называется поверхность, каноническое уравнение которой имеет вид :

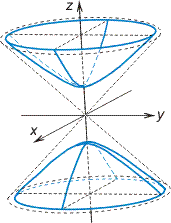
 б) Двуполостный гиперболоид. Двуполостным гиперболоидом (рис. 2.30) называется поверхность, каноничное уравнение которой имеет вид: 

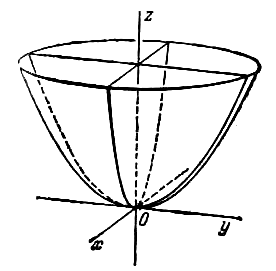
Параболоиды

а) Эллиптическим параболоидом (рис. 2.31) называется поверхность, каноничное уравнение которой имеет вид: 

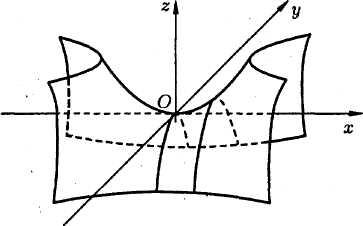
б) Гиперболичным параболоидом (рис. 2.32) называется поверхность, каноничное уравнение которой имеет вид: 

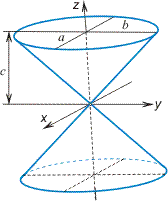
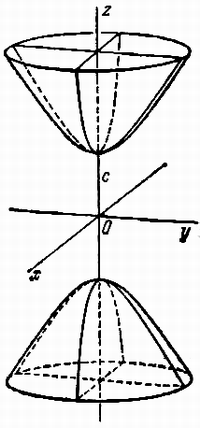
Конические поверхности 

конической поверхностью называется поверхность, которая описана прямой, что проходит через точку – вершину конуса – и что пересекает заданную линию – направляющую конуса. 

Уравнение конуса (рис. 2.33) второго порядка имеет вид: 

Поверхность вращения 

Пусть в плоскости  задана линия  что имеет уравнение  Тогда чтобы получить уравнение поверхности, что образована вращением линии  что лежит в плоскости  около оси  нужно в уравнение этой линии заменить  на  Искомое уравнение поверхности вращения будет 

Аналогично правила будут иметь место и по отношению к поверхностям, которые образуют обращение плоских линий около других координатных осей. 

Примеры:  1) уравнение поверхности, что образуются вращением эллипса  около оси  будет  (эллипсоид вращения). 

2) уравнение поверхности, что образуются вращением гиперболы  около оси  будет  или  (двуполостный гиперболоид). 

Примеры решения задач:

Задача 2.126

Обозначить координаты центра сферы и ее радиус: 

Решение. Предоставим заданное уравнение в виде (2.43), для этого: 1) объединяем в группы члены, которые содержат одноименные координаты; 

2) выделим в группах полные квадраты. Получим: 

Соизмеряя с (2.43), получим  Следует, центр сферы – точка  радиус 

Задача 2.127 

Эллипс с полуосями 5 и 3 вращается около своей большей оси. которая совпадает с началом координат. Сложить уравнение поверхности, что описывает эллипс при вращении. 

Решение. Сложим каноническое уравнение эллипса с центром в начале координат, который размещен в плоскости 

чтобы получить уравнение поверхности, которая образована вращением в плоскости  около оси  необходимо в уравнении эллипса заменить  на  Получим эллипсоид вращения, который протянул вдоль оси 

 или 

Задача 2.128 

Сложим уравнение конуса с вершиной в начале координат и направляющей: 

Решение. Канонические уравнения образующих, что проходят через вершину  конуса и точки  направляющей, будут: 

Исключим   в заданных уравнениях. Изменяя   через  обозначим   и  из остальных двух уравнений: 

подставим полученные значения   и  в первое уравнение направляющей, получим: 

 или 

Задача 2.129 

Какие поверхности обозначаются уравнениями: 

Решение. Каждое из уравнений содержит только две переменные   и   и обозначает на плоскости  кривые: 1) круг, 2) эллипс, 3) параболу, 4) гиперболу. 

В пространстве же каждое из них обозначается цилиндрическую поверхность с образующими, что параллельны оси   так как эти уравнения не содержат переменной . Направляющими этих цилиндрических поверхности являются указанные кривые: 

 – уравнение прямого углового цилиндра; 

 – уравнение эллиптического цилиндра;

 – уравнение параболического цилиндра; 

  – уравнение гиперболичного цилиндра. 

Задача 2.130 

Гипербола с полуосями 3 и 4 вращается около своей мнимой оси, которая совпадает с осью  Центры гиперболы совпадает с началом координат. Сложить уравнение поверхности, которое получим при вращении гиперболы. 

Решение. Сложим каноничное уравнение гиперболы с центром в начале координат, что находятся в плоскости 

Чтобы сложить уравнение поверхности, образованной вращением гиперболы, что находится в уравнение гиперболы вместо  подставить 

 или 

Следует, получим однополосный гиперболоид вращения: 

Понятие о поверхности второго порядка

Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению.

Общее уравнение поверхности второго порядка, основные определения

Поверхностью второго порядка называется множество точек пространства , описывается уравнением , левая часть которого является многочленом второй степени относительно переменных :

где коэффициенты уравнения при текущих переменных ; – свободный член; и по крайней мере один из коэффициентов отличается от нуля

Уравнение (10.27) называют общим уравнением поверхности второго порядка. Вид поверхности и ее расположение относительно координатных плоскостей зависит от значений параметров в (10.27).

Если не существует ни одной точки , которая удовлетворяет общее уравнение, говорится, что оно определяет мнимую поверхность.
Поверхность называется вырожденной, если ее общее уравнение описывает точку, одну или две плоскости. К примеру:

уравнение точки в 

уравнения двух плоскостей, параллельных 

уравнения двух биссекторных плоскостей.

При изучении поверхностей второго порядка решаются две взаимно обратные основные задачи:
1) по известным геометрическим свойствам точек поверхности составить уравнение соответствующей поверхности;
2) по известным уравнением поверхности установить геометрические свойства ее точек.

Примером решения первой основной задачи является построение уравнения сферы (9.2). Уравнение других важнейших поверхностей рассматриваются ниже.

Цилиндрические и конические поверхности

Цилиндрической поверхностью, или просто цилиндром, называется поверхность, образованная движением прямой, перемещается параллельно самой себе вдоль фиксированной линии (кривой). Подвижную прямую называют образующей, а фиксированную кривую – направляющей цилиндрической поверхности. Направляющей может быть любая сомкнутая или разомкнутая линия.

Цилиндром второго порядка называется цилиндрическая поверхность, направляющей которой является кривая второго порядка: эллипс (круг), гипербола, парабола. Название цилиндра определяется названием его направляющей. Если образующая параллельна одной из координатных осей, а направляющая лежит в плоскости, перпендикулярной этой оси, то уравнение цилиндра совпадает с уравнением направляющей. При геометрической интерпретации изображается, как правило, часть поверхности между двумя плоскостями, перпендикулярными образующей.
К примеру:

 уравнения эллиптического цилиндра (рис. 10.9 а)

 уравнения гиперболического цилиндра (рис. 10.9 б)

 уравнения параболического цилиндра (рис. 10.9 в).

Рис. 10.9

Отсутствие переменной  в приведенных уравнениях означает, что аппликанта точек поверхности может быть любым действительным числом, потому что коэффициент при переменной  в уравнениях следует считать равными нулю. Например, уравнение параболического цилиндра можно записать в виде: . Итак, образующая цилиндра параллельна оси, совпадающей с переменной, которая отсутствует в уравнении поверхности.

Если в уравнениях эллипса и гиперболы положить , то получим соответственно круговой и равносторонний гиперболический цилиндры.

Конической поверхностью, или конусом, называется поверхность, образованная движением прямой, проходящей через заданную точку, вдоль фиксированной кривой. Подвижную прямую называют образующей, заданную точку – вершиной, а фиксированную кривую – направляющей конуса. Если образующей является кривая второго порядка, то поверхность называется конусом второго порядка.
На рис. 10.10 изображен конус второго порядка, определяется уравнением

Рис. 10.10

с вершиной в начале координат, направляющей которого является эллипс

в плоскости 

Поверхность симметрична относительно начала координат, а координатные плоскости является ее плоскостями симметрии. Множество точек поверхности с неотъемлемыми (неположительные) аппликатами называется верхней (нижней) полостью конуса.

Если направляющей конуса является круг , то он называется круговым.

Эллипс, парабола, гипербола – кривые второго порядка – можно получить сечением прямого кругового конуса плоскостями, которые не проходят через его вершину (рис. 10.11). А именно: если плоскость пересекает только одну полость конуса и непараллельных одной из его образующих, то кривой сечения является эллипс; в частном случае – круг;
если секущая плоскость параллельна одной из образующих конуса, то результат сечения – парабола;
если плоскость сечения пересекает обе полости конуса, то кривой сечения является гипербола.

Рис. 10.11

Исследование формы поверхностей второго порядка методом сечений

Приведенные выше уравнения поверхностей второго порядка складывались по геометрическим свойствам их точек в соответствии с определений поверхностей. Для решения обратной задачи (по данным уравнением поверхности определить ее вид) применяется метод сечений, суть которого заключается в следующем:

1) анализируют поверхность, устанавливая за ее уравнением линии пересечения (сечения) данной поверхности координатными плоскостями параллельными им;

2) синтезируют определенные на предыдущем шаге геометрические свойства поверхности, что позволяет представить вид поверхности и изобразить ее.

Продемонстрируем применение метода сечений к исследованию уравнения эллиптического параболоида:

Исследование предполагает такие шаги:
1) найдем линии пересечения поверхности (10.28) с плоскостью и плоскостями, параллельными ей :

Если:

а) , то уравнение (10.29) удовлетворяют лишь координаты точки , то есть плоскость является касательной к данной поверхности;
б) , то получаем воображаемую линию, поскольку плоскости заданную поверхность не пересекают;
в) , то уравнение (10.29) можно записать в виде:

то есть сечением поверхности плоскостями, параллельными , есть эллипсы, полуоси которых увеличиваются вместе с увеличением (рис. 10.12);

2) установим линию пересечения поверхности с плоскостью :

Это уравнение параболы, расположенной в плоскости , с осью симметрии .

Рис. 10.12

3) определим (аналогичным образом) сечение поверхности плоскостью : это парабола, которая описывается уравнением , и расположена в плоскости (с осью симметрии ).
4) изображаем согласно рассмотренным выше соответствующие линии (рис. 10.12), что позволяет составить представление о форме исследуемой поверхности. Наконец намечаем обвод – линию, получается как множество точек прикосновения к поверхности прямых, параллельных выбранном направления проектирования.

Аналогично осуществляется построение параболоида , сечения которого – параболы ветвями вниз, и параболоидов, оси которых совпадают с координатными осями . Уравнение таких поверхностей получаемых из рассмотренного выше с помощью циклической перестановки переменных.

Поверхностью вращения называется поверхность, для которой каждый из ее сечений плоскостью, перпендикулярной одной из координатных осей или произвольной оси , является кругом. Круговой конус и круговой цилиндр являются примерами таких поверхностей: конус образуется вращением вокруг оси прямой, проходящей через начало координат, а цилиндр – прямой, параллельной оси , причем прямые не принадлежат плоскости, перпендикулярной оси вращения.

Уравнения поверхностей, симметричные относительно координатных осей или / и координатных плоскостей, называют каноническими, или стандартными.

В заключение отметим, что приведенные сведения используются при изучении интегрирования функций двух переменных и является фундаментом для более глубокого изучения теории поверхностей второго порядка.

Далее в таблице 10.1 приводятся канонические уравнения и изображения важнейших поверхностей второго порядка.

Важнейшие поверхности второго порядка                                                                    Таблица 10.1

Лекция 4. Поверхности
второго порядка

Цилиндрические
поверхности

Название цилиндра
определяется названием направляющей.
Если направляющей служит эллипс

в плоскости
,
то соответствующая цилиндрическая
поверхность назы­вается эллиптическим
цилиндром
(см. рис. 1).

Рис. 2	Рис. 1

Ч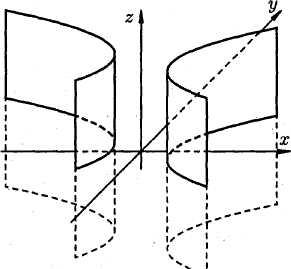астным
случаем эллиптического цилиндра является
круговой
цилиндр,
его уравнение
.
Уравнение

определяет в
пространстве параболи­ческий
цилиндр
(см. рис. 2). Уравнение

определяет в пространстве гиперболи­ческий
цилиндр

(см. рис. 3).

Все эти поверхности
называются цилиндрами
второго порядка,
так как их уравнения есть уравнения
второй степени относительно текущих
коорди­нат
,

и
.

Канонические
уравнения поверхностей второго порядка

По заданному
уравнению поверхности второго порядка
(т. е. поверхности, уравнение которой в
прямоугольной системе координат является
алгебраическим уравнением второй
степени) будем определять ее геометрический
вид. Для этого применим так называемый
метод сечений: исследование вида
поверхности будем производить при
помощи изучения ли­ний пересечения
данной поверхности с координатными
плоскостями или плоскостями, им
параллельными.

Эллипсоид.
Исследуем
поверхность, заданную уравнением

.
(1)

Рассмотрим сечения
поверхности (1) плоскостями, параллельными
плоскости
.
Уравнения таких плоскостей:
,
где

— любое число.

Линия,
получаемая в сечении, определяется
двумя уравнениями

,

.
(2)

Исследуем уравнения
(2):

а) Если
,

,
то
.
Точек пересечения поверхно­сти (1) с
плоскостями

не существует.

б) Если
,
т. е.
,
то
.
Линия пересечения (2) вырождается в две
точки

и
.
Плоскости

и

касаются данной поверхности.

в)
Если
,
то уравнения (2) можно переписать в виде:

,

.

Как видно, линия
пересечения есть эллипс с Рис. 4
полу­осями

и
.

При
этом чем меньше
,
тем больше полуоси

и
.
При

они достигают своих наибольших значений:

,

.
Уравнения (2) примут вид

,

.

Аналогичные
результаты получим, если рассмотрим
сечения поверхности (1) плоскостями

и
.

Таким образом,
рассмотренные сечения позволяют
изобразить поверхность (1) как замкнутую
овальную поверхность. Поверхность (1)
называется эллипсоидом.
Величины a,

и

называются полуосями
эллипсоида.
Если все они различны, то эллипсоид
называется трехосным;
если какие-либо две полуоси равны,
трехосный эллипсоид превращается в
эллипсоид
вращения;
если
,
то – в сферу
.
Однополостный
гиперболоид. Исследуем
поверхность, заданную уравнением

.
(3)

Анализ этих сечений
показывает, что поверхность, определяемая
уравнением(3), имеет форму бесконечной
расширяющейся трубки см. рис.5.

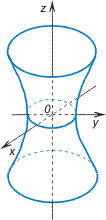
Рис. 5

Двухполостный
гиперболоид. Каноническое
уравнение имеет вид

₍₄₎

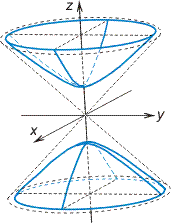
Рис.
6

Эллиптический
параболоид. Исследуем
поверхность, заданную уравнением

,
(5)

При пересечении
поверхности (5) координатными плоскостями

и

получатся соответственно параболы

и
.
Таким образом, поверхность, определяемая
уравнением (5), имеет вид выпук­лой,
бесконечно расширяющейся чаши (см. рис.
7).

Поверхность (5)
называется эллиптическим
параболоидом.

Гиперболический
параболоид. Исследуем
поверхность, определяемую уравнением

,
(6)

При пересечении
поверхности плоскостями, параллельными
плоскости

(

), будут получаться параболы

,

,

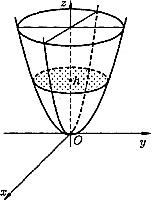
Рис. 8

Рис.7

ветви которых
направлены вверх. При

в сечении получается парабола

,

с вершиной в начале
координат и осью симметрии
.

Пересекая
поверхность (6) плоскостями
,
получим параболы
,
ветви которых направлены вниз.

Анализ линии
пересечения позволяет определить вид
поверхности: она

имеет вид седла
(см. рис. 8). Поверхность (6) называется
гиперболическим
параболоидом.

Конус второго
порядка.
Исследуем уравнение поверхности

.
(7)

Пересечем поверхность
(7)
плоскостями
.
Линия пересечения

,

. При

она вырождается в точку

. При

в сечении будем получать эллипсы

.

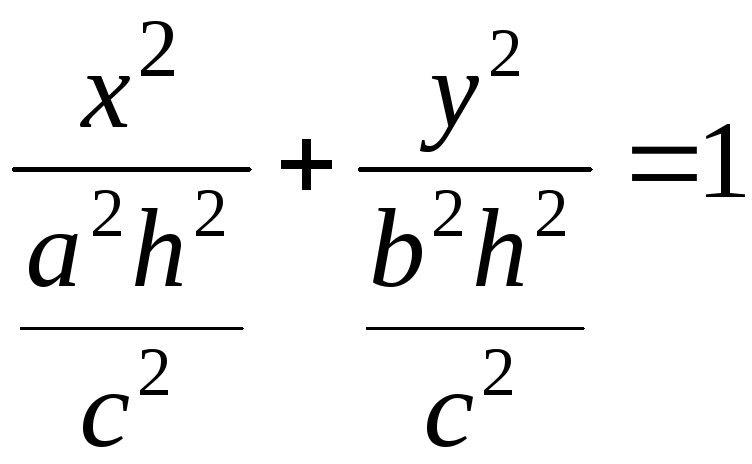
Полуоси этих
эллипсов будут возрастать при возрастании

.

Поверхность,
определяемая уравнени­ем (7), называется
конусом
второго порядка,
имеет вид, изобра­женный на рисунке
9.

Примеры тестовых заданий

1) Поверхность, определяемая уравнением
,
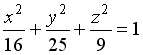является…

Варианты ответов:

однополостным гиперболоидом; сферой;
конусом; эллипсоидом

2) Поверхность, определяемая уравнением
,
является…

Варианты ответов:

сферой; эллиптическим параболоидом;
эллиптическим цилиндром; конусом

3) Поверхность, определяемая уравнением
,
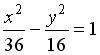является…

Варианты ответов: эллиптическим
цилиндром; гиперболическим цилиндром;
конусом; эллипсоидом

4) Поверхность, определяемая уравнением
,
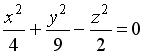является…

Варианты ответов: эллипсоидом;
эллиптическим цилиндром; конусом;
сферой

5) Поверхность, определяемая уравнением
,
является…

Варианты ответов: гиперболическим
цилиндром; сферой; конусом; эллиптическим
цилиндром

Уравнения
поверхностей второго порядка

Эллипсоид a, b, c — полуоси
Однополостный гиперболоид c — действительная полуось, a и b — мнимые полуоси
Двуполостный гиперболоид c — действительная полуось, a и b — мнимые полуоси
Конус Вершина конуса в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат
Эллиптический параболоид
Гиперболический параболоид
Эллиптический цилиндр a и b — полуоси
Гиперболический цилиндр
Параболический цилиндр p — фокальный параметр

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

(1).

Уравнение (1) называется каноническим
уравнением эллипсоида. Величины a,
b, c суть полуоси эллипсоида (рис. 1). Если все
они различны, эллипсоид называется трехосным; в
случае, когда какие-нибудь две из них одинаковы,
эллипсоид называется вытянутым, при a=b>c – сжатым. В случае, когда a=b=c, эллипсоид представляет
собой сферу.

Гиперболоидами называются
поверхности, которые в некоторой системе
декартовых прямоугольных координат
определяются уравнениями

, (2)

. (3)

Гиперболоид, определяемый уравнением
(2), называется однополостным (рис. 2); гиперболоид,
определяемый уравнением (3), – двуполостным (рис. 3);
уравнения (2) и (3) называются каноническими
уравнениями соответствующих гиперболоидов.
Величины a, b, c называются
полуосями гиперболоида. В случае однополостного
гиперболоида, заданного уравнением (2), только
первые из них (а и b) показаны
на рис. 2. В случае двуполостного гиперболоида,
заданного уравнением (3), одна из них (именно, с)
показана на рис. 3. Гиперболоиды, определяемые
уравнениями (2) и (3), при a=b
являются поверхностями вращения.

Параболоидами называются поверхности,
которые в некоторой системе декартовых
прямоугольных координат определяются
уравнениями

, (4)

, (5)

где p и q – положительные числа,
называемые параметрами параболоида. Параболоид,
определяемый уравнением (4), называется
эллиптическим (рис. 4); параболоид, определяемый
уравнением (5), – гиперболическим (рис. 5). Уравнения
(4) и (5) называют каноническими уравнениями
соответствующих параболоидов. В случае, когда p=q, параболоид, определяемый
уравнением (4), является поверхностью вращения
(вокруг Oz).

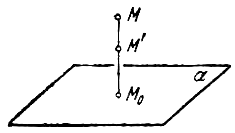
Рассмотрим теперь преобразование
пространства, которое называется равномерным
сжатием (или равномерным растяжением).

Выберем какую-нибудь плоскость;
обозначим ее буквой
. Зададим, кроме
того, некоторое положительное число q. Пусть М – произвольная точка
пространства, не лежащая на плоскости
,
– основание
перпендикуляра, опущенного на плоскость

из точки М. Переместим точку М по прямой
в
новое положение
так, чтобы имело
место равенство

и чтобы после перемещения точка
осталась с той же стороны от плоскости
,
где она была первоначально (рис. 6). Точно так же мы
поступим со всеми точками пространства, не
лежащими на плоскости
; точки, которые
расположены на плоскости
, оставим на своих
местах. Таким образом, все точки пространства, за
исключением тех, что лежат на плоскости
,
переместятся; при этом расстояние от каждой
точки до плоскости
изменится в
некоторое определенное число раз, общее для всех
точек. Описываемое сейчас перемещение точек
пространства называется его равномерным сжатием
к плоскости
; число q
носит название коэффициента сжатия.

Пусть дана некоторая поверхность F; при равномерном сжатии
пространства точки, которые ее составляют,
переместятся и в новых положениях сотавят
поверхность F’. Будем
говорить, что поверхность F’
получено из F в результате
равномерного сжатия пространства. Оказывается,
что многие поверхности второго порядка (все,
кроме гиперболического параболоида) можно
получить в результате равномерного сжатия из
поверхностей вращения).

ПРИМЕР. Доказать, что произвольный
трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных
равномерных сжатий пространства к координатным
плоскостям: к плоскости Oxy с
коэффициентом сжатия
и к плоскости Oxz с коэффициентом сжатия
.

ДОКАЗАТЕЛЬСТВО. Пусть производится
равномерное сжатие пространства к плоскости Oxy с коэффициентом
и
пусть
– точка, в которую переходит при этом
точка
. Выразим координаты x’,
y’, z’ точки М’ через координаты x, y, z точки М. Так как прямая MM’ перпендикулярна к плоскости Oxy, то x’=x, y’=y.
С другой стороны, так как расстояние от точки М’
до плоскости Oxy равно
расстоянию от точки М до этой плоскости,
умноженному на число
, то
.

Таким образом, мы получаем искомые
выражения:

,
,
(6)

или

,
,
(7)

Предположим, что M(x; y; z)
– произвольная точка сферы

.

Заменим здесь x, y, z
их выражениями (7); получим

,

откуда

.

Следовательно, точка M’(x’;
y’; z’) лежит на эллипсоиде вращения.
Аналогично, мы должны осуществить сжатие
пространства к плоскости Oxz
по формулам

,
,
;

тогда получим трехосный эллипсоид и
именно тот, уравнение которого дано в условии
задачи.

Отметим еще, что однополостный
гиперболоид и гиперболический параболоид суть
линейчатые поверхности, то есть они состоят из
прямых; эти прямые называются прямолинейными
образующими указанных поверхностей.

Однополостный гиперболоид

имеет две системы прямолинейных
образующих, которые определяются уравнениями:

,
;

,
,

где
и
– некоторые
числа, не равные одновременно нулю.
Гиперболический параболоид

также имеет две системы прямолинейных
образующих, которые определяются уравнениями

,
;

,
.

Конической поверхностью, или конусом,
называется поверхность, которая описывается
движущейся прямой (образующей) при условии, что
эта прямая проходит через постоянную точку S и пересекает некоторую
определенную линию L. Точка S называется вершиной конуса;
линия L – направляющей.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

L — образующая цилиндра;

H — высота цилиндра;

S_бок — площадь боковой поверхности;

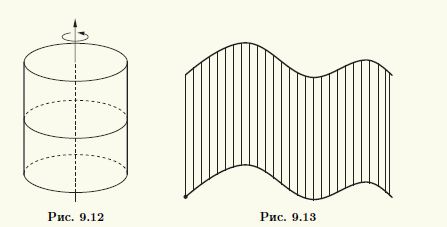
При вращении прямой вокруг некоторой оси, параллельной этой прямой, образуется по-верхность, которую называют круговым цилиндром (рис. 9.12). Эта поверхность является частным случаем цилиндрической поверхности, получающейся при движении прямой в пространстве, которая остается параллельной своему исходному положению (рис. 9.13). Если на движущейся прямой фиксировать точку, то она опишет кривую, которую называют направляющей цилиндрической поверхности (см. рис. 9.13). Можно также сказать, что цилиндрическая поверхность представляет собой множество точек прямых, параллельных фиксированной прямой. Эти параллельные прямые называют образующими цилиндрической поверхности.

В качестве направляющей цилиндра можно взять любую кривую, образованную пересечением цилиндрической поверхности с плоскостью, не параллельной образующим. Выберем прямоугольную систему координат так, чтобы образующие цилиндрической поверхности были параллельны оси Oz. В качестве направляющей выберем кривую, являющуюся пересечением цилиндрической поверхности с координатной плоскостью xOy (рис. 9.14).

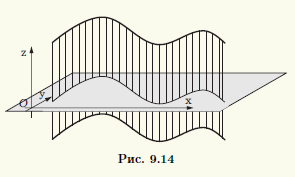
Направляющая в плоскости xOy описывается некоторым уравнением φ(x,y) = 0 двух переменных. Точка M(x; y; z) лежит на цилиндрической поверхности тогда и только тогда, когда ее абсцисса и ордината (фактически координаты точки N(x; у; 0) на плоскости xOy) подчиняются уравнению направляющей. Поэтому в выбранной системе координат цилиндрическая поверхность описывается уравнением φ(x,y) = 0 — уравнением своей направляющей, которое трактуется как уравнение трех переменных x, у и z. Верно и обратное утверждение: если в некоторой прямоугольной системе координат в пространстве поверхность описывается уравнением, не содержащим одного из переменных, то эта поверхность является цилиндрической. Итак, критерием для цилиндрической поверхности является отсутствие в ее уравнении в подходящей системе координат одного из переменных.

Цилиндр второго порядка — это цилиндрическая поверхность, направляющая которой в плоскости, перпендикулярной образующим, представляет собой кривую второго порядка. В выбранной выше прямоугольной системе координат цилиндр второго порядка описывается уравнением второй степени Ax 2 + 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0, где A 2 + B 2 + C 2 ≠ 0.

Это уравнение можно упростить подходящим выбором системы координат. Фактически речь идет о приведении к каноническому виду уравнений второго порядка от двух переменных (см. 8.3). Канонические уравнения кривых второго порядка приводят к трем видам цилиндров второго порядка:

— эллиптическому (рис. 9.15, а) с каноническим уравнением x 2 /a 2 + y 2 /b 2 = 1;

— гиперболическому (рис. 9.15, б) с каноническим уравнением x 2 /a 2 + y 2 /b 2 = 1;

— параболическому с каноническим уравнением y 2 = 2px (рис. 9.15, в).

Отметим, что если направляющей является пара пересекающихся (параллельных, совпадающих) прямых, то соответствующая им цилиндрическая поверхность представляют собой пару пересекающихся (параллельных, совпадающих) плоскостей.

Глава 46. Поверхности второго порядка

Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

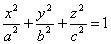(1).

Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.

Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

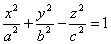, (2)

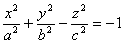. (3)

Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

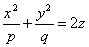, (4)

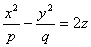, (5)

где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

Выберем какую-нибудь плоскость; обозначим ее буквой 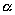. Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости 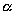, 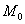— основание перпендикуляра, опущенного на плоскость 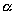из точки М. Переместим точку М по прямой 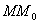в новое положение 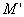так, чтобы имело место равенство

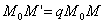
и чтобы после перемещения точка осталась с той же стороны от плоскости 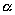, где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости 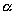; точки, которые расположены на плоскости 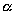, оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости 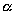, переместятся; при этом расстояние от каждой точки до плоскости 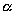изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости 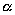; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

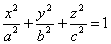
может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия 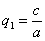и к плоскости Oxz с коэффициентом сжатия .

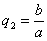ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом 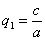и пусть 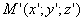— точка, в которую переходит при этом точка 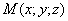. Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на числ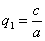о , то .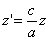

Таким образом, мы получаем искомые выражения:

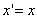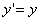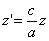, , (6)

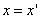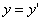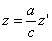, , (7)

Предположим, что M(x; y; z ) — произвольная точка сферы

.

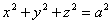Заменим здесь x, y, z их выражениями (7); получим

,

.

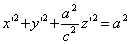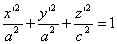Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

, , ;

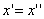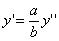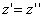тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

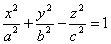
имеет две системы прямолинейных образующих, которые определяются уравнениями:

, ;

, ,

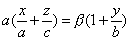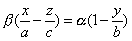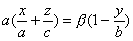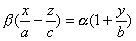где 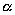и 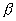— некоторые числа, не равные одновременно нулю. Гиперболический параболоид

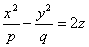
также имеет две системы прямолинейных образующих, которые определяются уравнениями

, ;

, .

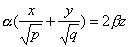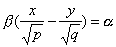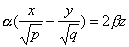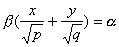Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).

На этой странице вы узнаете

• Как вода в кружке иллюстрирует сечение цилиндра?
• Как лист бумаги превратить в цилиндр?

Что общего у джентльмена 19 века, Вилли Вонка из «Чарли и шоколадная фабрика», Шерлока Холмса в экранизации «Безобразная невеста» и некоторых сценических костюмов? Цилиндр! О нем, вернее о фигуре цилиндра и поговорим в статье.

Понятие цилиндра

Сейчас мы говорим про мужской головной убор, который был популярен в 19 веке и стал достаточно узнаваем в массовой культуре. Оказывается, в математике также существует цилиндр. И они похожи по форме.

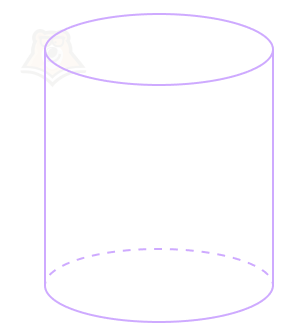
Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон. 

Возможно, для уточнения некоторых терминов вам захочется заглянуть в статью «Тела вращения». 

Если посмотреть на форму шляпы, то она действительно будет похожа на геометрическую фигуру.  Встретить цилиндр можно и в наше время. Обычная кружка является цилиндром.

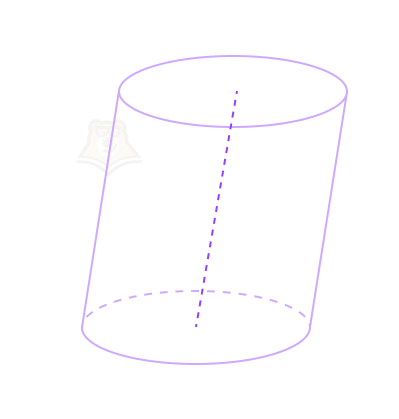
Прямая, вокруг которой мы крутили прямоугольник, чтобы получить цилиндр, — это ось цилиндра. 

Также, как у Земли есть ось вращения, она есть и у цилиндра. 

Наша кружка стоит на круглом дне. Это дно, как и самый верх кружки, будут называться основаниями цилиндра. 

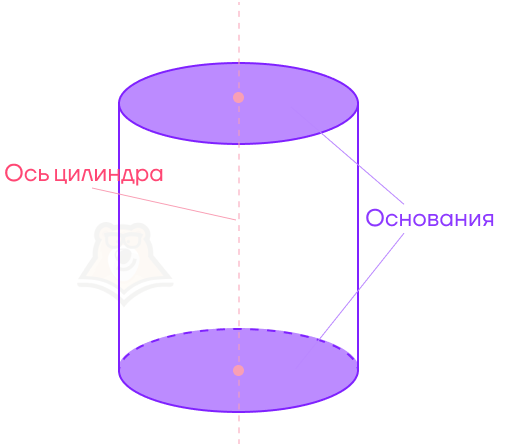
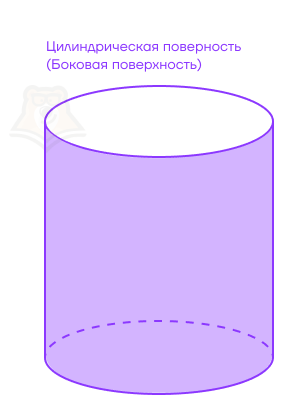
Снова посмотрим на стенки кружки. В цилиндре эта поверхность будет называться цилиндрической поверхностью. Ее также могут называть боковой поверхностью цилиндра. 

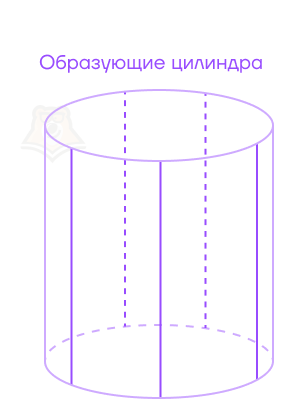
Представим, что наша кружка раскрашена вертикальными линиями. Эти линии будут лежать на цилиндрической поверхности и перпендикулярны основаниям. У них есть название:

Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований. 

Все образующие, — а в цилиндре их очень-очень много, —лежат только на цилиндрической поверхности. Эта поверхность и состоит из множества образующих. 

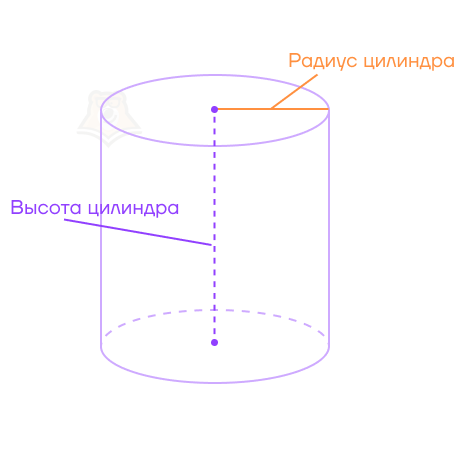
Узнаем ширину кружки. Для этого нужно измерить радиус дна. Этот же радиус будет радиусом основания, а в цилиндре он называется радиусом цилиндра. 

Теперь найдем высоту кружки. Для этого нужно измерить расстояние от дна до самого верха кружки. 

В математике это будет расстоянием между плоскостями, а ищется оно как длина перпендикуляра, опущенного из одной плоскости на другую. Подробнее про это можно прочесть в статье «Расстояния между фигурами». 

Высота цилиндра — перпендикуляр, опущенный из плоскости одного основания на плоскость второго основания. 

Свойства цилиндра

Рассмотрим, какими свойствами обладает цилиндр. 

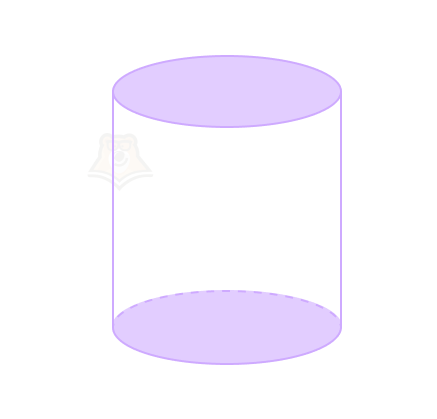
Свойство 1. Основания цилиндра равны и параллельны. 

Это всегда два равных круга, лежащих в параллельных плоскостях. 

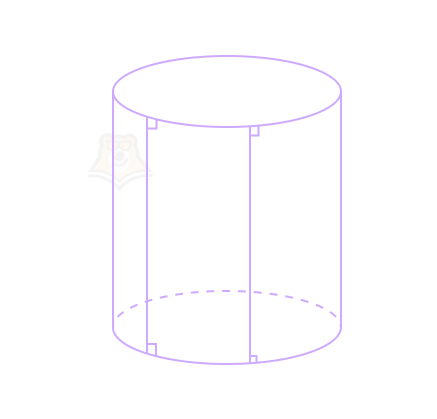
Свойство 2. Образующие цилиндра равны и параллельны. 

Поскольку все образующие перпендикулярны основаниям, то они параллельны между собой по свойству прямой и перпендикулярной ей плоскости. Подробнее про это свойство можно прочесть в статье «Углы в пространстве». 

А равны они потому, что являются перпендикуляром к основаниям, то есть равны высоте цилиндра.

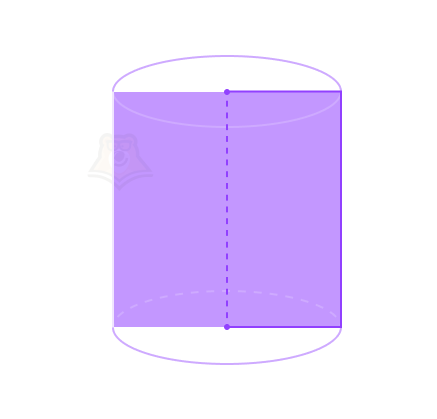
Свойство 3. Сечение цилиндра, проходящее через ось цилиндра, является прямоугольником. Такое сечение в цилиндре будет называться осевым сечением цилиндра. 

Например, если разрезать тортик по диаметру, то место среза как раз будет прямоугольником. 

Подробности про сечения фигур можно найти в статье «Сечения». 

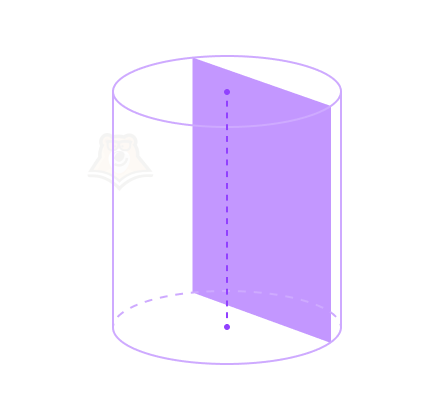
Свойство 4. Сечение цилиндра, проходящее параллельно оси цилиндра и перпендикулярно его основаниям, будет являться прямоугольником. 

Свойство 5. Сечение цилиндра, перпендикулярное оси цилиндра, является кругом с радиусом, равным радиусу цилиндра. Такое сечение в цилиндре называется перпендикулярным сечением цилиндра. 

Заметим, что все вышеописанные свойства относятся к прямому цилиндру. 

Цилиндр также может быть наклонным. В этом случае ось цилиндра и его образующие не будут перпендикулярны основаниям. 

Если мы разрежем поверхность цилиндра по одной из его образующих и как бы “развернем” ее, у нас получится прямоугольник. 

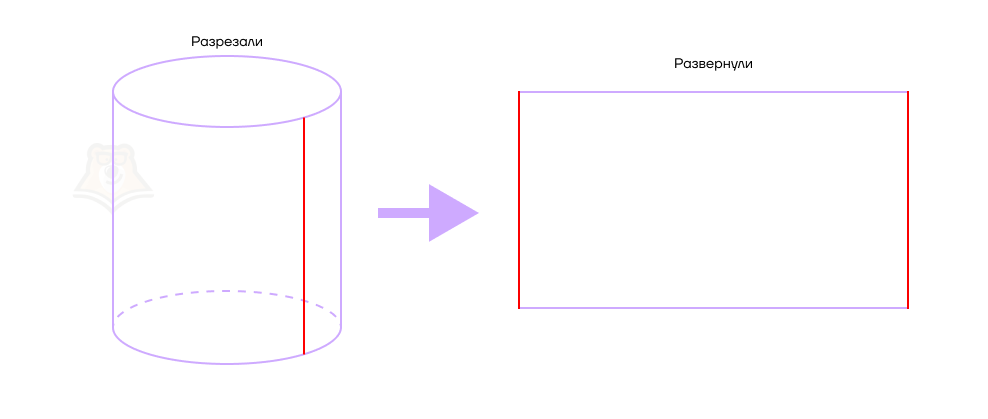
Это также легко увидеть, если вспомнить художников с тубусами. Тубус имеет форму цилиндра, и свернутый прямоугольный лист принимает такую же форму. 

Развертка боковой поверхности цилиндра — прямоугольник, одна сторона которого равна высоте цилиндра, а вторая — длине окружности его основания. 

Формулы цилиндра

А если это прямоугольник, то мы знаем, как найти его площадь. Нам нужно умножить его длину на высоту. Так мы получаем площадь боковой поверхности цилиндра. 

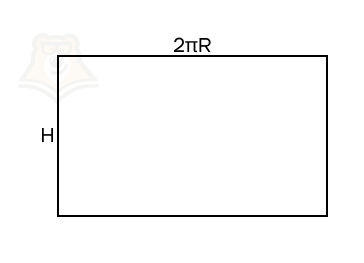
(S_{бок.} = 2 pi RH)

В этой формуле 2R — длина окружности основания, где R — его радиус, а Н — образующая (или высота) цилиндра. Подробнее про площадь прямоугольника и длину окружности (а также про площадь круга) можно прочесть в статьях «Параллелограмм» и «Окружность и круг». 

Мы нашли площадь боковой поверхности. Как же теперь найти площадь полной поверхности?

Для этого нужно сложить площади боковой поверхности и оснований. Следовательно, мы получаем следующую формулу. 

(S = S_{бок.} + 2S_{осн.} = 2 pi RH+2 pi R^2 = 2 pi R(H + R))

Допустим, мы решили сделать чашку очень вкусного чая, но чтобы правильно его заварить нам нужно знать точный объем воды. Для этого вычислим объем цилиндра. Воспользуемся следующей формулой:

(V = S_{осн.}H = pi R^2H)

В этой формуле R — радиус цилиндра, Н — высота. 

Часто формулу объема можно применить для решения жизненных задач. Например, чтобы найти объем детали, погруженной в воду. 

Пример 1. В цилиндрическом сосуде налито 1650 см³ жидкости. В этот сосуд опустили деталь. При этом уровень жидкости увеличился в 1,2 раза. Найдите объем детали. Ответ выразите в см³. 

Решение. 

Шаг 1. Выразим высоту жидкости в первый и второй раз. Пусть вначале уровень жидкости был равен х, значит после того, как в нее опустили деталь, он стал равен 1,2х. 

Шаг 2. Вспомним физику и заметим, что объем жидкости в сосуде после того, как в него опустили деталь, будет равен сумме объемов жидкости и детали: V = V_ж + V_д. 

Шаг 3. С помощью объема жидкости выразим площадь основания сосуда:

V_ж = S_осн.H
1650 = S_осн.x
(S_{осн} = frac{1650}{x})

Шаг 4. Подставим площадь основания в формулу объема жидкости после того, как в нее опустили деталь:

(V = S_{осн.}H = frac{1650}{x} * 1,2x = 1980)

Шаг 5. Тогда объем детали будет равен:

V_д = V — V_ж
V_д = 1980 — 1650 =330 

Ответ: 330 см³

Фактчек

• Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон. Цилиндр может быть прямым и наклонным. В наклонном цилиндре ось не перпендикулярна основаниям цилиндра. 
• Цилиндр состоит из двух оснований и цилиндрической поверхности (боковой поверхности цилиндра). Основания имеют форму кругов, равны между собой и лежат в параллельных плоскостях. Развертка боковой поверхности имеет форму прямоугольника. 
• Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований. В прямом цилиндре образующая равна высоте цилиндра. Образующие равны и параллельны друг другу, а также образуют боковую поверхность цилиндра. 
• Осевое сечение цилиндра проходит через его ось и является прямоугольником. Любое сечение, параллельное осевому, также будет являться прямоугольником. Перпендикулярное сечение проходит перпендикулярно оси цилиндра и параллельно его основаниям. Перпендикулярное сечение имеет форму круга. 

Проверь себя

Задание 1. 
Что такое образующая цилиндра?

1. Ось вращения, с помощью которой получен цилиндр.
2. Диаметр оснований цилиндра.
3. Любой перпендикуляр, проведенный от одного основания к другому.
4. Отрезок, соединяющий точки окружности основания. 

Задание 2. 
Площадь боковой поверхности цилиндра равняется 44. Его радиус равен 8. Найдите высоту цилиндра. 

1. 2,75
2. 5,5
3. (2,75 pi)
4. 2

Задание 3. 
Площадь основания цилиндра равна 16. Его высота равна 4. Найдите площадь полной поверхности цилиндра. 

1. 64
2. (64 pi)
3. 32
4. (32 pi)

Задание 4. 
Объем цилиндра равен 28, а его высота равняется 7. Найдите диаметр основания.

1. 4
2. 2
3. 16
4. 8

Ответы: 1. – 4 2. – 1 3. – 2  4. – 1