Как найти уравнение директрисы параболы онлайн - Сайт, где вы сможете решить свои вопросы

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	– twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{”}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	–
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

директриса:(y-2)=3(x-5)^2
директриса:3x^2+2x+5y-6=0
директриса:x=y^2
директриса:(y-3)^2=8(x-5)
директриса:(x+3)^2=-20(y-1)
Показать больше

Описание

Рассчитать директрису параболы по заданному уравнению шаг за шагом

parabola-directrix-calculator

Блог-сообщения, имеющие отношение к Symbolab

My Notebook, the Symbolab way

Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Пусть дана некоторая парабола (x^2+3y=16). Требуется найти уравнение директрисы для этой параболы. Нет, директриса – это не директор-женщина в вашей школе. Это такая специальная прямая, что каждая точка параболы равноудалена от фокуса параболы и директрисы. 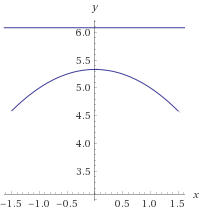Ну вам об этом лучше не думать – просто вставьте уравнение параболы в калькулятор как показано в примере. И вы получите все что вам требуется. Справа приведет пример параболы и ее директрисы (прямая горизонтальная линия). Вы можете воспользоваться нашим примером – кликните на пиктограмму копирования и код запроса будет добавлен в калькулятор. вам остается только нажать кнопку “Решить”. Что может быть проще? Ну и на всякий случай – определение параболы:
Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

directrix of parabola x^2+3y=16

Похожие публикации: калькулятор

Источник

Уравнение директрисы параболы

Содержание:

Что такое директриса параболы
Каноническое уравнение параболы
Уравнение директрисы параболы, если вершина не в пересечении осей координат
- Алгоритм расчета
Фокус параболы
Примеры решения задач

Что такое директриса параболы

Определение

Директриса параболы — такая прямая, кратчайшее расстояние от которой до любой точки, принадлежащей параболе, точно такое же, как расстояние от этой точки до фокуса.

Вершина параболы — точка пересечения параболы с ее осью. Она считается началом системы координат, канонической для данной кривой.

Вершина — середина перпендикуляра, опущенного из фокуса на директрису. Таким образом, директриса перпендикулярна оси симметрии и проходит на расстоянии р/2 от вершины параболы. Число р — фокальный параметр, расстояние от фокуса до директрисы. Поскольку все параболы подобны, именно эта характеристика определяет масштаб конкретной параболы.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Каноническое уравнение параболы

Каноническое уравнение параболы:

(y^2;=;2px)

Парабола

Если расположить параболу слева от оси ординат, уравнение примет вид:

(y^2;=;-;2px)

Парабола отрицательное уравнение

Уравнение директрисы параболы, если вершина не в пересечении осей координат

Формула директрисы параболы имеет вид:

(х;=;-frac р2)

Если вершину перенести в точку ((x_0;;y_0)), отличную от начала осей координат, каноническое уравнение примет вид:

({(y;-;y_0)}^2;=;2p;times;(x;-;x_0))

Алгоритм расчета

Если уравнение параболы приведено в виде квадратного многочлена, перенесем все слагаемые с y в левую часть уравнения, а с х — в правую.
Упростим выражение, выделив полный квадрат относительно одной из переменных.
Введем новые переменные ((x_1;;y_1)), чтобы привести уравнение к каноническому виду, ведя при этом отсчет с новой точки начала координат.
Вычислим параметр р и фокус, запишем уравнение директрисы.
Вернемся к старым координатам, заменив ((x_1;;y_1)) на х и y.

Фокус параболы

Определение

Расстояние от точки фокуса (F) до любой точки параболы равняется расстоянию от этой точки к директрисе.

Фокус параболы

Чтобы составить уравнение директрисы, нужно знать фокальный параметр.

Определение

Фокальный параметр — половина длины хорды, проходящей через её фокус перпендикулярно фокальной оси.

Примеры решения задач

Задача №1

Составить уравнение директрисы параболы (y^2;=;6x).

Решение

Сравнив каноническое уравнение с данным, получим:

(2р = 6 )

(р = 3)

(frac р2;=;frac32)

Уравнение директрисы — (х;=;-frac р2.)

В данном случае оно будет выглядеть так:

(х;=;-;frac32)

Задача №2

Найти директрису параболы, заданной уравнением (4х^2;-;12х;+;y;+;6;=;0.)

Решение

Преображаем многочлен, находим полный квадрат относительно переменной х:

(4х^2;-;12х;+;y;+;6;=;0;Rightarrow;4(х^2;-;3х);+;y;+;6;=;0;Rightarrow;;4((х^2;-;2;timesfrac32х;+;frac94);-;frac94);+;y;+;6;=;0;Rightarrow;)

(;Rightarrow;(4;{(х;-;frac32)}^2;-;9;+;y;+;6;=;0;Rightarrow;y;-;3;=-;4;{(х;-;frac32)}^2;Rightarrow;{(х;-;frac32)}^2;=;-;frac14;(y;-;3))

Пусть ((y — 3)) будет (y_1), а ((х;-;frac32)) — (х_1).

Тогда, перенеся начало координат в точку ((x_1;;y_1)), получим каноническое уравнение (х_1^2;=;-{textstylefrac14}y_1).

(2р;=;frac14;Rightarrow;р;=;frac18;Rightarrow;frac р2;=;frac1{16})

Тогда уравнение директрисы — (y_1=;frac1{16}).

Заменив (y_1) на ((y — 3)), получим уравнение: (y;–;3;=;frac1{16})

Следовательно, (y;–;frac{49}{16};=;0).

В старой системе координат уравнение директрисы:

(16у — 49 = 0, у;=;frac{49}{16}).

Насколько полезной была для вас статья?

Рейтинг: 3.17 (Голосов: 18)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

The directrix is a fixed line used in describing a curve or surface. This curve can be a parabola. Here is a simple online Directrix calculator to find the parabola focus, vertex form and parabola directrix. In this below online Parabola focus directrix calculator just enter the input values in the form of a standard equation, y = ax² + bx + c to get the result. Use our free online Parabola calculator to solve your academic mathematical and engineering problems.

Code to add this calci to your website

Formula:

x = – b / 2a
y = c – ( ( b² – 1) / 4a)
u = – b / 2a
v = ax² + bx + c
d = c – ( ( b² + 1) / 4a)

Where,
a = X² Coefficient
b = X Coefficient
c = Constant
x = Parabola Focus x-coordinate
y = Parabola Focus y-coordinate
u,v = Vertex Form
d = Parabola Directrix

All the parabola directrix calculations can be made in easier and quicker manner by using this Parabola directrix calculator.

Источник

Директриса параболы

оксана николаевна кузнецова

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Определение 1

Директрисой параболы называют такую прямую, кратчайшее расстояние от которой до любой точки $M$, принадлежащей параболе точно такое же, как и расстояние от этой же точки до фокуса параболы $F$.

Рисунок 1. Фокус и директриса параболы

Основные понятия параболы

Отношение расстояний от точки $M$, лежащей на параболе, до этой прямой и от этой же точки до фокуса $F$ параболы называют эксцентриситетом параболы $ε$.

Сделаем домашку
с вашим ребенком за 380 ₽

Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online

Бесплатное пробное занятие

*количество мест ограничено

Чтобы найти эксцентриситет параболы, достаточно воспользоваться следующей формулой из определения эксцентриситета:
$ε =frac{MF}{MM_d}$, где точка $M_d$ – точка пересечения перпендикуляра, опущенного из точки $M$ c прямой $d$.

Определение 2

Каноническая парабола задается уравнением вида $y^2 = px$, где $p$ обязательно должно быть больше нуля.

Более часто приходится иметь дело с параболой, вершина которой не находится в точке начала координатных осей, и тогда уравнение параболы приобретает следующий вид:

$y = ax^2 + bx + c$, при этом коэффициент $a$ не равен нулю.

Чтобы найти директрису такой параболы, необходимо от такой формы перейти к канонической, ниже в примерах показано, как это сделать.

Расстояние от фокуса до директрисы параболы называется её фокальным параметром $p$.
Уравнение директрисы канонической параболы имеет следующий вид: $x=-p/2$

Алгоритм составления уравнения директрисы параболы, заданной не каноническим уравнением

«Директриса параболы» 👇

Чтобы составить уравнение директрисы параболы, вершина которой не находится на пересечении осей координат, достаточно воспользоваться следующим алгоритмом:

Перенесите все слагаемые с $y$ в левую часть уравнения, а с $x$ – в правую.
Упростите полученное выражение.
Введите дополнительные переменные чтобы прийти к каноническому виду уравнения.

Пример 1

Составьте уравнение директрисы параболы, описанной уравнением $4x^2 + 24 x – 4y + 36 = 0$

Переносим все слагаемые с $y$ в левую часть и избавляемся от множителя, получаем:

$y^2 = x^2 + 6x – y + 9$
Приводим в форму квадрата:

$(x + 3)^2 = y$
Вводим дополнительные переменные $t = x + 3$ и $y = z$
Получаем следующее уравнение: $t^2 = z$
Выражаем $p$ из канонического уравнения параболы, получаем $p = frac{y^2}{2x}$, следовательно, в нашем случае $p = frac{1}{2}$.
Уравнение директрисы приобретает следующий вид: $t = -frac{1}{4} cdot t$. Подставляем $t$ и получаем следующее уравнение директрисы $x = -3frac{1}{4}$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 09.12.2022

Источник

Номер Строки

Уравнение директрисы параболы

Что такое директриса параболы

Каноническое уравнение параболы

Уравнение директрисы параболы, если вершина не в пересечении осей координат

Алгоритм расчета

Фокус параболы

Примеры решения задач

Текст с ошибкой:

Поиск по содержимому

Formula:

Директриса параболы

Основные понятия параболы

Алгоритм составления уравнения директрисы параболы, заданной не каноническим уравнением

Вам также может понравиться

Как найти архивное сообщение в gmail

Как исправить холодец если получился густой

Как с телефона найти часы apple watch

Добавить комментарий Отменить ответ