Как найти уравнение этой поверхности

Уравнения поверхности и линии в пространстве с примерами решения

Содержание:

Уравнения поверхности и линии в пространстве

Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если

— уравнение поверхности Р (рис. 189), то при М(х, у, z)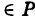

Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.

Пример (уравнения координатных плоскостей):

Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,

— уравнение координатной плоскости Oyz. Аналогично,

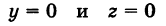
— соответственно уравнения координатных плоскостей Oxz и Оху.

Формула 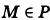обозначает, что точка М принадлежит Р. Формула 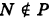обозначает, что точка N не принадлежит Р.

В более общем случае

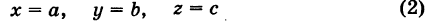
— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные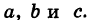

Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.

Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой 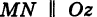(образующая) вдоль заданной линии L, лежащей в плоскости Оху (направляющая) (рис. 190).

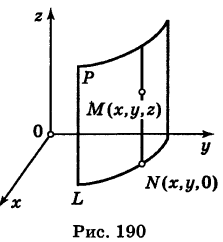
Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).

— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,

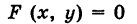
является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.

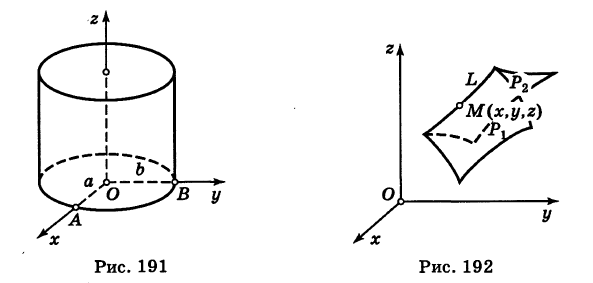
Пример (уравнение эллиптического цилиндра):

Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение

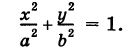
В частности, при а = b получаем уравнение кругового цилиндра

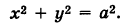
Линию L в пространстве можно задать как пересечение двух данных поверхностей 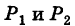(рис. 192). Точка 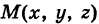, лежащая на линии L, принадлежит как поверхности 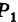так и поверхности 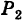, и, следовательно, координаты этой точки удовлетворяют уравнениям обеих поверхностей.

Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:

являющихся уравнениями поверхностей, определяющих данную линию.

Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки 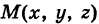, координаты которых удовлетворяют обоим уравнениям системы (4).

Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.

Определение: Уравнениями линии в пространстве называется такая пара уравнений между переменными , которой удовлетворяют координаты каждой точки, лежащей на данной линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Пример (уравнения координатных осей):

Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому

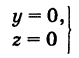
— уравнения оси Ох. Аналогично,

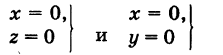
— уравнения осей Оу и Oz соответственно.

Пример:

Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).

Решение:

Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть

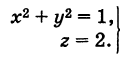
В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем

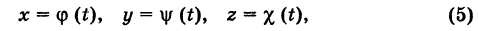
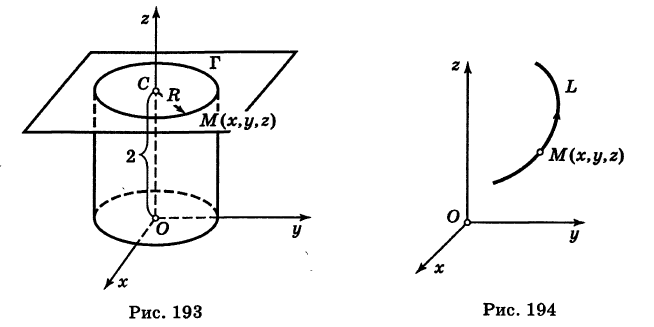
где 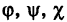— некоторые определенные функции. Обобщая уравнения (5), под t понимают вспомогательную переменную (параметр)> не обязательно время; поэтому уравнения (5) носят название параметрических уравнений линии в пространстве.

Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.

Пример:

Написать уравнения винтовой линии радиуса а и шага 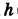(рис. 195).

Решение:

Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.

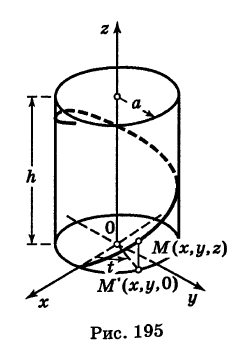
Приняв за параметр 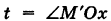и учитывая, что аппликата г винтовой линии растет пропорционально углу поворота t, будем иметь

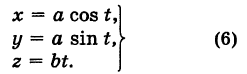
Для определения коэффициента пропорциональности b положим 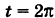; тогда 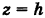. Следовательно,

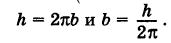
Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем

Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости 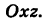. Из уравнений (6′) также вытекает, что проекция винтовой линии (6′) на координатную плоскость Оху есть окружность, а на координатную плоскость 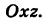— косинусоида.

Текущую точку 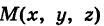кривой L можно характеризовать ее радиусом-вектором («следящий радиус-вектор») (рис. 196)

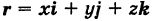
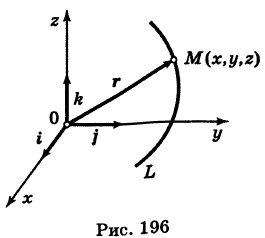
( — орты). Тогда из (5) получаем векторное уравнение линии

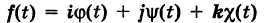
— так называемая вектор-функция скалярного аргумента t.

В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).

Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).

Пример:

Какой геометрический образ соответствует уравнению

Решение:

Из уравнения (8) получаем или 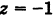. Следовательно, графиком уравнения (8) является пара плоскостей, параллельных координатной плоскости Оху и отстоящих от нее на расстояниях, равных единице (рис. 197).

Пример:

Какой геометрический образ соответствует паре уравнений

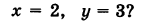
Решение:

Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Общее уравнение плоскости
• Угол между плоскостями
• Понятие о производной вектор-функции
• Криволинейные интегралы
• Прямоугольная система координат на плоскости и ее применение
• Линии второго порядка
• Полярные координаты
• Непрерывность функции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Поверхности второго порядка: их виды, уравнения, примеры

Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат

Общее уравнение поверхности второго порядка имеет вид

Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты – это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:

Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:

В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.

Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому

I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 , λ 2 , λ 3 – корни характеристического уравнения

.

В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.

Эллипсоид

Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.

После решения характеристического уравнения общее уравнение можно переписать в следующем виде:

.

Тогда полуоси эллипсоида будут

, , .

Поэтому каноническое уравнение эллипсоида имеет вид

.

Мнимый эллипсоид

Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:

,

, , .

Мнимый конус

Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:

,

, , .

Однополостный гиперболоид

Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:

.

, , ,

то каноническое уравнение однополостного гиперболоида будет иметь вид

.

Двуполостный гиперболоид

Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:

.

Последняя запись и есть каноническое уравнение двуполостного гиперболоида.

Конус

Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.

Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:

,

известном как каноническое уравнение конуса.

II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 и λ 2 – отличные от нуля корни характеристического уравнения.

Эллиптический параболоид

Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.

Общее уравнение можно переписать в виде:

.

Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая

,

,

получим каноническое уравнение эллиптического параболоида:

.

Гиперболический параболоид

Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.

Обозначая через λ 1 положительный корень, а через λ 2 – отрицательный и беря перед корнем знак минус, переписываем уравнение в виде:

.

, ,

получим каноническое уравнение гиперболического параболоида:

.

III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 и λ 2 – отличные от нуля корни характеристического уравнения.

Эллиптический цилиндр

Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

, ,

получим каноническое уравнение эллиптического цилиндра:

.

Мнимый эллиптический цилиндр

Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

Последняя запись – каноническое уравнение мнимого эллиптического цилиндра.

Мнимые пересекающиеся плоскости

Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

, ,

получим каноническое уравнение мнимых пересекающихся плоскостей:

.

Гиперболический цилиндр

Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

,

, .

Таким образом, каноническое уравнение гиперболического цилиндра:

.

Пересекающиеся плоскости

Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

,

, .

Таким образом, пересекающихся плоскостей:

.

IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 = I 1 – отличный от нуля корень характеристического уравнения.

Параболический цилиндр

Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:

,

.

Это уравнение параболического цилиндра, в каноническом виде оно записывается так:

.

V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

.

Параллельные плоскости

Если K 2 , то общее уравнение поверхности второго порядка определяет две параллельные плоскости.

,

перепишем его в виде

.

Мнимые параллельные плоскости

Если K 2 > 0 , то общее уравнение поверхности второго порядка определяет две мнимые параллельные плоскости.

,

перепишем его в виде

.

Совпадающие плоскости

Если K 2 = 0 , то общее уравнение поверхности второго порядка определяет две совпадающие плоскости:

.

Решение примеров на определение вида поверхности второго порядка

Пример 1. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Решение. Найдём I 3 :

(как вычислить определитель).

I 1 = 1 + 5 + 1 = 7 ,

Следовательно, данная поверхность – однополостный гиперболоид.

.

Составляем и решаем характеристическое уравнение:

;

.

,

, , .

Пример 2. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Решение. Найдём I 3 :

.

.

Следовательно, общее уравнение определяет эллиптический параболоид.

.

I 1 = 2 + 2 + 3 = 7 .

Решаем характеристическое уравнение:

.

.

,

, .

Пример 3. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

,

,

,

I 1 = 5 + 2 + 5 = 12 .

Так как I 3 = К 4 = 0 , I 2 > 0 , I 1 K 3 , то данное общее уравнение определяет эллиптический цилиндр.

.

.

Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение

Пример 4. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Общее уравнение плоскости: основные сведения

Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

1. Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .

Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x – x 0 , y – y 0 , z – z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:

n → , M 0 M → = A x – x 0 + B ( y – y 0 ) + C ( z – z 0 ) = A x + B y + C z – ( A x 0 + B y 0 + C z 0 )

Примем D = – ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.

1. Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.

В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида

A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 задает некоторую плоскость.

Уравнение A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x – x 0 , y – y 0 , z – z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.

Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x – 2 · y + 3 · z – 7 = 0 и – 2 · x + 4 · y – 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.

Раскроем чуть шире смысл теорем.

В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.

Укажем пример как иллюстрацию этих утверждений.

Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , – 1 , – 3 ) и N 0 ( 0 , 2 , – 8 ) и плоскость, определяемая уравнением 2 x + 3 y – z – 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( – 1 ) – ( – 3 ) – 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , – 1 , – 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 – ( – 8 ) – 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , – 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) – нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y – z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , – 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , – λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , – λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x – x 0 , y – y 0 , z – z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) = 0

Задана точка М 0 ( – 1 , 2 , – 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , – 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

1. Исходные условия позволяют получить следующие данные:

x 0 = – 1 , y 0 = 2 , z 0 = – 3 , A = 3 , B = 7 , C = – 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) = 0

3 ( x – ( – 1 ) ) + 7 ( y – 2 ) – 5 ( z – ( – 3 ) ) = 0 ⇔ 3 x + 7 y – 5 z – 26 = 0

1. Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x – x 0 , y – y 0 , z – z 0 ) = ( x + 1 , y – 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y – 2 ) – 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y – 5 z – 26 = 0

Ответ: 3 x + 7 y – 5 z – 26 = 0

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

1. В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

1. Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.

1. При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = – D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = – D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = – D A ⇔ x = λ , λ ∈ R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , – D C , 0 , – D B , 0 и – D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0

Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , – 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.

Р​​ешение

У​​​​​словием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , – 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = – 7 , тогда требуемое уравнение имеет вид: x – 7 = 0 .

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) = 0 ⇔ ⇔ 1 · ( x – 7 ) + 0 · ( y + 2 ) + 0 · ( z – 3 ) = 0 ⇔ ⇔ x – 7 = 0

Ответ: x – 7 = 0

Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( – 3 , 1 , 2 ) .

Решение

Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .

Найдем значение B A . В исходных данных фигурирует точка М 0 ( – 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: – 3 + B A · 1 = 0 , откуда определяем B A = 3 .

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .

[spoiler title=”источники:”]

http://function-x.ru/surfaces_of_the_second_order.html

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-ploskosti/

[/spoiler]

Содержание:

Уравнения поверхности и линии в пространстве

Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если

— уравнение поверхности Р (рис. 189), то при М(х, у, z)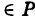

Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.

Пример (уравнения координатных плоскостей):

Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,

х = 0

— уравнение координатной плоскости Oyz. Аналогично,

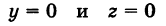
— соответственно уравнения координатных плоскостей Oxz и Оху.

Формула 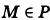обозначает, что точка М принадлежит Р. Формула 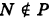обозначает, что точка N не принадлежит Р.

В более общем случае

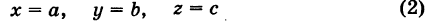
— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные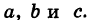

Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.

Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой 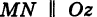(образующая) вдоль заданной линии L, лежащей в плоскости Оху (направляющая) (рис. 190).

Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).

Пусть

— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,

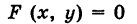
является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.

Пример (уравнение эллиптического цилиндра):

Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение

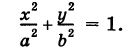
В частности, при а = b получаем уравнение кругового цилиндра

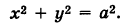
Линию L в пространстве можно задать как пересечение двух данных поверхностей 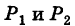(рис. 192). Точка 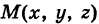, лежащая на линии L, принадлежит как поверхности 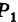так и поверхности 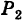, и, следовательно, координаты этой точки удовлетворяют уравнениям обеих поверхностей.

Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:

являющихся уравнениями поверхностей, определяющих данную линию.

Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки 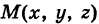, координаты которых удовлетворяют обоим уравнениям системы (4).

Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.

Определение: Уравнениями линии в пространстве 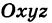называется такая пара уравнений между переменными 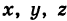, которой удовлетворяют координаты каждой точки, лежащей на данной линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Пример (уравнения координатных осей):

Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому

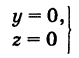
— уравнения оси Ох. Аналогично,

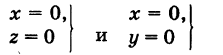
— уравнения осей Оу и Oz соответственно.

Пример:

Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).

Решение:

Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть

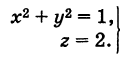
В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем

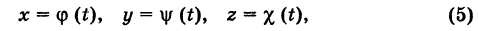
где 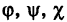— некоторые определенные функции. Обобщая уравнения (5), под t понимают вспомогательную переменную (параметр)} не обязательно время; поэтому уравнения (5) носят название параметрических уравнений линии в пространстве.

Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.

• Заказать решение задач по высшей математике

Пример:

Написать уравнения винтовой линии радиуса а и шага 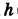(рис. 195).

Решение:

Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.

Приняв за параметр 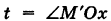и учитывая, что аппликата г винтовой линии растет пропорционально углу поворота t, будем иметь

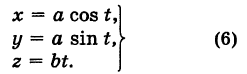
Для определения коэффициента пропорциональности b положим 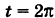; тогда 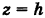. Следовательно,

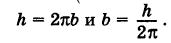
Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем

Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости 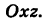. Из уравнений (6′) также вытекает, что проекция винтовой линии (6′) на координатную плоскость Оху есть окружность, а на координатную плоскость 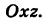— косинусоида.

Текущую точку 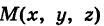кривой L можно характеризовать ее радиусом-вектором («следящий радиус-вектор») (рис. 196)

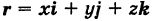
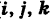( — орты). Тогда из (5) получаем векторное уравнение линии

где

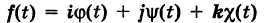
— так называемая вектор-функция скалярного аргумента t.

В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).

Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).

Пример:

Какой геометрический образ соответствует уравнению

Решение:

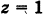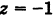Из уравнения (8) получаем или . Следовательно, графиком уравнения (8) является пара плоскостей, параллельных координатной плоскости Оху и отстоящих от нее на расстояниях, равных единице (рис. 197).

Пример:

Какой геометрический образ соответствует паре уравнений

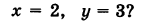
Решение:

Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).

§12. Уравнения поверхности и линии в пространстве

12.1. Основные понятия

Поверхность
и ее уравнение.

Поверхность
в пространстве, как правило, можно
рассматривать как геометрическое место
точек, удовлетворяющих какому-либо
условию. Например, сфера радиуса

с центром в точке

есть гео­метрическое место всех точек
пространства, находящихся от точки

на расстоянии

.

Прямоугольная
система координат

в пространстве позволя­ет установить
взаимно однозначное соответствие между
точками пространства и тройками чисел

,

и

— их координатами. Свойство, общее всем
точкам поверхности, можно записать в
виде уравнения, свя­зывающего координаты
всех точек поверхности.

Уравнением
данной поверхности в прямоугольной
системе координат

называется такое уравнение

с тремя переменными

,

и

,
которому удовлетворяют координаты
каждой точки, лежащей на поверхности,
и не удовлетворяют координаты то­чек,
не лежащих на этой поверхности. Переменные

,

и

в уравнении поверхности называются
текущими координатами точек поверх­ности.

Уравнение
поверхности, позволяет изучение
геометрических свойств поверхности
заменить исследованием его уравнения.
Так, для того, чтобы узнать, лежит ли
точка

на данной поверхно­сти, достаточно
подставить координаты точки

в уравнение поверх­ности вместо
переменных: если эти координаты
удовлетворяют урав­нению, то точка
лежит на поверхности, если не удовлетворяют
— не лежит.

Уравнение
сферы.

Найдем
уравнение сферы радиуса

с центром в точке

.
Согласно определению сферы расстояние
любой ее точки

от центра

равно радиусу

,
т.е.

.
Но

,
где

.
Следовательно,

или

.

Это
и есть искомое уравнение сферы. Ему
удовлетворяют координаты любой ее точки
и не удовлетворяют координаты точек,
не лежащих на данной сфере.

Если
центр сферы

совпадает с началом координат, то
уравнение сферы принимает вид

.

Если
же дано уравнение вида

,
то оно, вообще говоря, определяет в
пространстве некоторую поверхность.

Выражение
«вообще говоря» означает, что в отдельных
случаях уравнение

может определять не поверхность, а
точку, линию или вовсе не определять
никакой геометрический образ. Говорят,
«поверхность вырождается».

Так,
уравнению

не удовлетворяют никакие действительные
значения

,

,

.
Уравнению

удовлетворяют лишь координаты точек,
лежащих на оси

(из уравнения следует:

,


,
а

— любое число).

Итак,
поверхность в пространстве можно задать
геометрически и аналитически. Отсюда
вытекает постановка двух основных
задач:

1. Дана
   поверхность как геометрическое место
   точек. Найти уравнение этой поверхности.

2. Дано
   уравнение

   .
   Исследовать форму поверхности,
   определяемой этим уравнением.

Уравнения
линии в пространстве.

Линию
в пространстве можно рассматривать как
линию пересечения двух поверхностей
(см. рис. 12.1) или как геометрическое место
точек, общих двум поверхностям.

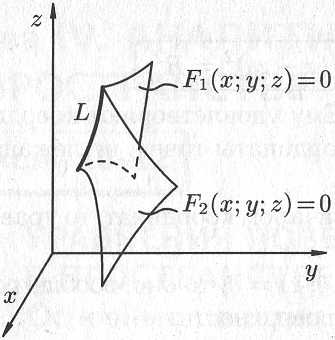
Рис. 12.1

Если

и

— уравнения двух поверхностей,
определяющих линию

,
то координаты точек этой линии
удовлетворяют системе двух уравнений
с тремя неизвестными:

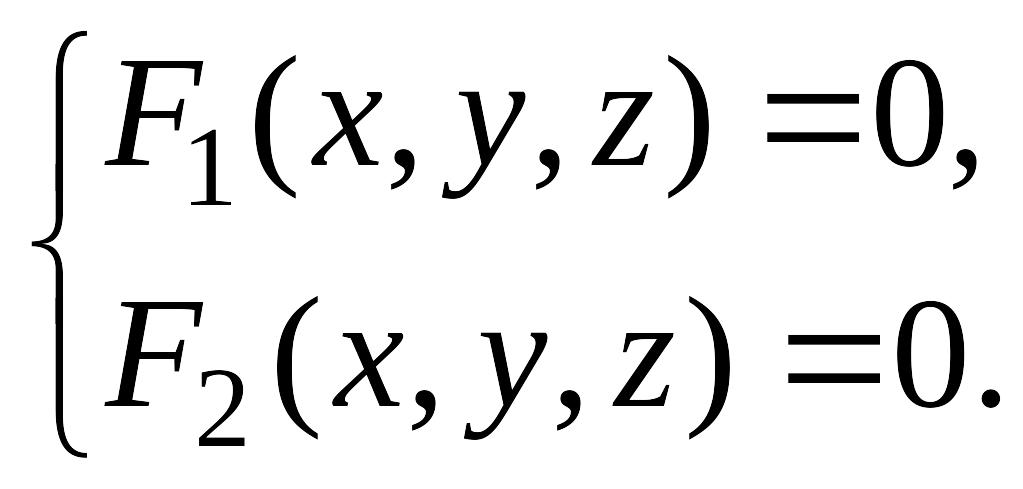
(12.1)

Уравнения
системы (12.1) называются уравнениями
линии в пространстве.
Например,

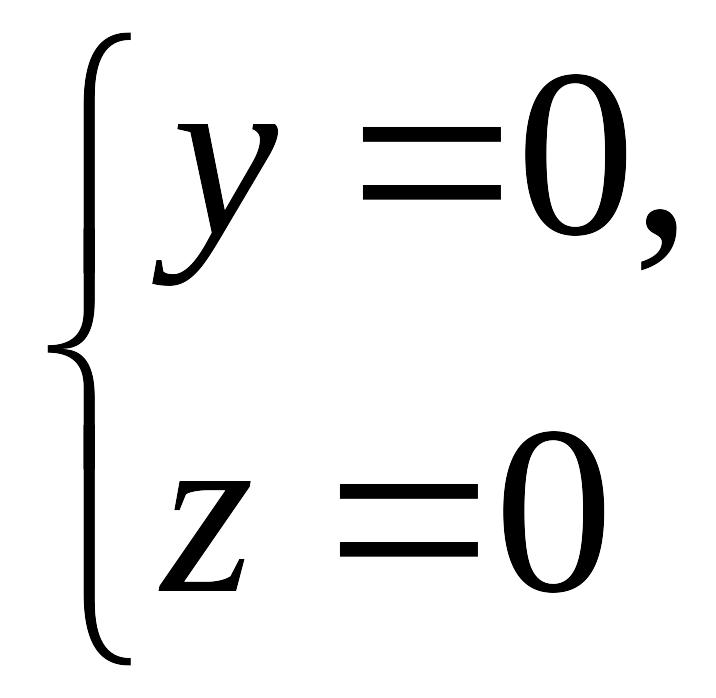
есть уравнения оси

.

Линию
в пространстве можно рассматривать как
траекторию движения точки (см. рис.
12.2).

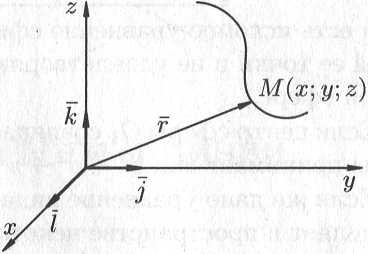
Рис. 12.2

В этом случае ее
задают векторным уравнением

(12.2)

или параметрическими
уравнениями

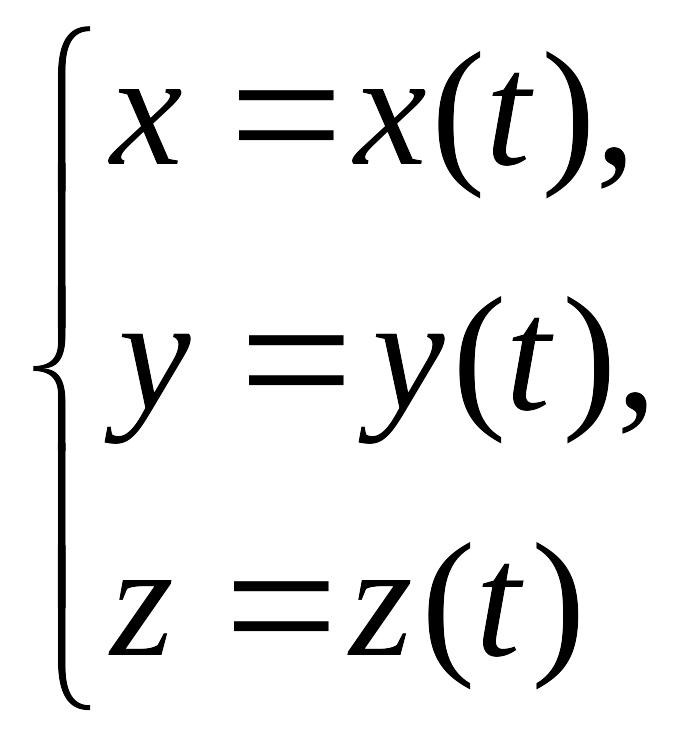
проекций вектора
(12.2) на оси координат.

Например,
параметрические уравнения винтовой
линии имеют вид

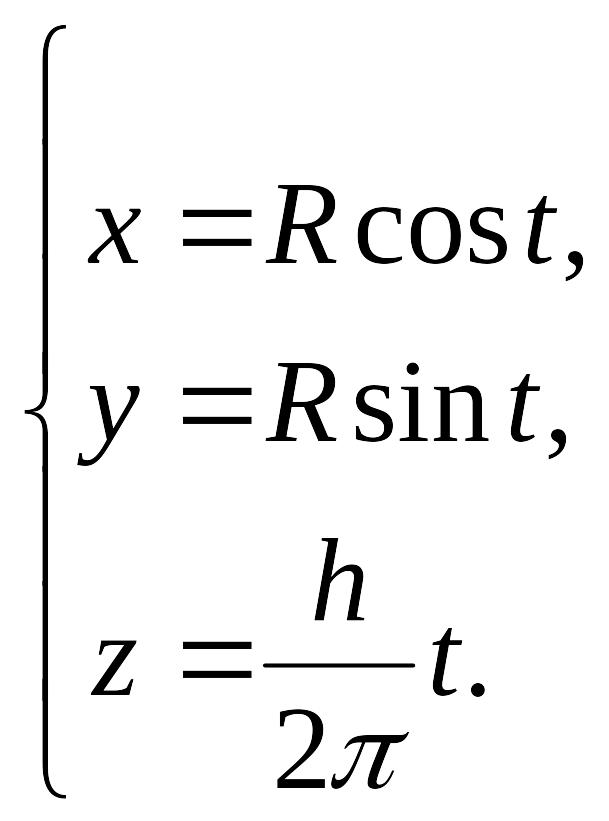
Если
точка

равномерно движется по образующей
кругового ци­линдра, а сам цилиндр
равномерно вращается вокруг оси, то
точка

описывает винтовую линию (см. рис. 12.3).

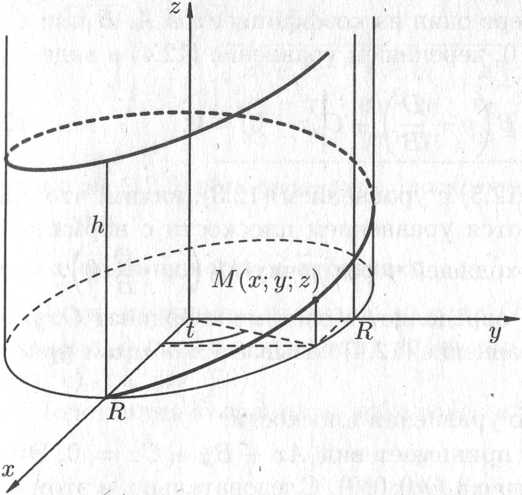
Рис. 12.3

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Канонические уравнения поверхностей второго порядка

Рассмотрим задачу приведения уравнения поверхности второго порядка к наиболее простому (каноническому) виду.

Напомним, что алгебраической поверхностью второго порядка называется геометрическое место точек плоскости, которое в какой-либо аффинной системе координат может быть задано уравнением вида

где левая часть — многочлен трех переменных второй степени. Коэффициенты при первых степенях переменных , а также при их произведениях взяты удвоенными просто для удобства дальнейших преобразований.

Уравнение (4.41) можно записать в матричном виде: где — матрица квадратичной формы, — столбец коэффициентов линейной формы (см. пункты 5,6, замечаний 4.1).

Требуется найти прямоугольную систему координат , в которой уравнение поверхности приняло бы наиболее простой вид.

Результатом решения поставленной задачи является следующая основная теорема.

---

Классификация алгебраических поверхностей второго порядка

Теорема 4.3. Для любой алгебраической поверхности второго порядка существует прямоугольная система координат , в которой уравнение этой поверхности принимает один из следующих семнадцати канонических видов:

В этих уравнениях , причем в уравнениях 1,2; в уравнениях 3,4,5,6,7,9,10.

Теорема 4.3 дает аналитические определения поверхностей второго порядка. Согласно п.2 замечаний 4.1, поверхности (1),(4),(5),(6),(7),(8),(9), (12),(13),(14),(15),(17) называются вещественными (действительными), а поверхности (2),(3),(10),(11),(16) — мнимыми.

Поясним доказательство теоремы. Оно аналогично доказательству теоремы 3.3 и фактически содержит алгоритм решения поставленной задачи.

Без ограничения общности можно предполагать, что уравнение поверхности второго порядка задано в прямоугольной системе координат. В противном случае можно перейти от непрямоугольной системы координат к прямоугольной , при этом уравнение линии будет иметь тот же вид и ту же степень согласно теореме 4.1.

Пусть в прямоугольной системе координат алгебраическая поверхность второго порядка задана уравнением (4.41), в котором хотя бы один из старших коэффициентов ап, отличен от нуля,n поскольку левая часть уравнения — многочлен трех переменных второй степени.

Упрощение общего уравнения (4.41) производится в два этапа. На первом этапе при помощи однородного ортогонального преобразования координат “уничтожаются” члены с произведением неизвестных, как и в случае уравнения линии второго порядка, при этом достаточно сделать три поворота (см. углы Эйлера).

Докажем, что существует однородная ортогональная замена переменных

где — столбцы старых и новых переменных, — ортогональная матрица , при которой квадратичная форма

приводится к каноническому виду

для которого матрица квадратичной формы диагональная:

Действительно, подставляя в квадратичную форму , получаем

т.е. при однородной ортогональной замене переменных (4.42) матрица квадратичной формы преобразуется по закону

Составим характеристическое уравнение для матрицы (см. пункт 3 замечаний 3.12):

Так как это уравнение третьей степени, то оно имеет хотя бы один действительный корень. Обозначим его . Однородная система уравнений

или

определитель которой равен нулю, имеет бесконечно много ненулевых решений. Обозначим через вектор, координатный столбец которого совпадает с ненулевым решением системы, удовлетворяющим условию нормировки . Дополним этот единичный вектор векторами до ортонормированного базиса пространства. Координатные столбцы векторов удовлетворяют условиям

кроме того столбец удовлетворяет равенству или, что то же самое, . Из координатных столбцов базисных векторов составим матрицу , которая в силу (4.44) является ортогональной, так как

и, следовательно, . Сделаем в квадратичной форме замену переменных с ортогональной матрицей . По закону (4.43) находим

Последний столбец этой матрицы, учитывая равенство и ортогональность , имеет вид

Следовательно, в матрице элементы и . Поэтому квадратичная форма имеет вид

Как показано при доказательстве теоремы 3.3, многочлен двух переменных при помощи поворота системы координат можно привести к виду . Этот поворот соответствует повороту найденной системы координат вокруг оси аппликат.

Таким образом, существует преобразование прямоугольной системы координат, приводящее квадратичную форму к каноническому виду. При этом уравнение (4.41) не содержит членов с произведением неизвестных:

На втором этапе, при помощи параллельного переноса “уничтожаются” один, два или все три члена первой степени. В результате всех преобразований получаем систему координат , в которой уравнение (4.45) становится приведенным (одного из следующих пяти типов):

Уравнения (I), (II), (II) совпадают с приведенными уравнениями линии второго порядка, поскольку не зависят от неизвестной . В разделе показано, что они сводятся к каноническим уравнениям эллипсов, гиперболы, параболы или пар прямых. Поэтому уравнения (I), (II), (III) соответственно сводятся к каноническим уравнениям цилиндров (9), (10), (12), (14): эллиптического, гиперболического, параболического, или пар плоскостей (11), (13), (15), (16), (17).

Уравнение (IV) в зависимости от знаков коэффициентов сводится к каноническим уравнениям параболоидов (7) или (8). Например, если все коэффициенты положительны, то, перенося линейный член в правую часть и разделив обе части уравнения на , получим . Обозначим положительные величины и изменим направление оси аппликат, т.е. сделаем замену: , , . В результате получим уравнение эллиптического параболоида (7): Если окажется, что , то переименуем координатные оси:

Уравнение (V) в зависимости от знаков коэффициентов сводится к каноническим уравнениям эллипсоидов (1),(2), гиперболоидов (4),(5) или конусов (3),(6).

---

Замечания 4.7.

1. Система координат, в которой уравнение алгебраической поверхности второго порядка имеет канонический вид, называется канонической. Каноническая система координат определяется неоднозначно. Например, изменяя направление оси ординат на противоположное, снова получаем каноническую систему координат, так как замена переменной на не изменяет уравнений (1)–(17).

2. Поверхности второго порядка, приведенные в формулировке теоремы 4.3, изображены в канонической системе координат. Изображение мнимых поверхностей дается штриховыми линиями только для иллюстрации.

3. В случаях (11),(13),(15)-(17) поверхности называются распадающимися, поскольку соответствующие им многочлены второй степени разлагаются в произведение многочленов первой степени.

4. Напомним, что ненулевой столбец , удовлетворяющий равенству , называется собственным вектором матрицы , а число — собственным значением этой матрицы. Говорят, что собственный вектор соответствует (принадлежит) собственному значению .

Как показано при доказательстве теоремы 4.3, при помощи однородной ортогональной замены переменных (4.42) или, что то же самое, при помощи поворотов прямоугольной системы координат вокруг ее начала , квадратичную форму

можно привести к каноническому виду

где — собственные числа матрицы квадратичной формы, т.е. корни характеристического уравнения: , а матрица замены переменных составлена из попарно ортогональных единичных собственных векторов матрицы , соответствующих собственным значениям . Другими словами, для любой квадратичной формы (трех переменных) существует ортонормированный базис , составленный из собственных векторов матрицы , в котором квадратичная форма имеет канонический вид.

5. При ортогональном преобразовании координат собственные векторы матрицы квадратичной формы не изменяются, а именно, если собственный вектор матрицы (соответствующий собственному значению ), то вектор является собственным для матрицы , где — ортогональная матрица.

Действительно, учитывая, что и , получаем

т.е. . Следовательно, — собственный вектор, соответствующий собственному значению .

6. При однородной невырожденной замене переменных линейная форма меняется следующим образом , т.е. столбец коэффициентов линейной формы изменяется по закону . Свободный член квадратичной функции при однородной замене переменных не изменяется.

Продолжение Порядок приведения уравнения поверхности второго порядка к каноническому виду

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Содержание:

1. Цилиндры
2. Упражнение
3. Поверхности второго порядка
4. Сфера и ее уравнение
5. Цилиндрические поверхности 
6. Цилиндры второго порядка
7. Эллипсоид 
8. Гиперболоиды
9. Параболоиды
10. Конические поверхности 
11. Поверхность вращения 
12. Понятие о поверхности второго порядка
13. Общее уравнение поверхности второго порядка, основные определения
14. Цилиндрические и конические поверхности
15. Исследование формы поверхностей второго порядка методом сечений

Поверхностью второго порядка в пространстве называется поверхность, определяемая уравнением второй степени относительно текущих координат

Рассмотрим частные виды поверхностей второго порядка. Сфера с центром в точке и радиусом имеет уравнение где — заданные числа (рис. 2.18).

Раскрыв скобки и перенеся в левую часть, получим Нетрудно проверить, что уравнение второй степени относительно в котором коэффициенты при равны, а члены с произведениями координат отсутствуют, представляет собой уравнение сферы (кроме случаев, когда это уравнение не определяет никакой поверхности).

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Цилиндры

Цилиндрической называется поверхность, описываемая прямой, остающейся параллельной некоторому направлению и пересекающей данную линию. Последняя называется направляющей цилиндрической поверхности, а сама прямая — образующей. Пусть, например, образующие цилиндрической поверхности параллельны оси и направляющей служит эллипс (рис. 2.19)

в плоскости с уравнением Эта поверхность называется эллиптическим цилиндром. Пусть — произвольная точка этого цилиндра, а точка — проекция на плоскость

Ясно, что абсциссы и ординаты точек и совпадают. Так как точка лежит на эллипсе, то ее координаты х и у удовлетворяют уравнению (2.55). Но тогда этому уравнению удовлетворяют координаты х и у точки цилиндра. Значит, (2.55) есть уравнение цилиндра.

Итак, уравнение (2.55) на плоскости определяет эллипс, а в пространстве — эллиптический цилиндр с образующей, параллельной направляющей которого является указанный эллипс.

Возможно вам будут полезны данные страницы:

Упражнение

Изобразите самостоятельно:

1) гиперболический цилиндр с уравнением и образующей, параллельной оси

2) параболический цилиндр с уравнением и образующей, параллельной оси

Поверхности второго порядка

Определение. Поверхности второго порядка называют геометрическое место точек пространства, декартовые координаты которых удовлетворяют уравнению второй степени. 

Сфера и ее уравнение

Сферой называют геометрическое место точек пространства,  равноудаленное от заданной точки – центра сферы. 

Если центром сферы является точка  а радиус  тогда уравнение сферы будет: 

Если центр сферы находится в начале координат  и радиус  тогда уравнение сферы будет: 

Цилиндрические поверхности 

Поверхность называется цилиндрической, если она образуется прямой (образующая), параллельно к заданной прямой   и которая проходит через заданную линию  (направляющая линия). Пример цилиндрической линии изображен на рис. 2.24

Если образующая цилиндрической поверхности параллельна оси  а образующая  лежит на плоскости  и задана уравнением: 

тогда уравнение цилиндрической поверхности будет: 

Уравнение  обозначает цилиндрическую поверхность с образующей, что параллельна оси  уравнение  – цилиндрическая поверхность с образующей, что параллельна оси  

Цилиндры второго порядка

а) Эллиптичным цилиндром  называется поверхность (рис. 2.25), каноничное уравнение которой имеет вид: 

Если  то получим круговой цилиндр: 

б) Гиперболичным цилиндром называется поверхность, уравнение которой имеет вид (рис. 2.26): 

в) Параболическим цилиндром называется поверхность, каноничное уравнение которой имеет вид (рис. 2.27): 

Эллипсоид 

Эллипсоидом называется поверхность, каноничное уравнение которой имеет вид (рис. 2.28): 

 Отрезки  – называются полуосями эллипсоида. 

Гиперболоиды

а) однополосный гиперболоид. 

Однополосным гиперболоидом (рис. 2.29) называется поверхность, каноническое уравнение которой имеет вид :

 б) Двуполостный гиперболоид. Двуполостным гиперболоидом (рис. 2.30) называется поверхность, каноничное уравнение которой имеет вид: 

Параболоиды

а) Эллиптическим параболоидом (рис. 2.31) называется поверхность, каноничное уравнение которой имеет вид: 

б) Гиперболичным параболоидом (рис. 2.32) называется поверхность, каноничное уравнение которой имеет вид: 

Конические поверхности 

конической поверхностью называется поверхность, которая описана прямой, что проходит через точку – вершину конуса – и что пересекает заданную линию – направляющую конуса. 

Уравнение конуса (рис. 2.33) второго порядка имеет вид: 

Поверхность вращения 

Пусть в плоскости  задана линия  что имеет уравнение  Тогда чтобы получить уравнение поверхности, что образована вращением линии  что лежит в плоскости  около оси  нужно в уравнение этой линии заменить  на  Искомое уравнение поверхности вращения будет 

Аналогично правила будут иметь место и по отношению к поверхностям, которые образуют обращение плоских линий около других координатных осей. 

Примеры:  1) уравнение поверхности, что образуются вращением эллипса  около оси  будет  (эллипсоид вращения). 

2) уравнение поверхности, что образуются вращением гиперболы  около оси  будет  или  (двуполостный гиперболоид). 

Примеры решения задач:

Задача 2.126

Обозначить координаты центра сферы и ее радиус: 

Решение. Предоставим заданное уравнение в виде (2.43), для этого: 1) объединяем в группы члены, которые содержат одноименные координаты; 

2) выделим в группах полные квадраты. Получим: 

Соизмеряя с (2.43), получим  Следует, центр сферы – точка  радиус 

Задача 2.127 

Эллипс с полуосями 5 и 3 вращается около своей большей оси. которая совпадает с началом координат. Сложить уравнение поверхности, что описывает эллипс при вращении. 

Решение. Сложим каноническое уравнение эллипса с центром в начале координат, который размещен в плоскости 

чтобы получить уравнение поверхности, которая образована вращением в плоскости  около оси  необходимо в уравнении эллипса заменить  на  Получим эллипсоид вращения, который протянул вдоль оси 

 или 

Задача 2.128 

Сложим уравнение конуса с вершиной в начале координат и направляющей: 

Решение. Канонические уравнения образующих, что проходят через вершину  конуса и точки  направляющей, будут: 

Исключим   в заданных уравнениях. Изменяя   через  обозначим   и  из остальных двух уравнений: 

подставим полученные значения   и  в первое уравнение направляющей, получим: 

 или 

Задача 2.129 

Какие поверхности обозначаются уравнениями: 

Решение. Каждое из уравнений содержит только две переменные   и   и обозначает на плоскости  кривые: 1) круг, 2) эллипс, 3) параболу, 4) гиперболу. 

В пространстве же каждое из них обозначается цилиндрическую поверхность с образующими, что параллельны оси   так как эти уравнения не содержат переменной . Направляющими этих цилиндрических поверхности являются указанные кривые: 

 – уравнение прямого углового цилиндра; 

 – уравнение эллиптического цилиндра;

 – уравнение параболического цилиндра; 

  – уравнение гиперболичного цилиндра. 

Задача 2.130 

Гипербола с полуосями 3 и 4 вращается около своей мнимой оси, которая совпадает с осью  Центры гиперболы совпадает с началом координат. Сложить уравнение поверхности, которое получим при вращении гиперболы. 

Решение. Сложим каноничное уравнение гиперболы с центром в начале координат, что находятся в плоскости 

Чтобы сложить уравнение поверхности, образованной вращением гиперболы, что находится в уравнение гиперболы вместо  подставить 

 или 

Следует, получим однополосный гиперболоид вращения: 

Понятие о поверхности второго порядка

Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению.

Общее уравнение поверхности второго порядка, основные определения

Поверхностью второго порядка называется множество точек пространства , описывается уравнением , левая часть которого является многочленом второй степени относительно переменных :

где коэффициенты уравнения при текущих переменных ; – свободный член; и по крайней мере один из коэффициентов отличается от нуля

Уравнение (10.27) называют общим уравнением поверхности второго порядка. Вид поверхности и ее расположение относительно координатных плоскостей зависит от значений параметров в (10.27).

Если не существует ни одной точки , которая удовлетворяет общее уравнение, говорится, что оно определяет мнимую поверхность.
Поверхность называется вырожденной, если ее общее уравнение описывает точку, одну или две плоскости. К примеру:

уравнение точки в 

уравнения двух плоскостей, параллельных 

уравнения двух биссекторных плоскостей.

При изучении поверхностей второго порядка решаются две взаимно обратные основные задачи:
1) по известным геометрическим свойствам точек поверхности составить уравнение соответствующей поверхности;
2) по известным уравнением поверхности установить геометрические свойства ее точек.

Примером решения первой основной задачи является построение уравнения сферы (9.2). Уравнение других важнейших поверхностей рассматриваются ниже.

Цилиндрические и конические поверхности

Цилиндрической поверхностью, или просто цилиндром, называется поверхность, образованная движением прямой, перемещается параллельно самой себе вдоль фиксированной линии (кривой). Подвижную прямую называют образующей, а фиксированную кривую – направляющей цилиндрической поверхности. Направляющей может быть любая сомкнутая или разомкнутая линия.

Цилиндром второго порядка называется цилиндрическая поверхность, направляющей которой является кривая второго порядка: эллипс (круг), гипербола, парабола. Название цилиндра определяется названием его направляющей. Если образующая параллельна одной из координатных осей, а направляющая лежит в плоскости, перпендикулярной этой оси, то уравнение цилиндра совпадает с уравнением направляющей. При геометрической интерпретации изображается, как правило, часть поверхности между двумя плоскостями, перпендикулярными образующей.
К примеру:

 уравнения эллиптического цилиндра (рис. 10.9 а)

 уравнения гиперболического цилиндра (рис. 10.9 б)

 уравнения параболического цилиндра (рис. 10.9 в).

Рис. 10.9

Отсутствие переменной  в приведенных уравнениях означает, что аппликанта точек поверхности может быть любым действительным числом, потому что коэффициент при переменной  в уравнениях следует считать равными нулю. Например, уравнение параболического цилиндра можно записать в виде: . Итак, образующая цилиндра параллельна оси, совпадающей с переменной, которая отсутствует в уравнении поверхности.

Если в уравнениях эллипса и гиперболы положить , то получим соответственно круговой и равносторонний гиперболический цилиндры.

Конической поверхностью, или конусом, называется поверхность, образованная движением прямой, проходящей через заданную точку, вдоль фиксированной кривой. Подвижную прямую называют образующей, заданную точку – вершиной, а фиксированную кривую – направляющей конуса. Если образующей является кривая второго порядка, то поверхность называется конусом второго порядка.
На рис. 10.10 изображен конус второго порядка, определяется уравнением

Рис. 10.10

с вершиной в начале координат, направляющей которого является эллипс

в плоскости 

Поверхность симметрична относительно начала координат, а координатные плоскости является ее плоскостями симметрии. Множество точек поверхности с неотъемлемыми (неположительные) аппликатами называется верхней (нижней) полостью конуса.

Если направляющей конуса является круг , то он называется круговым.

Эллипс, парабола, гипербола – кривые второго порядка – можно получить сечением прямого кругового конуса плоскостями, которые не проходят через его вершину (рис. 10.11). А именно: если плоскость пересекает только одну полость конуса и непараллельных одной из его образующих, то кривой сечения является эллипс; в частном случае – круг;
если секущая плоскость параллельна одной из образующих конуса, то результат сечения – парабола;
если плоскость сечения пересекает обе полости конуса, то кривой сечения является гипербола.

Рис. 10.11

Исследование формы поверхностей второго порядка методом сечений

Приведенные выше уравнения поверхностей второго порядка складывались по геометрическим свойствам их точек в соответствии с определений поверхностей. Для решения обратной задачи (по данным уравнением поверхности определить ее вид) применяется метод сечений, суть которого заключается в следующем:

1) анализируют поверхность, устанавливая за ее уравнением линии пересечения (сечения) данной поверхности координатными плоскостями параллельными им;

2) синтезируют определенные на предыдущем шаге геометрические свойства поверхности, что позволяет представить вид поверхности и изобразить ее.

Продемонстрируем применение метода сечений к исследованию уравнения эллиптического параболоида:

Исследование предполагает такие шаги:
1) найдем линии пересечения поверхности (10.28) с плоскостью и плоскостями, параллельными ей :

Если:

а) , то уравнение (10.29) удовлетворяют лишь координаты точки , то есть плоскость является касательной к данной поверхности;
б) , то получаем воображаемую линию, поскольку плоскости заданную поверхность не пересекают;
в) , то уравнение (10.29) можно записать в виде:

то есть сечением поверхности плоскостями, параллельными , есть эллипсы, полуоси которых увеличиваются вместе с увеличением (рис. 10.12);

2) установим линию пересечения поверхности с плоскостью :

Это уравнение параболы, расположенной в плоскости , с осью симметрии .

Рис. 10.12

3) определим (аналогичным образом) сечение поверхности плоскостью : это парабола, которая описывается уравнением , и расположена в плоскости (с осью симметрии ).
4) изображаем согласно рассмотренным выше соответствующие линии (рис. 10.12), что позволяет составить представление о форме исследуемой поверхности. Наконец намечаем обвод – линию, получается как множество точек прикосновения к поверхности прямых, параллельных выбранном направления проектирования.

Аналогично осуществляется построение параболоида , сечения которого – параболы ветвями вниз, и параболоидов, оси которых совпадают с координатными осями . Уравнение таких поверхностей получаемых из рассмотренного выше с помощью циклической перестановки переменных.

Поверхностью вращения называется поверхность, для которой каждый из ее сечений плоскостью, перпендикулярной одной из координатных осей или произвольной оси , является кругом. Круговой конус и круговой цилиндр являются примерами таких поверхностей: конус образуется вращением вокруг оси прямой, проходящей через начало координат, а цилиндр – прямой, параллельной оси , причем прямые не принадлежат плоскости, перпендикулярной оси вращения.

Уравнения поверхностей, симметричные относительно координатных осей или / и координатных плоскостей, называют каноническими, или стандартными.

В заключение отметим, что приведенные сведения используются при изучении интегрирования функций двух переменных и является фундаментом для более глубокого изучения теории поверхностей второго порядка.

Далее в таблице 10.1 приводятся канонические уравнения и изображения важнейших поверхностей второго порядка.

Важнейшие поверхности второго порядка                                                                    Таблица 10.1