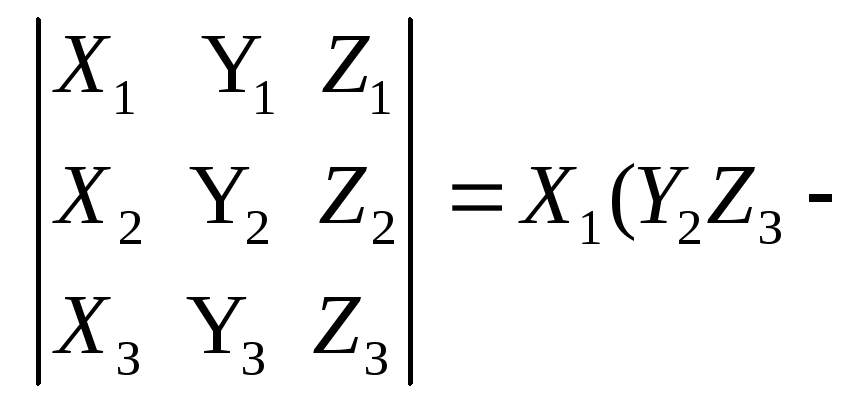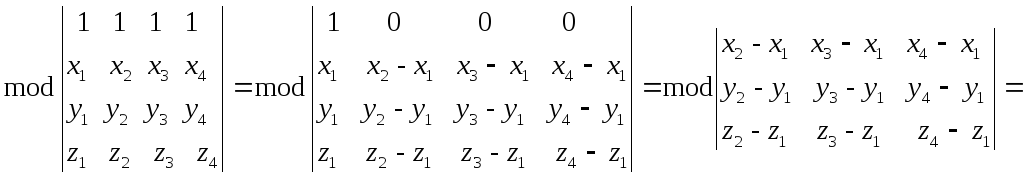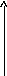Как найти уравнение грани параллелепипеда

Прямоугольный параллелепипед. Что это такое?

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

1. Противолежащие грани параллелепипеда равны и параллельны друг другу.
2. Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3. Параллелепипед симметричен относительно середины его диагонали.
4. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

1. Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
2. Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
3. Высота прямого параллелепипеда равна длине бокового ребра.
4. Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
5. Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

• Площадь боковой поверхности прямого параллелепипеда
  Sб = Ро*h
  Ро — периметр основания
  h — высота
• Площадь полной поверхности прямого параллелепипеда
  Sп = Sб+2Sо
  Sо — площадь основания
• Объем прямого параллелепипеда
  V = Sо*h

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

1. Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
2. Противолежащие грани параллелепипеда попарно параллельны и равны.
3. Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
4. Диагонали прямоугольного параллелепипеда равны.
5. В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7. Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы прямоугольного параллелепипеда:

• Объем прямоугольного параллелепипеда
  V = a · b · h
  a — длина, b — ширина, h — высота
• Площадь боковой поверхности
  Sбок = Pосн·c=2(a+b)·c
  Pосн — периметр основания, с — боковое ребро
• Площадь поверхности
  Sп.п = 2(ab+bc+ac)

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = d₁² + c² = a² + b² + c²

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

1. В кубе 6 граней, каждая грань куба — квадрат.
2. Противолежащие грани параллельны друг другу.
3. Все углы куба, образованные двумя гранями, равны 90°.
4. У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
5. Диагонали куба равны.
6. Диагональ куба в √3 раз больше его ребра.
7. Диагональ грани куба в √2 раза больше длины ребра.

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

• Объем куба через длину ребра a
  V = a3
• Площадь поверхности куба
  S = 6a2
• Периметр куба
  P = 12a

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a – длина, b – ширина, c – высота. Тогда a = 10, b = 5, c = 8.

Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) – сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) – суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) – сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) – сумма длин всех ребер прямоугольного параллелепипеда.

Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X – сумма длин ребер).

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°.

По теореме Пифагора:
BD₁ 2 = DD₁ 2 + BD 2
BD 2 = BD₁ 2 – DD₁ 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 – AD 2 = (√17)2 — 4 2 = 1
A₁B₁ = AB = 1.

Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77
BD₁ = √77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

• прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
• параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
• основание прямоугольного параллелепипеда — прямоугольник;
• три измерения прямоугольного параллелепипеда: длина, ширина, высота;
• диагональ параллелепипеда равна сумме квадратов его измерений.

Прямоугольный параллелепипед

Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.

Свойства прямоугольного параллелепипеда:

1. В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
2. Противоположные грани попарно равны и параллельны.
3. Все двугранные углы прямоугольного параллелепипеда – прямые.
4. Диагонали прямоугольного параллелепипеда равны.
5. Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$с$ – высота(она же боковое ребро);

$P_<осн>$ – периметр основания;

$S_<осн>$ – площадь основания;

$S_<бок>$ – площадь боковой поверхности;

$S_<п.п>$ – площадь полной поверхности;

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

$S_<бок>=P_<осн>·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.

Дополнительные сведения, которые пригодятся для решения задач:

$а$ – длина стороны.

$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) – треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Объем любой пирамиды равен трети произведения основания и высоты.

В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

• $S=/<2>$, где $h_a$ – высота, проведенная к стороне $а$.
• $S=/<2>$, где $a,b$ – соседние стороны, $α$ – угол между этими соседними сторонами.
• Формула Герона $S=√$, где $р$ – это полупериметр $p=/<2>$.
• $S=p·r$, где $r$ – радиус вписанной окружности.
• $S=/<4R>$, где $R$ – радиус описанной окружности.
• Для прямоугольного треугольника $S=/<2>$, где $а$ и $b$ – катеты прямоугольного треугольника.
• Для равностороннего треугольника $S=/<4>$, где $а$ – длина стороны.

В основании лежит четырехугольник.

1. Прямоугольник.
   $S=a·b$, где $а$ и $b$ – смежные стороны.
2. Ромб.
   $S=/<2>$, где $d_1$ и $d_2$ – диагонали ромба.
   $S=a^2·sin⁡α$, где $а$ – длина стороны ромба, а $α$ – угол между соседними сторонами.
3. Трапеция.
   $S=<(a+b)·h>/<2>$, где $а$ и $b$ – основания трапеции, $h$ – высота трапеции.
4. Квадрат.
   $S=a^2$, где $а$ – сторона квадрата.

Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.

Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.

Объем пирамиды, в основании которой лежит прямоугольник

Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.

В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.

Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Прямоугольный параллелепипед. Площадь поверхности прямоугольного параллелепипеда

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы узнаем, что такое прямоугольный параллелепипед, его свойства. Кроме того, будет выведена формула площади поверхности параллелепипеда, решена задача с применением данной формулы.

[spoiler title=”источники:”]

http://examer.ru/ege_po_matematike/teoriya/pryamiugolnyi_parallelepiped

http://interneturok.ru/lesson/matematika/5-klass/bplowadi-i-obyomyb/pryamougolnyy-parallelepiped-ploschad-poverhnosti-pryamougolnogo-parallelepipeda

[/spoiler]

Задача 29325 5.2.55) Даны уравнения трех граней…

Для трех ребер $OA$, $OB$ и $OC$ параллелепипеда с общей вершиной $O$ заданы координаты соответствующих вершин $Oleft(7,2,2right)$, $Aleft(8,9,1right)$, $Bleft(3,5,3right)$ и $Cleft(6,3,8right)$. Найти углы в основании параллелепипеда, считая, что его образует параллелограмм, построенный на ребрах $OA$ и $OB$. Найти площадь основания параллелепипеда. Найти объем параллелепипеда.

Призмою называют многогранник, две грани которого — основания — являются одинаковыми многоугольниками, лежащими в параллельных плоскостях, а другие грани — боковые — являются параллелограммами, имеющими общие стороны с этими многоугольниками. Параллелепипедом называется призма, основаниями которой являются параллелограммы.

Пусть начало пространственного вектора $overline{AB}$ находится в точке $Aleft(x_{a} ,; y_{a} ,z_{a} right)$, а конец — в точке $Bleft(x_{b} ,; y_{b} ,z_{b} right)$. Алгебраически этот вектор записывают так: $overline{AB}=left(x_{b} -x_{a} right)cdot overline{i}+left(y_{b} -y_{a} right)cdot overline{j}+left(z_{b} -z_{a} right)cdot overline{k}$.

Используем эту формулу для представления каждого из ребер в виде вектора, имеющего начало в точке $O$. Используем для них обозначения: $bar{a}=overline{OA}$, $bar{b}=overline{OB}$ и $bar{c}=overline{OC}$. Алгебраическая запись этих векторов:

$bar{a}=left(8-7right)cdot bar{i}+left(9-2right)cdot bar{j}+left(1-2right)cdot bar{k}$ или $bar{a}=bar{i}+7cdot bar{j}-bar{k}$;

$bar{b}=left(3-7right)cdot bar{i}+left(5-2right)cdot bar{j}+left(3-2right)cdot bar{k}$ или $bar{b}=-4cdot bar{i}+3cdot bar{j}+bar{k}$;

$bar{c}=left(6-7right)cdot bar{i}+left(3-2right)cdot bar{j}+left(8-2right)cdot bar{k}$ или $bar{c}=-bar{i}+bar{j}+6cdot bar{k}$.

Находим угол между векторами $overline{a}$ и $overline{b}$ в основании параллелепипеда. Для этого сначала вычислим скалярное произведение этих векторов.

Известно, что скалярное произведение $overline{a}cdot overline{b}$ двух векторов $overline{a}=x_{1} cdot overline{i}+y_{1} cdot overline{j}+z_{1} cdot overline{k}$ и $overline{b}=x_{2} cdot overline{i}+y_{2} cdot overline{j}+z_{2} cdot overline{k}$ вычисляется по формуле $overline{a}cdot overline{b}=x_{1} cdot x_{2} +y_{1} cdot y_{2} +z_{1} cdot z_{2} $ или по формуле $overline{a}cdot overline{b}=left|overline{a}right|cdot left|overline{b}right|cdot cos phi $, где $phi $ — угол между векторами.

В нашем случае имеем:

[overline{a}cdot overline{b}=x_{1} cdot x_{2} +y_{1} cdot y_{2} +z_{1} cdot z_{2} =1cdot left(-4right)+7cdot 3+left(-1right)cdot 1=-4+21-1=16.]

Теперь вычисляем длины этих векторов. Для этого используем следующую формулу: $left|overline{AB}right|=sqrt{left(x_{b} -x_{a} right)^{2} +left(y_{b} -y_{a} right)^{2} +left(z_{b} -z_{a} right)^{2} } $.

Получаем:

[left|bar{a}right|=sqrt{1^{2} +7^{2} +left(-1right)^{2} } =sqrt{1+49+1} =sqrt{51} approx 7,1414;]

[left|bar{b}right|=sqrt{left(-4right)^{2} +3^{2} +1^{2} } =sqrt{16+9+1} =sqrt{26} approx 5,0990.]

Теперь можем вычислить косинус угла между векторами $overline{a}$ и $overline{b}$:

[cos phi =frac{bar{a}cdot bar{b}}{left|bar{a}right|cdot left|bar{b}right|} =frac{16}{7,1414cdot 5,0990} approx 0,44.]

Отсюда получаем значение угла между векторами $overline{a}$ и $overline{b}$ в основании параллелепипеда: $phi =1,12; радиан=64{}^circ $. Смежный угол $phi _{1} =180-64=116{}^circ $.

Вычисляем площадь основания параллелепипеда. При этом известно, что если сторонами параллелограмма являются два неколлинеарных вектора, приведенные к общему началу, то площадь параллелограмма равна длине их векторного произведения.

Известно также, что векторное произведение $overline{v}=overline{a}times overline{b}$ двух векторов $overline{a}$ и $overline{b}$ вычисляется по формуле $overline{v}=left|begin{array}{ccc} {overline{i}} & {overline{j}} & {overline{k}} \ {x_{1} } & {y_{1} } & {z_{1} } \ {x_{2} } & {y_{2} } & {z_{2} } end{array}right|$.

Находим векторное произведение векторов $bar{a}=bar{i}+7cdot bar{j}-bar{k}$ и $bar{b}=-4cdot bar{i}+3cdot bar{j}+bar{k}$: $overline{v}=left|begin{array}{ccc} {overline{i}} & {overline{j}} & {overline{k}} \ {1} & {7} & {-1} \ {-4} & {3} & {1} end{array}right|=10cdot bar{i}+3cdot bar{j}+31cdot bar{k}$.

Теперь находим площадь основания параллелепипеда как длину векторного произведения: $S=left|overline{v}right|=sqrt{10^{2} +3^{2} +31^{2} } =32,7109$ кв.од.

Находим объем параллелепипеда. При этом известно, что если ребрами параллелепипеда являются три некомпланарных вектора, приведенные к общему началу, то объем параллелепипеда равен модулю их смешанного произведения.

Известно также, что смешанное произведение трех векторов $overline{a}=x_{1} cdot overline{i}+y_{1} cdot overline{j}+z_{1} cdot overline{k}$, $overline{b}=x_{2} cdot overline{i}+y_{2} cdot overline{j}+z_{2} cdot overline{k}$ и $overline{c}=x_{3} cdot overline{i}+y_{3} cdot overline{j}+z_{3} cdot overline{k}$ вычисляется по формуле $left(overline{a}times overline{b}right)cdot overline{c}=left|begin{array}{ccc} {x_{1} } & {y_{1} } & {z_{1} } \ {x_{2} } & {y_{2} } & {z_{2} } \ {x_{3} } & {y_{3} } & {z_{3} } end{array}right|$.

Находим смешанное произведение векторов $bar{a}=bar{i}+7cdot bar{j}-bar{k}$, $bar{b}=-4cdot bar{i}+3cdot bar{j}+bar{k}$ и $bar{c}=-bar{i}+bar{j}+6cdot bar{k}$:

[left(overline{a}times overline{b}right)cdot overline{c}=left|begin{array}{ccc} {1} & {7} & {-1} \ {-4} & {3} & {1} \ {-1} & {1} & {6} end{array}right|==1cdot 17-7cdot left(-23right)+left(-1right)cdot left(-1right)=17+161+1=179.]

Получаем объем параллелепипеда: $V=left|179right|=179$ куб.од.

Задача 2

Доказательство.
Если векторы
компланарны, то, согласно доказанной
теореме, их смешанное произведение
равно нулю. Если смешанное произведение
векторов равно нулю, то по этой же теореме
проекция одного из векторов на ось,
определяемую векторным произведением
двух других векторов, равна нулю, т. е.
он параллелен плоскости, в которой лежат
два другие вектора. Это означает, что
векторы компланарны. Следствие доказано.

Следствие 3.
Смешанное
произведение трех векторов, два из
которых совпадают, равно нулю.

Доказательство.
Если два вектора из трех совпадают, то
такие три вектора компланарны и их
смешанное произведение равно нулю.
Следствие доказано.

Теорема 14.
Если векторы
,изаданы своими координатами, т. е.,,,
то смешанное произведение векторов,ивычисляется по формуле

.
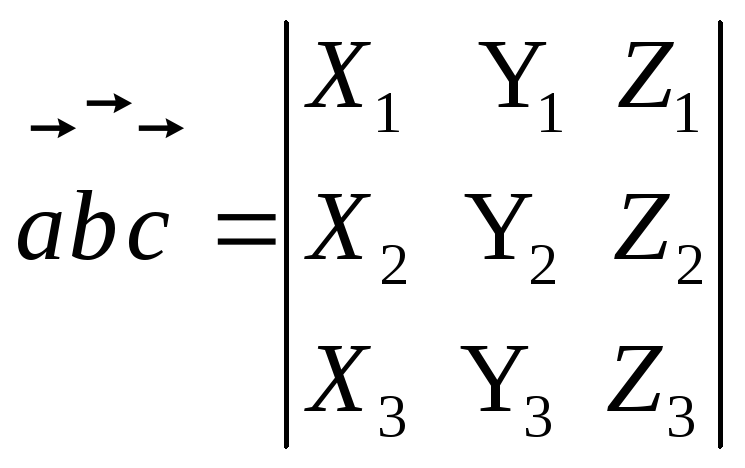
(2.34)

Доказательство.
Разложим определитель, стоящий в правой
части выражения (2.34), по первой строке.
Получим:
.
Теорема доказана.

Теорема 15. Пусть
даны точки
,,,.
Тогда объем параллелепипеда, построенного
на векторах,икак на сторонах, вычисляется по формуле

.
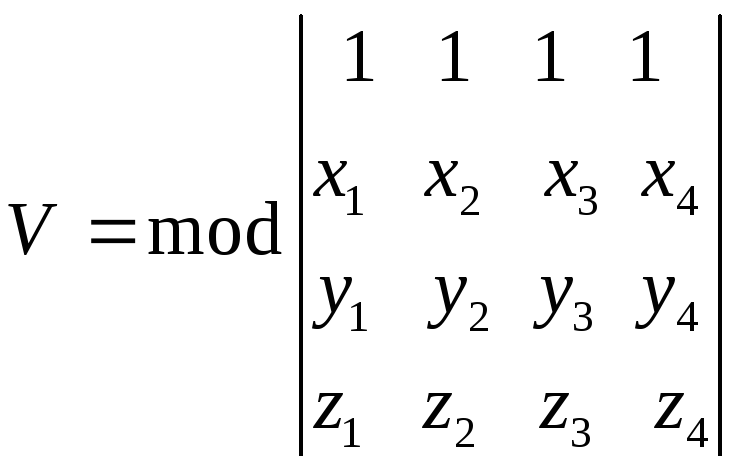
(2.35)

Доказательство.
Преобразуем правую часть (2.35), используя
свойства определителей:

.
Теорема доказана.

Следствие.
Объем треугольной пирамиды с вершинами
в точках
,,,вычисляется по формуле

.
(2.36)

Доказательство.
Если четыре вершины параллелепипеда,
не лежащие в одной плоскости, являются
вершинами треугольной пирамиды, то
объем пирамиды составляет
объема параллелепипеда. Учитывая, что
объем параллелепипеда вычисляется по
формуле (2.35), получаем доказываемое
тождество. Следствие доказано.

П р и м е р 29.
Вершины тетраэдра находятся в точках
,,и.
Найти длину высотытетраэдра, опущенной из вершины.

Решение.
Так как объем
тетраэдра и его высотасвязаны соотношением,
где
площадь грани
,
то.
Объемтетраэдра и площадьгранинайдем, используя векторное и смешанное
произведения векторов. По формуле (2.36)
имеем:.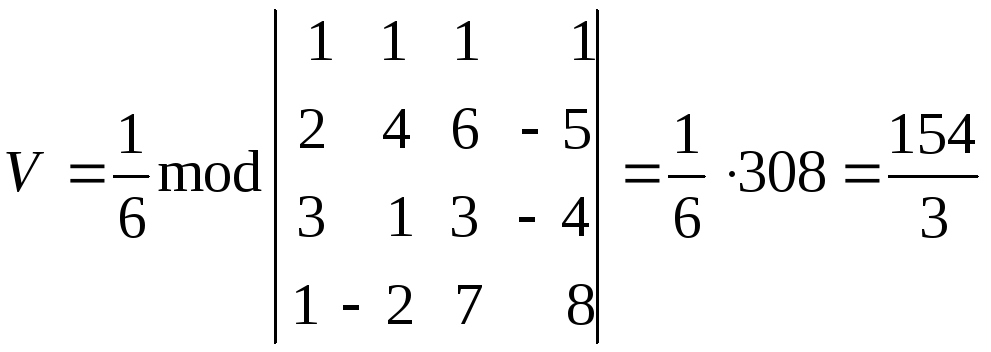
Из определения векторного произведения
следует, что.
Так как,,
то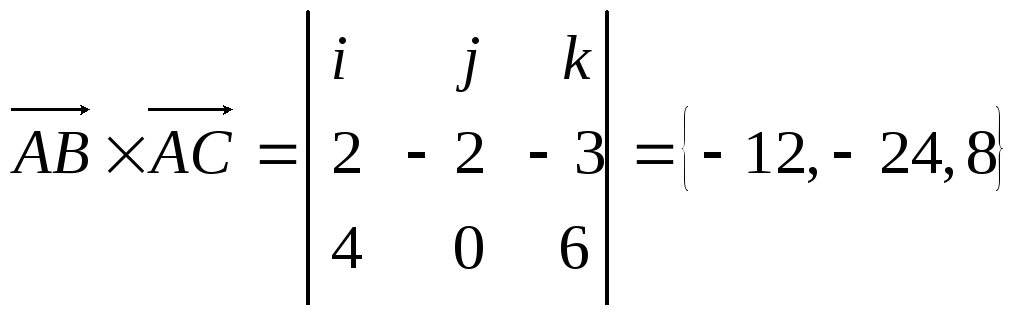и.
Таким образом,.

3.1. Общее уравнение плоскости

Пусть
в пространстве задана прямоугольная
система координат
,
точкаи вектор.
Выведем уравнение плоскости,
проходящей через точкуи перпендикулярной вектору.

Пусть

произвольная точка плоскости
.
Точкалежит в плоскоститогда и только тогда, когда векторыивзаимно перпендикулярны.

z

M₀

y

M

O

x

Вектор
имеет координаты.
Необходимым и достаточным условием
перпендикулярности векторов является
равенство нулю их скалярного произведения,
т. е. должно выполняться равенство.
Воспользовавшись формулой (2.21), получим:

.
(3.1)

Уравнение
(3.1) 
искомое уравнение плоскости
,
проходящей через точкуи перпендикулярной вектору,
так как ему удовлетворяют координатылюбой точки,
лежащей на плоскости,
и не удовлетворяют координаты никакой
точки, не лежащей на этой плоскости.

Если
в уравнении (3.1) раскрыть скобки и
обозначить
,
то получимобщее уравнение
плоскости:

.
(3.2)

Таким образом,
плоскость является поверхностью первого
порядка, так как определяется уравнением
первой степени.

Теорема 1.
Всякое уравнение первой степени вида
(3.2) определяет в заданной системе
координат плоскость.

Доказательство.
Пусть заданы
прямоугольная система координат
и уравнение,
коэффициенты которого удовлетворяют
условию,
т. е. хотя бы один из коэффициентовотличен от нуля. Для определенности
будем считать, что.
Уравнение (3.2) имеет решение,
так как при фиксированныхииз уравнения (3.2) получим.
Следовательно, существует хотя бы одна
точка,
координаты которой удовлетворяют
уравнению (3.2), т. е..
Вычитая это числовое равенство из
уравнения (3.2), получим уравнение,
эквивалентное данному,
поэтому уравнениеопределяет плоскость, проходящую через
точкуи перпендикулярную вектору.
Теорема доказана.

П р и м е р 30.
Составить общее уравнение плоскости,
проходящей через точку
перпендикулярно вектору.

Решение.
С использованием (3.1) имеем:
,
или.

Определение.
Вектор
,
перпендикулярный плоскости,
задаваемой уравнением,
называетсянормальным вектором
этой плоскости.

Теорема 2.
Если два уравнения
иопределяют одну и ту же плоскость, то
найдется такое число,
что справедливы равенства,,,,
т.е. коэффициенты уравнений пропорциональны.

Доказательство.
Уравнения
иопределяют одну и ту же плоскость,
поэтому векторыиколлинеарны. Согласно условию (2.28)
коллинеарности имеем:,
т. е.,,.
Подставим выражения для коэффициентовв первое уравнение плоскости, получим:.
Выражение, стоящее в скобках, равно,
поэтому.
Теорема доказана.

3.2. Угол между плоскостями

Рассмотрим
две плоскости
и,
которые задаются уравнениямии.

При
любом расположении плоскостей в
пространстве один из углов
между ними равен углу между их нормальными
векторамиии вычисляется по формуле:

.
(3.3)

Второй
угол
между плоскостями равени.

Две
плоскости
ипараллельны тогда и только тогда, когда
их нормальные векторыиколлинеарны. В этом случае

.
(3.4)

Условие
(3.4) является условием параллельности
двух плоскостей, задаваемых уравнениями
и.

Две
плоскости
ивзаимно перпендикулярны тогда и только
тогда, когда их нормальные векторыиортогональны, т. е. косинус угламежду ними равен нулю. Поэтому условие
перпендикулярности плоскостей
определяется соотношением

.
(3.5)

Соседние файлы в папке 20-12-2012_21-26-59

• #
• #
• #
• #
• #
• #
• #

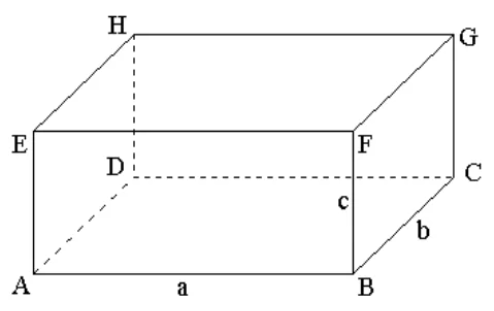
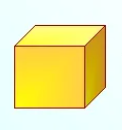
Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).

Определение

Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.

Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.

У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.

Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.

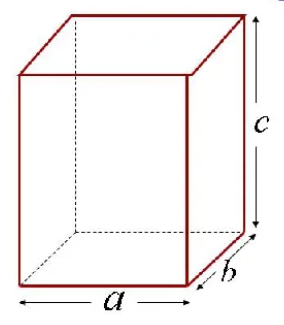
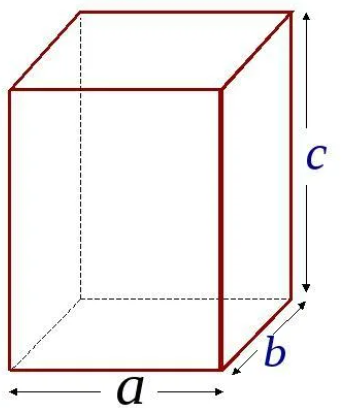
Длина, ширина, высота

Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.

Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.

Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.

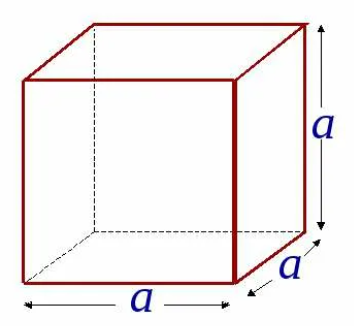
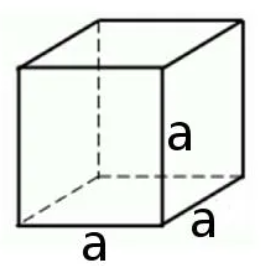
Куб

Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).

Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a². Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a²

Объем прямоугольного параллелепипеда

С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.

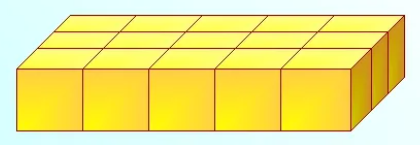
Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.

 

За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.

Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм³; с ребром 1 см – кубическим сантиметром (см³) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.

Формула объема прямоугольного параллелепипеда

Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.

Объем куба

Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:

V=a³

Пирамида

Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).

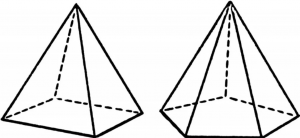
Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).

Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.

Даниил Романович | Просмотров: 882