Как найти уравнение грани пирамиды а1а2а3

Онлайн решение Пирамиды по координатам вершин

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Пример 1:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти:

1) координаты и модули векторов А₁ А₂и А₁ А₄;  

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) площадь грани А₁ А₂ А₃;         

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂ А₃;

7) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3.

Сделать чертеж.

А₁ (0; 4; -4), А₂ (5; 1; -1), А₃ (-1; -1; 3), А₄ (0; -3; 7).

Решение от преподавателя:

Пример 2:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

8) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

1. А₁ (7; 7; 3), А₂ (6; 5; 8), А₃ (3; 5; 8), А₄ (8; 4; 1).

Решение от преподавателя:

Пример 3:

Решение от преподавателя:

 Уравнение плоскости. 
Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением: 

x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 x3-x1 y3-y1 z3-z1

= 0

Уравнение плоскости A₁A₂A₃ 

(x-3)(1*2-0*3) – (y-2)((-2)*2-3*3) + (z+2)((-2)*0-3*1) = 2x + 13y – 3z-38 = 0 

Угол между прямой A₁A₄ и плоскостью A₁A₂A₃. 
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 

Уравнение плоскости A₁A₂A₃: 2x + 13y – 3z-38 = 0 
Уравнение прямой A₁A₄: 

γ = arcsin(0.267) = 15.486^o 

Уравнение высоты пирамиды через вершину A₄(0,2,2) 
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями: 
Уравнение плоскости A₁A₂A₃: 2x + 13y – 3z-38 = 0 

Уравнение плоскости через вершину A₄(0,2,2) 
Плоскость, проходящая через точку M₀(x₀;y₀;z₀) и параллельная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением: 
A(x-x₀) + B(y-y₀) + C(z-z₀) = 0 
Уравнение плоскости A₁A₂A₃: 2x + 13y – 3z-38 = 0 
2(x-0)+13(y-2)-3(z-2) = 0 
или 
2x+13y-3z-20 = 0

Пример 4:

Решение от преподавателя:

Даны координаты пирамиды: A₁(0,1,1), A₂(3,4,4), A₃(-3,9,3), A₄(0,5,4) 

1. Уравнение плоскости. 
   Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением: 

x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 x3-x1 y3-y1 z3-z1

= 0

Уравнение плоскости A₁A₂A₃ 

(x-0)(3*2-8*3) – (y-1)(3*2-(-3)*3) + (z-1)(3*8-(-3)*3) = -18x – 15y + 33z-18 = 0 
Упростим выражение: -6x – 5y + 11z-6 = 0 

2) Угол между прямой A₁A₄ и плоскостью A₁A₂A₃. 
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 

Уравнение плоскости A₁A₂A₃: -6x – 5y + 11z-6 = 0 
Уравнение прямой A₁A₄: 

γ = arcsin(0.193) = 11.128^o 

3) Уравнение высоты пирамиды через вершину A₄(0,5,4) 
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями: 
Уравнение плоскости A₁A₂A₃: -6x – 5y + 11z-6 = 0 

4) Уравнение плоскости через вершину A₄(0,5,4) 
Плоскость, проходящая через точку M₀(x₀;y₀;z₀) и параллельная плоскости

5)  Координаты вектора  A₁A₄(0;4;3) 

Уравнение прямой, проходящей через точку А₁(0,1,1) параллельно вектору А₁А₂(0,4,3) имеет вид:

Пример 5:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

8) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

А₁ (4; 4; 10), А₂ (4; 10; 2), А₃ (2; 8; 4), А₄ (9; 6; 9).

Решение от преподавателя:

Пример 6:

Решение от преподавателя:

1) Даны координаты  вершин пирамиды: A₁(0,1,1), A₂(3,4,4), A₃(-3,9,3), A₄(0,5,4) 
Координаты векторов. 
Координаты векторов:       A₁A₂(3;3;3)        A₁A₄(0;4;3) 

 Угол между векторами a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂) можно найти по формуле: 
   ,    где a₁a₂ = X₁X₂ + Y₁Y₂ + Z₁Z₂ 
Найдем угол между ребрами A₁A₂(3;3;3) и A₁A₃(0;4;3): 

А₁ = arccos(0,808)

Найдем площадь грани с учётом геометрического смысла векторного произведения: 
S =
Найдем векторное произведение

=i(3*2-8*3) – j(3*2-(-3)*3) + k(3*8-(-3)*3) = -18i – 15j + 33k 

3) Объем пирамиды. 
Объем пирамиды, построенный на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен: 

Координатывекторов:A₁A₂(3;3;3)    A₁A₃(-3;8;2) A₁A₄(0;4;3) :      

Пример 7:

Решение от преподавателя:

1. Угол между ребрами. 
   Угол между векторами a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂) можно найти по формуле: 
   
   где a₁a₂ = X₁X₂ + Y₁Y₂ + Z₁Z₂ 
   Найдем угол между ребрами A₁A₂(-2;1;3) и A₁A₃(3;0;2): 
   
   γ = arccos(0) = 90.003⁰ 
2. Площадь грани 
   Площадь грани можно найти по формуле: 
   
   где 
   
   Найдем площадь грани A₁A₂A₃ 
   Найдем угол между ребрами A₁A₂(-2;1;3) и A₁A₃(3;0;2): 
   
   
   Площадь грани A₁A₂A₃ 
3. Объем пирамиды, построенный на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен: 

где определитель матрицы равен: 
∆ = (-2)*(0*4-0*2)-3*(1*4-0*3)+(-3)*(1*2-0*3) = -18 

Пример 8:

Даны координаты вершин пирамиды А₁А₂А₃А₄ . Найти:

1) длину ребра А₁А₂;

2) угол между рёбрами А₁А₂  и А₁А₄ ;

3) угол между ребром А₁А₄ и гранью А₁А₂А₃;

4) площадь грани А₁А₂А₃;

5) объём пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

8) уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃;

Сделать чертёж.

А₁(3; 5; 4),        А₂(8; 7; 4),            А₃(5; 10; 4),          А₄(4; 7; 8).

Решение от преподавателя:

1) Длина ребра A₁A₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) угол между ребрами А₁А₄ и гранью А₁А₂А₃;

Найдем уравнение стороны А₁А₄:

Вектор нормали:  к плоскости А₁А₂А₃.

4) площадь грани А₁А₂А₃;

5) объем пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

Итак: z=4 – уравнение плоскости А₁А₂А₃.

8) уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃.

A₄O – высота:

Уравнение A₄O:

Т.к. , то

В результате получаем уравнение высоты:

Пример 9:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

8) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

А₁ (4; 4; 10), А₂ (4; 10; 2), А₃ (2; 8; 4), А₄ (9; 6; 9).

Решение от преподавателя:

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Контрольная работа по мат. анализу 06

Элементы векторной алгебры и аналитической геометрии

Контрольная работа 1

1. Даны координаты вершин пирамиды. Найти: 1) длину рёбер А1А2 и А1А3; 2) Угол между рёбрами А1А2 и А1А3; 3) Площадь грани А1А2А3; 4) Объём пирамиды; 5) Уравнение прямой А1А2; 6) Уравнение плоскости А1А2А3; 7) Угол между ребром А1А4 и гранью А1А2А3; 8) Уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Координаты вершин: А1(5;1;0), А2 (0;1;2), А3(3;0;1), А4(2;2;2).

Координаты векторов находим по формуле: X = xj – xi; Y = yj – yi; Z = zj – zi

Здесь X, Y,Z координаты вектора; xi, yi, zi – координаты точки Аi; xj, yj, zj – координаты точки Аj; Для вектора A1A2 : X = x2 – x1; Y = y2 – y1; Z = z2 – z1

X = 0-5; Y = 1-1; Z = 2-0

1) Длина рёбер А1А2 и А1А3;

Длина вектора a(X;Y;Z) выражается через его координаты формулой:

2) Угол между рёбрами А1А2 и А1А3;

Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:

, где a1a2 = X1X2 + Y1Y2 + Z1Z2

Найдем угол между ребрами A1A2 и A1A3

, γ = arccos(0.91) = 24.50

3) Площадь грани А1А2А3;

Найдем площадь грани с учётом геометрического смысла векторного произведения:

4) Объём пирамиды;

Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:

Находим Определитель матрицы

∆ = (-5) • ((-1) • 2-1 • 1)-(-2) • (0 • 2-1 • 2)+(-3) • (0 • 1-(-1) • 2) = 5

5) Уравнение прямой А1А2;

Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:

Уравнение прямой A1A2

6) Уравнение плоскости А1А2А3;

Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:

Уравнение плоскости A1A2A3

(x-5)(0 • 1-(-1) • 2) – (y-1)((-5) • 1-(-2) • 2) + (z-0)((-5) • (-1)-(-2) • 0) = 2x+y+5z-11=0

7) Угол между ребром А1А4 и гранью А1А2А3;

Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле

8) Уравнение высоты, опущенной из вершины А4 на грань А1А2А3.

Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:

2. Линия задана уравнением В полярной системе координат

1. построить линию по точкам, начиная от До И придавая значения через промежуток ;

2. найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной осью;

3. по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

1) Построим линию по точкам, начиная от До и придавая Значения через промежуток

2) Построим уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.

3) Найдём уравнение данной линии в декартовой системе координат:

Используем формулы перехода от полярной системы координат к декартовой:

Тогда

По уравнению в декартовой прямоугольной системе координат определяем, что это линия – гипербола.

Элементы линейной алгебры

Контрольная работа 2

I. Даны две матрицы А и В. Найти (2АТ-3В)*(А+2ВТ)

,

, ,

, ,

II. Определить собственные значения и собственные векторы матрицы третьего порядка.

Исходная матрица имеет вид:

Составляем систему для определения координат собственных векторов:

(5 – λ)x1-2×2 + 2×3 = 0

0x1 + (5 – λ)x2 + 0x3 = 0

0x1 + 2×2 + (3 – λ)x3 = 0

Составляем характеристическое уравнение и решаем его.

Для этого находим определитель матрицы и приравниваем полученное выражение к нулю.

(5 – λ) • ((5 – λ) • (3 – λ)-2 • 0)-0 • (-2 • (3 – λ)-2 • 2)+0 • (-2 • 0-(5 – λ) • 2) = 0

После преобразований, получаем: – λ3 + 13λ2 – 55λ + 75 = 0

Один из корней уравнения равен λ1 = 3

Тогда характеристическое уравнение можно записать как

(λ -3)( – λ2 + 10λ – 25)=0.

D = 102 – 4 • (-1) • (-25) = 0

Получили собственные числа: λ1 = 3,

Найдём собственный вектор для λ1.

Составляем систему для определения координат собственных векторов:

Подставляя λ = 3 в систему, имеем:

Пусть x1 – свободное неизвестное, тогда выразим через него все остальные x1.

Множество собственных векторов, отвечающих собственному числу λ1= 3 , имеет вид: , где x1 – любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x1 = 1: .

Рассуждая аналогично, находим собственный вектор, отвечающий собственным числам:

. Следовательно, – любое,

Множество собственных векторов, отвечающих собственным числам , имеет вид: . При x1 = 1 и x3 = 0: , при x1 = 0 и x3 = 1: .

Ответ: Собственные числа: λ1=3, , собственные векторы: , , .

III. Дано комплексное число z. Требуется: 1) записать число z в алгебраической и тригонометрической формах; 2) Найти все корни уравнения w3+z=0

1) – алгебраическая форма

– тригонометрическая форма

2) Найдем корни уравнения w3 =0,

Применим формулу извлечения корней из комплексного числа:

, к=0,1,…,n-1

,

Так как a=, то

Контрольная работа 3

I. Найти пределы функций, не пользуясь правилом Лопиталя.

1.

2.

3.

4.

1.

3.

Использовали эквивалентности бесконечно малых величин при :

4.

II. Задана функция . Найти точки разрыва функции, если они существуют. Сделать чертёж

Построим график заданной функции:

Функция определена на всём множестве чисел и неэлементарная.

Каждая из составляющих функций непрерывна на своём промежутке; заданная функция может иметь точки разрыва только в точках смены аналитических выражений, то есть в точках и .

Исследуем поведение функции в этих точках: найдём значение функции в этих точках и пределы справа и слева,

, . Так как , Следовательно, в этой точке функция имеет разрыв 1-го рода – скачок

, . Так как , то в этой точке функция имеет разрыв 1-го рода – скачок.

III. Найти производные первого порядка данных функций.

1) ;

2) ;

3) ;

4) ;

5)

4) ;

Прологарифмируем данную функцию:

Найдём производную от правой и левой части по х, считая у сложной функцией, зависящей от х.

Тогда

5)

Дифференцируем обе части равенства по х:

Разрешаем равенство относительно :

Окончательно:

IV. Найти и для заданных функций:

1) ;

2)

1) ;

2)

Приложение дифференциального исчисления

Контрольная работа 4

Контрольная работа 5

I. Вычислить определённые интегралы. В п. 1) и 2) результаты проверить дифференцированием.

1)

2)

3)

4)

1)

– верно

– верно

3)

Разложим подынтегральное выражение на простые дроби:

II. Вычислить несобственный интеграл или доказать его расходимость.

III. Вычислить (с точностью до двух знаков после запятой) длину дуги данной линии

По формуле .

В нашем случае

Тогда

Имеем

Ответ:

Даны вершины пирамиды а1 а2 а3 а4 найти уравнение грани

1) правильно
2) нет
Площадь треугольника равна половине длины векторного произведения векторов
векторное произведение А1А2 и А1А3 – это вектор, который находится как формальный определитель
Википедия
А потом находится уже его длина

Помогите пожалуйста.
Даны координаты вершин пирамиды
A1(1,-1,2), A2(0,-1.6), A3(-1,0,2,), A4(1,1,4)
Найти:
длину ребер A1A2, A1A3.
угол между ребрами A1A2, A1A3
площадь грани A1A2A3
объём пирамиды
уровнения прямых A1A2 и A1A4 и А1А3
уровнения плоскостей A1A2A3 и A1A3A4
угол между плоскостями A1A2A3 и A1A3A4
уровнение высоты, опущенной из вершины A4 на грань A1A2A3
построить пирамиду по координатам верши.
Координаты точки А5, симметричной точке А4,относительно прямой А1А2
Координаты точки А6, симметричной точке А4, относительно плоскости А1А2А3
Расстояние между прямыми А1А2 и А3А4

Долго мучался, стараясь решить всё это, облазил весь интернет и этот сайт, и книжки скачивал и решебник онлайн только для проверки можно использовать. вообщем помогить решить

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=onlayn-resheniye-piramidy

http://matica.org.ua/primery/primery/kontrolnaia-rabota-po-mat-analizu6

http://diary.ru/~eek/p54502540_dany-koordinaty-vershiny-piramidy-a1-a2-a3-a4.htm

[/spoiler]

Решение:

Найдем уравнение плоскости А1А2А3:	x	y	z–2	= 0
3	0	3
-2	1	-5

-3x + 9y +3z – 6 = 0

Итак,
А₁А₂А₃:
x
– 3y
– z
+ 2 = 0.

Нормальный
вектор этой плоскости n{1,
-3, -1} будет направляющим для искомой
прямой. Значит, ее каноническое уравнение
имеет вид:

x – 4	=	y – 1	=	z – 2
1	-3	-1

Задача
10.
Составьте уравнения плоскостей, отстоящих
от плоскости 2x–3y+z–5
=0 на 3.

РЕШЕНИЕ:

1) Точка
М(0, 0, 5) принадлежит этой плоскости.
Действительно, 2∙0–3∙0+5–5=0. Найдем
уравнение прямой L,
проходящей через точку М перпендикулярно
данной плоскости:

L:	x=2t
y=-3t
z=5+t

2)
Плоскость, отстоящая от данной на 3 –
это плоскость, проходящая через точку
А(x₀,
y₀,
z₀)
параллельно данной (нормальный вектор
равен {2, -3, 1}), где x₀,
y₀,
z₀
являются
решениями системы:

x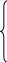
₀
=
2t₀,

y₀
=
-3t₀,

z₀
=
5+t₀,

(4t₀+9t₀+5+t₀-5)²=9∙14

;

3)
Плоскость Р₁,
проходящая через точку

и имеющая нормальный вектор {2, -3, 1}, будет
одной из искомых.

Плоскость
Р₂
проходящая через точку

и
имеющая нормальный вектор {2, -3, 1}, также
будет искомой.

Ответ:
P₁:

;
P₂:

Задача
11.
В пирамиде с вершинами А₁(1;-2;1),
А₂(3;-2;1),
А₃(-2;1;0),
А₄(2;2;5)
найдите:

1. уравнение
   грани А₁А₂А₃;

2. уравнение
   плоскости, проходящей через высоту
   пирамиды, опущенную из вершины А₄
   на грань А₁А₂А₃
   ,
   и
   вершину А₁
   пирамиды;

3. уравнение
   прямой, проходящей через вершину А₂
   параллельно ребру А₁А₄;

4. точку,
   симметричную вершине А₄,
   относительно
   грани А₁А₂А_3.

РЕШЕНИЕ:

1)

А1А2А3:	x–4	y	z	= 0
-6	1	2
4	2	0

–4x + 16 + 8y – 16z = 0

x – 2y + 4z – 4 =
0

2)
Найдем уравнение высоты A₄H
пирамиды, опущенной из вершины А₄
на грань А₁А₂А₃.
Направляющим для нее будет вектор {1,
-2, 4}.

A4H:	x=3+t
y=2–2t
z=7+4t

Точка
М(2, 4, 3) принадлежит этой прямой. Тогда
плоскость проходит через точки А₄(3;2;7),
М(2, 4, 3) и А₁(4,
0, 0) и ее уравнение будет иметь вид:

x–4	y	z	= 0
3	2	7
2	4	3

-22(x–4)
+
5y
+
8z = 0

22x – 5y – 8z – 88
= 0

3)
Найдем уравнение прямой А₁А₄:

.
Ее направляющий вектор {-1, 2, 7} будет
направляющим и для искомой прямой. Имеем
ее каноническое уравнение:

4)
Искомая точка

принадлежит прямой A₄H
и

Н=
–A₄H.

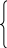
21t+23=–23

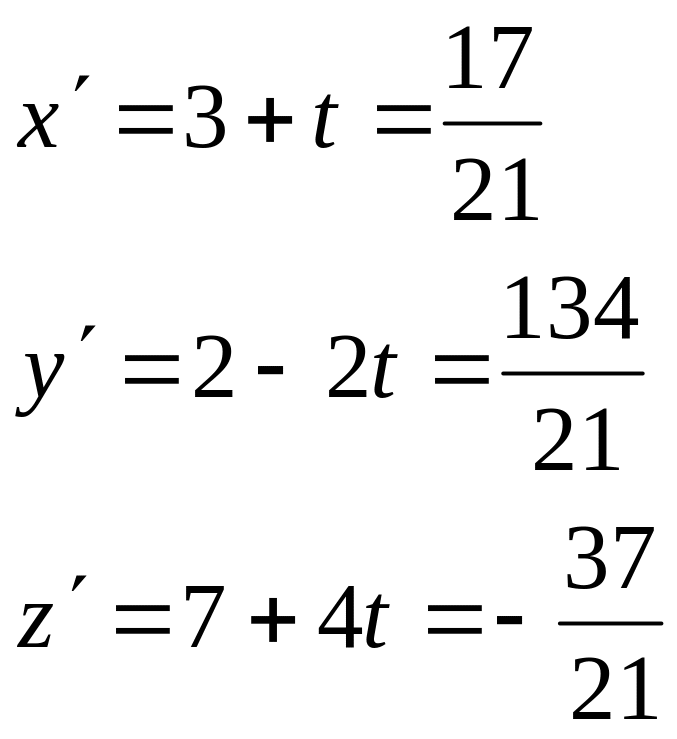
Т.е

имеет координаты

Ответ:
x
– 2y
+ 4z
– 4 = 0; 22x
– 5y
– 8z
– 88 = 0;

;

Задача
12. Найти точки пересечения
поверхности и прямой:

1+z2 =	x2	+	y2
16	9

y
+3 = 0,

x
+y
-4z
+3 = 0.

РЕШЕНИЕ:

1) Найдем параметрическое задание прямой:

q=[n1,n2] =	i	j	k	= -4i+j–k
0	1	0
1	1	-4

П
усть
z₁=2,
то y
= -3

x
+ y
= 5

y
= -3

x
= 8

Точка
А(8, -3, 2) принадлежит прямой. Тогда прямую
можно задать следующим образом:

x
= 8 – 4t

y
= –3 + t

z
= 2 – t

2) Пусть
М(x₀,
y₀,
z₀)
– точка пересечения прямой и плоскости,
тогда:

x₀
=
4(2-t₀),

y₀
=
-3+t₀,

z₀
=
2-t₀,

t₀=6,5
или t₀=
–4,5

Имеем:
M₁(8,
-3, 2) и М₂(-18,
3,5, -4,5).

Ответ:
M₁(8,
-3, 2) и М₂(-18,
3,5, -4,5).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Геометрия 10-11 класс

10 баллов

Даны координаты вершин пирамиды
A1A2A3A4. A1(2;5;8) A2(1;4;9) A3(2;1;6) A4(5;4;2)Найти:
1) длину ребра A1A2;
2) угол между ребрами A1A2 и A1A4;
3) уравнение плоскости A1A2A3 и угол между ребром A1A4 и плоскостью A1A2A3;
4) уравнение высоты, опущенной из вершины A4 на грань A1A2A3 и ее длину;
5) площадь грани A1A2A3 и объем пирамиды.
Сделать чертеж

Ирина Каминкова

14.12.2020 20:24:47

Ответ эксперта

Ирина Каминкова

14.12.2020 20:27:16

Ответ эксперта

Ирина Каминкова

14.12.2020 20:27:45

Ответ эксперта

Все предметы

Рейтинг пользователей