Задача 1.
Тетраэдр в пространстве задано вершинами
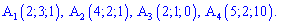
Необходимо найти:
1) уравнение грани 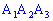 ;
;
2) уравнение высоты пирамиды, которая проходит через вершину 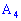 ;
;
3) длину этой высоты;
4) угол между ребром 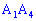 и гранью
и гранью 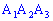 в градусах;
в градусах;
5) площадь грани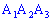 ;
;
6) Объем пирамиды.
Решение.
1) Уравнение грани 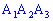
Запишем уравнение плоскости в виде.
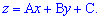 .
.
Поскольку все три точки принадлежат этой плоскости, то, подставляя их по очереди получим систему уравнений
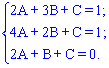
Решая ее получим.
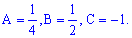 .
.
Подставляя в исходное уравнение получим
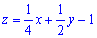 , Или
, Или 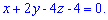 .
.
2) Уравнение высоты пирамиды, проходящей через вершину 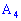
Запишем уравнение высоты пирамиды, проходящей через вершину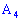
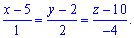 .
.
3) Высота с вершины 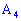
Найдем высоту, для этого найдем 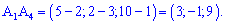
Высоту найдем учитывая уравнение грани 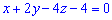 , по формуле
, по формуле
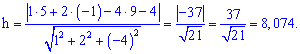
4)Угол между ребром  и гранью
и гранью 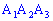 в градусах
в градусах
Найдем угол между ребром 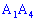 и гранью
и гранью 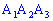 (
(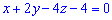 ) . Запишем уравнение прямой, проходящей через точки
) . Запишем уравнение прямой, проходящей через точки 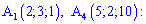
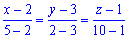 , или
, или 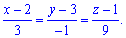 .
.
Найдем синус угла по формуле
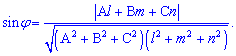 .
.
Подставим значения
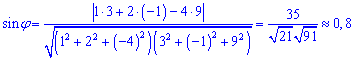
Найдем значение угла
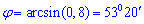
5) Площадь грани 
Площадь грани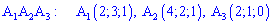 найдем по формуле
найдем по формуле
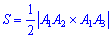
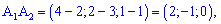
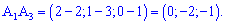
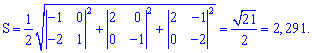
6) Объем пирамиды
Найдем объем пирамиды пирамиды по формуле
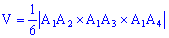 , где
, где
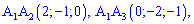
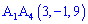
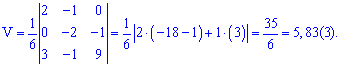
Математический калькулятор YukhymCalc решает эту задачу и немало типичных для студенческой практики математических задач. Фрагмент работы калькулятора приведены ниже.
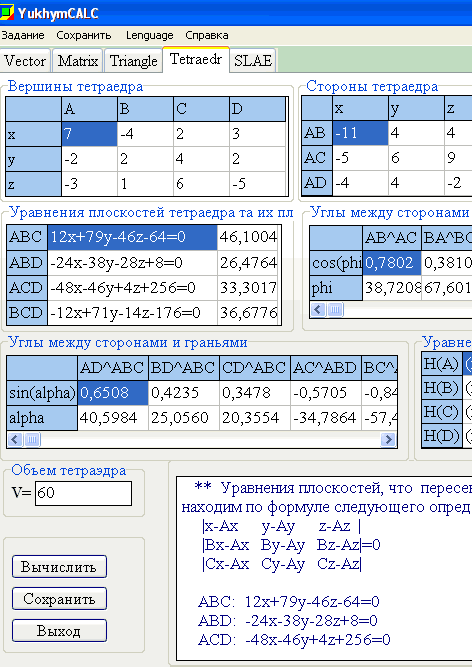
——————————
Посмотреть материалы:
- Длина вектора. Угол между векторами
- Разложение вектора по базису
- Проекция вектора на вектор
- Смешанное произведение векторов
- Деление отрезка в заданном отношении
-
Решение типовых задач
Задача 1.1. Составить
уравнение плоскости, проходящей через
точку
![]() ,если задан нормальный вектор
,если задан нормальный вектор![]() .
.
Р ешение.Воспользуемся уравнением (1.2):
ешение.Воспользуемся уравнением (1.2):
![]()
Подставляя координаты вектора
![]() и точки
и точки![]() ,
,
получим
![]()
![]()
![]()
Ответ:
![]()
Задача 1.2. Составить уравнение
плоскости, проходящей через точку![]() параллельно векторам
параллельно векторам![]() и
и![]() (их называют направляющими векторами
(их называют направляющими векторами
плоскости).
Решение.
П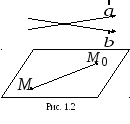 ервый
ервый
способ.Пусть![]() – произвольная точка на плоскости.Тогда векторы
– произвольная точка на плоскости.Тогда векторы
![]()
![]() и
и![]() (рис. 1.2) должны быть компланарны, т. е.
(рис. 1.2) должны быть компланарны, т. е.
их смешанное произведение должно быть
равно 0:![]() .Запишем смешанное произведение через
.Запишем смешанное произведение через
координаты векторов. Получим
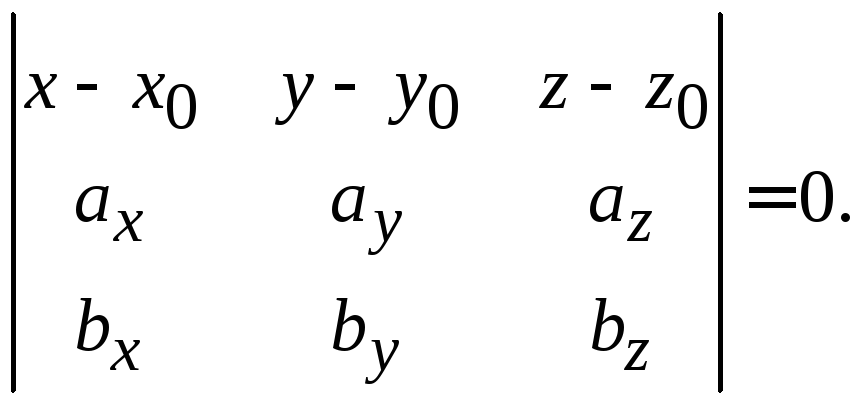
Подставим заданные координаты и вычислим
определитель разложением по элементам
первой строки:
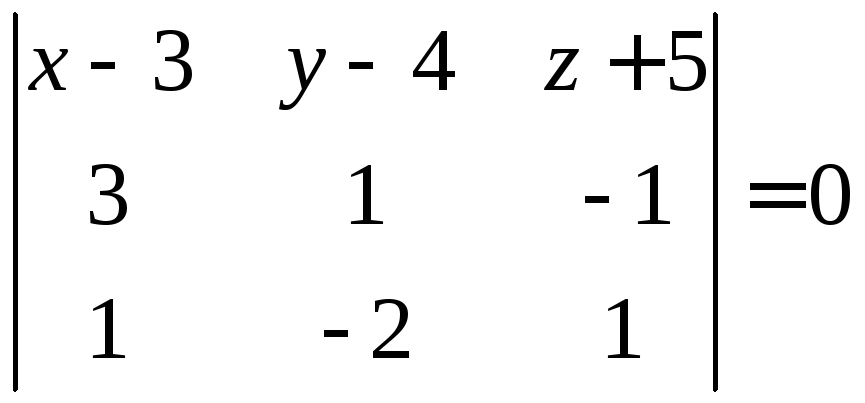 ,
,
или
![]() .
.
Окончательно:
![]()
Второй способ. Найдем сначала вектор![]() (рис. 1.1). Очевидно, что вектор
(рис. 1.1). Очевидно, что вектор
нормали
![]() к плоскости должен быть ортогонален
к плоскости должен быть ортогонален
также векторам![]() и
и![]() .
.
Поэтому его можно выбрать как
векторное произведение![]()
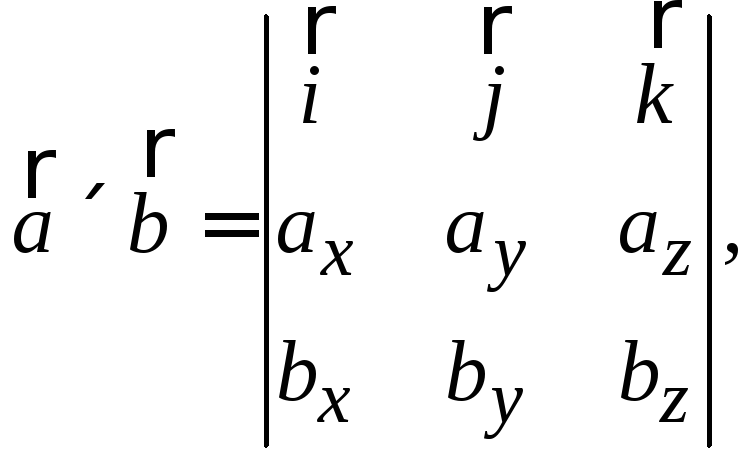
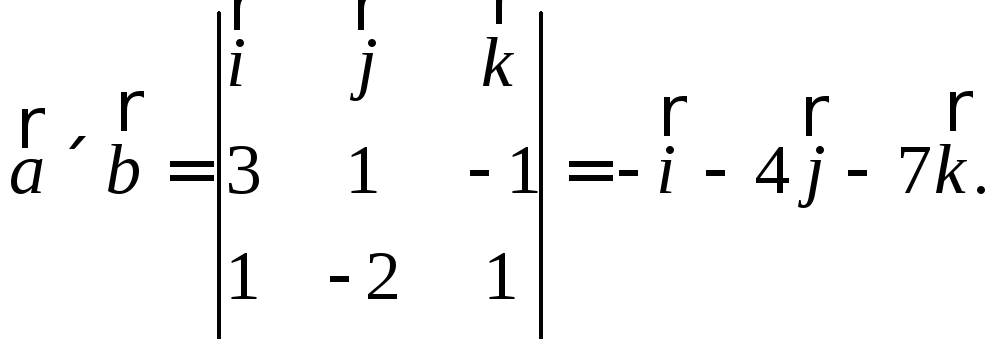
Затем выпишем общее уравнение плоскости,
используя
![]() ,
,![]() (см.
(см.
формулу (1.2)). Получим
![]()
![]()
![]()
Ответ: ![]()
![]() Полезная
Полезная
формула. Если
плоскость проходит через точку
![]() ,
,
![]() и
и![]() – ее направляющие векторы, то уравнение
– ее направляющие векторы, то уравнение
плоскости имеет вид
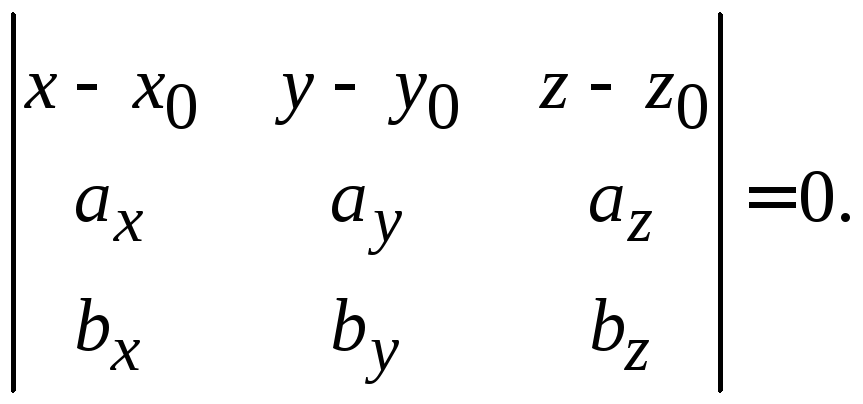 (1.7)
(1.7)
Замечание.Первый способ решения
задачи предпочтительнее. Второй способ
отличается лишь тем, что в нем смешанное
произведение трех векторов![]() ,
,![]() ,
,![]() вычисляется последовательно. А именно:
вычисляется последовательно. А именно:
сначала находим векторное произведение![]() и затем результат умножаем скалярно на
и затем результат умножаем скалярно на
вектор![]() .
.
В дальнейшем при решении задач будем
придерживаться первого способа.
Задача 1.3. Составить уравнение
плоскости, проходящей через точки![]() и
и![]() параллельно вектору
параллельно вектору![]() .
.
Р
![]()
ешение.Пусть![]()
произвольная точка на плоскости.
Тогда векторы![]() ,
,![]() и
и![]() компланарны (рис. 1.3). Запишем условие
компланарны (рис. 1.3). Запишем условие
компланарности векторов через их
координаты:
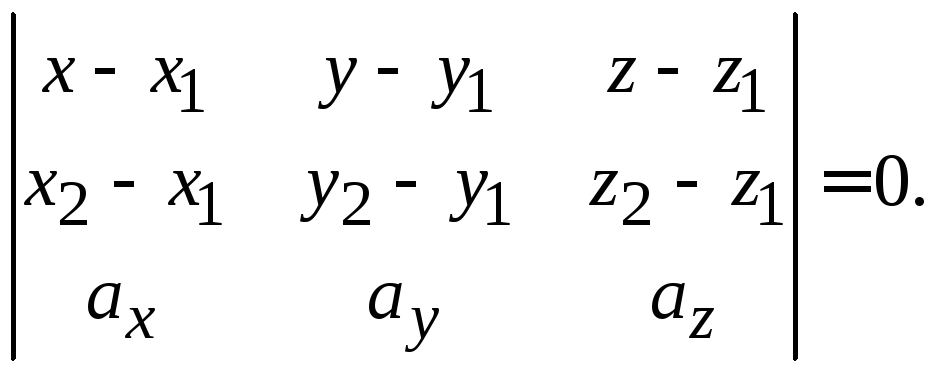
Подставляя заданные координаты, получим
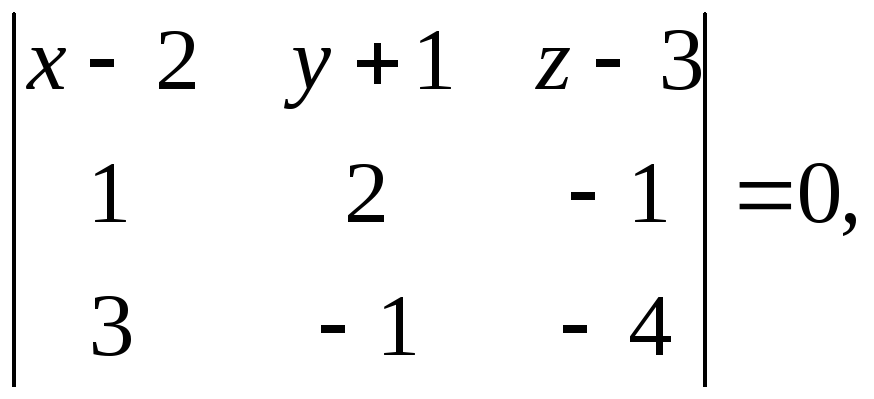
или
![]()
Окончательно:
![]()
Ответ:
![]()
![]() Полезная
Полезная
формула.Если плоскость проходит
через две заданные точки![]() и
и![]() параллельно вектору
параллельно вектору![]() ,
,
то ее уравнение имеет вид
 (1.8)
(1.8)
Задача 1.4. Составить уравнение
плоскости, проходящей через точку![]() параллельно плоскости
параллельно плоскости![]()
Решение. В качестве вектора![]() искомой плоскости можно выбрать
искомой плоскости можно выбрать
нормальный вектор заданной плоскости,
так как эти плоскости параллельны. Таким
образом, имеем![]() и
и![]() .
.
Подставляя координаты![]() и
и![]() в уравнение (1.2), получим
в уравнение (1.2), получим
![]()
Окончательно:
![]()
Ответ: ![]()
Задача 1.5. Найти величину острого
угла между плоскостями![]() и
и![]()
Решение. Угол между плоскостями
равен углу между нормальными векторами![]() и
и![]() (см. формулу 1.4)).
(см. формулу 1.4)).
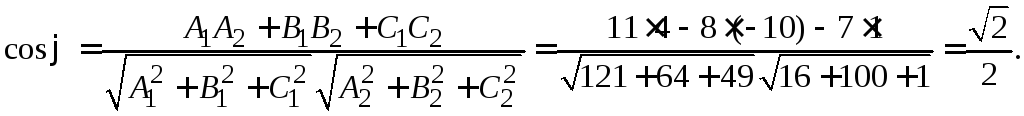
Отсюда
![]()
Ответ: ![]()
Задача 1.6. Чему равен угол между
плоскостями![]() и
и![]() ?
?
Решение. Найдем скалярное произведение
нормальных векторов
![]() и
и![]()
![]()
Следовательно, эти плоскости
перпендикулярны:
![]()
Ответ:
![]()
Задача 1.7. Составить уравнение
плоскостей, которые проходят через
точку![]() и отсекают на координатных осях отличные
и отсекают на координатных осях отличные
от нуля отрезки одинаковой длины.
Р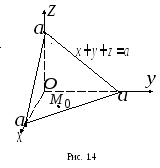 ешение.Воспользуемся уравнением плоскости
ешение.Воспользуемся уравнением плоскости
в отрезках на осях (1.3). Рассмотрим сначала
случай 1:![]() (рис. 1.4). Тогда
(рис. 1.4). Тогда
получим
![]()
![]()
![]()
Подставляя в уравнение координаты точки
![]() ,
,
найдем![]()
![]()
![]()
Уравнение плоскости:
![]()
Затем следует
аналогично рассмотреть случаи 2:
![]()
![]() 3:
3:![]()
![]()
4:
![]()
![]() Получим четыре различные плоскости.
Получим четыре различные плоскости.
Ответ:
![]()
![]()
![]()
![]()
Задача 1.8. Построить
плоскости, заданные уравнениями: 1)![]()
![]() ;2)
;2)![]()
![]() ;
;
3)
![]()
![]() ;
;
4) плоскость![]() ,
,
проходящую через точку![]() параллельно плоскости
параллельно плоскости![]() ;
;
5) плоскость![]() ,
,
проходящую через точку![]() и ось
и ось![]() .
.
Р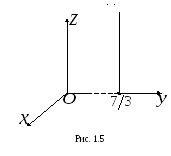
 ешение.1. Плоскость
ешение.1. Плоскость![]() параллельна плоскости
параллельна плоскости![]() и отсекает на оси
и отсекает на оси![]() отрезок,
отрезок,
равный![]()
(рис. 1.5).
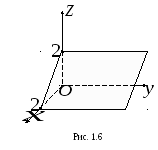
2. Плоскость
![]() параллельна оси
параллельна оси![]() ,
,
пересекает плоскость![]()
по прямой
![]() ,
,
отсекая на осях![]() и
и![]() отрезки, равные 2 (рис. 1.6).
отрезки, равные 2 (рис. 1.6).
3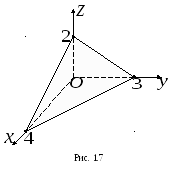
 . Уравнение
. Уравнение
плоскости запишем в отрезках на осях
(1.3):![]() .
.
Плоскость отсекает на осях![]() ,
,![]() ,
,![]() отрезки, длины которых равны соответственно
отрезки, длины которых равны соответственно
4, 3, 2 (рис. 1.7).
Рис. 1.8
4. Так как плоскость
![]() параллельна плоскости
параллельна плоскости![]() ,
,
то ее нормальный вектор можно выбрать
в виде![]() .
.
Тогда согласно формуле (1.2) уравнение
плоскости![]() будет
будет![]() ,
,
где![]() по условию задачи. Таким образом, получаем
по условию задачи. Таким образом, получаем![]() (рис. 1.8).
(рис. 1.8).
5 .
.
Плоскость![]() проходит через ось
проходит через ось![]() .
.
Поэтому ее нормальный вектор имеет вид![]() .
.
Так как плоскость проходит через начало
координат![]() ,
,
то коэффициент![]()
в уравнении
плоскости (1.1) равен 0. Подставляя
координаты точки
![]() в уравнение
в уравнение![]() ,
,
получаем![]() (рис. 1.9).
(рис. 1.9).
Задача 1.9. Составить уравнение
плоскости, проходящей через три заданные
точки![]()
![]()
![]()
Р ешение.Пусть
ешение.Пусть
![]() произвольная
произвольная
точка на плоскости. Тогда векторы![]() ,
,![]() ,
,![]() компланарны (рис. 1.10). Запишем условие
компланарны (рис. 1.10). Запишем условие
компланарности этих векторов через их
координаты:
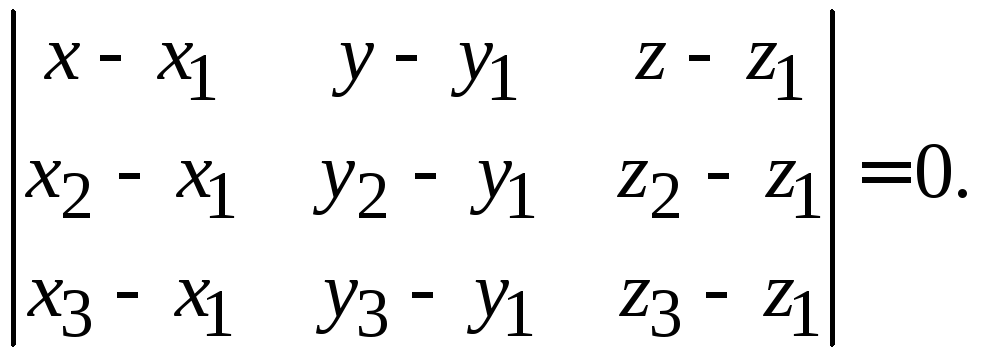 Подставим
Подставим
значения координат и найдем уравнение
плоскости:
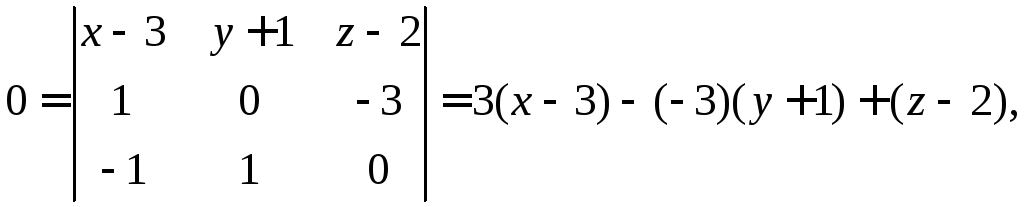
или
![]()
Ответ:
![]()
![]() Полезная
Полезная
формула. Если плоскость проходит
через три заданные точки![]()
![]()
![]() не лежащие на одной прямой, то ее уравнение
не лежащие на одной прямой, то ее уравнение
имеет вид
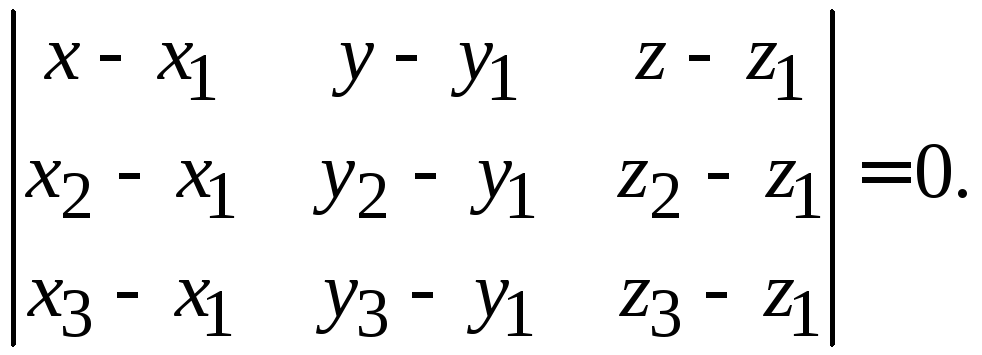 (1.9)
(1.9)
Задача 1.10. Даны
координаты вершин тетраэдра:
![]() ,
,![]() ,
,![]() ,
,![]() (рис. 1.11). Составить уравнения его граней.
(рис. 1.11). Составить уравнения его граней.
Р ешение.Найдем уравнение грани
ешение.Найдем уравнение грани![]() .
.
Для этого подставим в формулу (1.9)
координаты вершин![]() :
:
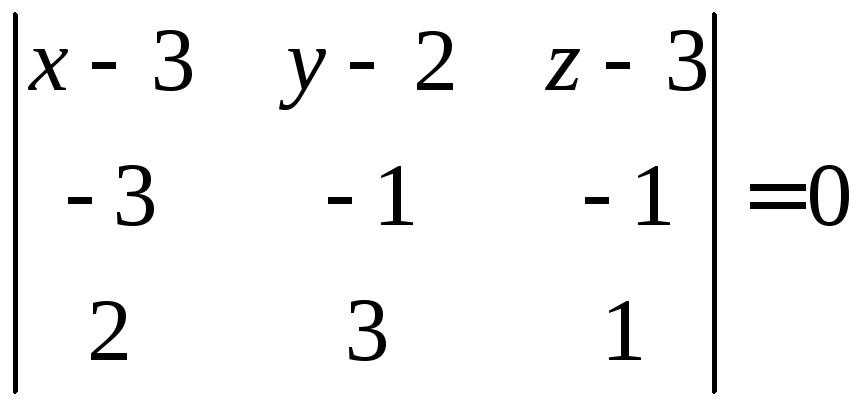 ,
,
или
![]() .
.
Уравнение искомой грани имеет вид
![]()
Уравнения
граней
![]() ,
,![]() ,
,![]() найдите самостоятельно.
найдите самостоятельно.
Ответ: ![]()
![]()
![]()
![]()
![]() .
.
Задача 1.11. Найти расстояние от точки![]() до плоскости
до плоскости![]()
Решение. Используем формулу (1.5): .
.
Ответ:
![]()
Задача 1.12. Найти расстояние между
параллельными плоскостями
![]()
![]()
![]()
![]() .
.
Решение.
Первый способ.
Выберем
произвольно точку
![]()
на плоскости
![]() .
.
Пусть, например,![]() Тогда
Тогда![]() Следовательно,
Следовательно,![]() Найдем расстояние
Найдем расстояние![]() от
от
точки![]() до плоскости
до плоскости![]() ,
,
по формуле (1.5):
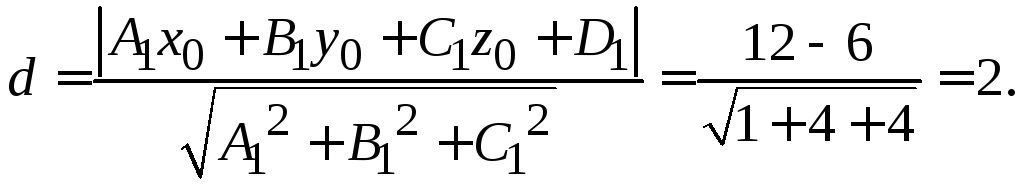
В торой
торой
способ.Очевидно, что плоскости![]() и
и![]() лежат по одну сторону относительно
лежат по одну сторону относительно
начала координат![]()
Обозначим через
![]() расстояние от начала координат
расстояние от начала координат
до плоскости![]() ,
,
через![]() – до плоскости
– до плоскости![]() (рис. 1.12).
(рис. 1.12).
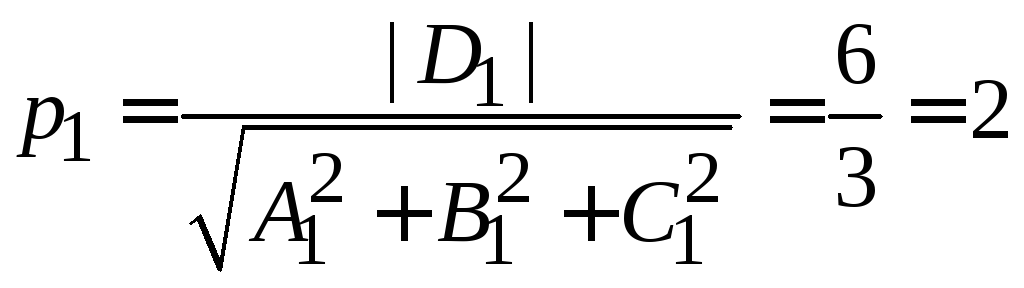

 ,
,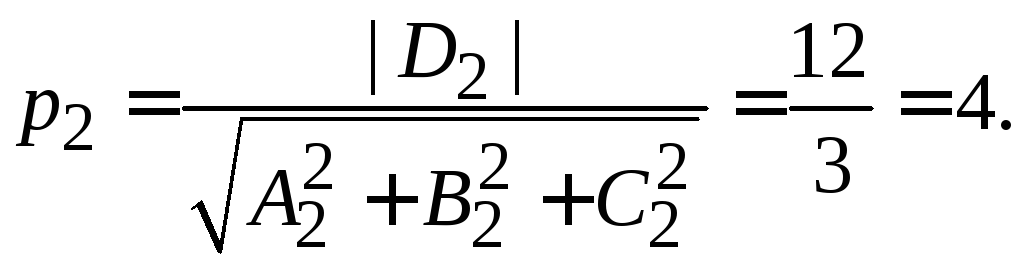
Расстояние между плоскостями равно
![]() .
.
Отсюда находим
![]()
Ответ:
![]()
Замечание. Если бы плоскости
находились по разные стороны от начала
координат (рис. 1.13), то расстояние между
ними было бы равно![]()
Задача 1.13. Составить уравнение
плоскости, проходящей через заданную
прямую![]() и точку
и точку![]() не лежащую на этой прямой.
не лежащую на этой прямой.
Решение. Уравнение произвольной
плоскости![]() ,
,
проходящей через заданную прямую, имеет
вид (см. формулу (1.6))
![]()
Отсюда
![]() :
:![]()
Подставляя в это уравнение координаты
точки
![]() ,
,
получим
![]()
![]()
![]() ,
,![]()
Положим, например,
![]() Тогда
Тогда![]() Остается подставить эти коэффициенты
Остается подставить эти коэффициенты
в уравнение плоскости. Получим![]()
Ответ:
![]()
Задача 1.14. Написать уравнение
биссектрисы![]() острого двугранного угла между плоскостями
острого двугранного угла между плоскостями![]() и
и![]()
Решение. Нормальные
векторы первой и второй плоскостей
соответственно равны
![]() и
и![]() Они образуют острый угол
Они образуют острый угол![]() ,
,
так как
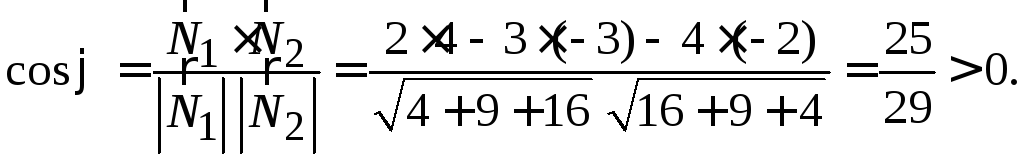
Очевидно, что
![]() (Нормальные векторы
(Нормальные векторы![]() и
и![]() всегда можно взять равными по длине,
всегда можно взять равными по длине,
например, единичными.) Так как![]() ,
,
то параллелограмм, построенный на
векторах![]() и
и![]() как на сторонах, является ромбом, а
как на сторонах, является ромбом, а
диагональ![]()
![]() биссектрисой его угла. Следовательно,
биссектрисой его угла. Следовательно,
вектор![]() может быть выбран в качестве нормального
может быть выбран в качестве нормального
вектора искомой биссектрисы![]() Далее следуем рассуждениям задачи 1.13.
Далее следуем рассуждениям задачи 1.13.
Уравнение биссектрисы![]() ищем в виде
ищем в виде
![]()
Отсюда
![]()
Учитывая, что
![]()
![]()
![]() получаем систему уравнений
получаем систему уравнений
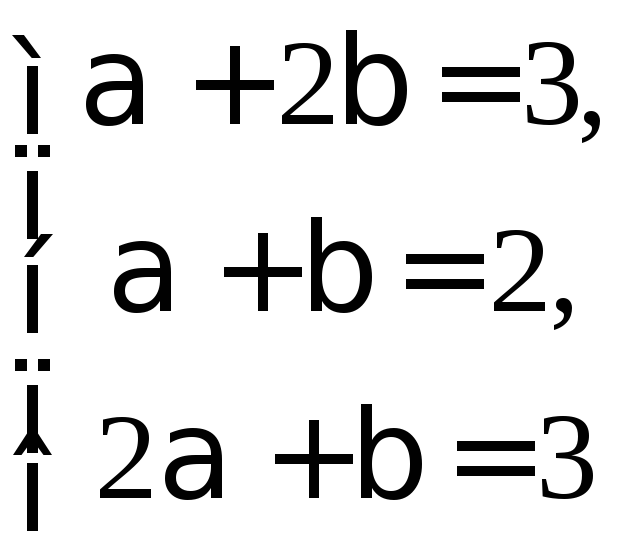
![]()
![]()
![]()
Подставляя эти значения в уравнение
биссектрисы
![]() ,
,
имеем
![]()
Окончательно:
![]()
Чертеж к этой задаче предлагаем сделать
самостоятельно.
Ответ:
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
C ( ; ; ), D ( ; ; )
Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Уравнение ребер и граней тетраэдра
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
Тетраэдр.
Тетраэдр – это частный случай правильной треугольной пирамиды.
Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.


Медиана тетраэдра – это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).
Бимедиана тетраэдра – это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).
Высота тетраэдра – это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).
Свойства тетраэдра.
Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.
Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.
Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.
Типы тетраэдров.
Правильный тетраэдр – это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.
У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.
Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.
Правильный тетраэдр – это один из 5-ти правильных многогранников.
Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:
– Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.
– Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.
– Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.
– Каркасный тетраэдр — тетраэдр, который таким условиям:
- есть сфера, которая касается каждого ребра,
- суммы длин ребер, что скрещиваются равны,
- суммы двугранных углов при противоположных ребрах равны,
- окружности, которые вписаны в грани, попарно касаются,
- каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
- перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.
– Соразмерный тетраэдр, бивысоты у него одинаковы.
– Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.
Формулы для определения элементов тетраэдра.
Высота тетраэдра:

где h – высота тетраэдра, a – ребро тетраэдра.
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.

где V – объем тетраэдра, a – ребро тетраэдра.
Основные формулы для правильного тетраэдра:

Где S – Площадь поверхности правильного тетраэдра;
h – высота, опущенная на основание;
r – радиус вписанной в тетраэдр окружности;
[spoiler title=”источники:”]
http://yukhym.com/ru/vektory/tetraedr-treugolnaya-piramida-v-prostranstve.html
http://www.calc.ru/1535.html
[/spoiler]

Аналитическая геометрия – задача на расчет пирамиды (тетраэдра)
Краткая теория
Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное – разобраться и уделить задаче достаточно времени.
Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.
Пример решения задачи
Задача
Даны координаты
вершин пирамиды
. Найти:
Сделать чертеж.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Длина ребра
Длину ребра
найдем по
формуле расстояния между 2-мя точками:
Угол между ребрами
Угол между ребрами
и
найдем как угол
между направляющими векторами
и
:
Косинус угла между
векторами:
Угол между ребром и гранью. Векторное произведение
Вычислим угол между
ребром
и гранью
.
Для этого вычислим
координаты нормального вектора плоскости
–им будет
векторное произведение векторов
и
.
Найдем векторное произведение. Для этого
вычислим определитель:
Нормальный вектор
плоскости:
Синус угла:
Площадь грани
Вычислим площадь
грани
. Она будет численно равна половине модуля векторного
произведения векторов
и
:
Искомая площадь:
Объем пирамиды. Смешанное произведение векторов
Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов
и
:
Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:
Искомый объем
пирамиды:
Уравнение прямой в пространстве
Вычислим уравнение
прямой
. Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Уравнение искомой
прямой:
Уравнение плоскости
Вычислим уравнение
плоскости
. Нормальный вектор плоскости
. кроме того, плоскость проходит через точку
-уравнение
грани
Уравнение высоты, опущенной на грань
Составим уравнение
высоты, опущенной на грань
из вершины
:
Нормальный вектор
является
направляющим вектором высоты, кроме того, высота проходит через точку
Искомое уравнение
высоты:
Сделаем схематический чертеж:
Онлайн решение Пирамиды по координатам вершин
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
