Как найти уравнение касательной дроби

Уравнение касательной к графику функции. 10-й класс

Класс: 10

Презентация к уроку

Тип урока: изучение нового материала.

Методы обучения: наглядный, частично поисковый.

Цель урока.

Ввести понятие касательной к графику функции в точке, выяснить в чем состоит геометрический смысл производной, вывести уравнение касательной и научить находить его для конкретных функций.
1. Развивать логическое мышление, математическую речь.
2. Воспитывать волю и упорство для достижения конечных результатов.

Оборудование: интерактивная доска, компьютер.

I. Организационный момент

Проверка готовности учащихся к уроку. Сообщение темы урока и целей.

II. Актуализация знаний.

(Вспомнить с учащимися геометрическое определение касательной к графику функции. Привести примеры, показывающие, что данное утверждение не полно.)

Вспомним, что же такое касательная?

“Касательная – это прямая, имеющая с данной кривой одну общую точку”. (Слайд № 2)

Обсуждение правильности данного определения. (После обсуждения, учащиеся приходят к выводу, что данное определение неверно.) Для наглядного доказательства их умозаключения приводим следующий пример.

Рассмотрим пример. (Слайд № 3)

Пусть дана парабола и две прямые , имеющая с данной параболой одну общую точку М (1;1). Проводится обсуждение, почему первая прямая не является к данной параболе касательной (Рис. 1), а вторая является (Рис.2).

На данном уроке, мы с вами должны выяснить, что же такое касательная к графику функции в точке, как составить уравнение касательной?

Рассмотреть основные задачи на составление уравнения касательной.

Для этого, вспомнить общий вид уравнения прямой, условия параллельности прямых, определение производной и правила дифференцирования. (Слайд № 4)

III. Подготовительная работа к изучению нового материала.

Сформулировать определение производной. (Слайд № 5)

Заполнить таблицу произвольных элементарных функций. (Слайд № 6)

Вспомнить правила дифференцирования. (Слайд № 7)

Какие из указанных прямых параллельны и почему? (Убедиться наглядно) (Слайд №8)

IV Изучение нового материала.

Чтобы задать уравнение прямой на плоскости нам достаточно знать угловой коэффициент и координаты одной точки.

Пусть дан график функции . На нем выбрана точка , в этой точке к графику функции проведена касательная (мы предполагаем, что она существует). Найти угловой коэффициент касательной.

Дадим аргументу приращение и рассмотрим на графике (Рис. 3) точку P с абциссой . Угловой коэффициент секущей MP, т.е. тангенс угла между секущей и осью x, вычисляется по формуле .

Если мы теперь устремим к нулю, то точка Р начнет приближаться по кривой к точке М. Касательную мы охарактеризовали как предельное положение секущей при этом приближении. Значит, естественно считать, что угловой коэффициент касательной будет вычисляться по формуле .

Следовательно, .

Если к графику функции y = f (x) в точке х = а можно провести касательную, непараллельную оси у, то выражает угловой коэффициент касательной. (Слайд № 10)

Или по другому. Производная в точке х = а равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке .

Это и есть геометрический смысл производной. (Слайд № 11)

Причем, если :

3. .

Выясним общий вид уравнения касательной.

Пусть, прямая задана уравнением . Мы знаем, что . Для вычисления m воспользуемся тем, что прямая проходит через точку . Подставим в уравнение. Получим , т.е. . Подставим найденные значения k и m в уравнение прямой:

– уравнение касательной к графику функции. (Слайд № 12)

Составим уравнение касательной:

1. к параболе в точке (Слайд № 13)
2. к графику функции в точке

Решая эти примеры мы воспользовались очень простым алгоритмом, который заключается в следующем: (Слайд № 15)

1. Обозначим абсциссу точки касания буквой a.
2. Вычислим .
3. Найдем и .
4. Подставим найденные числа , в формулу

Рассмотрим типичные задания и их решение.

№1 Составить уравнение касательной к графику функции в точке .

Решение. Воспользуемся алгоритмом, учитывая, что в данном примере .

1)

2)

3) ;

4) Подставим найденные числа ,, в формулу.

, т.е.

Ответ:

№2 К графику функции провести касательную так, чтобы она была параллельна прямой . (Слайд № 17)

Решение. Уточним формулировку задачи. Требование “провести касательную” обычно означает “составить уравнение касательной”. Воспользуемся алгоритмом составления касательной, учитывая, что в данном примере .

Искомая касательная должна быть параллельна прямой . Две прямые параллельны, тогда и только тогда, когда равны их угловые коэффициенты. Значит угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой: .Но . Следовательно: ; .

Из уравнения ,т.е. , находим, что и . Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 2, другая в точке с абсциссой -2.

Действуем по алгоритму.

1) ,

2) ,

3)

4) Подставив значения ,, , получим , т.е. .

Подставив значения ,, , получим , т.е.

Ответ: , .

V. Решение задач.

1. Решение задач на готовых чертежах (Слайд № 18 и Слайд № 19)

2. Решение задач из учебника: № 29.3 (а,в), № 29.12 (б,г), № 29.18, № 29.23 (а) (Слайд № 20)

VI. Подведение итогов.

1. Ответьте на вопросы:

• Что называется касательной к графику функции в точке?
• В чем заключается геометрический смысл производной?
• Сформулируйте алгоритм нахождения уравнения касательной?

2. В чем были трудности на уроке, какие моменты урока наиболее понравились?

3. Выставление отметок.

VII. Комментарии к домашней работе

№ 29.3 (б,г), № 29.12 (а,в), № 29.19, № 29.23 (б) (Слайд №22)

Литература. (Слайд 23)

1. Алгебра и начала математического анализа: Учеб. Для 10-11 кл. для учащихся общеобразовательных учреждений (базовый уровень) / Под редакцией А.Г. Мордковича. – М.: Мнемозина, 2009.
2. Алгебра и начала математического анализа: Задачник, Для 10-11 кл. для учащихся общеобразовательных учреждений (базовый уровень) / Под редакцией А.Г. Мордковича. – М.: Мнемозина, 2009.
3. Алгебра и начала анализа. Самостоятельные и контрольные работы для 10-11 классов. / Ершова А.П., Голобородько В.В. – М.: ИЛЕКСА, 2010.
4. ЕГЭ 2010. Математика. Задача В8. Рабочая тетрадь / Под редакцией А.Л.Семенова и И.В.Ященко – M.: Издательство МЦНМО, 2010.

1. Уравнение касательной к графику функции

Теория:

Даны функция (y=f(x)) и точка (M(a;f(a))); известно, что существует f ′ ( a ) .
Уравнение касательной к графику функции (y=f(x)) в точке (M) имеет вид (y=kx+m). Найдём значения коэффициентов (k) и (m).

Известно, что k = f ′ ( a ) . Для вычисления значения (m) воспользуемся тем, что искомая прямая проходит через точку (M(a;f(a))).
При подстановке координаты точки (M) в уравнение прямой, получим верное равенство (f(a)=ka+m), т. е. (m=f(a)-ka).

Подставим найденные значения коэффициентов (k) и (m) в уравнение прямой:

y = kx + m ; y = kx + ( f ( a ) − ka ) ; y = f ( a ) + k ( x − a ) ; y = f ( a ) + f ′ ( a ) ( x − a ) .

Нами получено уравнение касательной к графику функции (y=f(x)) в точке (x=a).

Алгоритм составления уравнения касательной к графику функции (y=f(x))

1. Обозначаем абсциссу точки касания буквой (a).

3. Находим f ′ ( x ) и вычисляем f ′ ( a ) .

4. Подставляем найденные числа (a), (f(a)), f ′ ( a ) в формулу y = f ( a ) + f ′ ( a ) ( x − a ) .

Для функции (y=f(x)), имеющей производную в фиксированной точке (x), справедливо приближенное равенство Δ y ≈ f ′ ( x ) ⋅ Δ x ;

или, подробнее, f ( x + Δ x ) − f ( x ) ≈ f ′ ( x ) ⋅ Δ x .

В этом приближённом равенстве заменим (x) на (a), вместо x + Δ x будем писать (x) и тогда Δ x будет равно (x-a). Получим:

f ( x ) − f ( a ) ≈ f ′ ( a ) ( x − a ) или f ( x ) ≈ f ( a ) + f ′ ( a ) ( x − a ) .

Смысл равенства заключается в том, что приближенное значение функции в точке (x) равно значению касательной в этой точке.

Уравнение касательной к графику функции

п.1. Уравнение касательной

Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.

Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end

Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace_<=k>x+underbrace_ <=b>$$

п.2. Алгоритм построения касательной

На входе: уравнение кривой (y=f(x)), абсцисса точки касания (x_0).
Шаг 1. Найти значение функции в точке касания (f(x_0))
Шаг 2. Найти общее уравнение производной (f’ (x))
Шаг 3. Найти значение производной в точке касания (f'(x_0 ))
Шаг 4. Записать уравнение касательной (y=f’ (x_0)(x-x_0)+f(x_0)), привести его к виду (y=kx+b)
На выходе: уравнение касательной в виде (y=kx+b)

Пусть (f(x)=x^2+3). Найдем касательную к этой параболе в точке (x_0=1).

(f(x_0)=1^2+3=4 )
(f'(x)=2x )
(f'(x_0)=2cdot 1=2)
Уравнение касательной: $$ y=2(x-1)+4=2x-2+4=2x+2 $$ Ответ: (y=2x+2)

п.3. Вертикальная касательная

Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода (x_0notin D), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку (x_0in D), входящую в область определения. График функции и касательная имеют одну общую точку ((x_0,y_0)).

Вертикальные касательные характерны для радикалов вида (y=sqrt[n]).

Пусть (f(x)=sqrt[5]+1). Найдем касательную к этой кривой в точке (x_0=1).

(f(x_0)=sqrt[5]<1-1>+1=1)
(f'(x)=frac15(x-1)^<frac15-1>+0=frac15(x-1)^<-frac45>=frac<1><5(x-1)^<frac45>> )
(f'(x_0)=frac<1><5(1-1)^<frac45>>=frac10=+infty)
В точке (x_0) проходит вертикальная касательная.
Её уравнение: (x=1)
Ответ: (y=2x+2)

п.4. Примеры

Пример 1. Для функции (f(x)=2x^2+4x)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

Находим точки пересечения, решаем уравнение: $$ 2x^2+4x=0Rightarrow 2x(x+2)=0Rightarrow left[ begin x=0\ x=-2 end right. $$ Две точки на оси: (0;0) и (-2;0). Касательная в точке (x_0=0): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot 0+4=4\ y=4(x-0)+0=4x end Касательная в точке (x_0=-2): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot (-2)+4=-4\ y=-4(x+2)+0=-4x-8 end

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

Общее уравнение касательной: (f'(x)=4x+4) По условию (f'(x_0)=tgalpha=tg45^circ=1) Решаем уравнение: $$ 4x_0+4=1Rightarrow 4x_0=-3Rightarrow x_0=-frac34 $$ Точка касания (x_0=-frac34) begin f(x_0)=2cdotleft(-frac34right)^2+4cdotleft(-frac34right)=frac98-3=-frac<15> <8>end Уравнение касательной: begin y=1cdotleft(x+frac34right)-frac<15><8>=x-frac98 end

в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.

Найдем угловой коэффициент заданной прямой: (y=-2x+6Rightarrow k=-2). Касательная должна быть параллельной, значит, её угловой коэффициент тоже (k=-2). Получаем уравнение: begin f'(x_0)=-2\ 4x_0+4=-2Rightarrow 4x_0=-6Rightarrow x_0=-frac32 end Точка касания (x_0=-frac32) begin f(x_0)=2cdotleft(-frac32right)^2+4cdotleft(-frac32right)=\ =frac92-6=-frac32 end Уравнение касательной: begin y=-2cdotleft(x+frac32right)-frac32=-2x-frac92 end Или, в каноническом виде: begin 2x+y+frac92=0 end

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

У горизонтальной прямой (k=0). Получаем уравнение: (f'(x_0)=0). begin 4x_0+4=0Rightarrow 4x_0=-4Rightarrow x_0=-1 end Точка касания (x_0=-1) begin f(x_0)=2cdot(-1)^2+4cdot(-1)=-2 end Уравнение касательной: begin y=0cdot(x+1)-2=-2 end

Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)

Пример 3*. Найдите точку, в которой касательная к графику функции (f(x)=frac-x) перпендикулярна прямой (y=11x+3). Напишите уравнение этой касательной.

Угловой коэффициент данной прямой (k_1=11).
Угловой коэффициент перпендикулярной прямой (k_2=-frac<1>=-frac<1><11>) begin f'(x)=left(fracright)’-x’=frac<2x(x+3)-(x^2+2)cdot 1><(x+3)^2>-1=frac<2x^2+6x-x^2-2-(x+3)^2><(x+3)^2>=\ =frac<(x+3)^2>=- frac<11> <(x+3)^2>end В точке касания: begin f'(x_0)=k_2Rightarrow=-frac<11><(x+3)^2>=-frac<1><11>Rightarrow (x+3)^2=121Rightarrow (x+3)^2-11^2=0Rightarrow\ Rightarrow (x+14)(x+8)=0Rightarrow left[ begin x=-14\ x=8 end right. end
Уравнение касательной при (x_0=-14) begin f(x_0)=frac<(-14)^2+2><-14+3>+14=frac<198><-11>+14=-18+14=-4\ y=-frac<1><11>(x+14)-4=-frac <11>end Уравнение касательной при (x_0=8) begin f(x_0)=frac<8^2+2><8+3>-8=frac<66><11>-8=-2\ y=-frac<1><11>(x-8)-2=-frac <11>end
Ответ: точка касания (-14;-4), уравнение (y=-frac<11>)
и точка касания (8;-2), уравнение (-frac<11>)

Пример 4*. Найдите уравнения общих касательных к параболам (y=x^2-5x+6) и (y=x^2+x+1). Укажите точки касания.

Найдем производные функций: begin f_1′(x)=2x-5, f_2′(x)=2x+1 end Пусть a – абсцисса точки касания для первой параболы, b – для второй.
Запишем уравнения касательных (g_1(x)) и (g_2(x)) через эти переменные. begin g_1(x)=f_1′(a)(x-a)+f_1(a)=(2a-5)(x-a)+a^2-5a+6=\ =(2a-5)x-2a^2+5a+a^2-5a+6=(2a-5)x+(6-a^2)\ \ g_2(x)=f_2′(b)(x-b)+f_2(b)=(2b+1)(x-b)+b^2+b+1=\ =(2b+1)x-2b^2-b+b^2+b+1=(2b+1)x+(1-b^2) end Для общей касательной должны быть равны угловые коэффициенты и свободные члены. Получаем систему уравнений: begin begin 2a-5=2b+1\ 6-a^2=1-b^2 end Rightarrow begin 2(a-b)=6\ a^2-b^2=5 end Rightarrow begin a-b=3\ (a-b)(a+b)=5 end Rightarrow begin a-b=3\ a+b=frac53 end Rightarrow \ Rightarrow begin 2a=3+frac53\ 2b=frac53-3 end Rightarrow begin a=frac73\ b=-frac23 end end Находим угловой коэффициент и свободный член из любого из двух уравнений касательных: $$ k=2a-5=2cdotfrac73-5=-frac13, b=6-a^2=6-frac<49><9>=frac59 $$ Уравнение общей касательной: $$ y=-frac x3+frac59 $$
Точки касания: begin a=frac73, f_1(a)=left(frac73right)^2-5cdotfrac73+6=frac<49><9>-frac<35><3>+6=frac<49-105+54><9>=-frac29\ b=-frac23, f_2(b)=left(-frac23right)^2-frac23+1=frac49-frac23+1frac<4-6+9><9>=frac79 end
Ответ: касательная (y=-frac x3+frac59); точки касания (left(frac73;-frac29right)) и (left(-frac23;frac79right))

Пример 5*. Докажите, что кривая (y=x^4+3x^2+2x) не пересекается с прямой (y=2x-1), и найдите расстояние между их ближайшими точками.

Решим уравнение: (x^4+3x^2+2x=2x-1) begin x^4+3x^2+1=0Rightarrow D=3^2-4=5Rightarrow x^2=frac<-3pmsqrt<5>> <2>end Оба корня отрицательные, а квадрат не может быть отрицательным числом.
Значит, (xinvarnothing) – решений нет, кривая и прямая не пересекаются.
Что и требовалось доказать.

Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом (k=2), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой (y=2x-1).
Строим уравнение касательной. По условию: (f'(x)=4x^3+6x+2=2) begin 4x^3+6x=0Rightarrow 2x(2x^2+3)=0Rightarrow left[ begin x=0\ 2x^2+3=0 end right. Rightarrow left[ begin x=0\ x^2=-frac32 end right. Rightarrow left[ begin x=0\ xinvarnothing end right. Rightarrow x=0 end Точка касания (x_0=0, y_0=0^4+3cdot 0^2+2cdot 0=0).
Уравнение касательной: (y=2(x-0)+0=2x)

Ищем расстояние между двумя параллельными прямыми: (y=2x) и (y=2x-1). Перпендикуляр из точки (0;0) на прямую (y=2x-1) имеет угловой коэффициент (k=-frac12), его уравнение: (y=-frac12 x+b). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и (b=0).

Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac<0,4><2>=-0,2 end Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt<0,4^2+(-0,2)^2>=0,2sqrt<2^2+1^2>=frac<sqrt<5>><5>)
Ответ: (frac<sqrt<5>><5>)

[spoiler title=”источники:”]

http://www.yaklass.ru/p/algebra/10-klass/proizvodnaia-primenenie-proizvodnoi-dlia-issledovaniia-funktcii-9147/kak-poluchit-uravnenie-kasatelnoi-k-grafiku-funktcii-11225/re-01fe2bca-fe21-491b-860a-b63304a86ea9

http://reshator.com/sprav/algebra/10-11-klass/uravnenie-kasatelnoj-k-grafiku-funkcii/

[/spoiler]

п.1. Уравнение касательной

Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.

Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin{gather*} (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end{gather*}

Уравнение касательной к кривой (y=f(x)) в точке (x_0) имеет вид: $$ y=f'(x_0)(x-x_0)+f(x_0) $$ при условии, что производная (f'(x_0)=aneinfty) – существует и конечна.

Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace{f'(x_0)}_{=k}x+underbrace{f(x_0)-f'(x_0)cdot x_0}_{=b} $$

Уравнение касательной с угловым коэффициентом: begin{gather*} y=kx+b\ k=f'(x_0), b=f(x_0)-f'(x_0)cdot x_0 end{gather*}

п.2. Алгоритм построения касательной

п.3. Вертикальная касательная

В случае, если производная (f'(x_0)=pminfty) – существует, но бесконечна, в точке (x_0) проходит вертикальная касательная (x=x_0).

п.4. Примеры

Пример 1. Для функции (f(x)=2x^2+4x)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)

Пример 2. Напишите уравнение касательной к графику функции в заданной точке:
a) ( f(x)=frac5x+frac x5, x_0=4 ) begin{gather*} f(x_0)=frac54+frac45=frac{25+16}{20}=frac{41}{20}\ f'(x)=left(frac5xright)’+left(frac x5right)’=-frac{5}{x^2}+frac15=frac{-25+x^2}{5x^2}=frac{x^2-25}{5x^2}\ f'(x_0)=frac{4^2-25}{5cdot 4^2}=-frac{9}{80} end{gather*} Уравнение касательной: $$ y=-frac{9}{80}(x-4)+frac{41}{20}=-frac{9}{80}x+frac{9}{20}+frac{41}{20}=-frac{9}{80}x+2,5 $$
б) ( f(x)=frac{x^2+5}{3-x}, x_0=2 ) begin{gather*} f(x_0)=frac{2^2+5}{3-2}=frac91=9\ f'(x)=frac{(x^2+5)'(3-x)-(x^2+5)(3-x)’}{(3-x)^2}=frac{2x(3-x)+(x^2+5)}{(3-x)^2}=\ =frac{6x-2x^2+x^2+5}{(3-x)^2}=frac{-x^2+6x+5}{(3-x)^2}\ f'(x_0)=frac{-2^2+6cdot 2+5}{(3-2)^2}=13 end{gather*} Уравнение касательной: $$ y=13(x-2)+9=13x-26+9=13x-17 $$

Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin{gather*} 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac{0,4}{2}=-0,2 end{gather*} Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt{0,4^2+(-0,2)^2}=0,2sqrt{2^2+1^2}=frac{sqrt{5}}{5})
Ответ: (frac{sqrt{5}}{5})

Уравнение касательной к графику функции

Чтобы закрепить
предыдущий параграф, рассмотрим задачу
нахождения касательной к графику функции
в данной точке. Это задание встречалось
нам в школе, и оно же встречается в курсе
высшей математики.

Рассмотрим
«демонстрационный» простейший пример.

Составить
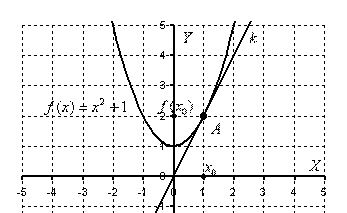
уравнение касательной к графику
функции 
 в
точке с абсциссой 
.
Я сразу приведу готовое графическое
решение задачи (на практике этого делать
в большинстве случаев не надо):

Строгое
определение касательной дается с помощью
определения самой производной функции,
и с этим пока повременим. Наверняка
практически всем интуитивно понятно,
что такое касательная. Если объяснять
«на пальцах», то касательная к графику
функции – этопрямая,
которая касается графика функции
в единственной точке.
При этом все близлежащие точки прямой
расположены максимально близко к графику
функции.

Применительно
к нашему случаю: при 
 касательная 
 (стандартное
обозначение) касается графика функции
в единственной точке 
.

И наша
задача состоит в том, чтобы найти
уравнение прямой 
.

Как
составить уравнение касательной в точке
с абсциссой 
?

Общая формула
знакома нам еще со школы:

Значение 
 нам
уже дано в условии.

Теперь
нужно вычислить, чему равна сама
функция в
точке 
:

 

На
следующем этапе находим производную:

Находим
производную в точке (задание, которое
мы недавно рассмотрели):

Подставляем
значения 
, 
 и 
 в
формулу 
:

Таким
образом, уравнение касательной:

Это
«школьный» вид уравнения прямой с
угловым коэффициентом. В высшей математике
уравнение прямой принято записывать в
так называемой общей
форме 
,
поэтому перепишем найденное уравнение
касательной в соответствии с традицией:  

Очевидно,
что точка 
 должна
удовлетворять данному уравнению:

 –
верное равенство.

Следует
отметить, что такая проверка является
лишь частичной. Если мы неправильно
вычислили производную в точке 
,
то выполненная подстановка нам ничем
не поможет.

Рассмотрим еще
два примера.

Пример 5

Составить
уравнение касательной к графику
функции 
 в
точке с абсциссой 

Уравнение
касательной составим по формуле 

1)
Вычислим значение функции в точке 
:

2)
Найдем производную. Дважды используем
правило дифференцирования сложной
функции:

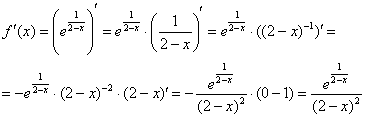
3)
Вычислим значение производной в
точке 
:

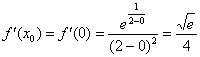
4)
Подставим значения 
, 
 и 
 в
формулу 
:

Готово.

Выполним
частичную проверку:

Подставим
точку 
 в
найденное уравнение:

 –
верное равенство.

Пример 6

Составить
уравнение касательной к графику
функции 
 в
точке с абсциссой 

Полное решение и
образец оформления в конце урока.

В задаче на
нахождение уравнения касательной очень
важно ВНИМАТЕЛЬНО и аккуратно выполнить
вычисления, привести уравнение прямой
к общему виду.

Дифференциал функции одной переменной

Коль скоро я не
объяснил (на данный момент), что такое
производная функции, то не имеет смысла
объяснять, и что такое дифференциал
функции. В самой примитивной формулировке
дифференциал – это «почти то же самое,
что и производная».

Производная
функции чаще всего обозначается через 
.

Дифференциал
функции стандартно обозначается
через 
 (так
и читается – «дэ игрек»)

Дифференциал
функции одной переменной записывается
в следующем виде:

Другой
вариант записи: 

Простейшая
задача: Найти дифференциал функции 

1) Первый этап.
Найдем производную:

2) Второй этап.
Запишем дифференциал:

Готово.

Дифференциал
функции одной или нескольких переменных
чаще всего используют дляприближенных
вычислений.

Помимо других
задач с дифференциалом время от времени
встречается и «чистое» задание на
нахождение дифференциала функции. Кроме
того, как и для производной, для
дифференциала существует понятие
дифференциала в точке. И такие примеры
мы тоже рассмотрим.

Пример 7

Найти
дифференциал функции 

Перед
тем, как находить производную или
дифференциал, всегда целесообразно
посмотреть, а нельзя ли как-нибудь
упростить функцию (или запись функции)
ещё додифференцирования?
Смотрим на наш пример. Во-первых, можно
преобразовать корень:

 (корень
пятой степени относится именно к синусу).

Во-вторых, замечаем,
что под синусом у нас дробь, которую,
очевидно, предстоит дифференцировать.
Формула дифференцирования дроби очень
громоздка. Нельзя ли избавиться от
дроби? В данном случае – можно, почленно
разделим числитель на знаменатель:

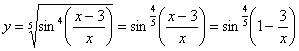
Функция
сложная. В ней два вложения: под степень
вложен синус, а под синус вложено
выражение 
.
Найдем производную, используя правило
дифференцирования сложной функции 
 два
раза:

Запишем
дифференциал, при этом снова представим 
 в
первоначальном «красивом» виде:

Готово.

Когда
производная представляет собой дробь,
значок 
 обычно
«прилепляют» в самом конце числителя
(можно и справа на уровне дробной черты).

Пример 8

Найти
дифференциал функции 

Это пример для
самостоятельного решения.

Следующие два
примера на нахождение дифференциала в
точке.

Пример 9

Вычислить
дифференциал функции 
 в
точке 

Найдем
производную:

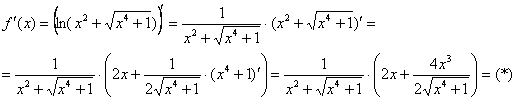
Опять, производная
вроде бы найдена. Но в эту бодягу еще
предстоит подставлять число, поэтому
результат максимально упрощаем:

Труды
были не напрасны, записываем дифференциал:

Теперь
вычислим дифференциал в точке 
:

В
значок дифференциала 
 единицу
подставлять не нужно, он немного из
другой оперы.

Ну и
хорошим тоном в математике считается
устранение иррациональности в знаменателе.
Для этого домножим числитель и знаменатель
на 
.
Окончательно:

Пример 10

Вычислить
дифференциал функции 
 в
точке 
.
В ходе решения производную максимально
упростить.

Это пример для
самостоятельного решения. Примерный
образец оформления и ответ в конце
урока.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #

  08.02.20157.31 Mб91.rtf

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В этой статье мы разберем все типы задач на нахождение уравнения касательной.

Вспомним геометрический смысл производной: если к графику функции в точке проведена касательная, то коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси ) равен производной функции в точке .

Возьмем на касательной произвольную точку  с координатами :

И рассмотрим прямоугольный треугольник :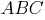

В этом треугольнике

Отсюда

Или

Это и есть уравнение касательной, проведенной к графику функции в точке .

Чтобы написать уравнение касательной, нам достаточно знать уравнение функции и точку, в которой проведена касательная. Тогда мы сможем найти и .

Есть три основных типа задач на составление уравнения касательной.

1. Дана точка касания 

2. Дан коэффициент наклона касательной, то есть значение производной функции в точке .

3. Даны координаты точки, через которую проведена касательная, но которая не является точкой касания.

Рассмотрим каждый тип задач.

1. Написать уравнение касательной к графику функции   в точке .

а) Найдем значение функции в точке .

.

б) Найдем значение производной в точке . Сначала найдем производную функции

Подставим найденные значения в уравнение касательной:

Раскроем скобки в правой части уравнения. Получим:

Ответ: .

2. Найти абсциссы точек, в которых касательные к графику функции параллельны оси абсцисс.

Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции в точках касания равно нулю.

а) Найдем производную функции .

б) Приравняем производную к нулю и найдем значения , в которых касательная параллельна оси :

Приравняем каждый множитель к нулю, получим:

Ответ: 0;3;5

3. Написать уравнения касательных к графику функции , параллельных  прямой .

Касательная параллельна прямой . Коэффициент наклона этой прямой равен -1. Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -1. То есть мы знаем коэффициент наклона касательной, а, тем самым, значение производной в точке касания.

Это второй тип задач на нахождение уравнения касательной.

Итак, у нас дана функция и значение производной в точке касания.

а) Найдем точки, в которых производная функции равна -1.

Сначала найдем уравнение производной.

Нам нужно найти производную дроби.

Приравняем производную к числу -1.

или

или

б) Найдем уравнение касательной к графику функции в точке .

Найдем значение функции в точке .

(по условию)

Подставим эти значения в уравнение касательной:

.

б) Найдем уравнение касательной к графику функции в точке .

Найдем значение функции в точке .

(по условию).

Подставим эти значения в уравнение касательной:

.

Ответ:

4. Написать уравнение касательной к кривой , проходящей через точку

Сначала проверим, не является ли точка точкой касания. Если точка является точкой касания, то она принадлежит графику функции, и её координаты должны удовлетворять уравнению функции. Подставим координаты  точки   в уравнение функции.

. Мы получили под корнем отрицательное число, равенство не верно, и точка не принадлежит графику функции и не является точкой касания.

Это последний тип задач на нахождение уравнения касательной. Первым делом нам нужно найти абсциссу точки касания.

Найдем значение .

Пусть – точка касания. Точка  принадлежит касательной к графику функции . Если мы подставим координаты этой точки в уравнение касательной, то получим верное равенство:

.

Значение функции в точке равно .

Найдем значение производной функции в точке .

Сначала найдем производную функции . Это сложная функция.

Производная в точке равна .

Подставим выражения для и в уравнение касательной. Получим уравнение относительно :

Решим это уравнение.

Сократим числитель и знаменатель дроби на 2:

Приведем правую часть уравнения к общему знаменателю. Получим:

Упростим числитель дроби и умножим обе части на – это выражение строго больше нуля.

Получим уравнение

Это иррациональное уравнение.

Решим его. Для этого возведем обе части в квадрат и перейдем к системе.

Решим первое уравнение.

Решим квадратное уравнение, получим

или

Второй корень не удовлетворяет условию , следовательно, у нас только одна точка касания и её абсцисса равна .

Напишем уравнение касательной к кривой в точке . Для этого подставим значение в уравнение   – мы его уже записывали.

Получим:

Ответ:
И.В. Фельдман, репетитор по математике.

Уравнение касательной онлайн

Оставить свой комментарий:

---