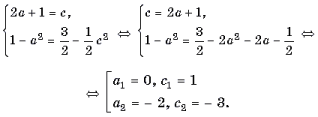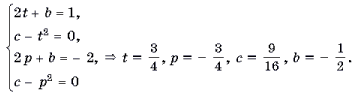Касательная к параболе
Воскресенье, 3 ноября, 2019
Иногда в заданиях ЕГЭ и даже ОГЭ по математике, особенно в заданиях с параметром, возникают ситуации, когда нужно установить, при каком условии некоторая прямая касается параболы. Составить уравнение касательной к функции можно с помощью производной, и старшеклассникам обычно рассказывают в школе, как это делать. Но в случае с параболой можно обойтись без этих премудростей. Достаточно уметь решать квадратные уравнения, а этому учат уже в основой школе. В данной статье профессиональный репетитор по математике рассказывает о том, как получить уравнение касательной к параболе в некоторой точке без использования производной.
Уравнение касательной к параболе
Давайте изобразим координатную плоскость и нарисуем в ней параболу, которая проходит через начало координат. Так бывает, конечно, не всегда. Но эту проблему можно легко устранить. Достаточно просто перенести начало координат в вершину параболы, и мы получим нужную нам ситуацию. Поэтому целесообразно рассматривать именно случай, когда парабола проходит через начало координат. В этом случае уравнение такой параболы имеет вид :
Мы для определённости взяли положительный коэффициент , поэтому ветви данной параболы направлены вверх. Но на самом деле все дальнейшие рассуждения будут справедливы и для отрицательных
.
Отметим некоторую точку A, которая принадлежит нашей параболе. Пусть она имеет координаты . Проведём касательную к параболе в этой точке. Касательная – это прямая. А в общем виде уравнение прямой записывается как
. То есть ситуация получается следующая:
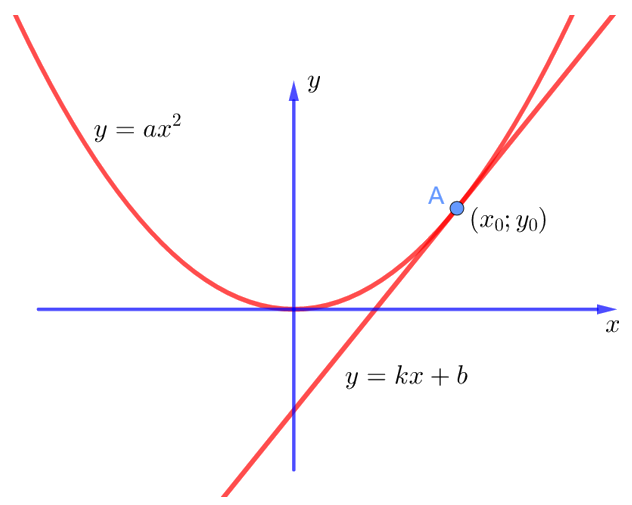
Ну и давайте зададимся целью найти неизвестные коэффициенты и
через известные значения
и
. Так у нас и получится касательная к параболе, а точнее её уравнение в точке
. Но давайте сразу договоримся, что делать мы это будем без помощи производной, чтобы этот материал был понятен не только старшеклассникам.
Итак, что же у нас есть? У нас есть парабола , причём
. Иначе это была бы не парабола, а просто прямая линия, которая совпадает с осью OX. Также у нас есть касательная
. Но важно то, что эта касательная и парабола имеют общую точку с координатами
.
А это значит, что координаты этой точки должны удовлетворять и уравнению параболы, и уравнению касательной. Значит, если мы подставим координаты этой точки в уравнение параболы и в уравнение касательной, то мы должны при этом получить верные равенства. Итак, имеет место следующая система уравнений:
Именно её нам и нужно решить. Но как это сделать? Ну, во-первых, обратим сразу внимание, что у этих уравнений одинаковые левые части. А значит, равны и правые. То есть получается вот такое уравнение:
Это квадратное уравнение, которое может иметь от нуля до двух решений, в зависимости от дискриминанта. Вот здесь и возникает самая главная идея! Поскольку прямая касается параболы (ведь это касательная к параболе), то у них есть только одна общая точка. А это означает, что данное уравнение должно иметь единственное решение. Ну а единственное решение оно имеет только в том случае, если дискриминант равен нулю. Осталось его посчитать:
(1)
Ну а сам корень уравнения при нулевом дискриминанте равен:
(2)
Ну а дальше подставляем выражение (2) в уравнение (1) и получаем следующее уравнение:
(3)
Ну и получилось, что мы смогли выразить коэффициент и коэффициент
через
и
(уравнения (2) и (3), соответственно), как и было нужно. Подставляя их в уравнение прямой, получаем искомое уравнение касательной к параболе:
Уравнение касательной к параболе в общем виде
В общем виде парабола задаётся формулой: . Как уже отмечалось выше, такую параболу можно всегда свести к параболе
путём простого переноса начала системы координат в вершину исходной параболы. Но зададимся вопросом, как будет выглядеть уравнение касательной к такой параболе, если мы не будем осуществлять такой перенос.
Касательная к параболе — это прямая, поэтому в общем виде уравнение этой прямой записывается по аналогии с предыдущим пунктом: . Только здесь мы используем букву
, поскольку буква
уже занята:
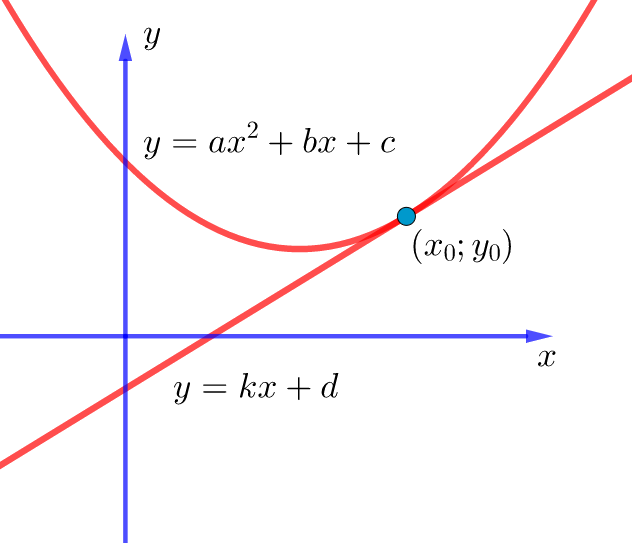
И вновь мы ссылаемся на тот факт, что данная касательная и парабола будут иметь общую точку . Значит, координаты этой точки должны удовлетворять следующей системе уравнений:
У записанных уравнений равны левые части, значит, равны и правые. То есть имеет место следующее квадратное уравнение:
Ну и поскольку у касательной с параболой есть только одна общая точка, то последнее уравнение должно иметь единственное решение. Такое возможно только в том случае, если его дискриминант равен нулю. То есть имеет место равенство:
(4)
При этом сам корень уравнения должен быть равен:
(5)
Подставляем выражение (5) в выражение (4) и получаем:
(6)
Итак, мы получили искомые коэффициенты. Значит, уравнение касательной к параболе в общем виде будет выглядеть так:
При этом легко убедиться, что в частном случае при (то есть когда парабола проходит через начало координат) мы получаем то же самое уравнение, которое уже было нами получено в предыдущем пункте.
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
Угол наклона прямой y=kx+b называется угол α, который отсчитывается от положительного направления оси ох к прямой y=kx+b в положительном направлении.
На рисунке направление ох обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Угловой коэффициент прямой y=kx+b называют числовым коэффициентом k.
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k=tg α.
- Угол наклона прямой равняется 0 только при параллельности ох и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0. Значит, вид уравнения будет y=b.
- Если угол наклона прямой y=kx+b острый, тогда выполняются условия 0<α<π2 или 0°<α<90°. Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию tg α>0, причем имеется возрастание графика.
- Если α=π2, тогда расположение прямой перпендикулярно ох. Равенство задается при помощи равенства x=c со значением с, являющимся действительным числом.
- Если угол наклона прямой y=kx+b тупой, то соответствует условиям π2<α<π или 90°<α<180°, значение углового коэффициента k принимает отрицательное значение, а график убывает.
Секущей называют прямую, которая проходит через 2 точки функции f(x). Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что АВ является секущей, а f(x) – черная кривая, α – красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника АВС можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
k=tg α=BCAC=f(xB)-fxAxB-xA, где абсциссами точек А и В являются значения xA, xB, а f(xA), f(xB) – это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k=f(xB)-f(xA)xB-xA или k=f(xA)-f(xB)xA-xB, причем уравнение необходимо записать как y=f(xB)-f(xA)xB-xA·x-xA+f(xA) или
y=f(xA)-f(xB)xA-xB·x-xB+f(xB).
Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у=0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Касательная к графику функции f(x) в точке x0; f(x0) называется прямая, проходящая через заданную точку x0; f(x0), с наличием отрезка, который имеет множество значений х, близких к x0.
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y=x+1, считается касательной к y=2x в точке с координатами (1; 2). Для наглядности, необходимо рассмотреть графики с приближенными к (1; 2) значениями. Функция y=2x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Очевидно, что y=2x сливается с прямой у=х+1.
Для определения касательной следует рассмотреть поведение касательной АВ при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.
Секущая АВ, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной αx.
Касательной к графику функции y=f(x) в точке А считается предельное положение секущей АВ при В стремящейся к А, то есть B→A.
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей АВ для функции f(x), где А и В с координатами x0, f(x0) и x0+∆x, f(x0+∆x), а ∆x обозначаем как приращение аргумента. Теперь функция примет вид ∆y=∆f(x)=f(x0+∆x)-f(∆x). Для наглядности приведем в пример рисунок.
Рассмотрим полученный прямоугольный треугольник АВС. Используем определение тангенса для решения, то есть получим отношение ∆y∆x=tg α. Из определения касательной следует, что lim∆x→0∆y∆x=tg αx. По правилу производной в точке имеем, что производную f(x) в точке x0 называют пределом отношений приращения функции к приращению аргумента, где ∆x→0, тогда обозначим как f(x0)=lim∆x→0∆y∆x.
Отсюда следует, что f'(x0)=lim∆x→0∆y∆x=tg αx=kx, где kx обозначают в качестве углового коэффициента касательной.
То есть получаем, что f’(x) может существовать в точке x0 причем как и касательная к заданному графику функции в точке касания равной x0, f0(x0), где значение углового коэффициента касательной в точке равняется производной в точке x0. Тогда получаем, что kx=f'(x0).
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x0 при пересечении.
Уравнение касательной к графику функции y=f(x) в точке x0, f0(x0) принимает вид y=f'(x0)·x-x0+f(x0).
Имеется в виду, что конечным значением производной f'(x0) можно определить положение касательной, то есть вертикально при условии limx→x0+0f'(x)=∞ и limx→x0-0f'(x)=∞ или отсутствие вовсе при условии limx→x0+0f'(x)≠limx→x0-0f'(x).
Расположение касательной зависит от значения ее углового коэффициента kx=f'(x0). При параллельности к оси ох получаем, что kk=0, при параллельности к оу – kx=∞, причем вид уравнения касательной x=x0 возрастает при kx>0, убывает при kx<0.
Произвести составление уравнения касательной к графику функции y=ex+1+x33-6-33x-17-33 в точке с координатами (1; 3) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1; 3) является точкой касания, тогда x0=-1, f(x0)=-3.
Необходимо найти производную в точке со значением -1. Получаем, что
y’=ex+1+x33-6-33x-17-33’==ex+1’+x33′-6-33x’-17-33’=ex+1+x2-6-33y'(x0)=y'(-1)=e-1+1+-12-6-33=33
Значение f’(x) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда kx=tg αx=y'(x0)=33
Отсюда следует, что αx=arctg33=π6
Ответ: уравнение касательной приобретает вид
y=f'(x0)·x-x0+f(x0)y=33(x+1)-3y=33x-9-33
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Выяснить наличие существования касательной к графику заданной функции
y=3·x-15+1 в точке с координатами (1;1). Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y’=3·x-15+1’=3·15·(x-1)15-1=35·1(x-1)45
Если x0=1, тогда f’(x) не определена, но пределы записываются как limx→1+035·1(x-1)45=35·1(+0)45=35·1+0=+∞ и limx→1-035·1(x-1)45=35·1(-0)45=35·1+0=+∞, что означает существование вертикальной касательной в точке (1;1).
Ответ: уравнение примет вид х=1, где угол наклона будет равен π2.
Для наглядности изобразим графически.
Найти точки графика функции y=115x+23-45×2-165x-265+3x+2, где
- Касательная не существует;
- Касательная располагается параллельно ох;
- Касательная параллельна прямой y=85x+4.
Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x∈-∞; 2 и [-2; +∞). Получаем, что
y=-115×3+18×2+105x+176, x∈-∞; -2115×3-6×2+9x+12, x∈[-2; +∞)
Необходимо продифференцировать функцию. Имеем, что
y’=-115×3+18×2+105x+176′, x∈-∞; -2115×3-6×2+9x+12′, x∈[-2; +∞)⇔y’=-15(x2+12x+35), x∈-∞; -215×2-4x+3, x∈[-2; +∞)
Когда х=-2, тогда производная не существует, потому что односторонние пределы не равны в этой точке:
limx→-2-0y'(x)=limx→-2-0-15(x2+12x+35=-15(-2)2+12(-2)+35=-3limx→-2+0y'(x)=limx→-2+015(x2-4x+3)=15-22-4-2+3=3
Вычисляем значение функции в точке х=-2, где получаем, что
- y(-2)=115-2+23-45(-2)2-165(-2)-265+3-2+2=-2, то есть касательная в точке (-2;-2) не будет существовать.
- Касательная параллельна ох, когда угловой коэффициент равняется нулю. Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.
Когда x∈-∞; -2, тогда -15(x2+12x+35)=0, а при x∈(-2; +∞) получаем 15(x2-4x+3)=0.
Решим:
-15(x2+12x+35)=0D=122-4·35=144-140=4×1=-12+42=-5∈-∞; -2×2=-12-42=-7∈-∞; -2 15(x2-4x+3)=0D=42-4·3=4×3=4-42=1∈-2; +∞x4=4+42=3∈-2; +∞
Вычисляем соответствующие значения функции
y1=y-5=115-5+23-45-52-165-5-265+3-5+2=85y2=y(-7)=115-7+23-45(-7)2-165-7-265+3-7+2=43y3=y(1)=1151+23-45·12-165·1-265+31+2=85y4=y(3)=1153+23-45·32-165·3-265+33+2=43
Отсюда -5; 85, -4; 43, 1; 85, 3; 43 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 . Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
-15×2+12x+35=85×2+12x+43=0D=122-4·43=-28<0
Другое уравнение имеет два действительных корня, тогда
15(x2-4x+3)=85×2-4x-5=0D=42-4·(-5)=36×1=4-362=-1∈-2; +∞x2=4+362=5∈-2; +∞
Перейдем к нахождению значений функции. Получаем, что
y1=y(-1)=115-1+23-45(-1)2-165(-1)-265+3-1+2=415y2=y(5)=1155+23-45·52-165·5-265+35+2=83
Точки со значениями -1; 415, 5; 83 являются точками, в которых касательные параллельны прямой y=85x+4.
Ответ: черная линия – график функции, красная линия – график y=85x+4, синяя линия – касательные в точках -1; 415, 5; 83.
Возможно существование бесконечного количества касательных для заданных функций.
Написать уравнения всех имеющихся касательных функции y=3cos32x-π4-13, которые располагаются перпендикулярно прямой y=-2x+12.
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется -1, то есть записывается как kx·k⊥=-1. Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k⊥=-2, тогда kx=-1k⊥=-1-2=12.
Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x0 получаем, что kx=y'(x0). Из данного равенства найдем значения х для точек касания.
Получаем, что
y'(x0)=3cos32x0-π4-13’=3·-sin32x0-π4·32×0-π4’==-3·sin32x0-π4·32=-92·sin32x0-π4⇒kx=y'(x0)⇔-92·sin32x0-π4=12⇒sin32x0-π4=-19
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
32×0-π4=arcsin-19+2πk или 32×0-π4=π-arcsin-19+2πk
32×0-π4=-arcsin19+2πk или 32×0-π4=π+arcsin19+2πk
x0=23π4-arcsin19+2πk или x0=235π4+arcsin19+2πk, k∈Z
Z- множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у:
y0=3cos32x0-π4-13
y0=3·1-sin232x0-π4-13 или y0=3·-1-sin232x0-π4-13
y0=3·1–192-13 или y0=3·-1–192-13
y0=45-13 или y0=-45+13
Отсюда получаем, что 23π4-arcsin19+2πk; 45-13, 235π4+arcsin19+2πk; -45+13 являются точками касания.
Ответ: необходимы уравнения запишутся как
y=12x-23π4-arcsin19+2πk+45-13,y=12x-235π4+arcsin19+2πk-45+13, k∈Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [-10;10], где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y=-2x+12. Красные точки – это точки касания.
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке xcenter; ycenter и радиусом R применяется формула x-xcenter2+y-ycenter2=R2.
Данное равенство может быть записано как объединение двух функций:
y=R2-x-xcenter2+ycentery=-R2-x-xcenter2+ycenter
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Для составления уравнения окружности в точке x0; y0, которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y=R2-x-xcenter2+ycenter или y=-R2-x-xcenter2+ycenter в указанной точке.
Когда в точках xcenter; ycenter+R и xcenter; ycenter-R касательные могут быть заданы уравнениями y=ycenter+R и y=ycenter-R, а в точках xcenter+R; ycenter и
xcenter-R; ycenter будут являться параллельными оу, тогда получим уравнения вида x=xcenter+R и x=xcenter-R.
Касательная к эллипсу
Когда эллипс имеет центр в точке xcenter; ycenter с полуосями a и b, тогда он может быть задан при помощи уравнения x-xcenter2a2+y-ycenter2b2=1.
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y=ba·a2-(x-xcenter)2+ycentery=-ba·a2-(x-xcenter)2+ycenter
Если касательные располагаются на вершинах эллипса, тогда они параллельны ох или оу. Ниже для наглядности рассмотрим рисунок.
Написать уравнение касательной к эллипсу x-324+y-5225=1 в точках со значениями x равного х=2.
Решение
Необходимо найти точки касания, которые соответствуют значению х=2. Производим подстановку в имеющееся уравнение эллипса и получаем, что
x-324x=2+y-5225=114+y-5225=1⇒y-52=34·25⇒y=±532+5
Тогда 2; 532+5 и 2; -532+5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y. Получим, что
x-324+y-5225=1y-5225=1-x-324(y-5)2=25·1-x-324y-5=±5·1-x-324y=5±524-x-32
Очевидно, что верхний полуэллипс задается с помощью функции вида y=5+524-x-32, а нижний y=5-524-x-32.
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2; 532+5 будет иметь вид
y’=5+524-x-32’=52·124-(x-3)2·4-(x-3)2’==-52·x-34-(x-3)2⇒y'(x0)=y'(2)=-52·2-34-(2-3)2=523⇒y=y'(x0)·x-x0+y0⇔y=523(x-2)+532+5
Получаем, что уравнение второй касательной со значением в точке
2; -532+5 принимает вид
y’=5-524-(x-3)2’=-52·124-(x-3)2·4-(x-3)2’==52·x-34-(x-3)2⇒y'(x0)=y'(2)=52·2-34-(2-3)2=-523⇒y=y'(x0)·x-x0+y0⇔y=-523(x-2)-532+5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке xcenter; ycenter и вершины xcenter+α; ycenter и xcenter-α; ycenter, имеет место задание неравенства x-xcenter2α2-y-ycenter2b2=1, если с вершинами xcenter; ycenter+b и xcenter; ycenter-b, тогда задается при помощи неравенства x-xcenter2α2-y-ycenter2b2=-1.
Гипербола может быть представлена в виде двух объединенных функций вида
y=ba·(x-xcenter)2-a2+ycentery=-ba·(x-xcenter)2-a2+ycenter или y=ba·(x-xcenter)2+a2+ycentery=-ba·(x-xcenter)2+a2+ycenter
В первом случае имеем, что касательные параллельны оу, а во втором параллельны ох.
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Составить уравнение касательной к гиперболе x-324-y+329=1 в точке 7; -33-3.
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x-324-y+329=1⇒y+329=x-324-1⇒y+32=9·x-324-1⇒y+3=32·x-32-4 или y+3=-32·x-32-4⇒y=32·x-32-4-3y=-32·x-32-4-3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7; -33-3.
Очевидно, что для проверки первой функции необходимо y(7)=32·(7-3)2-4-3=33-3≠-33-3, тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y(7)=-32·(7-3)2-4-3=-33-3≠-33-3, значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
Получаем, что
y’=-32·(x-3)2-4-3’=-32·x-3(x-3)2-4⇒kx=y'(x0)=-32·x0-3×0-32-4×0=7=-32·7-37-32-4=-3
Ответ: уравнение касательной можно представить как
y=-3·x-7-33-3=-3·x+43-3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y=ax2+bx+c в точке x0, y(x0), необходимо использовать стандартный алгоритм, тогда уравнение примет вид y=y'(x0)·x-x0+y(x0). Такая касательная в вершине параллельна ох.
Следует задать параболу x=ay2+by+c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что
x=ay2+by+c⇔ay2+by+c-x=0D=b2-4a(c-x)y=-b+b2-4a(c-x)2ay=-b-b2-4a(c-x)2a
Графически изобразим как:
Для выяснения принадлежности точки x0, y(x0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна оу относительно параболы.
Написать уравнение касательной к графику x-2y2-5y+3, когда имеем угол наклона касательной 150°.
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
-2y2-5y+3-x=0D=(-5)2-4·(-2)·(3-x)=49-8xy=5+49-8x-4y=5-49-8x-4
Значение углового коэффициента равняется значению производной в точке x0 этой функции и равняется тангенсу угла наклона.
Получаем:
kx=y'(x0)=tg αx=tg 150°=-13
Отсюда определим значение х для точек касания.
Первая функция запишется как
y’=5+49-8x-4’=149-8x⇒y'(x0)=149-8×0=-13⇔49-8×0=-3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150° для такой функции не существует.
Вторая функция запишется как
y’=5-49-8x-4’=-149-8x⇒y'(x0)=-149-8×0=-13⇔49-8×0=-3×0=234⇒y(x0)=5-49-8·234-4=-5+34
Имеем, что точки касания – 234; -5+34.
Ответ: уравнение касательной принимает вид
y=-13·x-234+-5+34
Графически изобразим это таким образом:
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Вспомним определение секущей для лучшего понимания что такое касательная.
Определение 1
Секущей называют прямую, пересекающую график кривой в двух точках одновременно.
Касательной прямой к графику кривой называют прямую, проходящую через некую точку кривой и совпадающую с ней в этой точке так, что это прямая лишь касается кривой.
Другое и более ёмкое определение касательной дал Лейбниц.
Определение 2
Лейбниц касательной называл прямую, проведённую через пару точек на рассматриваемой кривой, не совпадающих между собой, но находящихся бесконечно близко друг к другу. Из определения Лейбница видно, что касательная является частным случаем секущей.
Геометрический смысл производной в точке и касательной
Рассмотрим определение касательной подробнее.
Рисунок 1. Касательная и секущая к графику. Автор24 — интернет-биржа студенческих работ
Пусть дана некая кривая $L$, а на ней выбрана произвольная точка $M$. Возьмём ещё одну точку $P$, расположенную также на этой кривой и проведём через точки $M$ и $P$ секущую. Теперь поставим точку $P$ ещё ближе к точке $M$ и проведём новую секущую.
Проделаем так ещё несколько раз, каждый раз получая новую секущую, как бы поворачивающуюся вокруг точки $M$.
В момент, когда очередная точка $P$ находится бесконечно близко к точке $M$, секущая как бы достигает своего предельного положения, в котором по сути она лишь касается графика.
«Уравнение касательной» 👇
Это положение называется касательной к графику кривой $L$ в точке $M$.
Уравнение касательной через производную
Теперь узнаем, как найти уравнение касательной.
Рассмотрим некую функцию $y(x)$ и выберем на ней точку $M$ с координатами $(a; y(a))$.
Сделаем приращение к аргументу $x$ в этой точке, равное $Δx$ и рассмотрим точку $P$ на графике функции с абсциссой, равной $x=x+Δx$. Значение функции в этой точке будет равно $y(a+ Δx)$. Проведём через точки $M$ и $P$ секущую.
Как мы помним из курса математики, угловой коэффициент равен тангенсу угла прямой с осью абсцисс. Это значит, что угловой коэффициент рассматриваемой нами секущей равен приращению функции $y$ к приращению функции $x$:
$k_{секущ.}=frac{Δy}{Δx}left(1right)$.
Теперь рассмотрим приращение $Δx$ как бесконечно малую величину. В этом случае точка $P$ с координатами $(a; y(a)+ Δy)$ будет приближаться к точке $M$, стремясь к ней. Следовательно, угловой коэффициент нашей секущей, которая в данном случае является касательной, равен пределу:
$k_{кас.}=lim_{ Δx to 0}(k_{секущ.})$
Воспользуемся формулой $(1)$ для секущей:
$k_{кас.}=lim_{ Δx to 0} frac{Δy}{Δx}$
Данный предел также носит название производной функции $y=f(x)$ в точке $x$ и обозначается как $y’(x)$.
Определение 3
Геометрический смысл производной состоит в том, что при условии возможности проведения касательной в точке $x$ к графику исследуемой кривой, такой, что эта касательная не параллельна оси $OX$, значение производной является угловым коэффициентом проведённой касательной в этой точке.
Иначе данное утверждение можно записать как
$k_{кас.}(a)=f’(a)$.
То есть, при составлении уравнения касательной через производную, производная функции является угловым коэффициентом.
Заметим на всякий случай, что сама функция $y=f(x)$ и её производная $y’(x)$ — две разные функции, равные между собой в точке $x$.
Таким образом, в общем виде уравнение касательной будет иметь вид:
$y=f(x_0)+f’(x_0)(x-x_0) left(2right)$,
где $f(x_0)$ — значение функции в точке $x_0$, а $f’(x_0)$ — её производная.
Уравнение касательной для параболы

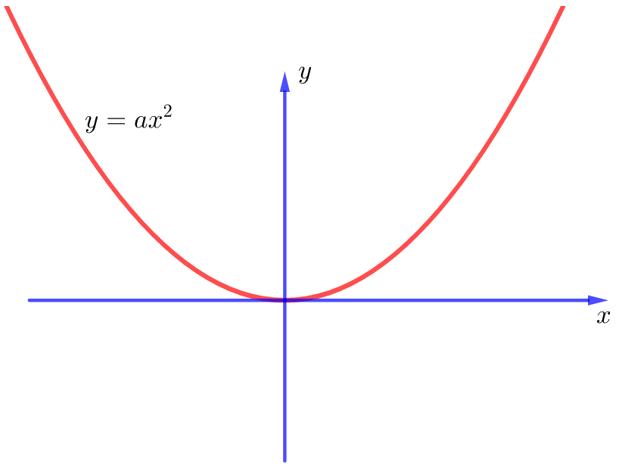
Рисунок 2. Уравнение касательной к графику параболической функции. Автор24 — интернет-биржа студенческих работ
Рассмотрим получение уравнения касательной к графику функции на параболе $y=ax^2$ в точке $M$ c координатами $(x; y)$.
Придадим этой точке приращение по оси $OX$, равное $Δx$, приращение по оси $y$ тогда составит $y+Δy=a(x+ Δx)^2$. Точку с координатами $(x+ Δx; y+Δy)$ назовём $P$.
Теперь чтобы определить тангенс угла секущей $MP$с осью абсцисс, рассмотрим прямоугольный треугольник $triangle MNP$. В нём катет $MN$ равен $Δx$, а второй катет $Δy$ — это приращение ординаты, равное $Δy=a(2x cdot Δx + Δx^2)$.
Выразим используя эти данные тангенс угла $φ$.
$mathrm{tg}φ=frac{Δy}{Δx}=2ax + a cdot Δx$
Теперь для получения углового коэффициента рассмотрим это отношение при бесконечно малой величине $Δx$. Как известно, в этом случае мы имеем дело с пределом:
$mathrm{tg}φ= lim_{Δx to 0}(2ax+a cdot x)=2ax$.
Благодаря такому соотношению становится легко построить касательную к параболе (рис. 2, б).
Для этого достаточно рассмотреть треугольник $triangle MPT$, так как отрезок $TP$ будет равен:
$TP=frac{y}{mathrm{tg}α}=frac{ax^2}{2ax}=frac{x}{2}$
То есть, для того чтобы получить касательную, необходимо соединить середину отрезка $OP$ с точкой $M$.
Расположение касательной в зависимости от значения её углового коэффициента
Рассмотрим несколько различных случаев значения углового коэффициента для касательной.
Если её угловой коэффициент, то есть, тангенс, равен нулю, то касательная расположена параллельно оси $OX$, а сама прямая принимает вид $y=b$.
Если тангенс положительный, то касательная образует острый угол с осью абсцисс, что значит, что вместе с ростом $x$ растёт и $y$.
В случае если тангенс отрицательный, прямая образует тупой угол с горизонтальной осью, а это значит, что с увеличением значения икса происходит уменьшение значения игрека.
Есть ещё один случай расположения касательной — параллельно оси $OY$, в этом случае её уравнение описывается как $x=c$, где $c$ — некая константа.
Другим числом, определяющим положение касательной, является число $b$, являющееся свободным членом в уравнении прямой $y=kx+b$. Число $b$ характеризует значение функции $y(x)$ в точке её пересечения с осью ординат, иначе говоря, оно есть не что иное, как значение уравнения касательной к графику функции в точке $x=0$.
Пример 1
Составить уравнение касательной в точке $x=3$ для графика функции $y(x)=2x^2+3x-6$.
Сначала найдём значение функции в точке $x=3$:
$y=2 cdot 3^2 +3 cdot 3 – 6 = 21$
Теперь определим значение производной для исследуемой функции:
$(2x^2+3x-6)’=4x+3$
Теперь получим значение углового коэффициента, для этого подставим $x=3$ в производную:
$y’(x)=4 cdot 3 + 3 = 15$
Подставим это значение в формулу для касательной $(2)$:
$y_{кас.}=21+15 cdot (x-3)$
$y=15x-24$ — уравнение касательной получено.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
3. Аналитическая геометрия на плоскости
3.9 Касательные
Пусть на плоскости задана кривая уравнением $F(x,y)=0$ (т.е. неявным образом). Пусть точка $(x_0, y_0)$ принадлежит этой кривой. Выпишем уравнение касательной к кривой в этой точке.
Напомним, что если кривая задана уравнением $y=f(x)$, то, как известно из курса дифференциального исчисления, угловой коэффициент касательной в точке $(x_0,y_0)$, лежащей на кривой, равен значению производной $f(x)$ в этой точке, т.е. $k=f'(x_0)$. Таким образом, уравнение касательной (уравнение прямой с заданным угловым коэффициентом, проходящей через заданную точку) имеет вид:
[
y-y_0=f'(x_0)(x-x_0).
]
Если кривая задана неявно, то производная $f'(x_0)$ вычисляется согласно соотношению
[
f'(x_0)=-frac{frac{partial F}{partial x}}{frac{partial F}{partial y}}|_{x_0, y_0}.
]
Подставляя в уравнение касательной, получаем уравнение касательной в окончательном виде:
begin{equation}
(y-y_0)cdot frac{partial F}{partial y}(x_0, y_0)+(x-x_0)cdot frac{partial F}{partial x}(x_0, y_0)=0. (26)
label{kasat}
end{equation}
Рассмотрим с помощью этого соотношения касательные к кривым второго порядка.
1. Касательная к эллипсу.
Исходное уравнение
[
frac{x^2}{a^2}+frac{y^2}{b^2}=1,
]
так что $frac{partial F}{partial x}=frac{2x}{a^2}$, $frac{partial F}{partial y}=frac{2y}{b^2}$. При этом уравнение (26) принимает вид
[
frac{2(x-x_0)x_0}{a^2}+frac{2(y-y_0)y_0}{b^2}=0.
]
Сокращая на 2 и учитывая, что точка $(x_0,y_0)$ лежит на эллипсе, получаем уравнение касательной эллипса, проходящей через эту точку:
begin{equation}
frac{xx_0}{a^2}+frac{yy_0}{b^2}=1. (27)
label{kasell}
end{equation}
2. Касательная к гиперболе.
Исходное уравнение
[
frac{x^2}{a^2}-frac{y^2}{b^2}=1,
]
так что $frac{partial F}{partial x}=frac{2x}{a^2}$, $frac{partial F}{partial y}=-frac{2y}{b^2}$. При этом уравнение (26) принимает вид
[
frac{2(x-x_0)x_0}{a^2}-frac{2(y-y_0)y_0}{b^2}=0.
]
Сокращая на 2 и учитывая, что точка $(x_0,y_0)$ лежит на гиперболе, получаем уравнение касательной гиперболы, проходящей через эту точку:
begin{equation}
frac{xx_0}{a^2}-frac{yy_0}{b^2}=1. (28)
label{kashyp}
end{equation}
3. Касательная к параболе.
Исходное уравнение
[
y^2-2px=0,
]
так что $frac{partial F}{partial x}=-2p$, $frac{partial F}{partial y}=2y$. При этом уравнение (26) принимает вид
[
-2p(x-x_0)+2(y-y_0)y_0=0.
]
Сокращая на 2 и учитывая, что точка $(x_0,y_0)$ лежит на параболе, получаем уравнение касательной параболы, проходящей через эту точку:
begin{equation}
yy_0=p(x+x_0). (29)
label{kaspar}
end{equation}
Пример.
Задачи.
Уравнение касательной к графику функции
П. Романов, Т. Романова,г. Магнитогорск,
Челябинская обл.
Уравнение
касательной к графику функции
Статья опубликована при поддержке Гостиничного комплекса «ИТАКА+». Останавливаясь в городе судостроителей Северодвинске, вы не столкнетесь с проблемой поиска временного жилья. Тут, на сайте гостиничного комплекса «ИТАКА+» http://itakaplus.ru, вы сможете легко и быстро снять квартиру в городе, на любой срок, с посуточной оплатой.
На современном этапе развития
образования в качестве одной из основных его
задач выступает формирование творчески мыслящей
личности. Способность же к творчеству у учащихся
может быть развита лишь при условии
систематического привлечения их к основам
исследовательской деятельности. Фундаментом для
применения учащимися своих творческих сил,
способностей и дарований являются
сформированные полноценные знания и умения. В
связи с этим проблема формирования системы
базовых знаний и умений по каждой теме школьного
курса математики имеет немаловажное значение.
При этом полноценные умения должны являться
дидактической целью не отдельных задач, а
тщательно продуманной их системы. В самом
широком смысле под системой понимается
совокупность взаимосвязанных взаимодействующих
элементов, обладающая целостностью и устойчивой
структурой.
Рассмотрим методику обучения
учащихся составлению уравнения касательной к
графику функции. По существу, все задачи на
отыскание уравнения касательной сводятся к
необходимости отбора из множества (пучка,
семейства) прямых тех из них, которые
удовлетворяют определенному требованию
– являются касательными к графику некоторой
функции. При этом множество прямых, из которого
осуществляется отбор, может быть задано двумя
способами:
а) точкой, лежащей на
плоскости xOy (центральный пучок прямых);
б) угловым коэффициентом (параллельный пучок
прямых).
В связи с этим при изучении
темы «Касательная к графику функции» с целью
вычленения элементов системы нами были выделены
два типа задач:
1) задачи на касательную,
заданную точкой, через которую она проходит;
2) задачи на касательную, заданную ее угловым
коэффициентом.
Обучение решению задач на
касательную осуществлялось при помощи
алгоритма, предложенного А.Г. Мордковичем [2].
Его принципиальное отличие от уже известных
заключается в том, что абсцисса точки касания
обозначается буквой a (вместо x0), в связи с чем
уравнение касательной приобретает вид
y = f(a) + f ‘(a)(x – a)
(сравните с y = f(x0) + f ‘(x0)(x
– x0)). Этот методический прием, на наш
взгляд, позволяет учащимся быстрее и легче
осознать, где в общем уравнении касательной
записаны координаты текущей точки, а где
– точки касания.
Алгоритм
составления уравнения касательной к графику
функции y = f(x)
1. Обозначить буквой a
абсциссу точки касания.
2. Найти f(a).
3. Найти f ‘(x) и f ‘(a).
4. Подставить найденные числа a, f(a), f ‘(a) в
общее уравнение касательной y = f(a) = f ‘(a)(x – a).
Этот алгоритм может быть
составлен на основе самостоятельного выделения
учащимися операций и последовательности их
выполнения.
Практика показала, что
последовательное решение каждой из ключевых
задач при помощи алгоритма позволяет
формировать умения написания уравнения
касательной к графику функции поэтапно, а шаги
алгоритма служат опорными пунктами действий.
Данный подход соответствует теории поэтапного
формирования умственных действий, разработанной
П.Я. Гальпериным и Н.Ф. Талызиной [3].
В первом типе задач были
выделены две ключевые задачи:
- касательная проходит через
точку, лежащую на кривой (задача 1); - касательная проходит через
точку, не лежащую на кривой (задача 2).
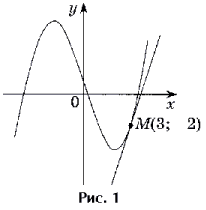
касательной к графику функции в точке M(3; – 2).
Решение. Точка M(3; – 2)
является точкой касания, так как
1. a = 3 – абсцисса точки
касания.
2. f(3) = – 2.
3. f ‘(x) = x2 – 4, f ‘(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – уравнение
касательной.
Задача 2. Напишите уравнения
всех касательных к графику функции y = – x2
– 4x + 2, проходящих через точку M(– 3; 6).
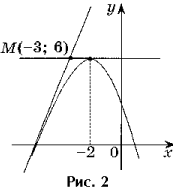
является точкой касания, так как f(– 3) 6 (рис. 2).
1. a – абсцисса точки
касания.
2. f(a) = – a2 – 4a + 2.
3. f ‘(x) = – 2x – 4, f ‘(a) = – 2a – 4.
4. y = – a2 – 4a + 2 – 2(a + 2)(x – a)
– уравнение касательной.
Касательная проходит через
точку M(– 3; 6), следовательно, ее координаты
удовлетворяют уравнению касательной.
6 = – a2 – 4a + 2 – 2(a +
2)(– 3 – a),
a2 + 6a + 8 = 0 ^ a1 = – 4, a2 = – 2.
Если a = – 4, то уравнение
касательной имеет вид y = 4x + 18.
Если a = – 2, то уравнение
касательной имеет вид y = 6.
Во втором типе ключевыми
задачами будут следующие:
- касательная параллельна
некоторой прямой (задача 3); - касательная проходит под
некоторым углом к данной прямой (задача 4).
Задача 3. Напишите уравнения
всех касательных к графику функции y = x3 – 3x2
+ 3, параллельных прямой y = 9x + 1.
Решение.
1. a – абсцисса точки
касания.
2. f(a) = a3 – 3a2 + 3.
3. f ‘(x) = 3x2 – 6x, f ‘(a) = 3a2 – 6a.
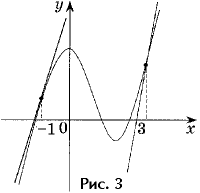
(условие параллельности). Значит, надо решить
уравнение 3a2 – 6a = 9. Его корни a = – 1, a = 3
(рис. 3).
4. 1) a = – 1;
2) f(– 1) = – 1;
3) f ‘(– 1) = 9;
4) y = – 1 + 9(x + 1);
y = 9x + 8 – уравнение
касательной;
1) a = 3;
2) f(3) = 3;
3) f ‘(3) = 9;
4) y = 3 + 9(x – 3);
y = 9x – 24 – уравнение
касательной.
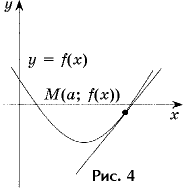
касательной к графику функции y = 0,5x2 – 3x + 1,
проходящей под углом 45° к прямой y = 0 (рис. 4).
Решение. Из условия f ‘(a) =
tg 45° найдем a: a – 3 = 1 ^ a = 4.
1. a = 4 – абсцисса точки
касания.
2. f(4) = 8 – 12 + 1 = – 3.
3. f ‘(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).
y = x – 7 – уравнение
касательной.
Несложно показать, что
решение любой другой задачи сводится к решению
одной или нескольких ключевых задач. Рассмотрим
в качестве примера следующие две задачи.
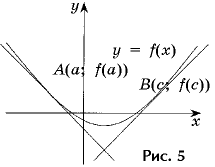
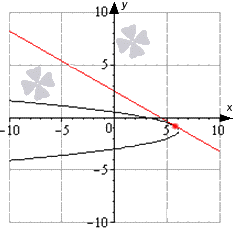
касательных к параболе y = 2x2 – 5x – 2, если
касательные пересекаются под прямым углом и одна
из них касается параболы в точке с абсциссой 3
(рис. 5).
Решение. Поскольку дана
абсцисса точки касания, то первая часть решения
сводится к ключевой задаче 1.
1. a = 3 – абсцисса точки
касания одной из сторон прямого угла.
2. f(3) = 1.
3. f ‘(x) = 4x – 5, f ‘(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – уравнение первой
касательной.
Пусть a – угол наклона первой
касательной. Так как касательные
перпендикулярны, то – угол наклона второй касательной. Из
уравнения y = 7x – 20 первой касательной имеем tg a = 7. Найдем
Это значит, что угловой
коэффициент второй касательной равен .
Дальнейшее решение сводится к
ключевой задаче 3.
Пусть B(c; f(c)) есть точка
касания второй прямой, тогда
1.
– абсцисса второй точки касания.
2.
3.
4.
– уравнение
второй касательной.
Примечание. Угловой
коэффициент касательной может быть найден проще,
если учащимся известно соотношение
коэффициентов перпендикулярных прямых k1•k2
= – 1.
2. Напишите уравнения всех
общих касательных к графикам функций
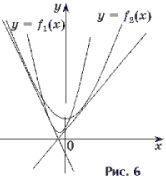
отысканию абсцисс точек касания общих
касательных, то есть к решению ключевой задачи 1 в
общем виде, составлению системы уравнений и
последующему ее решению (рис. 6).
1. Пусть a – абсцисса
точки касания, лежащей на графике функции y = x2
+ x + 1.
2. f(a) = a2 + a + 1.
3. f ‘(a) = 2a + 1.
4. y = a2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a2.
1. Пусть c – абсцисса
точки касания, лежащей на графике функции
2.
3. f ‘(c) = c.
4.
Так как касательные общие, то
Итак, y = x + 1 и y = – 3x – 3
– общие касательные.
Основная цель рассмотренных
задач – подготовить учащихся к
самостоятельному распознаванию типа ключевой
задачи при решении более сложных задач,
требующих определенных исследовательских
умений (умения анализировать, сравнивать,
обобщать, выдвигать гипотезу и т. д.). К числу
таких задач можно отнести любую задачу, в которую
ключевая задача входит как составляющая.
Рассмотрим в качестве примера задачу (обратную
задаче 1) на нахождение функции по семейству ее
касательных.
3. При каких b и c прямые y = x и
y = – 2x являются касательными к графику функции
y = x2 + bx + c?
Решение.
Пусть t – абсцисса точки
касания прямой y = x с параболой y = x2 + bx + c; p
– абсцисса точки касания прямой y = – 2x с
параболой y = x2 + bx + c. Тогда уравнение
касательной y = x примет вид y = (2t + b)x + c – t2, а
уравнение касательной y = – 2x примет вид y = (2p +
b)x + c – p2.
Составим и решим систему
уравнений
Ответ:
Задачи для
самостоятельного решения
1. Напишите уравнения
касательных, проведенных к графику функции y = 2x2
– 4x + 3 в точках пересечения графика с прямой y = x +
3.
Ответ: y = – 4x + 3, y = 6x – 9,5.
2. При каких значениях a
касательная, проведенная к графику функции y = x2
– ax в точке графика с абсциссой x0 = 1,
проходит через точку M(2; 3)?
Ответ: a = 0,5.
3. При каких значениях p
прямая y = px – 5 касается кривой y = 3x2 – 4x – 2?
Ответ: p1 = – 10, p2
= 2.
4. Найдите все общие точки
графика функции y = 3x – x3 и касательной,
проведенной к этому графику через точку P(0; 16).
Ответ: A(2; – 2), B(– 4; 52).
5. Найдите кратчайшее
расстояние между параболой y = x2 + 6x + 10 и
прямой
Ответ:
6. На кривой y = x2 – x + 1
найдите точку, в которой касательная к графику
параллельна прямой y – 3x + 1 = 0.
Ответ: M(2; 3).
7. Напишите уравнение
касательной к графику функции y = x2 + 2x –
| 4x |, которая касается его в двух точках.
Сделайте чертеж.
Ответ: y = 2x – 4.
8. Докажите, что прямая y = 2x
– 1 не пересекает кривую y = x4 + 3x2 + 2x.
Найдите расстояние между их ближайшими точками.
Ответ:
9. На параболе y = x2
взяты две точки с абсциссами x1 = 1, x2 = 3.
Через эти точки проведена секущая. В какой точке
параболы касательная к ней будет параллельна
проведенной секущей? Напишите уравнения секущей
и касательной.
Ответ: y = 4x – 3 – уравнение
секущей; y = 4x – 4 – уравнение касательной.
10. Найдите угол q между касательными
к графику функции y = x3 – 4x2 + 3x + 1,
проведенными в точках с абсциссами 0 и 1.
Ответ: q = 45°.
11. В каких точках
касательная к графику функции образует с осью Ox угол в 135°?
Ответ: A(0; – 1), B(4; 3).
12. В точке A(1; 8) к кривой 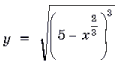
касательная. Найдите длину отрезка касательной,
заключенного между осями координат.
Ответ:
13. Напишите уравнение всех
общих касательных к графикам функций y = x2 –
x + 1 и y = 2x2 – x + 0,5.
Ответ: y = – 3x и y = x.
14. Найдите расстояние между
касательными к графику функции параллельными оси абсцисс.
Ответ:
15. Определите, под какими
углами парабола y = x2 + 2x – 8 пересекает ось
абсцисс.
Ответ: q1 = arctg 6, q2 = arctg (– 6).
16. На графике функции найдите все
точки, касательная в каждой из которых к этому
графику пересекает положительные полуоси
координат, отсекая от них равные отрезки.
Ответ: A(– 3; 11).
17. Прямая y = 2x + 7 и парабола y
= x2 – 1 пересекаются в точках M и N. Найдите
точку K пересечения прямых, касающихся параболы в
точках M и N.
Ответ: K(1; – 9).
18. При каких значениях b
прямая y = 9x + b является касательной к графику
функции y = x3 – 3x + 15?
Ответ: – 1; 31.
19. При каких значениях k
прямая y = kx – 10 имеет только одну общую точку с
графиком функции y = 2x2 + 3x – 2? Для найденных
значений k определите координаты точки.
Ответ: k1 = – 5, A(– 2;
0); k2 = 11, B(2; 12).
20. При каких значениях b
касательная, проведенная к графику функции y = bx3
– 2x2 – 4 в точке с абсциссой x0 = 2,
проходит через точку M(1; 8)?
Ответ: b = – 3.
21. Парабола с вершиной на
оси Ox касается прямой, проходящей через точки A(1;
2) и B(2; 4), в точке B. Найдите уравнение параболы.
Ответ:
22. При каком значении
коэффициента k парабола y = x2 + kx + 1 касается
оси Ox?
Ответ: k = д 2.
23. Найдите углы между
прямой y = x + 2 и кривой y = 2x2 + 4x – 3.
Ответ:
24. Определите, под какими
углами пересекаются графики функций y = 2x2 +
3x – 3 и y = x2 + 2x + 3.
Ответ:
25. При каком значении k угол
между кривыми y = x2 + 2x + k и y = x2 + 4x + 4
будет равен 45°?
Ответ: k = – 3.
26. Найдите все значения x0,
при каждом из которых касательные к графикам
функции y = 5cos 3x + 2 и y = 3cos 5x в точках в
абсциссой x0 параллельны.
Ответ:
27. Под каким углом видна
окружность x2 + y2 = 16 из точки (8; 0)?
Ответ:
28. Найдите геометрическое
место точек, из которых парабола y = x2 видна
под прямым углом?
Ответ: прямая
29. Найдите расстояние между
касательными к графику функции образующими с
положительным направлением оси Ox угол 45°.
Ответ:
30. Найдите геометрическое
место вершин всех парабол вида y = x2 + ax + b,
касающихся прямой y = 4x – 1.
Ответ: прямая y = 4x + 3.
Литература
1. Звавич Л.И., Шляпочник Л.Я.,
Чинкина М.В. Алгебра и начала анализа: 3600 задач
для школьников и поступающих в вузы. – М., Дрофа,
1999.
2. Мордкович А. Семинар четвертый для молодых
учителей. Тема «Приложения производной». – М.,
«Математика», № 21/94.
3. Формирование знаний и умений на основе
теории поэтапного усвоения умственных действий.
/ Под ред. П.Я. Гальперина, Н.Ф. Талызиной.
– М., МГУ, 1968.

![Rendered by QuickLaTeX.com [ begin{cases} y_0=ax_0^2 \ y_0 = kx_0 + b end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-81c3b8b33bf77426c6a92221ff2a65ff_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} y_0 = ax_0^2+bx_0+c \ y_0 = kx_0+d end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8176337792ada69638b8aeac2cbe1cf9_l3.png)