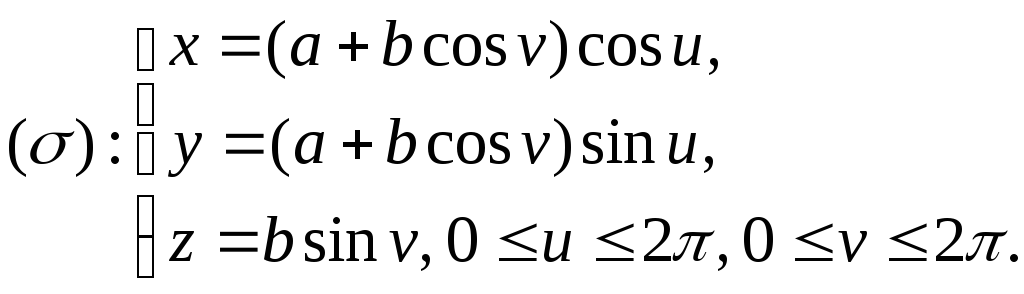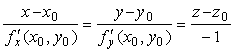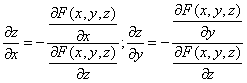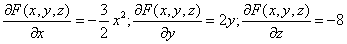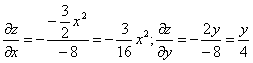Задача 22350 3. Составить уравнение касательной…
Условие
3. Составить уравнение касательной плоскости к сфере (x-1)^2+(y+2)^2+(z-2)^2=27 в точке M0(2;-1;-3).
математика ВУЗ
15828
Решение
★
Точка M0(2;–1;–3) принадлежит сфере, так как ее координаты удовлетворяют уравнению сферы
(2–1)^2+(-1+2)^2+(-3–2)^2=27,
1+1+25=27 – верно.
R=sqrt(27)=3sqrt(3)
C(1;-2;2)- центр сферы.
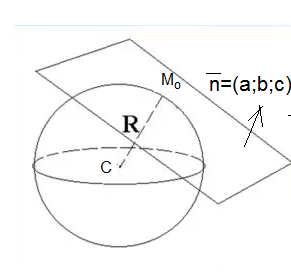
Касательная плоскость перпендикулярна радиусу, проведенному в точку касания.
Значит вектор vector{СM} – нормальный вектор касательной плоскости.
vector{СM} =(2-1;-1-(-2);-3-2)=(1;1;-5)
Уравнение плоскости с нормальным вектором vector{n}=(a;b;c) и проходящей через точку М_(о)(x_(o);y_(o);z_(o)) имеет вид
a*(x-x_(o))+b*(y-y_(o))+c*(z-z_(o))=0
1*(x-2)+1*(y+1)-5*(z+3)=0
x+y-5z-16=0
О т в е т. x+y-5z-16=0
Написать комментарий
На этом уроке мы более подробно рассмотрим
случай взаимного расположения сферы и плоскости, когда расстояние от центра
сферы до плоскости равно радиусу сферы. Сформулируем и докажем свойство и
признак касательной плоскости к сфере. А также поговорим о прямой касательной к
сфере.
Прежде чем приступить к рассмотрению данной
темы, давайте вспомним, что такое сфера.
Итак, сферой называется поверхность, состоящая из всех точек
пространства, расположенных на данном расстоянии от данной точки. Причём, данная
точка называется центром сферы, а данное расстояние – радиусом
сферы.
Также вы уже знаете, что в зависимости от
соотношения расстояния от центра сферы до плоскости и радиуса сферы возможны
три случая взаимного расположения сферы и плоскости в пространстве.
Сфера и плоскость могут:
1) пересекаться по окружности. Случай, когда
расстояние от центра сферы до плоскости меньше радиуса сферы.
Тогда сечение сферы плоскостью есть
окружность;
2) не пересекаться. Случай, когда расстояние
от центра сферы до плоскости больше радиуса сферы.
Тогда сфера и плоскость не имеют общих точек.
3) и иметь только одну общую точку. Случай,
когда расстояние от центра сферы до плоскости равно радиусу сферы.
Давайте более подробно остановимся на последнем
случае, когда сфера и плоскость имеют только одну общую точку.
Определение:
Плоскость, имеющая со сферой только одну общую
точку, называется касательной плоскостью к сфере, а их общая
точка называется точкой касания плоскости и сферы.
На экране вы видите сферу с центром в точке О
и плоскость . Эта
плоскость является касательной плоскостью к сфере, а точка А – есть точка
касания.
Касательной плоскостью к шару
называется касательная плоскость к сфере, которая является границей этого шара.
Вообще касательная плоскость к сфере обладает
свойством, аналогичным свойству касательной к окружности.
Это свойство выражается в следующей теореме:
Итак, теорема или свойство касательной
плоскости к сфере: радиус сферы, проведённый в точку касания сферы и
плоскости, перпендикулярен к касательной плоскости.
Доказательство: плоскость касается
сферы с центром в точке
. Докажем,
что .
По определению касательной плоскости точка А
будет единственной общей точкой плоскости и сферы.
Другие точки плоскости лежат вне сферы. Следовательно, они расположены дальше
от центра сферы.
Тогда ОА – это кратчайшее расстояние от точки
до плоскости. Напомним, что кратчайшее расстояние измеряется длиной
перпендикуляра. Значит, перпендикуляр .
Следовательно, радиус . Теорема
доказана.
Справедлива и обратная теорема (признак
касательной плоскости к сфере).
Сформулируем и докажем её.
Итак, обратная теорема или признак
касательной плоскости к сферы: если радиус сферы перпендикулярен к
плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость
является касательной к сфере.
Доказательство: из условия теоремы вытекает,
что данный радиус является перпендикуляром, проведённым из центра сферы к
данной плоскости.
Поэтому расстояние от центра сферы до плоскости
равно радиусу сферы , и,
следовательно, сфера и плоскость имеют только одну общую точку. По определению
такая плоскость является касательной к сфере. Значит, плоскость – есть
касательная плоскость к сфере. Что и требовалось доказать.
Задача: диаметр шара равен см. На
каком расстоянии от центра шара находится плоскость, касающаяся его?
Решение: напомним, что
касательной плоскостью к шару называется касательная плоскость к сфере, которая
является границей этого шара. Плоскость, имеющая со сферой только одну общую
точку, называется касательной плоскостью к сфере, а их общая точка называется
точкой касания плоскости и сферы.
По свойству касательной плоскости к сфере:
радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к
касательной плоскости .
Радиус нашего шара и будет расстоянием от
центра шара до точки касания с плоскостью .
Так как по условию задачи диаметр шара равен
18 см, то радиус равен (см). Запишем
ответ.
Задача: сфера касается плоскости
равностороннего треугольника с высотой см в его
центре. Расстояние от центра сферы до стороны треугольника равно см.
Найдите радиус сферы.
Решение: так как по условию
задачи треугольник равносторонний, то его центр будет находиться в центре
вписанной и описанной окружностей.
Напомним, что в равностороннем треугольнике
высота является и биссектрисой, и медианой. А по свойству медиан треугольника:
три медианы треугольника пересекаются в одной точке, являющейся центром тяжести
треугольника. Эта точка делит каждую медиану в отношении , считая от
вершины.
Так как по условию задачи высота треугольника
равна 12 см, а она же является и медианой, значит, расстояние (см).
Рассмотрим . Он
прямоугольный, так как . А по
свойству касательной плоскости к сфере: радиус сферы, проведённый в точку
касания сферы и плоскости, перпендикулярен к касательной плоскости.
Применим теорему Пифагора и найдем чему равен
катет . Получаем,
что (см). Не
забудем записать ответ.
Определение:
Прямая, лежащая в касательной плоскости сферы
и проходящая через точку касания, называется касательной прямой к
сфере.
По определению касательная плоскость имеет со
сферой только одну общую точку, следовательно, касательная прямая также имеет
со сферой только одну общую точку – точку касания.
На экране вы видите сферу с центром в точке О
и прямые ,
и
, лежащие в
плоскости . Прямые
,
и
являются касательными прямыми к сфере, а точка А – есть
точка касания.
Для касательной прямой в сфере также
справедливы следующие утверждения:
Радиус, проведённый в точку касания прямой и
сферы, перпендикулярен к касательной прямой.
Прямая, перпендикулярная радиусу сферы в
конечной его точке на сфере, является касательной к сфере.
А теперь давайте рассмотрим две касательные
прямые к сфере с центром О, проходящие через точку А и касающиеся сферы в
точках В и С.
Отрезки и
– отрезки
касательных, проведёнными из точки .
Они обладают следующим свойством: отрезки
касательных к сфере, проведенные из одной точки, равны и составляют равные углы
с прямой, проходящей через эту точку и центр сферы.
Это легко увидеть из равенства прямоугольных
треугольников . У этих
треугольников гипотенуза общая,
а катеты .
Задача: расстояние от точки до центра
сферы с
радиусом см равно
. Найдите
расстояние от данной точки до точки касания
прямой и сферы.
Решение: соединим точку А, точку
касания, с центром сферы.
Отрезок . Напомним,
что радиус, проведённый в точку касания прямой и сферы, перпендикулярен к
касательной прямой.
Рассмотрим . Он
прямоугольный. Применяя теорему Пифагора найдём чему равен катет , который и
является расстоянием от точки до точки А.
Имеем, (см).
Итоги:
На этом уроке мы более подробно рассмотрели
случай взаимного расположения сферы и плоскости, когда расстояние от центра
сферы до плоскости равно радиусу сферы. Узнали, что плоскость, имеющая со
сферой только одну общую точку, называется касательной плоскостью к сфере, а их
общая точка называется точкой касания плоскости и сферы. Сформулировали и
доказали свойство и признак касательной плоскости. А также узнали, что прямая,
лежащая в касательной плоскости сферы и проходящая через точку касания,
называется касательной прямой к сфере.
Геометрия, 11 класс
Урок №8. Сфера и шар
Перечень вопросов, рассматриваемых в теме:
- что такое сфера, какие у неё есть элементы (центр, радиус, диаметр сферы);
- что такое шар и его элементы;
- уравнение сферы;
- формула для нахождения площади поверхности сферы;
- взаимное расположение сферы и плоскости;
- теорема о радиусе сферы, который проведён в точку касания и теорему обратную данной.
Глоссарий по теме:
Определение
Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.
Определение
Круг – это часть плоскости, ограниченная окружностью.
Определение
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.
Определение
Тело, ограниченное сферой, называется шаром.
Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.
Уравнение сферы

Определение
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.
Определение
Сегмент шара – это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Определение
Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.
Основная литература:
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.
Дополнительная литература:
Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177
Теоретический материал для самостоятельного изучения
1. Основные теоретические факты
По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.
Рисунок 1 – Сфера с центром в точке О и радиусом R
Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.
Определение
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.
Определение
Тело, ограниченное сферой, называется шаром.
Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.
Сферу можно получить ещё одним способом – вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.
2. Уравнение сферы
Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.
Пусть сфера имеет центром точку С (x0; y0; z0) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:
МС=
Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС2=R2, то есть координаты точки М удовлетворяют уравнению:

Это выражение называют уравнением сферы радиуса R и центром С(x0; y0; z0).
3. Взаимное расположение сферы и плоскости
Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.
1. Пусть d
2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.
3. Пусть d
Рассмотрим случай касания более подробно.
Определение
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.
Теорема (свойство касательной плоскости).
Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Теорема (признак касательной плоскости):
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.
4. Основные формулы
Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:

Формула для вычисления площади поверхности сферы и ее элементов:
S=4πR2 – площадь сферы.
S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

Примеры и разбор решения заданий тренировочного модуля
1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.
Решение:
Площадь круга вычисляется по формуле: Sкр=πR2.
Площадь поверхности шара вычисляется по формуле: Sсф=4πR2. Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.
Ответ: 36
2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.
Решение:
Площадь сферы равна Sсф=4πR2. То есть Sсф=100π.
По условию площадь круга некоторого радиуса r также равна 100π. Значит, r2 =100, то есть r=10.
Ответ: 10.
3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15
Решение:
Окружность, вписанная в треугольник, является сечением сферы.
Найдем ее радиус.
Площадь треугольника с известными сторонами можно вычислить по формуле Герона:

p=0,5(AB+BC+AC)=21

S=84.
С другой стороны, S=p·r.
Отсюда r=4.
Теперь найдем расстояние от центра шара до секущей плоскости.
Используем соотношение:



h=3.
Ответ: 3.
4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.
Решение:
Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.
Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.
По условию задачи R=10.
Используем соотношение:



h=6.
Ответ: 6.
– 181–
Тема поверхностные интегралы
§1. Параметрическое задание поверхности
Линию на плоскости
можно задавать явно (
– парабола), неявно (
– лемниската
Бернулли)
и параметрически
– эллипс). Для поверхностей в пространстве
мы знакомы с явным заданием– параболоид вращения) и неявным заданием
– коническая поверхность). Осталось
познакомиться ещё с одним способом –
параметрическим.
Сразу заметим,
что система трёх однопараметрических
уравнений
задаёт в пространстве
некоторую линию
Для такого задания линии удобно
использовать векторную форму записи,
а именно: линиясостоит из тех точек
радиус-векторы которых имеют вид
(Подробнее об этом
смотри «Математический анализ, ч.1»,
тема «Функции нескольких переменных»).
Для параметрического
задания поверхности необходимы два
параметра. Пусть на плоскости с декартовой
прямоугольной системой координат в некоторой области
заданы три функции
Другими словами,
каждой точке
поставлена в соответствие тройка чисел
,
которые
естественно понимать как координаты
точки пространства
Множество всех таких точек, и есть
некоторая поверхность:

Здесь также удобна
векторная форма записи: поверхность состоит из точек
радиус-векторы которых задаются
вектор-функцией двух переменных
.
Замечание
1. Исключая
из параметрических уравнений оба
параметра, можно получить неявное
уравнение поверхности и тем самым
идентифицировать поверхность.
Пример 1.
Уравнения

определяют сферу
.
Пример
2. Уравнения
определяют
коническую поверхность
Пример
3. Пусть в
плоскости
дана окружность
с центром в точке
,
причёмПри вращении этой окружности вокруг
осиполучается поверхность, называемая
тором.
Выведем параметрические
уравнения тора. Пусть
– текущая точка тора. В качестве
параметров возьмём два угла:– угол между
и плоскостью
,
– угол между
и осью
,
где
Обозначим
Тогда
а
кроме
того
Окончательно имеем
для тора:
Пример 4.
Уравнения
определяют т.н.
геликоид (прямой), т.е. поверхность,
описываемую прямой
,
которая вращается вокруг осии одновременно перемещается вдоль этой
оси, причем,
скорости вращения и перемещения
постоянные, в начальный моментсовпадает с
Замечание
2. Явное
задание поверхности
является частным случаем параметрического:
В параметрических
уравнениях (1) зафиксируем значение
одного из параметров: пусть, например,
Получим систему однопараметрических
уравнений
определяющую
некоторую линию
,
которая называется координатной линией.
Меняя значение,
получим целое семейство таких линий.
Аналогично можно получить ещё одно
семейство координатных линий:
Через каждую точку
(за исключением некоторых точек, таких,
как полюса сферы или вершина конуса)
проходит по одной линии каждого семейства
координатных линий. Соответствующие
значения параметров называются
криволинейными координатами точки
поверхности.
Для сферы (2)
координатные линии – это параллели ()
и меридианы ().
§2. Касательная плоскость к поверхности, заданной параметрически
Напомним, что
направляющий вектор касательной к линии
имеет вид .
Здесь
– значение параметра, которое соответствует
точке касания.
Далее, касательная
линия к поверхности – это касательная
к линии, лежащей на поверхности, а
касательная плоскость – это плоскость,
в которой лежат все касательные прямые
(Подробно обо всём этом смотри
«Математический анализ, ч.1», тема
«Функции нескольких переменных», §8 и
§9).
Что касается
нормального вектора касательной
плоскости к поверхности
можно рассуждать
таким образом. Через точку
проходят две координатные линии:
и .
Их векторные уравнения:
Направляющие
векторы касательных к этим линиям
и
соответственно. Векторное произведение
этих векторов
можно взять в
качестве нормального вектора касательной
плоскости. Зная точку касания ,
криволинейные координаты которой ,
и нормальный вектор ,
нетрудно написать уравнение касательной
плоскости
Можно написать
готовую формулу касательной плоскости
(без вычисления вектора ),
если воспользоваться общим приёмом.
Берём текущую точку касательной плоскости
и
рассматриваем три вектора: ,
и .
Они компланарны и, следовательно, их
смешанное произведение равно нулю.
Отсюда получаем уравнение касательной
плоскости
Здесь производные
функций
вычисляются при значениях параметров
и ,
которые соответствуют точке касания
.
Пример.
Составить уравнения касательной
плоскости к винтовой поверхности
в токе ,
криволинейные координаты которой .
Решение.
Находим частные производные функций
и подставляем в соответствующую формулу:

Разлагаем
определитель по 1й
строке:
.
Оставим в левой
части уравнения только члены, содержащие
текущие координаты
и разделим обе части уравнения на :
Соседние файлы в папке Лекции по мат.анализу
- #
- #
- #
- #
- #
- #
- #
- #
Касательная плоскость и нормаль к поверхности
Касательной плоскостью к поверхности σ в её точке М0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М0.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M0(x0,y0,z0) имеет вид:
Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M0(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z0 = f’x(x0,y0,z0)(x — x0) + f’y(x0,y0,z0)(y — y0)
По условию задачи x0 = 0 , y0 = 1 , тогда z0 = 5
Найдем частные производные функции z = x^3+5*y :
f’x(x,y) = (x 3 +5•y)’x = 3•x 2
f’x(x,y) = (x 3 +5•y)’y = 5
В точке М0(0,1) значения частных производных:
f’x(0;1) = 0
f’y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0
Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M0(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:
Для нашей функции:
Тогда:
В точке М0(1,0,1) значения частных производных:
f’x(1;0;1) = -3 /16
f’y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z — 1 = -3 /16(x — 1) + 0(y — 0) или 3 /16•x+z- 19 /16 = 0
Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
fx’(x, y) = (y/x + xy – 5x 3 )’x = – y/x 2 + y – 15x 2 ;
fy’ (x, y) = (y/x + xy – 5x 3 )’y = 1/x + x.
Точка М0(x0, y0, z0) принадлежит поверхности σ, поэтому можно вычислить z0, подставив заданные x0 = –1 и y0 = 2 в уравнение поверхности:
Пример №1 . Дана функция z=f(x,y) и две точки А(х0, y0) и В(х1,y1). Требуется: 1) вычислить значение z1 функции в точке В; 2) вычислить приближенное значение z1 функции в точке В исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x0,y0,z0).
Решение.
Запишем уравнения касательной в общем виде:
z — z0 = f’x(x0,y0,z0)(x — x0) + f’y(x0,y0,z0)(y — y0)
По условию задачи x0 = 1, y0 = 2, тогда z0 = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’x(x,y) = (x 2 +3•x•y•+y 2 )’x = 2•x+3•y 3
f’x(x,y) = (x 2 +3•x•y•+y 2 )’y = 9•x•y 2
В точке М0(1,2) значения частных производных:
f’x(1;2) = 26
f’y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0
Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение
Касательная плоскость и нормаль к поверхности.
Пусть поверхность задана в неявном виде: $F(x,y,z)=0$ и пусть точка $M_0(x_0,y_0,z_0)$ принадлежит данной поверхности. Тогда уравнение касательной плоскости к этой поверхности в точке $M_0$ таково:
Уравнение нормали имеет вид:
Если же уравнение поверхности задано в явном виде $z=f(x,y)$, то уравнение касательной плоскости имеет вид:
Уравнение нормали в случае явного задания поверхности таково:
Примечание (желательное для более полного понимания текста): показатьскрыть
Формулы (3) и (4) легко получить из формул (1) и (2). Если $z=f(x,y)$, то перенося $z$ в правую часть равенства получим: $f(x,y)-z=0$. Обозначая $F(x,y,z)=f(x,y)-z$, получим: $F_^<‘>=left(f(x,y)-zright)_^<‘>=f_^<‘>(x,y)-0=f_^<‘>(x,y)$. Аналогично и $F_^<‘>=left(f(x,y)-zright)_^<‘>=f_^<‘>(x,y)-0=f_^<‘>(x,y)$. Что же касается последней производной (т.е. производной по переменной $z$), то тут нужно учесть, что выражение $f(x,y)$ не содержит $z$, поэтому: $F_^<‘>=left(f(x,y)-zright)_^<‘>=0-1=-1$. Подставляя в формулы (1) и (2) вместо $F_^<‘>$, $F_^<‘>$, $F_^<‘>$ соответственно $f_^<‘>$, $f_^<‘>$ и $-1$ и получим формулы (3) и (4).
Найти уравнение касательной плоскости и нормали к поверхности $z=3x^2y^4-6xy^3+5x-4y+10$ в точке $M_0(-2;1;20)$.
Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$, $y_0$, $z_0$ (координаты точки $M_0$) в нашем случае таковы: $x_0=-2$, $y_0=1$, $z_0=20$. Но перед тем, как переходить к решению, осуществим небольшую проверку. Убедимся, что точка $M_0$ действительно лежит на заданной поверхности. Эта проверка не является обязательной, но желательна, ибо ошибка в условиях подобных задач – дело вовсе не редкое. Подставим $x=x_0$, $y=y_0$ в уравнение нашей поверхности и убедимся, что $z_0$ действительно равно 20:
$$ z_0=3x_<0>^<2>y_<0>^<4>-6x_0y_<0>^<3>+5x_0-4y_0+10=3cdot (-2)^2cdot 1^4-6cdot (-2)cdot 1^3-4cdot 1+10=12+12-4=20. $$
Проверка пройдена, точка $M_0$ действительно лежит на заданной поверхности. Теперь найдём частные производные, т.е. $z_^<‘>$ и $z_^<‘>$:
Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ в выражения частных производных:
Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_^ <‘>left(x_0, y_0right)=-13$, $z_^ <‘>left(x_0, y_0right)=80$ в формулу (3) получим уравнение касательной плоскости:
Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_^ <‘>left(x_0, y_0right)=-13$, $z_^ <‘>left(x_0, y_0right)=80$ в формулу (4) получим уравнение нормали:
Ответ: Касательная плоскость: $-13x+80y-z-86=0$; нормаль: $frac<-13>=frac<80>=frac<-1>$.
Найти уравнение касательной плоскости и нормали к поверхности $z=5sqrt-2xy-39$ в точке $M_0(3;-4;z_0)$.
Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=3$, $y_0=-4$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:
Теперь, как и в предыдущем примере, перейдём к нахождению частных производных $z_^<‘>$ и $z_^<‘>$. После того, как мы найдём эти производные в общем виде, укажем их значения при $x=x_0$ и $y=y_0$:
Подставляя $x_0=3$, $y_0=-4$, $z_0=10$, $z_^ <‘>left(x_0, y_0right)=11$, $z_^ <‘>left(x_0, y_0right)=-10$ в формулы (3) и (4) получим уравнения касательной плоскости и нормали:
Ответ: Касательная плоскость: $11x-10y-z-63=0$; нормаль: $frac<11>=frac<-10>=frac<-1>$.
Найти уравнение касательной плоскости и нормали к поверхности $3xy^2z+5xy+z^2=10xz-2y+1$ в точке $M_0(1;-2;3)$.
Перенесём все слагаемые в левую часть равенства и обозначим полученное в левой части выражение как $F(x,y,z)$:
Используем формулы (1) и (2). Значения $x_0$, $y_0$ и $z_0$ как и ранее обозначают координаты точки $M_0$, т.е. $x_0=1$, $y_0=-2$, $z_0=3$.
Проверим, действительно ли точка $M_0$ лежит на данной поверхности. Для этого подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражение $3xy^2z+5xy+z^2-10xz+2y-1$ и выясним, равен ли нулю полученный результат:
Итак, точка $M_0$ действительно лежит на данной поверхности. Естественно, что данная проверка не является обязательной, но она крайне желательна. Перейдём к дальнейшему решению. Нам нужно найти $F_^<‘>$, $F_^<‘>$ и $F_^<‘>$:
Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражения частных производных:
Подставляя $x_0=1$, $y_0=-2$, $z_0=3$, $F_^ <‘>left(M_0right)=-4$, $F_^ <‘>left(M_0right)=-29$ и $F_^ <‘>left(M_0right)=8$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:
Ответ: Касательная плоскость: $-4x-29y+8z-78=0$; нормаль: $frac<-4>=frac<-29>=frac<8>$.
Найти уравнение касательной плоскости и нормали к поверхности $z^3+4xyz=-3x^2+5y+7$ в точке $M_0(0;-3;z_0)$.
Поверхность задана в неявном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (1) и (2). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=0$, $y_0=-3$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:
Перенесём все слагаемые в левую часть равенства:
Обозначим $F(x,y,z)=z^3+4xyz+3x^2-5y-7$ и применим формулы (1) и (2). Найдём частные производные первого порядка $F_^<‘>$, $F_^<‘>$ и $F_^<‘>$. После того, как мы найдём эти производные в общем виде, укажем их значения в точке $M_0$:
Подставляя $x_0=0$, $y_0=-3$, $z_0=-2$, $F_^ <‘>left(M_0right)=-24$, $F_^ <‘>left(M_0right)=-5$ и $F_^ <‘>left(M_0right)=12$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:
Ответ: Касательная плоскость: $-24x-5y+12z+9=0$; нормаль: $frac<-24>=frac<-5>=frac<12>$.
Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Поверхности. Касательная плоскость и нормаль
Краткие теоретические сведения
Способы задания поверхностей
Рассматриваем вектор–функцию двух скалярных аргументов: $$vec=vec(u,v).$$ Годографом такой функции является поверхность.
Запишем четыре способа задания поверхности: 1. Векторное уравнение: $$vec=vec(u,v).$$ 2. Параметрическое уравнение: $$x=x(u,v),,, y=y(u,v),,, z=z(u,v).$$ 3. Неявное уравнение: $$varPhi(x,y,z)=0.$$ 4. Явное уравнение: $$z=z(x,y).$$
Поверхность называется регулярной ($k$ раз дифференцируемой), если у каждой точки этой поверхности есть окрестность, допускающая регулярную параметризацию (то есть функции $x(u,v), y(u,v),z=z(u,v)$ $k$ раз непрерывно дифференцируемы). При $k=1$ поверхность называется гладкой.
Регулярная поверхность в окрестности каждой своей точки допускает бесчисленное множество параметризаций.
Кривая, лежащая на поверхности $vec=vec(u,v)$, задается уравнениями $$ u=u(t),,, v=v(t).$$ Линии $u=mbox$, $v=mbox$ являются координатными линиями данной параметризации поверхности.
Решение задач
Задача 1 (Феденко №544)
Дана поверхность begin x=u+v, ,, y=u-v,,, z=uv. end Проверить, принадлежат ли ей точки $A(4,2,3)$ и $B(1,4,-2)$.
Ответ. Точка $A$ принадлежит, так как ее координаты удовлетворяют системе уравнений, задающих поверхность. Точка $B$ не принадлежит поверхности.
Задача 2 (Феденко № 546)
Найдите неявное уравнение поверхности, заданной параметрическими уравнениями: begin begin x & = x_0 + a,mbox,u,mbox,v, \ y & = y_0 + b,mbox,u,mbox,v, \ z & = z_0 + c,mbox,u. end end
Ответ. Эллипсоид с полуосями $a$, $b$, $c$ и центром в точке $(x_0, y_0, z_0)$: begin frac<(x-x_0)^2>+frac<(y-y_0)^2>+frac<(z-z_0)^2>=1. end
Задача 3 (Феденко №528)
В плоскости $xOz$ задана кривая $x=f(u)$, $z=g(u)$, не пересекающая ось $Oz$. Найдите параметризацию поверхности, полученной при вращении этой кривой вокруг оси $Oz$.
Решение задачи 3
Произвольная точка $M$, принадлежащая кривой и имеющая координаты $x_0=f(u_0)$, $y_0=0$, $z_0=g(u_0)$, движется по окружности с центром на оси $Oz$ и радиусом $R=f(u_0)$ в плоскости, параллельной плоскости $xOy$: $z=g(u_0)$. Поэтому изменение ее координат можно записать следующими уравнениями: begin left< begin x_0 & = & f(u_0),mbox,v, \ y_0 & = & f(u_0),mbox,v, \ z_0 & = & g(u_0). \ end right. end
Поскольку точка $M$ произвольная, уравнение искомой поверхности: begin left< begin x & = & f(u),mbox,v, \ y & = & f(u),mbox,v, \ z & = & g(u). \ end right. end
Касательная плоскость. Нормаль
Краткие теоретические сведения
Пусть $vec=vec(u,v)in C^1$ — поверхность, проходящая через точку $P(u_0, v_0)$. Пусть $u=u(t)$, $v=v(t)$ — уравнения гладкой кривой, проходящей через точку $P(u_0, v_0)$ и лежащей на заданной поверхности.
Пусть точка $P$ не является особой, то есть ранг матрицы begin left( begin x_u & y_u & z_u \ x_v & y_v & z_v \ end right) end в точке $P$ равен $2$ (для особой точки ранг меньше $2$). Если поверхность задана неявно $varPhi(x,y,z)=0$, то в не особой точке $P$ выполняется условие: $varPhi_x^2+varPhi_y^2+varPhi_z^2neq0.$
Касательная к кривой $u=u(t)$, $v=v(t)$ на поверхности $vec=vec(u,v)$ определяется вектором: begin displaystylefrac>
Обозначения:
— $vec=$ — радиус-вектор произвольной точки касательной плоскости.
— $vec=$ — радиус вектор точки $P(u_0, v_0)$.
— Частные производные $x_u$, $y_u$, $z_u$, $x_v$, $y_v$, $z_v$ вычисляются в точке $P(u_0, v_0)$.
Уравнение касательной плоскости:
1. Если поверхность задана векторно, то уравнение касательной плоскости можно записать через смешанное произведение трех линейно зависимых векторов: $$ left(vec-vec, , vec_u, , vec_v right)=0. $$ 2. Если поверхность задана параметрически, запишем определитель: begin left| begin X-x & Y-y & Z-z \ x_u & y_u & z_u\ x_v & y_v & z_v\ end right|=0 end 3. Если поверхность задана неявным уравнением: begin varPhi_x(X-x)+varPhi_y(Y-y)+varPhi_z(Z-z)=0. end 4. В случая явного задания поверхности, уравнение касательной плоскости примет вид: begin (Z-z)=z_x(X-x)+z_y(Y-y). end
Нормалью поверхности в точке $P$ называется прямая, проходящая через $P$ перпендикулярно касательной плоскости в этой точке.
Уравнение нормали:
1.$$ vec=vec + lambdavec, ,, vec=vec_utimesvec_v. $$ 2. begin displaystylefrac< left| begin y_u & z_u\ y_v & z_v\ end right|>= displaystylefrac< left| begin z_u & x_u\ z_v & x_v\ end right|>= displaystylefrac< left| begin x_u & y_u\ x_v & y_v\ end right|>. end 3. begin displaystylefrac<varPhi_x>=displaystylefrac<varPhi_y>=displaystylefrac<varPhi_z>. end 4. begin displaystylefrac=displaystylefrac=displaystylefrac<-1>. end
Решение задач
Задача 1 (Феденко №574)
Дана поверхность begin x=u,mbox,v,,, y=u,mbox,v,,, z=u. end Написать:
а) уравнение касательной плоскости к поверхности;
б] уравнение нормали к поверхности;
в) касательной к линии $u=2$
в точке $Mleft(u=2, v=displaystylefrac<pi><4>right)$ поверхности.
Задача 2
Через точки $A(0,1,0)$ и $B(1,0,0)$ провести плоскость, касательную к поверхности $vec=$.
Ответ. $z=0, -2X-2Y+Z+2=0$.
Задача 3
Построить касательную плоскость к поверхности $y=x^2+z^2$, перпендикулярную вектору $vec<2,1,-1>$.
Задача 4
Через точку $M(1,2,1)$ провести плоскость, касательную к поверхности $x^2+y^2-z^2=0$.
Ответ. $X-Z=0$, $3X-4Y+5Z=0$.
Задача 5 (Феденко №594)
Докажите, что поверхности begin z=mbox(xy), ,, x^2-y^2=a end ортогональны в точках их пересечения.
Решение задачи 5
Запишем направляющие векторы нормалей к поверхностям, проведенным в точках их пересечения: begin begin vec_1&=left<frac<mbox^2(x_0y_0)>,frac<mbox^2(x_0y_0)>,-1right>,\ vec_2&=left<2x_0,-2y_0,0right>. end end Скалярные произведения векторов $n_1$ и $n_2$ равны нулю, следовательно векторы ортогональны. begin n_1cdot n_2=0. end
источники:
http://math1.ru/education/funct_sev_var/tannorm.html
http://vmath.ru/vf5/diffgeom/seminar5