Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Задача.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Решение:
Подставив координаты вершин треугольника в уравнение окружности
получим систему уравнений
Вычтем из первого уравнения системы второе:
Теперь из второго уравнения системы вычтем третье:
Приравняем правые части равенств b=-2a+10 и b=3a-20:
Подставим в первое уравнение системы a=6 и b=-2:
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Как найти уравнение описанной окружности по координатам
Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
получим систему уравнений
Вычтем из первого уравнения системы второе:
Теперь из второго уравнения системы вычтем третье:
Приравняем правые части равенств b=-2a+10 и b=3a-20:
Подставим в первое уравнение системы a=6 и b=-2:
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) |
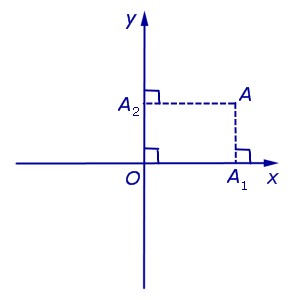
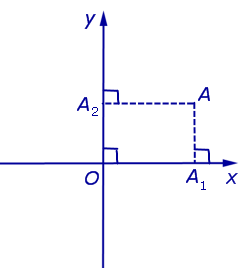
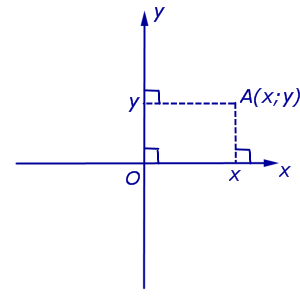
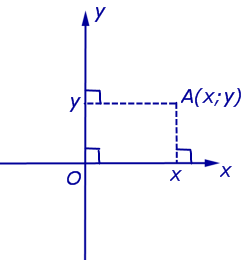
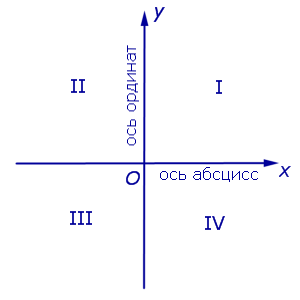
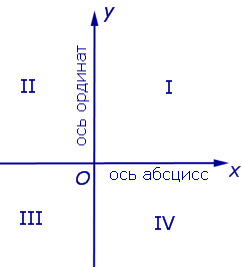
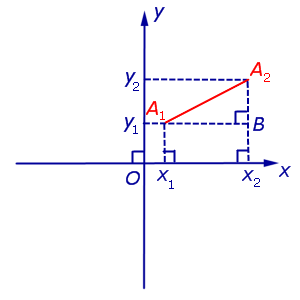
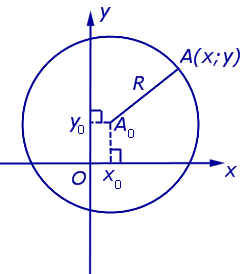
Примечание: дробные числа записывайте Округлять до -го знака после запятой. Декартовы координаты точек плоскости. Уравнение окружностиЧисловая осьОпределение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины. Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом . Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA . Прямоугольная декартова система координат на плоскостиОпределение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2). Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо. Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA1 и AA2 на прямые Ox и Oy соответственно (рис.3). Определение 4 . Абсциссой точки A называют координату точки A1 на числовой оси Ox , ординатой точки A называют координату точки A2 на числовой оси Oy . Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y). Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) . Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5). Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5. Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью . Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0. Формула для расстояния между двумя точками координатной плоскостиУтверждение 1 . Расстояние между двумя точками координатной плоскости вычисляется по формуле Доказательство . Рассмотрим рисунок 6.
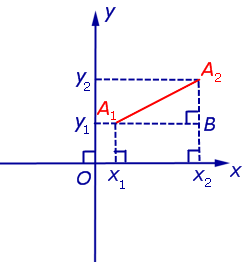
что и требовалось доказать. Уравнение окружности на координатной плоскостиПоскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем: Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A0 (x0 ; y0) . Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид источники: http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik http://www.resolventa.ru/demo/him/diagege.htm |
Описанная окру́жность многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать 
Свойства[править | править код]
- Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если около n-угольника описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).
- Около любого правильного многоугольника (все углы и стороны равны) можно описать окружность, и притом только одну.
- Вокруг каждого треугольника может быть описана единственная окружность.
Уравнения окружности[править | править код]
Уравнение описанной окружности можно выразить через декартовы координаты вершин вписанного в неё треугольника. Предположим, что
являются координатами вершин A, B и C. Тогда окружность — геометрическое место точек v = (vx,vy), в декартовой плоскости удовлетворяющих уравнениям
,
гарантирующих то, что вершины A, B, C, и v находятся на одном и том же расстоянии r от общего центра u окружности. Используя поляризационное тождество, эти уравнения можно свести к условию, что линейное отображение, задаваемое матрицей
имеет ненулевое ядро. Таким образом, описанная окружность может быть описана как множество нулей определителя этой матрицы:
Раскладывая этот определитель по первой строке и вводя обозначения
мы приводим уравнение окружности к виду a|v|2 − 2Sv − b = 0,
или, предполагая, что точки A, B, C не лежали на одной прямой (в противном случае окружность вырождается в прямую линию, которая также может рассматриваться как обобщённая окружность с центром S на бесконечности), |v − S/a|2 = b/a + |S|2/a2,
выражая центр окружности как S / а и её радиус как √(b/a + |S|2/a2). Сходный подход позволяет вывести уравнение сферы, описанной вокруг тетраэдра.
Параметрическое уравнение[править | править код]
Единичный вектор перпендикулярный к плоскости, содержащую круг даётся в виде
Следовательно, с учётом радиуса r с центром Pc, точка на окружности P0 единичная нормаль к плоскости, содержащей окружность: 

Трилинейные и барицентрические координаты окружности[править | править код]
Уравнение окружности в трилинейных координатах x : y : z есть[1]:p. 199 a/x + b/y + c/z = 0. Уравнение окружности в барицентрических координатах есть x : y : z is a2/x + b2/y + c2/z = 0.
Изогональное сопряжение окружности есть бесконечно удалённая прямая, записываемая в трилинейных координатах в виде ax + by + cz = 0 и в барицентрических координатах в виде x + y + z = 0.
Координаты центра описанной окружности[править | править код]
Декартовы координаты центра[править | править код]
Декартовы координаты центра описанной окружности есть
,
где
Без ограничения общности это можно выразить в упрощённом виде после перевода вершины A в начало координат декартовой системы координат, то есть, когда
A′ = A − A = (A′x,A′y) = (0,0). В этом случае координаты вершин B′ = B − A и C′ = C − A представляют собой векторы из вершины A′ к этим вершинам.
Заметим, что этот тривиальный перевод возможен для всех треугольников и координат центра описанной окружности треугольника A′B′C′ в следующем виде:
,
где
Трилинейные координаты центра[править | править код]
Центр описанной окружности имеет трилинейные координаты[1]:p.19
- cos α : cos β : cos γ,
где α, β, γ внутренние углы треугольника.
В терминах сторон треугольника a, b, c трилинейные координаты центра описанной окружности имеют вид[2]
Барицентрические координаты центра[править | править код]
Барицентрические координаты центра описанной окружности имеют вид
[3],
где a, b, c длины сторон (BC, CA, AB соответственно) треугольника.
В терминах углов треугольника 
Вектор центра описанной окружности[править | править код]
Так как декартовы координаты любой точки являются средневзвешенным тех вершин, со своими весами, то барицентрические координаты точки нормируются в сумме единицей, тогда вектор центра описанной окружности, можно записать в виде
Здесь U есть вектор центра описанной окружности, A, B, C являются векторами вершин. Делитель здесь равен 16S 2, где S — площадь треугольника.
Для треугольника[править | править код]
Окружность, описанная около треугольника
- Около треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров или медиатрис.
Углы[править | править код]
|
Равные углы у вписанного треугольника |
Равные углы у вписанного треугольника |
На рисунке показаны равные углы у треугольника, вписанного в окружность.
Углы, образуемые описанной окружностью со сторонами треугольника, совпадают с углами, которые образуют стороны треугольника, соединяясь друг с другом в вершинах. Сторона, противоположная углу α, дважды касается окружности: один раз на каждом конце; в каждом случае под одинаковым углом α (см. рис.) (аналогично для двух других углов). Это связано с теоремой об отрезке круга, дополнительном данному (the alternate segment theorem,), в которой говорится, что угол между касательной и хордой равен вписанному в окружность углу, опирающемуся на эту хорду.
Треугольные центры на окружности, описанной около треугольника ABC[править | править код]
В этом параграфе вершины углов обозначены, как A, B, C и все координаты являются трилинейными координатами.
Следующие точки на окружности, описанной около треугольника ABC:
- Точка Штейнера = bc / (b2 − c2) : ca / (c2 − a2) : ab / (a2 − b2) = невершинная точка пересечения описанной окружности с эллипсом Штейнера. (Эллипс Штейнера с центром, расположенном в центроиде треугольника ABC представляет собой эллипс с наименьшей площадью из всех, что проходят через вершины A, B и C. Уравнение эллипса Штейнера имеет вид: 1/(ax) + 1/(by) + 1/(cz) = 0.)
- Точка Тарри (Tarry point) = sec (A + ω) : sec (B + ω) : sec (C + ω) = диаметрально противоположная точке Штейнера
- Фокус параболы Киперта (Kiepert parabola) = csc (B − C) : csc (C − A) : csc (A − B). (см. рис.)
Свойства вписанной параболы
- Перспекторы вписанных в треугольник парабол лежат на описанном эллипсе Штейнера[4]. Фокус вписанной параболы лежит на описанной окружности, а директриса проходит через ортоцентр[5]. Парабола, вписанная в треугольник, имеющая директрисой прямую Эйлера, называется параболой Киперта. Её перспектор — четвёртая точка пересечения описанной окружности и описанного эллипса Штейнера, называемая точкой Штейнера.
- Теорема Лестера[6]. В любом разностороннем треугольнике две точки Торричелли, центр девяти точек и центр описанной окружности лежат на одной окружности (окружности Лестера).
Свойства центра описанной окружности треугольника[править | править код]
- У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.
-
Остроугольный
-
Тупоугольный
-
Прямоугольный
Обозначаем буквой О точку пересечения серединных перпендикуляров к его сторонам и проведём отрезки ОА, ОВ и ОС.
Так как точка О равноудалена от вершин треугольника АВС, то ОА = OB = ОС.
Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и,
значит, является описанной около треугольника ABC.
- Центр описанной окружности изогонально сопряжен ортоцентру.
- 3 из 4 окружностей, описанных относительно серединных треугольников (образованных средними линиями треугольника), пересекаются в одной точке внутри треугольника. Эта точка и есть центр описанной окружности основного треугольника.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника (называемого дополнительным треугольником).
- Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
- Математически последнее утверждение означает, что
расстояние от центра описанной окружности например до стороны 
расстояние от ортоцентра например до вершины 
- Из последних трёх утверждений следует то, что сумма расстояний от ортоцентра остроугольного треугольника до трёх его вершин в два раза больше, чем сумма расстояний от центра описанной окружности до трёх его сторон, и равна
. В тупоугольном треугольнике надо брать знак «-» в случае, если перпендикуляр из центра описанной окружности на сторону целиком лежит вне треугольника или если отрезок, проведённый из ортоцентра к вершине, целиком лежит вне треугольника. Остальные члены берутся со знаком «+».
- Математически последнее утверждение (Формула Карно) означает, что[7]:
где 



Радиус[править | править код]
Формулы радиуса описанной окружности
-
,
- где:
— стороны треугольника,
— углы, лежащие против сторон
соответственно,
— площадь треугольника.
— полупериметр треугольника, то есть
.
Положение центра описанной окружности[править | править код]
Пусть 

где
При этом 

Уравнение описанной окружности[править | править код]
Пусть
координаты вершин треугольника в некоторой декартовой системе координат на плоскости,

Тогда уравнение описанной окружности
Координаты центра описанной окружности могут быть вычислены
где
В явном виде координаты центра окружности определяются по формулам:
Теоремы, связанные с описанной окружностью[править | править код]
- Теорема о трезубце, или теорема трилистника, или теорема Клайнэра: Если
— точка пересечения биссектрисы угла
с описанной окружностью треугольника
,
и
— соответственно центры вписанной и вневписанной окружности, касающейся стороны
, тогда
.
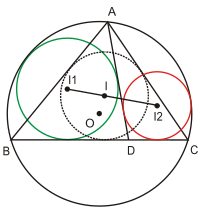
- Теорема Мансиона. Отрезок, соединяющий центры вписанной и вневписанной окружностей треугольника, делится описанной окружностью пополам.
- Теорема Мансиона (продолжение). Середина дуги
описанной окружности треугольника
, не содержащая вершину
, равноудалена от вершин
и
, центра
вписанной окружности и центра
вневписанной окружности. Середина дуги
описанной окружности треугольника
, содержащая вершину
, равноудалена от вершин
и
, и центров
и
вневписанных окружностей.
- Окружностно-чевианным треугольником называют треугольник с вершинами во вторых точках пересечения трёх прямых, проведённых через вершины подерного треугольника и данную точку
, с описанной окружностью. Теорема. Окружностно-чевианный треугольник подобен подерному (Доказательство в: http://www.problems.ru/view_problem_details_new.php?id=108130 Архивная копия от 4 марта 2016 на Wayback Machine).
- Теорема Симсона: Основания перпендикуляров, опущенных из точки
описанной окружности треугольника
на его стороны или их продолжения, лежат на одной прямой. Эта прямая называется прямой Симсона.
- Согласно теореме Лестера центр девяти точек лежит на одной окружности (на окружности Лестера) вместе с тремя другими точками — двумя точками Торричелли и центром описанной окружности [6].
- Прямая Эйлера проходит через: 1) Центроид треугольника, 2) Ортоцентр треугольника, 3) центр описанной окружности, 4) Центр окружности девяти точек и другие известные точки (см. Прямая Эйлера).
- Радиус описанной окружности, проведенный из вершины треугольника в ее центр, всегда перпендикулярен одной из трех сторон ортотреугольника, которую он пересекает (Зетель, следствие 2, § 66, с. 81).
Связь описанной окружности со вписанной окружностью, с ортоцентром и другими точками[править | править код]
Или через стороны треугольника:
,
где 
- Расстояние от центра O до ортоцентра H есть[9][10]:p. 449
- Для центроида G и центра девяти точек N имеем:
- Произведение радиусов описанной и вписанной окружностей треугольника связано со сторонами a, b и c в виде[11]: p. 189, #298(d):
- Отношение радиусов вписанной и описанной окружностей треугольника [12]:
.
- Если медиана m, высота h и внутренняя биссектриса t выходят из одной и той же вершины треугольника, около которого описана окружность радиуса R, тогда[13] :p.122,#96
- Центр описанной окружности изогонально сопряжён с ортоцентром.
- Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности[14].
- В треугольнике есть три окружности, которые касаются двух сторон треугольника и описанной окружности. Такие окружности называют полувписанными или окружностями Веррьера. Отрезки, соединяющие вершины треугольника и соответствующие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке, называемой точкой Веррьера. Она служит центром гомотетии, которая переводит описанную окружность во вписанную. Точки касания окружностей Веррьера со сторонами лежат на прямой, которая проходит через центр вписанной окружности.
- Теорема Тебо 3 утверждает (см. рис.):
- Формула Карно утверждает, что в треугольнике ABC сумма расстояний от центра D описанной окружности до сторон треугольника ABC, взятых со знаком «-», когда высота из D на сторону целиком лежит вне треугольника (иначе со знаком «+»), будет равна
, где r и R — радиусы вписанной и описанной окружностей[13]:p.83.
Формула Карно:
Например для рисунка формула Карно примет вид: 
- В другой формулировке формула Карно утверждает, что[7]:
где 



- Расстояние от центра описанной окружности например до стороны
треугольника равно:
расстояние от ортоцентра например до вершины 
Определения к последней теореме[править | править код]
- Треугольник с вершинами в проекциях данной точки на стороны называется подерным или педальным треугольником этой точки.
- Окружностно-чевианный треугольник — треугольник с тремя вершинами во вторых точках пересечения с описанной окружностью трёх прямых, проведённых через вершины и данную точку.
Вариации по теме[править | править код]
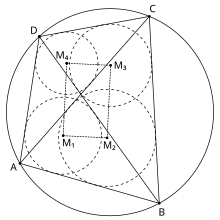
Японская теорема (Japanese theorem)
- Теорема[15]. Если во вписанном в окружность четырёхугольнике провести диагональ, а в полученные два треугольника вписать две окружности, затем аналогично поступить, проведя вторую диагональ, тогда центры четырёх образовавшихся окружностей являются вершинами прямоугольника (то есть лежат на одной окружности). Эту теорему называют японской теоремой (Japanese theorem). (см. рис.).
Для четырёхугольника[править | править код]
Вписанный простой (без самопересечений) четырёхугольник является выпуклым.
Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 180° (
Можно описать окружность около:
- любого антипараллелограмма
- любого прямоугольника (частный случай квадрат)
- любой равнобедренной трапеции
- любого четырёхугольника, у которого два противоположных угла прямые
- любого четырёхугольника, у которого сумма противоположных углов равна 180 градусов
- любого четырёхугольника, у которого пересекаются в одной точке четыре серединных перпендикуляра его сторон (или медиатрисы его сторон, то есть перпендикуляры к сторонам, проходящие через их середины)
- Первая теорема Птолемея. У четырёхугольника, вписанного в окружность, произведение длин диагоналей равно сумме произведений длин пар противоположных сторон:[16]:
.
- Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство.[17] :

- Радиус окружности, описанной около четырёхугольника:

- Площадь четырёхугольника, вписанного в окружность, можно вычислить по формуле Брахмагупты:
- Та же Формула Брахмагупты для площади вписанного в окружность четырёхугольника может быть записана через определитель[18]:

- Подробнее о четырёхугольниках, вписанных в окружность, можно прочитать в статье «Вписанный четырёхугольник».
Для вписано-описанного четырехугольника[править | править код]
Аналог теоремы Эйлера для вписано-описанного четырёхугольника[править | править код]
- Для радиусов R и r соответственно описанной и вписанной окружностей данного вписано-описанного четырёхугольника и расстояния d между центрами этих окружностей выполняется соотношение:
.
или
.
Для многоугольника[править | править код]
- Если из отрезков составить многоугольник, то его площадь будет максимальна, когда он вписанный.
- Если точка равноудалена от вершин многоугольника, то она совпадает с центром окружности, описанной около этого многоугольника.
В сферическом треугольнике[править | править код]
Описанная окружность для сферического треугольника — это окружность, содержащая все его вершины.
- Если A, B, C — углы сферического треугольника, P — их полусумма, то тангенс радиуса[19] описанной окружности будет равен[20]:78,83
- Описанная окружность принадлежит сфере. Радиус, проведённый из центра сферы через центр описанной окружности пересечёт сферу в точке пересечения серединных перпендикуляров (больших кругов сферы, перпендикулярных сторонам в их середине) к сторонам сферического треугольника[20]:21-22.
См. также[править | править код]
- Вписанная и вневписанные в треугольник окружности
- Вписанная окружность
- Вневписанная окружность
- Окружность
- Ортоцентр
- Серединный перпендикуляр
- Четырехугольник
- Четырехугольники, вписанные в окружность
- Центр описанной окружности
Примечания[править | править код]
- ↑ 1 2 Whitworth, William Allen. Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions, Forgotten Books, 2012 (orig. Deighton, Bell, and Co., 1866). http://www.forgottenbooks.com/search?q=Trilinear+coordinates&t=books Архивная копия от 24 марта 2016 на Wayback Machine
- ↑ 1 2 Clark Kimberling’s Encyclopedia of Triangles http://faculty.evansville.edu/ck6/encyclopedia/ETC.html Архивная копия от 19 апреля 2012 на Wayback Machine
- ↑ Wolfram page on barycentric coordinates. Дата обращения: 29 апреля 2016. Архивировано 20 июля 2017 года.
- ↑ , . Геометрические свойства кривых второго порядка. — 2-е изд., дополн.. — 2011. — С. 110.
- ↑ , . Геометрические свойства кривых второго порядка. — 2-е изд., дополн.. — 2011. — С. 27—28.
- ↑ 1 2 Yiu, 2010, с. 175–209.
- ↑ 1 2 Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.: Учпедгиз, 1962. задача на с. 120—125. параграф 57, с.73.
- ↑ The Orthopole (21 января 2017). Дата обращения: 22 июня 2020. Архивировано 22 июня 2020 года. (англ.)
- ↑ Marie-Nicole Gras, «Distances between the circumcenter of the extouch triangle and the classical centers»,
Forum Geometricorum 14 (2014), 51-61. http://forumgeom.fau.edu/FG2014volume14/FG201405index.html Архивная копия от 28 апреля 2021 на Wayback Machine - ↑ Smith, Geoff, and Leversha, Gerry, «Euler and triangle geometry», Mathematical Gazette 91, November 2007, 436—452.
- ↑ Johnson, Roger A., Advanced Euclidean Geometry, Dover, 2007 (orig. 1929).
- ↑ Longuet-Higgins, Michael S., «On the ratio of the inradius to the circumradius of a triangle», Mathematical Gazette 87, March 2003, 119—120.
- ↑ 1 2 Altshiller-Court, Nathan, College Geometry, Dover, 2007.
- ↑ Мякишев А. Г. Элементы геометрии треугольника. Серия: «Библиотека „Математическое просвещение“». М.:МЦНМО,2002. c. 11, п. 5.
- ↑ Вокруг задачи Архимеда. Упр. 8, рис. 13, c. 6 Архивная копия от 29 апреля 2016 на Wayback Machine // geometry.ru
- ↑ Теорема Птолемея. Дата обращения: 15 марта 2009. Архивировано 10 мая 2009 года.
- ↑ Четырёхугольники Архивная копия от 16 сентября 2015 на Wayback Machine. Вписанные четырёхугольники .
- ↑ Стариков В. Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. Выпуск 1/ Гл. ред. Романова И. В. Чебоксары: ЦДИП «INet», 2014. С. 37-39
- ↑ Здесь радиус окружности измеряется по сфере, то есть представляет собой градусную меру дуги большого круга, соединяющей точку пересечения радиуса сферы, проведённого из центра сферы через центр окружности, со сферой и вершину треугольника.
- ↑ 1 2 Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — 154 с.
Литература[править | править код]
- Paul Yiu. The Circles of Lester, Evans, Parry, and Their Generalizations // Forum Geometricorum. — 2010. — Т. 10.
- Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. 153 с.
Ссылки[править | править код]
На Викискладе есть медиафайлы по теме Описанная окружность
|
Заблокирован |
|
|
1 |
|
Координаты центра описанной окружности27.05.2014, 16:53. Показов 74975. Ответов 6 Миниатюры
2 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,061 |
|
|
27.05.2014, 18:32 |
2 |
|
Что-то сложновато. Известно, что уравнение окружности при известных координатах вершин записывается следующей красивой формулой (для продвинутых школьников).
1 |
|
Заблокирован |
|
|
28.05.2014, 14:47 [ТС] |
3 |
|
Спасибо вам за формулу. Я такой не знал.
0 |
|
753 / 458 / 49 Регистрация: 13.05.2012 Сообщений: 947 |
|
|
28.05.2014, 15:38 |
4 |
|
Интересно, можно эту формулу модифицировать, если треугольник задан в пространстве координатами своих вершин, т.е.
1 |
|
Заблокирован |
|
|
28.05.2014, 15:55 [ТС] |
5 |
|
Вы задали очень хороший вопрос. Я правда над этим не
0 |
|
2833 / 1642 / 254 Регистрация: 03.12.2007 Сообщений: 4,222 |
|
|
28.05.2014, 17:58 |
6 |
|
Решение Альтернативное начало: центр описанной окружности лежит на пересечении серединных перпендикуляров, отсюда 3 скалярных произведения равны нулю:
1 |
|
Заблокирован |
|
|
28.05.2014, 18:10 [ТС] |
7 |
|
Я восхищен вами!! Я что-то подобное сначала попробовал, но
0 |

В геометрии, описанная окружность или описанная окружность в многоугольнике является окружностью, которая проходит через все вершины многоугольник. Центр этой окружности называется центром описанной окружности, а ее радиус называется радиусом описанной окружности .
Не каждый многоугольник имеет описанную окружность. Многоугольник, у которого он есть, называется циклическим многоугольником или иногда конциклическим многоугольником, потому что его вершины конциклические. Все треугольники, все правильные простые многоугольники, все прямоугольники, все равнобедренные трапеции и все Правые воздушные змеи циклические.
Связанное понятие – это минимальный ограничивающий круг, который является наименьшим кругом, который полностью содержит многоугольник внутри него, если центр круга находится внутри многоугольника. Каждый многоугольник имеет уникальный минимальный ограничивающий круг, который может быть построен с помощью алгоритма линейного времени. Даже если у многоугольника есть описанная окружность, она может отличаться от минимальной ограничивающей окружности. Например, для тупого треугольника минимальная ограничивающая окружность имеет самую длинную сторону в качестве диаметра и не проходит через противоположную вершину.
Содержание
- 1 Треугольники
- 1.1 Строение линейки и циркуля
- 1.2 Альтернативное построение
- 1.3 Уравнения окружности
- 1.3.1 Декартовы координаты
- 1.3.2 Параметрическое уравнение
- 1.3. 3 Трилинейные и барицентрические координаты
- 1.3.4 Более высокие измерения
- 1.4 Координаты окружности центра
- 1.4.1 Декартовы координаты
- 1.4.2 Трилинейные координаты
- 1.4.3 Барицентрические координаты
- 1.4.4 Окружность центра вектор
- 1.4.5 Декартовы координаты из перекрестных и скалярных произведений
- 1.4.6 Местоположение относительно треугольника
- 1.5 Углы
- 1.6 Центры треугольника на описанной окружности треугольника ABC
- 1.7 Другие свойства
- 2 циклических четырехугольника
- 3 циклических n-угольника
- 3.1 Точка на описанной окружности
- 3.2 Константа, описывающая многоугольник
- 4 См. Также
- 5 Ссылки
- 6 Внешние ссылки
- 6.1 MathWorld
- 6.2 Интерактивные
Треугольники
Все треугольники циклические; то есть каждый треугольник имеет описанную окружность.
Построение линейки и циркуля
Центр описанной окружности треугольника может быть построен путем рисования любые две из трех серединных перпендикуляров. Для трех неколлинеарных точек эти две прямые не могут быть параллельны, а центр описанной окружности – это точка, где они пересекаются. Любая точка на биссектрисе равноудалена от двух точек, которые она делит пополам, из чего следует, что эта точка на обеих биссектрисах равноудалена от всех трех вершин треугольника. Радиус описанной окружности – это расстояние от нее до любой из трех вершин.
Альтернативное построение

Альтернативный метод определения центра описанной окружности – это рисование любых двух линий, каждая из которых выходит из одной из вершин под углом к общей стороне, общий угол вылета равен 90 ° минус угол противоположной вершины. (В случае, если противоположный угол тупой, рисование линии под отрицательным углом означает выход за пределы треугольника.)
В прибрежной навигации описанная окружность треугольника иногда используется как способ получения строки положения с помощью секстанта , когда нет компаса. Горизонтальный угол между двумя ориентирами определяет описанную окружность, на которой лежит наблюдатель.
Уравнения окружности
Декартовы координаты
В евклидовой плоскости можно явно задать уравнение описанной окружности в терминах Декартовы координаты вершин вписанного треугольника. Предположим, что
- A = (A x, A y) B = (B x, B y) C = (C x, C y) { displaystyle { begin {align} mathbf {A} = (A_ {x}, A_ {y}) \ mathbf {B} = (B_ {x}, B_ {y}) \ mathbf {C} = (C_ {x}, C_ {y}) end {align}}}
– координаты точек A, B и C. Описанная окружность является геометрическим местом точек v = (v x,vy) в декартовой плоскости, удовлетворяющих уравнениям
- | v – u | 2 = r 2 | A – u | 2 = r 2 | B – u | 2 = r 2 | C – u | 2 = р 2 { Displaystyle { begin {align} | mathbf {v} – mathbf {u} | ^ {2} = r ^ {2} \ | mathbf {A} – mathbf {u } | ^ {2} = r ^ {2} \ | mathbf {B} – mathbf {u} | ^ {2} = r ^ {2} \ | mathbf {C} – mathbf {u} | ^ {2} = r ^ {2} end {align}}}
гарантирует, что точки A, B, Cи v находятся на одинаковом расстоянии r от общего центр u круга. Используя поляризационное тождество, эти уравнения сводятся к условию, что матрица
- [| v | 2 – 2 v x – 2 v y – 1 | А | 2 – 2 A x – 2 A y – 1 | B | 2 – 2 B x – 2 B y – 1 | C | 2 – 2 C x – 2 C y – 1] { displaystyle { begin {bmatrix} | mathbf {v} | ^ {2} – 2v_ {x} – 2v_ {y} – 1 \ | mathbf {A} | ^ {2} – 2A_ {x} – 2A_ {y} – 1 \ | mathbf {B} | ^ {2} – 2B_ {x} – 2B_ {y} -1 \ | mathbf {C} | ^ {2} – 2C_ {x} – 2C_ {y} – 1 end {bmatrix}}}
имеет ненулевое ядро . Таким образом, описанная окружность может быть альтернативно описана как геометрическое место нулей детерминанта этой матрицы:
- det [| v | 2 v x v y 1 | А | 2 A x A y 1 | B | 2 B x B y 1 | C | 2 C x C y 1] = 0. { displaystyle det { begin {bmatrix} | mathbf {v} | ^ {2} v_ {x} v_ {y} 1 \ | mathbf {A} | ^ {2} A_ {x} A_ {y} 1 \ | mathbf {B} | ^ {2} B_ {x} B_ {y} 1 \ | mathbf {C} | ^ {2} C_ { x} C_ {y} 1 end {bmatrix}} = 0.}
Используя расширение кофактора, пусть
- S x = 1 2 det [| А | 2 A y 1 | B | 2 Б у 1 | C | 2 C y 1], S y = 1 2 det [A x | А | 2 1 B x | B | 2 1 C x | C | 2 1], a = det [A x A y 1 B x B y 1 C x C y 1], b = det [A x A y | А | 2 B x B y | B | 2 C x C y | C | 2] { displaystyle { begin {align} S_ {x} = { frac {1} {2}} det { begin {bmatrix} | mathbf {A} | ^ {2} A_ {y} 1 \ | mathbf {B} | ^ {2} B_ {y} 1 \ | mathbf {C} | ^ {2} C_ {y} 1 end {bmatrix}}, \ [5pt] S_ {y} = { frac {1} {2}} det { begin {bmatrix} A_ {x} | mathbf {A} | ^ {2} 1 \ B_ {x} | mathbf {B} | ^ {2} 1 \ C_ {x} | mathbf {C} | ^ {2} 1 end {bmatrix}}, \ [5pt] a = det { begin {bmatrix} A_ {x} A_ {y} 1 \ B_ {x} B_ {y} 1 \ C_ {x} C_ {y} 1 end {bmatrix}}, \ [5pt] b = det { begin {bmatrix} A_ {x} A_ {y} | mathbf {A} | ^ {2} \ B_ {x} B_ {y} | mathbf {B} | ^ {2} \ C_ {x } C_ {y} | mathbf {C} | ^ {2} end {bmatrix}} end {align}}}
тогда у нас есть | v | – 2 Sv – b = 0 и, если предположить, что три точки не были на одной линии (в противном случае описанная окружность – это та линия, которую также можно рассматривать как обобщенную окружность с S на бесконечности), | v− S/ а | = b / a + | S | / a, что дает центр описанной окружности S / a и радиус описанной окружности √b / a + | S | / a. Подобный подход позволяет вывести уравнение описанной сферы тетраэдра .
Параметрическое уравнение
A единичный вектор , перпендикулярный плоскости, содержащей окружность дается как
- n ^ = (P 2 – P 1) × (P 3 – P 1) | (P 2 – P 1) × (P 3 – P 1) |. { displaystyle { widehat {n}} = { frac {(P_ {2} -P_ {1}) times (P_ {3} -P_ {1})} {| (P_ {2} -P_ { 1}) times (P_ {3} -P_ {1}) |}}.}
Следовательно, учитывая радиус r, центр, P c, точку на окружности, P 0 и единичная нормаль плоскости, содержащей круг, n ^ { textstyle { widehat {n}}}

- R (s) = P c + cos (sr) (P 0 – P c) + sin (sr) [n ^ × (P 0 – P c)]. { displaystyle mathrm {R} (s) = mathrm {P_ {c}} + cos left ({ frac { mathrm {s}} { mathrm {r}}} right) (P_ { 0} -P_ {c}) + sin left ({ frac { mathrm {s}} { mathrm {r}}} right) left [{ widehat {n}} times (P_ { 0} -P_ {c}) right].}
Трилинейные и барицентрические координаты
Уравнение описанной окружности в трилинейных координатах x: y: z равно a / x + b / y + c / z = 0. Уравнение описанной окружности в барицентрических координатах x: y: z равно a / x + b / y + c / z = 0.
изогонально сопряженное описанной окружности – линия на бесконечности, заданная в трилинейных координатах как ax + by + cz = 0 и в барицентрических координатах как x + y + z = 0.
Высшие измерения
Кроме того, описанная окружность треугольника, вложенного в измерения d, может быть найдена с использованием обобщенного метода. Пусть A, Bи C будут d-мерными точками, которые образуют вершины треугольника. Начнем с транспонирования системы, чтобы поместить C в начало координат:
- a = A – C, b = B – C. { displaystyle { begin {align} mathbf {a} = mathbf {A} – mathbf {C}, \ mathbf {b} = mathbf {B} – mathbf {C}. end {align}}}
Радиус описанной окружности r равен
- r = ‖ a ‖ ‖ b ‖ ‖ a – b ‖ 2 ‖ a × b ‖ = ‖ a – b ‖ 2 sin θ = ‖ A – В ‖ 2 грех θ, { displaystyle r = { frac { left | mathbf {a} right | left | mathbf {b} right | left | mathbf {a} – mathbf {b} right |} {2 left | mathbf {a} times mathbf {b} right |}} = { frac { left | mathbf { a} – mathbf {b} right |} {2 sin theta}} = { frac { left | mathbf {A} – mathbf {B} right |} {2 sin theta}},}
где θ – это внутренний угол между a и b . Центр описанной окружности, p 0, задается как
- p 0 = (‖ a ‖ 2 b – ‖ b ‖ 2 a) × (a × b) 2 ‖ a × b ‖ 2 + C. { displaystyle p_ {0} = { frac {( left | mathbf {a} right | ^ {2} mathbf {b} – left | mathbf {b} right | ^ {2} mathbf {a}) times ( mathbf {a} times mathbf {b})} {2 left | mathbf {a} times mathbf {b} right | ^ { 2}}} + mathbf {C}.}
Эта формула работает только в трех измерениях, поскольку перекрестное произведение не определено в других измерениях, но ее можно обобщить на другие измерения, заменив перекрестные произведения следующими идентичностями :
- (a × b) × c = (a ⋅ c) b – (b ⋅ c) a, a × (b × c) = (a ⋅ c) b – (a ⋅ b) c, ‖ a × b ‖ знак равно ‖ a ‖ 2 ‖ b ‖ 2 – (a ⋅ b) 2. { Displaystyle { begin {выровнен} ( mathbf {a} times mathbf {b}) times mathbf {c} = ( mathbf {a} cdot mathbf {c}) mathbf {b } – ( mathbf {b} cdot mathbf {c}) mathbf {a}, \ mathbf {a} times ( mathbf {b} times mathbf {c}) = ( mathbf {a} cdot mathbf {c}) mathbf {b} – ( mathbf {a} cdot mathbf {b}) mathbf {c}, \ left | mathbf {a} times mathbf {b} right | = { sqrt { left | mathbf {a} right | ^ {2} left | mathbf {b} right | ^ {2} – ( mathbf {a} cdot mathbf {b}) ^ {2}}}. end {align}}}
Координаты окружности центра
Декартовы координаты
Декартовы координаты центра описанной окружности U = (U x, U y) { displaystyle U = left (U_ {x}, U_ {y} right)}
- U x = 1 D [(A x 2 + A y 2) (B y – C y) + (B x 2 + B y 2) (C y – A y) + (C x 2 + C y 2) (A y – B y)] U y = 1 D [(A x 2 + A y 2) (C x – B x) + (B x 2 + B y 2) (A x – C x) + ( С Икс 2 + С Y 2) (В Икс – А Икс)] { Displaystyle { begin {Выровнено} U_ {x} = { frac {1} {D}} left [(A_ {x } ^ {2} + A_ {y} ^ {2}) (B_ {y} -C_ {y}) + (B_ {x} ^ {2} + B_ {y} ^ {2}) (C_ {y } -A_ {y}) + (C_ {x} ^ {2} + C_ {y} ^ {2}) (A_ {y} -B_ {y}) right] \ [5pt] U_ {y} = { frac {1} {D}} left [(A_ {x} ^ {2} + A_ {y} ^ {2}) (C_ {x} -B_ {x}) + (B_ {x } ^ {2} + B_ {y} ^ {2}) (A_ {x} -C_ {x}) + (C_ {x} ^ {2} + C_ {y} ^ {2}) (B_ {x } -A_ {x}) right] end {align}}}
с
- D = 2 [A x (B y – C y) + B x (C y – A y) + C x (А у – Б у)]. { displaystyle D = 2 left [A_ {x} (B_ {y} -C_ {y}) + B_ {x} (C_ {y} -A_ {y}) + C_ {x} (A_ {y} -B_ {y}) right]. ,}
Без ограничения общности это можно выразить в упрощенной форме после перевода вершины A в начало декартовых систем координат, т. Е. Когда A ′ = A – A = (A ′ x, A ′ y) = (0,0). В этом случае координаты вершин B = B – A и C = C – A представляют векторы из вершины A в эти вершины. Обратите внимание, что этот тривиальный перевод возможен для всех треугольников и центра описанной окружности U ′ = (U x ′, U y ′) { displaystyle U ‘= (U’ _ {x}, U ‘_ {y})}
- U x ′ = 1 D ′ [C y ′ (B x ′ 2 + B y ′ 2) – B y ′ (C x ′ 2 + C y ′ 2)], U y ′ = 1 D ′ [B x ′ (C x ′ 2 + C y ′ 2) – C x ′ (B x ′ 2 + B y ′ 2)] { displaystyle { begin {align} U ‘_ {x} = { frac {1} {D’}} left [C ‘_ {y} ({B’ _ {x}} ^ {2} + {B ‘_ {y}} ^ {2}) – B’ _ {y} ({C ‘_ {x}} ^ {2} + {C’ _ {y}} ^ {2}) right], [5pt] U ‘_ {y} = { frac {1} {D’}} left [B ‘_ {x} ({C’ _ {x}} ^ {2} + {C’_ {y}} ^ {2}) – C ‘_ {x} ({B’ _ {x}} ^ {2} + {B ‘_ {y}} ^ {2}) right] end {выровнено }}}
с
- D ′ = 2 (B x ′ C y ′ – B y ′ C x ′). { displaystyle D ‘= 2 (B’ _ {x} C ‘_ {y} -B’ _ {y} C ‘_ {x}). ,}
Из-за перевода вершины A в origin радиус описанной окружности r может быть вычислен как
- r = ‖ U ′ ‖ = U x ′ 2 + U y ′ 2 { displaystyle r = | U ‘ | = { sqrt {{U’ _ {x }} ^ {2} + {U ‘_ {y}} ^ {2}}}}
и фактический центр описанной окружности ABC выглядит следующим образом:
- U = U’ + A { displaystyle U = U ‘+ A}
Трилинейные координаты
Центр описанной окружности имеет трилинейные координаты
- cos α: cos β: cos γ
где α, β, γ – углы треугольника.
В терминах длин сторон a, b, c трилинейные линии равны
- a (b 2 + c 2 – a 2): b (c 2 + a 2 – b 2): c ( а 2 + б 2 – в 2). { displaystyle a left (b ^ {2} + c ^ {2} -a ^ {2} right): b left (c ^ {2} + a ^ {2} -b ^ {2} справа): c left (a ^ {2} + b ^ {2} -c ^ {2} right).}
Барицентрические координаты
Центр описанной окружности имеет барицентрические координаты
- a 2 (b 2 + c 2 – a 2): b 2 (c 2 + a 2 – b 2): c 2 (a 2 + b 2 – c 2), { displaystyle a ^ {2} left (b ^ {2} + c ^ {2} -a ^ {2} right): ; b ^ {2} left (c ^ {2} + a ^ {2} -b ^ {2} right): ; c ^ {2} left (a ^ {2} + b ^ {2} -c ^ {2} right), ,}
где a, b, c – длины ребер ( BC, CA, AB соответственно) треугольника.
С точки зрения углов треугольника α, β, γ, { displaystyle alpha, beta, gamma,}
- грех 2 α: грех 2 β: грех 2 γ. { displaystyle sin 2 alpha: sin 2 beta: sin 2 gamma.}
Вектор окружности центра
Поскольку декартовы координаты любой точки являются средневзвешенными координатами вершин, с весами, являющимися барицентрическими координатами точки, нормализованными к единице, вектор центра описанной окружности может быть записан как
- U = a 2 (b 2 + c 2 – a 2) A + b 2 (c 2 + a 2 – b 2) B + c 2 (a 2 + b 2 – c 2) C a 2 (b 2 + c 2 – a 2) + b 2 (c 2 + a 2 – b 2) + c 2 (a 2 + b 2 – в 2). { displaystyle U = { frac {a ^ {2} left (b ^ {2} + c ^ {2} -a ^ {2} right) A + b ^ {2} left (c ^ { 2} + a ^ {2} -b ^ {2} right) B + c ^ {2} left (a ^ {2} + b ^ {2} -c ^ {2} right) C} { a ^ {2} left (b ^ {2} + c ^ {2} -a ^ {2} right) + b ^ {2} left (c ^ {2} + a ^ {2} -b ^ {2} right) + c ^ {2} left (a ^ {2} + b ^ {2} -c ^ {2} right)}}.}
Здесь U – вектор центр описанной окружности, а A, B, C – векторы вершин. Делитель здесь равен 16S, где S – площадь треугольника. Как указано ранее
- a = A – C, b = B – C. { displaystyle { begin {align} mathbf {a} = mathbf {A} – mathbf {C}, \ mathbf {b} = mathbf {B} – mathbf {C}. end {align}}}
Декартовы координаты из перекрестных и скалярных произведений
В евклидовом пространстве существует уникальный круг, проходящий через любые заданные три неколлинеарные точки P 1, P 2 и P 3. Используя декартовы координаты для представления этих точек как пространственных векторов, можно использовать скалярное произведение и векторное произведение для вычисления радиуса. и центр круга. Пусть
- P 1 = [x 1 y 1 z 1], P 2 = [x 2 y 2 z 2], P 3 = [x 3 y 3 z 3] { displaystyle mathrm {P_ {1}} = { begin {bmatrix} x_ {1} \ y_ {1} \ z_ {1} end {bmatrix}}, mathrm {P_ {2}} = { begin {bmatrix} x_ {2} y_ {2} \ z_ {2} end {bmatrix}}, mathrm {P_ {3}} = { begin {bmatrix} x_ {3} \ y_ {3} \ z_ {3} end {bmatrix}}}
Тогда радиус круга определяется как
- r = | П 1 – П 2 | | П 2 – П 3 | | P 3 – P 1 | 2 | (P 1 – P 2) × (P 2 – P 3) | { displaystyle mathrm {r} = { frac { left | P_ {1} -P_ {2} right | left | P_ {2} -P_ {3} right | left | P_ {3} -P_ {1} right |} {2 left | left (P_ {1} -P_ {2} right) times left (P_ {2} -P_ {3} right) right |} }}
Центр круга задается линейной комбинацией
- P c = α P 1 + β P 2 + γ P 3 { displaystyle mathrm {P_ {c}} = alpha , P_ {1} + beta , P_ {2} + gamma , P_ {3}}
, где
- α = | П 2 – П 3 | 2 (P 1 – P 2) ⋅ (P 1 – P 3) 2 | (P 1 – P 2) × (P 2 – P 3) | 2 β = | P 1 – P 3 | 2 (P 2 – P 1) ⋅ (P 2 – P 3) 2 | (P 1 – P 2) × (P 2 – P 3) | 2 γ = | П 1 – П 2 | 2 (P 3 – P 1) ⋅ (P 3 – P 2) 2 | (P 1 – P 2) × (P 2 – P 3) | 2 { displaystyle { begin {align} alpha = { frac { left | P_ {2} -P_ {3} right | ^ {2} left (P_ {1} -P_ {2} right) cdot left (P_ {1} -P_ {3} right)} {2 left | left (P_ {1} -P_ {2} right) times left (P_ {2} -P_ {3} right) right | ^ {2}}} \ beta = { frac { left | P_ {1} -P_ {3} right | ^ {2} left (P_ {2} -P_ {1} right) cdot left (P_ {2} -P_ {3} right)} {2 left | left (P_ {1} -P_ {2} right) times left (P_ {2} -P_ {3} right) right | ^ {2}}} \ gamma = { frac { left | P_ {1} -P_ {2} right | ^ {2} left (P_ {3} -P_ {1} right) cdot left (P_ {3} -P_ {2} right)} {2 left | left (P_ {1} -P_ {2} right) times left (P_ {2} -P_ {3} right) right | ^ {2}}} end {align}}}
Местоположение относительно треугольника
Положение центра описанной окружности зависит от типа треугольника:
- Для острого треугольника (все углы меньше прямого) центр описанной окружности всегда лежит внутри треугольника.
- Для прямоугольного треугольника центр описанной окружности всегда лежит в середине гипотенузы. Это одна из форм теоремы Фалеса.
- Для тупого треугольника (треугольник с одним углом больше прямого) центр описанной окружности всегда лежит за пределами треугольника.



Эти особенности местоположения можно увидеть, рассматривая трилинейные или барицентрические координаты, указанные выше для центр описанной окружности: все три координаты положительны для любой внутренней точки, по крайней мере одна координата отрицательна для любой внешней точки, а одна координата равна нулю, а две положительны для не вершинной точки на стороне треугольника.
Углы

Углы, которые описанная окружность образует со сторонами треугольника, совпадают с углами, под которыми стороны встречаются друг с другом. Сторона, противоположная углу α, пересекает окружность дважды: по одному на каждом конце; в каждом случае под углом α (аналогично для двух других углов). Это связано с теоремой об альтернативном сегменте, которая утверждает, что угол между касательной и хордой равен углу в альтернативном сегменте.
Центры треугольника находятся на описанной окружности треугольника ABC
В этом разделе углы вершин помечены как A, B, C, а все координаты – трилинейные координаты :
- точка Штейнера = bc / (b – c): ca / (c – a): ab / (a - b) = невершинная точка пересечения описанной окружности с эллипсом Штейнера. (Эллипс Штейнера с центром = центроид (ABC) – это эллипс наименьшей площади, проходящий через A, B и C.Уравнение для этого эллипса: 1 / (ax) + 1 / ( by) + 1 / (cz) = 0.)
- Точка выдержки = sec (A + ω): sec (B + ω): sec (C + ω) = антипод точки Штейнера
- Фокус = csc (B – C): csc (C – A): csc (A – B).
Другие свойства
диаметр описанной окружности, называемый окружным диаметром и равным удвоенному описанному радиусу, может быть вычислен как длина любой стороны треугольника, деленная на синус противоположного угол :
- диаметр = a sin A = b sin B = c sin C. { displaystyle { text {Diameter}} = { frac {a} { sin A}} = { frac {b} { sin B}} = { frac {c} { sin C}}. }
Как следствие закона синусов, не имеет значения, какая сторона и противоположный угол взяты: результат будет таким же.
Диаметр описанной окружности можно также выразить как
- диаметр = a b c 2 ⋅ площадь = | A B | | B C | | C A | 2 | Δ A B C | = abc 2 s (s – a) (s – b) (s – c) = 2 abc (a + b + c) (- a + b + c) (a – b + c) (a + b – c) { displaystyle { begin {align} { text {Diameter}} {} = { frac {abc} {2 cdot { text {area}}}} = { frac {| AB || BC || CA |} {2 | Delta ABC |}} \ [5pt] {} = { frac {abc} {2 { sqrt {s (sa) (sb) (sc)}}}} [5pt] {} = { frac {2abc} { sqrt {(a + b + c) (- a + b + c) (a-b + c) (a + bc)}}} end {align}}}
где a, b, c – длины сторон треугольника, а s = (a + b + c) / 2 – полупериметр. Выражение s (s – a) (s – b) (s – c) { displaystyle { sqrt { scriptstyle {s (sa) (sb) (sc)}}}}
- диаметр = 2 sin площадь sin A sin B sin. C. { displaystyle { text {Diameter}} = { sqrt { frac {2 cdot { text {area}}} { sin A sin B sin C}}}.}
Треугольник окружность из девяти точек имеет половину диаметра описанной окружности.
В любом данном треугольнике центр описанной окружности всегда коллинеарен центроиду и ортоцентру. Линия, которая проходит через все из них, известна как линия Эйлера.
. Изогональное сопряжение центра описанной окружности – это ортоцентр.
Полезный минимальный ограничивающий круг трех точек определяется либо описанной окружностью (где три точки находятся на минимальной ограничивающей окружности), либо двумя точками самой длинной стороны треугольника (где две точки определяют диаметр окружности). Обычно минимальную ограничивающую окружность путают с описанной.
Описанная окружность трех коллинеарных точек – это линия, на которой лежат три точки, часто называемая окружностью бесконечного радиуса. Почти коллинеарные точки часто приводят к численной нестабильности при вычислении описанной окружности.
Окружности треугольников тесно связаны с триангуляцией Делоне набора точек.
Согласно теореме Эйлера в геометрии, расстояние между центром описанной окружности O и центром I составляет
- OI = R (R – 2 r), { displaystyle OI = { sqrt {R (R-2r)}},}
где r – радиус вписанной окружности, а R – радиус описанной окружности; следовательно, радиус описанной окружности как минимум в два раза больше внутреннего радиуса (неравенство треугольника Эйлера ), с равенством только в равностороннем случае.
Расстояние между O и ортоцентр H равен
- OH = R 2-8 R 2 cos A cos B cos C = 9 R 2 – (a 2 + b 2 + c 2). { displaystyle OH = { sqrt {R ^ {2} -8R ^ {2} cos A cos B cos C}} = { sqrt {9R ^ {2} – (a ^ {2} + b ^ {2} + c ^ {2})}}.}
Для центроида G и девятиточечного центра N мы имеем
- IG < I O, 2 I N < I O, O I 2 = 2 R ⋅ I N. {displaystyle {begin{aligned}IG
Произведение радиуса вписанной окружности и радиуса описанной окружности треугольника со сторонами a, b и c составляет
- r R = abc 2 (a + b + c). { displaystyle rR = { frac {abc} {2 (a + b + c)}}.}
С описанным радиусом R, сторонами a, b, c и медианами ma, m b и m c, имеем
- 3 3 R ≥ a + b + c 9 R 2 ≥ a 2 + b 2 + c 2 27 4 R 2 ≥ ma 2 + мб 2 + мс 2. { displaystyle { begin {align} 3 { sqrt {3}} R geq a + b + c \ [5pt] 9R ^ {2} geq a ^ {2} + b ^ {2} + c ^ {2} \ [5pt] { frac {27} {4}} R ^ {2} geq m_ {a} ^ {2} + m_ {b} ^ {2} + m_ {c} ^ {2}. End {align}}}
Если медиана m, высота h и внутренняя биссектриса t исходят из одной и той же вершины треугольника с описанным радиусом R, то
- 4 R 2 h 2 (t 2 – h 2) = t 4 (м 2 – h 2). { displaystyle 4R ^ {2} h ^ {2} (t ^ {2} -h ^ {2}) = t ^ {4} (m ^ {2} -h ^ {2}).}
Теорема Карно утверждает, что сумма расстояний от центра описанной окружности до трех сторон равна сумме радиуса описанной окружности и внутреннего радиуса. Здесь длина сегмента считается отрицательной тогда и только тогда, когда сегмент полностью лежит вне треугольника.
Если треугольник имеет две определенные окружности в качестве описанной окружности и вписанной окружности, существует бесконечное количество других треугольников с такими же описанными и вписанными окружностями, с любой точкой на описанной окружности в качестве вершины. (Это n = 3 случай поризмы Понселе ). Необходимым и достаточным условием существования таких треугольников является указанное выше равенство O I = R (R – 2 r). { displaystyle OI = { sqrt {R (R-2r)}}.}
Циклические четырехугольники

Четырехугольники, которые можно описать, обладают особыми свойствами, включая тот факт, что противоположные углы равны дополнительные углы (в сумме 180 ° или π радиан).
Циклические n-угольники
Для циклического многоугольника с нечетным числом сторон все углы равны тогда и только тогда, когда многоугольник правильный. У циклического многоугольника с четным числом сторон все углы равны тогда и только тогда, когда альтернативные стороны равны (то есть стороны 1, 3, 5,… равны, а стороны 2, 4, 6,… равны).
Циклический пятиугольник с рациональными сторонами и площадью известен как пятиугольник Роббинса ; во всех известных случаях его диагонали также имеют рациональную длину.
В любом циклическом n-угольнике с четным n сумма одного набора альтернативных углов (первого, третьего, пятого и т. д.) равна сумме другого набора альтернативных углов. Это может быть доказано индукцией из случая n = 4, в каждом случае заменяя сторону еще тремя сторонами и отмечая, что эти три новые стороны вместе со старой стороной образуют четырехугольник, который сам обладает этим свойством; Альтернативные углы последнего четырехугольника представляют собой прибавления к альтернативным суммам углов предыдущего n-угольника.
Пусть один n-угольник вписан в круг, а другой n-угольник будет касательным к этой окружности в вершинах первого n-угольника. Тогда из любой точки P на окружности произведение перпендикулярных расстояний от P до сторон первого n-угольника равно произведению перпендикулярных расстояний от P до сторон второго n-угольника.
Точка на описанной окружности
Пусть циклический n-угольник имеет вершины A 1,…, A n на единичной окружности. Тогда для любой точки M на вспомогательной дуге A 1Anрасстояния от M до вершин удовлетворяют
- {MA 1 + MA 3 + ⋯ + MA n – 2 + MA n < n / 2 if n is odd ; M A 1 + M A 3 + ⋯ + M A n − 3 + M A n − 1 ≤ n / 2 if n is even. {displaystyle {begin{cases}MA_{1}+MA_{3}+cdots +MA_{n-2}+MA_{n}
Константа, описывающая многоугольник

Любой правильный многоугольник является циклическим. Рассмотрим единичный круг, затем опишем правильный треугольник так, чтобы каждая сторона касалась круга. Опишите круг, а затем квадрат. Опять описываем круг, затем описываем правильный 5-угольник и так далее. Радиусы описанных окружностей сходятся к так называемой константе, описывающей многоугольник
- ∏ n = 3 ∞ 1 cos (π n) = 8.7000366…. { displaystyle prod _ {n = 3} ^ { infty} { frac {1} { cos left ({ frac { pi} {n}} right)}} = 8.7000366 ldots.}
(последовательность A051762 в OEIS ). Обратной величиной этой константы является постоянная Кеплера – Боукампа.
![Rendered by QuickLaTeX.com [ left{ begin{array}{l} (2 - a)^2 + (1 - b)^2 = R^2 , \ (6 - a)^2 + (3 - b)^2 = R^2 , \ (9 - a)^2 + (2 - b)^2 = R^2 . \ end{array} right. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-82dd95fa041ab9c8ca35f00eaea5d2ba_l3.png)
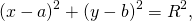
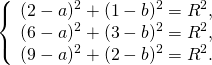
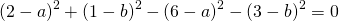
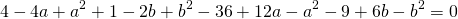
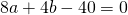
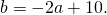
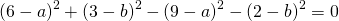
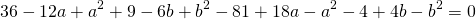
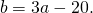
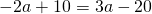
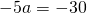
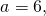
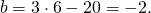
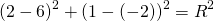
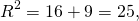
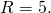
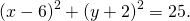

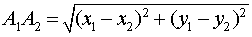












![{displaystyle mathrm {R} left(sright)=mathrm {P_{c}} +cos left({frac {mathrm {s} }{mathrm {r} }}right)left(P_{0}-P_{c}right)+sin left({frac {mathrm {s} }{mathrm {r} }}right)left[{hat {n}}times left(P_{0}-P_{c}right)right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1c6c1115dde943f477602b69e5a0cba324c4031)
![{displaystyle U_{x}=left[(A_{x}^{2}+A_{y}^{2})(B_{y}-C_{y})+(B_{x}^{2}+B_{y}^{2})(C_{y}-A_{y})+(C_{x}^{2}+C_{y}^{2})(A_{y}-B_{y})right]/D,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e16bf02ada8f34e0681c8ccff86dda27646ef5ab)
![{displaystyle U_{y}=left[(A_{x}^{2}+A_{y}^{2})(C_{x}-B_{x})+(B_{x}^{2}+B_{y}^{2})(A_{x}-C_{x})+(C_{x}^{2}+C_{y}^{2})(B_{x}-A_{x})right]/D}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69e0d594fa5173934dd8eaed061df764a43bfaa6)
![{displaystyle D=2left[A_{x}(B_{y}-C_{y})+B_{x}(C_{y}-A_{y})+C_{x}(A_{y}-B_{y})right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9dbe2e53bfcc5e249910bad7534e60d1c30a3a8b)
![{displaystyle left[C'_{y}(B_{x}^{'2}+B_{y}^{'2})-B'_{y}(C_{x}^{'2}+C_{y}^{'2})right]/D',}](https://wikimedia.org/api/rest_v1/media/math/render/svg/979835c7ebb809943501983695147c1a854cc844)
![{displaystyle left[B'_{x}(C_{x}^{'2}+C_{y}^{'2})-C'_{x}(B_{x}^{'2}+B_{y}^{'2})right]/D'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1397bc08e6b08f01d51bd56e582c378f0887a0cd)














































![{displaystyle d=OI={sqrt {{frac {a,b,c,}{a+b+c}}left[{frac {a,b,c,}{(a+b-c),(a-b+c),(-a+b+c)}}-1right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96d414c32e06726f47e1711b71229497899dff1a)

















 Сообщение было отмечено gehh как решение
Сообщение было отмечено gehh как решение


![{displaystyle {begin{aligned}S_{x}={frac {1}{2}}det {begin{bmatrix}|mathbf {A} |^{2}A_{y}1\|mathbf {B} |^{2}B_{y}1\|mathbf {C} |^{2}C_{y}1end{bmatrix}},\[5pt]S_{y}={frac {1}{2}}det {begin{bmatrix}A_{x}|mathbf {A} |^{2}1\B_{x}|mathbf {B} |^{2}1\C_{x}|mathbf {C} |^{2}1end{bmatrix}},\[5pt]a=det {begin{bmatrix}A_{x}A_{y}1\B_{x}B_{y}1\C_{x}C_{y}1end{bmatrix}},\[5pt]b=det {begin{bmatrix}A_{x}A_{y}|mathbf {A} |^{2}\B_{x}B_{y}|mathbf {B} |^{2}\C_{x}C_{y}|mathbf {C} |^{2}end{bmatrix}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1649c42b7532a101a98ee8d0eb5f18f72a4922a1)

![{ displaystyle mathrm {R} (s) = mathrm {P_ {c}} + cos left ({ frac { mathrm {s}}) { mathrm {r}}} right) (P_ {0} -P_ {c}) + sin left ({ frac { mathrm {s}} { mathrm {r}}} right) left [{ widehat {n}} times (P_ {0} -P_ {c}) right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a70aa6cf6f613352caa88916c82a86f03bbc8b4)




![{displaystyle {begin{aligned}U_{x}={frac {1}{D}}left[(A_{x}^{2}+A_{y}^{2})(B_{y}-C_ {y})+(B_{x}^{2}+B_{y}^{2})(C_{y}-A_{y})+(C_{x}^{2}+C_{y}^{2})(A_{y}-B_{y})right]\[5pt]U_{y}={frac {1}{D}}left[(A_{x}^{2}+A_{y}^{2})(C_{x}-B_{x})+(B_{x}^{2}+B_{y}^{2})(A_{x}-C_{x})+(C_{x}^{2}+C_{y}^{2})(B_{x}-A_{x})right]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79248a1cfbeff74ea283e3c6c07a289fe188fb4d)
![D=2left[A_{x}(B_{y}-C_{y})+B_{x}(C_{y}-A_{y})+C_{x}(A_{y}-B_{y})right].,](https://wikimedia.org/api/rest_v1/media/math/render/svg/34c6178eff86289b6ec6f7dd49c95d675180f944)
![{displaystyle {begin{aligned}U'_{x}={frac {1}{D'}}left[C'_{y}({B'_{x}}^{2}+{B'_{y}}^{2})-B'_{y}({C'_{x}}^{2}+{C'_{y}}^{2})right],\[5pt]U'_{y}={frac {1}{D'}}left[B'_{x}({C'_{x}}^{2}+{C'_{y}}^{2})-C'_{x}({B'_{x}}^{2}+{B'_{y}}^{2})right]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae86c30103fce308b05684855b6c7241218358ad)












![{displaystyle {begin{aligned}{text{diameter}}{}={frac {abc}{2cdot {text{area}}}}={frac {|AB||BC||CA|}{2|Delta ABC|}}\[5pt]{}={frac {abc}{2{sqrt {s(s-a)(s-b)(s-c)}}}}\[5pt]{}={frac {2abc}{sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47584c5d8064a85b773192bd5c30ff505b51ac6a)



![{displaystyle {begin{aligned}3{sqrt {3}}Rgeq a+b+c\[5pt]9R^{2}geq a^{2}+b^{2}+c^{2}\[5pt]{frac {27}{4}}R^{2}geq m_{a}^{2}+m_{b}^{2}+m_{c}^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/790d28d5425086fee0f7465ed10d65aab26b5586)



