Как найти уравнение оси симметрии параболы формула

Была ли эта статья полезной?

Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.

Оглавление:

• Что такое парабола и как она выглядит
• Каноническое уравнение параболы
• Свойства и график квадратичной функции
• Как определить, куда направлены ветви параболы
• Как найти вершину параболы по формуле
• Смещение параболы
• Как строить параболу по квадратному уравнению
• Директриса, эксцентриситет, фокус параболы
• Заключение

Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.

Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.

Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.

Что такое парабола и как она выглядит

Алгебра: под этим термином понимается график квадратичной функции.

Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:

1. Любая прямая пересекает на плоскости искомую линию в 2-х точках – так называемые, «нули» (кроме основного экстремума графика).
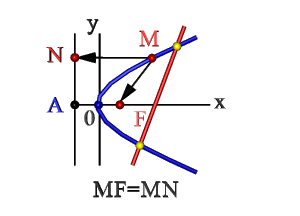
2. Множество точек плоскости ХОY (М), расстояние FM которых до F = расстоянию MN до прямой Где F – фокус, AN – директриса. Эти понятия рассмотрим ниже.

Каноническое уравнение параболы

На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.

Каноническое уравнение имеет вид:

y² = 2 * p * x,

где коэффициент p – фокальный параметр параболы (AF).

В алгебре оно запишется иначе:

y = a x² + b x + c (узнаваемый шаблон: y = x²).

Свойства и график квадратичной функции

Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.

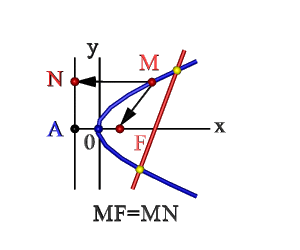
Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.

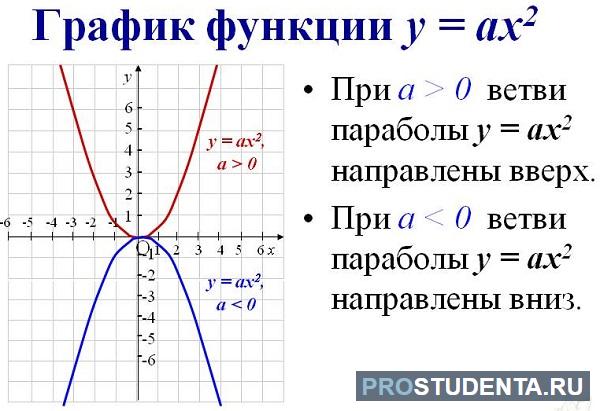
Как определить, куда направлены ветви параболы

Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.

Как найти вершину параболы по формуле

Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.

Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.

Формулы нахождения вершины:

• x₀ = -b / (2 * a);
• y₀ = y (x₀).

Пример.

Имеется функция у = 4 * x² + 16 * x – 25. Найдём вершины этой функции.

Для такой линии:

• х = -16 / (2 * 4) = -2;
• y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.

Получаем координаты вершины (-2, -41).

Смещение параболы

Классический случай, когда в квадратичной функции y = a x² + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0; 0).

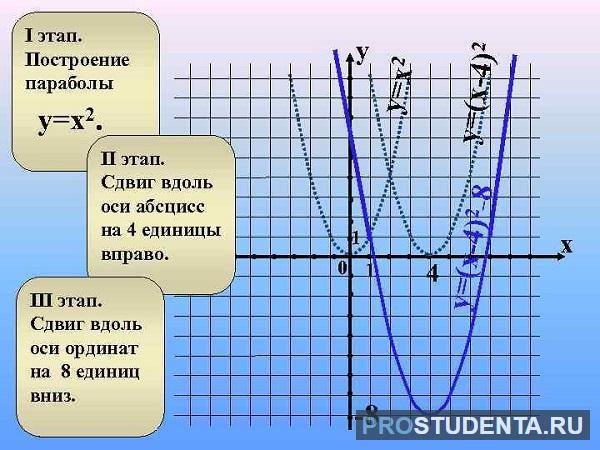
Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.

Пример.

Имеем: b = 2, c = 3.

Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 – по оси ординат.

Как строить параболу по квадратному уравнению

Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.

Анализируя выражения и уравнения, можно увидеть следующее:

1. Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.
2. Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.

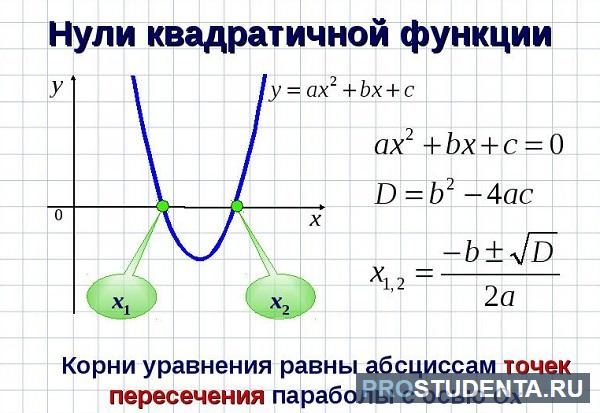
Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:

D = (b² – 4 * a * c).

Для этого нужно приравнять выражение к нулю.

Наличие корней параболы зависит от результата:

• D ˃ 0, то х_{1, 2} = (-b ± D^0,5) / (2 * a);
• D = 0, то х_{1, 2} = -b / (2 * a);
• D ˂ 0, то нет точек пересечения с вектором ОХ.

Получаем алгоритм построения параболы:

• определить направление ветвей;
• найти координаты вершины;
• найти пересечение с осью ординат;
• найти пересечение с осью абсцисс.

Пример 1.

Дана функция у = х² – 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:

1. а = 1, следовательно, ветви направлены вверх;
2. координаты экстремума: х = – (-5) / 2 = 5/2; y = (5/2)² — 5 * (5/2) + 4 = -15/4;
3. с осью ординат пересекается в значении у = 4;
4. найдем дискриминант: D = 25 — 16 = 9;
5. ищем корни:

• Х₁ = (5 + 3) / 2 = 4; (4, 0);
• Х₂ = (5 — 3) / 2 = 1; (1, 0).

По полученным точкам можно построить параболу.

Пример 2.

Для функции у = 3 * х² – 2 * х – 1 нужно построить параболу. Действуем по приведенному алгоритму:

1. а = 3, следовательно, ветви направлены вверх;
2. координаты экстремума: х = – (-2) / 2 * 3 = 1/3; y = 3 * (1/3)² — 2 * (1/3) — 1 = -4/3;
3. с осью у будет пересекаться в значении у = -1;
4. найдем дискриминант: D = 4 + 12 = 16. Значит корни:

• Х₁ = (2 + 4) / 6 = 1; (1;0);
• Х₂ = (2 — 4) / 6 = -1/3; (-1/3; 0).

По полученным точкам можно построить параболу.

Директриса, эксцентриситет, фокус параболы

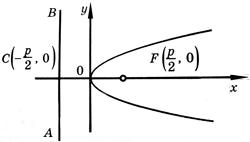
Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).

Прямая АВ – директриса (своего рода хорда параболы определенной длины). Ее уравнение: х = -р/2.

Эксцентриситет (константа) = 1.

Заключение

Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 декабря 2022 года; проверки требует 1 правка.

Парабола
Парабола как коническое сечение
Парабола, её фокус и директриса
Эксцентриситет
Уравнения
Другие конические сечения
Гипербола Парабола Эллипс Окружность

Пара́бола (греч. παραβολή — приближение^[1]) — плоская кривая, один из типов конических сечений.

Определение[править | править код]

Античные математики определяли параболу как результат пересечения кругового конуса с плоскостью, которая не проходит через вершину конуса и параллельна его образующей (см. рисунок). В аналитической геометрии удобнее эквивалентное определение: парабола есть геометрическое место точек на плоскости, для которых расстояние до заданной точки (фокуса) равно расстоянию до заданной прямой (директрисы) (см. рисунок)^[2].

Если фокус лежит на директрисе, то парабола вырождается в ломаную.

Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

Вершина[править | править код]

Точка параболы, ближайшая к её директрисе, называется вершиной этой параболы. Вершина является серединой перпендикуляра, опущенного из фокуса на директрису.

Уравнения[править | править код]

Каноническое уравнение параболы в прямоугольной системе координат:

(или , если поменять местами оси координат).

Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы^[3]. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии от обоих.

Вывод
Уравнение директрисы PQ: , фокус F имеет координаты Таким образом, начало координат O — середина отрезка CF. По определению параболы, для любой точки M, лежащей на ней, выполняется равенство KM = FM. Далее, поскольку и , то равенство приобретает вид: После возведения в квадрат и некоторых преобразований получается равносильное уравнение

Парабола, заданная квадратичной функцией[править | править код]

Квадратичная функция при также является уравнением параболы и графически изображается той же параболой, что и но в отличие от последней имеет вершину не в начале координат, а в некоторой точке A, координаты которой вычисляются по формулам:

где  — дискриминант квадратного трёхчлена.

Ось симметрии параболы, заданной квадратичной функцией, проходит через вершину параллельно оси ординат. При a > 0 (a < 0) фокус лежит на этой оси над (под) вершиной на расстоянии 1/4a, а директриса — под (над) вершиной на таком же расстоянии и параллельна оси абсцисс. Уравнение может быть представлено в виде а в случае переноса начала координат в точку A уравнение параболы превращается в каноническое. Таким образом, для каждой квадратичной функции можно найти систему координат такую, что в этой системе уравнение соответствующей параболы представляется каноническим. При этом

Общее уравнение параболы[править | править код]

В общем случае парабола не обязана иметь ось симметрии, параллельную одной из координатных осей. Однако, как и любое другое коническое сечение, парабола является кривой второго порядка и, следовательно, её уравнение на плоскости в декартовой системе координат может быть записано в виде квадратного многочлена:

Если кривая второго порядка, заданная в таком виде, является параболой, то составленный из коэффициентов при старших членах дискриминант равен нулю.

Уравнение в полярной системе[править | править код]

Парабола в полярной системе координат с центром в фокусе и нулевым направлением вдоль оси параболы (от фокуса к вершине) может быть представлена уравнением

где p — фокальный параметр (расстояние от фокуса до директрисы или удвоенное расстояние от фокуса до вершины)

Расчёт коэффициентов квадратичной функции[править | править код]

Если для уравнения параболы с осью, параллельной оси ординат, известны координаты трёх различных точек параболы то его коэффициенты могут быть найдены так:

Если же заданы вершина и старший коэффициент , то остальные коэффициенты и корни вычисляются по формулам:

Свойства[править | править код]

• Парабола — кривая второго порядка.
• Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.
• Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей. Сигнал также придет в одной фазе, что важно для антенн.
• Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
• Отрезок, соединяющий середину произвольной хорды параболы и точку пересечения касательных к ней в концах этой хорды, перпендикулярен директрисе, а его середина лежит на параболе.
• Парабола является антиподерой прямой.
• Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
• Траектория фокуса параболы, катящейся по прямой, есть Цепная линия^[4].
• Описанная окружность треугольника, описанного около параболы, проходит через её фокус, а точка пересечения высот лежит на её директрисе

Связанные определения[править | править код]

• При вращении параболы вокруг оси симметрии получается эллиптический параболоид.

Вариации и обобщения[править | править код]

Графики степенной функции при натуральном показателе называются параболами порядка ^[5][6]. Ранее рассмотренное определение соответствует то есть параболе 2-го порядка.

Парабола также представляет собой синусоидальную спираль при ;

Параболы в физическом пространстве[править | править код]

Траектории некоторых космических тел (комет, астероидов и других), проходящих вблизи звезды или другого массивного объекта (звезды или планеты) на достаточно большой скорости, имеют форму параболы (или гиперболы). Эти тела, вследствие своей большой скорости, не захватываются гравитационным полем звезды и продолжают свободный полёт. Это явление используется для гравитационных манёвров космических кораблей (в частности, аппаратов Вояджер).

Для создания невесомости в земных условиях проводятся полёты самолётов по параболической траектории, так называемой параболе Кеплера.

При отсутствии сопротивления воздуха траектория полёта тела в приближении однородного гравитационного поля представляет собой параболу.

Также параболические зеркала используются в любительских переносных телескопах систем Кассегрена, Шмидта — Кассегрена, Ньютона, а в фокусе параболы устанавливают вспомогательные зеркала, подающие изображение на окуляр.

При вращении сосуда с жидкостью вокруг вертикальной оси поверхность жидкости в сосуде и вертикальная плоскость пересекаются по параболе.

Свойство параболы фокусировать пучок лучей, параллельных оси параболы, используется в конструкциях прожекторов, фонарей, фар, а также телескопов-рефлекторов (оптических, инфракрасных, радио- …), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанций и в других областях.

Форма параболы иногда используется в архитектуре для строительства крыш и куполов.

• 

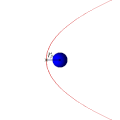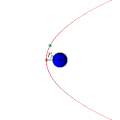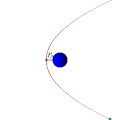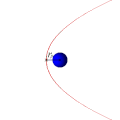
  Параболическая орбита и движение спутника по ней (анимация)

• 

• 

• 

  Параболические траектории струй воды

• 

  Вращающийся сосуд с жидкостью

Примечания[править | править код]

Литература[править | править код]

• Акопян А. А., Заславский А. В. Геометрические свойства кривых второго порядка. — М.: МЦНМО, 2007. — 136 с.
• Бронштейн И. Парабола // Квант. — 1975. — № 4. — С. 9—16.
• Маркушевич А. И. Замечательные кривые. — Гостехиздат, 1952. — 32 с. — (Популярные лекции по математике, выпуск 4).
• Парабола // Математическая энциклопедия (в 5-и томах). — М.: Советская Энциклопедия, 1984. — Т. 4. — С. 191—192. — 1216 с.

Ссылки[править | править код]

• Статья в справочнике «Прикладная математика».
• Анимированные рисунки, иллюстрирующие некоторые свойства параболы.
• Информация (англ.) о связи параболы с физикой.
• Учебный фильм о параболе

Уравнение оси симметрии

Этот калькулятор позволит вам найти уравнение оси симметрии для заданной квадратичной функции, показывая все этапы процесса.

Вам необходимо предоставить действительное выражение квадратичной функции. Например, допустимой квадратичной функцией является что-то вроде 2x² – 5x + 1, но вы также можете ввести не полностью упрощенную квадратичную функцию, например 2x² + 5x +3/4 x – x² , так как калькулятор проведет необходимое упрощение квадратичной функции.

Как только вы зададите действительную квадратичную функцию, вам нужно нажать кнопку “Вычислить”, и будут предоставлены решения со всеми шагами.

Ось симметрии имеет сильное геометрическое значение, именно она служит “зеркалом” для графика квадратичной функции, которая является параболой, и она тесно связана с корнями квадратичной функции.

Формула оси симметрии

график

из

квадратичная функция

ax² +b x + c – парабола, и эта парабола будет симметрична вокруг своей оси симметрии. Уравнение оси симметрии имеет вид:

[x = displaystyle -frac{b}{2a} ]

Каковы шаги для нахождения уравнения оси симметрии?

• Шаг 1: Определите квадратичную функцию и упростите ее до вида ax² +b x + c
• Шаг 2: Упростив квадратичную функцию, убедитесь, что a ≠ 0, иначе вы не сможете продолжать
• Шаг 3: Уравнение оси симметрии имеет вид (x = displaystyle -frac{b}{2a} )
• Шаг 4: Это означает, что ось симметрии – вертикальная линия, проходящая через точку (left(displaystyle -frac{b}{2a}, 0right) )

Обратите внимание, что это относится к обычным параболам, без вращения осей, что выходит за рамки данного учебника.

Калькулятор оси симметрии

Этот

Калькулятор параболы

получит квадратичную функцию, упростит ее до вида ax² +b x + c и подставит значения a и b в формулу:

[x = displaystyle -frac{b}{2a} ]

Но есть и другие способы поиска

Ось симметрии

параболы. Предположим, что вы

решить квадратное уравнение

ax² +b x + c = 0, и вы находите корни u и v. Как вы находите

Ось симметрии

когда вы знаете корни квадратного уравнения?

• Шаг 1: Определите заданные корни квадратных уравнений
• Шаг 2: У вас будет два корня u и v. Если есть только один корень, вы определяете u и v как одно и то же значение
• Шаг 3: Ось симметрии находится путем вычисления средней точки корней u и v: Таким образом, мы получаем формулу оси симметрии (x = displaystyle frac{u+v}{2}). Это работает как для вещественных, так и для комплексных корней

Когда у вас

сложные корни

то они будут сопряженными комплексными числами, и тогда их среднее даст действительное число.

Зачем заботиться об оси симметрии?

Ось симметрии соответствует симметричной линии для графика квадратичной функции, которая является параболой. Таким образом, наличие ссылки на симметрию дает много информации о параболе.

Например, корни уравнения будут располагаться симметрично относительно этой оси симметрии.

Пример: ось симметрии

Рассмотрим следующее квадратное уравнение: (f(x) = 3x^2 + 2x + 1). Найдите его ось симметрии.

Решение:

чем завершается расчет.

Пример: уравнение оси симметрии

Предположим, что у вас есть следующее квадратичное выражение: (f(x) = x^2 + frac{2}{3}x + frac{5}{4}). Используйте формулу для вычисления его оси симметрии.

Решение:

чем завершается расчет.

Пример: формула оси симметрии из корней

Предположим, что корнями квадратного уравнения являются (r_1 = 3) и (r_2 = 5). Найдите уравнение оси симметрии параболы.

Отвечать:

Мы знаем, что при наличии корней необходимо усреднить корни. Следовательно, уравнение оси симметрии параболы имеет вид

[x = displaystyle frac{u+v}{2} = displaystyle frac{3+5}{2} = 4]

чем завершается расчет.

Больше квадратичных калькуляторов

Нахождение оси симметрии параболы – это лишь одна из многих задач, которые можно решить с помощью функции

квадратичные функции

. Вы можете

решать квадратные уравнения

и

вычислить вершину

.

Кроме того, как вы, вероятно, уже заметили, существует тесная связь между

формула вершины

и ось симметрии: Действительно, ось симметрии – это вертикальная линия, проходящая через вершину.

Как найти ось симметрии квадратичной функции

Содержание

• Что такое квадратичная функция
• Как найти ось симметрии квадратичной функции
• Как найти ось симметрии квадратичной функции – Примеры

Что такое квадратичная функция

Полиномиальная функция второй степени называется квадратичной функцией. Формально f (x) = ax²+ bx + c – квадратичная функция, где a, b и c – действительные постоянные и a ≠ 0 для всех значений x. График квадратичной функции является параболой.

Как найти ось симметрии квадратичной функции

Любая квадратичная функция показывает поперечную симметрию поперек оси y или линии, параллельной ей. Ось симметрии квадратичной функции может быть найдена следующим образом:

F (X) = ах²+ bx + c, где a, b, c, x∈R и a ≠ 0

Написание х терминов в виде полного квадрата у нас есть,

Переставляя члены вышеприведенного уравнения

Это означает, что для каждого возможного значения f (x) есть два соответствующих значения x. Это хорошо видно на диаграмме ниже.

Эти значения расположены,

 

расстояние влево и вправо от значения -b / 2a. Другими словами, значение -b / 2a всегда является средней точкой линии, соединяющей соответствующие значения x (точки) для любого заданного f (x).

Следовательно ,
x = -b / 2a – уравнение оси симметрии для заданной квадратичной функции в виде f (x) = ax²+ BX + C

Как найти ось симметрии квадратичной функции – Примеры

• Квадратичная функция определяется как f (x) = 4x²+ Х + 1. Найдите симметричную ось.

х = -b / 2a = -1 / (2 × 4) = – 1/8

Следовательно, уравнение оси симметрии имеет вид х = -1 / 8

• Квадратичная функция задается выражением f (x) = (x-2) (2x-5)

Упрощая выражение, мы получаем f (x) = 2x²-5x-4x + 10 = 2x²-9x + 10

Мы можем сделать вывод, что a = 2 и b = -9. Следовательно, мы можем получить ось симметрии как

х = – (-9) / (2 × 2) = 9/4