Как легко составить уравнение параболы по графику
В данной статье репетитор по математике рассказывает о простом и эффективном способе составления уравнения параболы по её графику, которому вас не научат в школе. Дочитайте эту статью до конца или посмотрите видео с подробным объяснением, потому что эта информация может вам пригодиться на экзамене.
Задача состоит в том, чтобы по графику параболы (см. рисунок) определить коэффициенты a, b и c соответствующей квадратичной функции ![]() :
:
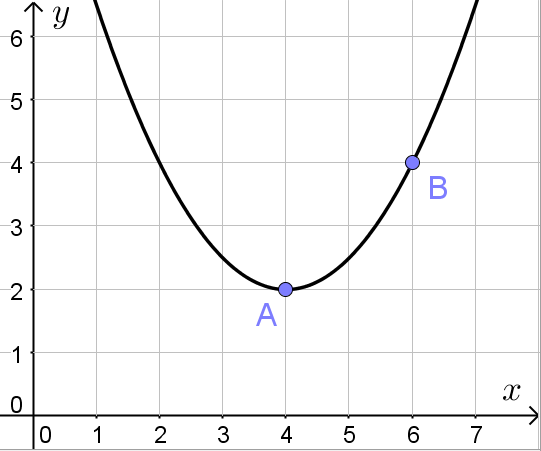
Существует стандартный и крайне неэффективный способ решения этой задачи. Он заключается в том, чтобы через координату ![]() вершины параболы связать коэффициенты a и b, используя формулу
вершины параболы связать коэффициенты a и b, используя формулу ![]() . Затем взять координаты двух точек, которые принадлежат параболе, составить систему уравнений и решить её относительно искомых коэффициентов. Считать придётся долго и муторно.
. Затем взять координаты двух точек, которые принадлежат параболе, составить систему уравнений и решить её относительно искомых коэффициентов. Считать придётся долго и муторно.
Мы не пойдём этим путём. Предлагаемый в данной статье способ намного более прост и изящен. Введём новую систему координат ![]() с центром в вершине параболы и осями, сонаправленными с исходной системой координат. В данной системе координат уравнение нашей параболы будет иметь вид:
с центром в вершине параболы и осями, сонаправленными с исходной системой координат. В данной системе координат уравнение нашей параболы будет иметь вид: ![]() , где
, где ![]() . Изобразим в новой системе координат график квадратичной функции
. Изобразим в новой системе координат график квадратичной функции ![]() (синяя пунктирная линия на рисунке):
(синяя пунктирная линия на рисунке):
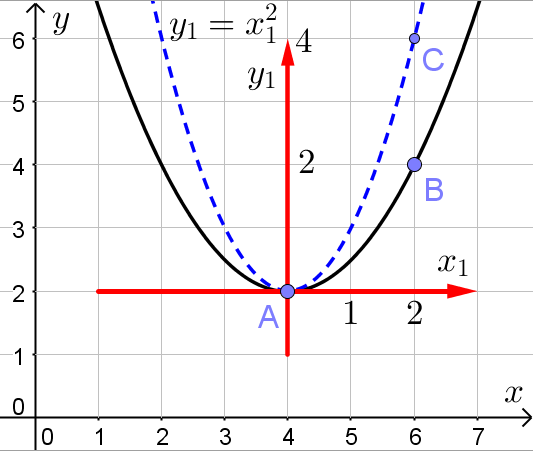
Абсциссы точек C и B в новой системе координат равны. Ордината точки C в 2 раза больше ординаты точки B. Значит график исходной параболы в новой системе координат получен умножением на ![]() всех ординат точек графика функции
всех ординат точек графика функции ![]() . Откуда получаем, что
. Откуда получаем, что ![]() . Значит исходная парабола может быть представлена в виде следующего выражения в новой системе координат:
. Значит исходная парабола может быть представлена в виде следующего выражения в новой системе координат: ![]() .
.
Осталось перейти в исходную систему координат. Поскольку новая система координат получена путём параллельного переноса исходной системы координат на 4 единичных отрезка вправо и 2 единичных отрезка вверх, то в исходной системе координат наша парабола может быть представлена в виде следующего выражения:
![]()
Как видите, данный способ требует минимум вычислений и фактически является полуустным. Запомните этот способ, он может пригодиться вам при решений задач из ЕГЭ, ОГЭ или вступительных экзаменов в вузы и школы с углубленным изучением математики.
Квадратичная функция. Построение параболы

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило, в соответствии с которым каждому значению аргумента соответствует единственное значение функции. Вот какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек координатной плоскости, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0.
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 в частном случае при b = 0, c = 0:
Точки, обозначенные фиолетовыми кружками, называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:
x
y
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов. При увеличении старшего коэффициента график сужается, при уменьшении — расширяется.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
x
y
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
- Если старший коэффициент больше нуля (a > 0), то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля (a < 0), то ветви параболы напрaвлены вниз.
Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.
Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.
Для наглядности возьмем функцию y = ax 2 + bx + c. Чтобы найти точки пересечения с осью Ox, нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
- Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
Теперь понятно, что, зная направление ветвей параболы и знак дискриминанта, мы можем схематично представить график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
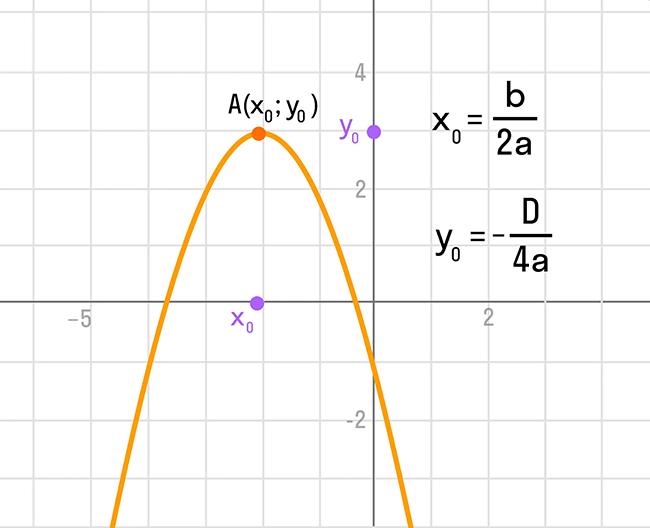
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
- Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.
D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
- Координаты вершины параболы:
Точка пересечения с осью OY находится: (0; -5) относительно оси симметрии.
Нанесем эти точки на координатную плоскость и построим график параболы:
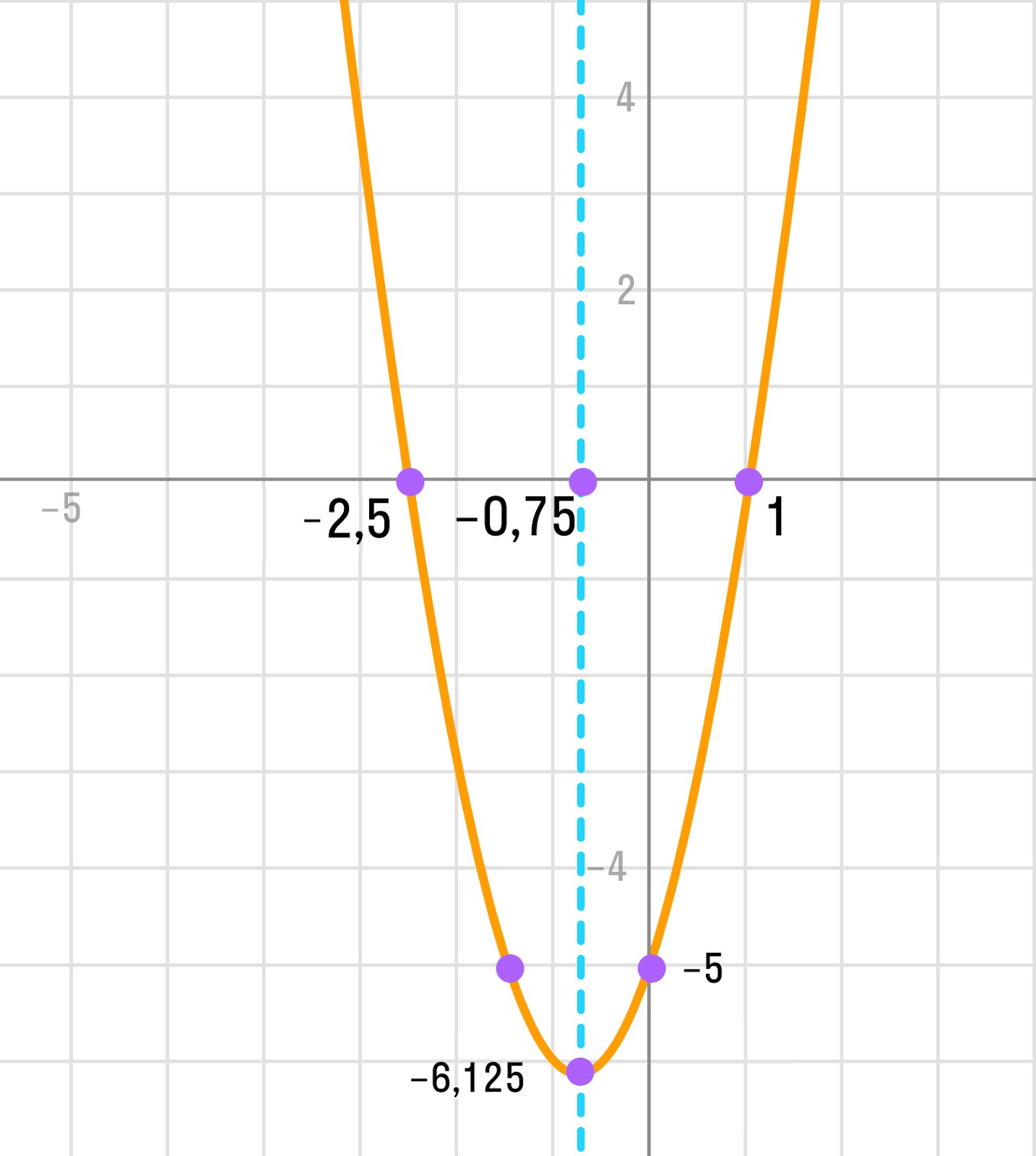
Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀
Зная координаты вершины параболы и старший коэффициент, можно записать уравнение квадратичной функции в виде у = a(x − x0) + y0, где x0, y0 — координаты вершины параболы.
Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.
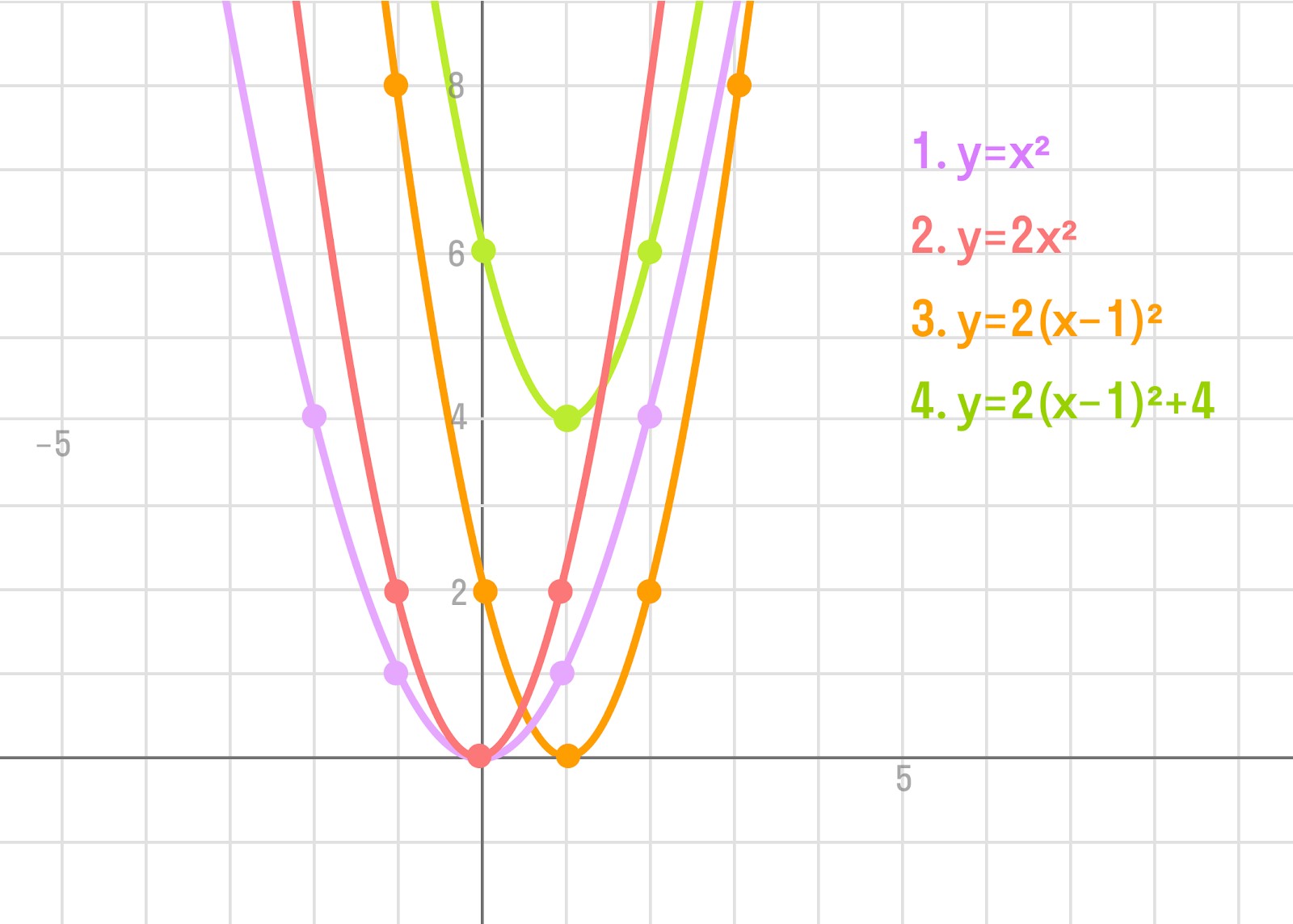
Рассмотрим пример: y = 2 * (x — 1) 2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить график функции y = x 2 ,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
Построить график параболы для каждого случая.
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид функции позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:

Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная относительно оси симметрии параболы.
Отметим эти точки на координатной плоскости и соединим плавной прямой линией.
Как построить параболу
Соавтор(ы): Jake Adams. Джейк Адамс — репетитор и владелец онлайн-сервиса Simplifi EDU с офисом в Санта-Монике, Калифорния, который предлагает образовательные ресурсы и услуги репетиторов по предметам от уровня детского сада до колледжа, помощь в подготовке к тестам SAT и ACT и консультирование по вопросам поступления в колледж. Имеет более 14 лет опыта в качестве профессионального репетитора, нацелен на предоставление клиентам репетиторских услуг высочайшего качества и доступа к сети, объединяющей выскоквалифицированных репетиторов с высшим образованием из лучших колледжей страны. Получил диплом бакалавра по международному бизнесу и маркетингу в Университете Пеппердайна.
Количество источников, использованных в этой статье: 7. Вы найдете их список внизу страницы.
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило, в соответствии с которым каждому значению аргумента соответствует единственное значение функции. Вот какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек координатной плоскости, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно
на курсах по математике в онлайн-школе Skysmart.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.

Построение квадратичной функции
Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0.
График квадратичной функции — парабола, которая имеет следующий вид для y = x2 в частном случае при b = 0, c = 0:
Точки, обозначенные фиолетовыми кружками, называют базовыми точками. Чтобы найти их координаты для функции y = x2, нужно составить таблицу:
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y |
4 |
1 |
0 |
1 |
4 |
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x2 при любых значениях остальных коэффициентов. При увеличении старшего коэффициента график сужается, при уменьшении — расширяется.
График функции y = –x2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y |
−4 |
−1 |
0 |
−1 |
−4 |
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
- Если старший коэффициент больше нуля (a > 0), то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля (a < 0), то ветви параболы напрaвлены вниз.
Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.
Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.
Для наглядности возьмем функцию y = ax2 + bx + c. Чтобы найти точки пересечения с осью Ox, нужно решить квадратное уравнение ax2 + bx + c = 0. В процессе найдем дискриминант D = b2 – 4ac, который даст нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
- Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
Теперь понятно, что, зная направление ветвей параболы и знак дискриминанта, мы можем схематично представить график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax2 + bx + c.
Разберем общий алгоритм на примере y = 2x2 + 3x – 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
- Найдем дискриминант квадратного трехчлена 2x2 + 3x – 5.
D = b2 – 4ac = 9 – 4 * 2 * (-5) = 49 > 0
√D = 7
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
2x2 + 3x – 5 = 0
,
- Координаты вершины параболы:
- Точка пересечения с осью OY находится: (0; -5) относительно оси симметрии.
-
Нанесем эти точки на координатную плоскость и построим график параболы:

Уравнение квадратичной функции имеет вид y = a * (x – x₀)2 + y₀
Зная координаты вершины параболы и старший коэффициент, можно записать уравнение квадратичной функции в виде у = a(x − x0) + y0, где x0, y0 — координаты вершины параболы.
Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x2 + 3x – 5 при а = 1, то второй коэффициент является четным числом.
Рассмотрим пример: y = 2 * (x – 1)2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить график функции y = x2,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
-
Построить график параболы для каждого случая.

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
-
Данный вид функции позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
-
Определим координаты вершины параболы:

-
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная относительно оси симметрии параболы.
-
Отметим эти точки на координатной плоскости и соединим плавной прямой линией.
Сообщения без ответов | Активные темы
Как по точкам составить уравнение параболы
Модераторы: Prokop, mad_math
| Автор | Сообщение | ||
|---|---|---|---|
|
alexa125 |
|
||
|
Дан график параболы. Точки (-8;0), (1;0) и (0,3) Я забыла как по точкам составить уравнение параболы
|
||
| Вернуться к началу |
|
||
|
alexa125 |
|
||
|
Спасибо:) с=3 я сразу же нашла:)
|
|||
| Вернуться к началу |
|
||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Составить уравнение параболы
в форуме Начала анализа и Другие разделы школьной математики |
sniperghost |
1 |
986 |
11 ноя 2014, 21:11 |
|
Составить уравнение параболы
в форуме Аналитическая геометрия и Векторная алгебра |
HUEHUEHUE |
1 |
1064 |
22 окт 2014, 15:36 |
|
Составить каноническое и полярное уравнение параболы
в форуме Аналитическая геометрия и Векторная алгебра |
middle |
2 |
355 |
06 янв 2017, 16:37 |
|
Составить уравнение параболы зная фокус и вершину
в форуме Аналитическая геометрия и Векторная алгебра |
bhelp |
1 |
770 |
19 дек 2016, 16:37 |
|
Получение коэф наклонной параболы по точкам
в форуме Аналитическая геометрия и Векторная алгебра |
Ignatyyy |
0 |
329 |
27 ноя 2015, 19:59 |
|
Составить канонические уравнения эллипса, гиперболы,параболы
в форуме Аналитическая геометрия и Векторная алгебра |
LuluHate |
0 |
87 |
23 ноя 2022, 15:16 |
|
Алгебраическое уравнение поверхности по точкам min max
в форуме Аналитическая геометрия и Векторная алгебра |
Zink |
7 |
450 |
04 сен 2016, 10:53 |
|
Уравнение кривой по точкам и касательным
в форуме Аналитическая геометрия и Векторная алгебра |
rusty_cat |
0 |
1067 |
24 авг 2015, 19:27 |
|
Уравнение параболы
в форуме Аналитическая геометрия и Векторная алгебра |
yaroslav1997 |
1 |
516 |
16 дек 2014, 01:24 |
|
Найти уравнение параболы
в форуме Аналитическая геометрия и Векторная алгебра |
ArsPol |
1 |
668 |
25 окт 2013, 19:36 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 8 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
Как легко составить уравнение параболы по графику
Среда, 3 августа, 2016
В данной статье репетитор по математике рассказывает о простом и эффективном способе составления уравнения параболы по её графику, которому вас не научат в школе. Дочитайте эту статью до конца или посмотрите видео с подробным объяснением, потому что эта информация может вам пригодиться на экзамене.
Задача состоит в том, чтобы по графику параболы (см. рисунок) определить коэффициенты a, b и c соответствующей квадратичной функции ![]() :
:

Существует стандартный и крайне неэффективный способ решения этой задачи. Он заключается в том, чтобы через координату ![]() вершины параболы связать коэффициенты a и b, используя формулу
вершины параболы связать коэффициенты a и b, используя формулу ![]() . Затем взять координаты двух точек, которые принадлежат параболе, составить систему уравнений и решить её относительно искомых коэффициентов. Считать придётся долго и муторно.
. Затем взять координаты двух точек, которые принадлежат параболе, составить систему уравнений и решить её относительно искомых коэффициентов. Считать придётся долго и муторно.
Мы не пойдём этим путём. Предлагаемый в данной статье способ намного более прост и изящен. Введём новую систему координат ![]() с центром в вершине параболы и осями, сонаправленными с исходной системой координат. В данной системе координат уравнение нашей параболы будет иметь вид:
с центром в вершине параболы и осями, сонаправленными с исходной системой координат. В данной системе координат уравнение нашей параболы будет иметь вид: ![]() , где
, где ![]() . Изобразим в новой системе координат график квадратичной функции
. Изобразим в новой системе координат график квадратичной функции ![]() (синяя пунктирная линия на рисунке):
(синяя пунктирная линия на рисунке):

Абсциссы точек C и B в новой системе координат равны. Ордината точки C в 2 раза больше ординаты точки B. Значит график исходной параболы в новой системе координат получен умножением на ![]() всех ординат точек графика функции
всех ординат точек графика функции ![]() . Откуда получаем, что
. Откуда получаем, что ![]() . Значит исходная парабола может быть представлена в виде следующего выражения в новой системе координат:
. Значит исходная парабола может быть представлена в виде следующего выражения в новой системе координат: ![]() .
.
Осталось перейти в исходную систему координат. Поскольку новая система координат получена путём параллельного переноса исходной системы координат на 4 единичных отрезка вправо и 2 единичных отрезка вверх, то в исходной системе координат наша парабола может быть представлена в виде следующего выражения:
![]()
Как видите, данный способ требует минимум вычислений и фактически является полуустным. Запомните этот способ, он может пригодиться вам при решений задач из ЕГЭ, ОГЭ или вступительных экзаменов в вузы и школы с углубленным изучением математики.
Статья написана репетитором по математике в Москве, Сергеем Валерьевичем
|
19 / 18 / 7 Регистрация: 16.05.2017 Сообщений: 447 |
|
|
1 |
|
Составить уравнение параболы по двум точкам18.12.2017, 15:41. Показов 23450. Ответов 12
Что я уже на час подзавис. Коэффициент c нашел, а что дальше делать не знаю. Вообще нужно решить криволинейный интеграл первого порядка, но не дана функция, а только написано, что часть параболы от точек (0;0) и (2;4). Понятно, что с=0 и что один из корней тоже равен 0. Т.е. y = x(ax + b), но как найти a и b? Нужна помощь. С интегралом и сам справлюсь. Сасибо
0 |
|
Диссидент
27465 / 17154 / 3780 Регистрация: 24.12.2010 Сообщений: 38,635 |
|
|
18.12.2017, 15:58 |
2 |
|
Вообще-то через 2 точки можно построить много парабол вида y = ax2+bx…Может быть (0,0) – вершина? Тогда и b=0 Добавлено через 1 минуту
0 |
|
6353 / 4062 / 1509 Регистрация: 09.10.2009 Сообщений: 7,550 Записей в блоге: 4 |
|
|
18.12.2017, 16:03 |
3 |
|
Байт, так первого же рода, не второго. ТС не договаривает что-то.
0 |
|
19 / 18 / 7 Регистрация: 16.05.2017 Сообщений: 447 |
|
|
18.12.2017, 18:10 [ТС] |
4 |
|
Вот задание: Но возможно, ваш интеграл не зависит от пути интегрирования… Ну я не сильно силен, учусь, но как я понял что не зависит. Добавлено через 1 минуту Добавлено через 20 минут Добавлено через 1 час 20 минут
0 |
|
3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,668 Записей в блоге: 4 |
|
|
18.12.2017, 18:52 |
5 |
|
Наверняка имеется в виду парабола
0 |
|
19 / 18 / 7 Регистрация: 16.05.2017 Сообщений: 447 |
|
|
18.12.2017, 18:54 [ТС] |
6 |
|
Да я тоже в этом уверен, но имеется в виду без доказательства вряд ли прокатит)
0 |
|
Диссидент
27465 / 17154 / 3780 Регистрация: 24.12.2010 Сообщений: 38,635 |
|
|
18.12.2017, 22:19 |
7 |
|
никто не может помочь. А как тут помочь? Данных явно мало. Придумать дополнительные данные за тебя?
0 |
|
19 / 18 / 7 Регистрация: 16.05.2017 Сообщений: 447 |
|
|
18.12.2017, 22:40 [ТС] |
8 |
|
А как тут помочь? Данных явно мало. Придумать дополнительные данные за тебя? Ну во первых мы с вами не так близко знакомы, чтобы переходить на ты. А во вторых, я полное условие написал выше, только там нет под интегралом обозначения кривой L, так как я не знаю как ее туда поместить. Я конечно тоже склоняюсь, что должно быть простое уравнение параболы y=x2, но повторюсь, что это надо как то обосновать, а не мне кажется.
0 |
|
19 / 18 / 7 Регистрация: 16.05.2017 Сообщений: 447 |
|
|
18.12.2017, 22:44 [ТС] |
9 |
|
Ну вот скрин задания, если поможет. Но оо ничем не отличается от того что я выше написал Миниатюры
0 |
|
6353 / 4062 / 1509 Регистрация: 09.10.2009 Сообщений: 7,550 Записей в блоге: 4 |
|
|
18.12.2017, 22:45 |
10 |
|
BaredJJ, а может быть ветвь параболы, положенной на бок:
0 |
|
Диссидент
27465 / 17154 / 3780 Регистрация: 24.12.2010 Сообщений: 38,635 |
|
|
18.12.2017, 22:49 |
11 |
|
чтобы переходить на ты. Простите, ради Бога, за мой шальной язык. Тут как-то не принято так жестко следить за этикетом. Но если Вас это коробит, то я, во избежании повторения таких ошибок, постараюсь избегать общения с Вами.
0 |
|
6353 / 4062 / 1509 Регистрация: 09.10.2009 Сообщений: 7,550 Записей в блоге: 4 |
|
|
18.12.2017, 22:55 |
12 |
|
Вот общий вид парабол, проходящих через указанные две точки ( (0;0) – не вершина):
1 |
|
19 / 18 / 7 Регистрация: 16.05.2017 Сообщений: 447 |
|
|
19.12.2017, 13:52 [ТС] |
13 |
|
Простите, ради Бога, за мой шальной язык. Тут как-то не принято так жестко следить за этикетом. Но если Вас это коробит, то я, во избежании повторения таких ошибок, постараюсь избегать общения с Вами. Ну вы же взрослый человек, сами меня тыкнули, а теперь из меня виноватого делаете. Будьте благоразумны и умейте спокойно относится к замечаниям и в свой адрес. Тем более, что я вам ничего плохого не сделал и не сказал, а только обратил внимание на то, что мне не очень приятно. Добавлено через 28 минут
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
19.12.2017, 13:52 |
|
13 |








