Как найти уравнение плоскости через вектор нормали

35

36

9. Расстояние от точки до плоскости

Расстояние от произвольной точки M0 (x0 , y0 , z0 ) до плоскости Ax + By + Cz + D = 0 равно:

d = Ax0 + By0 + Cz0 + D

A2 + B2 + C 2

Пример. Найти уравнение плоскости, проходящей через точки А(2,-1,4) и В(3,2,-1) перпендикулярно плоскости x + y + 2z − 3 = 0 .

Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0 , вектор нормали к этой плоскости n1 (A,B,C). Вектор AB (1,3,-5) принадлежит плоскости. Заданная нам плоскость,

перпендикулярная искомой имеет вектор нормали n2 (1,1,2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то

n = AB × n			i	j	k	= i		3	− 5		− j		1	− 5		+ k		1	3		= 11i − 7 j − 2k.
2	=	1	3	− 5
1							1	2				1	2				1	1
			1	1	2

Таким образом, вектор нормали n1 (11,-7,-2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е.

11.2+ 7.1− 2.4 + D = 0; D = −21. Итого, получаем уравнение плоскости: 11x − 7 y − 2z − 21 = 0

10.Уравнение линии в пространстве

Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:

F(x, y, z) = 0 . Это уравнение называется уравнением линии в пространстве.

Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана какимлибо уравнением.

Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L.

F(x, y, z) = 0

Тогда пару уравнений Ф(x, y, z) = 0 назовем уравнением линии в пространстве.

11. Уравнение прямой в пространстве по точке и направляющему вектору

Возьмем произвольную прямую и вектор S (m, n, p), параллельный данной прямой. Вектор S называется направляющим вектором прямой.

На прямой возьмем две произвольные точки M0 (x0 , y0 , z0 ) и M (x, y, z) .

z

37

38

Для того, чтобы однозначно построить плоскость, необходимы три точки, которые не лежат на одной прямой.

Общее уравнение плоскости принимает вид:

Общее уравнение плоскости

Ax+By+Cz+D=0Ax+By+Cz+D=0,

где A,B,C,DA, B, C, D — коэффициенты, задающие плоскость. Они не могут быть одновременно равны нулю.

Здесь будет калькулятор

Составление уравнения плоскости по трем точкам

Текст цитаты

Заголовок

Текст цитаты

В случае, когда известны координаты всех трех точек, уравнение плоскости, проходящей через эти точки составляется с помощью определителя:

Уравнение плоскости через определитель

∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0,

где (x1;y1;z1),(x2;y2;z2),(x3;y3;z3)(x_1;y_1;z_1), (x_2;y_2;z_2), (x_3;y_3;z_3) — координаты точек, через которые проходит данная плоскость, а (x;y;z)(x; y; z) — всевозможные координаты точек этой плоскости.

Задача 1

Составить уравнения плоскости проходящей через три точки с координатами (1;3;0),(5;6;4),(−1;−4;0)(1;3;0), (5;6;4), (-1;-4;0).

Решение

Пусть:

x1=1x_1=1
y1=3y_1=3
z1=0z_1=0
x2=5x_2=5
y2=6y_2=6
z2=4z_2=4
x3=−1x_3=-1
y3=−4y_3=-4
z3=0z_3=0

Составляем определитель:

∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0

∣x−15−1−1−1y−36−3−4−3z−04−00−0∣=0begin{vmatrix}
x-1 & 5-1 & -1-1 \
y-3 & 6-3 & -4-3 \
z-0 & 4-0 & 0-0 \
end{vmatrix}=0

∣x−14−2y−33−7z40∣=0begin{vmatrix}
x-1 & 4 & -2 \
y-3 & 3 & -7 \
z & 4 & 0 \
end{vmatrix}=0

28x−8y−22z−4=028x-8y-22z-4=0 — уравнение искомой плоскости.

Ответ

28x−8y−22z−4=028x-8y-22z-4=0

Уравнение плоскости по точке и вектору нормали

Если дана точка, лежащая на плоскости и вектор нормали к этой плоскости, то сама плоскость задается уравнением:

Уравнение плоскости по точке и нормали

(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0,

где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, принадлежащей плоскости, а (n1;n2;n3)(n_1;n_2;n_3) — координаты вектора нормали к этой плоскости.

Задача 2

Выпишите уравнение плоскости, если даны: координата точки плоскости (8;−2;9)(8;-2;9) и вектор нормали (1;3;5)(1;3;5).

Решение

x0=8x_0=8
y0=−2y_0=-2
z0=9z_0=9
n1=1n_1=1
n2=3n_2=3
n3=5n_3=5

(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0

(x−8)⋅1+(y−(−2))⋅3+(z−9)⋅5=0(x-8)cdot 1+(y-(-2))cdot 3+(z-9)cdot 5=0

x−8+3y+6+5z−45=0x-8+3y+6+5z-45=0

x+3y+5z−47=0x+3y+5z-47=0 — уравнение плоскости.

Проверка

Чтобы убедиться в том, что задача решена правильно, без ошибок, необходимо в полученное уравнение подставить координаты точки, которые даны в условии задачи:

8+3⋅(−2)+5⋅9−47=08+3cdot(-2)+5cdot9-47=0

0=00=0 — верно, значит ответ правильный.

Ответ

x+3y+5z−47=0x+3y+5z-47=0

Статья раскрывает суть нормального (нормированного) уравнения и показывает, при каких видах задач его чаще всего применяют. Рассмотрим выведение нормального уравнения плоскости с примерами решений.  Приведем примеры приведения общего уравнения плоскости к нормальному виду. Решим задачи по нахождению расстояния от точки до плоскости при помощи нормального уравнения плоскости.

Нормальное уравнение плоскости – описание и пример

Возьмем прямоугольную систему координат Охуz трехмерного пространства. Если плоскость удалена на расстояние p≥0 в положительном направлении нормального вектора n→.  Возьмем за единицу длину вектора n→. Получим, что координатами направляющего косинуса являются n→=(cos α, cos β, cos γ),  тогда n→=cos2 α, cos2 β, cos2 γ=1.

Примем обозначение ON за расстояние от точки до плоскости, таким образом, точка N принадлежит плоскости, где длиной отрезка ON будет значение p. Представим это на рисунке, изображенном ниже.

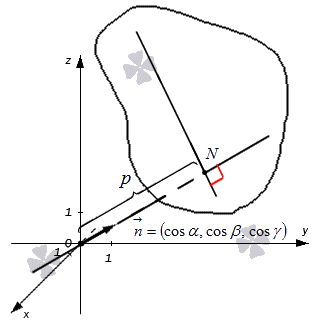
Теперь найдем уравнение заданной плоскости.

В трехмерном пространстве обозначим точку M (x, y, z). Отсюда получим, что OM→, являющийся ее радиус вектором, с координатами (x, y, z). Запись примет вид OM→=(x, y, z). Отсюда получаем, что плоскость определена множеством точек M (x, y, z), тогда числовая проекция вектора OM→ по направлению n→ равна значению p. Запись принимает вид npn→OM→=p. Рассмотрим на приведенном ниже рисунке.

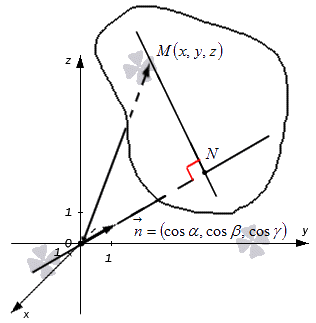
Из вышесказанного получим, что определение скалярного произведения векторов по формуле n→=(cos α, cos β, cos γ) и OM→=(x, y, z) в результате дают равенство

n→, OM→=n→·OM→·cos n⇀, OM→^=n→·npn→OM→=1·p=p

Данная формула представляет скалярное произведение в координатной форме. Тогда получаем следующее выражение:

n→, OM→=cos α·x+cos β·y+cos γ·z

При сопоставлении двух последних равенств получаем уравнение плоскости такого вида cos α·x+cos β·y+cos γ·z=p. Упростим выражения. Для этого необходимо перенести значение p в левую сторону, получим cos α·x+cos β·y+cos γ·z-p=0.

cos α·x+cos β·y+cos γ·z-p=0 называют нормальным уравнением плоскости или уравнением плоскости в нормальном виде. Реже его называют нормированным уравнением заданной плоскости.

Теперь заданное в прямоугольной системе координат Охуz нормальное уравнение принимает вид cos α·x+cos β·y+cos γ·z-p=0. Р имеет значение расстояния положительного направления единичного нормального вектора плоскости n→=(cos α, cos β, cos γ).

Чаще всего косинус не представляется явно  в уравнении плоскости, потому как cos α, cos β и cos γ является некоторыми действительными числами, сумма квадратов которых равна единице.

Рассмотрим пример нормального уравнения плоскости.

Если имеется плоскость, заданная в прямоугольной системе координат Oxyz при помощи уравнения нормального вида, -14·x-34·y+64·z-7=0.

Отсюда cos α=-14, cos β=-34, cos γ=64.

Из выражения находим, что  -14, -34, 64 – координаты нормального вектора плоскости n→. Его длина вычисляется из формулы n→=-142+-342+642=1. Плоскость располагается относительно координат в направлении вектора n→ на расстоянии 7 единиц, потому как p=7.

Отсюда ясно, что нормальное уравнение плоскости представляет собой общее уравнение плоскости Ax+By+Cz+D=0, где A, B, C – некоторые действительные числа, при которых длина нормального вектора плоскости n→=(A, B, C) равняется 1, причем D является неотрицательным числом.

Чтобы выявить, является представленное уравнение нормальным уравнением плоскости, необходимо выполнение обоих условий n→=cos2 α+cos2 β+cos2 γ=1 и p≥0, тогда получим уравнение плоскости нормального вида. При невыполнении хотя бы одного условия, уравнение не является нормальным.

Рассмотрим на примере.

Приведение общего уравнения плоскости к нормальному виду

Для приведения уравнения плоскости Ax+By+Cz+D=0 к нормальному виду, обе части умножаются на нормированный множитель ±1A2+B2+C2. Знак определятся по числу D, он должен быть противоположным значения числа D.

Когда D=0, знак может быть любым.

Нормальным уравнением плоскости  считается общее уравнение плоскости после умножения на нормирующий множитель, потому как  длина вектора с кооординатами ±AA2+B2+C2, ±BA2+B2+C2, ±CA2+B2+C2 равна 1.

Отсюда получаем, что ±AA2+B2+C2, ±BA2+B2+C2, ±CA2+B2+C2=A2+B2+C2A2+B2+C2=1.

Знак множителя необходим для того, что проверять выполнимость условия p≥0.

Нахождение расстояния от точки до плоскости

Теперь раскроем тему нормального уравнения плоскости, где уравнение плоскости нормального вида применимо для нахождения расстояния от заданной точки в пространстве до плоскости.

При заданной системе координат Охуz трехмерного пространства имеем плоскость с уравнением cos α·x+cos β·y+cos γ·z-p=0, где необходимо определить расстояние от p до точки M0 (x0, y0, z0) заданной плоскости. Его вычисляют по формуле p=cos α·x0+cos β·y0+cos γ·z0-p. Само расстояние является числом, которое получается при подстановке координат точки  в левую сторону уравнения. Для вывода формулы необходимо обратиться к статье расстояния от точки до плоскости.

Если плоскость задана другим уравнением, а необходимо произвести вычисление от заданной точки до плоскости, необходимо привести уравнение к виду нормального уравнения плоскости, используя формулу p=cos α·x0+cos β·y0+cos γ·z0-p.



5.2.4. Как составить уравнение плоскости
по точке и вектору нормали?

Вытяните вперёд руку и мысленно зафиксируйте произвольную точку пространства… прямо, как Владимир Ильич Ленин :). Очевидно, что эта конструкция тоже однозначно определяет плоскость:

Уравнение плоскости, проходящей через точку  перпендикулярно вектору  , в декартовой системе координат выражается формулой:

Выглядит значительно привлекательнее, чем предыдущие мытарства. И поэтому если в какой-то задаче вам известен вектор нормали, то, конечно же, уравнение выгодно составлять через него.

Но ещё раз обращаю внимание, что формулы, касаемые вектора нормали, работают лишь  в декартовой системе координат, но не в общем аффинном случае.

Задача 135

Составить уравнение плоскости по точке  и вектору нормали .

Решение: используем формулу :

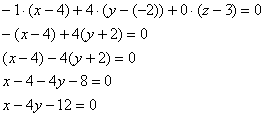
Ответ:

Проверка выполняется очень легко:

1) Из полученного уравнения  «снимаем» вектор нормали:  – всё хорошо, полученный вектор совпал с вектором из условия (в ряде случаев может получиться коллинеарный вектор).

2) Подставим координаты точки  в уравнение плоскости:

  – верное равенство, значит, точка  принадлежит данной плоскости.

Вывод: уравнение плоскости найдено правильно.

Пример настолько прозрачен, что хочется немного завуалировать условие:

Задача 136

Найти уравнение плоскости, проходящей через точку  перпендикулярно оси абсцисс.

Это задача для самостоятельного решения. Просто, но со вкусом.

И тема получает закономерное продолжение, рассмотрим простейшие задачи с плоскостью:

5.3.1. Как найти плоскость, параллельную данной?

5.2.3. Вектор нормали плоскости (нормальный вектор)

| Оглавление |



Автор: Aлeксaндр Eмeлин

Нормальное уравнение плоскости: описание, примеры, решение задач

Статья раскрывает суть нормального (нормированного) уравнения и показывает, при каких видах задач его чаще всего применяют. Рассмотрим выведение нормального уравнения плоскости с примерами решений. Приведем примеры приведения общего уравнения плоскости к нормальному виду. Решим задачи по нахождению расстояния от точки до плоскости при помощи нормального уравнения плоскости.

Нормальное уравнение плоскости – описание и пример

Возьмем прямоугольную систему координат О х у z трехмерного пространства. Если плоскость удалена на расстояние p ≥ 0 в положительном направлении нормального вектора n → . Возьмем за единицу длину вектора n → . Получим, что координатами направляющего косинуса являются n → = ( cos α , cos β , cos γ ) , тогда n → = cos 2 α , cos 2 β , cos 2 γ = 1 .

Примем обозначение O N за расстояние от точки до плоскости, таким образом, точка N принадлежит плоскости, где длиной отрезка O N будет значение p . Представим это на рисунке, изображенном ниже.

Теперь найдем уравнение заданной плоскости.

В трехмерном пространстве обозначим точку M ( x , y , z ) . Отсюда получим, что O M → , являющийся ее радиус вектором, с координатами ( x , y , z ) . Запись примет вид O M → = ( x , y , z ) . Отсюда получаем, что плоскость определена множеством точек M ( x , y , z ) , тогда числовая проекция вектора O M → по направлению n → равна значению p . Запись принимает вид n p n → O M → = p . Рассмотрим на приведенном ниже рисунке.

Из вышесказанного получим, что определение скалярного произведения векторов по формуле n → = ( cos α , cos β , cos γ ) и O M → = ( x , y , z ) в результате дают равенство

n → , O M → = n → · O M → · cos n ⇀ , O M → ^ = n → · n p n → O M → = 1 · p = p

Данная формула представляет скалярное произведение в координатной форме. Тогда получаем следующее выражение:

n → , O M → = cos α · x + cos β · y + cos γ · z

При сопоставлении двух последних равенств получаем уравнение плоскости такого вида cos α · x + cos β · y + cos γ · z = p . Упростим выражения. Для этого необходимо перенести значение p в левую сторону, получим cos α · x + cos β · y + cos γ · z – p = 0 .

cos α · x + cos β · y + cos γ · z – p = 0 называют нормальным уравнением плоскости или уравнением плоскости в нормальном виде. Реже его называют нормированным уравнением заданной плоскости.

Теперь заданное в прямоугольной системе координат О х у z нормальное уравнение принимает вид cos α · x + cos β · y + cos γ · z – p = 0 . Р имеет значение расстояния положительного направления единичного нормального вектора плоскости n → = ( cos α , cos β , cos γ ) .

Чаще всего косинус не представляется явно в уравнении плоскости, потому как cos α , cos β и cos γ является некоторыми действительными числами, сумма квадратов которых равна единице.

Рассмотрим пример нормального уравнения плоскости.

Если имеется плоскость, заданная в прямоугольной системе координат O x y z при помощи уравнения нормального вида, – 1 4 · x – 3 4 · y + 6 4 · z – 7 = 0 .

Отсюда cos α = – 1 4 , cos β = – 3 4 , cos γ = 6 4 .

Из выражения находим, что – 1 4 , – 3 4 , 6 4 – координаты нормального вектора плоскости n → . Его длина вычисляется из формулы n → = – 1 4 2 + – 3 4 2 + 6 4 2 = 1 . Плоскость располагается относительно координат в направлении вектора n → на расстоянии 7 единиц, потому как p = 7 .

Отсюда ясно, что нормальное уравнение плоскости представляет собой общее уравнение плоскости A x + B y + C z + D = 0 , где A , B , C – некоторые действительные числа, при которых длина нормального вектора плоскости n → = ( A , B , C ) равняется 1 , причем D является неотрицательным числом.

Чтобы выявить, является представленное уравнение нормальным уравнением плоскости, необходимо выполнение обоих условий n → = cos 2 α + cos 2 β + cos 2 γ = 1 и p ≥ 0 , тогда получим уравнение плоскости нормального вида. При невыполнении хотя бы одного условия, уравнение не является нормальным.

Рассмотрим на примере.

Выявить уравнение плоскости нормального вида из заданных уравнений:

1 7 x – 4 7 y + 4 2 7 – 3 = 0 1 3 x + 7 6 y – 5 6 z + 2 5 = 0 1 3 x + 1 2 y + 1 4 z – 11 = 0

Начнем решение с первого уравнения. Для этого необходимо проверить, равняется ли длина нормального вектора n → = 1 7 , – 4 7 , 4 2 7 единице.

Вычисляем длину по формуле и получаем: n → = 1 7 2 + – 4 7 2 + 4 2 7 2 = 1 49 + 16 49 + 32 49 = 1

Необходимо поработать с числом p , так как его значение должно быть положительным. Это верно, так как p = 3 . Значит, первое заданное уравнение плоскости можно считать уравнением плоскости в нормальном виде.

Второе уравнение из заданных нельзя считать нормальным уравнением плоскости, так как условие p ≥ 0 не выполняется, ибо в данном уравнении p = – 2 5 .

Третье уравнение имеет нормальный вектор с координатами n → = 1 3 , 1 2 , 1 4 , длина которого не равняется единице из вычислений:

n → = 1 3 2 + 1 2 2 + 1 4 2 = 1 9 + 1 4 + 1 16 = 61 12 ≠ 1

Отсюда следует, что его нельзя считать за уравнение плоскости в нормальном виде.

Ответ: 1 7 x – 4 7 y + 4 2 7 z – 3 = 0 уравнение является нормальным уравнением плоскости.

Приведение общего уравнения плоскости к нормальному виду

Для приведения уравнения плоскости A x + B y + C z + D = 0 к нормальному виду, обе части умножаются на нормированный множитель ± 1 A 2 + B 2 + C 2 . Знак определятся по числу D , он должен быть противоположным значения числа D .

Когда D = 0 , знак может быть любым.

Нормальным уравнением плоскости считается общее уравнение плоскости после умножения на нормирующий множитель, потому как длина вектора с кооординатами ± A A 2 + B 2 + C 2 , ± B A 2 + B 2 + C 2 , ± C A 2 + B 2 + C 2 равна 1 .

Отсюда получаем, что ± A A 2 + B 2 + C 2 , ± B A 2 + B 2 + C 2 , ± C A 2 + B 2 + C 2 = A 2 + B 2 + C 2 A 2 + B 2 + C 2 = 1 .

Знак множителя необходим для того, что проверять выполнимость условия p ≥ 0 .

Привести уравнение 2 x – 3 y + z + 5 = 0 к нормальному виду.

Из условия имеем, что A = 2 , B = – 3 , C = 1 , D = 5 . Исходя из того, что D является положительным числом, нормирующий множитель дожжен иметь противоположный знак. Отсюда получим, что получим отрицательный результат.

– 1 A 2 + B 2 + C 2 = – 1 2 2 + ( – 3 ) 2 + 1 2 = – 1 14

Чтобы получить искомое нормальное уравнение плоскости, обе части уравнения необходимо умножить на нормирующий множитель. Получим:

– 1 14 · 2 x – 3 y + z + 5 = – 1 14 · 0 ⇔ ⇔ – 2 14 x + 3 14 y – 1 14 z – 5 14 = 0

Ответ: – 2 14 x + 3 14 y – 1 14 z – 5 14 = 0 .

Написать нормальное уравнение плоскости, если оно задано уравнением 3 x – 4 z = 0 прямоугольной системы координат O x y z .

Из условия видно, что A = 3 , B = 0 , C = – 4 , D = 0 . Знака перед множителем нет, потому как D = 0 . Значит, возьмем со знаком « + ». Получаем выражение вида:

1 A 2 + B 2 + C 2 = 1 3 2 + 0 2 + ( – 4 ) 2 = 1 5

При умножении обеих частей уравнения на нормирующий множитель, получаем уравнение плоскости нормального вида 3 5 x – 4 5 z = 0 .

Ответ: 3 5 x – 4 5 z = 0 .

Нахождение расстояния от точки до плоскости

Теперь раскроем тему нормального уравнения плоскости, где уравнение плоскости нормального вида применимо для нахождения расстояния от заданной точки в пространстве до плоскости.

При заданной системе координат О х у z трехмерного пространства имеем плоскость с уравнением cos α · x + cos β · y + cos γ · z – p = 0 , где необходимо определить расстояние от p до точки M 0 ( x 0 , y 0 , z 0 ) заданной плоскости. Его вычисляют по формуле p = cos α · x 0 + cos β · y 0 + cos γ · z 0 – p . Само расстояние является числом, которое получается при подстановке координат точки в левую сторону уравнения. Для вывода формулы необходимо обратиться к статье расстояния от точки до плоскости.

Имеется уравнение плоскости вида – 1 3 x + 2 3 y – 2 3 z – 1 = 0 , которое располагается в прямоугольной системе координат. Определить расстояние от точки с координатами M 0 ( 1 , – 3 , 0 ) до плоскости.

Координаты точки M необходимо подставить в левую часть уравнения плоскости. Тогда получаем:

– 1 3 · 1 + 2 3 · ( – 3 ) – 2 3 · 0 – 1 = 0

Искомое расстояние – величина абсолютная, значит p = – 3 1 3 = 3 1 3 .

Если плоскость задана другим уравнением, а необходимо произвести вычисление от заданной точки до плоскости, необходимо привести уравнение к виду нормального уравнения плоскости, используя формулу p = cos α · x 0 + cos β · y 0 + cos γ · z 0 – p .

Найти расстояние от заданной точки с координатами M 0 ( 5 , – 1 , 2 ) до плоскости x 5 + y – 2 + z 4 = 1 .

По условию имеем уравнение плоскости в отрезках. Это значит, что необходимо привести его к нормальному уравнению плоскости. Для этого переходим к общему уравнению, после чего приведем к нормальному виду.

Получаем: x 5 + y – 2 + z 4 = 1 ⇔ 1 5 x – 1 2 y + 1 4 z – 1 = 0

Для вычисления нормирующего множителя применяем: 1 1 5 2 + – 1 2 2 + 1 4 2 = 1 141 25 · 16 = 20 141

Обе части уравнения 1 5 x – 1 2 y + 1 4 z – 1 = 0 умножаем на нормирующий множитель. Теперь получено нормальное уравнение исходной плоскости вида:

4 141 x – 10 141 y + 5 141 z – 20 141 = 0

Отсюда видно, что cos α = 4 141 , cos β = – 10 141 , cos γ = 5 141 , p = – 20 141 , x 0 = 5 , y 0 = – 1 , z 0 = 2

Все имеющиеся данные помогут использовать формулу для нахождения искомого расстояния от точки до плоскости:

p = cos α · x 0 + cos β · y 0 + cos γ · z 0 – p = 4 141 · 5 – 10 141 · – 1 + 5 141 · 2 – 20 141 = 20 141

Уравнения плоскости: общее, через три точки, нормальное

Плоскость, общее уравнение плоскости

Чтобы получить общее уравнение плоскости, разберём плоскость, проходящую через заданную точку.

Пусть в пространстве есть три уже известные нам оси координат – Ox, Oy и Oz. Подержим лист бумаги так, чтобы он оставался плоским. Плоскостью будет сам лист и его продолжение во всех направлениях.

Пусть P произвольная плоскость в пространстве. Всякий перпендикулярный ей вектор называется вектором нормали к этой плоскости. Естественно, речь идёт о ненулевом векторе.

Если известна какая-нибудь точка плоскости P и какой-нибудь вектор нормали к ней, то этими двумя условиями плоскость в пространстве вполне определена (через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору). Общее уравнение плоскости будет иметь вид:

Итак, условия, которыми задаётся уравнение плоскости, есть. Чтобы получить само уравнение плоскости, имеющее приведённый выше вид, возьмём на плоскости P произвольную точку M с переменными координатами x, y, z. Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис. 1). Для этого, согласно условию перпендикулярности векторов, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, то есть

.

Вектор задан по условию. Координаты вектора найдём по формуле :

.

Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме:

. (1)

Так как точка M(x; y; z) выбрана на плоскости произвольно, то последнему уравнению удовлетворяют координаты любой точки, лежащей на плоскости P. Для точки N, не лежащей на заданной плоскости, , т.е. равенство (1) нарушается.

Перед решением задач может пригодиться урок о декартовой системе координат. Также хорошо бы владеть материалом о скалярном произведении векторов.

Пример 1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .

Решение. Используем формулу (1), еще раз посмотрим на неё:

.

В этой формуле числа A , B и C координаты вектора , а числа x 0 , y 0 и z 0 – координаты точки .

Вычисления очень простые: подставляем эти числа в формулу и получаем

.

Умножаем всё, что нужно умножить и складываем просто числа (которые без букв). Результат:

.

Требуемое уравнение плоскости в этом примере оказалось выражено общим уравнением первой степени относительно переменных координат x, y, z произвольной точки плоскости.

Итак, уравнение вида

(2)

называется общим уравнением плоскости.

Пример 2. Построить в прямоугольной декартовой системе координат плоскость, заданную уравнением .

Решение. Для построения плоскости необходимо и достаточно знать какие-либо три её точки, не лежащие на одной прямой, например, точки пересечения плоскости с осями координат.

Как найти эти точки? Чтобы найти точку пересечения с осью Oz , нужно в уравнение, данное в условии задачи, вместо икс и игрека подставить нули: x = y = 0 . Поэтому получаем z = 6 . Таким образом, заданная плоскость пересекает ось Oz в точке A(0; 0; 6) .

Точно так же находим точку пересечения плоскости с осью Oy . При x = z = 0 получаем y = −3 , то есть точку B(0; −3; 0) .

И, наконец, находим точку пересечения нашей плоскости с осью Ox . При y = z = 0 получим x = 2 , то есть точку C(2; 0; 0) . По трём полученным в нашем решении точкам A(0; 0; 6) , B(0; −3; 0) и C(2; 0; 0) строим заданную плоскость.

Рассмотрим теперь частные случаи общего уравнения плоскости. Это случаи, когда те или иные коэффициенты уравнения (2) обращаются в нуль.

1. При D = 0 уравнение определяет плоскость, проходящую через начало координат, так как координаты точки 0(0; 0; 0) удовлетворяют этому уравнению.

2. При A = 0 уравнение определяет плоскость, параллельную оси Ox, поскольку вектор нормали этой плоскости перпендикулярен оси Ox (его проекция на ось Ox равна нулю). Аналогично, при B = 0 плоскость параллельная оси Oy, а при C = 0 плоскость параллельна оси Oz.

3. При A = D = 0 уравнение определяет плоскость, проходящую через ось Ox, поскольку она параллельна оси Ox (A = 0) и проходит через начало координат (D = 0). Аналогично, плоскость проходит через ось Oy, а плоскость через ось Oz.

4. При A = B = 0 уравнение определяет плоскость, параллельную координатной плоскости xOy, поскольку она параллельна осям Ox (A = 0) и Oy (B = 0). Аналогично, плоскость параллельна плоскости yOz, а плоскость – плоскости xOz.

5. При A = B = D = 0 уравнение (или z = 0) определяет координатную плоскость xOy, так как она параллельна плоскости xOy (A = B = 0) и проходит через начало координат (D = 0). Аналогично, уравнение y = 0 в пространстве определяет координатную плоскость xOz, а уравнение x = 0 – координатную плоскость yOz.

Пример 3. Составить уравнение плоскости P , проходящей через ось Oy и точку .

Решение. Итак, плоскость проходит через ось Oy . Поэтому в её уравнении y = 0 и это уравнение имеет вид . Для определения коэффициентов A и C воспользуемся тем, что точка принадлежит плоскости P .

Поэтому среди её координат есть такие, которые можно подставить в уравнению плоскости, которое мы уже вывели (). Смотрим ещё раз на координаты точки:

Среди них x = 2 , z = 3 . Подставляем их в уравнение общего вида и получаем уравнение для нашего частного случая:

Оставляем 2A в левой части уравнения, переносим 3C в правую часть и получаем

Подставив найденное значение A в уравнение , получим

или .

Это и есть уравнение, требуемое в условии примера.

Решить задачу на уравнения плоскости самостоятельно, а затем посмотреть решение

Пример 4. Определить плоскость (или плоскости, если больше одной) относительно координатных осей или координатных плоскостей, если плоскость (плоскости) задана уравнением .

Уравнение плоскости, проходящей через три точки

Как уже упоминалось, необходимым и достаточным условием для построения плоскости, кроме одной точки и вектора нормали, являются также три точки, не лежащие на одной прямой.

Пусть даны три различные точки , и , не лежащие на одной прямой. Так как указанные три точки не лежат на одной прямой, векторы и не коллинеарны, а поэтому любая точка плоскости лежит в одной плоскости с точками , и тогда и только тогда, когда векторы , и компланарны, т.е. тогда и только тогда, когда смешанное произведение этих векторов равно нулю.

Используя выражение смешанного произведения в координатах, получим уравнение плоскости

(3)

После раскрытия определителя это уравнение становится уравнением вида (2), т.е. общим уравнением плоскости.

Пример 5. Составить уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой:

, ,

и определить частный случай общего уравнения прямой, если такой имеет место.

Решение. По формуле (3) имеем:

Получили общее уравнение плоскости

или после деления на -2:

.

Это уравнение, в котором A = 0, т.е. оно определяет плоскость, параллельную оси Ox.

Нормальное уравнение плоскости. Расстояние от точки до плоскости

Нормальным уравнением плоскости называется её уравнение, записанное в виде

,

где – направляющие косинусы нормали плоскости, – расстояние от начала координат до плоскости.

Нормалью к плоскости называется вектор, направление которого совпадает с направлением прямой, проведённой через начало координат перпендикулярно данной плоскости. (Есть полная аналогия с нормалью к прямой на плоскости, с той лишь разницей, что нормальное уравнение прямой существует в двух измерениях, а нормальное уравнение плоскости – в трёх).

Пусть M – какая угодно точка пространства. Для нахождения отклонения точки M от плоскости следует в левую часть нормального уравнения плоскости подставить на место x, y и z подставить координаты этой точки.

Это правило позволяет найти и расстояние от точки M до плоскости: расстояние равно модулю отклонения, т.е.

,

так как расстояние не может быть отрицательным числом.

Общее уравнение плоскости

приводится к нормальному виду почленным умножением на нормирующий множитель, определяемый формулой

.

Знак нормирующего множителя берётся противоположным знаку свободного члена в общем уравнении плоскости.

Пример 6. Привести уравнение плоскости к нормальному виду.

Решение. Вычислим нормирующий множитель:

.

Знак нормирующего множителя положительный, то есть, противоположен знаку свободного члена в общем уравнении плоскости. Умножим общее уравнение почленно на нормирующий множитель и получим требуемое в условии примера нормальное уравнение плоскости:

.

Пример 7. Вычислить величину отклонения и расстояния от точки до прямой, если точка задана координатами (-2; -4; 3) , а плоскость задана общим уравнением .

Решение. Сначала приведём уравнение плоскости к нормальному виду. Вычислим нормирующий множитель:

.

Знак нормирующего множителя отрицательный, то есть, противоположен знаку свободного члена в общем уравнении плоскости. Умножим общее уравнение почленно на нормирующий множитель и получим нормальное уравнение плоскости:

.

Вычислим отклонение точки от плоскости:

Найдём теперь расстояние от точки до плоскости как модуль отклонения:

Уравнение плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через три точки, и уравнение плоскости, проходящей через одну точку и имеющий заданный нормаль плоскости. Дается подробное решение с пояснениями. Для построения уравнения плоскости выберите вариант задания исходных данных, введите координаты точек в ячейки и нажимайте на кнопку “Решить”.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение плоскости, проходящей через три точки

Рассмотрим цель − вывести уравнение плоскости, проходящей через три различные точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃), не лежащие на одной прямой. Так как эти точки не лежат на одной прямой, векторы и не коллинеарны. Следовательно точка M(x, y, z) лежит в одной плоскости с точками M₁, M₂, M₃ тогда и тольно тогда, когда векторы M₁M₂, M₁M₃ и компланарны. Но векторы M₁M₂, M₁M₃, M₁M компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Используя смешанное произведение векторов M₁M₂, M₁M₃, M₁M в координатах, получим необходимое и достаточное условие принадлежности точки M(x, y, z) к указанной плоскости:

Разложив определитель в левой части выражения, например, по первому столбцу и упростив, получим уравнение плоскости в общей форме, проходящий по точкам M₁, M₂, M₃:

Пример 1. Построить уравнение плоскости, проходящую через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2).

Подставляя координаты точек A, B, C в (1), получим:

Разложим определитель по первому столбцу:

Уравнение плоскости, проходящей через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2) имеет вид:

Уравнение плоскости, проходящей через одну точку и имеющий нормаль n

Пример 2. Построить плоскость, проходящую через точку M₀(-1, 2, 1) и имеюший нормаль n(1, 4/5, 1).

Подставляя координаты векторов M₀ и n в (2), получим:

[spoiler title=”источники:”]

http://function-x.ru/equations_of_plane.html

http://matworld.ru/analytic-geometry/uravnenie-ploskosti-online.php

[/spoiler]