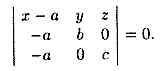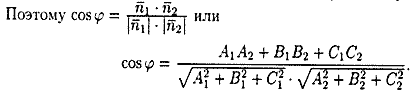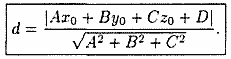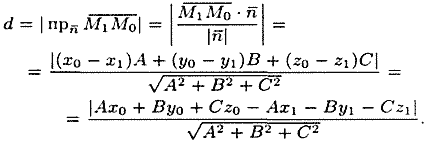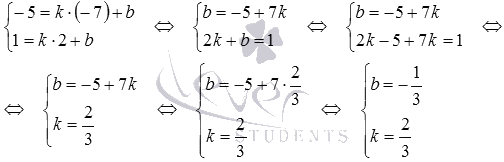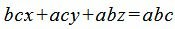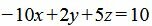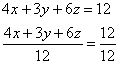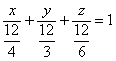Данный раздел будет полностью посвящен теме «Уравнение плоскости в отрезках». Мы последовательно рассмотрим, какой вид имеет уравнение плоскости в отрезках, применение этого уравнения для построения заданной плоскости в прямоугольной системе координат, переход от общего уравнения плоскости к уравнению плоскости в отрезках. В статье мы рассмотрим большое количество примеров, которые облегчат усвоение информации.
Уравнение плоскости в отрезках – описание и примеры
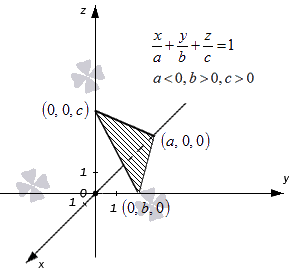
Уравнение плоскости в отрезках имеет вид xa+yb+zc=1 , где a, b и c – это действительные числа, отличные от нуля. Абсолютные величины чисел a, b и c равны длинам отрезков, которые отсекаются плоскостью на осях координат Oх, Oу и Oz в трехмерной системе координат Oхуz. Откладываются длины отрезков от начала координат. Направление, в котором необходимо отложить длину отрезка, определяет знак, стоящий перед числом. Наличие «-» свидетельствует о том, что отрезок надо откладывать от нуля в отрицательном направлении оси.
Действительно, координаты точек a, 0, 0, 0, b, 0, 0, 0, c удовлетворяют уравнению плоскости в отрезках:
aa+0b+0c=1=1⇔1=10a+bb+0c=1=1⇔1=10a+0b+cc=1=1⇔1=1
Поясним этот момент, расположив заданные точки на графике.
Проиллюстрируем описанное выше примером.
Плоскость проходит через точки -2, 0, 0, 0, 3, 0 и 0, 0, -12 на осях координат в прямоугольной системе координат Oxyz. Необходимо записать уравнение плоскости в отрезках.
Решение
Определим положение отрезков, отсекаемых плоскостью на осях координат. На оси абсцисс откладываем в отрицательном направлении отрезок длиной 2 единицы. На оси ординат в положительном направлении откладываем отрезок длиной 3 . На оси аппликат в отрицательном направлении откладываем отрезок длиной 12 .
При этом, уравнение плоскости в отрезках будет иметь вид: x-2+y3+z-12=1 .
Ответ: x-2+y3+z-12=1
Уравнение плоскости в отрезках удобно использовать для построения чертежей. Проиллюстрируем это утверждение примером.
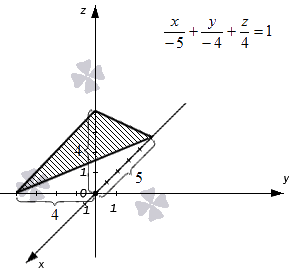
Плоскость в прямоугольной системе координат Oхуz задана уравнением плоскости в отрезках вида x-5+y-4+z4=1 . Необходимо изобразить эту плоскость на графике.
Решение
Изобразим оси координат, обозначаем начало координат и единичные отрезки на осях. Отмечаем длины отрезков, отсекаемых плоскостью, на каждой из осей. Соединяем концевые точки отрезков прямыми линиями. Полученная плоскость имеет вид треугольника. Она соответствует заданному уравнению плоскости в отрезках x-5+y-4+z4=1 .
Ответ:
Плоскость может быть задана уравнением плоскости другого вида. Для того, чтобы изобразить заданную плоскость на чертеже, можно сначала перейти к уравнению плоскости в отрезках. Получив уравнение плоскости в отрезках, нам останется лишь отметить точки a, 0, 0, 0, b, 0, 0, 0, c и соединить их прямыми линиями.
Приведение общего уравнения плоскости к уравнению плоскости в отрезках
Мы имеем общее уравнение плоскости в пространстве вида Ax+By+Cz+D=0 . И мы можем получить уравнение плоскости в отрезках. Сделать это можно в том случае, если плоскость пересекает все координатные оси, причем не в начале координат.
Не получится перевести общее уравнение плоскости в пространстве в уравнение плоскости в отрезках в тех случаях, когда плоскость проходит через одну из координатных осей или располагается параллельно оси. Другими словами, мы можем работать лишь с полным уравнением плоскости вида Ax+By+Cz+D=0, где A≠0, B≠0, C≠0, D≠0 .
Приведение общего уравнения плоскости к уравнению плоскости в пространстве производится следующим образом. Переносим слагаемое D в правую часть уравнения с противоположным знаком.
Ax+By+Cz+D=0⇔Ax+By+Cz=-D
Так как D≠0 , то обе части полученного уравнения можно разделить на –D: A-Dx+B-Dy+C-Dz=1 .
Так как A≠0, B≠0, C≠0 , то мы можем отправить в знаменатели коэффициенты перед переменными x, y и z. Последнее уравнение эквивалентно равенству x-DA+y-DB+z-DC=1 . При этом мы использовали очевидное равенство pq=1qp, p, q∈R, p≠0, q≠0 .
В итоге, мы получаем уравнение плоскости в отрезках. Это становится хорошо видно в том случае, если обозначить -DA=a, -DB=b, -DC=c.
Разберем решение примера.
Плоскость в прямоугольной системе координат Oxyz в пространстве задана уравнением вида 3x+9y-6z-6=0 . Переведем это уравнение в уравнение плоскости в отрезках.
Решение
Данное в условии задачи уравнение является полным уравнением плоскости. Это дает нам возможность привески его к уравнению плоскости в отрезках. Перенесем -6 в правую часть равенства, а затем разделим обе части равенства на 6:
3x+9y-6z-6=0⇔3x+9y+6z=63x+9y-6z=6⇔12x+32y-z=1
Коэффициенты при переменных x, y и z отправим в знаменатели: 12x+32y-z=1⇔x2+y23+z-1=1 . Полученное уравнение и есть уравнение плоскости в отрезках.
Ответ: x2+y23+z-1=1
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Уравнение плоскости в отрезках
В данной статье мы рассмотрим уравнение плоскости в отрезках. Представим методы преобразования уравнения плоскости в отрезках в уравнение плоскости в общем виде и обратно. Рассмотрим численные примеры.
Уравнение плоскости в отрезках представляется следующей формулой:
где a, b, c отличные от нуля числа.
Отметим, что числа a, b, c в уравнении (1) имеют простой геометрический смысл. Они равны длинам отрезков, которые отсекает плоскость на осях Ox, Oy, Oz (Рис.1, Рис.2).
Действительно. Подставляя в (1) y=0, z=0 получим x=a, если же подставить в (1) x=0, y=0 то получим z=c, подставвляя, наконец, x=0, z=0 получим y=b. Таким образом плоскость, определяемая уравнением (1) проходит через точки M1(a, 0, 0), M2(0, b, 0) и M3(0, 0, с).
Пример 1. Составить уравнение прямой, которая пересекает оси Ox, Oy и Oz в точках −1,3 и 7, соответственно.
Решение. Подставляя значения a=−1, b=3 и c=7 в (1), получим:
Ответ:
Приведение уравнения плоскости в отрезках к общему виду
Левая часть уравнения (1) приведем к общему знаменателю:
Далее, умножив обе части уравнения на abc, получим:
или
Пример 2. Уравнение плоскости в отрезках представлено следующим уравнением:
Перевести уравнение к общему виду.
Решение. Приведем левую часть уравнения к общему знаменателю:
Умножив обе части уравнения на 10, получим:
или
Ответ:
Приведение общего уравнения плоскости к уравнению плоскости в отрезках
Пусть задано общее уравнение плоскости:
где A, B, C, D − отличные от нуля числа, т.е. уравнение плокости является полным (о полных и неполных уравнениях плоскости смотрите здесь).
Сделаем следующие преобразования. Переведем свободный член D на правую часть уравнения и разделим обе части уравнения на −D:
Уравнение (2) можно переписать в следующем виде:
Сделаем следующие обозначения:
Тогда получим уравнение прямой в отрезках (1).
Пример 3. Привести общее уравнение прямой
к уравнению прямой в отрезках.
Решение. Так как все коэффициенты уравнения отличны от нуля, можно построить уравнение плоскости в отрезках. Воспользуемся формулой (3). Имеем: A=−2, B=3, C=5, D=−4. Подставив эти значения в формулу (3), получим:
или
Ответ:
Уравнение
плоскости в отрезках
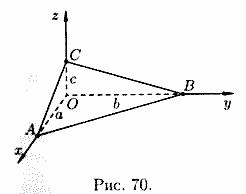
Пусть
плоскость отсекает на осях Ох, Оу и Оz
соответственно отрезки a,
b
и c,
т. е. проходит через три точки A(a;0;0),
B(0;b;0)
и C(0;0;c)
(см.рис. 70). Подставляя координаты этих
точек в уравнение (12.6), получаем
Раскрыв
определитель, имеем
,
т. е.или
(12.7)
Уравнение
(12.7) называется уравнением плоскости в
отрезках на осях. Им удобно пользоваться
при построении плоскости.
25. Уравнение плоскости, проходящей через три точки (вывод).
Три
точки пространства, не лежащие на одной
прямой, определяют единственную
плоскость. Найдем уравнение плоскости
Q, проходящей через три данные точки
M1(x1;y1;z1),
М2(x2;y2;z2)
и М3(х3,y3,z3),
не лежащие на одной прямой.
Возьмем
на плоскости произвольную точку M(x;y;z)
и составим векторы
,
,
.
Эти векторы лежат на плоскости Q,
следовательно, они компланарны. Используем
условие компланарности трех векторов
(их смешанное произведение равно нулю),
получаем,
т. е.

Уравнение
(12.6) есть уравнение плоскости, проходящей
через три данные точки.
26. Угол между плоскостями (вывод).
Пусть
заданы две плоскости Q1
и Q2:
Под
углом между плоскостями Q1
и Q2
понимается один из двугранных углов,
образованных этими плоскостями.
Угол
между нормальными векторами
и
плоскостей
Q1
и Q2
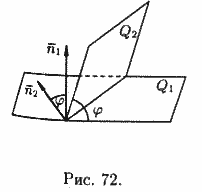
равен одному из этих углов (см. рис. 72).
Для
нахождения острого угла следует взять
модуль правой части.
Если
плоскости Q1
и Q2
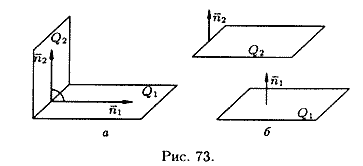
перпендикулярны (см. рис. 73,
а), то таковы же их нормали, т. е.
(и
наоборот). Но тогда,
т. е..
Полученное равенство есть условие
перпендикулярности двух плоскостей Q1
и Q2.
Если
плоскости Q1
и Q2
параллельны (см. рис. 73, б), то будут
параллельны и их нормали
и
(и
наоборот). Но тогда, как известно
координаты векторов пропорциональны:.
Это и есть уcловиє параллельности двух
плоскостей Q1
и Q2.
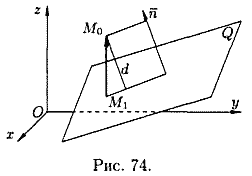
27. Расстояние от точки до плоскости (вывод).
Пусть
задана точка
и
плоскость Q своим уравнением.
Расстояние d от точкидо
плоскости Q находится по формуле
Вывод
этой формулы такой же, как вывод формулы
расстояния от точки
до
прямой.
Расстояние
d от точки M0
до плоскости Q равно модулю проекции
вектора
,
где—
произвольная точка плоскости Q, на
направление нормального вектора(см.
рис. 74). Следовательно,
А
так как точка
принадлежит
плоскости Q, то
Поэтому
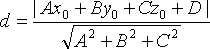
Отметим, что если плоскость Q задана
уравнением,
то расстояние от точкидо
плоскости Q может быть найдено по формуле
28. Условия параллельности и перпендикулярности плоскостей (вывод).
Если
плоскости Q1
и Q2
перпендикулярны (см. рис. 73,
а), то таковы же их нормали, т. е.
(и
наоборот). Но тогда,
т. е..
Полученное равенство есть условие
перпендикулярности двух плоскостей Q1
и Q2.
Если
плоскости Q1
и Q2
параллельны (см. рис. 73, б), то будут
параллельны и их нормали
и
(и
наоборот). Но тогда, как известно
координаты векторов пропорциональны:.
Это и есть условие параллельности двух
плоскостей Q1
и Q2.
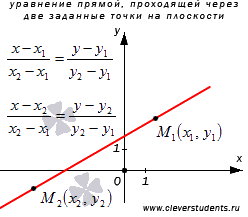
29. Уравнения прямой в r3. Уравнения прямой, проходящей через две фиксированные точки (вывод).
Прежде
чем получить уравнение прямой, проходящей
через две заданные точки в прямоугольной
системе координат на плоскости, вспомним
некоторые факты.
Одна
из аксиом геометрии гласит, что через
две несовпадающие точки на плоскости
можно провести единственную прямую.
Другими словами, задав две точки на
плоскости, мы однозначно определяем
прямую линию, которая через эти две
точки проходит (при необходимости
обращайтесь к разделу способы
задания прямой на плоскости).
Пусть
на плоскости зафиксирована прямоугольная
декартова система координатOxy.
В этой системе координат любой прямой
линии соответствует некотороеуравнение
прямой на плоскости. С этой же прямой
неразрывно связаннаправляющий
вектор прямой. Этих знаний вполне
достаточно, чтобы составить уравнение
прямой, проходящей через две заданные
точки.
Сформулируем
условие задачи: составить уравнение
прямой a, которая в прямоугольной
декартовой системе координатOxyпроходит через две несовпадающие точкии
.
Покажем
самое простое и универсальное решение
этой задачи.
Нам
известно, что каноническое
уравнение прямой на плоскостивида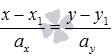
в прямоугольной системе координатOxyпрямую линию, проходящую через точкуи
имеющую направляющий вектор.
Напишем
каноническое уравнение прямой a,
проходящей через две заданные точкии
.
Очевидно,
направляющим вектором прямой a,
которая проходит через точкиМ1иМ2, является вектор,
он имеет координаты(при
необходимости смотрите статьювычисление
координат вектора по координатам точек
его конца и начала). Таким образом, мы
имеем все необходимые данные, чтобы
написать каноническое уравнение прямойa– координаты ее направляющего
вектораи
координаты лежащей на ней точки(и
).
Оно имеет вид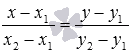
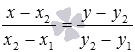
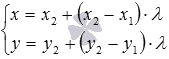
Также
мы можем записать параметрические
уравнения прямой на плоскости,
проходящей через две точкии
.
Они имеют вид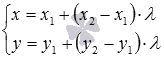
Разберем
решение примера.
Пример.
Напишите
уравнение прямой, которая проходит
через две заданные точки
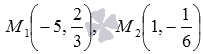
Решение.
Мы
выяснили, что каноническое уравнение
прямой, проходящей через две точки с
координатами
и
,
имеет вид
Из
условия задачи имеем
.
Подставим эти данные в уравнение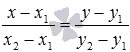
Получаем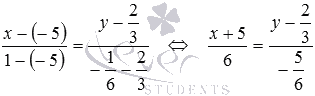
Ответ:
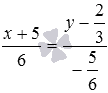
Если
нам потребуется не каноническое уравнение
прямой и не параметрические уравнения
прямой, проходящей через две заданные
точки, а уравнение прямой другого вида,
то от канонического уравнения прямой
всегда можно к нему прийти.
Пример.
Составьте
общее
уравнение прямой, которая в прямоугольной
системе координатOxyна плоскости
проходит через две точкии
.
Решение.
Сначала
напишем каноническое уравнение прямой,
проходящей через две заданные точки.
Оно имеет вид
.
Теперь приведем полученное уравнение
к требуемому виду:.
Ответ:
.
На
этом можно и закончить с уравнением
прямой, проходящей через две заданные
точки в прямоугольной системе координат
на плоскости. Но хочется напомнить, как
мы решали такую задачу в средней школе
на уроках алгебры.
В
школе нам было известно лишь уравнение
прямой с угловым коэффициентомвида.
Найдем значение углового коэффициентаkи числаb, при которых уравнениеопределяет
в прямоугольной системе координатOxyна плоскости прямую линию, проходящую
через точкии
при
.
(Если жеx1=x2,
то угловой коэффициент прямой бесконечен,
а прямуюМ1М2определяетобщее
неполное уравнение прямойвидаx-x1=0).
Так
как точки М1иМ2лежат на прямой, то координаты этих
точек удовлетворяют уравнению прямой,
то есть, справедливы равенстваи
.
Решая систему уравнений вида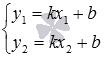
неизвестных переменныхkиb,
находим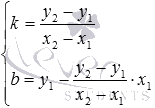
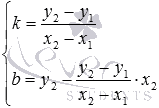
При этих значенияхkиbуравнение
прямой, проходящей через две точкии
,
принимает вид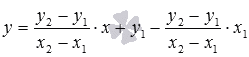
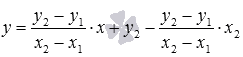
Запоминать
эти формулы не имеет смысла, при решении
примеров проще повторять указанные
действия.
Пример.
Напишите
уравнение прямой с угловым коэффициентом,
если эта прямая проходит через точки
и
.
Решение.
В
общем случае уравнение прямой с угловым
коэффициентом имеет вид
.
Найдемkиb, при которых уравнениесоответствует
прямой, проходящей через две точкии
.
Так
как точки М1иМ2лежат на прямой, то их координаты
удовлетворяют уравнению прямой,
то есть, верны равенстваи
.
Значенияkиbнаходим как решение
системы уравнений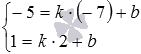
необходимости обращайтесь к статьерешение
систем линейных уравнений):
Осталось
подставить найденные значения
и
в
уравнение.
Таким образом, искомое уравнение прямой,
проходящей через две точкии
,
имеет вид.
Колоссальный
труд, не так ли?
Намного
проще записать каноническое уравнение
прямой, проходящей через две точки
и
,
оно имеет вид
и от него перейти к уравнению прямой с
угловым коэффициентом:.
Ответ:
.
К
началу страницы
Уравнения прямой, которая проходит
через две заданные точки в трехмерном
пространстве.
Пусть
в трехмерном пространстве зафиксирована
прямоугольная система координат Oxyz,
и заданы две несовпадающие точкии
,
через которые проходит прямаяM1M2.
Получим уравнения этой прямой.
Нам
известно, что канонические
уравнения прямой в пространствевида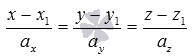
уравнения прямой в пространствевида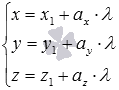
в прямоугольной системе координатOxyzпрямую линию, которая проходит через
точку с координатамии
имеет направляющий вектор.
Направляющим
вектором прямой M1M2является вектор,
и эта прямая проходит через точку(и
),
тогда канонические уравнения этой
прямой имеют вид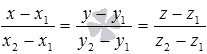
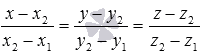
а параметрические уравнения –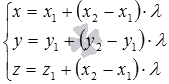
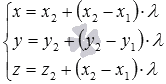
Пример.
Напишите
уравнение прямой, которая в прямоугольной
системе координат Oxyzв трехмерном
пространстве проходит через две точкии
.
Решение.
Мы
выяснили, что в прямоугольной системе
координат Oxyzв трехмерном пространстве
канонические уравнения прямой, которая
проходит через две точкии
,
имеют вид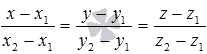
Из
условия имеем
,
тогда искомые уравнения прямой запишутся
как
Ответ:
.
Если
потребуется задать прямую М1М2с помощьюуравнений
двух пересекающихся плоскостей, то
сначала следует составить канонические
уравнения прямой, проходящей через две
точкии
,
и из этих уравнений получить нужные
уравнения плоскостей.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уравнение плоскости в отрезках
В данной статье мы рассмотрим уравнение плоскости в отрезках. Представим методы преобразования уравнения плоскости в отрезках в уравнение плоскости в общем виде и обратно. Рассмотрим численные примеры.
Уравнение плоскости в отрезках представляется следующей формулой:
 , , |
(1) |
где a, b, c отличные от нуля числа.
Отметим, что числа a, b, c в уравнении (1) имеют простой геометрический смысл. Они равны длинам отрезков, которые отсекает плоскость на осях Ox, Oy, Oz (Рис.1, Рис.2).
Действительно. Подставляя в (1) y=0, z=0 получим x=a, если же подставить в (1) x=0, y=0 то получим z=c, подставвляя, наконец, x=0, z=0 получим y=b. Таким образом плоскость, определяемая уравнением (1) проходит через точки M1(a, 0, 0), M2(0, b, 0) и M3(0, 0, с).
Пример 1. Составить уравнение прямой, которая пересекает оси Ox, Oy и Oz в точках −1,3 и 7, соответственно.
Решение. Подставляя значения a=−1, b=3 и c=7 в (1), получим:
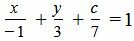
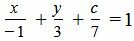
Приведение уравнения плоскости в отрезках к общему виду
Левая часть уравнения (1) приведем к общему знаменателю:
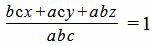
Далее, умножив обе части уравнения на abc, получим:
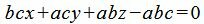
Пример 2. Уравнение плоскости в отрезках представлено следующим уравнением:
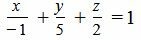
Перевести уравнение к общему виду.
Решение. Приведем левую часть уравнения к общему знаменателю:
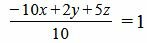
Умножив обе части уравнения на 10, получим:
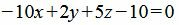
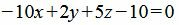
Приведение общего уравнения плоскости к уравнению плоскости в отрезках
где A, B, C, D − отличные от нуля числа, т.е. уравнение плокости является полным (о полных и неполных уравнениях плоскости смотрите здесь).
Сделаем следующие преобразования. Переведем свободный член D на правую часть уравнения и разделим обе части уравнения на −D:
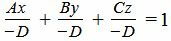 . . |
(2) |
Уравнение (2) можно переписать в следующем виде:
 . . |
(3) |
Сделаем следующие обозначения:
Тогда получим уравнение прямой в отрезках (1).
Пример 3. Привести общее уравнение прямой
к уравнению прямой в отрезках.
Решение. Так как все коэффициенты уравнения отличны от нуля, можно построить уравнение плоскости в отрезках. Воспользуемся формулой (3). Имеем: A=−2, B=3, C=5, D=−4. Подставив эти значения в формулу (3), получим:
Уравнение плоскости в отрезках: описание, примеры, решение задач
Данный раздел будет полностью посвящен теме «Уравнение плоскости в отрезках». Мы последовательно рассмотрим, какой вид имеет уравнение плоскости в отрезках, применение этого уравнения для построения заданной плоскости в прямоугольной системе координат, переход от общего уравнения плоскости к уравнению плоскости в отрезках. В статье мы рассмотрим большое количество примеров, которые облегчат усвоение информации.
Уравнение плоскости в отрезках – описание и примеры
Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 , где a , b и c – это действительные числа, отличные от нуля. Абсолютные величины чисел a , b и c равны длинам отрезков, которые отсекаются плоскостью на осях координат O х , O у и O z в трехмерной системе координат O х у z . Откладываются длины отрезков от начала координат. Направление, в котором необходимо отложить длину отрезка, определяет знак, стоящий перед числом. Наличие «-» свидетельствует о том, что отрезок надо откладывать от нуля в отрицательном направлении оси.
Действительно, координаты точек a , 0 , 0 , 0 , b , 0 , 0 , 0 , c удовлетворяют уравнению плоскости в отрезках:
a a + 0 b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + b b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + 0 b + c c = 1 = 1 ⇔ 1 = 1
Поясним этот момент, расположив заданные точки на графике.
Проиллюстрируем описанное выше примером.
Плоскость проходит через точки – 2 , 0 , 0 , 0 , 3 , 0 и 0 , 0 , – 1 2 на осях координат в прямоугольной системе координат O x y z . Необходимо записать уравнение плоскости в отрезках.
Решение
Определим положение отрезков, отсекаемых плоскостью на осях координат. На оси абсцисс откладываем в отрицательном направлении отрезок длиной 2 единицы. На оси ординат в положительном направлении откладываем отрезок длиной 3 . На оси аппликат в отрицательном направлении откладываем отрезок длиной 1 2 .
При этом, уравнение плоскости в отрезках будет иметь вид: x – 2 + y 3 + z – 1 2 = 1 .
Ответ: x – 2 + y 3 + z – 1 2 = 1
Уравнение плоскости в отрезках удобно использовать для построения чертежей. Проиллюстрируем это утверждение примером.
Плоскость в прямоугольной системе координат O х у z задана уравнением плоскости в отрезках вида x – 5 + y – 4 + z 4 = 1 . Необходимо изобразить эту плоскость на графике.
Решение
Изобразим оси координат, обозначаем начало координат и единичные отрезки на осях. Отмечаем длины отрезков, отсекаемых плоскостью, на каждой из осей. Соединяем концевые точки отрезков прямыми линиями. Полученная плоскость имеет вид треугольника. Она соответствует заданному уравнению плоскости в отрезках x – 5 + y – 4 + z 4 = 1 .
Ответ:
Плоскость может быть задана уравнением плоскости другого вида. Для того, чтобы изобразить заданную плоскость на чертеже, можно сначала перейти к уравнению плоскости в отрезках. Получив уравнение плоскости в отрезках, нам останется лишь отметить точки a , 0 , 0 , 0 , b , 0 , 0 , 0 , c и соединить их прямыми линиями.
Приведение общего уравнения плоскости к уравнению плоскости в отрезках
Мы имеем общее уравнение плоскости в пространстве вида A x + B y + C z + D = 0 . И мы можем получить уравнение плоскости в отрезках. Сделать это можно в том случае, если плоскость пересекает все координатные оси, причем не в начале координат.
Не получится перевести общее уравнение плоскости в пространстве в уравнение плоскости в отрезках в тех случаях, когда плоскость проходит через одну из координатных осей или располагается параллельно оси. Другими словами, мы можем работать лишь с полным уравнением плоскости вида A x + B y + C z + D = 0 , где A ≠ 0 , B ≠ 0 , C ≠ 0 , D ≠ 0 .
Приведение общего уравнения плоскости к уравнению плоскости в пространстве производится следующим образом. Переносим слагаемое D в правую часть уравнения с противоположным знаком.
A x + B y + C z + D = 0 ⇔ A x + B y + C z = – D
Так как D ≠ 0 , то обе части полученного уравнения можно разделить на – D : A – D x + B – D y + C – D z = 1 .
Так как A ≠ 0 , B ≠ 0 , C ≠ 0 , то мы можем отправить в знаменатели коэффициенты перед переменными x , y и z . Последнее уравнение эквивалентно равенству x – D A + y – D B + z – D C = 1 . При этом мы использовали очевидное равенство p q = 1 q p , p , q ∈ R , p ≠ 0 , q ≠ 0 .
В итоге, мы получаем уравнение плоскости в отрезках. Это становится хорошо видно в том случае, если обозначить – D A = a , – D B = b , – D C = c .
Разберем решение примера.
Плоскость в прямоугольной системе координат O x y z в пространстве задана уравнением вида 3 x + 9 y – 6 z – 6 = 0 . Переведем это уравнение в уравнение плоскости в отрезках.
Решение
Данное в условии задачи уравнение является полным уравнением плоскости. Это дает нам возможность привески его к уравнению плоскости в отрезках. Перенесем – 6 в правую часть равенства, а затем разделим обе части равенства на 6 :
3 x + 9 y – 6 z – 6 = 0 ⇔ 3 x + 9 y + 6 z = 6 3 x + 9 y – 6 z = 6 ⇔ 1 2 x + 3 2 y – z = 1
Коэффициенты при переменных x, y и z отправим в знаменатели: 1 2 x + 3 2 y – z = 1 ⇔ x 2 + y 2 3 + z – 1 = 1 . Полученное уравнение и есть уравнение плоскости в отрезках.
Ответ: x 2 + y 2 3 + z – 1 = 1
Уравнение плоскости.
Общее уравнение плоскости
Любую плоскость можно задать уравнением плоскости первой степени вида
A x + B y + C z + D = 0
где A, B и C не могут быть одновременно равны нулю.
Уравнение плоскости в отрезках
Если плоскость пересекает оси OX, OY и OZ в точках с координатами ( a , 0, 0), (0, b , 0) и (0, 0, с ), то она может быть найдена, используя формулу уравнения плоскости в отрезках
| x | + | y | + | z | = 1 |
| a | b | c |
Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали
Чтобы составить уравнение плоскости, зная координаты точки плоскости M( x 0, y 0, z 0) и вектора нормали плоскости n = < A; B; C >можно использовать следующую формулу.
Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой
Если заданы координаты трех точек A( x 1, y 1, z 1), B( x 2, y 2, z 2) и C( x 3, y 3, z 3), лежащих на плоскости, то уравнение плоскости можно найти по следующей формуле
| x – x 1 | y – y 1 | z – z 1 | = 0 |
| x 2 – x 1 | y 2 – y 1 | z 2 – z 1 | |
| x 3 – x 1 | y 3 – y 1 | z 3 – z 1 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-ploskosti-v-otrezkah/
http://ru.onlinemschool.com/math/library/analytic_geometry/plane/
[/spoiler]
5.1.5. Уравнение плоскости в отрезках
Важнейшая прикладная разновидность. Если все коэффициенты общего уравнения плоскости отличны от нуля, то оно представимо в виде
, который называется уравнением плоскости в отрезках. Очевидно, что плоскость пересекает координатные оси в
точках , и большое преимущество такого уравнения состоит в лёгкости построения
чертежа:
Задача 128
Построить плоскость
Решение: составим уравнение плоскости в отрезках. Перебросим свободный член направо и разделим обе части на 12:
,
Делаем дроби трёхэтажными:
Именно так! – ведь знаменатели могут оказаться и дробными. Но в данном случае всё разделилось нацело:
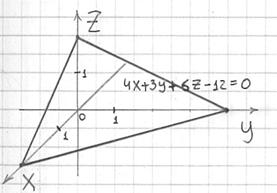
Таким образом, плоскость проходит через точки . В целях самоконтроля координаты каждой точки устно подставим в исходное уравнение
. После чего выполним чертёж:
В отличие от предыдущих примеров здесь фрагмент плоскости изображается в виде треугольника, который, как я уже отмечал, может «прорисоваться» в
любом из 8 октантов.
Уравнение содержит длины
трёх отрезков, которые «исходят» из начала координат и однозначно определяют плоскость (отсюда и название уравнения).
Задание для тренировки:
Задача 129
Построить плоскость
После чего возвращаемся к аналитике.


| Оглавление |
Автор: Aлeксaндр Eмeлин