Уравнение плоскости, проходящей через данную прямую параллельно другой прямой онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через прямую L1 параллельно другой прямой L2 (прямые L1 и L2 не параллельны). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямых (канонический или параметрический) введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку “Решить”.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через данную прямую параллельно другой прямой − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2, которые не параллельны:
Задача заключается в построении уравнения плоскости α, проходящей через прямую L1 параллельно прямой L2(Рис.1).
Решение. Уравнение прямой L1 проходит через точку M1(x1, y1, z1) и имеет направляющий вектор q1={m1, p1, l1}. Уравнение прямой L2 проходит через точку M2(x2, y2, z2) и имеет направляющий вектор q2={m2, p2, l2}.
Прамая L1 должна лежать на искомой плоскости α, следовательно точка M1 должна нежать на плоскости α.
Уравнение плоскости можно записать формулой
и поскольку M1(x1, y1, z1) принадлежит этой плоскости, то справедливо следующее равенство:
Для того, чтобы плоскость α проходила через прямую L1, нормальный вектор плоскости n={A, B, C} должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:
Для того, чтобы плоскость α была параллельна прямой L2, нормальный вектор плоскости n={A, B, C} должен быть ортогональным направляющему вектору q2 прямой L2, т.е. скалярное произведение этих векторов должен быть равным нулю:
Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (4)−(6). Представим систему линейных уравнений (4)−(6) в матричном виде:
Решив однородную систему линейных уравнений (7) найдем частное решение. (как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн). Подставляя полученные коэффициенты A, B, C и D в уравнение (3), получим уравнение плоскости, проходящей через прямую L1 параллельно прямой L2.
Пример 1.Найти уравнение плоскости α, проходящей через прямую L1:
паралленьно другой прямой L2 :
Решение. Прямая L1 проходит через точку M1(x1, y1, z1)=M1(1, 1, 5) и имеет направляющий вектор
Прямая L2 проходит через точку M2(x2, y2, z2)=M2(1, 1, −2) и имеет направляющий вектор
Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(1, 1, 5) и нормальный вектор плоскости n={A, B, C} перпендикулярна направляющему вектору q1={m1, p1, l1}={1, 1, −3} прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:
Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:
Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (10)−(12). Подставим значения m1, p1, l1, m2, p2, l2, x1, y1, z1 в (10),(11) и (12):
Представим эти уравнения в матричном виде:
Решим систему линейных уравнений (16) отностительно A, B, C, D:
Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n={A, B, C}={−13/24,1/6,−1/8} то она может быть представлена формулой:
Подставляя значения A,B,C,D в (17), получим:
Уравнение плоскости можно представить более упрощенном виде, умножив на число −24:
Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (19).
——————
Пример 2. Найти уравнение плоскости α, проходящей через прямую L1:
и паралленьной другой прямой L2
Решение. Прямая L1 проходит через точку M1(x1, y1, z1)=M1( −2, 0, 1) и имеет направляющий вектор
Прямая L2 проходит через точку M2(x2, y2, z2)=M2(1, 1,−2) и имеет направляющий вектор
Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(−2, 0, 1) и нормальный вектор плоскости n={A, B, C} перпендикулярна направляющему вектору q1={m1, p1, l1}={5, −8, 3} прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:
Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:
Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (22)−(24). Подставим значения m1, p1, l1, m2, p2, l2, x1, y1, z1 в (22),(23) и (24):
Представим эти уравнения в матричном виде:
Решим систему линейных уравнений (28) отностительно A, B, C, D:
Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n={A, B, C}={11/35,2/35,−13/35} то она может быть представлена формулой:
Подставляя значения A,B,C,D в (30), получим:
Уравнение плоскости можно представить более упрощенном виде, умножив на число 35:
Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (32).
Уравнение плоскости, проходящей через данную прямую параллельно другой прямой онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через прямую L1 параллельно другой прямой L2 (прямые L1 и L2 не параллельны). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямых (канонический или параметрический) введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку “Решить”.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через данную прямую параллельно другой прямой − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2, которые не параллельны:
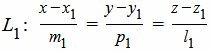 . . |
(1) |
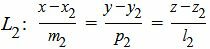 . . |
(2) |
Задача заключается в построении уравнения плоскости α, проходящей через прямую L1 параллельно прямой L2(Рис.1).
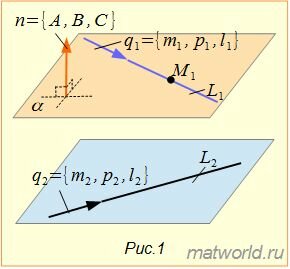
Прамая L1 должна лежать на искомой плоскости α, следовательно точка M1 должна нежать на плоскости α.
Уравнение плоскости можно записать формулой
и поскольку M1(x1, y1, z1) принадлежит этой плоскости, то справедливо следующее равенство:
Для того, чтобы плоскость α проходила через прямую L1, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:
Для того, чтобы плоскость α была параллельна прямой L2, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q2 прямой L2, т.е. скалярное произведение этих векторов должен быть равным нулю:
Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (4)−(6). Представим систему линейных уравнений (4)−(6) в матричном виде:
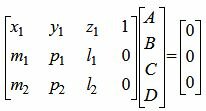
|
(7) |
Решив однородную систему линейных уравнений (7) найдем частное решение. (как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн). Подставляя полученные коэффициенты A, B, C и D в уравнение (3), получим уравнение плоскости, проходящей через прямую L1 параллельно прямой L2.
Пример 1. Найти уравнение плоскости α, проходящей через прямую L1:
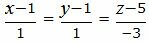 |
(8) |
паралленьно другой прямой L2 :
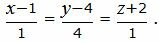 |
(9) |
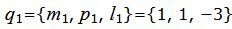
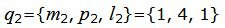
Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(1, 1, 5) и нормальный вектор плоскости n=<A, B, C> перпендикулярна направляющему вектору q1=<m1, p1, l1>= <1, 1, −3>прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
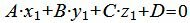 |
(10) |
а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:
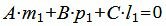 |
(11) |
Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:
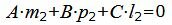 |
(12) |
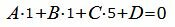 |
(13) |
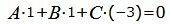 |
(14) |
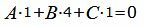 |
(15) |
Представим эти уравнения в матричном виде:
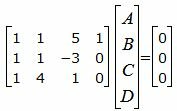 |
(16) |
Решим систему линейных уравнений (16) отностительно A, B, C, D:
 |
(17) |
Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n=<A, B, C>= <−13/24,1/6,−1/8>то она может быть представлена формулой:
Подставляя значения A,B,C,D в (17), получим:
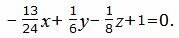 |
(18) |
Уравнение плоскости можно представить более упрощенном виде, умножив на число −24:
Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (19).
Пример 2. Найти уравнение плоскости α, проходящей через прямую L1:
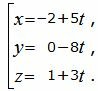 |
(20) |
Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(−2, 0, 1) и нормальный вектор плоскости n=<A, B, C> перпендикулярна направляющему вектору q1=<m1, p1, l1>= <5, −8, 3>прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:
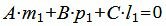 |
(23) |
Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:
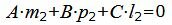 |
(24) |
Представим эти уравнения в матричном виде:
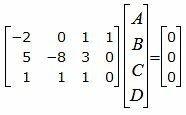 |
(28) |
Решим систему линейных уравнений (28) отностительно A, B, C, D:
 |
(29) |
Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n=<A, B, C>= <11/35,2/35,−13/35>то она может быть представлена формулой:
Подставляя значения A,B,C,D в (30), получим:
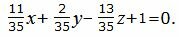 |
(31) |
Уравнение плоскости можно представить более упрощенном виде, умножив на число 35:
Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (32).
Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости
Статья рассматривает понятия параллельность прямой и плоскости. Будут рассмотрены основные определения и приведены примеры. Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.
Параллельные прямые и плоскость – основные сведения
Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.
Параллельность обозначается « ∥ ». Если в задании по условию прямая a и плоскость α параллельны, тогда обозначение имеет вид a ∥ α . Рассмотрим рисунок, приведенный ниже.
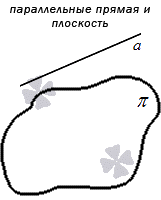
Считается, что прямая a , параллельная плоскости α и плоскость α , параллельная прямой a , равнозначные, то есть прямая и плоскость параллельны друг другу в любом случае.
Параллельность прямой и плоскости – признак и условия параллельности
Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.
Если заданная прямая a , не лежащая в плоскости α , параллельна прямой b , которая принадлежит плоскости α , тогда прямая a параллельна плоскости α .
Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.
Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.
Подробное доказательство рассмотрено в учебнике 10 – 11 класса по геометрии. Необходимым и достаточным условием параллельности прямой с плоскостью возможно при наличии определения направляющего вектора прямой и нормального вектора плоскости.
Для параллельности прямой a , не принадлежащей плоскости α , и данной плоскости необходимым и достаточным условием является перпендикулярность направляющего вектора прямой с нормальным вектором заданной плоскости.
Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.
Допустим, прямая а в систему координат О х у задается каноническими уравнениями прямой в пространстве , которые имеют вид x – x 1 a x = y – y 1 a y = z – z 1 a z или параметрическими уравнениями прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , плоскостью α с общими уравнениями плоскости A x + B y + C z + D = 0 .
Отсюда a → = ( a x , a y , a z ) является направляющим вектором с координатами прямой а, n → = ( A , B , C ) – нормальным вектором заданной плоскости альфа.
Чтобы доказать перпендикулярность n → = ( A , B , C ) и a → = ( a x , a y , a z ) , нужно использовать понятие скалярного произведения. То есть при произведении a → , n → = a x · A + a y · B + a z · C результат должен быть равен нулю из условия перпендикулярности векторов.
Значит, что необходимым и достаточным условием параллельности прямой и плоскости запишется так a → , n → = a x · A + a y · B + a z · C . Отсюда a → = ( a x , a y , a z ) является направляющим вектором прямой a с координатами, а n → = ( A , B , C ) – нормальным вектором плоскости α .
Определить, параллельны ли прямая x = 1 + 2 · λ y = – 2 + 3 · λ z = 2 – 4 · λ с плоскостью x + 6 y + 5 z + 4 = 0 .
Получаем, что предоставленная прямая не принадлежит плоскости, так как координаты прямой M ( 1 , – 2 , 2 ) не подходят. При подстановке получаем, что 1 + 6 · ( – 2 ) + 5 · 2 + 4 = 0 ⇔ 3 = 0 .
Необходимо проверить на выполнимость необходимое и достаточное условие параллельности прямой и плоскости. Получим, что координаты направляющего вектора прямой x = 1 + 2 · λ y = – 2 + 3 · λ z = 2 – 4 · λ имеют значения a → = ( 2 , 3 , – 4 ) .
Нормальным вектором для плоскости x + 6 y + 5 z + 4 = 0 считается n → = ( 1 , 6 , 5 ) . Перейдем к вычислению скалярного произведения векторов a → и n → . Получим, что a → , n → = 2 · 1 + 3 · 6 + ( – 4 ) · 5 = 0 .
Значит, перпендикулярность векторов a → и n → очевидна. Отсюда следует, что прямая с плоскостью являются параллельными.
Ответ: прямая с плоскостью параллельны.
Определить параллельность прямой А В в координатной плоскости О у z , когда даны координаты A ( 2 , 3 , 0 ) , B ( 4 , – 1 , – 7 ) .
По условию видно, что точка A ( 2 , 3 , 0 ) не лежит на оси О х , так как значение x не равно 0 .
Для плоскости O x z вектор с координатами i → = ( 1 , 0 , 0 ) считается нормальным вектором данной плоскости. Обозначим направляющий вектор прямой A B как A B → . Теперь при помощи координат начала и конца рассчитаем координаты вектора A B . Получим, что A B → = ( 2 , – 4 , – 7 ) . Необходимо выполнить проверку на выполнимость необходимого и достаточного условия векторов A B → = ( 2 , – 4 , – 7 ) и i → = ( 1 , 0 , 0 ) , чтобы определить их перпендикулярность.
Запишем A B → , i → = 2 · 1 + ( – 4 ) · 0 + ( – 7 ) · 0 = 2 ≠ 0 .
Отсюда следует, что прямая А В с координатной плоскостью О y z не являются параллельными.
Ответ: не параллельны.
Не всегда заданное условие способствует легкому определению доказательства параллельности прямой и плоскости. Появляется необходимость в проверке принадлежности прямой a плоскости α . Существует еще одно достаточное условие, при помощи которого доказывается параллельность.
При заданной прямой a с помощью уравнения двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 , плоскостью α – общим уравнением плоскости A x + B y + C z + D = 0 .
Необходимым и достаточным условием для параллельности прямой a и плоскости α яляется отсутствие решений системы линейных уравнений, имеющей вид A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 .
Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат О х у z не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:
A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 , а также уравнению плоскости A x + B y + C z + D = 0 .
Следовательно, система уравнений, имеющая вид A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 , называется несовместной.
Верно обратное: при отсутствии решений системы A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не существует точек в О х у z , удовлетворяющих всем заданным уравнениям одновременно. Получаем, что нет такой точки с координатами, которая могла бы сразу быть решениями всех уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 и уравнения A x + B y + C z + D = 0 . Значит, имеем параллельность прямой и плоскости, так как отсутствуют их точки пересечения.
Система уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.
Доказать , что прямая x – 1 = y + 2 – 1 = z 3 параллельна плоскости 6 x – 5 y + 1 3 z – 2 3 = 0 .
Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:
x – 1 = y + 2 – 1 = z 3 ⇔ – 1 · x = – 1 · ( y + 2 ) 3 · x = – 1 · z 3 · ( y + 2 ) = – 1 · z ⇔ x – y – 2 = 0 3 x + z = 0
Чтобы доказать параллельность заданной прямой x – y – 2 = 0 3 x + z = 0 с плоскостью 6 x – 5 y + 1 3 z – 2 3 = 0 , необходимо уравнения преобразовать в систему уравнений x – y – 2 = 0 3 x + z = 0 6 x – 5 y + 1 3 z – 2 3 = 0 .
Видим, что она не решаема, значит прибегнем к методу Гаусса.
Расписав уравнения, получаем, что 1 – 1 0 2 3 0 1 0 6 – 5 1 3 2 3
1 – 1 0 2 0 3 1 – 6 0 1 1 3 – 11 1 3
1 – 1 0 2 0 3 1 – 6 0 0 0 – 9 1 3 .
Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.
Делаем вывод, что прямая x – 1 = y + 2 – 1 = z 3 и плоскость 6 x – 5 y + 1 3 z – 2 3 = 0 параллельны, так как было выполнено необходимое и достаточное условие для параллельности плоскости с заданной прямой.
Ответ: прямая и плоскость параллельны.
Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости.
В этой статье всесторонне раскрыта тема «параллельность прямой и плоскости». Сначала дано определение параллельных прямой и плоскости, приведена графическая иллюстрация и пример. Далее сформулирован признак параллельности прямой и плоскости, а также озвучены необходимые и достаточные условия параллельности прямой и плоскости. В заключении приведены развернутые решения задач, в которых доказывается параллельность прямой и плоскости.
Навигация по странице.
Параллельные прямая и плоскость – основные сведения.
Начнем с определения параллельных прямой и плоскости.
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Для обозначения параллельности используется символ «». То есть, если прямая a и плоскость параллельны, то можно кратко записать a .
Заметим, что выражения «прямая a и плоскость параллельны», «прямая a параллельна плоскости » и «плоскость параллельна прямой a » одинаково употребимы.
В качестве примера параллельных прямой и плоскости приведем натянутую гитарную струну и плоскость грифа этой гитары.
Параллельность прямой и плоскости – признак и условия параллельности.
Параллельность прямой и плоскости далеко не всегда является очевидным фактом. Другими словами, параллельность прямой и плоскости приходится доказывать. Существует достаточное условие, выполнение которого гарантирует параллельность прямой и плоскости. Это условие называют признаком параллельности прямой и плоскости. Прежде чем ознакомиться с формулировкой этого признака, рекомендуем повторить определение параллельных прямых.
Если прямая a , не лежащая в плоскости , параллельна некоторой прямой b , которая лежит в плоскости , то прямая a параллельна плоскости .
Озвучим еще одну теорему, которую можно использовать для установления параллельности прямой и плоскости.
Если одна из двух параллельных прямых параллельна некоторой плоскости, то вторая прямая либо также параллельна этой плоскости, либо лежит в ней.
Доказательство признака параллельности прямой и плоскости и доказательство озвученной теоремы приводятся в учебнике геометрии за 10 – 11 классы, который указан в конце статьи в списке рекомендованной литературы.
Определение направляющего вектора прямой и определение нормального вектора плоскости позволяют записать необходимое и достаточное условие параллельности прямой и плоскости.
Для параллельности прямой a , не лежащей в плоскости , и плоскости необходимо и достаточно, чтобы направляющий вектор прямой a был перпендикулярен нормальному вектору плоскости .
Это условие удобно использовать для доказательства параллельности прямой и плоскости, которые заданы в прямоугольной системе координат в трехмерном пространстве некоторыми уравнениями.
Пусть прямую a в прямоугольной системе координат Oxyz задают канонические уравнения прямой в пространстве вида или параметрические уравнения прямой в пространстве вида , а плоскости соответствует общее уравнение плоскости . Тогда – направляющий вектор прямой a , а – нормальный вектор плоскости . Для перпендикулярности векторов и необходимо и достаточно, чтобы скалярное произведение равнялось нулю (об этом написано в статье условие перпендикулярности двух векторов).
Следовательно, необходимое и достаточное условие параллельности прямой a и плоскости ( a не лежит в плоскости ) примет вид , где – направляющий вектор прямой a , – нормальный вектор плоскости .
Разберем решения нескольких примеров.
Являются ли прямая и плоскость параллельными?
Заданная прямая не лежит в плоскости, так как координаты точки прямой не удовлетворяют уравнению плоскости: . Проверим выполнение необходимого и достаточного условия параллельности прямой и плоскости. Очевидно, – направляющий вектор прямой , – нормальный вектор плоскости . Вычислим скалярное произведение векторов и : . Таким образом, векторы и перпендикулярны. Следовательно, заданные прямая и плоскость параллельны.
да, прямая и плоскость параллельны.
Параллельна ли прямая АВ координатной плоскости Oyz , если .
Точка не лежит в координатной плоскости Oyz , так как абсцисса этой точки отлична от нуля.
Нормальным вектором плоскости Oyz является вектор . В качестве направляющего вектора прямой AB возьмем вектор . Координаты точек начала и конца вектора позволяют вычислить координаты этого вектора, тогда . Проверим выполнение необходимого и достаточного условия перпендикулярности векторов и : . Следовательно, прямая AB и координатная плоскость Oyz не параллельны.
нет, не параллельны.
Разобранное условие не совсем удобно для доказательства параллельности прямой a и плоскости , так как отдельно приходится проверять, что прямая a не лежит в плоскости . Поэтому, доказывать параллельность прямой a и плоскости удобнее с помощью следующего необходимого и достаточного условия.
Пусть прямая a задана уравнениями двух пересекающихся плоскостей ,
а плоскость – общим уравнением плоскости .
Для параллельности прямой a и плоскости необходимо и достаточно, чтобы система линейных уравнений вида не имела решений.
Действительно, если прямая a параллельна плоскости , то они по определению не имеют общих точек. Следовательно, не существует ни одной точки в прямоугольной системе координат Oxyz , координаты которой удовлетворяли бы одновременно и уравнениям прямой и уравнению плоскости . Значит, система уравнений вида несовместна.
И обратно: если система уравнений вида не имеет решений, то не существует ни одной точки в прямоугольной системе координат Oxyz , координаты которой удовлетворяли бы одновременно всем уравнениям системы. Тогда, не существует точки, координаты которой одновременно удовлетворяют и уравнениям прямой и уравнению плоскости . Следовательно, прямая a и плоскость не имеют общих точек, то есть, они параллельны.
В свою очередь система уравнений не имеет решений, когда ранг основной матрицы системы меньше ранга расширенной матрицы (это следует из теоремы Кронекера-Капелли, при необходимости смотрите статью решение систем линейных уравнений). Несовместность этой системы уравнений можно также показать, используя метод Гаусса для решения систем линейных уравнений.
Докажите параллельность прямой и плоскости .
Перейдем от канонических уравнений прямой к уравнениям двух пересекающихся плоскостей:
Для доказательства параллельности прямой и плоскости покажем, что система уравнений не имеет решения. Воспользуемся методом Гаусса:
Действительно, система уравнений несовместна, следовательно, заданные прямая и плоскость не имеют общих точек. Этим доказана параллельность прямой и плоскости .
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/parallelnye-prjamaja-i-ploskost-priznak-i-uslovija/
http://www.cleverstudents.ru/line_and_plane/parallel_line_and_plane.html
[/spoiler]
Пусть  непараллельные прямые. Тогда плоскость, проходящая через прямую
непараллельные прямые. Тогда плоскость, проходящая через прямую  и параллельная прямой
и параллельная прямой  представляется уравнением
представляется уравнением

 где
где  координаты какой-либо точки
координаты какой-либо точки  прямой
прямой  Здесь имеем частный случай § 158 (роль точки
Здесь имеем частный случай § 158 (роль точки  играет
играет  Замечание к § 158 тоже остается в силе.
Замечание к § 158 тоже остается в силе.
Уравнение плоскости, проходящей через прямую и параллельной другой прямой
Если даны не параллельные прямые L1 и L2, тогда плоскость, проходящая через прямую L1 и параллельная прямой L2 представляется уравнением:
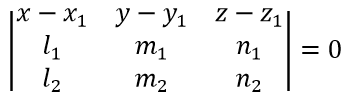
Это и есть уравнение плоскости, проходящей через данную прямую и параллельной другой данной прямой.
где
х1, y1, z1 — координаты какой-либо точки прямой L1
ι1, m1, n1 — направляющие коэффициенты прямой L1
ι2, m2, n2 — направляющие коэффициенты прямой L2
![]() 7422
7422
Уравнение плоскости, проходящей через прямую параллельно прямой
Материал из Циклопедии
Перейти к навигации
Перейти к поиску
Уравнение плоскости, проходящей через прямую параллельно прямой, задаётся равенством нулю смешанного произведения вектора-разности радиусов-векторов точек и направляющих векторов прямых.
Обозначения[править]
Введём обозначения:




Формулы[править]
Векторная форма: 
Координатная форма:
- Заметим, что формулы уравнения плоскости, проходящей через прямую параллельно прямой, аналогичны формулам уравнения плоскости, проходящей через точку параллельно двум прямым.
Уравнения плоскости[править]
- уравнение плоскости, проходящей через три точки;
- уравнение плоскости, равноудалённой от двух точек;
- уравнение плоскости, проходящей через две точки параллельно прямой;
- уравнение плоскости, проходящей через две точки перпендикулярно плоскости;
- уравнение плоскости, проходящей через точку и прямую;
- уравнение плоскости, проходящей через точку перпендикулярно прямой;
- уравнение плоскости, проходящей через точку параллельно плоскости;
- уравнение плоскости, проходящей через точку параллельно двум прямым;
- уравнение плоскости, проходящей через точку перпендикулярно двум плоскостям;
- уравнение плоскости, проходящей через прямую параллельно прямой;
- уравнение плоскости, проходящей через прямую перпендикулярно плоскости.
Литература[править]
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970.
- Выгодский М. Я. Справочник по высшей математике — М.: Наука, 1964, стр.187.


