В данном материале мы расскажем, как правильно вычислить уравнение плоскости, которая проходит через 2 пересекающиеся или параллельные прямые. Начнем с формулировки основного принципа, а потом, как всегда, разберем несколько задач, где можно применить этот принцип на практике.
Как найти уравнение плоскости, проходящей через пересекающиеся прямые?
Для того чтобы вывести это уравнение, нам понадобится вспомнить одну теорему. Она звучит так:
Через две пересекающиеся прямые может проходить только одна плоскость.
Доказательство этого утверждения основано на двух аксиомах:
- через три точки с разными координатами, которые не лежат на одной прямой, проходит только одна плоскость;
- если у нас есть две точки прямой с разными координатами, расположенные в некоторой плоскости, то все точки этой прямой находятся в этой плоскости.
В итоге мы можем утверждать, что с помощью указания двух пересекающихся прямых мы можем задать определенную плоскость в трехмерном пространстве.
Далее нам нужно доказать, что плоскость, которая проходит через две определенные прямые, совпадет с той, что проходит через три заданные точки, две из которых находятся на тех самых прямых.
Допустим, у нас есть две прямые a и b с пересечением в некой точке M. Теперь расположим на первой прямой две точки М1 и М2. У них должны быть разные координаты, но при этом одна из них может совпадать с точкой пересечения. На второй прямой отметим точку М3 (но она совпадать с точкой M не должна). Теперь нам надо показать, что плоскость, проходящая через М1М2М3, – это та же самая плоскость, что проходит через пересекающиеся прямые a и b.
Посмотрим на схему:
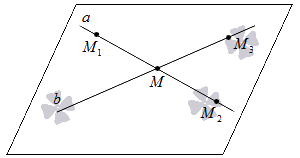
Поскольку мы имеем точки прямой a, которые находятся в плоскости М1М2М3 (М1 и М2), то, используя аксиому, которую мы приводили выше, можно утверждать, что все точки этой прямой находятся в данной плоскости. Все точки прямой b тоже будут находиться в ней, поскольку там расположены две несовпадающие точки данной прямой (М и М3). Таким образом, мы доказали, что плоскости, в которых лежат данные прямые, совпадают.
Теперь перейдем непосредственно к формулировке уравнения плоскости, которая проходит через пересекающиеся прямые. Возьмем a и b, которые заданы в прямоугольной системе координат Oxyz в трехмерном пространстве и являются пересекающимися. Напишем уравнение плоскости, которая проходит через эти прямые.
Все решение можно свести к нахождению уже изученного уравнения плоскости, проходящей через три точки. Сначала нам надо найти координаты двух точек M1 и M2, которые расположены на пересекающихся прямых, и точки M3, которая находится на другой прямой и не является точкой их пересечения. Для этого можно использовать разные способы. Так, мы можем составить параметрические уравнения для первой прямой в пространстве. В итоге получим:
x=x1+ax·λy=y1+ay·λz=z1+az·λ
Отсюда можно вывести координаты x1, y1, z1 точки M1, если λ=0. Для М2 эти данные можно вычислить, если придать параметру любое действительное значение, отличное от нуля, например, единицу.
Далее мы можем составить такие же параметрические уравнения для второй прямой и, используя некоторое значение параметра, высчитать координаты М3. Важно проверить, чтобы она не лежала в точке пересечения прямых и вообще не находилась на прямой a.
Итак, мы нашли координаты всех нужных точек – М1, М2 и М3. Переходим к написанию уравнения плоскости, которая через них проходит. Запишем:
x-x1y-y1z-z1x2-x1y2-y1z2-z1x3-x1y3-y1z3-z1=0
Теперь найдем определитель матрицы x-x1y-y1z-z1x2-x1y2-y1z2-z1x3-x1y3-y1z3-z1 и получим общее уравнение для нужной нам плоскости, которая будет проходит через две заданные прямые a и b.
Как найти уравнение плоскости, проходящей через параллельные прямые?
Для этого нам понадобится вспомнить теорему, которая формулируется так:
Через две параллельные прямые проходит только одна плоскость.
Ее можно доказать, используя аксиому о единственной плоскости, которая проходит через три точки, а также утверждение о двух параллельных прямых (если одна из параллельных прямых пресекает некоторую плоскость, то это же делает и другая).
Итак, возможно задать плоскость в пространстве, если указать две параллельные прямые, которые в ней находятся.
Очевиден тот факт, что плоскость, которая проходит через 2 параллельные прямые и плоскость, которая проходит через три точки, две из которой лежат на одной из этих прямых, будут совпадать.
После этого мы можем найти уравнение плоскости, проходящей через две заданные параллельные прямые.
У нас есть прямоугольная система координат в трехмерном пространстве, которая обозначается Oxyz. Составим уравнение плоскости, которая проходит через параллельные прямые a и b.
Сводим задачу опять же к нахождению уравнения для плоскости с тремя точками. В самом деле, можно определить, какие точно координаты будут иметь М1 и М2, лежащие на одной из параллельных прямых, и М3, расположенная на другой прямой. После этого просто запишем нужное нам уравнение для плоскости, проходящей через три точкиM1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в следующем виде:
x-x1y-y1z-z1x2-x1y2-y1z2-z1x3-x1y3-y1z3-z1=0
Это и есть нужное нам уравнение плоскости, проходящей через заданные параллельные прямые.
Примеры задач на нахождение подобных уравнений
Таким образом, для того чтобы составить уравнение плоскости, которая проходит через 2 пересекающиеся или параллельные прямые, требуется вычислить координаты трех точек, которые расположены на этих прямых (две точки на одной прямой и третья на другой). Посмотрим, как это принцип реализуется на практике.
У нас задана прямоугольная система координат в трехмерном пространстве. Расположенная в ней прямая a проходит через точку M1(-3,1, -4) и пересекает координатную прямую Oy в точке M2(0, 5, 0). Составьте уравнение плоскости, которая будет проходить через пересекающиеся a и Oy.
Решение
Изначально у нас заданы координаты двух точек, которые расположены на исходной прямой. Для составления уравнения нам нужна третья. Возьмем точку начала координат O (0, 0, 0). Она расположена на Oy и не совпадает с координатами двух точек, которые были заданы в условии. Та плоскость, что будет проходить через них, и есть та, для которой нам надо вывести уравнение. Запишем его в координатном виде:
x-x1y-y1z-z1x2-x1y2-y1z2-z1x3-x1y3-y1z3-z1=0 ⇔ x-0y-0z-0-3-01-0-4-00-05-00-0=0 ⇔⇔xyz-31-4050=0⇔20x-15z=0⇔4x-3z=0
Ответ: 4x-3z=0.
Возьмем более сложный пример, где координаты нужных точек не будут столь очевидными.
У нас есть две пересекающиеся прямые a и b, которые заданы с помощью уравнений.
x-74=y-75=z+5-6x-31=y-2-3=z-15
Составьте уравнение плоскости, которая проходит через них.
Решение
Начнем с вычисления координат трех необходимых точек. Две из них расположены на прямой a, третья – на b.
Прямая в условии задана с помощью канонических уравнений в пространстве вида x-74=y-75=z+5-6, следовательно, она будет проходить через точку x-74=y-75=z+5-6.
Для вычисления координат второй точки нам надо записать параметрическое уравнение:
x-74=y-75=z+5-6⇔x=7+4·λy=7+5·λz=-5-6·λ
Если мы примем λ=1 , то сможем подсчитать координаты второй точки:
x=7+4·λy=7+5·λz=-5-6·λ⇔x=11y=12z=-11
Мы получили, что M2 (11, 12, -11).
Понятно, что прямая, заданная с помощью уравнения x-31=y-2-3=z-15, будет проходить через точку M3 (3, 2, 1). Перед вычислениями надо проверить, не лежит ли она в точке пересечения прямых. Для этого надо подставить ее координаты во второе уравнение:
3-74=2-75=1+5-6⇔-1≡-1≡-1
Мы видим, что канонические уравнения прямой свелись к тождествам. Тогда наша третья точка лежит именно в месте пересечения прямых, значит, нам надо взять еще одну, которая будет находится на прямой b. Для этого также запишем параметрические уравнения:
x-31=y-2-3=z-15⇔x=3+μy=2-3·μz=1+5·μ
Высчитаем нужные координаты, приняв μ=1.
x=3+1y=2-3·1z=1+5·1⇔x=4y=-1z=6⇔M3 (4, -1, 6)
Далее мы можем переходить непосредственно у формулированию уравнения нужной нам плоскости, которая будет проходить через M1( 7, 7, -5), M2 (11, 12, -11), M3 (4, -1, 6):
x-x1y-y1z-z1x2-x1y2-y1z2-z1x3-x1y3-y1z3-z1=0 ⇔ x-7y-7z-(-5)11-712-7-11-(-5)4-7-1-76-(-5)=0 ⇔⇔x-7y-7z+545-6-3-811=0⇔7x-26y-17z+48=0
Ответ: 7x-26y-17z+48=0.
Очевидно, что процесс вычисления координат нужных нам точек занимает больше всего времени при решении подобных задач.
Нам осталось разобрать пример плоскости, которая проходит через две прямые, являющиеся параллельными.
Составьте уравнение плоскости, которая проходит через две параллельные прямые. Они выражены с помощью уравнений x=2·λy=1+λz=-1-λ и x-32=y1=z+5-1.
Решение
Вычисляем координаты двух нужных точек по параметрическим уравнениям, приняв λ=0 и λ=1.
λ=0: x=2·0y=1+0z=-1-0⇔x=0y=1z=-1⇔M1(0, 1, -1)λ=1: x=2·1y=1+1z=-1-1⇔x=2y=2z=-2⇔M2 (2, 2, -2)
У нас получается, что прямая x-32=y1=z+5-1 будет проходить через точку M3(3, 0, -5).
Переходим к уравнению плоскости для трех точек М1, М2 и М3:
x-x1y-y1z-z1x2-x1y2-y1z2-z1x3-x1y3-y1z3-z1=0 ⇔ x-0y-1z-(-1)2-02-1-2-(-1)3-00-1-5-(-1)=0 ⇔⇔xy-1z+121-13-1-4=0⇔-5x+5y-5z-10=0⇔x-y-z+2=0
Ответ: x-y-z+2=0.
Уравнение плоскости, которая проходит через две пересекающиеся или две параллельные прямые.
В этой статье собрана информация, необходимая для нахождения уравнения плоскости, проходящей через две заданные пересекающиеся или параллельные прямые. Сначала разобран принцип составления уравнения плоскости, которая проходит через две заданные прямые, после этого приведены подробные решения характерных примеров.
Навигация по странице.
Нахождение уравнения плоскости, проходящей через две пересекающиеся прямые.
Прежде чем приступать к нахождению уравнения плоскости, проходящей через две заданные пересекающиеся прямые, напомним одну теорему: в трехмерном пространстве через две пересекающиеся прямые проходит единственная плоскость. Это утверждение является следствием из двух аксиом геометрии:
- через три различные и не лежащие на одной прямой точки проходит единственная плоскость;
- если две несовпадающие точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Таким образом, конкретную плоскость в трехмерном пространстве можно задать, указав две пересекающиеся прямые, лежащие в этой плоскости.
Теперь покажем, что плоскость, проходящая через две заданные пересекающиеся прямые, совпадает с плоскостью, проходящей через три различные точки, две из которых лежат на одной из заданных прямых, а третья – на другой прямой.
Пусть заданные прямые a и b пересекаются в точке М . Отметим на прямой a две различные точки М1 и М2 (одна из них может совпадать с точкой M ), а на прямой b точку М3 , отличную от точки М . Покажем, что плоскость М1М2М3 есть плоскость, проходящая через заданные пересекающиеся прямые a и b .
Так как в плоскости М1М2М3 лежат две точки прямой a (точки М1 и М2 ), то из озвученной в начале этого пункта аксиомы следует, что все точки прямой a лежат в плоскости М1М2М3 , в частности, точка М . Тогда в плоскости М1М2М3 лежат все точки прямой b , так как две несовпадающие точки прямой b (точки М и М3 ) лежат в указанной плоскости. Следовательно, плоскость, проходящая через пересекающиеся прямые a и b , и плоскость, проходящая через три точки М1 , М2 и М2 , совпадают.
Итак, поставим перед собой следующую задачу.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , заданы две пересекающиеся прямые a и b , и требуется написать уравнение плоскости, проходящей через пересекающиеся прямые a и b .
Сведем решение этой задачи к нахождению уравнения плоскости, проходящей через три точки. Для этого нужно определить координаты двух различных точек M1 и M2 , лежащих на одной из заданных пересекающихся прямых, и координаты точки M3 , лежащей на другой прямой и не являющейся точкой пересечения заданных прямых. Для нахождения координат точек М1 , М2 и М3 все средства хороши. Например, можно получить параметрические уравнения прямой a в пространстве вида . Из них видны координаты точки М1 (они получаются при ), а координаты точки М2 можно вычислить, придав параметру любое ненулевое действительное значение (к примеру, ). После этого можно получить параметрические уравнения прямой b и при некотором значении параметра вычислить координаты точки М3 , не забыв удостовериться, что она не является точкой пересечения заданных прямых (что она не лежит на прямой a ).
Будем считать, что координаты точек М1 , М2 и М3 найдены. После этого мы можем написать уравнение плоскости, проходящей через три точки и в виде . Вычислив определитель матицы вида , мы получим общее уравнение плоскости М1М2М3 , которое и будет уравнением плоскости, проходящей через две пересекающиеся прямые a и b .
Нахождение уравнения плоскости, проходящей через две параллельные прямые.
Прежде чем получить уравнение плоскости, проходящей через две заданные параллельные прямые, вспомним теорему: через две параллельные прямые проходит единственная плоскость. Эта теорема доказывается на основе аксиомы о единственной плоскости, проходящей через три заданные точки, с использованием утверждения: если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.
Таким образом, мы можем задать конкретную плоскость в трехмерном пространстве, указав две параллельные прямые, лежащие в этой плоскости.
Очевидно, что плоскость, проходящая через две заданные параллельные прямые, совпадает с плоскостью, проходящей через три различные точки, две из которых лежат на одной из заданных параллельных прямых, а третья лежит на другой прямой.
Теперь можно приступать к нахождению уравнения плоскости, проходящей через две заданные параллельные прямые.
Пусть в трехмерном пространстве введена прямоугольная система координат Oxyz , заданы две параллельные прямые a и b и требуется составить уравнение плоскости, которая проходит через параллельные прямые a и b .
Эта задача, также как и задача о нахождении уравнения плоскости, проходящей через две заданные пересекающиеся прямые, сводится к составлению уравнения плоскости, проходящей через три точки. Действительно, мы можем определить координаты двух точек М1 и М2 , лежащих на одной из заданных параллельных прямых, и координаты точки М3 , лежащей на другой прямой. После этого нам лишь нужно написать уравнение плоскости, проходящей через три точки и , в виде . Это уравнение является искомым уравнением плоскости, проходящей через две заданные параллельные прямые.
Примеры составления уравнения плоскости, проходящей через две прямые.
Итак, чтобы написать уравнение плоскости, проходящей через две заданные параллельные или пересекающиеся прямые, нужно найти координаты трех различных точек, две из которых лежат на одной из заданных прямых, а третья точка – на другой прямой, после чего записать уравнение плоскости, проходящей через три точки. Покажем применение этого алгоритма при решении примеров.
Известно, что прямая a в прямоугольной системе координат Oxyz в трехмерном пространстве проходит через точку и пересекает координатную прямую Oy в точке . Напишите уравнение плоскости, проходящей через пересекающиеся прямые a и Oy .
Из условия нам известны координаты двух точек М1 и М2 , лежащих на прямой a . Очевидно, что точка лежит на координатной прямой Oy и не совпадает с точками М1 и М2 . Тогда плоскость, проходящая через три точки , и , есть плоскость, проходящая через пересекающиеся прямые a и Oy . Напишем ее уравнение:
.
Рассмотрим еще один пример, в котором координаты точек, лежащих на заданных пересекающихся прямых, не так очевидны.
Составьте уравнение плоскости, которая проходит через две пересекающиеся прямые a и b , заданные уравнениями и соответственно.
Сначала найдем координаты двух точек, лежащих на прямой a , и координаты точки, лежащей на прямой b .
Прямая, которую в прямоугольной системе координат Oxyz задают канонические уравнения прямой в пространстве вида , проходит через точку . Перейдем к параметрическим уравнениям этой прямой, чтобы определить координаты еще одной точки (обозначим ее М2 ), лежащей на ней. Имеем , примем и из параметрических уравнений прямой вычислим координаты точки М2 : . Следовательно, .
Очевидно, что прямая проходит через точку . Проверим, не является ли точка точкой пересечения заданных прямых, подставив ее координаты в уравнения прямой a : . Канонические уравнения прямой a обратились в тождества, следовательно, точка М3 лежит на прямой a и является точкой пересечения заданных прямых. Таким образом, нам нужно взять другую точку М3 , лежащую на прямой b , так как сейчас найденные точки М1 , М2 и М3 лежат на одной прямой. Для этого мы также переходим к параметрическим уравнениям прямой b : , и вычисляем координаты точки М3 , приняв : .
Теперь мы можем получить уравнение плоскости, проходящей через три точки , и , которое является искомым уравнением плоскости, проходящей через две заданные пересекающиеся прямые:
.
Не правда ли, что нахождение координат точек, лежащих на заданных прямых, является самым трудоемким процессом при составлении уравнения плоскости, проходящей через две пересекающиеся прямые?
Осталось рассмотреть пример составления уравнения плоскости, проходящей через две заданные параллельные прямые.
Напишите уравнение плоскости, проходящей через две параллельные прямые и .
По параметрическим уравнениям прямой при и вычислим координаты двух точек М1 и М2 :
Очевидно, что прямая проходит через точку .
Найдем уравнение плоскости, проходящей через три точки М1 , М2 и М3 :
Это уравнение и есть искомое уравнение плоскости, проходящей через две заданные параллельные прямые.
.
Уравнение плоскости, которая проходит через две пересекающиеся или две параллельные прямые
В данном материале мы расскажем, как правильно вычислить уравнение плоскости, которая проходит через 2 пересекающиеся или параллельные прямые. Начнем с формулировки основного принципа, а потом, как всегда, разберем несколько задач, где можно применить этот принцип на практике.
Как найти уравнение плоскости, проходящей через пересекающиеся прямые?
Для того чтобы вывести это уравнение, нам понадобится вспомнить одну теорему. Она звучит так:
Через две пересекающиеся прямые может проходить только одна плоскость.
Доказательство этого утверждения основано на двух аксиомах:
- через три точки с разными координатами, которые не лежат на одной прямой, проходит только одна плоскость;
- если у нас есть две точки прямой с разными координатами, расположенные в некоторой плоскости, то все точки этой прямой находятся в этой плоскости.
В итоге мы можем утверждать, что с помощью указания двух пересекающихся прямых мы можем задать определенную плоскость в трехмерном пространстве.
Далее нам нужно доказать, что плоскость, которая проходит через две определенные прямые, совпадет с той, что проходит через три заданные точки, две из которых находятся на тех самых прямых.
Допустим, у нас есть две прямые a и b с пересечением в некой точке M . Теперь расположим на первой прямой две точки М 1 и М 2 . У них должны быть разные координаты, но при этом одна из них может совпадать с точкой пересечения. На второй прямой отметим точку М 3 (но она совпадать с точкой M не должна). Теперь нам надо показать, что плоскость, проходящая через М 1 М 2 М 3 , – это та же самая плоскость, что проходит через пересекающиеся прямые a и b .
Посмотрим на схему:
Поскольку мы имеем точки прямой a , которые находятся в плоскости М 1 М 2 М 3 ( М 1 и М 2 ), то, используя аксиому, которую мы приводили выше, можно утверждать, что все точки этой прямой находятся в данной плоскости. Все точки прямой b тоже будут находиться в ней, поскольку там расположены две несовпадающие точки данной прямой ( М и М 3 ). Таким образом, мы доказали, что плоскости, в которых лежат данные прямые, совпадают.
Теперь перейдем непосредственно к формулировке уравнения плоскости, которая проходит через пересекающиеся прямые. Возьмем a и b , которые заданы в прямоугольной системе координат O x y z в трехмерном пространстве и являются пересекающимися. Напишем уравнение плоскости, которая проходит через эти прямые.
Все решение можно свести к нахождению уже изученного уравнения плоскости, проходящей через три точки. Сначала нам надо найти координаты двух точек M 1 и M 2 , которые расположены на пересекающихся прямых, и точки M 3 , которая находится на другой прямой и не является точкой их пересечения. Для этого можно использовать разные способы. Так, мы можем составить параметрические уравнения для первой прямой в пространстве. В итоге получим:
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ
Отсюда можно вывести координаты x 1 , y 1 , z 1 точки M 1 , если λ = 0 . Для М 2 эти данные можно вычислить, если придать параметру любое действительное значение, отличное от нуля, например, единицу.
Далее мы можем составить такие же параметрические уравнения для второй прямой и, используя некоторое значение параметра, высчитать координаты М 3 . Важно проверить, чтобы она не лежала в точке пересечения прямых и вообще не находилась на прямой a .
Итак, мы нашли координаты всех нужных точек – М 1 , М 2 и М 3 . Переходим к написанию уравнения плоскости, которая через них проходит. Запишем:
x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0
Теперь найдем определитель матрицы x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 и получим общее уравнение для нужной нам плоскости, которая будет проходит через две заданные прямые a и b .
Как найти уравнение плоскости, проходящей через параллельные прямые?
Для этого нам понадобится вспомнить теорему, которая формулируется так:
Через две параллельные прямые проходит только одна плоскость.
Ее можно доказать, используя аксиому о единственной плоскости, которая проходит через три точки, а также утверждение о двух параллельных прямых (если одна из параллельных прямых пресекает некоторую плоскость, то это же делает и другая).
Итак, возможно задать плоскость в пространстве, если указать две параллельные прямые, которые в ней находятся.
Очевиден тот факт, что плоскость, которая проходит через 2 параллельные прямые и плоскость, которая проходит через три точки, две из которой лежат на одной из этих прямых, будут совпадать.
После этого мы можем найти уравнение плоскости, проходящей через две заданные параллельные прямые.
У нас есть прямоугольная система координат в трехмерном пространстве, которая обозначается O x y z . Составим уравнение плоскости, которая проходит через параллельные прямые a и b .
Сводим задачу опять же к нахождению уравнения для плоскости с тремя точками. В самом деле, можно определить, какие точно координаты будут иметь М 1 и М 2 , лежащие на одной из параллельных прямых, и М 3 , расположенная на другой прямой. После этого просто запишем нужное нам уравнение для плоскости, проходящей через три точки M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) в следующем виде:
x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0
Это и есть нужное нам уравнение плоскости, проходящей через заданные параллельные прямые.
Примеры задач на нахождение подобных уравнений
Таким образом, для того чтобы составить уравнение плоскости, которая проходит через 2 пересекающиеся или параллельные прямые, требуется вычислить координаты трех точек, которые расположены на этих прямых (две точки на одной прямой и третья на другой). Посмотрим, как это принцип реализуется на практике.
У нас задана прямоугольная система координат в трехмерном пространстве. Расположенная в ней прямая a проходит через точку M 1 ( – 3 , 1 , – 4 ) и пересекает координатную прямую O y в точке M 2 ( 0 , 5 , 0 ) . Составьте уравнение плоскости, которая будет проходить через пересекающиеся a и O y .
Решение
Изначально у нас заданы координаты двух точек, которые расположены на исходной прямой. Для составления уравнения нам нужна третья. Возьмем точку начала координат O ( 0 , 0 , 0 ) . Она расположена на O y и не совпадает с координатами двух точек, которые были заданы в условии. Та плоскость, что будет проходить через них, и есть та, для которой нам надо вывести уравнение. Запишем его в координатном виде:
x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0 ⇔ x – 0 y – 0 z – 0 – 3 – 0 1 – 0 – 4 – 0 0 – 0 5 – 0 0 – 0 = 0 ⇔ ⇔ x y z – 3 1 – 4 0 5 0 = 0 ⇔ 20 x – 15 z = 0 ⇔ 4 x – 3 z = 0
Ответ: 4 x – 3 z = 0 .
Возьмем более сложный пример, где координаты нужных точек не будут столь очевидными.
У нас есть две пересекающиеся прямые a и b , которые заданы с помощью уравнений.
x – 7 4 = y – 7 5 = z + 5 – 6 x – 3 1 = y – 2 – 3 = z – 1 5
Составьте уравнение плоскости, которая проходит через них.
Решение
Начнем с вычисления координат трех необходимых точек. Две из них расположены на прямой a , третья – на b .
Прямая в условии задана с помощью канонических уравнений в пространстве вида x – 7 4 = y – 7 5 = z + 5 – 6 , следовательно, она будет проходить через точку x – 7 4 = y – 7 5 = z + 5 – 6 .
Для вычисления координат второй точки нам надо записать параметрическое уравнение:
x – 7 4 = y – 7 5 = z + 5 – 6 ⇔ x = 7 + 4 · λ y = 7 + 5 · λ z = – 5 – 6 · λ
Если мы примем λ = 1 , то сможем подсчитать координаты второй точки:
x = 7 + 4 · λ y = 7 + 5 · λ z = – 5 – 6 · λ ⇔ x = 11 y = 12 z = – 11
Мы получили, что M 2 ( 11 , 12 , – 11 ) .
Понятно, что прямая, заданная с помощью уравнения x – 3 1 = y – 2 – 3 = z – 1 5 , будет проходить через точку M 3 ( 3 , 2 , 1 ) . Перед вычислениями надо проверить, не лежит ли она в точке пересечения прямых. Для этого надо подставить ее координаты во второе уравнение:
3 – 7 4 = 2 – 7 5 = 1 + 5 – 6 ⇔ – 1 ≡ – 1 ≡ – 1
Мы видим, что канонические уравнения прямой свелись к тождествам. Тогда наша третья точка лежит именно в месте пересечения прямых, значит, нам надо взять еще одну, которая будет находится на прямой b . Для этого также запишем параметрические уравнения:
x – 3 1 = y – 2 – 3 = z – 1 5 ⇔ x = 3 + μ y = 2 – 3 · μ z = 1 + 5 · μ
Высчитаем нужные координаты, приняв μ = 1 .
x = 3 + 1 y = 2 – 3 · 1 z = 1 + 5 · 1 ⇔ x = 4 y = – 1 z = 6 ⇔ M 3 ( 4 , – 1 , 6 )
Далее мы можем переходить непосредственно у формулированию уравнения нужной нам плоскости, которая будет проходить через M 1 ( 7 , 7 , – 5 ) , M 2 ( 11 , 12 , – 11 ) , M 3 ( 4 , – 1 , 6 ) :
x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0 ⇔ x – 7 y – 7 z – ( – 5 ) 11 – 7 12 – 7 – 11 – ( – 5 ) 4 – 7 – 1 – 7 6 – ( – 5 ) = 0 ⇔ ⇔ x – 7 y – 7 z + 5 4 5 – 6 – 3 – 8 11 = 0 ⇔ 7 x – 26 y – 17 z + 48 = 0
Ответ: 7 x – 26 y – 17 z + 48 = 0 .
Очевидно, что процесс вычисления координат нужных нам точек занимает больше всего времени при решении подобных задач.
Нам осталось разобрать пример плоскости, которая проходит через две прямые, являющиеся параллельными.
Составьте уравнение плоскости, которая проходит через две параллельные прямые. Они выражены с помощью уравнений x = 2 · λ y = 1 + λ z = – 1 – λ и x – 3 2 = y 1 = z + 5 – 1 .
Решение
Вычисляем координаты двух нужных точек по параметрическим уравнениям, приняв λ = 0 и λ = 1 .
λ = 0 : x = 2 · 0 y = 1 + 0 z = – 1 – 0 ⇔ x = 0 y = 1 z = – 1 ⇔ M 1 ( 0 , 1 , – 1 ) λ = 1 : x = 2 · 1 y = 1 + 1 z = – 1 – 1 ⇔ x = 2 y = 2 z = – 2 ⇔ M 2 ( 2 , 2 , – 2 )
У нас получается, что прямая x – 3 2 = y 1 = z + 5 – 1 будет проходить через точку M 3 ( 3 , 0 , – 5 ) .
Переходим к уравнению плоскости для трех точек М 1 , М 2 и М 3 :
x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0 ⇔ x – 0 y – 1 z – ( – 1 ) 2 – 0 2 – 1 – 2 – ( – 1 ) 3 – 0 0 – 1 – 5 – ( – 1 ) = 0 ⇔ ⇔ x y – 1 z + 1 2 1 – 1 3 – 1 – 4 = 0 ⇔ – 5 x + 5 y – 5 z – 10 = 0 ⇔ x – y – z + 2 = 0
Ответ: x – y – z + 2 = 0 .
Уравнение плоскости, проходящей через точку и прямую онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и через данную прямую (точка не лежит на этой прямой). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку “Решить”.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через точку и прямую − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L:
Задача заключается в построении уравнения плоскости α, проходящей через точку M0 и и через прямую L(Рис.1).
Решение. Уравнение плоскости, проходящей через точку M0 и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (2) |
Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
| A(x−x1)+B(y−y1)+C(z−z1)=0. | (3) |
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
Вычитая уравнение (3) из уравнения (2), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (5) |
Решая совместно уравнения (4) и (5) отностительно коэффициентов A, B, C получим такие значения A, B, C, при которых уравнение (2) проходит через точку M0 и через прямую (1). Для решения систему уравнений (4), (5), запишем их в матричном виде:
Как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн.
Получив частное решение уравнения (6) и подставив полученные значения A, B, C в (2), получим решение задачи.
Решение. Уравнение плоскости α, проходящей через точку M0(x0, y0, z0)=M0(1, 2, 5) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).
Вычитая уравнение (3) из уравнения (2), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (8) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
Решим систему линейных уравнений (10) и (11) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
Решив однородную систему линейных уравнений (12) используя метод Гаусса, найдем следующее частное решение:
Подставляя значения коэффициентов A, B, C в уравнение плоскости (2), получим:
Упростим уравнение (13):
Ответ: Уравнение плоскости, проходящей через точку M0(1, 2, 5) и через прямую (7) имеет вид (14).
Пример 2. Найти уравнение плоскости α, проходящую через точку M0(4, 3, −6) и через прямую L, заданной параметрическим уравнением:
Решение. Приведем параметрическое уравнение (15) к каноническому виду:
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (17) |
Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1)=(0, 2, 4). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
| A(x−x1)+B(y−y1)+C(z−z1)=0. | (18) |
Вычитая уравнение (18) из уравнения (17), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (19) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n должен быть ортогональным направляющему вектору прямой L :
Решим систему линейных уравнений (21) и (22) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
Решив однородную систему линейных уравнений (23) используя метод Гаусса, найдем следующее частное решение:
Подставляя значения коэффициентов A, B, C в уравнение плоскости (17), получим:
Упростим уравнение (24):
Уравнение плоскости можно представить более упрощенном виде, умножив на число 23.
Ответ: Уравнение плоскости, проходящей через точку M0(4, 3, −6) и через прямую (16) имеет вид (26).
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-ploskosti-kotoraja-prohodit-cherez-dve-p/
http://matworld.ru/analytic-geometry/uravnenie-ploskosti4-online.php
[/spoiler]
Нахождение уравнения плоскости, проходящей через две параллельные прямые.
Прежде
чем получить уравнение
плоскости, проходящей через две заданные
параллельные прямые,
вспомним теорему: через две параллельные
прямые проходит единственная плоскость.
Эта теорема доказывается на основе
аксиомы о единственной плоскости,
проходящей через три заданные точки, с
использованием утверждения: если одна
из двух параллельных прямых пересекает
плоскость, то и другая прямая пересекает
эту плоскость.
Таким
образом, мы можем задать конкретную
плоскость в трехмерном пространстве,
указав две параллельные прямые, лежащие
в этой плоскости.
Очевидно,
что плоскость, проходящая через две
заданные параллельные прямые, совпадает
с плоскостью, проходящей через три
различные точки, две из которых лежат
на одной из заданных параллельных
прямых, а третья лежит на другой прямой.
Теперь
можно приступать к нахождению уравнения
плоскости, проходящей через две заданные
параллельные прямые.
Пусть
в трехмерном пространстве введена
прямоугольная система координат Oxyz,
заданы две параллельные прямые a и b и
требуется составить уравнение плоскости,
которая проходит через параллельные
прямые a и b.
Эта
задача, также как и задача о нахождении
уравнения плоскости, проходящей через
две заданные пересекающиеся прямые,
сводится к составлению уравнения
плоскости, проходящей через три точки.
Действительно, мы можем определить
координаты двух точек М1 и М2,
лежащих на одной из заданных параллельных
прямых, и координаты точки М3,
лежащей на другой прямой. После этого
нам лишь нужно написать уравнение
плоскости, проходящей через три
точки ![]() и
и ![]() ,
,
в виде  .
.
Это уравнение является искомым уравнением
плоскости, проходящей через две заданные
параллельные прямые.
Нахождение
уравнения плоскости, проходящей через
заданную точку пространства параллельно
заданной плоскости.
Задача
нахождения уравнения плоскости,
проходящей через заданную точку
пространства параллельно заданной
плоскости, возникает из следующей
теоремы: через любую точку пространства,
не лежащую в данной плоскости, проходит
единственная плоскость, параллельная
данной. Доказательство этой теоремы
можно найти в учебнике геометрии
для 10–11
классов, указанном в конце статьи.
Пусть
в трехмерном пространстве
зафиксирована прямоугольная
система координат Oxyz,
в ней задана плоскость и
точка![]() ,
,
не лежащая в плоскости![]() .
.
Поставим перед собой задачу: написать
уравнение плоскости![]() ,
,
проходящей через точку![]() параллельно
параллельно
плоскости![]() .
.
Решим
ее.
Нам
известно, что общее
уравнение плоскости,
проходящей через точку ![]() и
и
имеющей нормальный вектор плоскости![]() ,
,
имеет вид![]() .
.
Таким образом, мы сможем записать
требуемое уравнение плоскости![]() ,
,
если определим координаты ее нормального
вектора.
При
изучении темы «нормальный
вектор плоскости»
мы отметили, что нормальный вектор одной
из двух параллельных плоскостей является
нормальным вектором второй плоскости.
Следовательно, в силу параллельности
плоскостей ![]() и
и![]() ,
,
нормальным вектором плоскости![]() является
является
любой нормальный вектор заданной
плоскости![]() .
.
Таким образом, задача составления
уравнения плоскости![]() ,
,
проходящей через заданную точкуМ1 параллельно
заданной плоскости![]() ,
,
сводится к определению координат
нормального вектора плоскости![]() .
.
В свою очередь координаты нормального
вектора плоскости![]() проще
проще
всего получить, если иметь перед глазами
общее уравнение плоскости![]() вида
вида![]() .
.
В этом случае коэффициентыA, B,C перед
переменными x, y, z являются
соответствующими координатами нормального
вектора плоскости ![]() .
.
Итак,
запишем алгоритм
нахождения уравнения плоскости ![]() ,
,
проходящей через заданную точку![]() параллельно
параллельно
заданной плоскости![]() :
:
Следует
заметить, что если точка М1 лежит
в плоскости ![]() ,
,
то, действуя по записанному алгоритму,
мы получим уравнение плоскости![]() ,
,
которая совпадает с плоскостью![]() .
.
Нахождение
уравнения плоскости, проходящей через
заданную точку пространства перпендикулярно
к заданной прямой.
Поставим
перед собой следующую задачу.
Пусть
в трехмерном пространстве
зафиксирована прямоугольная
система координат Oxyz,
задана точка ![]() ,
,
прямаяa и
требуется написать уравнение плоскости ![]() ,
,
проходящей через точкуМ1 перпендикулярно
к прямой a.
Сначала
вспомним один важный факт.
На
уроках геометрии в средней школе
доказывается теорема: через заданную
точку трехмерного пространства проходит
единственная плоскость, перпендикулярная
к данной прямой (доказательство этой
теоремы Вы можете найти в учебнике
геометрии за 10–11 классы,
указанном в списке литературы в конце
статьи).
Теперь
покажем, как находится уравнение этой
единственной плоскости, проходящей
через заданную точку перпендикулярно
к заданной прямой.
Мы
можем написать общее
уравнение плоскости,
если нам известны координаты точки,
лежащей в этой плоскости, и координаты
нормального вектора плоскости.
В
условии задачи нам даны
координаты x1, y1, z1 точки М1,
через которую проходит плоскость ![]() .
.
Тогда, если мы найдем координаты
нормального вектора плоскости![]() ,
,
то мы сможем составить требуемое
уравнение плоскости, проходящей через
заданную точку перпендикулярно к
заданной прямой.
Любой направляющий
вектор прямой a представляет
собой нормальный вектор плоскости ![]() ,
,
так как он ненулевой и лежит на прямойa,
перпендикулярной к плоскости ![]() .
.
Таким образом, нахождение координат
нормального вектора плоскости![]() сводится
сводится
к нахождению координат направляющего
вектора прямойa.
В
свою очередь, координаты направляющего
вектора прямой a могут
определяться различными способами,
зависящими от способа задания прямой a в
условии задачи. Например, если прямуюa в
прямоугольной системе координат
задают канонические
уравнения прямой в пространстве
вида  илипараметрические
илипараметрические
уравнения прямой в пространстве вида  ,
,
то направляющий вектор этой прямой
имеет координатыax, ay и az;
если же прямая a проходит
через две точки ![]() и
и![]() ,
,
то координаты ее направляющего вектора
определяются как![]() .
.
Итак,
получаем алгоритм
для нахождения уравнения плоскости ![]() ,
,
проходящей через заданную
точку![]() перпендикулярно
перпендикулярно
к заданной прямойa:
Из
найденного общего уравнения плоскости
вида ![]() можно,
можно,
при необходимости, получитьуравнение
плоскости в отрезках и нормальное
уравнение плоскости.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для того, чтобы однозначно построить плоскость, необходимы три точки, которые не лежат на одной прямой.
Общее уравнение плоскости принимает вид:
Ax+By+Cz+D=0Ax+By+Cz+D=0,
где A,B,C,DA, B, C, D — коэффициенты, задающие плоскость. Они не могут быть одновременно равны нулю.
Здесь будет калькулятор
Составление уравнения плоскости по трем точкам
Текст цитаты
Заголовок Текст цитаты
В случае, когда известны координаты всех трех точек, уравнение плоскости, проходящей через эти точки составляется с помощью определителя:
∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0,
где (x1;y1;z1),(x2;y2;z2),(x3;y3;z3)(x_1;y_1;z_1), (x_2;y_2;z_2), (x_3;y_3;z_3) — координаты точек, через которые проходит данная плоскость, а (x;y;z)(x; y; z) — всевозможные координаты точек этой плоскости.
Составить уравнения плоскости проходящей через три точки с координатами (1;3;0),(5;6;4),(−1;−4;0)(1;3;0), (5;6;4), (-1;-4;0).
Решение
Пусть:
x1=1x_1=1
y1=3y_1=3
z1=0z_1=0
x2=5x_2=5
y2=6y_2=6
z2=4z_2=4
x3=−1x_3=-1
y3=−4y_3=-4
z3=0z_3=0
Составляем определитель:
∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0
∣x−15−1−1−1y−36−3−4−3z−04−00−0∣=0begin{vmatrix}
x-1 & 5-1 & -1-1 \
y-3 & 6-3 & -4-3 \
z-0 & 4-0 & 0-0 \
end{vmatrix}=0
∣x−14−2y−33−7z40∣=0begin{vmatrix}
x-1 & 4 & -2 \
y-3 & 3 & -7 \
z & 4 & 0 \
end{vmatrix}=0
28x−8y−22z−4=028x-8y-22z-4=0 — уравнение искомой плоскости.
Ответ
28x−8y−22z−4=028x-8y-22z-4=0
Уравнение плоскости по точке и вектору нормали
Если дана точка, лежащая на плоскости и вектор нормали к этой плоскости, то сама плоскость задается уравнением:
(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0,
где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, принадлежащей плоскости, а (n1;n2;n3)(n_1;n_2;n_3) — координаты вектора нормали к этой плоскости.
Выпишите уравнение плоскости, если даны: координата точки плоскости (8;−2;9)(8;-2;9) и вектор нормали (1;3;5)(1;3;5).
Решение
x0=8x_0=8
y0=−2y_0=-2
z0=9z_0=9
n1=1n_1=1
n2=3n_2=3
n3=5n_3=5
(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0
(x−8)⋅1+(y−(−2))⋅3+(z−9)⋅5=0(x-8)cdot 1+(y-(-2))cdot 3+(z-9)cdot 5=0
x−8+3y+6+5z−45=0x-8+3y+6+5z-45=0
x+3y+5z−47=0x+3y+5z-47=0 — уравнение плоскости.
Проверка
Чтобы убедиться в том, что задача решена правильно, без ошибок, необходимо в полученное уравнение подставить координаты точки, которые даны в условии задачи:
8+3⋅(−2)+5⋅9−47=08+3cdot(-2)+5cdot9-47=0
0=00=0 — верно, значит ответ правильный.
Ответ
x+3y+5z−47=0x+3y+5z-47=0
Все ответы
|
|
 |
|


