Как найти уравнение прямой перпендикулярной данной онлайн

bold{mathrm{Basic}}	bold{alphabetagamma}	bold{mathrm{ABGamma}}	bold{sincos}	bold{gedivrightarrow}	bold{overline{x}spacemathbb{C}forall}	bold{sumspaceintspaceproduct}	bold{begin{pmatrix}square&square\square&squareend{pmatrix}}	bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx} ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square} left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec alpha beta gamma delta zeta eta theta iota kappa lambda mu nu xi pi rho sigma tau upsilon phi chi psi omega A B Gamma Delta E Z H Theta K Lambda M N Xi Pi P Sigma T Upsilon Phi X Psi Omega sin cos tan cot sec csc sinh cosh tanh coth sech arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge (square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset vee wedge neg oplus cap cup square^{c} subset subsete superset supersete int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x} (2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5) (1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1) mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить} arcsin sin sqrt{square} 7 8 9 div arccos cos ln 4 5 6 times arctan tan log 1 2 3 – pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

• перпендикуляр:y=4x+6,:(-8,-26)
  

• перпендикуляр:2x-2y+4=0,:(2,:4)
  

• перпендикуляр:y=5x+2,:x=1
  

• перпендикуляр:y=-5x+2,:x=1
  

• перпендикуляр:4x-2y+6=0,:(2,7)
  

• перпендикуляр:y=3x-2,:x=-1
  

• Показать больше

Описание

Поэтапное решение уравнения перпендикулярной прямой

perpendicular-line-calculator

ru

Блог-сообщения, имеющие отношение к Symbolab

High School Math Solutions – Perpendicular & Parallel Lines Calculator

Parallel lines have the same slope, to find the parallel line at a given point you should simply calculate the…

Read More

Введите Задачу

Сохранить в блокнот!

Войти

Calculate the equation of a perpendicular line. Enter the equation of the original line and the point it passes through to calculate the perpendicular line equation.

• Perpendicular Bisector Calculator
• Parallel Line Calculator
• Slope Calculator
• Midpoint Calculator

Perpendicular Line Formula

Linear lines are almost always displayed in the form of

Where m is the slope and b is the y-intercept. The first step in finding the equation of a line perpendicular to another is understanding the relationship of their slopes. The slope of a perpendicular line is always the inverse of the other. This means that the product of the two slopes is equal to -1.

With that in mind we can formulate the following equations.

a * m = -1

a = -1 / m

Where m is the original slope, and a is the slope of the perpendicular line. Now that we have the slope of our new line, all we need now is the y-intercept, b.

To calculate the y-intercept, we can use a similar formula to the one used to calculate the equation of a parallel line.

b = y₀ + 1 * x₀ / m

• Where b is the y-intercept
• y0 is the y coordinate the line passes through
• X0 is the x coordinate the line passes through
• m is the slope of the original line.

What Is a Perpendicular Line?

A perpendicular line is a line that forms a 90-degree angle with another line. Such lines can be positioned in any plane.

On the grid, the perpendicular lines can be positioned crosswise, vertically and horizontally, or sideways.

They don’t have to be pointing upwards; they should only be at a 90-degree angle with respect to another line.

The Difference Between Parallel, Perpendicular, and Intersecting Lines

While it’s easy to confuse the lines with each other, they’re three very different concepts.

Parallel

Lines in a grid that are always the same spacing apart are known as parallel lines. Parallel lines never cross one other and they never have the same slope.

Perpendicular

Lines that connect at a right 90-degree angle are known as perpendicular lines. They’re perpendicular if the slope of one line is the negative reciprocal of the slope of the other.

The only thing that parallel lines and perpendicular lines have in common is that they’re both made up of straight lines.

Intersecting

Intersecting lines are formed when lines in a grid intersect with each other at a point of intersection. However, unlike perpendicular lines, they don’t form a right angle.

Do All Shapes Have Perpendicular Lines?

Perpendicular lines can be found in many shapes, but not all of them.

There will be no perpendicular sides on many polygons, but some might have perpendicular lines. Perpendicular lines will always exist in squares, right-angled triangles, and rectangles.

You can also find perpendicular lines on everyday objects such as decorations, fences, and doors.

What Is the Equation for Perpendicular Slope?

The perpendicular slope will be the reciprocal of the initial slope in the opposite direction.

To calculate the slope, use the slope-intercept equation (y = mx + b) and substitute in the provided point and the new slope.

Then, restore the equation to its standard form (ax + by = c).

Do Perpendicular Lines Have The Same Slope?

The slope of perpendicular lines is not the same. If two lines are perpendicular, one line’s slope is the negative reciprocal of the other line’s slope.

A number’s product and its reciprocal equals 1. When the slopes of two perpendicular lines in the plane are multiplied, however, the result is -1.

This indicates the slopes of perpendicular lines are reciprocals in the opposite direction.

Do Perpendicular Lines Have to Touch?

If two nonvertical lines in the same plane intersect at a right angle, then they’re considered to be perpendicular. If the lines aren’t in the same plane, the term perpendicular doesn’t apply to the shape.

Visualize a 3D square object if you’re having trouble understanding this information.

Even if it doesn’t appear to be the case, the lines on a 3D square are perpendicular. This is due to the lines existing on the same plane.

Summary

Two intersecting lines that make a right angle are called perpendicular lines.

The slope of the lines differs because the slope of one line is the negative reciprocal of the slope of the other.

Perpendicular lines aren’t present in all shapes, although they’re always found in squares, right-angled triangles, and rectangles.

Perpendicular lines don’t have to touch to be deemed perpendicular if they’re on the same plane.

How to calculate a perpendicular line

Let’s look at an example of how to use these equations. First, let’s assume you know the equation of the first line. It happens to be y=4x+5. Let’s also assume you know the x and y coordinates of a point that the perpendicular line passes through, say (4,5).

First, we need to calculate the slope. From the equation a = -1 / m we get a value of -1/4.

Next, we need to calculate the y-intercept of the new line using the equation b = y₀ + 1 * x₀ / m. From this, we get a value of 6.

Finally, we need to put this all together in the form: y=-1/4x + 6.

Finding Parallel and Perpendicular Lines

in the 2-Dimension Cartesian Plane, all straight lines can be represented as an equation of the form y=mx+b, where m is the slope and x and y are points along the line. Since all lines can be described this way, it makes calculating parallel and perpendicular lines simple.

It’s just a matter of manipulating the equation. Let’s look at how the equation is manipulated in order to calculate the equation of a perpendicular line.

Conceptually, a perpendicular line is a line that crosses through the original line at any point and forms a 90-degree angle at intercept. Since there can be an infinite number of perpendicular lines, calculating any specific line requires a point.

The slope of a perpendicular line is the reciprocal of the slope of the original line. This simply means if the original slope is m, the reciprocal is 1/m. With this in mind, we can now manipulate the equation to determine the perpendicular line.

y=mx+b —> y2=(1/m)x2+b

The only thing left to do is solve for be using the point given along the perpendicular line.

Steps to calculate a perpendicular line

We’ve gone over how to calculate the equation of a perpendicular line, and how manipulation of the original equation yields the results, but the following steps will outline the specific steps.

1. Calculate the slope of the original line. This can be done through the use of two points along the original line. To learn more about calculating the slope of a line click here.
2. Take the reciprocal of the original slope. If the slope is m, the reciprocal is 1/m.
3. Calculate b, the y-intercept of the new line using the new slope and the point given along that line.
4. Put all of the information together in point-slope form.

For more math related calculators, click here.

---

Узнайте больше об этом калькуляторе перпендикулярных линий.

Линии в значительной степени определяются их наклоном (наклоном). Горизонтальные линии — это линии с наклоном, равным нулю, а вертикальные линии — это линии, где наклон не определен (отрицательная или положительная бесконечность).

Перпендикулярные линии – это линии, которые пересекаются, образуя прямой угол. Существует особое условие для

уклон и перпендикулярный уклон

, всякий раз, когда заданы наклоны, чтобы линии были перпендикулярны, то есть произведение наклонов равно -1.

Заметим, что к одной заданной прямой перпендикулярно бесконечное число прямых. Чтобы найти тот, который вы ищете, вам нужно зафиксировать точку, через которую он проходит.

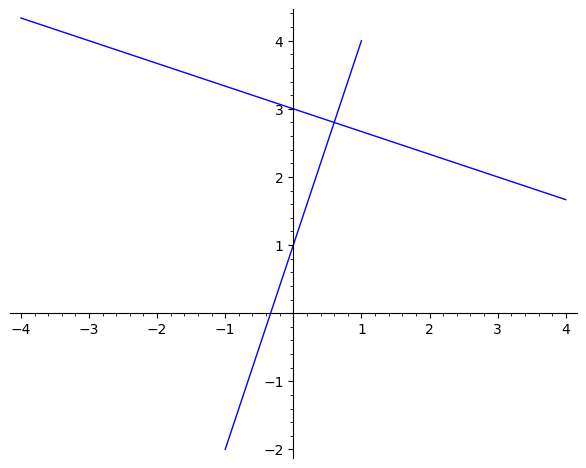
Как найти перпендикуляр прямой?

Стратегия проста. Шаг состоит в том, чтобы найти наклон данной линии. Если вам предоставлены наклон и точка пересечения для определения линии, значит, у вас уже есть наклон.

В противном случае, возможно, у вас есть

две точки, через которые проходит линия

, и в этом случае вы можете вычислить наклон напрямую.

В конечном счете, если вы определяете заданную линию уравнением, вам нужно ввести это уравнение в

форма пересечения наклона

, чтобы получить наклон.

Когда у вас есть наклон данной линии, вы используете формулу для перпендикулярного наклона, умножая на минус один обратную величину исходного наклона.

Что такое перпендикуляр к горизонтальной линии

Линия, перпендикулярная горизонтальной линии, является вертикальной линией.

Что такое перпендикуляр к вертикальной линии

Линия, перпендикулярная вертикальной линии, является горизонтальной линией.

Можете ли вы вычислить перпендикулярную линию без точек

Если у вас есть линия, существует не одна, а множество (бесконечных) перпендикулярных линий к данной линии. Чтобы определить одну конкретную перпендикулярную линию, вам необходимо указать одну точку, через которую проходит линия.

Как правило, вы указываете точку на исходной линии, через которую должна проходить перпендикулярная линия.

Пример расчета перпендикулярной линии для заданной линии:

Рассмотрим линию с уравнением (2x + 3y = 5)). Найдите уравнение перпендикуляра, проходящего через ((1, 1)).

Отвечать:

Сначала мы получаем уравнение пересечения наклона для ДАННОЙ линии, если это возможно

Нам было предложено следующее уравнение:

[displaystyle 2x+3y=5]

Помещая (y) в левую часть и (x) и константу в правую часть, мы получаем

[displaystyle 3y = -2x +5]

Затем, находя (y) путем деления обеих частей уравнения на (3), получается следующее

[displaystyle y=-frac{2}{3}x+frac{5}{3}]

Формула Перпендикулярного Уклона

В общем, формула, необходимая для вычисления перпендикулярного наклона (m_{perp}), выглядит следующим образом:

[m_{perp} = displaystyle -frac{1}{m}]

Подставляя значение (m = ) в формулу, мы находим, что перпендикулярный наклон равен

[m_{perp} = displaystyle -frac{1}{m} = displaystyle -frac{1}{} = frac{3}{2}]

Построение Перпендикулярной Линии

Теперь мы рассчитали, что перпендикулярный наклон равен (m_{perp} = frac{3}{2}), и мы знаем, что перпендикулярная линия проходит через точку ((1, 1)).

Следовательно, с имеющейся у нас информацией мы можем напрямую построить форму точки-наклона линии, которая

[displaystyle y – y_1 = m_{perp} left(x – x_1right)]

а затем подставляя известные значения (displaystyle m_{perp} = frac{3}{2}) и (displaystyle left( x_1, y_1 right) = left( 1, 1right)), мы получаем, что

[displaystyle y-1 = frac{3}{2} left(x-1right)]

Теперь нам нужно расширить правую часть уравнения, распределив наклон, чтобы мы получили [displaystyle y = frac{3}{2} x + frac{3}{2} left(-1right) + 1]

и упрощая, получаем, что [displaystyle y=frac{3}{2}x-frac{1}{2}]

Отсюда заключаем, что уравнение данной прямой есть (displaystyle y=-frac{2}{3}x+frac{5}{3}), а уравнение перпендикулярной прямой есть (displaystyle y=frac{3}{2}x-frac{1}{2}).

Если вы хотите сделать вещи более прямыми, используйте это

Калькулятор перпендикулярного уклона

и используйте формулу перпендикулярной линии, чтобы получить непосредственно наклон линии, которая является перпендикулярной линией.

Это на тот случай, если вы только

в поисках склона

в контексте того, что вы делаете.

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку “Решить”.

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости

Наша цель построить уравнение прямой, проходящей через данную точку M₀ и перпендикулярной к данной плоскости Ax+By+Cz+D=0.

Общее уравнение плоскости имеет вид:

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональный плоскости (1) имеет следующий вид:

Пример 1. Построить прямую, проходящую через точку M₀(5, -4, 4) и перпендикулярной плоскости

Решение.

Общее уравнение плоскости имеет вид (1), где :

Подставляя координаты точки M₀(5, -4, 4) и координаты нормального вектора плоскости (4) в (3), получим:

Ответ: