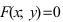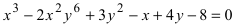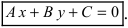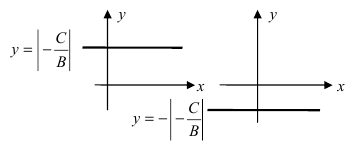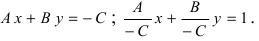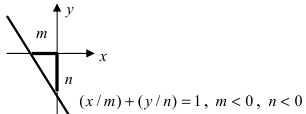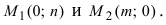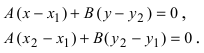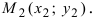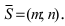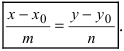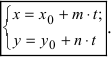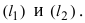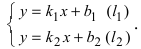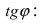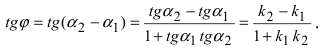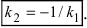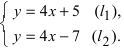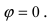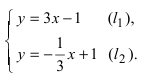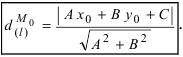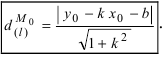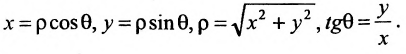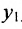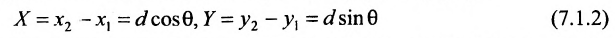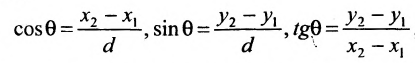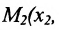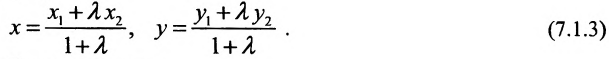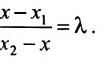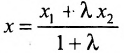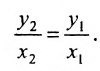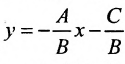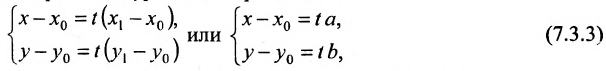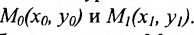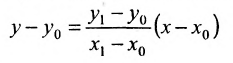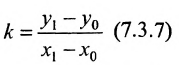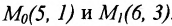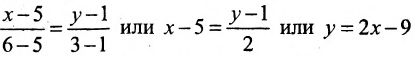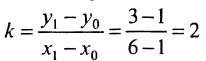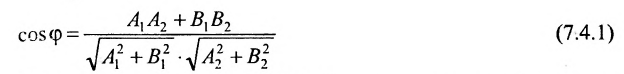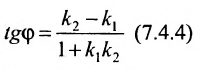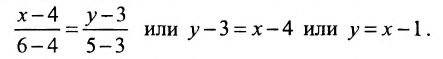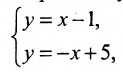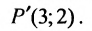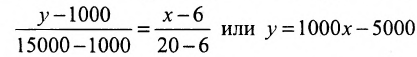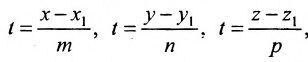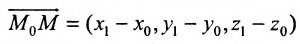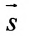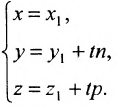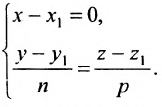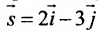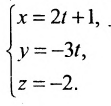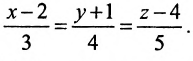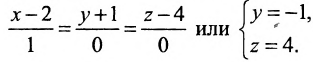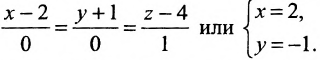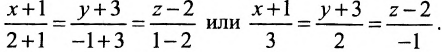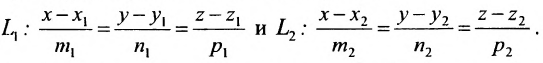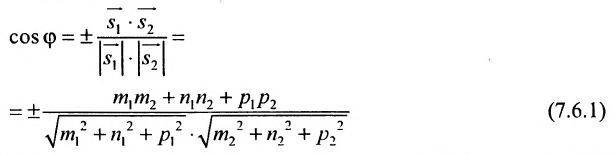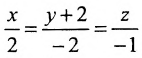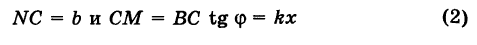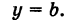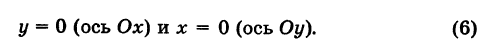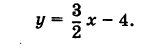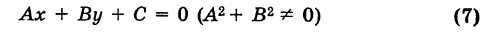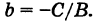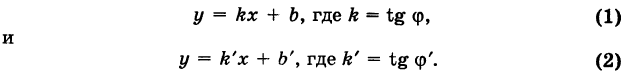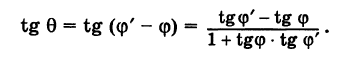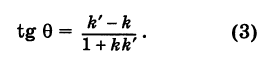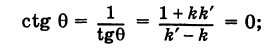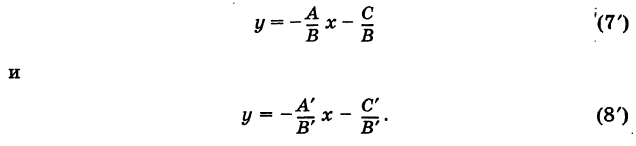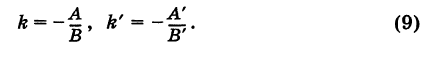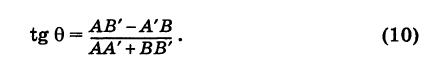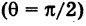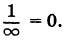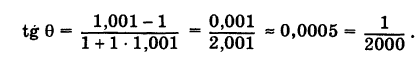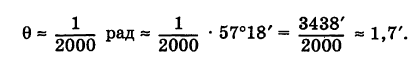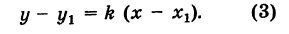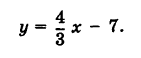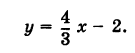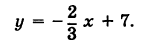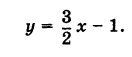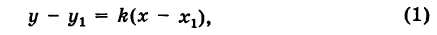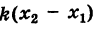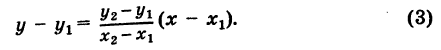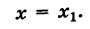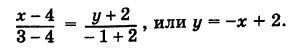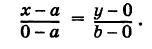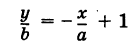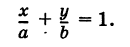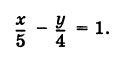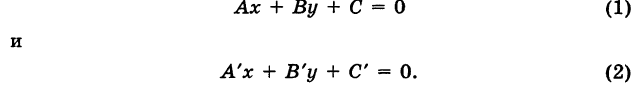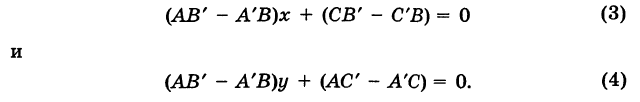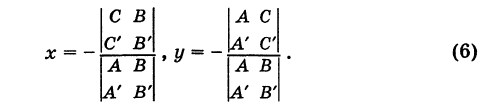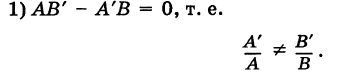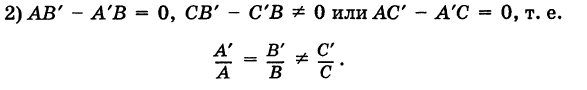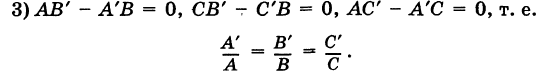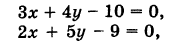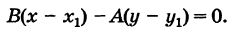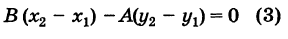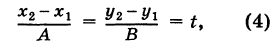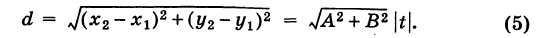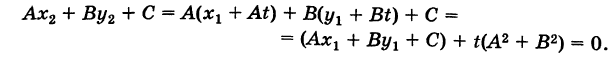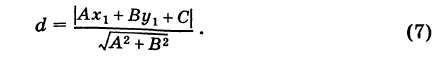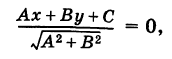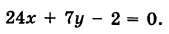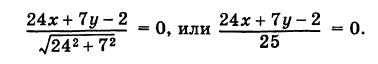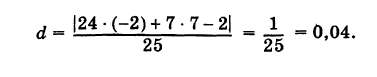ГДЗ учебник по алгебре 7 класс Мордкович. §9. Линейная функция y = kx. Номер №9.18.
Составьте уравнение прямой y = kx + m, изображенной на заданном рисунке:
а) рис. 17 ; 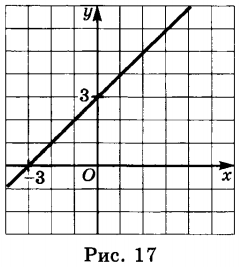
б) рис. 18 ; 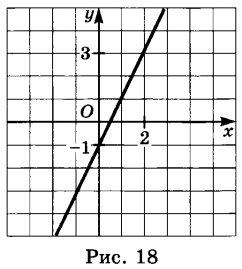
в) рис. 19 ; 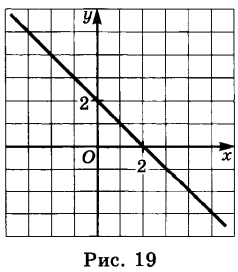
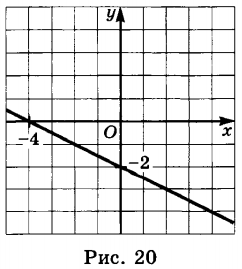
г) рис. 20 .
Решение а
График пересекает ось y в точке 3, значит m = 3 .
График пересекает ось x в точке − 3, значит ему принадлежит точка (− 3 ; 0 ).
y = kx + m
0 = − 3 k + 3
3 k = 3
k = 1
y = x + 3
Решение б
График пересекает ось y в точке − 1, значит m = − 1 .
Графику принадлежит точка ( 2 ; 3 ).
y = kx + m
3 = 2 k − 1
2 k = 3 + 1
2 k = 4
k = 2
y = 2 x − 1
Решение в
График пересекает ось y в точке 2, значит m = 2 .
График пересекает ось x в точке 2, значит ему принадлежит точка ( 2 ; 0 ).
y = kx + m
0 = 2 k + 2
2 k = − 2
k = − 1
y = −x + 2
Решение г
График пересекает ось y в точке − 2, значит m = − 2 .
График пересекает ось x в точке − 4, значит ему принадлежит точка (− 4 ; 0 ).
y = kx + m
0 = − 4 k − 2
4 k = − 2
k = − 0,5
y = − 0,5 x − 2
Практика. Решение задач. Часть 1. Уравнения прямой
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Мы изучили новые инструменты – координаты и действия с векторами в координатах, операцию скалярного умножения векторов. Этот урок мы посвятим решению задач и потренируемся применять эти новые инструменты на практике.
Общее уравнение прямой: описание, примеры, решение задач
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.
Общее уравнение прямой: основные сведения
Пусть на плоскости задана прямоугольная система координат O x y .
Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.
Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x – x 0 ) + B ( y – y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .
Полученное уравнение A ( x – x 0 ) + B ( y – y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x – x 0 , y – y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x – x 0 , y – y 0 ) не являлись бы перпендикулярными, и равенство A ( x – x 0 ) + B ( y – y 0 ) = 0 не было бы верным.
Следовательно, уравнение A ( x – x 0 ) + B ( y – y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .
Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .
Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x – x 0 , y – y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n → , M 0 M → = A ( x – x 0 ) + B ( y – y 0 ) = 0
Перепишем уравнение A x + B y – A x 0 – B y 0 = 0 , определим C : C = – A x 0 – B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .
Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2 x + 3 y – 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.
Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y – 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение – C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу – C B .
- Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
- Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
- Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
- Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.
Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , – 11 . Необходимо записать общее уравнение заданной прямой.
Решение
Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:
Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = – 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x – 2 = 0
Ответ: 7 x – 2 = 0
На чертеже изображена прямая, необходимо записать ее уравнение.
Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .
Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = – 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y – 3 = 0 .
Ответ: y – 3 = 0 .
Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x – x 0 ) + B ( y – y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М 0 ( – 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , – 2 ) . Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = – 2 , x 0 = – 3 , y 0 = 4 . Тогда:
A ( x – x 0 ) + B ( y – y 0 ) = 0 ⇔ 1 · ( x – ( – 3 ) ) – 2 · y ( y – 4 ) = 0 ⇔ ⇔ x – 2 y + 22 = 0
Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:
A x + B y + C = 0 ⇔ 1 · x – 2 · y + C = 0 ⇔ x – 2 · y + C = 0
Теперь найдем значение С, используя заданную условием задачи точку М 0 ( – 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x – 2 · y + C = 0 , т.е. – 3 – 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x – 2 · y + 11 = 0 .
Ответ: x – 2 · y + 11 = 0 .
Задана прямая 2 3 x – y – 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна – 3 . Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = – 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
2 3 x 0 – y 0 – 1 2 = 0
Определяем y 0 : 2 3 · ( – 3 ) – y 0 – 1 2 = 0 ⇔ – 5 2 – y 0 = 0 ⇔ y 0 = – 5 2
Ответ: – 5 2
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x – x 1 a x = y – y 1 a y .
Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = – B y .
Это равенство возможно записать как пропорцию: x + C A – B = y A .
В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = – B y – C . Выносим – В за скобки, тогда: A x = – B y + C B .
Перепишем равенство в виде пропорции: x – B = y + C B A .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3 y – 4 = 0 . Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3 y – 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим – 3 за скобки; получаем: 0 x = – 3 y – 4 3 .
Запишем полученное равенство как пропорцию: x – 3 = y – 4 3 0 . Так, мы получили уравнение канонического вида.
Ответ: x – 3 = y – 4 3 0 .
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Прямая задана уравнением 2 x – 5 y – 1 = 0 . Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2 x – 5 y – 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2
Теперь примем обе части полученного канонического уравнения равными λ , тогда:
x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = – 1 5 + 2 · λ , λ ∈ R
Ответ: x = 5 · λ y = – 1 5 + 2 · λ , λ ∈ R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = – A x – C . Разделим обе части полученного равенство на B , отличное от нуля: y = – A B x – C B .
Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2 x + 7 y = 0 ⇔ 7 y – 2 x ⇔ y = – 2 7 x
Ответ: y = – 2 7 x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :
A x + B y + C = 0 ⇔ A x + B y = – C ⇔ ⇔ A – C x + B – C y = 1 ⇔ x – C A + y – C B = 1
Необходимо преобразовать общее уравнение прямой x – 7 y + 1 2 = 0 в уравнение прямой в отрезках.
Решение
Перенесем 1 2 в правую часть: x – 7 y + 1 2 = 0 ⇔ x – 7 y = – 1 2 .
Разделим на -1/2 обе части равенства: x – 7 y = – 1 2 ⇔ 1 – 1 2 x – 7 – 1 2 y = 1 .
Преобразуем далее в необходимый вид: 1 – 1 2 x – 7 – 1 2 y = 1 ⇔ x – 1 2 + y 1 14 = 1 .
Ответ: x – 1 2 + y 1 14 = 1 .
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
x a + y b ⇔ 1 a x + 1 b y – 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y – k x – b = 0 ⇔ A x + B y + C = 0
Каноническое уравнение преобразуется к общему по следующей схеме:
x – x 1 a x = y – y 1 a y ⇔ a y · ( x – x 1 ) = a x ( y – y 1 ) ⇔ ⇔ a y x – a x y – a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x – x 1 a x = y – y 1 a y ⇔ A x + B y + C = 0
Заданы параметрические уравнения прямой x = – 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x = – 1 + 2 · λ y = 4 ⇔ x = – 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y – 4 0 ⇔ x + 1 2 = y – 4 0
Перейдем от канонического к общему:
x + 1 2 = y – 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y – 4 ) ⇔ y – 4 = 0
Ответ: y – 4 = 0
Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y – 1 = 0
Ответ: 1 3 x + 2 y – 1 = 0 .
Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x – x 0 ) + B ( y – y 0 ) = 0 . Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2 x – 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , – 3 ) : 2 x – 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A ( x – x 0 ) + B ( y – y 0 ) = 0 ⇔ 2 ( x – 4 ) – 3 ( y – 1 ) = 0 ⇔ 2 x – 3 y – 5 = 0
Ответ: 2 x – 3 y – 5 = 0 .
Заданная прямая проходит через начало координат перпендикулярно прямой x – 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x – 2 3 = y + 4 5 .
Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:
A ( x – x 0 ) + B ( y – y 0 ) = 0 ⇔ 3 ( x – 0 ) + 5 ( y – 0 ) = 0 ⇔ 3 x + 5 y = 0
[spoiler title=”источники:”]
http://interneturok.ru/lesson/geometry/9-klass/effektivnye-kursy/praktika-reshenie-zadach-chast-1-uravneniya-pryamoy
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-prjamoj/
[/spoiler]
Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.
Здесь будет калькулятор
Уравнение прямой с угловым коэффициентом
y=kx+by=kx+b,
где kk — угловой коэффициент, а bb — свободный коэффициент.
Уравнения данного вида составляются следующим образом по формуле:
y−y0=k(x−x0)y-y_0=k(x-x_0),
где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.
Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.
Решение
Подставляем значения в формулу:
y−y0=k(x−x0)y-y_0=k(x-x_0)
y−2=1⋅(x−1)y-2=1cdot(x-1)
Приводим подобные слагаемые:
y=x+1y=x+1
Ответ
y=x+1y=x+1
Общее уравнение прямой
Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:
y−x−1=0y-x-1=0
Уравнение прямой по двум точкам
Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},
где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.
Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).
Решение
x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}
x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}
x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}
x−4=−y−12x-4=frac{-y-1}{2}
y+1=2⋅(4−x)y+1=2cdot(4-x)
y=8−2x−1y=8-2x-1
y=−2x+7y=-2x+7
Ответ
y=−2x+7y=-2x+7
Уравнение прямой при помощи точки и вектора нормали
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.
Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).
Решение
x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,
x−7+40−5y=0x-7+40-5y=0
x−5y=−40+7x-5y=-40+7
x−5y=−33x-5y=-33
5y=x+335y=x+33
y=x5+335y=frac{x}{5}+frac{33}{5}
Проверка
Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.
8=75+3358=frac{7}{5}+frac{33}{5}
8=88=8 — верно, ответ правильный.
Ответ
y=x5+335y=frac{x}{5}+frac{33}{5}
Прямая в пространстве
Уравнение прямой, заданной в пространстве имеет такой вид:
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},
где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.
Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).
Решение
x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Проверка
Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:
1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.
Такой вид уравнения прямой называется каноническим.
Ответ
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Тест по теме “Составление уравнения прямой”
Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.
Прямая – это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Уравнения прямой, проходящей через две точки могут быть следующих видов:
- каноническое уравнение,
- параметрическое уравнение,
- общее уравнение прямой,
- уравнение прямой с угловым коэффициентом,
- уравнение прямой в полярных координатах и другие.
Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.
Каноническое уравнение прямой на плоскости
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
xa и ya – координаты первой точки A,
xb и yb – координаты второй точки B
Параметрическое уравнение прямой на плоскости
{begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases}}
xa, ya – координаты точки, лежащей на прямой,
{l;m} – координаты направляющего вектора прямой,
t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Каноническое уравнение прямой в пространстве
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a} = dfrac{z-z_a}{z_b-z_a}}
xa, ya и za – координаты первой точки A,
xb, yb и zb – координаты второй точки B
Параметрическое уравнение прямой в пространстве
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a \ z=n cdot t + z_a end{cases} }
xa, ya и za – координаты точки, лежащей на прямой,
{l;m;n} – координаты направляющего вектора прямой,
t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Пример нахождения уравнения прямой, проходящей через две точки
Найдем уравнения прямой, проходящей через точки A(1,2) и B(3,8).
Каноническое уравнение прямой
Каноническое уравнение прямой, проходящей через две точки имеет вид {dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
Подставим в формулу координаты точек A и B: {dfrac{x-1}{3-1} = dfrac{y-2}{8-2}}
Получаем каноническое уравнение прямой: {dfrac{x-1}{2} = dfrac{y-2}{4}}
Уравнение прямой с угловым коэффициентом
Из канонического уравнения получаем уравнение прямой с угловым коэффициентом: {y=3x-1}
Параметрическое уравнение прямой
Параметрическое уравнение прямой имеет вид:
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases} }
где {x_a, y_b} – координаты точки, лежащей на прямой, {{l;m}} – координаты направляющего вектора прямой, t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении. В качестве координат используем координаты точки {A(x_a, y_b)}.
Найдем координаты направляющего вектора:
overline{AB} = {x_b – x_a; y_b – y_a} = {3-1; 8-2} = {2; 6}
Получаем параметрическое уравнение:
begin{cases} x=2 t + 1 \ y=6 t + 2 end{cases}
Используем калькулятор для проверки полученного ответа.
В данном материале рассмотрим, что такое уравнение прямой. Проанализируем каждый вид данного уравнения. Изучим основные формулы и графики. Применим весь рассмотренный материал на практике, в виде решения задач и уравнений.
Данное уравнение — характеризуется, как уравнение двух переменных значений.
Значения в математики, чаще всего обозначают буквами x и y. Это самое распространенное обозначение, однако можно встретить и другие буквенные обозначения. Например: z, n и другие значения.
Определение прямой линии- фигура, состоящая из множества простых точек. Каждая точка, имеет собственные, определенные координаты, относительно осей абсцисс и ординат.
Уравнение прямой на плоскости — уравнение, характеризующее взаимосвязь координатных значений точек на прямой.
Для решения уравнений необходимо помнить ряд важным математических функций, правил, значений.
Все их мы будем рассматривать подробно в каждом разделе на примерах решения.
Общее уравнение прямой линии системы координат
Рассмотрим соответствующую теорему, которая отражает уравнение прямой на плоскости в системе координат Oxy.
Подробно исследуем следующее уравнение: ax+by+c=0.
Значения х и y, являются переменными данными со значениями.
a и b — действительные простые числа. Обязательное условие, которых неравенство нулю.
Следовательно, прямая линия задается вышеупомянутым уравнением данного вида: ax+by+c=0.
Рассмотрим на примере изученную теорему:
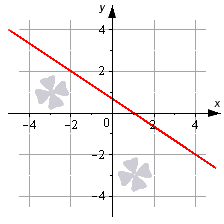
На данном рисунке, мы рассмотрим красную линию и запишем уравнение для нее.
2x+3y-2=0.
Координаты на данной прямой удовлетворяют составленному уравнению.
Уравнение может быть также полным и неполным. Рассмотрим случаи:
- Полное уравнение.
Все действительные числа, имеют любое значение, но не равные нулю. Поэтому такое определение относится к данному типу уравнений.
- Неполное уравнение.
Все числа в уравнении имеют любое значение. Характерно, также значения отрицательных знаков.
Уравнение прямой в отрезках прямой
Для отрезков уравнение будет иметь следующей вид:
[frac{x}{a}+frac{y}{b}=1]
Данные в знаменателе, являются действительными значениями, не равными нулевому значению. Величины действительных данных равняются отрезку. Он отсоединяется линией на оси координат. Протяженность начинает свой отсчет от начала координатной прямой.
Пример:
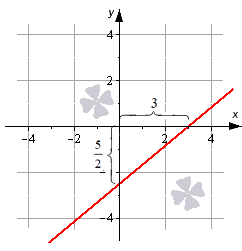
Нужно начертить прямую линию, которая задается формулой.
[frac{x}{3}+frac{y}{-frac{5}{2}}=1]
Обозначим на графике две точки ( 3 ; 0 ) , (0; [-frac{5}{2}]). Далее необходимо их соединить между собой.
Уравнение прямой с угловым коэффициентом
Записываем уравнение вида: [mathrm{y}=mathrm{k} cdot x+b];
x — значение, которое принимается, как переменное;
к — простое действительное число, является показателем углового коэффициента;
b — действительное число.
Угол наклона на плоскости в системе координат — угол, который берет свой отсчет значений от направления с положительным знаком до прямой, которая направлена против хода часовой стрелки.
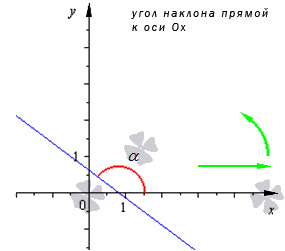
Угол будут считать нулевым, если прямая линии, имеют параллельное расположение относительно оси абсцисс либо совпадает с ней по расположению. Угол принимает значения, согласно интервалу (0, [pi]).
Формула
[text { Формула обозначения коэффициента: } k=operatorname{tg} alpha .]
Угловой коэффициент — значение тангенса угла наклона этой же прямой линии.
В случае, когда прямая линия параллельная другой оси, ординат, то принято считать, что угловой коэффициент не определяется. И соответствует интервалу бесконечности.
График функции будет возрастать, если значение коэффициента имеет положительное значение. Следовательно, убывание будет наблюдаться в противоположном значение, а именно с отрицательным значением.
На графиках показаны значения угловых коэффициентов и угол наклона. Когда есть разное расположение относительно осей.
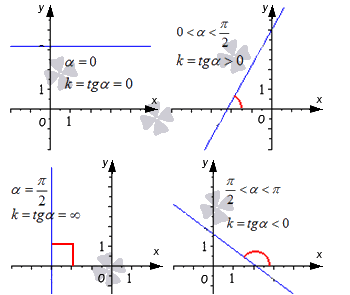
На примерах рассмотрим нахождение углового коэффициента. Для этого из прошлых тем, вспомним определение тангенса и его вычисление.
Пример №1:
Угол наклона прямой равен 120 градусов, относительно оси ох.
Нам нужно определить угловой коэффициент.
Применим известные нам формулы и подставим данные.
[alpha=120^{circ}, mathrm{k}=operatorname{tg} alpha=120=-sqrt{3}]
Следовательно правильный ответ задачи будет равняться [k=-sqrt{3}]
Пример №2:
В этом примере нам уже известно значение углового коэффициента.
Нужно определить угол наклона, относительно прямой. Для этого, нужно обязательно учитывать знак известного коэффициента. Если к>0, следует что угол будет острый и определяться как [alpha=operatorname{arctg} k].
Когда к<0, то угол будет характеризоваться как тупой. его значение определяется функцией: [alpha=pi-operatorname{arctg}|k|].
Например, угловое значение равно 3.
Значение коэффициента является положительным, значит угол будет острый. Вычисляться он будет по формуле: [alpha=operatorname{arctg} k=3]
Ответ задачи: [operatorname{arctg}=3].
Пример №3:
Значение углового коэффициента имеет отрицательное число в виде дроби. И равняется следующему значению: [-frac{1}{sqrt{3}}]
Для определения угла наклона, выполнить следующие действия: обозначим все значения. Угол наклона относительно оси имеет положительное значение. Следовательно формула для решения запишется следующим образом: [mathrm{k}=-frac{1}{sqrt{3}}<0 Rightarrow alpha=pi-operatorname{arctg}|k|].
Подставим данные, которые заданы в условии задания:
[alpha=pi-operatorname{arctg}left|-frac{1}{sqrt{3}}right|=pi-operatorname{arctg} frac{1}{sqrt{3}}=pi-frac{pi}{6}=frac{5 pi}{6} Rightarrow]ответ будет [frac{5 pi}{6}].
Пример №4:
Необходимо определить, относятся ли точки координат к прямой. Они равны: [m_{1}(3 ; 0) text { и } m_{2}(2 ;-2)]. Уравнение прямой задано следующее: [y=frac{1}{3} x-1].
Известные нам значения точек подставляем, в заданное уравнение прямой.
И получаем следующий вид формулы: [0=frac{1}{3} cdot 3-1 Leftrightarrow 0=0]. Так после вычисления, мы получаем равенство, которое считается верным. Можно утверждать, что точка принадлежит прямой.
Далее подставляем значения второй точки в уравнение.
[-2=frac{1}{3} cdot 2-1 Leftrightarrow-2=-frac{1}{3}] следовательно точка [m_{2}] не относится к прямой и не лежит на ней.
Вывод решения: только первая точка относится к прямой и лежит на ней, а вторая равная (2;-2) — нет.
Пример №5:
Нужно найти уравнение прямой, которая проходит через значение точки [m_{1}(4 ; 1)]. Значение углового коэффициента — (-2).
Запишем условие : [x_{1}=4, y_{1}=-1, k=-2]
Следовательно необходимое уравнение прямой равно: [y-y_{1}=k].
[left(x-x_{1}right) text { следовательно } y-(-1)=-2 cdot(x-4) Leftrightarrow y=-2 x+7]
Искомое уравнение: [y=-2 x+7]
Пример №6:
Составить уравнение прямой, проходящей через значение (-2;4). Угол наклона положительного направления равен [frac{3 pi}{4}].
Решение необходимо начать с определения коэффициента угла.
[k=operatorname{tg} alpha frac{3 pi}{4}=-1]
Определив угловое значение, можно составить искомое уравнение вида: [y-y_{1}=k cdotleft(x-x_{1}right) text { из этого следует } y-4=-1 cdot(x-(-2) Leftrightarrow y=-x+2]
Каноническое уравнение прямой на плоскости
Определение канонического уравнения — это уравнение следующего вида [frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}}].
Данное уравнение задает на плоскости в прямоугольной системе прямую линию. Она, в свою очередь проходит через точку [m_{1}(x ; y)], которая имеет вектор направления, обозначающийся как [underline{alpha}=left(alpha_{x} ; a_{y}right)]
Запишем несколько примеров для данного вида уравнения.
[frac{x-2}{sqrt{3}}=frac{y-3}{1}]
Приведенное уравнение — это уравнение прямой для канонического вида. Прямая его будет проходить через значения точек [m_{1}(2 ; 3)]. Вектор направляющий равен [sqrt{3}, 1].
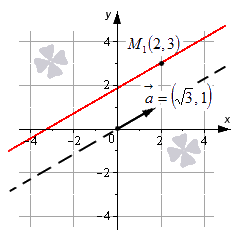
Важные моменты, которые следует помнить, при решении задач с каноническим уравнением.
Отметим следующие важные факты:
- если вектор является прямым и прямая линия проходит через точку, то ее уравнение имеет вид : [frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}}]
- когда вектор прямой по направлению, то любой из векторов может быть направляющим вектором прямой. И уравнение записывается следующим образом: [frac{x-x_{1}}{mu cdot alpha_{x}}=frac{y-y_{1}}{mu cdot alpha_{y}}]
Пример №1:
Прямая в системе координат проходит через точки (2;-4) и вектор направляющий равен (1;-3). Составьте и напишите каноническое уравнение, применяя известные нам данные.
[frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}}]
[x_{1}=2, y_{1}=2, alpha_{x}=1, alpha_{y}=-3]
Следовательно уравнение записывается следующим образом: [frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}} Leftrightarrow frac{x-2}{1}=frac{y-(-4)}{-3} Leftrightarrow frac{x-2}{1}=frac{y+4}{-3}]
[frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}} Leftrightarrow frac{x-2}{1}=frac{y-(-4)}{-3} Leftrightarrow frac{x-2}{1}=frac{y+4}{-3}] — окончательное искомое уравнение.
Пример №2:
Составить каноническое уравнение, проходящее через точки [sqrt[3]{2} ; quad-frac{1}{7}]
Прямая является параллельной относительно оси координат. Направляющий вектор принимается [underline{j}=(0 ; 1)]. Учитывая значение точек, через которые проходит прямая, записываем уравнение:
[frac{x-sqrt[3]{2}}{0}=frac{y-left(-frac{1}{7}right)}{1} Leftrightarrow frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}]
[text { Ответ: } frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}]
Пример №3:
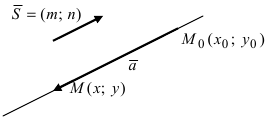
Составим уравнение, руководствуясь графиком, приведенным ниже.
Из рисунка видно, что прямая проходит через точки со значениями (0;3). Расположена параллельно относительно оси x (ось абсцисс). Координатный вектор [underline{i}=(1,0)] — направляющий вектор, для данной системы.
Собрав все данные, преобразовав их. можно записать уравнение:
[frac{x-0}{1}=frac{y-3}{0} Leftrightarrow frac{x}{1}=frac{y-3}{0}]
Нет времени решать самому?
Наши эксперты помогут!
Параметрическое уравнение на плоскости и его характеристики
Уравнение такого типа записываются в следующем виде:
[x=x_{1}+alpha_{x} cdot lambda]
[mathrm{y}=y_{1}+alpha_{y} cdot lambda]
[x_{1} y_{1} alpha_{x} alpha_{y} text { — действительные простые значения. }]
[alpha_{x} alpha_{y} text{ — значения, которые математически возможны равняться нулю.}]
[lambda text { — параметр, значение которого может быть различным. }]
Уравнение параметрического вида предназначено, для установления не очевидного взаимодействия между координатами точек системы. Для определения этого свойства и вводится параметр [lambda].
Пример №1:
Задана система уравнения:
[{x=-3-1 / 2 cdot lambda}]
[{y=3 cdot lambda}]
[{z=2 / 3}]
Необходимо определить все координаты, каждой направляющей системы.
[{x=-3-1 / 2 cdot lambda}]
[{y=3 cdot lambda}]
[{z=2 / 3} Leftrightarrow]
[Leftrightarrow{x=-3-1 / 2 cdot lambda}]
[{y=0+3 cdot lambda}]
[{z=2 / 3+0 cdot lambda}]
Коэффициенты перед значение [lambda] имеют соответствующие значения координат направляющего вектора и равняются: [underline{alpha}=(-1 / 2,3,0)] — для прямой по заданию.
Соответственно запишем все координаты направляющих векторов:
[left(-frac{1}{2} cdot mu, 3 cdot mu, 0 cdot muright)=left(-frac{1}{2} cdot mu, 3 cdot mu, 0 cdot muright), mu in R, mu neq 0 ]
[left(-frac{1}{2} cdot mu, 3 cdot mu, 0 cdot muright), mu in R, mu neq 0]
Пример №2
Составить параметрическое уравнение в пространстве:
[underline{alpha}=left(2 ;-frac{1}{sqrt{3}}, 0right)-text { вектор направляющий.}]
Точки (7, -1, 0) — значения точки на прямой координат.
[x_{1}=7, y_{1}=-1, z_{1}=0, alpha_{x}=2, alpha_{y}=-frac{1}{sqrt{3}}, alpha_{z}=0]
Полученные данные подставляем систему уравнения.
[x=x_{1}+alpha_{x} cdot lambda]
[mathrm{y}=y_{1}+alpha_{y} cdot lambda]
[z=z_{1}+alpha_{z} cdot lambda]
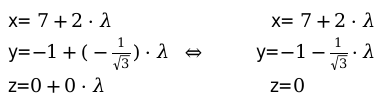
Особые моменты данного типа уравнений:
Имея любое значение [lambda], можно определить три числа (z, y,x).
К примеру точки [M_{1}left(x_{1} text { и так далее }right) text { находятсся в параметрах уравнения в системе. }]
[mathrm{x}=chi_{1}+alpha_{x} cdot lambda]
[mathrm{y}=y_{1}+alpha_{y} cdot lambda]
[z=z_{1}+alpha_{z} cdot lambda]
где значение [lambda]=0.
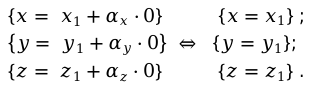
Пример №3:
Любые значения точек находятся на прямой, для определенной заданной системы координат.
[M_{1}(4 ; 3 ;-2)]
[N_{1}(-2 ; 3 ;-1)]
Запишем систему параметрических уравнение:
[x=2+2 cdot lambda]
[y=3 cdot lambda]
[z=-1-lambda]
Поставляя данные первой точки, получаем уравнения:
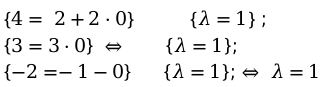
Следовательно значение [lambda=1 text {, для } M_{1}(4 ; 3 ;-2)]. следовательно она находится на прямой координат.
Аналогичные действия проводим для второй координаты точек.
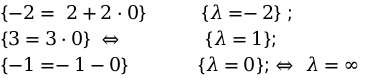
Выполнив вычисления, мы видим, что параметра для [lambda] не существует.
Нормальное уравнение для координатной прямой
Формула
Нормальное уравнение можно выразить в виде уравнения:
[A_{x}+B_{y}+C=0]
Где числа А, В, и C имеют такие значения, что, вектор [underline{n}=(mathrm{A}, quad mathrm{B})] равняется единице, [C leq 0].
Вектор [underline{n}=(mathrm{A}, quad mathrm{B})], будет является нормальным в системе координат.
Так же есть еще один способ записать нормальный вид уравнения, применяя для этого значения тригонометрических функций.
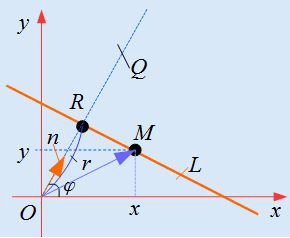
[cos alpha cdot x+cos beta cdot y-rho=0]
[cos alpha cos beta] — это действительные простые числа. Следовательно, они представлены направляющими косинусами. А также нормального вектора и единичной прямой.
Отсюда следует [underline{n}=left(begin{array}{lll} cos alpha & cos beta end{array}right)] равняется равенству: [underline{n}=cos ^{2} alpha+cos ^{2} beta=1]
Значение [rho geq 0]
Данное значение определяет длину расстояния от прямой линии до начала координатной прямой.
Пример №1:
В задаче имеется уравнение прямой для общего случая.
2x-3y+4=0
Нужно используя вышеуказанное уравнение составить простое уравнение для координатной прямой.
Для начала запишем А=2; В=-3; С=4.
Неизвестное значение t, сможем вычислить из равенства используя известные значения.
[mathrm{t}=pm frac{1}{sqrt{A^{2}+B^{2}}}=pm frac{1}{sqrt{13}}]
t- будет отрицательным значение, так как С>0.
[t=-frac{1}{sqrt{13}}]
Перемножим уравнение:
[frac{2}{sqrt{13}} x+frac{3}{sqrt{13}} y-frac{4}{sqrt{13}}=0]
Вывод решения: [frac{2}{sqrt{13}} x+frac{3}{sqrt{13}} y-frac{4}{sqrt{13}}=0]
Значение [frac{4}{sqrt{13}}] — будет являться, тем самым значение, которое показывает расстояние от начала до прямой координат прямой.
Пример №2.
Определим и составим нужное уравнение имея следующие известные нам данные: угол [varphi=60 text { градусов }]
Расстояние до прямой от начала координат равняется 4.
Используя данные решим задачу.
[cos varphi=cos left(60^{circ}right)=frac{1}{2}]
[sin varphi=sin left(60^{circ}right)=frac{sqrt{3}}{2}]
[frac{1}{2} x+frac{sqrt{3}}{2} y-4=0]
[text { Ответ: } frac{1}{2} x+frac{sqrt{3}}{2} y-4=0]
Пример №3:
Имея данные значения решим задачу согласно задания. Где угол [varphi=90 text { градусов }]
Расстояние до прямой от начала координат равняется 3.
Используя данные решим задачу.
[cos varphi=cos left(90^{circ}right)=0]
[sin varphi=sin left(90^{circ}right)=1]
[1 x+0 y-3=-2]
Ответ: [0 x+-1 y-3=-2] координата не лежит на прямой, так как имеет отрицательное значение.
Выводы по материалу:
Рассмотрев типы уравнения, для прямой в плоскости. Перечислив их категории и основные характеристики. Можно сказать, что это одна из составляющих математики.
В ней переплетаются все основные значения и функции этой технической науки.
Для решения задач, необходимо обладать следующими навыками:
- вспомнить весь изученный материал по работе с тригонометрическими функциями: косинус, синус. тангенс и другие.
- вычисление отрицательных значений и их правила;
- решение уравнений с дробными числами;
- помнить правило возведения числа в степень.
Учитывая все, рекомендации, процесс работы с материалом по данной теме значительно облегчит процесс.
Содержание:
Общее уравнение прямой:
Пусть на плоскости дана декартова система координат. Движение точки с произвольными координатами х и у по этой плоскости порождает линию.
Определение: Любое соотношение
Определение: Порядок линии определяется по высшему показателю степени переменных х и у или по сумме показателей степени в произведении этих величин.
Пример:
а) 2х + Зу-5 = 0 – линия первого порядка; точка A(l; 1) удовлетворяет этому соотношению, а точка, например, В(1; 0) – ему не удовлетворяет;
б)
в) 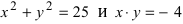
Рассмотрим другое определение линии:
Определение: Геометрическое место точек, координаты которых удовлетворяют уравнению F(x; у)=0, называется линией, а само уравнение F(x; у) = 0 – уравнением линии.
Определение: Общим уравнением прямой называется уравнение первого порядка вида
Рассмотрим частные случаи этого уравнения:
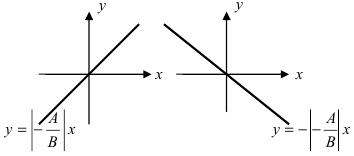
а) С = 0; 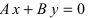
Рис. 20. Прямая, проходящая через начало координат.
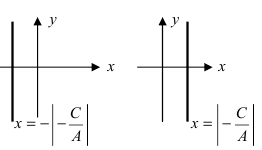
б) 5 = 0; Ах+С=0 – прямая проходит параллельно оси ординат Оу (Рис. 21):
Рис. 21. Прямая, проходящая параллельно оси ординат Оу.
в) А = 0; Ву+С=0 – прямая проходит параллельно оси абсцисс Ох (Рис. 22):
Рис. 22. Прямая, проходящая параллельно оси абсцисс Ох.
Виды уравнений прямой
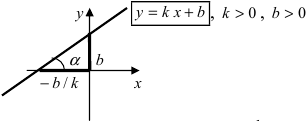
1. Уравнение прямой с угловым коэффициентом. Пусть дано общее уравнение прямой 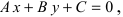
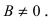
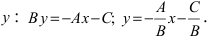
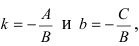
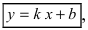
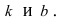
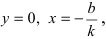
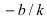
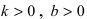
Рис. 23. Отрезки, отсекаемые прямой на координатных осях.
Из рисунка видно, что 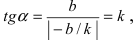
2. Уравнение прямой в отрезках.
Пусть в общем уравнении прямой параметр 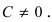
Обозначим через 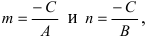
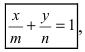
Рис. 24. Отрезки, отсекаемые прямой на координатных осях.
При у=о, х=m, т.е. прямая отсекает на оси абсцисс отрезок m. Следовательно, прямая проходит через 2 точки:
3. Уравнение прямой, проходящей через две заданные точки. Пусть дано общее уравнение прямой Ах + Ву + С = 0, которая проходит через две известные точки 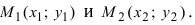
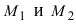
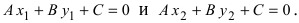
Пусть 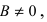
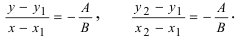
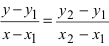
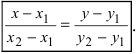
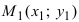
4. Уравнение прямой, проходящей через заданную точку 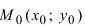
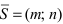
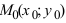
Определение: Вектор 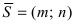
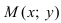
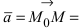
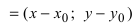
Рис. 25. Прямая, проходящая через данную точку параллельно направляющему вектору.
В силу того, что вектора 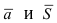
Определение: Полученное уравнение называется либо уравнением, проходящим через заданную точку параллельно направляющему вектору, либо каноническим уравнением прямой.
5. Параметрическое уравнение прямой. Если каждую дробь в каноническом уравнении прямой приравнять некоторому параметру t, то получим параметрическое уравнение прямой
Основные задачи о прямой на плоскости
1. Координаты точки пересечения двух прямых. Пусть две прямые заданы общими уравнениями 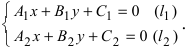
2. Угол между двумя пересекающимися прямыми. Пусть даны две пересекающиеся прямые, заданные уравнениями с угловыми коэффициентами
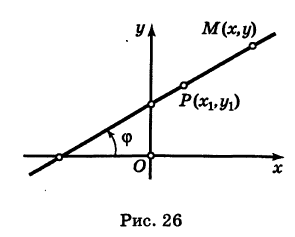
Требуется найти угол между этими прямыми (Рис. 26):
Рис. 26. Угол между двумя прямыми.
Из рисунка видно, что 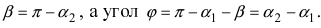
Наименьший угол между пересекающимися прямыми определим формулой 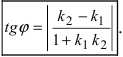
Отсюда следует условие перпендикулярности прямых: угловые коэффициенты прямых связаны между собой соотношением
Пример:
Определить угол между прямыми
Решение:
В силу того, что 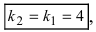
Пример:
Выяснить взаимное расположение прямых
Решение:
Так как угловые коэффициенты 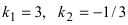
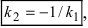
3. Расстояние от точки до прямой. Расстояние от точки до прямой определятся вдоль перпендикуляра, опущенного из точки 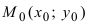
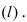
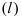
Если прямая 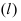
Прямая линия на плоскости и в пространстве. Системы координат на плоскости
Рассмотрим произвольную прямую. Выберем на этой прямой начальную точку, обозначаемую буквой О, определим положительное направление, выберем некоторый отрезок в качестве линейной единицы, благодаря чему прямая станет осью. После этого условимся называть координатой любой точки М на этой оси величину отрезка 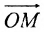
Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке, т.е. указано, какая из них считается первой, а какая – второй. Точка пересечения осей называется началом координат и обозначается через О, а сами оси – координатными осями, причем первую из них называют также осью абсцисс и обозначают через Ох, а вторую – осью ординат, обозначаемую Оу.
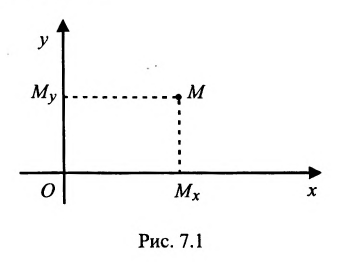
Пусть М- произвольная точка плоскости. Спроектируем точку M на координатные оси, т.е., проведем через М перпендикуляры к осям Ох и Оу; основания этих перпендикуляров обозначим соответственно 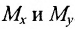
Координатами точки М в заданной системе называются числа 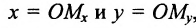
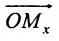
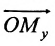
Если задана декартова прямоугольная система координат, то каждая точка М плоскости в этой системе имеет одну вполне определенную пару координат х, у – М(х, у). И обратно, для любых х и у на плоскости найдется одна вполне определенная точка с абсциссой х и ординатой у.
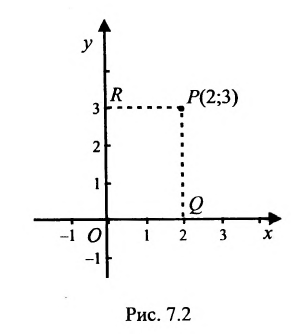
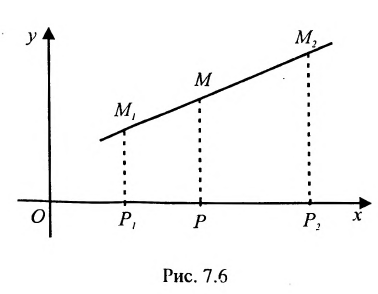
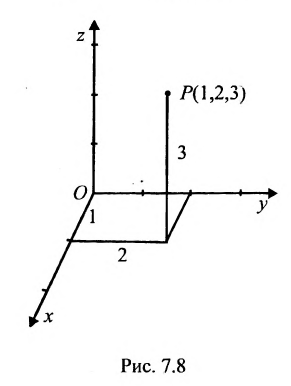
На рис. 7.2 положение точки Р полностью определяется ее координатами (2;3).
Две координатные оси разделяют всю плоскость на четыре части, называемыми координатными плоскостями, определяемыми соответственно:
Декартова прямоугольная система координат является наиболее употребительной. Однако, в отдельных случаях могут оказаться более удобными или косоугольная декартова или полярная системы координат.
Косоугольная система координат от прямоугольной декартовой системы координат отличается только произвольным углом между осями координат.
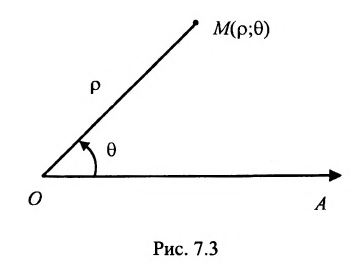
Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча OA, называемого полярной осью, масштаба для измерения длин и направления- вращения в плоскости, считаемого положительным (рис. 7.3).
Каждая точка М в полярной системе координат задается парой координат 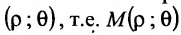
Декартова прямоугольная система координат связана с полярной системой формулами:
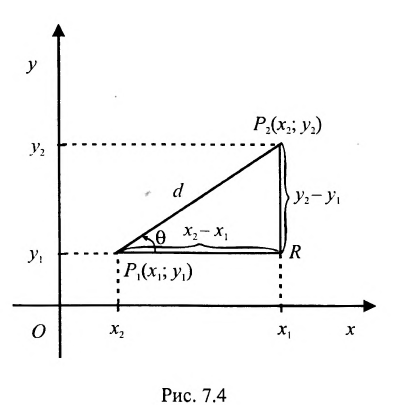
Основным инструментом аналитической геометрии служит формула для вычисления расстояния между двумя точками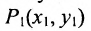
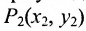
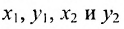
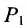
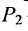
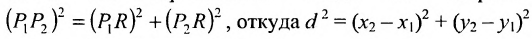
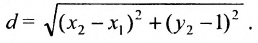
Это и есть формула для вычисления расстояния между двумя точками.
Важно иметь в виду, что эта формула остается в силе независимо от того, как расположены точки 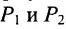
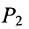
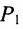
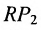
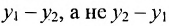
Расстояние между точками, вычисляемое по формуле (7.1.1), от этого не изменится, так как 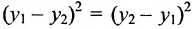
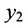
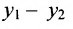
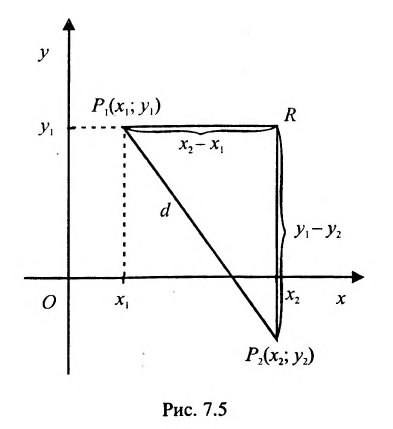
Если обозначить через 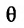
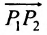
выражают проекции произвольного отрезка на координатные оси через его длину и полярный угол. Из формул (7.1.2) получаем формулы:
позволяющие определить полярный угол отрезка по координатам его конца и начала. Кроме того, если u – произвольная ось, а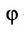
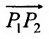
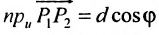
Пусть на плоскости даны две произвольные точки, из которых одна считается первой, другая – второй. Обозначим их в заданном порядке через 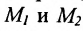
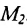
Определение 7.1.1. Число 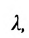
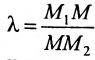
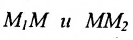
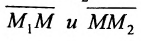
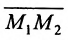
Число 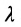
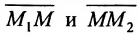
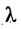
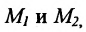
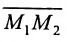
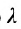
Задача о делении отрезка в данном отношении формулируется следующим образом:
Считая известными координаты двух точек 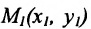
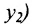
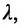
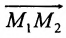
Решение задачи определяется следующей теоремой.
Теорема 7.1.1. Если точка М(х, у) делит направленный отрезок 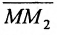
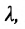
Доказательство:
Спроектируем точки 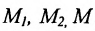
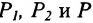
Подставив в (7.1.4) величины отрезков 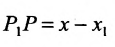
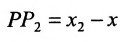
Разрешая это уравнение относительно х, находим:
Вторая формула (7.1.3) получается аналогично.
Если 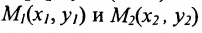
середина отрезка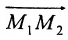
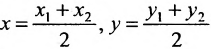
получаются из (7.1.3) при 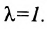
Основная теорема о прямой линии на плоскости
Предположим, что в данной плоскости задана прямоугольная система координат и некоторая прямая l.
Всякий ненулевой вектор, коллинеарный данной прямой, называется её направляющим вектором. Всякие два направляющих вектора 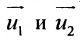
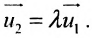
Для всех направляющих векторов 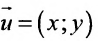
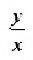
Действительно, если 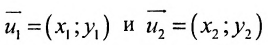
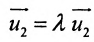
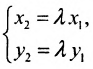
Угловой коэффициент прямой можно определить и по-другому: как тангенс угла, образованного положительным направлением оси абсцисс и заданной прямой.
Справедлива следующая теорема.
Теорема 7.3,1. Всякая прямая на плоскости определяется уравнением первой степени с двумя переменными х и у; и обратно, всякое уравнение первой степени с двумя переменными х и у определяет некоторую прямую на плоскости.
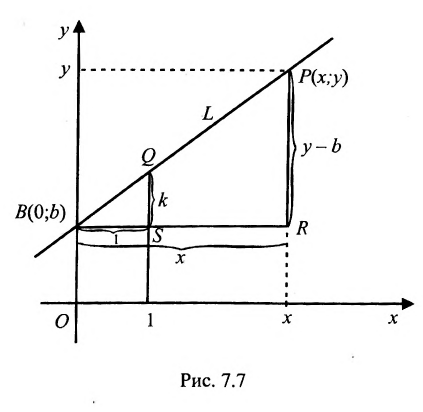
Доказательство: Пусть В = (О,b}- точка пересечения прямой L с осью у, а Р = (х,у) – любая другая точка на этой прямой. Проведем через точку В прямую, параллельную оси х, а через точку Р – прямую, параллельную оси у; проведем также прямую х = 1. Пусть k -угловой коэффициент прямой L (см. рис. 7.7). Случай к =0 не исключается.
Так как треугольники BSQ и BRP подобны, то 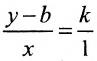
Следовательно, если точка Р принадлежит прямой L, то ее координаты удовлетворяют уравнению (7.2.1). Обратно, нетрудно показать, что если х и у связаны уравнением (7.2.1), то точка Р принадлежит прямой L, проходящей через точку (0;b) и имеющей угловой коэффициент k.
Таким образом, уравнение любой прямой можно записать в виде:
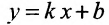
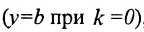
В обоих случаях мы получаем уравнение первой степени. Кроме того, каждое уравнение первой степени ио х и у можно привести к виду (7.2.2) либо (7.2.3).
Докажем обратное утверждение. Предположим, что задано произвольное уравнение первой степени:
Ах+Ву+С=0. (7.2.4)
Если 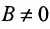
т.е. в виде (7.2.2). При В = 0 уравнение (7.2.3) сводится к уравнению
А х = —С,
или 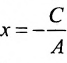
Таким образом, любая прямая описывается уравнением первой степени с неизвестными х и у, и обратно, каждое уравнение первой степени с неизвестными х и v определяет некоторую прямую.
Уравнение (7.2.4) называется общим уравнением прямой. Так
как 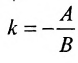
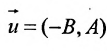
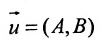
1. 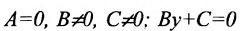
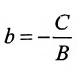
2. 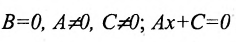
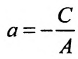
3. 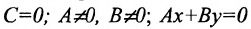
4. А=0; С=0; Ву-0 или у = 0 – это уравнение оси абсцисс Ох.
5. В=0;С=0; Ах=0 или х = 0 – это уравнение оси ординат Оу.
Различные виды уравнений прямой на плоскости
Положение прямой на плоскости относительно системы координат можно задать различными способами. Например, прямая однозначно определяется: двумя различными точками; точкой и направляющим вектором; отрезками, отсекаемыми прямой на осях координат и др. Однако, обязательно, должна быть точка, лежащая на этой прямой.
Пусть в уравнении (7.2.4) ни один из коэффициентов А, В, С не равен нулю. Перенесем свободные члены вправо и разделим на (-С). Получим уравнение прямой в отрезках:
где 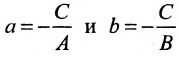
Рассмотрим прямую l на плоскости и выберем на этой прямой какие-нибудь точки 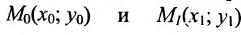
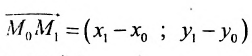
Геометрическое место концов всевозможных векторов вида 
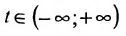
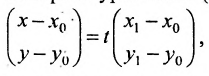
где 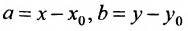
Система (7.3.3) равносильна уравнению
называемым каноническим уравнением прямой на плоскости. Из системы (7.3.3) можно получить уравнение
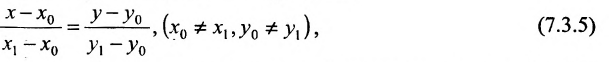
Если абсциссы точек 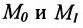

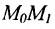
Если ординаты точек 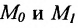
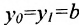
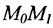
или
где
угловой коэффициент прямой.
Уравнение (7.3.6) называется уравнением прямой, проходящей через точку 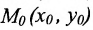
Пример:
Составить уравнение прямой, проходящей через две точки
Решение:
I способ. Воспользуемся уравнением (7.3.5). Подставив известные координаты точек 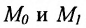
II способ. Зная координаты точек 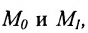
Тогда, воспользовавшись уравнением (7.3.6), найдём искомое уравнение прямой: 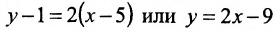
Заметим, что составленное уравнение можно записать как уравнение прямой в отрезках, разделив все члены уравнения
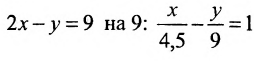
Взаимное расположение двух прямых на плоскости
Пусть на плоскости заданы две прямые общими уравнениями 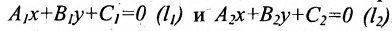
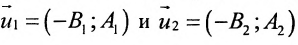
Если прямые параллельны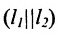
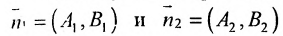
И обратно, если координаты при неизвестных х и у пропорциональны, то прямые параллельны. Следовательно, можно сформулировать следующую теорему:
Теорема 7.4.1. Две прямые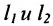
Например, прямые 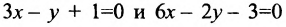
т. к.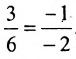
Если прямые перпендикулярны 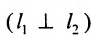
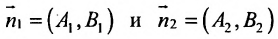
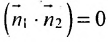
Справедливо и обратное утверждение: если скалярное произведение нормальных векторов равно нулю, то прямые /, и /2 перпендикулярны.
Теорема 7.4.2. Две прямые 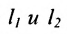
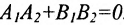
Например, прямые 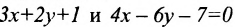
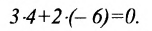
Если прямые заданы уравнениями вида 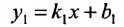
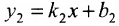
Для того чтобы прямые были параллельны, необходимо и достаточно, чтобы выполнялось равенство
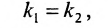
а для их перпендикулярности необходимо и достаточно, чтобы
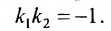
Пример:
Найти проекцию точки Р (2, 3) на прямую, проходящую через точки А (4, 3) и В (6, 5).
Решение:
Проекция точки Р на прямую АВ – это точка пересечения перпендикуляра, проведенного к этой прямой из точки Р.
Вначале составим уравнение прямой АВ. Воспользовавшись уравнением (7.3.5), последовательно получаем:
Для того, чтобы составить уравнение перпендикуляра, проведенного из точки Р на прямую АВ, воспользуемся уравнением (7.3.6). Угловой коэффициент k определим из условия перпендикулярности двух прямых, т. е. из формулы (7.4.6). Поскольку 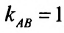
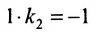
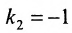
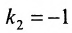
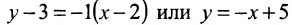
Решая систему уравнений, составленную из уравнений прямой АВ и перпендикуляра
найдём координаты проекции точки Р на прямую АВ: х=3 у=2, т.е.
Пример:
Издержки на производство шести автомобилей составляют 1000 млн. ден. ед., а на производство двадцати автомобилей- 15000 млн. ден. ед. Определить издержки на производство 22 автомобилей при условии, что функция К(х) издержек производства линейна, т.е. имеет вид у = ах + b .
Решение:
Обозначим через х количество автомобилей, а через y- издержки производства. Тогда из условия задачи следует, что заданы координаты двух точек- А(6; 1000) и В(20; 15000), принадлежащих линейной функции у = ах +b. Воспользовавшись уравнением (7.3.6 ), найдём искомое уравнение:
Подставив в найденную функцию х = 22, определим издержки на производство 22 автомобилей:
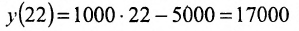
Пример:
Фирма продаёт свои изделия по 10 ден. ед. за единицу. Затраты на изготовление одного изделия составляют 6 ден. ед. Непроизводственные расходы фирмы равны 300 ден. ед. в год. Определить годовой выпуск продукции, необходимой для того, чтобы фирма работала с прибылью.
Решение:
Обозначим через х объём произведенной продукции. Тогда доход фирмы равен D = 10x. Затраты на производство определяются уравнением: 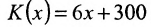
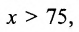
Прямая линия в пространстве
Системы координат в пространстве
В трехмерном пространстве система координат определяется тремя взаимно перпендикулярными осями, проходящими через начало координат О. Снабдив каждую ось единицей измерения длин, можно задать тремя упорядоченными числами (называемыми координатами) положение точки в пространстве. Например, точка Р задается упорядоченной тройкой чисел Р( 1,2,3).
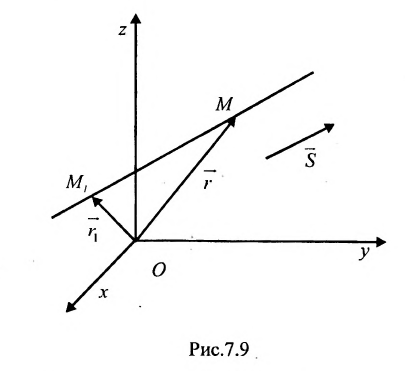
Пусть задано пространство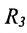
Положение прямой в пространстве вполне определяется заданием какой-либо сё фиксированной точки 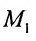
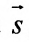
Вектор 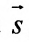
Итак, пусть прямая L проходит через точку 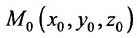
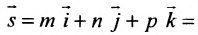
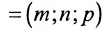
Рассмотрим произвольную точку M(x,y,z) на этой прямой. Из рисунка видно, что вектор 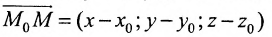
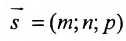
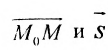
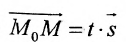
Уравнение 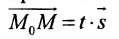
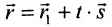
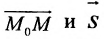
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты х, у и z и точка М перемещается по прямой.
Разрешив уравнения (7.5.2) относительно t
и приравняв найденные значенияt получим канонические уравнения прямой:
Если прямая L в пространстве задается двумя своими точками 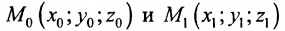
можно взять в качестве направляющего вектора и тогда уравнения (7.5.3) преобразуются в уравнения
где 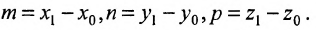
Пример:
Составить параметрические уравнения прямой, проходящей через точку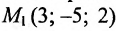
Решение:
В качестве направляющего вектора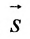
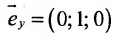
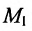
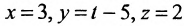
Пример:
Записать уравнения прямой 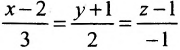
Обозначим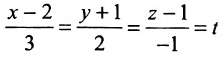
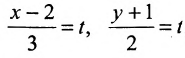
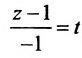
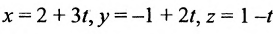
Замечание. Пусть прямая перпендикулярна одной из координатных осей, например, оси Ох. Тогда направляющий вектор
прямой перпендикулярный оси Ох, имеет координаты (о; n; р) и параметрические уравнения прямой примут вид
Исключая из уравнений параметр t, получим уравнения прямой в виде
Однако и в этом случае формально можно записывать канонические уравнения прямой в виде 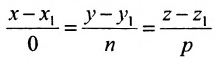
Аналогично, канонические уравнения
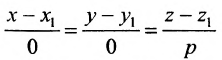
Пример:
Составить канонические и параметрические уравнения прямой, проходящей через точку 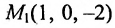
Решение:
Подставив координаты точки 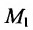
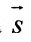
.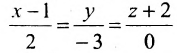
Пример:
Составить канонические уравнения прямой, проходящей через точку М(2, -1,4) параллельно
а) прямой 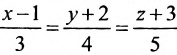
б) оси Ох;
в) оси Оу;
г) оси Oz.
Решение:
а) Поскольку направляющий вектор заданной прямой
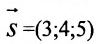
подставив координаты точки М(2; -1; 4) и вектора 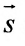
б) Поскольку единичный вектор оси О х: 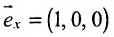
(7.5.3) координаты точки М(2; -1; 4 ) и вектора 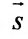
в) В качестве направляющего вектора 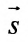
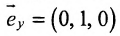
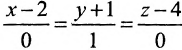
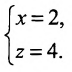
г) Единичный вектор оси Oz : 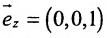
Пример:
Составить уравнение прямой, проходящей через две заданные точки
Решение:
Подставив координаты точек 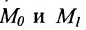
(7.5.4), получим:
Взаимное расположение двух прямых в пространстве
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным. Пусть в пространстве заданы две прямые:
Очевидно, что за угол 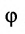
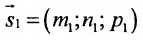
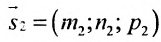
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов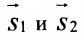
Две прямые параллельны тогда и только тогда, когда пропорциональны соответствующие координаты направляющих векторов:
т.е. 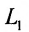
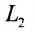
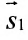
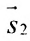
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих координат направляющих векторов равна нулю:
Пример:
Найти угол между прямыми 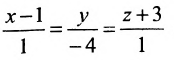
Решение:
Воспользуемся формулой (7.6.1), в которую подставим координаты направляющих векторов 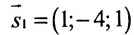
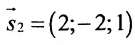
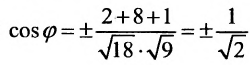
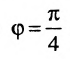
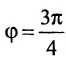
Вычисление уравнения прямой
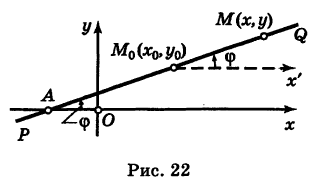
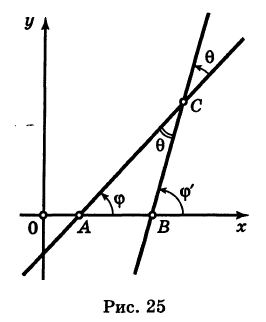
Пусть PQ — некоторая прямая на плоскости Оху (рис. 22). Через произвольную точку М0 (х0, у0) этой прямой (условно называемую «начальной точкой») проведем прямую М0х параллельную оси Ох и имеющую с ней одинаковое направление. Тогда наименьший неотрицательный угол 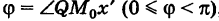
Очевидно, этот угол не зависит от выбора точки М0. Если прямая PQ пересекает ось Ох в некоторой точке А (а, 0), то ф есть обычный угол между направленными прямыми. Если PQ || Ох, то, очевидно, Ф = 0. Начальная точка М0 прямой и угол ф («направление прямой») однозначно определяют положение этой прямой на плоскости.
1) Пусть сначала 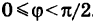
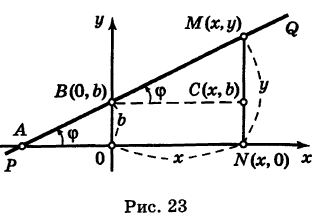
Ордината у = NM текущей точки М (х, у) прямой (рис. 23) состоит из двух частей:
из них первая постоянна, а вторая переменна. Введя угловой коэффициент tg ф = k9 из рис. 23 будем иметь
при х > 0.
Таким образом,
при х > 0.
Нетрудно проверить, что формула (3) остается справедливой также и при х < 0.
Мы доказали, что координаты любой точки М (х, у) прямой PQ удовлетворяют уравнению (3). Легко убедиться в обратном: если координаты какой-нибудь точки Ml 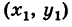
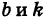
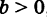
При k = 0 получаем уравнение прямой, параллельной оси Ох:
2) Если 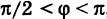
3) Если 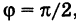
где а — абсцисса следа этой прямой на оси Ох (т. е. ее точки пересечения с осью Ох).
Замечание. Как частные случаи получаем уравнения осей координат:
Прямую легко построить по ее уравнению.
Пример:
Построить прямую, заданную уравнением
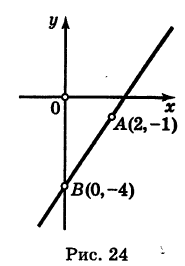
Решение:
Известно, что две точки вполне определяют положение прямой. Поэтому достаточно найти две точки, через которые проходит наша прямая. В данном уравнении b = -4. Следовательно, прямая проходит через точку В (0, -4). С другой стороны, координаты х и у любой точки, лежащей на нашей прямой, связаны заданным уравнением. Поэтому, задав абсциссу некоторой точки, лежащей на прямой, мы из уравнения прямой найдем ее ординату. Положим, например, х = 2; из уравнения прямой получим у = -1. Таким образом, наша прямая проходит через точки А (2, -1) и В (0, -4). Построив эти точки по их координатам и проведя через них прямую (рис. 24), мы получим искомую прямую.
Из предыдущего видно, что для произвольной прямой на плоскости можно составить ее уравнение; обратно, зная уравнение некоторой прямой, можно построить эту прямую. Таким образом, уравнение прямой полностью характеризует положение ее на плоскости.
Из формул (3) и (5) видно, что уравнение прямой есть уравнение первой степени относительно текущих координат х и у. Справедливо и обратное утверждение.
Теорема: Всякое невырожденное уравнение первой степени
представляет собой уравнение некоторой прямой линии на плоскости Оху (общее уравнение прямой линии).
Доказательство: 1) Пусть сначала В ^ 0. Тогда уравнение (7) можно представить в виде

2) Пусть теперь В = 0; тогда А 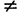
х = -С/А.
Уравнение (9) представляет собой уравнение прямой, параллельной оси Оу и отсекающей на оси Ох отрезок a = -С/А.
Так как все возможные случаи исчерпаны, то теорема доказана.
- Заказать решение задач по высшей математике
Угол между двумя прямыми
Рассмотрим две прямые (не параллельные оси Оу)у заданные их уравнениями с угловыми коэффициентами (рис. 25):
Требуется определить угол 9 между ними. Точнее, под углом 0 мы будем понимать наименьший угол, отсчитываемый против хода часовой стрелки, на который вторая прямая повернута относительно первой (0 < 0 < я). Этот угол 9 (рис. 25) равен углу АСВ треугольника ABC. Далее, из элементарной геометрии известно, что внешний угол треугольника равен сумме внутренних, с ним не смежных. Поэтому ф’ = ф + 0, или
0 = ф’ – ф;
отсюда на основании известной формулы тригонометрии получаем
Заменяя tg ф и tg ф’ соответственно на к и k окончательно будем иметь
Формула (3) дает выражение тангенса угла между двумя прямыми через угловые коэффициенты этих прямых.
Выведем теперь условия параллельности и перпендикулярности двух прямых.
Если прямые (1) и (2) параллельны, то ф’ = ф и, следовательно,
k’ = к. (4)
Обратно, если выполнено условие (4), то, учитывая, что ф’ и ф заключаются в пределах от 0 до я, получаем
Ф’ – ф, (5)
и, следовательно, рассматриваемые прямые или параллельны, или сливаются (параллельность в широком смысле).
Правило 1. Прямые на плоскости параллельны (в широком смысле) тогда и только тогдау когда их угловые коэффициенты равны между собой.
Если прямые перпендикулярны, то 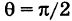
отсюда 1 + kk’ = 0 и
k’ = -l/k.
Справедливо также и обратное утверждение.
Правило 2. Две прямые на плоскости перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по величине и противоположны по знаку.
Пусть теперь уравнения прямых заданы в общем виде:
Ах + By + С = 0 (7)
и
А’х + В’у + С’ = 0. (8)
Отсюда, предполагая, что 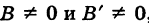
Следовательно, угловые коэффициенты этих прямых есть
Из формулы (3), производя несложные выкладки, находим тангенс угла между этими прямыми:
Отсюда получаем:
1) условие параллельности прямых (0 = 0)
2) условие перпендикулярности прямых
Отметим, в частности, что прямые
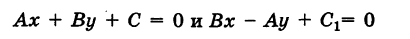
Для прямых, параллельных осям Ох и Оу, условно полагают 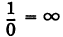
Пример:
Определить угол между прямыми у = х и у = 1,001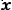
Решение:
По формуле (3) получаем
Так как для малых углов 0 справедливо приближенное равенство 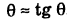
Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая РМ образует угол ф с положительным направлением оси Ох (рис. 26) и проходит через заданную точку Р 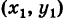
В этом случае, как мы видели, уравнение прямой имеет вид
у = kx + b, (1)
где k = tg ф — угловой коэффициент прямой, а Ь — длина отрезка, отсекаемого нашей прямой на оси Оу. Так как точка Р 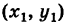
ух = kxt+ b. (2)
Вычитая из равенства (1) равенство (2), получим
Это и есть уравнение искомой прямой.
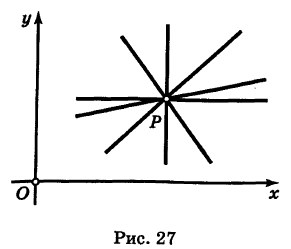
Если прямая, проходящая через точку Р 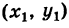
Если k — заданное число, то уравнение (3) представляет вполне определенную прямую. Если же k — переменный параметр, то это уравнение определит пучок прямых у проходящих через точку Р 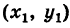
Пример:
Написать уравнение прямой, проходящей через точку Р (3, 2) и параллельной прямой:
Решение:
Так как искомая прямая параллельна данной прямой, то ее угловой коэффициент k = 4/3. Следовательно, на основании формулы (3) уравнение этой прямой имеет вид 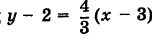
Пример:
Написать уравнение прямой, проходящей через точку Р (4, 5) и перпендикулярной к прямой:
Решение:
Так как искомая прямая перпендикулярна прямой с угловым коэффициентом k = -2/3, то ее угловой коэффициент k’ = -l/k = 3/2. Следовательно, на основании формулы (3) уравнение этой прямой таково:
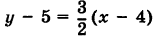
Уравнение прямой, проходящей через две данные точки
Известно, что через две не совпадающие между собой точки можно провести прямую, и притом только одну. Отыщем уравнение прямой, проходящей через точки 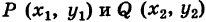
Предположим сначала, что 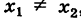
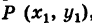
где k — неизвестный нам угловой коэффициент этой прямой. Однако так как наша прямая проходит также через точку Q 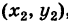
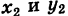
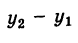
и, следовательно, при 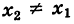
Подставляя выражение (2) для углового коэффициента k в уравнение (1), получим уравнение прямой PQ:
Это уравнение при 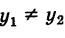
Если 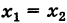
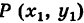
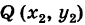
Пример:
Написать уравнение прямой, проходящей через точки Р(4, -2) и Q(3, -1).
Решение:
На основании уравнения (3) имеем
Уравнение прямой в «отрезках»
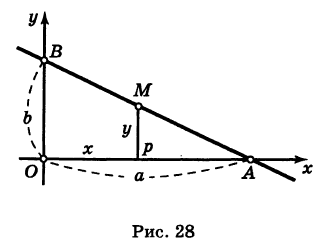
Выведем теперь уравнение прямой, положение которой на плоскости задано ненулевыми отрезками, отсекаемыми ею на осях координат. Предположим, например, что прямая АВ отсекает на оси Ох отрезок OA = а, а на оси Оу — отрезок О В = b (рис. 28), причем ясно, что тем самым положение прямой вполне определено.
Для вывода уравнения прямой АВ заметим, что эта прямая проходит через точки А (а, 0) и Б 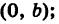
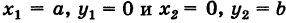
Отсюда
и окончательно
Это и есть так называемое уравнение прямой в «отрезках». Здесь х и у, как обычно, — координаты произвольной точки М (х, у), лежащей на прямой АВ (рис. 28).
Пример:
Написать уравнение прямой АВ, отсекающей на оси Ох отрезок OA = 5, а на оси Оу отрезок ОВ = -4.
Полагая в уравнении (1) а = 5 и b = -4, получим 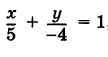
Примечание. Уравнение прямой, проходящей через начало координат или параллельной одной из осей координат, не может быть записано как уравнение прямой в «отрезках».
Точка пересечения двух прямых
Пусть имеем две прямые
Точка пересечения этих прямых лежит как на первой прямой, так и на второй. Поэтому координаты точки пересечения должны удовлетворять как уравнению первой, так и уравнению второй прямой. Следовательно, для того чтобы найти координаты точки пересечения двух данных прямых, достаточно решить совместно систему уравнений этих прямых.
Последовательно исключая из уравнений (1) и (2) неизвестные у и х, будем иметь
Отсюда если 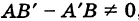
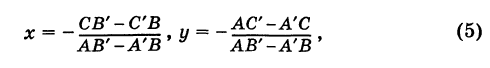
Для прямых (1) и (2) возможны следующие три случая.
На основании прямые не параллельны. Координаты их единственной точки пересечения определяются из формул (6).
Прямые параллельны и точки пересечения нет. Аналитически это видно из того, что по меньшей мере одно из уравнений (3) или (4) противоречиво и, значит, система (1) и (2) несовместна.
Прямые (1) и (2) сливаются, и, таким образом, существует бесчисленное множество точек пересечения. В этом случае левые части уравнений (1) и (2) отличаются только на постоянный множитель и, следовательно, система этих уравнений допускает бесконечно много решений.
Пример:
Решая совместно систему уравнений прямых
получаем х = 2 и у = 1. Следовательно, эти прямые пересекаются в точке N(2,1).
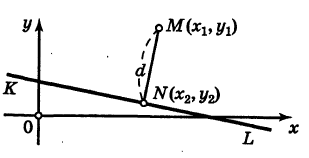
Расстояние от точки до прямой
Рассмотрим прямую KL, заданную общим уравнением
и некоторую точку М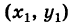
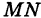
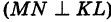
Уравнение перпендикуляра MN можно записать в виде
Отсюда для основания перпендикуляра N(x2, у2) будем иметь
и, следовательно,
где t — коэффициент пропорциональности. Поэтому
С другой стороны, учитывая, что точка N(*2, i/2) лежит на прямой KL, причем из (4) имеем 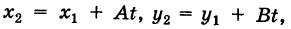
Следовательно,
Таким образом, в силу формулы (5) имеем
В частности, полагая 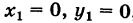
Замечание. Разделив обе части уравнения прямой (1) на 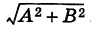
свободный член которого 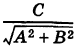
начала координат до прямой. Такое уравнение прямой будем называть нормированным.
Из формулы (7) получаем правило:
чтобы определить расстояние от точки до прямой, нужно в левую часть нормированного уравнения этой прямой подставить координаты данной точки и взять модуль полученного результата.
Пример:
Определить расстояние от точки М (-2, 7) до прямой
Решение:
Нормируя уравнение этой прямой, будем иметь
Отсюда искомое расстояние есть
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Приложения производной функции одной переменной
- Обратная матрица – определение и нахождение
- Ранг матрицы – определение и вычисление
- Определители второго и третьего порядков и их свойства
- Метод Гаусса – определение и вычисление