Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.
Уравнение прямой, проходящей через две заданные точки на плоскости
Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.
Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.
Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a, проходящей через две несовпадающие точки M1(x1, y1) и M2(x2, y2), находящиеся в декартовой системе координат.
В каноническом уравнении прямой на плоскости, имеющего вид x-x1ax=y-y1ay, задается прямоугольная система координат Оху с прямой, которая пересекается с ней в точке с координатами M1(x1, y1) с направляющим вектором a→=(ax, ay).
Необходимо составить каноническое уравнение прямой a, которая пройдет через две точки с координатами M1(x1, y1) и M2(x2, y2).
Прямая а имеет направляющий вектор M1M2→ с координатами(x2-x1, y2-y1), так как пересекает точки М1 и М2. Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M1M2→=(x2-x1, y2-y1) и координатами лежащих на них точках M1(x1, y1) и M2(x2, y2). Получим уравнение вида x-x1x2-x1=y-y1y2-y1 или x-x2x2-x1=y-y2y2-y1.
Рассмотрим рисунок, приведенный ниже.
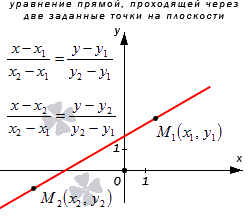
Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M1(x1, y1) и M2(x2, y2). Получим уравнение вида x=x1+(x2-x1)·λy=y1+(y2-y1)·λ или x=x2+(x2-x1)·λy=y2+(y2-y1)·λ.
Рассмотрим подробней на решении нескольких примеров.
Записать уравнение прямой, проходящей через 2 заданные точки с координатами M1-5, 23, M21, -16.
Решение
Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x1, y1 и x2, y2 принимает вид x-x1x2-x1=y-y1y2-y1. По условию задачи имеем, что x1=-5, y1=23, x2=1, y2=-16. Необходимо подставить числовые значения в уравнение x-x1x2-x1=y-y1y2-y1. Отсюда получим, что каноническое уравнение примет вид x-(-5)1-(-5)=y-23-16-23⇔x+56=y-23-56.
Ответ: x+56=y-23-56.
При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.
Составить общее уравнение прямой, проходящей через точки с координатами M1(1, 1) и M2(4, 2) в системе координат Оху.
Решение
Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида x-14-1=y-12-1⇔x-13=y-11.
Приведем каноническое уравнение к искомому виду, тогда получим:
x-13=y-11⇔1·x-1=3·y-1⇔x-3y+2=0
Ответ: x-3y+2=0.
Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y=kx+b. Если необходимо найти значение углового коэффициента k и числа b, при которых уравнение y=kx+b определяет линию в системе Оху, которая проходит через точки M1(x1, y1) и M2(x2, y2), где x1≠x2. Когда x1=x2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М1М2 определена общим неполным уравнением вида x-x1=0.
Потому как точки М1 и М2 находятся на прямой, тогда их координаты удовлетворяют уравнению y1=kx1+bи y2=kx2+b. Следует решить систему уравнений y1=kx1+by2=kx2+b относительно k и b.
Для этого найдем k=y2-y1x2-x1b=y1-y2-y1x2-x1·x1 или k=y2-y1x2-x1b=y2-y2-y1x2-x1·x2.
С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y=y2-y1x2-x1·x+y2-y2-y1x2-x1·x1 или y=y2-y1x2-x1·x+y2-y2-y1x2-x1·x2.
Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.
Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M2(2, 1) и y=kx+b.
Решение
Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y=kx+b. Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M1(-7, -5) и M2(2, 1).
Точки М1 и М2 располагаются на прямой, тогда их координаты должны обращать уравнение y=kx+b верное равенство. Отсюда получаем, что -5=k·(-7)+b и 1=k·2+b. Объединим уравнение в систему -5=k·-7+b1=k·2+bи решим.
При подстановке получаем, что
-5=k·-7+b1=k·2+b⇔b=-5+7k2k+b=1⇔b=-5+7k2k-5+7k=1⇔⇔b=-5+7kk=23⇔b=-5+7·23k=23⇔b=-13k=23
Теперь значения k=23 и b=-13 подвергаются подстановке в уравнение y=kx+b. Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y=23x-13.
Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.
Запишем каноническое уравнение прямой, проходящей через M2(2, 1) и M1(-7, -5), имеющее вид x-(-7)2-(-7)=y-(-5)1-(-5)⇔x+79=y+56.
Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x+79=y+56⇔6·(x+7)=9·(y+5)⇔y=23x-13.
Ответ: y=23x-13.
Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
Если в трехмерном пространстве имеется прямоугольная система координат Охуz с двумя заданными несовпадающими точками с координатами M1(x1, y1, z1) и M2(x2, y2, z2), проходящая через них прямая M1M2, необходимо получить уравнение этой прямой.
Имеем, что канонические уравнения вида x-x1ax=y-y1ay=z-z1az и параметрические вида x=x1+ax·λy=y1+ay·λz=z1+az·λспособны задать линию в системе координат Охуz, проходящую через точки, имеющие координаты (x1, y1, z1) с направляющим вектором a→=(ax, ay, az).
Прямая M1M2 имеет направляющий вектор вида M1M2→=(x2-x1, y2-y1, z2-z1), где прямая проходит через точку M1(x1, y1, z1) и M2(x2, y2, z2), отсюда каноническое уравнение может быть вида x-x1x2-x1=y-y1y2-y1=z-z1z2-z1 или x-x2x2-x1=y-y2y2-y1=z-z2z2-z1, в свою очередь параметрические x=x1+(x2-x1)·λy=y1+(y2-y1)·λz=z1+(z2-z1)·λ или x=x2+(x2-x1)·λy=y2+(y2-y1)·λz=z2+(z2-z1)·λ.
Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.
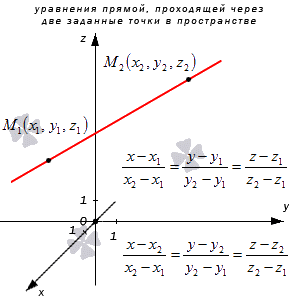
Написать уравнение прямой, определенной в прямоугольной системе координат Охуz трехмерного пространства, проходящей через заданные две точки с координатами M1(2, -3, 0) и M2(1, -3, -5).
Решение
Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x-x1x2-x1=y-y1y2-y1=z-z1z2-z1.
По условию имеем, что x1=2, y1=-3, z1=0, x2=1, y2=-3, z2=-5. Отсюда следует, что необходимые уравнения запишутся таким образом:
x-21-2=y-(-3)-3-(-3)=z-0-5-0⇔x-2-1=y+30=z-5
Ответ: x-2-1=y+30=z-5.
Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.
Прямая – это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Уравнения прямой, проходящей через две точки могут быть следующих видов:
- каноническое уравнение,
- параметрическое уравнение,
- общее уравнение прямой,
- уравнение прямой с угловым коэффициентом,
- уравнение прямой в полярных координатах и другие.
Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.
Каноническое уравнение прямой на плоскости
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
xa и ya – координаты первой точки A,
xb и yb – координаты второй точки B
Параметрическое уравнение прямой на плоскости
{begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases}}
xa, ya – координаты точки, лежащей на прямой,
{l;m} – координаты направляющего вектора прямой,
t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Каноническое уравнение прямой в пространстве
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a} = dfrac{z-z_a}{z_b-z_a}}
xa, ya и za – координаты первой точки A,
xb, yb и zb – координаты второй точки B
Параметрическое уравнение прямой в пространстве
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a \ z=n cdot t + z_a end{cases} }
xa, ya и za – координаты точки, лежащей на прямой,
{l;m;n} – координаты направляющего вектора прямой,
t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Пример нахождения уравнения прямой, проходящей через две точки
Найдем уравнения прямой, проходящей через точки A(1,2) и B(3,8).
Каноническое уравнение прямой
Каноническое уравнение прямой, проходящей через две точки имеет вид {dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
Подставим в формулу координаты точек A и B: {dfrac{x-1}{3-1} = dfrac{y-2}{8-2}}
Получаем каноническое уравнение прямой: {dfrac{x-1}{2} = dfrac{y-2}{4}}
Уравнение прямой с угловым коэффициентом
Из канонического уравнения получаем уравнение прямой с угловым коэффициентом: {y=3x-1}
Параметрическое уравнение прямой
Параметрическое уравнение прямой имеет вид:
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases} }
где {x_a, y_b} – координаты точки, лежащей на прямой, {{l;m}} – координаты направляющего вектора прямой, t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении. В качестве координат используем координаты точки {A(x_a, y_b)}.
Найдем координаты направляющего вектора:
overline{AB} = {x_b – x_a; y_b – y_a} = {3-1; 8-2} = {2; 6}
Получаем параметрическое уравнение:
begin{cases} x=2 t + 1 \ y=6 t + 2 end{cases}
Используем калькулятор для проверки полученного ответа.
Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.
Здесь будет калькулятор
Уравнение прямой с угловым коэффициентом
y=kx+by=kx+b,
где kk — угловой коэффициент, а bb — свободный коэффициент.
Уравнения данного вида составляются следующим образом по формуле:
y−y0=k(x−x0)y-y_0=k(x-x_0),
где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.
Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.
Решение
Подставляем значения в формулу:
y−y0=k(x−x0)y-y_0=k(x-x_0)
y−2=1⋅(x−1)y-2=1cdot(x-1)
Приводим подобные слагаемые:
y=x+1y=x+1
Ответ
y=x+1y=x+1
Общее уравнение прямой
Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:
y−x−1=0y-x-1=0
Уравнение прямой по двум точкам
Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},
где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.
Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).
Решение
x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}
x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}
x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}
x−4=−y−12x-4=frac{-y-1}{2}
y+1=2⋅(4−x)y+1=2cdot(4-x)
y=8−2x−1y=8-2x-1
y=−2x+7y=-2x+7
Ответ
y=−2x+7y=-2x+7
Уравнение прямой при помощи точки и вектора нормали
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.
Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).
Решение
x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,
x−7+40−5y=0x-7+40-5y=0
x−5y=−40+7x-5y=-40+7
x−5y=−33x-5y=-33
5y=x+335y=x+33
y=x5+335y=frac{x}{5}+frac{33}{5}
Проверка
Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.
8=75+3358=frac{7}{5}+frac{33}{5}
8=88=8 — верно, ответ правильный.
Ответ
y=x5+335y=frac{x}{5}+frac{33}{5}
Прямая в пространстве
Уравнение прямой, заданной в пространстве имеет такой вид:
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},
где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.
Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).
Решение
x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Проверка
Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:
1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.
Такой вид уравнения прямой называется каноническим.
Ответ
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Тест по теме “Составление уравнения прямой”
Получить уравнение прямой по двум точкам бывает необходимо, когда мы решаем задачи, связанные с анализом различных фигур на плоскости. В этом случае бывает полезно знать уравнение прямой, проходящей через две точки. Например, составляя такое уравнение мы уже знаем – как проходит прямая, с какие углом наклона к осям координат и можем рассчитать расположение прямой по отношению к другим прямым или к фигурам.
Составляем уравнение прямой по двум точкам
Итак, пусть нам даны две точки и
. Наша прямая проходит через две эти точки, давайте получим уравнение этой прямой. Уравнение пучка прямых, проходящих через точку с координатами
имеет вид:
![]()
То есть если прямая проходит через две точки и
она – одна из этого пучка прямых, проходящих через точку
и эта прямая имеет определенный коэффициент
. Значит, координаты точки
должны удовлетворять уравнению (1), то есть
![]()
.
Находим из (2) :
и подставим в уравнение (1):
![]()
.
Преобразовывая уравнение (3) получим:
Это и есть уравнение прямой, проходящей через две точки
и
.
Примечание: если точки и
лежат на прямой, которая параллельна оси
или оси
, то уравнение прямой будет иметь вид
или
соответственно.
Зная координаты любых двух точек прямой, мы всегда сможем определить угловой коэффициент прямой:
Геометрический вывод уравнения прямой
Действительно, давайте нарисуем прямую в системе координат и отметим на прямой две точки
и
, координаты которых известны
и
и отметим на этой прямой произвольную точку
.

Из подобия треугольников и
находим:
![]()
Из рисунка видно, что:
,
Таким образом, получаем уравнение прямой по двум точкам:
![]()
Задача
Составим уравнение прямой, проходящей через две точки и
.
Решение: Имеем ,
,
,
. Подставим эти значения в уравнение прямой, проходящей через две заданные точки:
![]()
Умножим левую и правую части уравнения на 5, получим:
– получившееся уравнение прямой.
Давайте сделаем проверку – если мы все решили правильно, то при подстановке координат точек и
мы получим верное равенство. Итак, подставим сначала координаты точки
:
Теперь координаты точки :
Значит, уравнение прямой мы нашли верно.
Ответ:
Условие прохождения прямой через три заданные точки
Если нам в задаче нужно убедиться, что три точки с заданными координатами лежат на одной прямой, можно рассуждать так:
- Если две точки с заданными координатами образуют прямую, то их координаты удовлетворяют уравнению прямой, проходящей через две точки.
- Если третья точка также лежит на этой прямой, то и ее координаты будут удовлетворять этому уравнению.
Таким образом, если нам даны три точки ,
и
, лежащие на одной прямой, то их координаты будут удовлетворять условию:
Теперь вы легко сможете составить уравнение прямой по двум точкам, а также найти угловой коэффициент прямой и проверить – принадлежит ли третья точка этой прямой.
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Как найти уравнение прямой по двум точкам?
Уравнение прямой, проходящей через две данные точки, можно получить, подставив координаты имеющихся точек в уравнения, приведённые ниже.
В случае, если прямая рассматривается относительно двух осей $OX$ и $OY$, уравнение прямой, проходящей через 2 точки, будет иметь вид:
$frac{x-x_1}{x_2 – x_1}= frac{y-y_1}{y_2-y_1}left(1right)$, где $(x_1; y_1)$ и $(x_2; y_2)$ — координаты точек.
Рисунок 1. Прямая, проходящая через 2 точки. Автор24 — интернет-биржа студенческих работ
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Выведем его.
$y-y_1=k cdot (x-x_1)$— уравнение прямой, проходящей через одну точку в заданном направлении, $k$ — неизвестный угловой коэффициент.
Подставим в него вторую точку и выразим $k$:
$y_2-y_1=k cdot (x_2-x_1)$
$k=frac{y_2-y_1}{ x_2-x_1}$.
Подставим $k$ в уравнение $(1)$ и получим зависимость прямой от значений двух лежащих на ней точек.
$frac{x-x_1}{x_2 – x_1}= frac{y-y_1}{y_2-y_1}$.
Для случая, когда прямая рассматривается относительно трёх осей $OX, OY$ и $OZ$, уравнение прямой, проходящей через две заданные точки, выглядит так:
$frac{x-x_1}{x_2 – x_1}= frac{y-y_1}{y_2-y_1}=frac{z-z_1}{z_2-z_1}$ — прямая в объёмной системе координат.
Пример 1
Составить уравнение прямой, проходящей через две точки $A$ и $B$ с положениями $(1;2)$ и $(3;4)$ соответственно.
Подставим значения для данных точек в уравнение $(1)$:
$frac{x-1}{3-1}=frac{y-2}{4-2}$
$frac{x-1}{2}=frac{y-2}{2}$
Получено искомое нами уравнение.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 14.03.2023
Похожие материалы по теме
Автор(ы):
Сергей Евгеньевич Грамотинский
Автор(ы):
Автор(ы):
Щебетун Виктор
Автор(ы):
Александр Мельник
Автор(ы):
Щебетун Виктор
Высшая математика
#Лекция
Высшая математика
#Лекция


