Уравнения, в которых неизвестное участвует под знаком корня называется иррациональным.
Содержание:
Рассмотрим методы решения некоторых видов иррациональных уравнений.
Рассмотрим простое иррациональное уравнение вида:

Пусть выражения f(х), g(x) принимают неотрицательные значения. Возводя обе части уравнения в квадрат, получим равносильное уравнение.
Так как 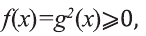
Значит, решение уравнения (1) осуществляется по правилу:
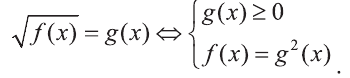
Аналогично уравнение вида 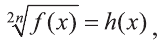 равносильно системе
равносильно системе 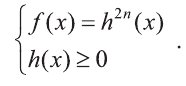
Пример:
Решите уравнение 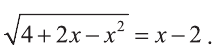
Решение:
Возводя обе части уравнения в квадрат, получим равносильное уравнение 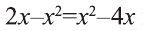 или
или 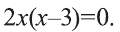 . Отсюда получим корни
. Отсюда получим корни 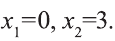 Так как х>2, то х=3 – решение данного уравнение.
Так как х>2, то х=3 – решение данного уравнение.
Уравнения вида 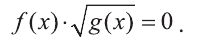
Для того чтобы произведение двух выражений обращалось в нуль, необходимо и достаточно равенство нулю, хотя бы одного из сомножителей.
Значит, для того чтобы 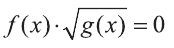 должно выполняться равенство или
должно выполняться равенство или 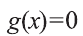 совокупность равенств
совокупность равенств 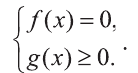
Этот факт мы кратко будем записывать так: 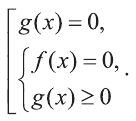
Пример:
Решите уравнение 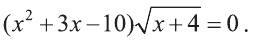
Решение:
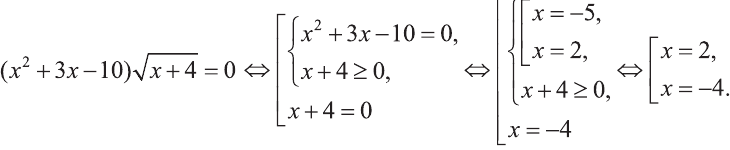
Ответ: 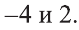
Пример:
Решите уравнение 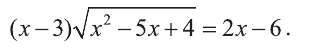
Решение:
Данное уравнение приводится к виду 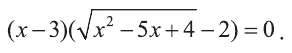 Так как система
Так как система 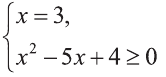 не имеет решении, то достаточно рассмотреть уравнение
не имеет решении, то достаточно рассмотреть уравнение 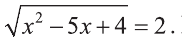 Возведем обе части этого уравнения в квадрат, получим равносильное ему уравнение
Возведем обе части этого уравнения в квадрат, получим равносильное ему уравнение 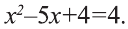
Ответ: 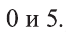
Уравнение вида 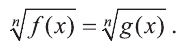
При решении таких уравнений сначала следует учесть четность-нечетность числа n, а затем привести его к равносильному уравнению.
Пусть n нечётно: 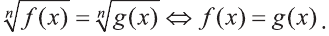
Например, уравнение 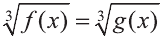 равносильно уравнению
равносильно уравнению 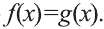
Пример:
Решите уравнение 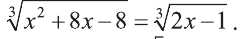
Решение:
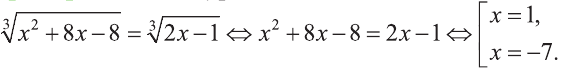
Ответ: 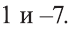
Пусть n четно, то есть n=2к. В этом случае данное уравнение равносильно каждой из систем: 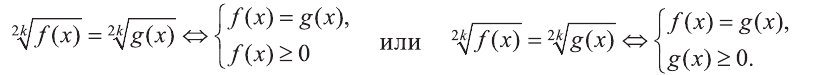
На практике из данных систем выбирается то, которое легче решается.
Пример:
Решите уравнение 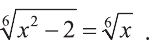
Решение:
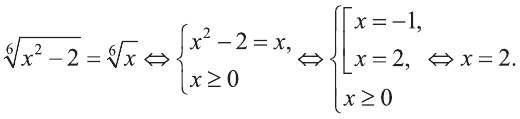
Ответ: 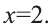
IV Замена переменных.
Пример:
Решите уравнение 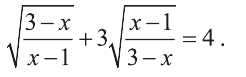
Решение:
Выполним замену 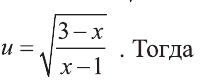
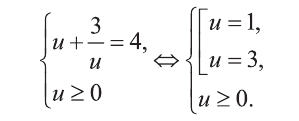
Найдем теперь корни данного уравнения.
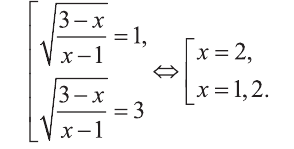
Ответ: х=2 и х=1,2.
Пример:
Решите уравнение 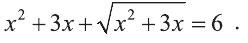
Решение:
Выполним замену 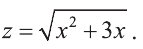 Тогда
Тогда
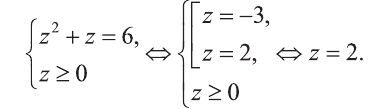
Найдем теперь корни данного уравнения
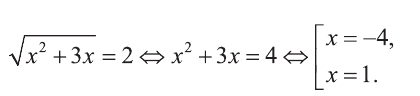
Ответ: х=4 и х=1.
Системы иррациональных уравнений
Решение систем, состоящих из иррациональных уравнений, опирается на известные нам методы сложения, подстановки и т.д. При этом следует учитывать области существования участвующих иррациональных выражений.
Пример:
Решите систему уравнений 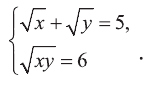
Решение:
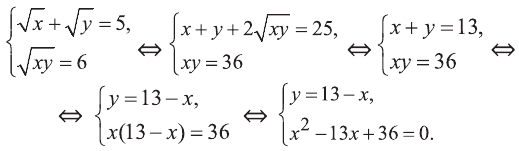
Данная система имеет решения 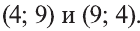
Пример:
Решите систему уравнений 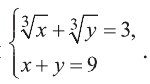
Решение:
Обозначим 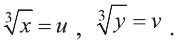 Воспользовавшись формулой сокращенного умножения, получим систему:
Воспользовавшись формулой сокращенного умножения, получим систему: 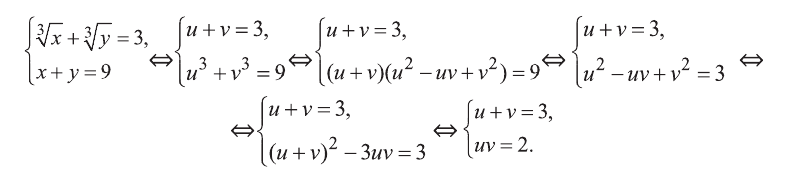
Эта система имеет решения 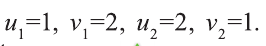 Отсюда получим решения (1; 8) и (8; 1) исходной системы.
Отсюда получим решения (1; 8) и (8; 1) исходной системы.
Пример:
Найдите точку С(х; 0), равноудаленную от точек А(3; 4) и В(-2; 5) плоскости.
Решение:
Из соотношения АС=ВС и формулы расстояния между двумя точками плоскости получим иррациональное уравнение
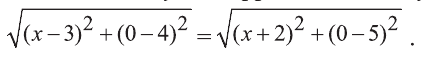
Делая равносильные преобразования, получим уравнение,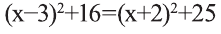 откуда -10х=4. Последнее уравнение имеет корень х=-0,4. Значит, С(-0,4; 0) – искомая точка.
откуда -10х=4. Последнее уравнение имеет корень х=-0,4. Значит, С(-0,4; 0) – искомая точка.
Пример:
Найдите точку на прямой у=3х, равноудаленную от точек А(-1;2) и В(3;—4) плоскости.
Решение:
По условию, ордината и абсцисса искомой точки удовлетворяет соотношению у=3х, поэтому она имеет координаты С(х;3х). Из соотношения АС=ВС и формулы расстояния между двумя точками плоскости получим иррациональное уравнение 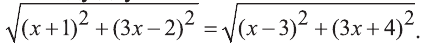 Делая равносильные преобразования, получим уравнение,
Делая равносильные преобразования, получим уравнение,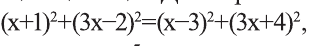 откуда -28х=20. Последнее уравнение имеет корень
откуда -28х=20. Последнее уравнение имеет корень 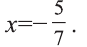
Значит, С(—5/7; -15/7) – искомая точка. Ответ: С(-5/7; -15/7).
Что называется иррациональным уравнением
Уравнение, содержащее переменную под знаком радикала (или в дробной степени) называется иррациональным уравнением.
Примеры: 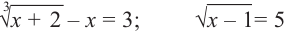
При решении рациональных уравнений, как правило, применяют возведение в степень. При этом необходимо учитывать следующее:
- решение рационального уравнения ищут на множестве действительных чисел;
- для радикала четной степени берутся арифметические корни, для радикала нечетной степени – действительные значения;
- при возведении обеих частей уравнения в нечетную степень получается равносильное уравнение;
- При возведении в четную степень множество допустимых значений переменной нового уравнения может расширяться. Возможно, что некоторые корни нового уравнения могут не удовлетворять иррациональному уравнению. Поэтому при возведении в четную степень надо проверять, удовлетворяют ли полученные значения переменных заданному иррациональному уравнению.
Пример:
Решите уравнение 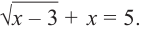
Решение:
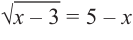 Оставим выражение содержащее радикал в
Оставим выражение содержащее радикал в
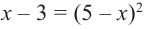 одной стороне уравнения возведем обе части
одной стороне уравнения возведем обе части
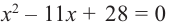 уравнения в квадрат, упростим и решим.
уравнения в квадрат, упростим и решим.
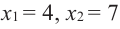
Проверка:
При 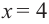 получаем
получаем 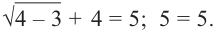
При 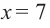 получаем
получаем 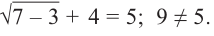
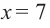 не удовлетворяет уравнению.
не удовлетворяет уравнению.
Ответ: {4}
Отметим, что решить уравнение 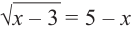 можно, приведя его к равносильной системе
можно, приведя его к равносильной системе 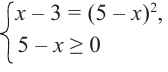
Определение иррационального уравнения
В этой лекции мы будем рассматривать уравнения, содержащие переменную (неизвестное) под знаком корня (радикала). Такие уравнения называют иррациональными.
Напомним на примерах два из возможных подходов к решению иррациональных уравнений.
Вычисление иррациональных уравнений
Первый подход состоит в замене исходного уравнения равносильным ему уравнением (системой или совокупностью уравнений и неравенств). Поскольку все равносильные уравнения имеют одни и те же решения, то при этом подходе проверка полученных значений переменной по условию исходного уравнения не является необходимой частью решения.
Например, при решении иррациональных уравнений часто пользуются следующими утверждениями о равносильности:
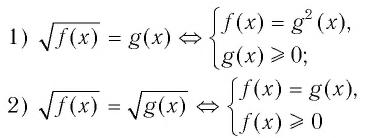
(вместо неравенства 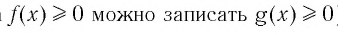 ).
).
Второй подход состоит в замене исходного уравнения его следствием. Поскольку решений в уравнении-следствии (системе или совокупности) может быть больше, чем в исходном уравнении, то необходимой частью процесса решения является проверка полученных значений переменной по условию исходного уравнения.
Переход к следствию из данного уравнения при оформлении записи решения можно обозначать символом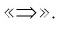
Примеры с решением
Пример №1
Решить уравнение:

Пример №2
Способ 1 (сохранение равносильности).
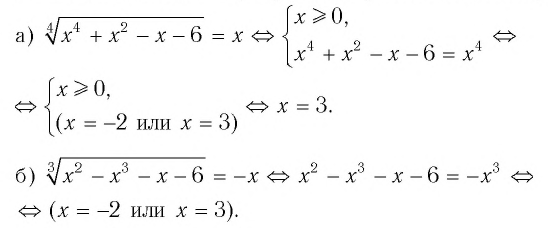
Ответ: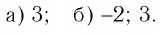
Для уравнения а) покажем решение способом 2 (использование уравнения-следствия):
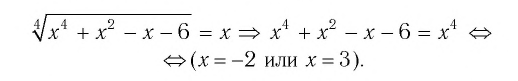
Проверка: при х = -2 получим 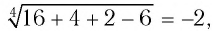 т. е.
т. е.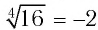 — неверное числовое равенство, значит, число -2 не является корнем уравнения а);
— неверное числовое равенство, значит, число -2 не является корнем уравнения а);
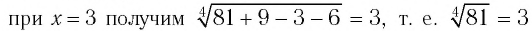 — верное числовое равенство, значит, число 3 — корень уравнения а);
— верное числовое равенство, значит, число 3 — корень уравнения а);
Пример №3
Решить уравнение 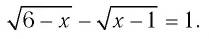
Решение:
Способ 1 (сохранение равносильности).
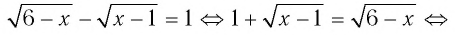
при любых допустимых значениях х обе части уравнения неотрицательны, поэтому, возведя их в квадрат, получим равносильное уравнение
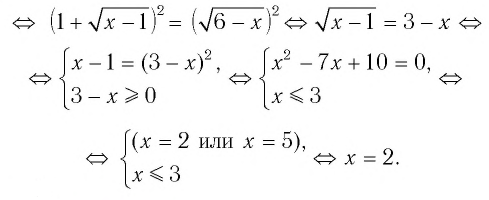
Ответ: 2.
Способ 2 (использование уравнения-следствия).
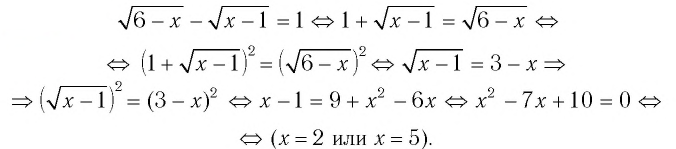
Проверка: х=2 удовлетворяет исходному уравнению, а х=5 не удовлетворяет (убедитесь в этом).
Пример №4
Решить уравнение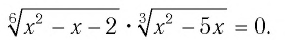
Решение:
Способ 1 (сохранение равносильности).
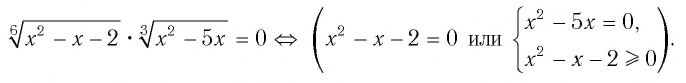
Решив это уравнение и систему, получим 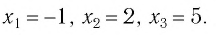
Ответ: -1; 2; 5.
Способ 2 (использование уравнения-следствия).
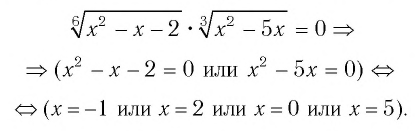
Проверка по условию исходного уравнения показывает, что 0 не является его корнем, так как при х = 0 выражение 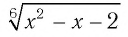 равно
равно 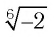 и не имеет смысла. А числа -1; 2; 5 — являются корнями заданного в условии уравнения.
и не имеет смысла. А числа -1; 2; 5 — являются корнями заданного в условии уравнения.
Пример №5
Решить уравнение с неизвестным х:
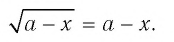
Решение:
Имеем (объясните почему):
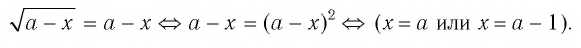
Ответ: при любом значении 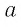 имеем
имеем 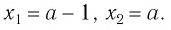
Пример №6
Решить уравнение 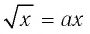 относительно х.
относительно х.
Решение:
Очевидно, что х = 0 — корень уравнения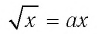 при любом значении а. При х>0 уравнение
при любом значении а. При х>0 уравнение 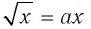 равносильно уравнению
равносильно уравнению 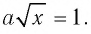 Если
Если 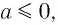 то это уравнение решений не имеет, а если а > 0, то
то это уравнение решений не имеет, а если а > 0, то 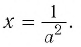
Ответ: 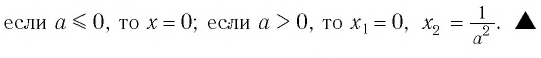
Решение иррациональных уравнений с использованием свойств функций
Уточним определение уравнения с одной переменной, данное в предыдущих классах.
Пусть 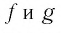 — функции от переменной
— функции от переменной 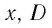 — множество всех значений переменной х, при которых определены обе эти функции. Равенство
— множество всех значений переменной х, при которых определены обе эти функции. Равенство
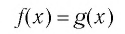
называется уравнением с переменной х, а множество D — областью определения этого уравнения (или областью допустимых значений переменной).
Переменную в уравнении называют также неизвестным. Корнем или решением уравнения 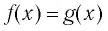 называется такое число
называется такое число 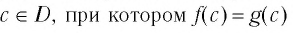 — верное числовое равенство.
— верное числовое равенство.
Теорема:
Уравнение

где 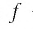 — возрастающая и
— возрастающая и 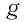 — убывающая функции, определенные на одном и том же множестве, имеет не более одного корня, т. е. либо вообще не имеет корней, либо имеет единственный корень.
— убывающая функции, определенные на одном и том же множестве, имеет не более одного корня, т. е. либо вообще не имеет корней, либо имеет единственный корень.
(Действительно, на рисунке 20, а, б видно, что графики возрастающей функции и убывающей функции
и убывающей функции 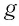 пересекаются на области определения не более чем в одной точке.)
пересекаются на области определения не более чем в одной точке.) 
▲ Доказательство. Пусть  — корень уравнения (1), т. е.
— корень уравнения (1), т. е.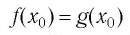 — верное числовое равенство.
— верное числовое равенство.
Если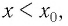 то по определению возрастающей и убывающей функций имеем
то по определению возрастающей и убывающей функций имеем
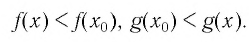
Следовательно,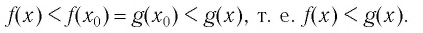
Значит, никакое число 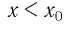 корнем уравнения (1) не является. Аналогично доказывается, что и никакое число
корнем уравнения (1) не является. Аналогично доказывается, что и никакое число 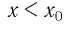 не является корнем уравнения (1).
не является корнем уравнения (1).
Замечание. Эта теорема справедлива и тогда, когда одна функция возрастающая (убывающая), а другая постоянная.
Приведем несколько примеров, где при решении иррациональных уравнений используются свойства возрастания и убывания функций.
Пример №7
Решить уравнение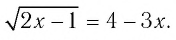
Решение:
Способ 1.
Подбором находим, что 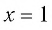 является корнем данного уравнения. Действительно,
является корнем данного уравнения. Действительно, 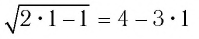 — верное числовое равенство.
— верное числовое равенство.
Так как функция 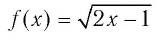 возрастающая, а функция
возрастающая, а функция 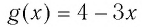 убывающая, то согласно теореме
убывающая, то согласно теореме 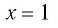 — единственный корень данного уравнения.
— единственный корень данного уравнения.
Ответ: 1.
Способ 2.
Возможно и другое решение:

Так как функция 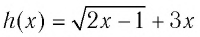 возрастающая, то (см. замечание) уравнение
возрастающая, то (см. замечание) уравнение 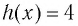 имеет не более одного решения. Подбором находим корень
имеет не более одного решения. Подбором находим корень 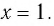
Пример №8
Решить уравнение 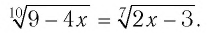
Решение:
Подбором находим, что число 2 — корень данного уравнения, поскольку 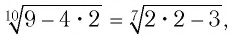 т. е. 1 = 1 — верное числовое равенство. Других корней уравнение не имеет, так как функция
т. е. 1 = 1 — верное числовое равенство. Других корней уравнение не имеет, так как функция 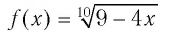 является убывающей, а функция
является убывающей, а функция 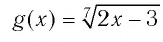 — возрастающей.
— возрастающей.
Ответ: 2.
▲ Иногда при решении иррациональных (и других) уравнений бывает полезно предварительно найти область определения уравнения.
Пример №9
Решить уравнение:
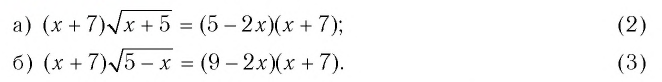
Решение:
а) Значение 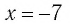 не принадлежит области определения уравнения (2), поскольку при этом значении выражение
не принадлежит области определения уравнения (2), поскольку при этом значении выражение 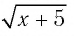 не имеет смысла. Поэтому
не имеет смысла. Поэтому 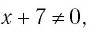 и уравнение (2) равносильно уравнению
и уравнение (2) равносильно уравнению

Решим это уравнение, переходя к уравнению-следствию:
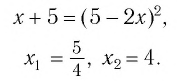
Проверка показывает, что корнем уравнения (4) (а значит, и уравнения (2)) является значение 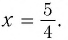
б) Очевидно, что значение 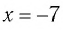 обращает уравнение (3) в верное числовое равенство и принадлежит области определения уравнения (3) — множеству
обращает уравнение (3) в верное числовое равенство и принадлежит области определения уравнения (3) — множеству 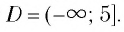 Значит,
Значит, 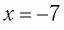 — корень уравнения (3).
— корень уравнения (3).
При 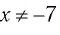 уравнение (3) равносильно уравнению
уравнение (3) равносильно уравнению

Решая это уравнение, получаем:
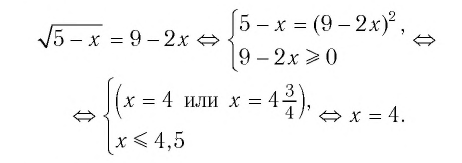
Ответ: 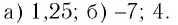
Решение уравнения (3) с помощью знаков равносильности можно записать так:
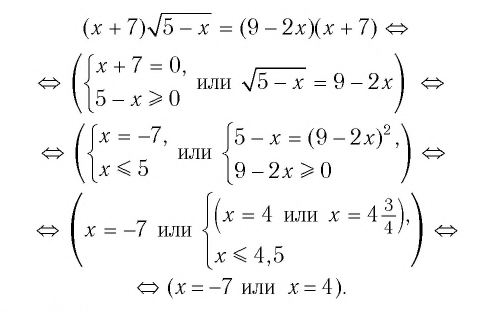
Пример №10
Решить уравнение:
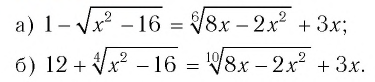
Решение:
а) Поскольку функция 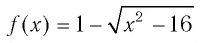 определена для значений
определена для значений 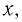 удовлетворяющих неравенству
удовлетворяющих неравенству 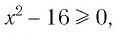 а функция
а функция 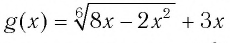 определена для значений
определена для значений 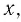 удовлетворяющих неравенству
удовлетворяющих неравенству 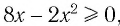 то область определения данного уравнения совпадает со множеством решений системы неравенств
то область определения данного уравнения совпадает со множеством решений системы неравенств
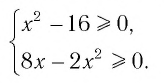
Решая эту систему, получаем равносильную ей систему:
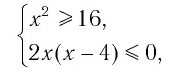
откуда имеем
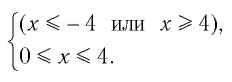
На рисунке 21 видно, что решением этой системы является только значение х = 4. Значит, область определения уравнения состоит из единственного числа 4, т. е. 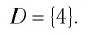
Осталось проверить, является ли число 4 корнем данного уравнения. Подставив 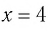 в исходное уравнение, получим
в исходное уравнение, получим
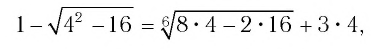
т. е. 1 = 12 — неверное числовое равенство, значит, 4 не является корнем данного уравнения.
б) Решение этого примера аналогично решению примера а). Выполните его самостоятельно.
Ответ: 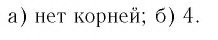
Пример №11
Решить уравнение
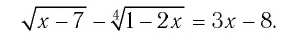
Решение:
Область определения данного уравнения совпадает со множеством решений системы неравенств:
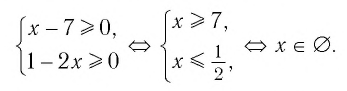 Поскольку система не имеет решений, то область определения не содержит ни одного числа. Значит, данное уравнение не имеет корней.
Поскольку система не имеет решений, то область определения не содержит ни одного числа. Значит, данное уравнение не имеет корней.
Ответ: нет корней.
Иногда при решении уравнений бывает полезно обратить внимание на наибольшее или наименьшее значения входящих в них функций.
Пример №12
Решить уравнение
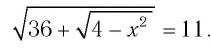
Решение:
Область определения уравнения совпадает со множеством решений неравенства 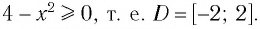
Очевидно, что функция 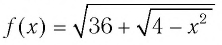 имеет наибольшее значение
имеет наибольшее значение 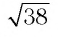 при х = 0. Таким образом, при любых значениях
при х = 0. Таким образом, при любых значениях 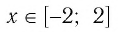 верно неравенство
верно неравенство 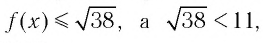 поэтому данное уравнение решений не имеет.
поэтому данное уравнение решений не имеет.
Ответ: нет решений. ▲
Напомним:
Уравнения, содержащие переменную под знаком корня, называются иррациональными.
При решении иррациональных уравнений не всегда удается от данного уравнения перейти к равносильному ему уравнению.
Например, решим уравнение 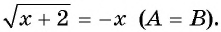
Первый способ.
Возведем обе части уравнения в квадрат, получим уравнение 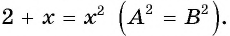 Оно имеет корни
Оно имеет корни 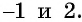 Очевидно, что число 2 не является корнем данного уравнения, так как
Очевидно, что число 2 не является корнем данного уравнения, так как 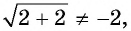 а число
а число 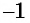 — корень данного уравнения, так как равенство
— корень данного уравнения, так как равенство 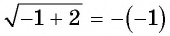 является верным.
является верным.
Посторонний корень уравнения (число 2) появился оттого, что уравнение 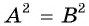 равносильно совокупности уравнений
равносильно совокупности уравнений 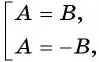 которая может иметь больше решений, чем данное уравнение
которая может иметь больше решений, чем данное уравнение 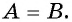 Поэтому после возведения обеих частей уравнения в четную степень без дополнительных условий следует выполнять проверку полученных корней.
Поэтому после возведения обеих частей уравнения в четную степень без дополнительных условий следует выполнять проверку полученных корней.
Второй способ.
Уравнение 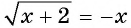 равносильно системе
равносильно системе 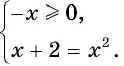 Действительно, обе части уравнения неотрициональны, поэтому при возведении в квадрат получим:
Действительно, обе части уравнения неотрициональны, поэтому при возведении в квадрат получим:
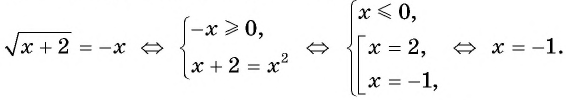
Третий способ.
Запишем уравнение 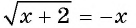 в виде
в виде 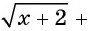
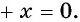 Рассмотрим функцию
Рассмотрим функцию 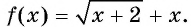 Эта функция возрастает на области определения, значит, данное уравнение не может иметь больше одного корня. Анализируя условие, заметим, что корень должен быть отрицательным и не превосходить по модулю число 2. Корнем данного уравнения является число -1.
Эта функция возрастает на области определения, значит, данное уравнение не может иметь больше одного корня. Анализируя условие, заметим, что корень должен быть отрицательным и не превосходить по модулю число 2. Корнем данного уравнения является число -1.
Рассмотрим некоторые виды иррациональных уравнений и методы их решения.
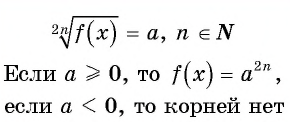
Уравнение вида=2n√f(x), где n∈N
Уравнение вида 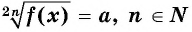
Если 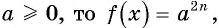 если
если 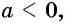 то корней нет.
то корней нет.
Пример №13
Решите уравнение:
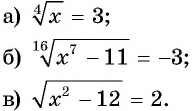
Решение:
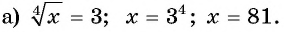
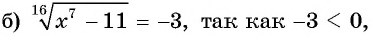 то уравнение не имеет корней.
то уравнение не имеет корней.
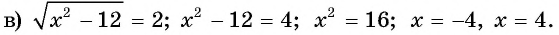
Ответ а) 81; б) нет корней; в) -4; 4.
- Заказать решение задач по высшей математике
Уравнение вида 2n+1√f(x)=a, где n∈N
Уравнение вида 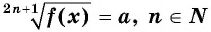
Уравнение 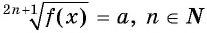 равносильно уравнению
равносильно уравнению 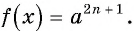
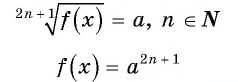
Пример №14
Решите уравнение:
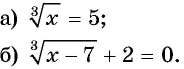
Решение:
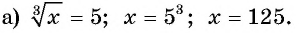
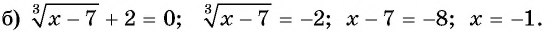
Ответ а) 125; б) -1.
Уравнение вида m√f(x)=g(x), m∈N, m>1
Уравнение вида 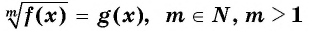
Пусть 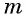 — четное число.
— четное число.
Рассмотрим способы решения уравнения вида 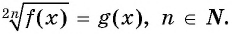
Первый способ.
Данное уравнение равносильно системе
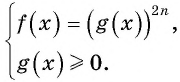
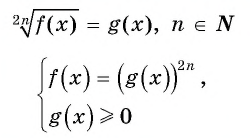
Пример №15
Решите уравнение 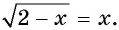
Решение:
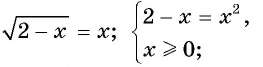
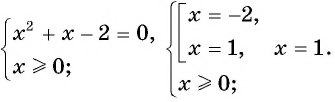 Ответ: 1
Ответ: 1
Второй способ.
Уравнение данного вида можно решить, возведя обе части уравнения в степень 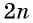 с последующей проверкой корней.
с последующей проверкой корней.
Пример №16
Решите уравнение 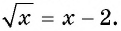
Решение:
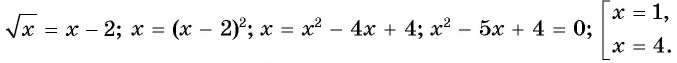
Проверка: при 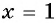 равенство
равенство 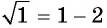 неверное; при
неверное; при 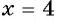 равенство
равенство 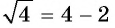 верное. Ответ: 4.
верное. Ответ: 4.
Если 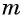 — нечетное число, то уравнение вида
— нечетное число, то уравнение вида 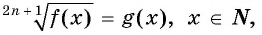 равносильно уравнению
равносильно уравнению 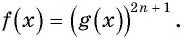
Пример №17
Решите уравнение 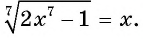
Решение:
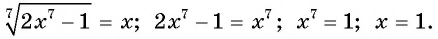
Ответ: 1.
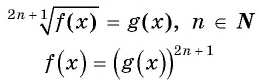
Уравнение вида m√f(x)=m√g(x), m∈N, m>1
Уравнение вида 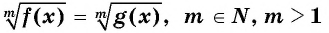
Пусть 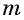 — четное число.
— четное число.
Рассмотрим способы решения уравнения вида 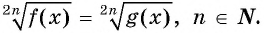
Первый способ.
Данное уравнение равносильно одной из систем
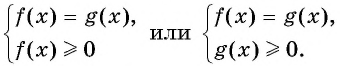
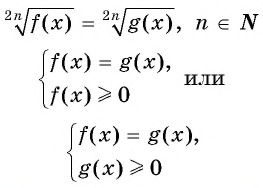
Пример №18
Решите уравнение
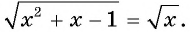
Решение:
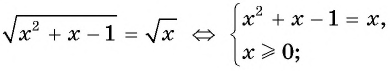
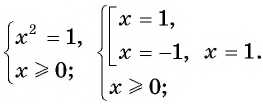
Ответ: 1
Второй способ.
Уравнение этого вида можно решить, возведя обе части уравнения в степень 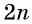 с последующей проверкой корней.
с последующей проверкой корней.
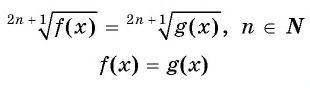
Пример №19
Решите уравнение 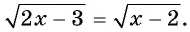
Решение:
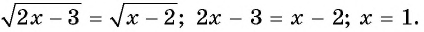
Проверка: при 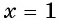 выражения в левой и правой частях равенства
выражения в левой и правой частях равенства 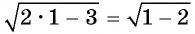 не имеют смысла, т. е. исходное уравнение не имеет корней.
не имеют смысла, т. е. исходное уравнение не имеет корней.
Ответ: нет корней.
Если 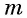 — нечетное число, то уравнение вида
— нечетное число, то уравнение вида 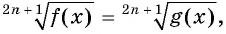
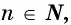 равносильно уравнению
равносильно уравнению 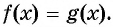
Пример №20
Решите уравнение 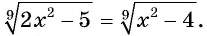
Решение:
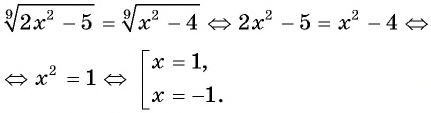
Ответ: -1; 1.
Уравнение вида √f(x)±√g(x)=a
Уравнение вида 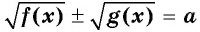
Первый способ.
Уравнение вида 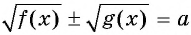 можно решить, возведя обе части уравнения в квадрат дважды с последующей проверкой найденных корней.
можно решить, возведя обе части уравнения в квадрат дважды с последующей проверкой найденных корней.
Пример №21
Решите уравнение 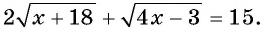
Решение:
Перенесем одно из слагаемых в правую часть, для того чтобы сократить преобразования.
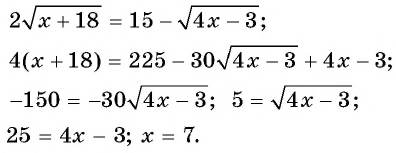
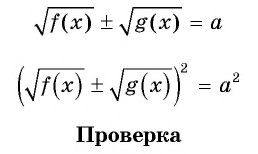
Проверка: 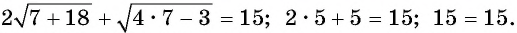 Значит, значение
Значит, значение 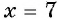 является корнем уравнения.
является корнем уравнения.
Ответ: 7.
Второй способ.
Некоторые уравнения этого вида можно решить, используя свойства функций.
Пример №22
Решите уравнение 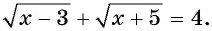
Решение:
Функция 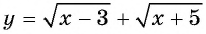 возрастает на всей области определения, поэтому, если данное уравнение имеет корень, то только один.
возрастает на всей области определения, поэтому, если данное уравнение имеет корень, то только один.
При 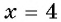 данное уравнение обращается в верное числовое равенство:
данное уравнение обращается в верное числовое равенство: 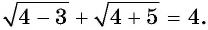 Значит, число 4 является единственным корнем данного уравнения.
Значит, число 4 является единственным корнем данного уравнения.
Ответ: 4.
Метод замены переменной
Пример №23
Решите уравнение 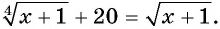
Решение:
Пусть 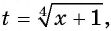 тогда
тогда 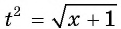 и уравнение принимает вид
и уравнение принимает вид 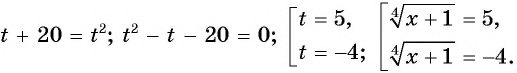 Второе уравнение совокупности не имеет корней.
Второе уравнение совокупности не имеет корней.
Тогда 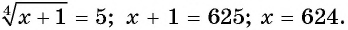
Ответ: 624.
Пример №24
Решите уравнение 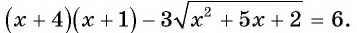
Решение:
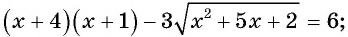
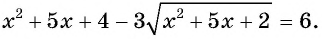
Пусть 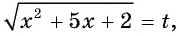 тогда
тогда 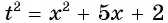 и уравнение принимает вид
и уравнение принимает вид 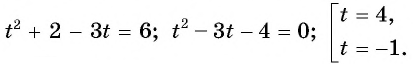 Так как
Так как 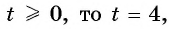 т.е.
т.е.
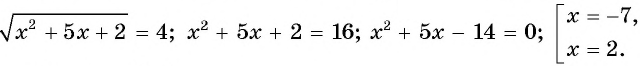
Ответ: -7; 2.
Примеры заданий и их решения
Пример №25
Решите уравнение:
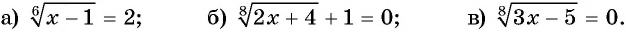
Решение:
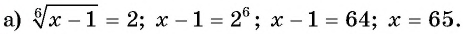
Ответ. 65.
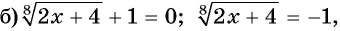 так как
так как 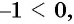 то уравнение не имеет корней.
то уравнение не имеет корней.
Ответ: нет корней.
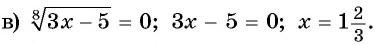
Ответ: 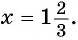
Пример №26
Решите уравнение:
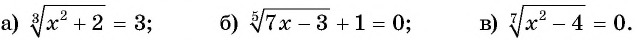
Решение:
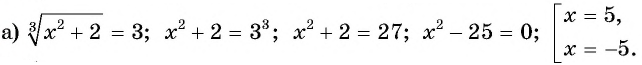
Ответ: -5; 5.
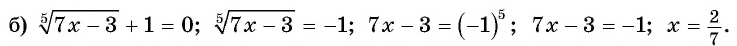
Ответ: 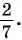
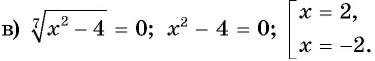
Ответ. -2; 2.
Пример №27
Решите уравнение:
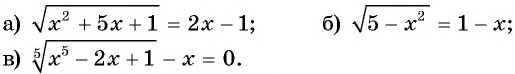
Решение:
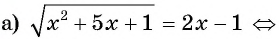
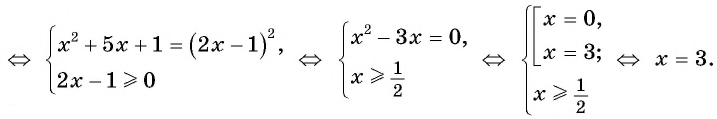
Ответ: 3.
б) Возведем обе части уравнения в квадрат и получим:
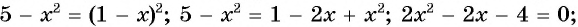
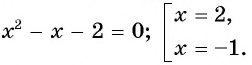
Проверка: при 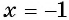 получим:
получим: 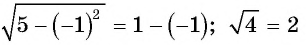 — верное равенство, значит,
— верное равенство, значит, 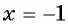 — корень данного уравнения. При
— корень данного уравнения. При 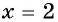 имеем:
имеем: 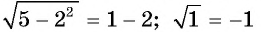 — неверное равенство, значит,
— неверное равенство, значит, 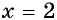 не является корнем данного уравнения.
не является корнем данного уравнения.
Ответ: -1.
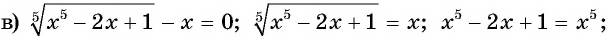
Ответ: 0,5.
Пример №28
Решите уравнение:
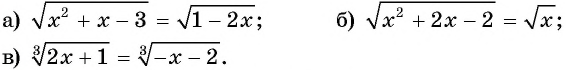
Решение:
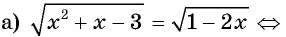
Ответ: -4.
б) Возведем обе части уравнения в квадрат и получим:
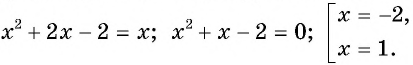
Проверка: при 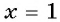 получим:
получим: 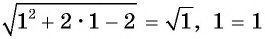 — верно, значит,
— верно, значит, 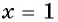 — корень данного уравнения. При
— корень данного уравнения. При 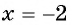 выражение
выражение  не имеет смысла, т. е.
не имеет смысла, т. е.  не является корнем данного уравнения.
не является корнем данного уравнения.
Ответ: 1.
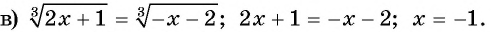
Ответ: -1
Пример №29
Решите уравнение: 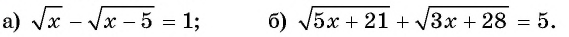
Решение:
а) Запишем уравнение в виде 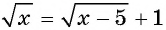 и возведем обе части полученного уравнения в квадрат:
и возведем обе части полученного уравнения в квадрат: 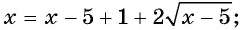
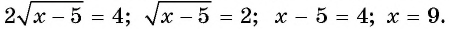 С помощью проверки убедимся, что
С помощью проверки убедимся, что 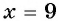 является корнем исходного уравнения.
является корнем исходного уравнения.
Ответ: 9.
б) Функция 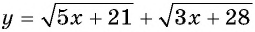 возрастает на всей области определения, поэтому если данное уравнение имеет корень, то только один.
возрастает на всей области определения, поэтому если данное уравнение имеет корень, то только один.
При 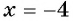 данное уравнение обращается в верное числовое равенство:
данное уравнение обращается в верное числовое равенство: 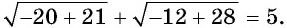 Значит, число
Значит, число 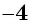 является единственным корнем данного уравнения.
является единственным корнем данного уравнения.
Ответ: 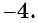
Пример №30
Решите уравнение 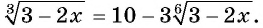
Решение:
Пусть 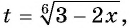 тогда
тогда 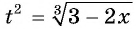 и исходное уравнение принимает вид
и исходное уравнение принимает вид 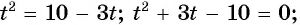
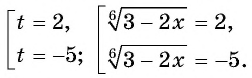
Второе уравнение совокупности не имеет корней. Тогда 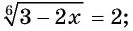
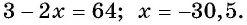
Ответ. 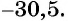
При решении иррациональных уравнений используют прием возведения левой и правой частей уравнения в одну степень.
Теорема 9.
Возведение левой и правой частей уравнения в нечетную натуральную степень дает уравнение, равносильное данному, а возведение в четную степень — уравнение, являющееся следствием данного уравнения.
Доказательство:
Пусть 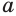 — корень уравнения
— корень уравнения 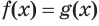 . Тогда истинно числовое равенство
. Тогда истинно числовое равенство 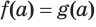 . Возведя его в степень
. Возведя его в степень 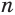 , по соответствующему свойству числовых равенств получим равенство
, по соответствующему свойству числовых равенств получим равенство 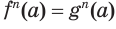 , которое также истинно. А это означает, что число
, которое также истинно. А это означает, что число 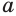 — корень уравнения
— корень уравнения 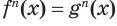 .
.
Поскольку каждый корень уравнения 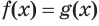 является корнем уравнения
является корнем уравнения 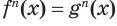 , то из уравнения
, то из уравнения 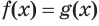 следует уравнение
следует уравнение 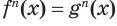 .
.
Пусть 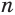 — нечетное натуральное число и
— нечетное натуральное число и 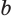 — корень уравнения
— корень уравнения 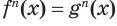 . Тогда истинно числовое равенство
. Тогда истинно числовое равенство 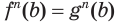 . Извлекая из обеих его частей корень степени
. Извлекая из обеих его частей корень степени 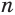 , по соответствующему свойству числовых равенств получим числовое равенство
, по соответствующему свойству числовых равенств получим числовое равенство 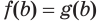 , которое истинно. Значит, число
, которое истинно. Значит, число 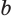 — корень уравнения
— корень уравнения 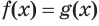 .
.
Поскольку при нечетном натуральном 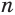 из уравнения
из уравнения 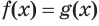 следует уравнение
следует уравнение 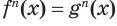 и из уравнения
и из уравнения 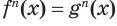 следует уравнение
следует уравнение 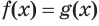 , то эти уравнения равносильны.
, то эти уравнения равносильны.
Пример №31
Решим уравнение 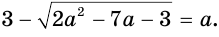
Данное уравнение равносильно уравнению  . Возведем обе его части в квадрат и приведем подобные:
. Возведем обе его части в квадрат и приведем подобные:
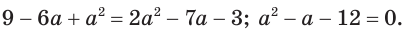
Полученное квадратное уравнение имеет корнями числа -3 и 4. Сделаем проверку. Подставив числа -3 и 4 в данное уравнение, получим числовые равенства
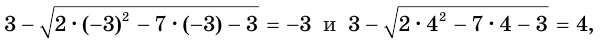
из которых истинно только первое равенство.
Ответ. -3.
Этот пример иллюстрирует ту часть теоремы 9, в которой утверждается, что возведение в четную степень обеих частей уравнения дает уравнение, которое является следствием данного уравнения. Появление постороннего корня 4 связано с тем, что возведением в квадрат к уравнению 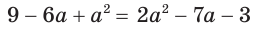 приводит не только данное уравнение, но и уравнение
приводит не только данное уравнение, но и уравнение 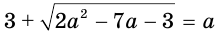 , которое и имеет корнем число 4.
, которое и имеет корнем число 4.
Вообще, при решении уравнений нужно быть внимательным к выполняемым преобразованиям. Полученные в результате решения числа включаются в ответ только в случае, когда все преобразования были преобразованиями равносильности.
Пример №32
Решим уравнение 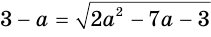 , используя только преобразования равносильности:
, используя только преобразования равносильности:
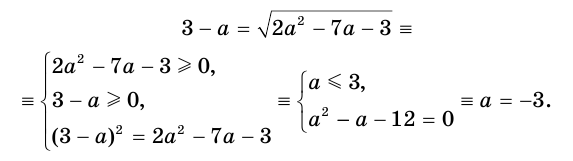
Некоторые иррациональные уравнения могут быть решены приемом введения вспомогательных переменных.
Пример №33
Решим уравнение 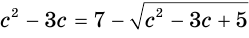 .
.
Обратим внимание на то, что данное уравнение равносильно уравнению 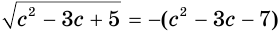 , в котором выражение
, в котором выражение 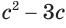 повторяется. Это наводит на мысль, что его или выражение, его содержащее, целесообразно рассматривать в качестве новой переменной. Обозначим через
повторяется. Это наводит на мысль, что его или выражение, его содержащее, целесообразно рассматривать в качестве новой переменной. Обозначим через 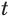 , например, выражение
, например, выражение 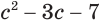 , т. е.
, т. е.
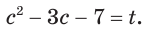
Тогда 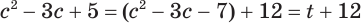 .
.
Это позволяет данное уравнение заменить уравнением 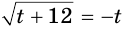 . Решим его:
. Решим его:
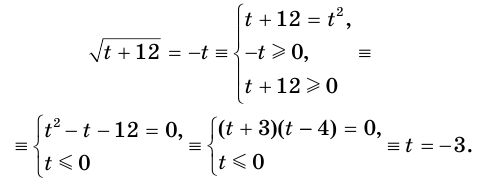
Вернемся к исходной переменной:
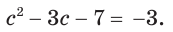
Полученное уравнение имеет корнями числа -1 и 4. Они и являются корнями исходного уравнения.
Ответ. -1; 4.
Иногда бывает удобно ввести две вспомогательные переменные.
Пример:
Решим уравнение 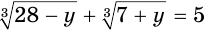 .
.
Обозначим 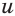 и
и 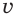 первый и второй радикалы соответственно:
первый и второй радикалы соответственно:
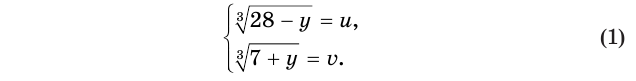
Тогда данное уравнение запишется как
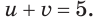
Из системы (1) получим еще одно уравнение, связывающее переменные 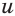 и
и 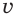 :
:
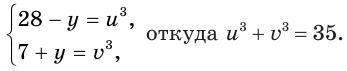
Таким образом, для нахождения значений переменных 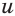 и
и 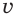 получилась система
получилась система 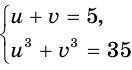 , которая решается так:
, которая решается так:
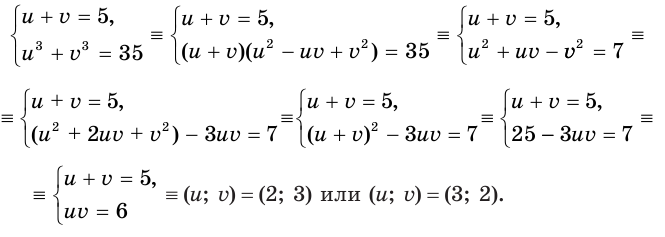
Теперь, чтобы найти значения исходной переменной, достаточно решить любое из уравнений системы (1).
Для 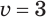 , а затем для
, а затем для 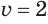 получим соответственно:
получим соответственно:
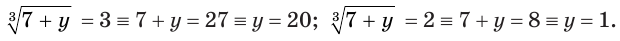
Анализ выполненных преобразований показывает, что все они являются преобразованиями равносильности. Поэтому оба полученных значения переменной 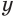 являются корнями данного уравнения.
являются корнями данного уравнения.
Ответ. 1; 20.
Пример №34
Решим систему уравнений
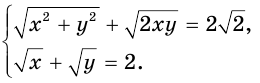
Обозначим 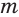 и
и 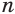 соответственно сумму и произведение радикалов
соответственно сумму и произведение радикалов 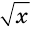 и
и 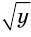 :
:
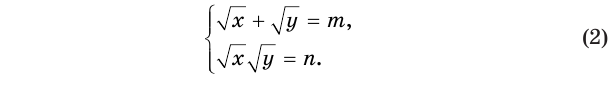
Выразим 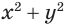 через
через 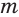 и
и 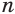 . Получим:
. Получим:
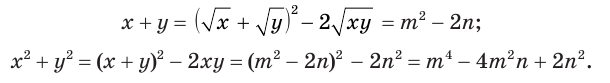
С учетом этого исходная система запишется так:
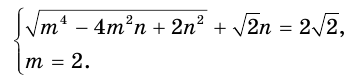
Поскольку 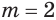 , то первое уравнение системы приводится к уравнению
, то первое уравнение системы приводится к уравнению 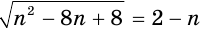 , решив которое, получим
, решив которое, получим 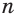 = 1.
= 1.
Учитывая, что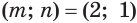 , из системы (2) находим, что
, из системы (2) находим, что 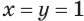 .
.
Ответ. (1; 1).
Иногда при решении системы бывает полезна тригонометрическая подстановка.
Пример №35
Решим систему уравнений 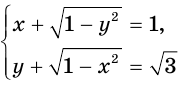 .
.
Обратим внимание на то, что модули переменных 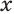 и
и  не превышают 1. Поэтому можно ввести вспомогательные переменные
не превышают 1. Поэтому можно ввести вспомогательные переменные  и
и  :
:
Выразим через них исходную систему и найдем ее решения:
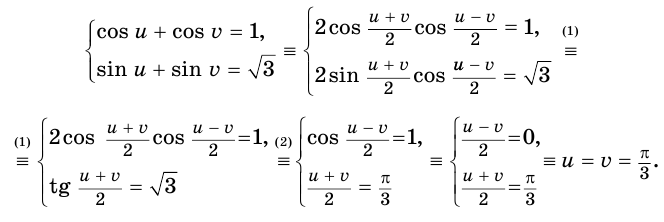
При переходе (1) мы покомпонентно второе уравнение разделили на первое, при переходе (2) учли то, что поскольку 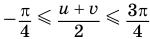 , то уравнение
, то уравнение 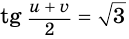 имеет корнем число
имеет корнем число 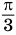 , но
, но 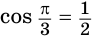 , поэтому первое уравнение записывается в виде
, поэтому первое уравнение записывается в виде 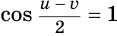 .
.
Вернувшись к исходным переменным, получим, что 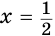 и
и 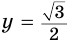 .
.
Ответ. 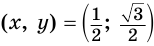 .
.
- Иррациональные неравенства
- Производная в математике
- Как найти производную функции
- Асимптоты графика функции
- Формулы двойного аргумента
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Свойства и график функции y=ⁿ√x (n>1, n∈N)
Алгебра
План урока:
Целое уравнение и его степень
Ранее мы уже изучали понятие целого выражения. Так называют любое выражение с переменной, в котором могут использоваться любые арифметические операции, а также возведение в степень. Однако есть важное ограничение – в целом выражении переменная НЕ может находиться в знаменателе какой-нибудь дроби или быть частью делителя. Также переменная не может находиться под знаком корня. Для наглядности приведем примеры целых выражений:
(n 3 + 7)/5 (в знаменателе находится только число, без переменной);
А вот примеры нецелых выражений:
Отличительной особенностью целых выражений является то, что в них переменная может принимать любое значение. В нецелых же выражениях возникают ограничения на значения переменной, ведь знаменатель дроби не должен равняться нулю, в выражение под знаком корня не должно быть отрицательным.
Введем понятие целого уравнения.
Приведем примеры целых ур-ний:
0,75х 7 + 0,53х 6 – 45х = 18
Напомним, что в математике существует понятие равносильных уравнений.
Когда мы решаем ур-ния, мы в каждой новой строчке записываем ур-ние, равносильное предыдущему. Для этого используются равносильные преобразования (перенос слагаемых через знак «=» с противоположным знаком, деление обоих частей равенства на одинаковые числа и т. д.).
Можно доказать (мы этого делать не будем), что любое целое ур-ние можно возможно преобразовать так, чтобы получилось иное, равносильное ему ур-ние, где в левой части будет находиться многочлен, а справа – ноль. Для этого надо лишь раскрыть скобки и умножить ур-ние на какое-нибудь число, чтобы избавиться от дробей.
Пример. Преобразуйте целое ур-ние
так, чтобы слева стоял многочлен, а справа – ноль.
Решение. В ур-нии есть дроби со знаменателями 5 и 4. Если умножить обе части на 20 (это наименьшее общее кратное чисел 5 и 4), то дроби исчезнут:
Теперь раскроем скобки:
4(5х 3 – 3х 4 + 45х – 27х 2 ) – 40 = 10х 2 + 5х + 35
20х 3 – 12х 4 + 180х – 108х 2 – 40 = 10х 2 + 5х + 35
Осталось перенести все слагаемые влево и привести подобные слагаемые:
20х 3 – 12х 4 + 180х – 108х 2 – 40 – 10х 2 – 5х – 35 = 0
– 12х 4 + 20х 3 – 118х 2 + 175х – 75 = 0
Получили ур-ние в той форме, которую и надо было найти по условию.
Ответ:– 12х 4 + 20х 3 – 118х 2 + 175х – 75 = 0
В математике любой полином можно обозначить как Р(х). Если ур-ние привели к тому виду, когда в одной части многочлен, а в другой ноль, то говорят, что получили ур-ние вида Р(х) = 0.
Получается, что решение целого уравнения всегда можно свести к решению равносильного ему ур-ния Р(х) = 0. Именно поэтому многочлены играют такую большую роль в математике
Напомним, что степенью многочлена называется максимальная степень входящего в его состав одночлена. Это же число является и степенью целого уравнения Р(х) = 0, а также степенью любого равносильного ему целого ур-ния.
Пример. Определите степень ур-ния
(х 3 – 5)(2х + 7) = 2х 4 + 9
Решение. Приведем ур-ние к виду Р(х) = 0. Для этого раскроем скобки:
(х 3 – 5)(2х + 7) = 2х 4 + 9
2х 4 + 7х 3 – 10х – 35 = 2х 4 + 9
Перенесем все слагаемые влево и приведем подобные слагаемые:
2х 4 + 7х 3 – 10х – 35 – 2х 4 – 9 = 0
7х 3 – 10х – 44 = 0
Получили в левой части многочлен 3-ей степени. Следовательно, и исходное ур-ние имело такую же степень
Приведем примеры ур-ний первой степени:
5,4568у + 0,0002145 = 0
Все они являются линейными ур-ниями, метод их решения изучался ранее. Они имеют 1 корень.
Приведем примеры ур-ний второй степени:
6t 2 + 98t – 52 = 0
Это квадратные ур-ния. У них не более двух действительных корней. Для их нахождения в общем случае надо вычислить дискриминант и использовать формулу
Квадратные и линейные ур-ния умели решать ещё в Древнем Вавилоне 4 тысячи лет назад! А вот с ур-ния 3-ей степени (их ещё называют кубическими уравнениями) оказались значительно сложнее. Приведем их примеры:
2х 3 + 4х 2 – 19х + 17 = 0
Лишь в 1545 году итальянец Джералимо Кардано опубликовал книгу, в которой описывался общий алгоритм решения кубических ур-ний. Он достаточно сложный и не входит в школьный курс математики. Его ученик, Лодовико Феррари, предложил метод решения ур-ний четвертой степени. В качестве примера такого ур-ния можно привести:
5х 4 + 6х 3 – 2х 2 – 10х + 1 = 0
Лишь в XIX веке было доказано, что для ур-ний более высоких степеней (5-ой, 6-ой и т. д.) не существует универсальных формул, с помощью которых можно было бы найти их корни.
Отметим, что если степень целого ур-ния равна n, то у него не более n корней (но их число может быть и меньше). Так, количество корней кубического уравнения не превышает трех, а у ур-ния 4-ой степени их не более 4.
Чтобы доказать это утверждение, сначала покажем способ составления уравнения Р(х) = 0, имеющего заранее заданные корни. Пусть требуется составить ур-ние, имеющее корни k1, k2,k3,…kn. Приравняем к нулю следующее произведение скобок:
Составленное ур-ние имеет все требуемые корни и никаких других корней. Действительно, произведение множителей может равняться нулю только в случае, если хотя бы один из множителей нулевой. Поэтому для решения ур-ния
надо каждую скобку приравнять к нулю:
х – k1 = 0 или х – k2 = 0 или х – k3 = 0 или…х – kn = 0
Перенесем второе слагаемое вправо в каждом равенстве и получим:
Чтобы вместо произведения скобок слева стоял многочлен, надо просто раскрыть скобки.
Пример. Составьте уравнение в виде Р(х) = 0, имеющее корни 1, 2, 3 и 4.
Запишем целое ур-ние, имеющее требуемые корни:
(х – 1)(х – 2)(х – 3)(х – 4) = 0
Будем поочередно раскрывать скобки, умножая 1-ую скобку на 2-ую, полученный результат на 3-ю и т.д.:
(х 2 – 3х + 2)(х – 3)(х – 4) = 0
(х 3 – 6х 2 + 11х – 6)(х – 4) = 0
х 4 – 10х 3 + 35х 2 – 50х +24 = 0
Получили ур-ние вида Р(х) = 0. Для проверки вычислений можно подставить в него числа 1, 2, 3 и 4 и убедиться, что они обращают ур-ние в верное равенство.
Ответ: х 4 – 10х 3 + 35х 2 – 50х +24 = 0
Заметим, что в рассмотренном примере, когда мы перемножали многочлены, мы получали новый полином, чья степень увеличивалась на единицу. Мы перемножили 4 скобки (х – k1), а потому получили полином 4 степени. Если бы мы перемножали, скажем, 10 таких скобок, то и многочлен бы получился 10-ой степени. Именно поэтому ур-ние n-ой степени не более n корней.
Действительно, предположим, что какое-то ур-ние n-ой степени имеет хотя бы (n + 1) корень. Обозначим эти корни как k1, k2,k3,…kn, kn+1 и запишем уравнение:
Оно, по определению, равносильно исходному ур-нию, ведь оно имеет тот же набор корней. Слева записаны (n + 1) скобок, поэтому при их раскрытии мы получим полином степени (n + 1). Значит, и исходное ур-ние на самом деле имеет степень n + 1, а не n. Получили противоречие, которое означает, что на самом деле у уравнения n-ой степени не более n корней.
Особо акцентируем внимание на том факте, что если корнями уравнения являются некоторые числа k1, k2,k3,…kn, то этому ур-нию равносильна запись (х – k1)(х – k2)(х – k3)…(х – kn) = 0
Этот факт будет использован далее при решении ур-ний.
Решение уравнений методом подбора корня
Необязательно преобразовывать ур-ние, чтобы найти его корни. Одним из приемов решения целых уравнений является метод подбора корня. Ведь если надо доказать, что какое-то число – это корень ур-ния, достаточно просто подставить это число в ур-ние и получить справедливое равенство!
Пример. Докажите, что корнями ур-ния
х 3 – 2х 2 – х + 2 = 0
являются только числа (– 1), 1 и 2.
Решение. Подставим в ур-ние каждую из предполагаемых корней и получим справедливое равенство. При х = – 1 имеем:
(– 1) 3 – 2(– 1) 2 – (– 1) + 2 = 0
При х = 1 получаем:
1 3 – 2•1 2 – 1 + 2 = 0
Наконец, рассмотрим случай, когда х = 2
2 3 – 2•2 2 – 2 + 2 = 0
Исходное ур-ние имеет 3-ю степень, поэтому у него не более 3 корней. То есть других корней, кроме (– 1), 1 и 2 , у него нет.
Конечно, просто так подобрать корни довольно тяжело. Однако есть некоторые правила, которые помогают в этом. Для начала введем понятие коэффициентов уравнения.
Понятно, что ур-ние Р(х) = 0 в общем виде можно записать так:
Числа а0, а1, а2,…аnи называют коэффициентами уравнений.
Например, для уравнения
5х 4 – 7х 3 + 9х 2 – х + 12 = 0
Если одна из слагаемых «пропущено» в уравнении, то считают, что коэффициент перед ним равен нулю. Например, в ур-нии
нет слагаемого с буквенной частью х 2 . Можно считать, что ур-ние равносильно записи
х 3 + 0х 2 + 2х – 15 = 0
где слагаемое х 2 есть, но перед ним стоит ноль. Тогда коэффициент а1 = 0.
Для обозначения первого коэффициента а0 может использоваться термин старший коэффициент, а для последнего коэффициента аn – термин «свободный член» или «свободный коэффициент».
Изучение коэффициентов ур-ния помогает быстрее подобрать корень. Существует следующая теорема:
Докажем это утверждение. Пусть m – это целый корень уравнения с целыми коэффициентами
Тогда можно подставить туда число m и получить верное равенство:
Поделим обе его части на m и получим
Справа – целое число (ноль), значит, и сумма чисел слева также целая. Все числа а0m n –1 , a1m n –2 , аn–1, очевидно, целые (так как и целыми являются и m, и все коэффициенты). Значит, и число аn/m должно быть целым. Но это возможно лишь в том случае, если m является делителем числа аn.
Из доказанной теоремы следует, что при подборе корней ур-ния достаточно рассматривать только те из них, которые являются делителями свободного члена. При этом следует учитывать и отрицательные делители.
Пример. Найдите целые корни уравнения
2х 4 – х 3 – 9х 2 + 4х + 4 = 0
Решение. Все коэффициенты ур-ния – целые, а потому целый корень должен быть делителем свободного члена, то есть числа 4. Делителями четверки являются 1 и (– 1), 2 и (– 2), 4 и (– 4). Подставляя каждое из этих чисел в ур-ние, получим верные равенства только для чисел 1, 2 и (– 2):
2•1 4 – 1 3 – 9•1 2 + 4•1 + 4 = 2 – 1 – 9 + 4 + 4 = 0
2•2 4 – 2 3 – 9•2 2 + 4•2 + 4 = 32 – 8 – 36 + 8 + 4 = 0
2•(– 2) 4 – (– 2) 3 – 9•(– 2) 2 + 4(– 2) + 4 = 32 + 8 – 36 – 8 + 4 = 0
Таким образом, только эти числа и могут быть целыми корнями ур-ния. Так как мы рассматриваем ур-ние 4 степени, то, возможно, у него помимо 3 целых корней есть ещё один дробный.
Пример. Решите ур-ние
0,5х 3 + 0,5х + 5 = 0
Решение. У ур-ния дробные коэффициенты. Умножим обе части равенства на 2 и получим ур-ние с целыми коэффициентами:
0,5х 3 + 0,5х + 5 = 0
(0,5х 3 + 0,5х + 5)•2 = 0•2
Попытаемся подобрать целый корень ур-ния. Он должен быть делителем свободного члена, то есть десятки. Возможными кандидатами являются числа 1 и (– 1), 2 и (– 2), 5 и (– 5), 10 и (– 10). Подходит только корень х = – 2:
(– 2) 3 + (– 2) + 10 = – 8 – 2 + 10 = 0
Обратим внимание, что в левой части ур-ния стоит сумма функций, возрастающих на всей числовой прямой: у = х 3 и у = х + 10. Значит, и вся левая часть х 3 + х + 10 монотонно возрастает. Это значит, что у ур-ния есть только один корень, и мы его нашли ранее подбором.
Ещё быстрее можно узнать, является ли единица корнем уравнения.
Докажем это. Подставим в ур-ние
значение х = 1. Так как единица в любой степени равна самой единице, то получим:
Получили равенство, в котором слева стоит сумма коэффициентов, в справа – ноль. Если сумма коэффициентов действительно равна нулю, то равенство верное, а, значит, единица является корнем ур-ния.
Пример. Укажите хотя бы 1 корень ур-ния
499х 10 – 9990х 7 + 501х 6 – 10х 5 + 10000х 4 – 1000 = 0
Решение. Заметим, что при сложении коэффициентов ур-ния получается 0:
499 – 9990 + 501 – 10 + 10000 – 1000 = (499 + 501 – 1000) + (10000 – 9990 – 10) = 0 + 0 = 0
Следовательно, единица является его корнем.
Решение уравнений с помощью разложения многочлена на множители
Если в уравнении вида P(x) = 0в левой части удается выполнить разложение многочлена на множители, то дальше каждый из множителей можно отдельно приравнять к нулю.
Пример. Решите ур-ние
Решение. Степень х 4 можно представить как (х 2 ) 2 , а 16 – как 4 2 . Получается, что слева стоит разность квадратов, которую можно разложить на множители по известной формуле:
(х 2 – 4)(х 2 + 4) = 0
Приравняем каждую скобку к нулю и получим два квадратных ур-ния:
х 2 – 4 = 0 или х 2 + 4 = 0
х 2 = 4 или х 2 = – 4
Первое ур-ние имеет два противоположных корня: 2 и (– 2). Второе ур-ние корней не имеет.
Предположим, что у ур-ния 3-ей степени есть 3 корня, и подбором мы нашли один из них. Как найти оставшиеся корни? Здесь помогает процедура, известная как «деление многочленов в столбик». Продемонстрируем ее на примере. Пусть надо решить ур-ние
100х 3 – 210х 2 + 134х – 24 = 0
Можно заметить, сумма всех коэффициентов ур-ния равна нулю:
100 – 210 + 134 – 24 = 0
Следовательно, первый корень – это 1.
Предположим, что у исходного ур-нияР(х) = 0 есть 3 корня, k1, k2и k3. Тогда ему равносильно другое ур-ние
Мы нашли, что первый корень k1 = 1, то есть
Обозначим как P1(x) = 0 ещё одно ур-ние, корнями которого будут только числа k2 и k3. Очевидно, что корнями ур-ния
Будут числа 1, k2 и k3. Его корни совпадают с корнями исходного ур-ния, а потому запишем
(х – 1)•P1(x) = 100х 3 – 210х 2 + 134х – 24
Поделим обе части на (х – 1):
Итак, если «поделить» исходное ур-ние на х – 1, то получим какой-то многочлен Р1(х), причем решением уравнения P1(x) = 0 будут оставшиеся два корня, k2и k3. Деление можно выполнить в столбик. Для этого сначала запишем «делимое» и «делитель», как и при делении чисел:
Смотрим на первое слагаемое делимого. Это 100х 3 . На какой одночлен нужно умножить делитель (х – 1), чтобы получился полином со слагаемым 100х 3 ? Это 100х 2 . Действительно, (х – 1)100х 2 = 100х 3 – 100х 2 . Запишем слагаемое 100х 2 в результат деления, а результат его умножения на делитель, то есть 100х 3 – 100х 2 , вычтем из делимого:
Теперь вычтем из делимого то выражение, которое мы записали под ним. Слагаемые 100х 3 , естественно, сократятся:
(100х 3 – 210х 2 ) – (100х 3 – 100х 2 ) = 100х 3 – 210х 2 – 100х 3 + 100х 2 = – 110х 2
Далее снесем слагаемое 134х вниз:
На какое слагаемое нужно умножить (х – 1), что получился полином со слагаемым (– 110х 2 ). Очевидно, на (– 110х):
(х – 1)(– 110х 2 ) = –110х 2 + 110х
Запишем в поле «ответа» слагаемое (– 110х 2 ), а под делимый многочлен – результат его умножения на (х – 1):
При вычитании из (–110х 2 + 134х) полинома (–110х 2 + 110х) остается 24х. Далее сносим последнее слагаемое делимого многочлена вниз:
Выражение х – 1 нужно умножить на 24, чтобы получить 24х – 24. Запишем в поле «ответа» число 24, а в столбике произведение 24(х –1) = 24х – 24:
В результате в остатке получился ноль. Значит, всё сделано правильно. С помощью деления столбиком мы смогли разложить полином 100х 3 – 210х 2 + 134х – 24 на множители:
100х 3 – 210х 2 + 134х – 24 = (х – 1)(100х 2 – 110х + 24)
Теперь перепишем исходное ур-ние с учетом этого разложения:
100х 3 – 210х 2 + 134х – 24 = 0
(х – 1)(100х 2 – 110х + 24) = 0
Теперь каждую отдельную скобку можно приравнять нулю. Получим ур-ние х – 1 = 0, корень которого, равный единице, мы уже нашли подбором. Приравняв к нулю вторую скобку, получим квадратное ур-ние:
100х 2 – 110х + 24 = 0
D =b 2 – 4ас = (– 110) 2 – 4•100•24 = 12100 – 9600 = 2500
Итак, мы нашли три корня ур-ния: 1; 0,3 и 0,8.
В данном случае мы воспользовались следующим правилом:
Пример. Решите уравнение
2х 3 – 8х 2 + 16 = 0
Решение. Все коэффициенты целые, а потому, если у уравнения есть целый корень, то он должен быть делителем 16. Перечислим эти делители: 1, – 1, 2, – 2, 4, – 4, 8, – 8, 16, – 16. Из всех них подходит только двойка:
2•2 3 – 8•2 2 + 16 = 16 – 32 + 16 = 0
Итак, первый корень равен 2. Это значит, что исходный многочлен можно разложить на множители, один из которых – это (х – 2). Второй множитель найдем делением в столбик. Так как в многочлене 2х 3 – 8х 2 + 16 нет слагаемого с буквенной часть х, то искусственно добавим её:
2х 3 – 8х 2 + 16 = 2х 3 – 8х 2 + 0х + 16
Теперь возможно деление:
Получили, что 2х 3 – 8х 2 + 16 = (х – 2)(2х – 4х – 8)
С учетом этого перепишем исходное ур-ние:
2х 3 – 8х 2 + 16 = 0
(х – 2)(2х – 4х – 8) = 0
х – 2 = 0 или 2х – 4х – 8 = 0
Решим квадратное ур-ние
D =b 2 – 4ас = (– 4) 2 – 4•2•(– 8) = 16 + 64 = 80
В 8 классе мы узнали, что если у квадратного ур-ния ах 2 + bx + c = 0 есть два корня, то многочлен ах 2 + bx + c можно разложить на множители по формуле
где k1 и k2– корни квадратного ур-ния. Оказывается, такое же действие можно выполнять с многочленами и более высоких степеней. В частности, если у кубического ур-ния есть 3 корня k1, k2 и k3, то его можно разложить на множители по формуле
Пример. Разложите на множители многочлен 2х 3 – 4х 2 – 2х + 4.
Решение. Целые корни этого многочлена (если они есть), должны быть делителем четверки. Из всех таких делителей подходят три: 1, (– 1) и 2:
2•1 3 – 4•1 2 – 2•1 + 4 = 2 – 4 – 2 + 4 = 0
2•(– 1) 3 – 4•(– 1) 2 – 2•(– 1) + 4 = – 2 – 4 + 2 + 4 = 0
2•2 3 – 4•2 2 – 2•2 + 4 = 16 – 16 – 4 + 4 = 0
Значит, многочлен можно разложить на множители:
2х 3 – 4х 2 – 2х + 4 = 2(х + 1)(х – 1)(х – 2)
Возникает вопрос – почему перед скобками нужна двойка? Попробуем сначала перемножить скобки без ее использования:
(х + 1)(х – 1)(х – 2) = (х 2 – 1)(х – 2) = х 3 – 2х 2 – х + 2
Получили не тот многочлен, который стоит в условии. Однако ур-ние
х 3 – 2х 2 – х + 2 = 0
имеет те же корни (1, 2 и (– 1)), что и ур-ние
2х 3 – 4х 2 – 2х + 4 = 0
Дело в том, что это равносильные ур-ния, причем второе получено умножением первого на два:
2•(х 3 – 2х 2 – х + 2) = 2х 3 – 4х 2 – 2х + 4
Надо понимать, что хотя ур-ния 2х 3 – 4х 2 – 2х + 4 = 0 и х 3 – 2х 2 – х + 2 = 0, по сути, одинаковы, многочлены в их левой части различны. Заметим, что при перемножении скобок (х – k1), (х – k2), (х – k3) и т.д. всегда будет получаться полином, у которого старший коэффициент равен единице. Поэтому, чтобы учесть этот самый коэффициент, надо домножить произведение скобок на него:
2х 3 – 4х 2 – 2х + 4= 2•(х 3 – 2х 2 – х + 2) = 2(х + 1)(х – 1)(х – 2)
Ответ: 2(х + 1)(х – 1)(х – 2).
Графический метод решения уравнений
Любое ур-ние с одной переменной можно представить в виде равенства
где у(х) и g(x) – некоторые функции от аргумента х.
Построив графики этих функций, можно примерно найти точки их пересечений. Они и будут соответствовать корням уравнения.
Пример. Решите графически уравнение
Решение. Строить график уравнения х 3 – х 2 – 1 = 0 довольно сложно, поэтому перенесем слагаемое (– х 2 – 1) вправо:
Построим графики у = х 3 и у = х 2 + 1 (второй можно получить переносом параболы у = х 2 на единицу вверх):
Видно, они пересекаются в точке, примерно соответствующей значению х ≈ 1,4. Если построить графики уравнения более точно (с помощью компьютера), то можно найти, что х ≈ 1,46557.
Ответ: х ≈ 1,46557
Конечно, графический метод решения уравнений не является абсолютно точным, однако он помогает быстро найти примерное положение корня. Также с его помощью можно определить количество корней уравнения. В рассмотренном примере был только 1 корень.
Пример. Определите количество корней уравнений
б) х 3 – 2х + 0,5 = 0
Решение. Перенесем два последних слагаемых вправо в каждом ур-нии:
Построим графики функций у = х 3 , у = х + 3 и у = 2х – 0,5:
Видно, что прямая у = х + 3 пересекает график у = х 3 в одной точке, поэтому у первого ур-ния будет 1 решение.Прямая у = 2х – 0,5 пересекает кубическую параболу в трех точках, а потому у второго ур-ния 3 корня.
Ответ: а) один корень; б) три корня.
Решение дробно-рациональных уравнений
До этого мы рассматривали только целые ур-ния, где переменная НЕ находится в знаменателе какого-нибудь выражения. Однако, если в ур-нии есть выр-ние, содержащее переменную в знаменателе, или присутствует деление на выр-ние с переменной, то его называют дробно-рациональным уравнением.
Приведем несколько примеров ур-ний, считающихся дробно-рациональными:
С помощью равносильных преобразований любое дробно-рациональное ур-ние возможно записать в виде отношения двух полиномов:
Дробь равна нулю лишь тогда, когда ее числитель равен нулю, а знаменатель – не равен. Таким образом, нужно сначала решить ур-ние Р(х) = 0 и потом проверить, что полученные корни не обращают полином Q(x) в ноль.
Обычно для решения дробно-рациональных уравнений используют такой алгоритм:
1) Приводят все дроби к единому знаменателю, умножают на него ур-ние и получают целое ур-ние.
2) Решают полученное целое ур-ние.
3) Исключают из числа корней те, которые обращают знаменатель хотя бы одной из дробей в ноль.
Пример. Решите ур-ние
Умножим обе части равенства на знаменатель 1-ой дроби:
2х 2 – 3х – 2 = х 2 (х – 2)
Раскроем скобки и перенесем все слагаемые в одну сторону:
2х 2 – 3х – 2 = х 3 – 2х 2
х 3 – 2х 2 – 2х 2 + 3х + 2 = 0
х 3 – 4х 2 + 3х + 2 = 0
У ур-ния могут быть только те целые корни, которые являются делителями двойки. Из кандидатов 1, – 1, 2 и – 2 подходит только двойка:
2 3 – 4•2 2 + 3•2 + 2 = 8 – 16 + 6 + 2 = 0
Нашли один корень, а потому исходный многочлен можно поделить в столбик на (х – 2):
Получили, что х 3 – 4х 2 + 3х + 2 = (х – 2)(х 2 – 2х – 1)
Тогда ур-ние примет вид:
(х – 2)(х 2 – 2х – 1) = 0
х – 2 = 0 или х 2 – 2х – 1 = 0
Решим квадратное ур-ние:
D =b 2 – 4ас = (– 2) 2 – 4•1•(– 1) = 4 + 4 = 8
Мы нашли все 3 корня кубического ур-ния. Теперь надо проверить, не обращают ли какие-нибудь из них знаменатели дроби в исходном ур-нии
в ноль. Очевидно, что при х = 2 знаменатель (х – 2) превратится в ноль:
Это значит, что этот корень надо исключить из списка решений. Такой корень называют посторонним корнем ур-ния.
Также ясно, что два остальных корня не обращают знаменатель в ноль, а потому они НЕ должны быть исключены из ответа:
Пример. Найдите все корни ур-ния
Решение. Если сразу привести выражение слева к общему знаменателю 4(х 2 + х – 2)(х 2 + х – 20), то получится очень длинное и неудобное выражение. Однако знаменатели довольно схожи, поэтому можно провести замену. Обозначим х 2 + х как у:
Тогда уравнение примет вид
Приведем дроби к общему знаменателю 4(у – 2)(у – 20):
Знаменатель должен равняться нулю:
4(у – 20) + 28(у – 2) + (у – 2)(у – 20) = 0
4у – 80 + 28у – 56 + у 2 – 20у – 2у + 40 = 0
у 2 + 10у – 96 = 0
Решаем квадратное ур-ние:
D =b 2 – 4ас = (10) 2 – 4•1•(– 96) = 100 + 384 = 484
Получили, что у1 = – 16, а у2 = 6. Произведем обратную замену:
х 2 + х = – 16 или х 2 + х = 6
х 2 + х + 16 = 0 или х 2 + х – 6 = 0
Дискриминант 1-ого ур-ния отрицателен:
D =b 2 – 4ас = (1) 2 – 4•1•(16) = 1– 64 = – 63
А потому оно не имеет решений. Решим 2-ое ур-ние:
D = b 2 – 4ас = (1) 2 – 4•1•(– 6) = 1+ 24 = 25
Нашли два корня: 2 и (– 3). Осталось проверить, не обращают ли они знаменатели дробей в ур-нии
в ноль. Подстановкой можно убедиться, что не обращают.
При решении дробно-рациональных ур-ний может использоваться и графический метод.
Пример. Сколько корней имеет уравнение
Решение. Построим графики функций у = х 2 – 4 и у = 2/х:
Видно, что графики пересекаются в 3 точках, поэтому ур-ние имеет 3 корня.
Решение уравнений
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

На данном уроке подробно рассмотрены способы решения уравнений. Объяснены способы решения уравнений, как методом подбора, так и с учетом взаимосвязи компонентов действий сложения и вычитания.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Уравнения и неравенства».
Отбор корней в тригонометрическом уравнение
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x – cosx = 0
cosx(sqrt(2)cosx – 1) = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx – 1 = 0
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 – 1/2 меньше или равно n меньше или равно -2 – 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 – 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 – 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 – 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
[spoiler title=”источники:”]
http://interneturok.ru/lesson/matematika/3-klass/undefined/reshenie-uravneniy-2
http://reshimvse.com/article.php?id=100
[/spoiler]
Пример:
а) реши уравнение
sinx=cos2x
.
б) Найди все корни этого уравнения, принадлежащие отрезку
2π;7π2
.
a) Уравнение прежде всего иррациональное, поэтому решается возведением обеих частей в квадрат. С учётом области определения получаем:
sinx=cos2x;sinx≥0,cos2x≥0.
Стоит заметить, что рассматривать оба неравенства в системе нам не нужно, так как мы будем решать уравнение. Поэтому можно оставить только одно — более простое неравенство:
sinx=cos2x;(1)sinx≥0.
Решим уравнение системы ((1)). Прежде всего избавимся от двойного угла в уравнении:
sinx=cos2x;sinx−cos2x=0;sinx−(cos2x−sin2x)=0;sinx−(1−sin2x−sin2x)=0;sinx−(1−2sin2x)=0;2sin2x+sinx−1=0;sinx=−1,sinx=12.
(sin x= -1) исключаем, так как это значение не входит в область определения, а решения второго уравнения обозначим на тригонометрической окружности.

Рис. (1). Решения уравнения на единичной окружности
Эти решения можно записать в виде:
x=π6+2πn,n∈ℤ,x=5π6+2πm,m∈ℤ.
б) Рассмотрим три способа отбора корней, попадающих в отрезок
2π;7π2
.
(1) способ:
вернёмся к единичной окружности. Отметим на ней дугу, соответствующую указанному промежутку, подпишем начало и конец, отметим точки окружности, представляющие серии решений и принадлежащие дуге, укажем их значения, принадлежащие промежутку.
2π+π6=13π6,2π+5π6=17π6.

Рис. (2). Отбор корней с помощью единичной окружности
Обрати внимание!
Нельзя отмечать и подписывать посторонние точки на окружности!
(2) способ:
указанный отрезок соответствует неравенству
2π≤x≤7π2
. Подставим в него полученные корни:
| 2π≤π6+2πn≤7π2,n∈ℤ:π;2≤16+2n≤72,n∈ℤ−16;2−16≤2n≤72−16,n∈ℤ;116≤2n≤206,n∈ℤ:2;1112≤n≤2012,n∈ℤ;1112≤n≤1812,n∈ℤ;n=1;π6+2π⋅1=13π6 | 2π≤5π6+2πm≤7π2,m∈ℤ:π;2≤56+2m≤72,m∈ℤ−56;2−56≤2m≤72−56,m∈ℤ;76≤2m≤166,m∈ℤ:2;712≤m≤1612,m∈ℤ;712≤m≤1412,m∈ℤ;m=1;5π6+2π⋅1=17π6 |
Обрати внимание!
Обязательно выдели целые части дробей для оценки значений (n) и (m)!
(3) способ:
разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо (n) и (m) (0), а потом добавим к каждому корню периоды. На числовой прямой должен быть выделен заданный отрезок, обозначены его концы, отмечены все последовательные значения серий корней, начиная с точек, расположенных левее промежутка, и заканчивая точками, расположенными правее промежутка.

Рис. (3). Отбор корней с помощью координатной прямой
Нам останется только выбрать корни, которые попали в нужный нам отрезок.
Ответ: а)
π6+2πn,n∈ℤ;5π6+2πm,m∈ℤ
; б)
13π6,17π6.
Рекомендуем при решении тригонометрических уравнений использовать несколько разных способов отбора. Это поможет тебе убедиться в правильности отбора корней и выработать навык выбора наиболее удобного способа.
Источники:
Рис. 1. Решения уравнения на единичной окружности. © ЯКласс.
Рис. 2. Отбор корней с помощью единичной окружности. © ЯКласс.
Рис. 3. Отбор корней с помощью координатной прямой. © ЯКласс.
Что такое иррациональные уравнения?
Не секрет же, что большинство чисел можно представить в виде обыкновенной дроби с натуральными числами в числителе и знаменателе?
Например, число 7 – это (frac{21}{3})
Иррациональные числа не такие. Их невозможно представить в виде дроби. Они странные.
Гиппас создал античным математикам множество проблем: их теории о том, что все в мире соизмеримо целым числам, рушились одна за другой. И они боялись.
Но мы будем смелыми 🙂
Сначала разберемся, что такое рациональные уравнения, а потом научимся находить решение иррациональных уравнений.
Итак, что из себя представляют рациональные уравнения, а что – иррациональные:
- ( 3cdot (x+1)=x) – как думаешь, какое это? Тут сложение, умножение, нет корней, и степеней никаких – рациональное!
- ( 3cdot (x+1)=sqrt{x}) – вот тебе и корень из переменной, значит уравнение НЕ рациональное (или иррациональное);
- ( 3cdot (x+1)=frac{1}{x}) – а это – рациональное;
- ( 3cdot (x+1)={{x}^{2}}) – тут вот степень, но она с целым показателем степени (( 2)– целое число) – значит, это тоже рациональное уравнение;
- ( 3cdot (x+1)={{x}^{-1}}) – даже уравнение с отрицательным показателем степени тоже является рациональным, ведь, по сути, ( {{x}^{-1}}) – это ( frac{1}{x});
- ( 3cdot (x+1)={{x}^{0}}) – тоже рациональное, т.к. ( {{x}^{0}}=1);
- ( 3cdot (x+1)={{x}^{frac{1}{2}}}) – а с ним поосторожнее, степень-то дробная, а по свойству корней ( {{x}^{frac{1}{2}}}=sqrt{x}), как ты помнишь, корня в рациональных уравнениях не бывает.
Надеюсь, теперь ты сможешь различить, к какому виду относится то или иное уравнение.
Дадим oпределение:
Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня или знаком возведения в дробную степень.
А вот как это выглядит: ( sqrt{x}); ( {{x}^{frac{1}{3}}}).
Но только отличать рациональное от иррационального недостаточно, тебе же решать их надо! Вся сложность в корнях, так?
Так избавься от них, вот и все дела!
Если еще не догадался, как, то я подскажу: просто возведи в нужную степень обе части уравнения, а потом решай его как простое рациональное уравнение.
Но проверяй все корни! Позже ты поймешь, почему делать это необходимо.
Как рациональные уравнения решать помнишь? Если забыл, то советую почитать «Рациональные уравнения».
Если читать лень, напомню вкратце. Для верного решения рациональных уравнений, ты должен придерживаться следующего алгоритма:
Пример №3
( sqrt{12-x}=x)
После возведения обеих частей в квадрат имеем:
( 12-x={{x}^{2}}), упрощаем и решаем квадратное уравнение по теореме Виета
( {{x}^{2}}+{x}-12=0)
( left[ begin{array}{l}{{x}_{1}}=3\{{x}_{2}}=-4end{array} right.)
У нас два корня, пробуем их подставить в исходное для проверки.
Подставляем ( 3), ( sqrt{9}=3), ( 3=3) – подходит.
Подставим ( -4), получим ( sqrt{16}=-4)…
Но ведь ( 4ne -4)! Что же получается, ( -4) – посторонний корень.
Заговор какой-то!
Думаю, интрига затянулась, настало время объяснить, почему получаются какие-то посторонние корни.
Опять объяснять буду на примере:
( -2ne 2), но если мы возведем в квадрат обе части, ( {{(-2)}^{2}}={{(2)}^{2}}), ( 4=4).
Ну как тебе фокус? 🙂
То же самое получается и в нашем примере с иррациональным уравнением, в результате преобразования мы можем найти все корни, но могут примешаться и посторонние.
Их надо отфильтровать проверкой, проверив, будет ли соблюдаться равенство исходного уравнения при их подстановке.
А если взять не вторую, а третью степень:
( {{(-2)}^{3}}ne {{(2)}^{3}})
( -8ne 8)
Пример №4 (метод уединения радикала)
( sqrt{2x+1}+sqrt{x}=1)
В этом примере есть два подкоренных выражения и число ( 1).
Чтобы избавиться от корня, нужно обе части возвести в квадрат, но, прежде чем сделать это, перенесем ( sqrt{x}) в правую часть.
( sqrt{2x+1}=1-sqrt{x})
«Зачем?» – спросишь ты.
Дело в том, что, если возводить в квадрат в таком виде, упрощать придется дольше, не веришь – попробуй сам, а я, пожалуй, избавлю себя от расписывания этого 🙂
Теперь возводим в квадрат обе части и упрощаем.
( sqrt{2x+1}=1-sqrt{x})
( 2x+1=1-2sqrt{x}+x)
( x=-2sqrt{x})
Понял, в чем сложность?
Этот метод решения математики называют «метод уединения радикала».
Радикал (выражение с корнем) надо уединить в одной стороне уравнения. Но уединять и возводить в степень придется не один раз.
Чтобы избавиться от корней и получить нормальное (рациональное 🙂 ) уравнение, придется выполнять множество замысловатых махинаций, которые заключаются в уединении и возведении в степень.
С другой стороны, можно заметить, что на определенной стадии решения становится без дальнейших упрощений понятно, что в уравнении, например, нет решений.
Например…
Корни степени больше 2
Ты спросишь: а что всё про квадратные корни? Как же быть с остальными степенями?
Спрошу в ответ: а чем они отличаются?
Отличие, на самом деле, есть. Но важна не конкретная степень корня, а четность этой степени.
Корни четной степени
Корни ( displaystyle 2), ( displaystyle 4), ( displaystyle 6), и т.д. степеней очень похожи друг на друга, и принцип решения уравнений с ними абсолютно одинаковый. Дело в том, что корень четной степени можно всегда привести к квадратному (вспоминаем тему «Корень и его свойства»!):
( displaystyle sqrt[4]{x}=sqrt{sqrt{x}};text{ }sqrt[6]{x}=sqrt{sqrt[3]{x}};text{ }sqrt[2k]{x}=sqrt{sqrt[k]{x}})
Например:
( displaystyle sqrt[4]{A}=Btext{ }Leftrightarrow text{ }left{ begin{array}{l}A={{B}^{4}}\Bge 0end{array} right.)
Корни нечетной степени
С нечетными степенями (( displaystyle 3), ( displaystyle 5), …) все намного проще!
Дело в том, что корень нечетной степени можно извлекать из любого числа! (И снова, если ты этого не знал, вспомни тему «Корень и его свойства»!)
Что это значит?
Теперь никаких дополнительных условий, никаких ограничений – просто возводим все в нужную степень и решаем:
( displaystyle begin{array}{l}sqrt[3]{A}=Btext{ }Leftrightarrow text{ }A={{B}^{3}}\sqrt[5]{A}=Btext{ }Leftrightarrow text{ }A={{B}^{5}}end{array})
Примеры:
- ( displaystyle sqrt[5]{2-x}=-2)
- ( displaystyle sqrt[4]{3+2{x}-{{x}^{2}}+{{x}^{4}}}=x)
- ( displaystyle sqrt[3]{{{x}^{3}}+3x+5}=x)
- ( displaystyle sqrt[3]{6+{{x}^{2}}-{{x}^{3}}}=1-x)
Ответы:
Загрузить PDF
Загрузить PDF
Иррациональное уравнение – это уравнение, в котором переменная находится под знаком корня. Для решения такого уравнения необходимо избавиться от корня. Однако это может привести к появлению посторонних корней, которые не являются решениями исходного уравнения. Для выявления таких корней необходимо подставить все найденные корни в исходное уравнение и проверить, соблюдается ли равенство.
Шаги
-

1
Запишите уравнение.
- Рекомендуется использовать карандаш, чтобы иметь возможность исправлять ошибки.
- Рассмотрим пример: √(2x-5) – √(х-1) = 1.
- Здесь √ – это квадратный корень.
-

2
Обособьте один из корней на одной стороне уравнения.
- В нашем примере: √(2x-5) = 1 + √(х-1)
-

3
Возведите обе стороны уравнения в квадрат, чтобы избавиться от одного корня.
-

4
Упростите уравнение, сложив/вычтя подобные члены.
-
5
Повторите описанный выше процесс для избавления от второго корня.
- Для этого обособьте оставшийся корень на одной стороне уравнения.

- Возведите обе стороны уравнения в квадрат, чтобы избавиться от оставшегося корня.

- Для этого обособьте оставшийся корень на одной стороне уравнения.
-
6
Упростите уравнение, сложив/вычтя подобные члены.
-

- Сложите/вычтите подобные члены, а затем перенесите все члены уравнения влево и приравняйте их к нулю. Вы получите квадратное уравнение.

-
-
7
Решите квадратное уравнение через формулу нахождения корней квадратного уравнения.
- Решение квадратного уравнения показано на следующем рисунке:

- Вы получите: (х – 2,53)(х – 11,47) = 0.

- Таким образом, х1 = 2,53 и х2 = 11,47.

- Решение квадратного уравнения показано на следующем рисунке:
-
8
Подставьте найденные корни в исходное уравнение и отбросьте посторонние корни.
- Подставьте х = 2,53.

- – 1 = 1, то есть равенство не соблюдено и х1 = 2,53 является посторонним корнем.
- Подставьте х2 = 11,47.

- Равенство соблюдено и х2 = 11,47 является решением уравнения.
- Таким образом, отбросьте посторонний корень х1 = 2,53 и запишите ответ: x2 = 11,47.

Реклама
- Подставьте х = 2,53.
Об этой статье
Эту страницу просматривали 12 703 раза.
