Уравнение сферы
Пусть
сфера имеет радиус
,
а ее центр находится в точке
.
Точка
лежит на сфере тогда и только тогда,
когда модуль вектораравен
,
то есть.
А последнее равенство выполнено тогда
и только тогда, когда
(1)
Уравнение
(1) и является искомым уравнением сферы.
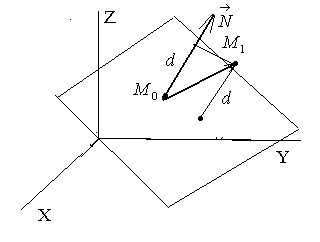
Уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору
Пусть
плоскость проходит через точку
перпендикулярно вектору
.
Точка
лежит на плоскости тогда и только тогда,
когда векторы
и
перпендикулярны. Векторы
и
перпендикулярны тогда и только тогда,
когда их скалярное произведение равно
нулю, то есть.
Тогда уравнение плоскости записываем
в виде
(2)
Рассмотрим
пример. Найти
уравнение плоскости, проходящей через
середину отрезка АВ перпендикулярно
этому отрезку если координаты точек
соответственно равны А(1;6;9), В(5;4;7).
Будем
рассуждать следующим образом. Чтобы
найти уравнение плоскости мы должны
знать точку, через которую эта плоскость
проходит, и вектор перпендикулярный
этой плоскости. Вектором, перпендикулярным
данной плоскости, будет вектор
,
поскольку, по условию задачи, плоскость
перпендикулярна отрезку АВ. Точку
определим
из условия, что плоскость проходит через
середину АВ. Имеем
.
Таким образоми уравнение примет вид
Выясним
вопрос, проходит ли эта плоскость через
точку М(7;3;0).
Имеем
,
значит, эта плоскость не проходит через
указанную точку.
Решим
еще одну задачу.
Найти уравнение плоскости, проходящей
через точку
,
параллельно векторам.
Чтобы
найти уравнение плоскости, мы должны
знать точку и вектор, перпендикулярный
этой плоскости. Точка у нас имеется, а
вот вектора не хватает. Но мы имеем в
качестве компенсации два параллельных
вектора. Теперь давайте вспомним свойства
векторного произведения векторов. А
оно гласит, что векторное произведение
двух векторов направлено перпендикулярно
плоскости, в которой эти векторы
расположены. Следовательно, в качестве
перпендикулярного вектора
может быть взято векторное произведение
векторов.
Имеем

Уравнение
плоскости примет вид
Еще
один пример.
Найти уравнение плоскости, проходящей
через точки
.
Как
видим в наличии целых три точки и ни
одного вектора. Но если вспомнить, что
вектор, соединяющий две точки параллелен
плоскости, в которой эти точки лежат,
то задача сводится к предыдущей.
Следовательно, плоскости параллельны
вектор
и вектор
.
Тогда

Уравнение
примет вид
Заметим,
что нетрудно получить общую
формулу уравнения плоскости, проходящей
через три точки
.
Она получается из следующих соображений.
Точка
лежит в данной плоскости тогда и только
тогда, когда векторы,
являются
компланарными, а значит, их смешанное
произведение равно нулю. Тогда получаем
или
окончательно

(3)
Общее
уравнение плоскости
Определение.
Общим уравнением поверхности первого
порядка на плоскости называется уравнение
вида
,
где.
Теорема.
Всякая плоскость может быть задана в
виде уравнения поверхности первого
порядка, и всякое уравнение поверхности
первого порядка является уравнением
некоторой плоскости.
Первая
часть этой теоремы доказывается просто.
На всякой плоскости можно указать
некоторую точку
перпендикулярный
ей вектор
.
Тогда, согласно (2), уравнение такойплоскости
имеет вид
.
Обозначим.
Тогда уравнение примет вид
.
Теперь
перейдем ко второй части теоремы. Пусть
имеется уравнение
,
где.
Будем считать для определенности.
Перепишем
уравнение в виде;
;
.
Рассмотрим
точку
,
где.
Тогда полученное уравнение имеет вид
,
и является уравнениемплоскости,
проходящей через точку
перпендикулярно вектору
.
Попутно
мы доказали, что если имеется уравнение
плоскости
вида
, то вектор
перпендикулярен даннойплоскости.
Итак,
уравнение вида
называется общим уравнением плоскости
в пространстве.
Далее
выведем
формулу вычисления расстояния от
произвольной точки до плоскости, заданной
общим уравнением.
Пусть
имеется плоскость
и точка
.
Требуется определить расстояние от
указанной точки доплоскости.
Рассмотрим
произвольную точку
наплоскости.
Имеем
.
Расстояниеот точки
доплоскости
равно модулю проекции вектора
на вектор
,
перпендикулярный данной плоскости.
Имеем

преобразуя,
получаем:
.
Пусть
даны две плоскости,
заданные общими уравнениями
,
. Тогда векторы
перпендикулярны первой и второй прямой
соответственно. Уголмежду прямыми равен углу между векторами
.
Тогдаформула
для определения угла имеет вид:
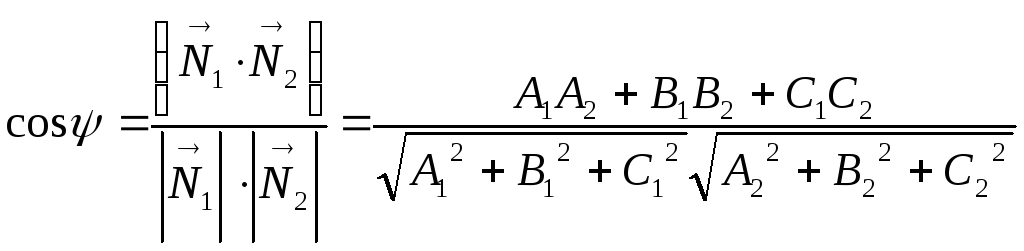
Условие
перпендикулярности плоскостей имеет
вид:
.
Плоскости
параллельны или совпадают тогда и только
тогда, когда векторы
колинеарны.
При
этом условие
совпадения плоскостей
имеет вид:
,
а
условие отсутствия пересечения
записывается в виде:
.
Последние
два условия докажите самостоятельно.
Исследуем
характер поведения плоскости
по ее общему уравнению.
Пусть
дано общее уравнение плоскости
.
Если
,
топлоскость
проходит через начало координат.
Рассмотрим
случай, когда ни один из коэффициентов
не равен нулю
.
Уравнение перепишем в виде
,
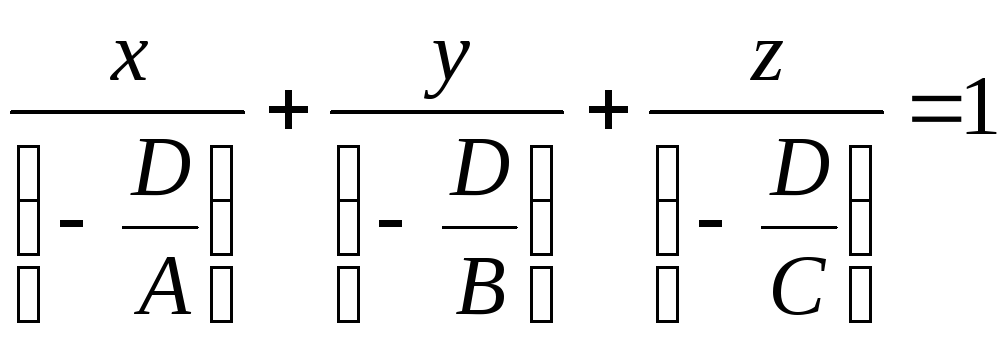
,
где.
Выясним смысл параметров
.
Найдем точки пересечения плоскости с
осями координат. Приимеем
,
а приимеем
,
при
имеем.
То есть
– это отрезки, которые отсекает плоскость
на координатных осях. Поэтомууравнение
называется
уравнением плоскости в отрезках.
В
случае
имеем
,

,
где.
То есть плоскость будет параллельна
оси
.
В
случае
имеем
,

,
где.
То есть плоскость будет параллельна
оси
.
В
случае
имеем
,

,
где.
То есть плоскость будет параллельна
оси
.
В
случае
имеем
,
,
где.
То есть плоскость будет перпендикулярна
оси
.
В
случае
имеем
,
,
где.
То есть плоскость будет перпендикулярна
оси
.
В
случае
имеем
,
,
где.
То есть плоскость будет перпендикулярна
оси
.
Соседние файлы в папке ВЕЧЕРНЕЕ 1 семестр 2012
- #
- #
- #
Уравнение сферы
Содержание:
- Уравнение сферы
- Задача пример №47
- Задача пример №48
Уравнение сферы
Определение. Сферой называется множество всех точек, расположенных на расстоянии 



Если точка 
Это уравнение сферы с центром в точке 

Если центр сферы находится в начале координат, то уравнение сферы радиуса 
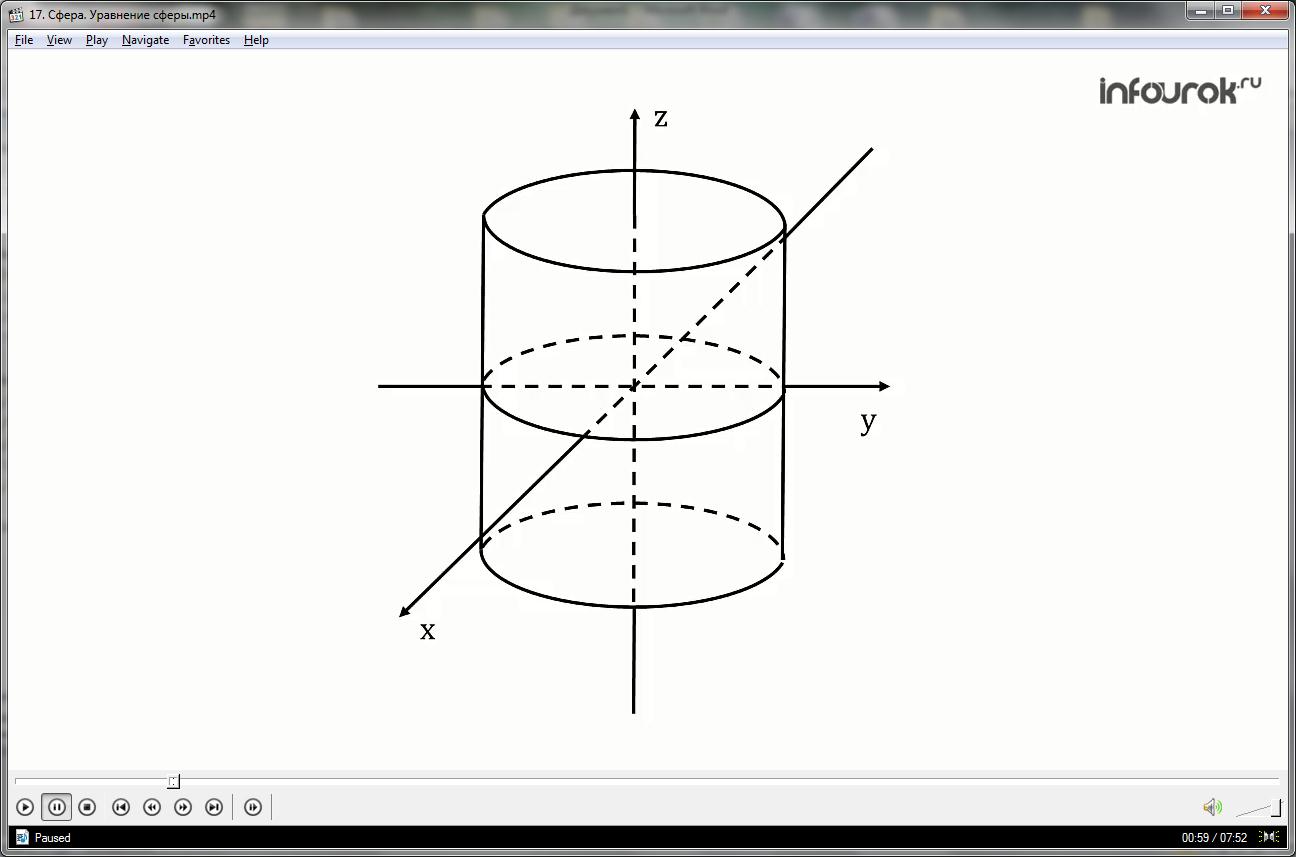
Как видно из рисунка, пересечение этой сферы с координатной плоскостью 

Задача пример №47
Запишите уравнение сферы, радиус которой равен 

Решение:
Задача пример №48
Представьте фигуру, которая получается при пересечении сферы 

Решение:
радиус сферы 


Пересечение плоскости 

Плоскость, имеющая со сферой только одну общую точку, называется плоскостью, касательной к сфере.
Например, плоскость 

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Пределы: примеры решения
- Площадь поверхности конуса
- Целые рациональные выражения
- Числовые ряды. Числовой ряд. Сумма ряда
- Метод Эйлера
- Линейные дифференциальные уравнения первого порядка
- Скрещивающиеся прямые
- Скалярное призведение двух векторов
- Теоремы, связанные с понятием производной
- Приближённые вычисления
Урок «Сфера. Уравнение сферы»
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Продолжаем изучение сферы.
На прошлых занятиях вы познакомились с определением сферы и шара.
Вспомним, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.
Данная точка — центр сферы.
Заданное расстояние — радиус сферы.
Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.
Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.
Уравнением поверхности F называется уравнение с тремя переменными x, y, z, если этому уравнению удовлетворяют координаты всех точек поверхности F и не удовлетворяют координаты точки, не принадлежащей этой поверхности.
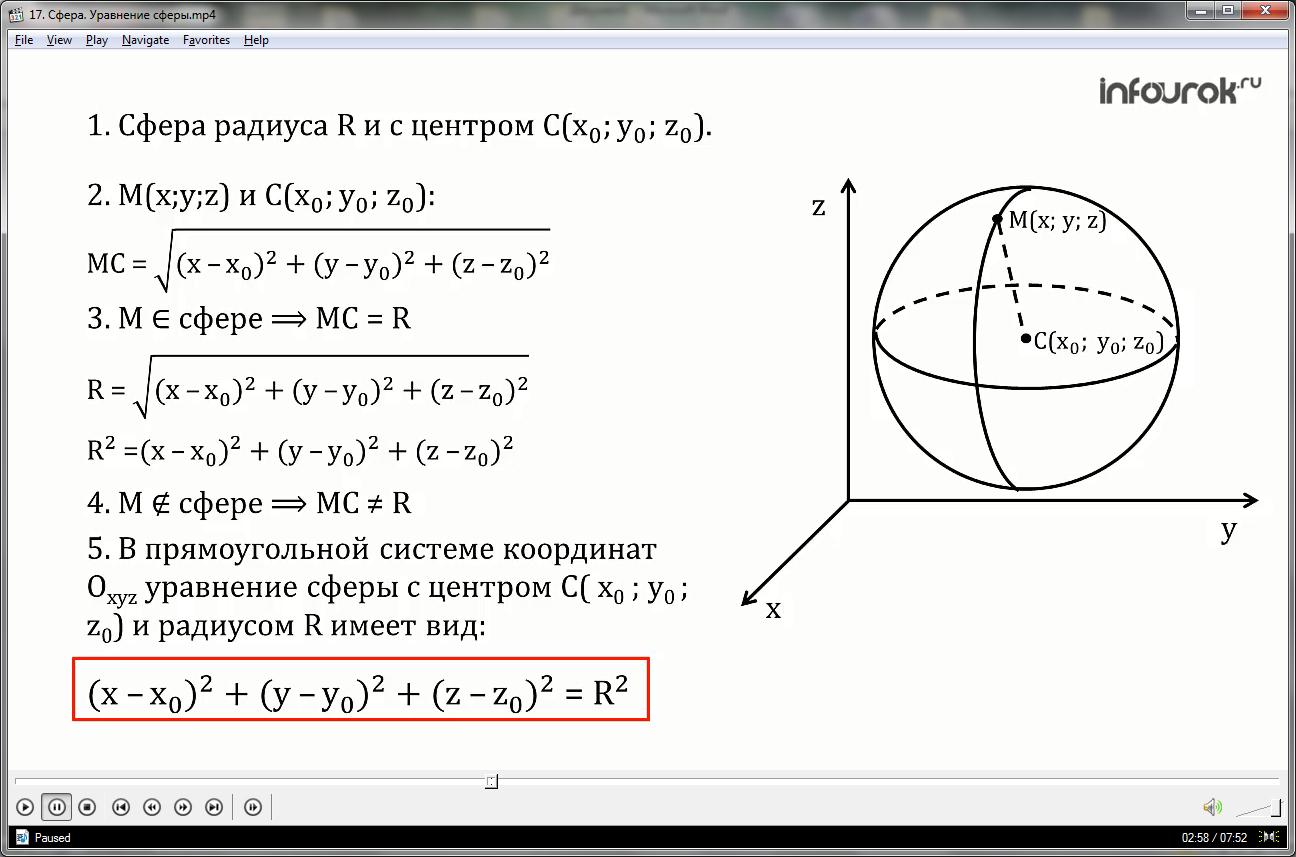
1.Рассмотрим сферу радиуса R и с центром С(x0; y0; z0).
2.Найдём расстояние от произвольной точки М(x; y; z) до центра С( x0 ; y0 ; z0) по формуле для вычисления расстояния между двумя точками с заданными координатами.
МС=√(x-x0)2+(y-y0)2+(z-z0)2.
3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть
R=√(x-x0)2+(y-y0)2+(z-z0)2 или
R2=(x-x0)2+(y-y0)2+(z-z0)2 .
4.В случае если точка М не принадлежит данной сфере, то R≠МС, значит, координаты точки М не удовлетворяют уравнению R2=(x-x0)2+(y-y0)2+(z-z0)2.
5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром
С (x0 ; y0 ; z0) и радиусом R имеет вид:
(x-x0)2+(y-y0)2+(z-z0)2 = R2
Применим полученные знания при решении задач.
Задача 1.
Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).
Решение:
1.Запишем уравнение сферы с центром
А (x0 ; y0 ; z0) и радиусом R:
(x-x0)2+(y-y0)2+(z-z0)2 = R2
2.Подставим соответствующие координаты центра сферы А в данное уравнение:
(x+2)2+(y-2)2+(z-0)2 = R2
Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:
(x+2)2+(y-2)2+z2 = R2
3.Так как сфера проходит через точку N с координатами (5;0;-1), то её координаты удовлетворяют уравнению сферы, подставим координаты этой точки в полученное уравнение:
R2=(5+2)2+(0-2)2+(-1)2 =49+4+1=54
Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:
(x+2)2+(y-2)2+z2 = 54
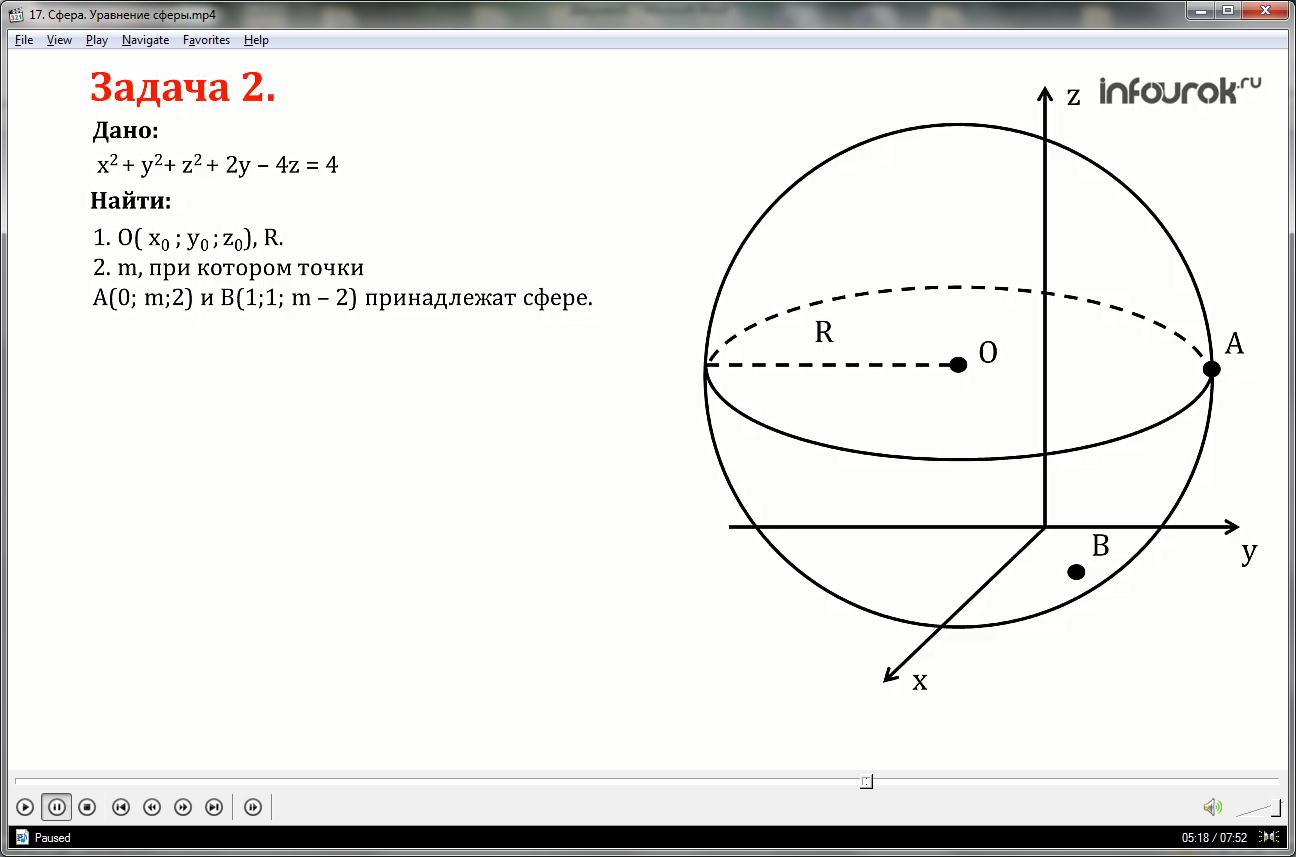
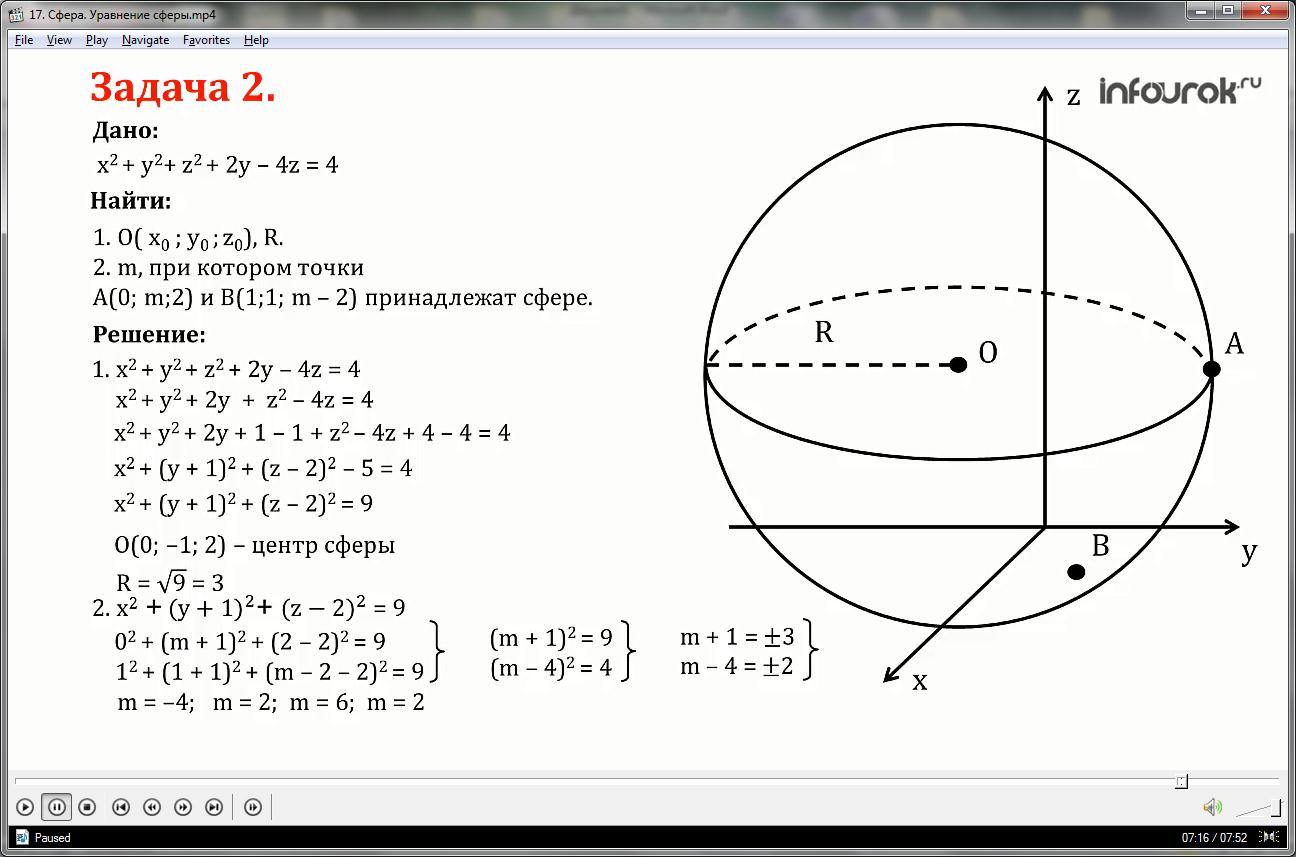
Задача 2.
Сфера задана уравнением:
x2+ y2+ z2+2y-4z=4
1) Найти координаты центра и радиус сферы;
2) Найти значение m, при котором точки
А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.
Решение:
1. Уравнение данной сферы имеет вид:
x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4
Выделим полный квадрат для переменных y и z, для этого прибавим и одновременно вычтем 1 и 4 в левой части уравнения:
x2+ y2+2y+1-1 + z2-4z+4-4=4
Уравнение примет вид:
x2+( y+1)2+( z-2)2-5=4 или
x2+( y+1)2+( z-2)2=9
Таким образом, центр сферы имеет координаты:
О (0;-1;2), радиус равен R=√9=3
2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:
x2+( y+1)2+( z-2)2=9
Точки А (0; m;2) и В (1;1; m-2) принадлежат данной сфере, значит их координаты удовлетворяют уравнению сферы. Подставим координаты этих точек в уравнение сферы и решим систему уравнений:
02+( m+1)2+(2-2)2=9
12+(1+1)2+( m-2-2)2=9
Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:
Таким образом, мы получили 4 значения m:
m=-4; m=2; m=6; m=2.
Несложно проверить, что при m=-4 и m=6 координаты точек А и В не удовлетворяют уравнению сферы. Проверьте самостоятельно.
Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением
x2+ y2+ z2+2y-4z=4 с центром в точке
О (0;-1;2) и радиусом R=3.
Запишем общее уравнение сферы с радиусом R=3;
В этом уравнение должны быть такие коэффициенты a,b,c, чтобы при подстановке координат всех точек, уравнение было верным. а,b,c можно найти из системы:
Из третьего уравнения выразим b^{2}+ c^{2}:
b^{2}+ c^{2} = 9 – (4-a)^{2}
Подставим в первое уравнение.
Раскрыв скобки и приведя подобные, получим, что a=2. Мы стали на шаг ближе к истине (которая, кст, всё же останется недостижимой)
Если умножить первое уравнение и прибавить ко второму, то после раскрытия скобок и привидения подобных b=2. Ну и теперь c ничего не остаётся, кроме как равняться 1, с=1.
Вот мы и получили искомое уравнение сферы:
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 62578 Составить уравнение сферы, проходящей…
Условие
61df57135e01221a629998de
13.01.2022 01:33:35
Составить уравнение сферы, проходящей через четыре точки: А(1;-2;-1), В(4;1;11), С(-8;-2;2) и D(-5;10;-1).
(x–a)2+(y–b)2+(z–c)2=R2 – каноническое уравнение сферы с центром в точке О(a;b;c) и радиусом R.
математика ВУЗ
513
Решение
5f3eaa23faf909182968dde0
13.01.2022 07:43:43
★
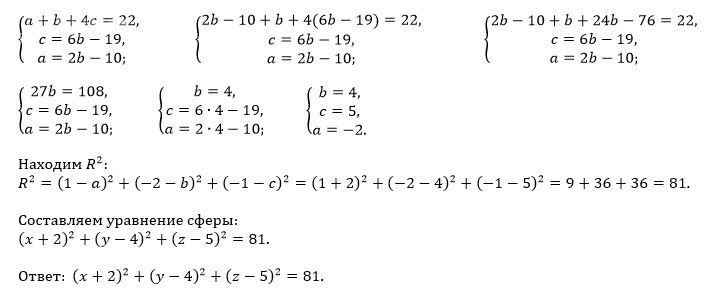
Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач