Ученик
(84),
закрыт
12 лет назад
Styx
Гений
(83658)
12 лет назад
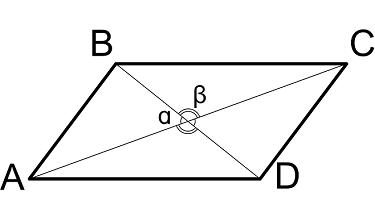
1) уравнение первой диагонали находится сразу- уравнение прямой, проходящей через две точки
2y+x-5=0
2) дальше школа- диагонали в точке пересечения делятся пополам
О (1,2)
3) диагонали взаимоперпендикулярны, поэтому K(AC)*K(BD)=-1
K(AC)=-1/2
K(BD)=2
y-2=2(x-1)- ур BD
3)- диагональ делит угол пополам
tg45=|K(AB)-2|/1+2K(AB)
k(AB)=+-3
AB: y-3=3(x+1)
K(BC)=-1/3
BC; y-1=-1/3(x-3)
K(AD)=K(BC)
K(AD)=-1/3
AD: y-3=-1/3(x+1)
Формулы параллелограмма
Для расчёта всех основных параметров параллелограмма воспользуйтесь калькулятором.
Признаки и свойства параллелограмма
- Противоположные стороны параллельны и равны.
- Противоположные углы равны
- Точка пересечения диагоналей делит их пополам.
- Сумма углов четырехугольника прилегающих к любой стороне равна 180°
- В четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон
- Сумма углов параллелограмма равна 360°
- Каждая диагональ делит параллелограмма на два равных треугольника
- Биссектрисы противоположных углов параллелограмма всегда параллельны
- Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)
Формулы стороны параллелограмма
Длины сторон через диагонали и угол между ними
Длина стороны через диагонали и известную сторону
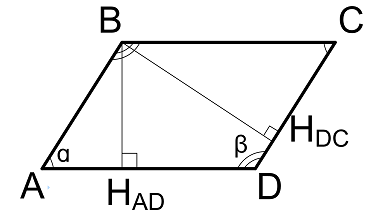
Длины сторон через высоты и угол между сторонами
Формулы диагоналей параллелограмма
Длина диагонали через стороны и углы между ними
Длина диагонали через стороны и известную диагональ
Длина диагонали через площадь параллелограмма, известную диагональ и угол между диагоналями
Формулы углов параллелограмма
Косинус острого угла
Косинус тупого угла
Синус острого и тупого угла через площадь и стороны параллелограмма
Формулы углов между диагоналями параллелограмма
Косинус острого угла через стороны и диагонали
Косинус тупого угла через стороны и диагонали
Синус острого и тупого угла через площадь и диагонали
Задача 43087 уравнения двух сторон параллелограмма x.
Условие
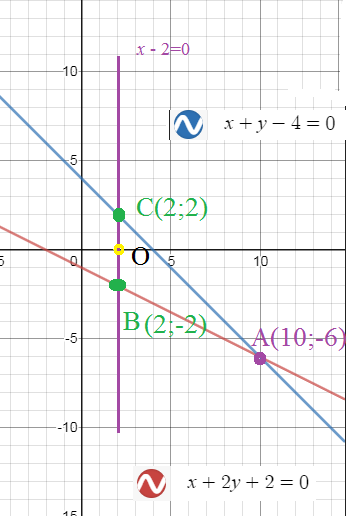
уравнения двух сторон параллелограмма x + 2y + 2 = 0 и x + y-4= 0, а уравнения одной из его диагоналей x-2 = 0. Найти координаты вершин параллелограмма. Сделать рисунок. Прошу решите
Решение
[b](10;-6)[/b] — координата вершины А
Так как точка А не принадлежит диагонали x-2=0
то диагональ пересекается со сторонами x + 2y + 2 = 0 и x + y–4= 0
Середина ВС — точка О
Так как О- середина AD, то координаты точки D легко найти из формул середины отрезка DA
[b]D(-6;6)[/b]
Как найти уравнения сторон параллелограмма
Даны уравнения двух сторон параллелограмма 8х+3у+1=0, 2х+у-1=0 и уравнение одной из его диагоналей 3х+2у+3=0. Определить координаты вершин этого параллелограмма.
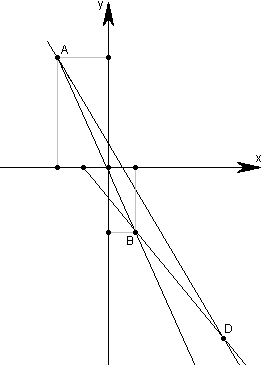
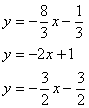
Для нахождения точки А приравняем эти два уравнения:
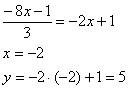
Мы видим, что уравнение 3х+2у+3=0 задает диагональ BD . Поэтому, приравняв сначала 1 и 3, а затем 2 и 3 уравнения, найдем соответственно точки D и В.
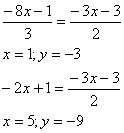
Как известно в параллелограмме противоположные стороны параллельны, то есть коэффициенты k при х равны. Поэтому для сторон ВС и CD остаются неизвестными только свободные члены d . Найдем их, подставив в уравнения прямых их известные точки D и В соответственно:
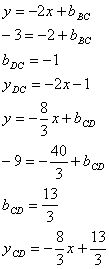
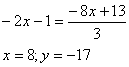
источники:
http://reshimvse.com/zadacha.php?id=43087
http://methmath.ru/zadatcha9.html
$begingroup$
Question:
The three vertices of a square $ABCD$ are $A(3,2), B(6,−2)$, and $C(2,−5)$. Find the equation of the side $CD$ and the equation of the diagonal $BD$.
My attempt:
- Equation of side $CD$: $4x+3y+7=0$
- Equation of diagonal $BD$: ??
Is my answer for the equation of the side $CD$ correct? I am not able to solve for the equation of the diagonal $BD$. Please help me. Thanks in advance.
slope of side $CD$:
$m_{CD}=m_{AB}=dfrac{(−2−2)}{(6−3)}=dfrac{-4}{3}=-1.33$ $left[because AB parallel CDright]$
equation of side $CD$:
$$y – y_1 = m(x – x_1) point slope form$$
$Rightarrow y+5=dfrac{−4}{3}(x−2) Rightarrow 4x+3y+7=0$
But I am not sure how to solve for the equation of the diagonal $BD$.
I have constructed the square in GeoGebra and I found that the coordinates of $D$ are $(-1,-1)$ and the slope of $BD$ is $dfrac{-1}{7}=-0.14$.
But I am not able to solve for the equation of the same. Please help me. Thanks in advance.
asked Oct 13, 2021 at 11:22
$endgroup$
1
$begingroup$
Slope of CD is equal to slope of AB and is equal to $(-2-2)/(6-3)=-4/3$, therefore equation of CD is $y=y_C-frac{4}{3}(x-x_C)=-5-frac{4}{3}(x-2)=-frac{4}{3}x-frac{7}{3}$. Multiplying by 3 to avoid fractions and moving all terms to left-hand side gives $4x+3y+7=0$.
Center of square is middle of AC and middle of BD.
Middle of AC is $(frac{x_A+x_C}{2},frac{y_A+y_C}{2})=(2.5,-1.5)$
Let D is $(x,y)$, then middle of BD is $(frac{x_B+x_D}{2},frac{y_B+y_D}{2})=(x/2+3,y/2-1)$
$2.5=x/2+3Rightarrow x=-1$
$-1.5=y/2-1Rightarrow y=-1$
So, D is $(-1,-1)$
Slope of BD is $(y_D-y_B)/(x_D-x_B)=(-1+2)/(-1-6)=-1/7$
Equation of BD is $y=y_B-frac{1}{7}(x-x_B)=-2-frac{1}{7}(x-6)=-frac{1}{7}x-frac{8}{7}$
Multiplying by 7 to avoid fractions and moving all terms to left-hand side gives $x+7y+8=0$.
answered Oct 13, 2021 at 15:20
$endgroup$
$begingroup$
It is very well known that the equation of the linear function is
$y=kx+b$, therefore, we have to determine the equation of $BD$ from the next system:
$$
begin{cases}
-1=-1*k+b,\
-2=6*k+b.
end{cases}
$$
Performing that system we get that $b=frac{-8}{7}$, but $k=(b+1)$, therefore, $k=frac{-1}{7}$.
$BD$ has the next equation: $y=-frac{1}{7}*x-frac{8}{7}$.
Good luck!
answered Oct 13, 2021 at 12:06
Vadim ChernetsovVadim Chernetsov
1,4131 gold badge9 silver badges11 bronze badges
$endgroup$
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Найдем концы диагоналей квадрата:
$$x=0$$
$$5*0+4у-20=0$$
$$y=5$$
$$y=0$$
$$5x+4*0-20=0$$
$$x=4$$
Следовательно, т. $%A(0; 5)$%, $%C(4; 0)$%
Найдем угловой коэффициент прямой:
$$5x+4y-20=0$$
$$4y=20-5x$$
$$y=-5/4 x+20$$
$$k_1=-5/4$$
$$(k_1-k_2)/(1+k_2 k_2 )=1$$
$$(-5/4-k_2)/(1-5/4 k_2 )=1$$
$$-5/4-k_2=1-5/4 k_2$$
$$k_2=9$$
Составим уравнение первой стороны квадрата проходящую через точку $%А(0; 5)$%
$$y-y_0=k(x-x_0 )$$
$$y-5=9(x-0)$$
$$y-5=9x$$
$$y=9x+5-AD $$
уравнение первой стороны квадрата
Составим уравнение стороны квадрата перпендикулярное стороне AD. Найдем угловой коэффициент
$$-5/4-k_2=-1+5/4 k_2$$
$$k_2=-1/9$$
Составим уравнение первой стороны квадрата проходящую через точку А(0; 5)
$$y-y_0=k(x-x_0 )$$
$$y-5=-1/9 (x-0)$$
$$y-5=-1/9 x$$
$$y=-x/9+5-AB$$
уравнение второй стороны квадрата
Найдем уравнение третьей стороны квадрата из условия параллельности сторон AD и BC через точку $%С(4; 0)$%
$$-y+9x+5=0$$
$$9(x-4)-1(y-0)=0$$
$$9x-y-36=0-BC$$
уравнение третьей стороны квадрата
Найдем уравнение третьей стороны квадрата из условия параллельности сторон AB и CD через точку $%С(4; 0)$%
$$-y-x/9+5=0$$
$$-1/9 (x-4)-1*(y-0)=0$$
$$-x/9-y+4/9=0-CD$$
mashkama
Преобразуем уравнение диагонали [math][BD][/math] к уравнению прямой с угловым коэффициентом:
[math]x+3y-3=0~Rightarrow~y=-frac{1}{3}x+1.[/math]
Диагональ [math][AC][/math] перпендикулярна диагонали [math][BD][/math] и проходит через точку [math]A.[/math] Значит, угловой коэффициент диагонали [math][AC][/math] равен [math]k_{AC}=-frac{1}{k_{BD}}=-frac{1}{-frac{1}{3}}=3,[/math] а её уравнение находится следующим образом:
[math]y-y_A=k_{AC}(x-x_A),~y-0=3(x-(-2)),~y=3x+6,[/math] или [math]3x-y+6=0.[/math]
Найдём координаты центра квадрата, решив совместно уравнения диагоналей:
[math]-frac{1}{3}x+1=3x+6~Rightarrow~frac{10}{3}x=-5,~x=-frac{15}{10}=-frac{3}{2},[/math]
[math]y=-frac{1}{3}bigg(-frac{3}{2}bigg)+1=frac{1}{2}+1=frac{3}{2}.[/math]
Центр квадрата находится в точке [math]Ebigg(-frac{3}{2};~frac{3}{2}bigg).[/math]
Попробуйте дальше продолжить сами. Например, чтобы найти координаты точки [math]C,[/math] можно воспользоваться тем, что точка [math]E[/math] делит отрезок [math][AC][/math] пополам. А можно найти расстояние [math]|AE|,[/math] составить уравнение окружности с центром в точке [math]E[/math] и радиусом [math]R=|AE|,[/math] а затем найти точки пересечения этой окружности с прямыми [math](AC)[/math] и [math](BD).[/math]