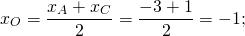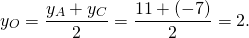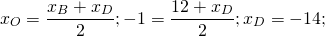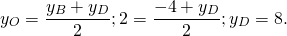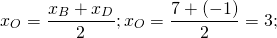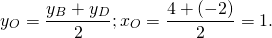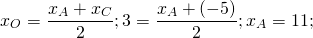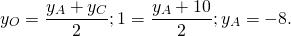Как найти уравнение сторон параллелограмма по координатам

Задача 43087 уравнения двух сторон параллелограмма x.

Условие

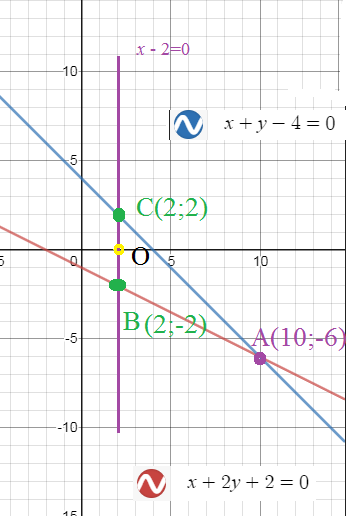
уравнения двух сторон параллелограмма x + 2y + 2 = 0 и x + y-4= 0, а уравнения одной из его диагоналей x-2 = 0. Найти координаты вершин параллелограмма. Сделать рисунок. Прошу решите

Решение

[b](10;-6)[/b] — координата вершины А

Так как точка А не принадлежит диагонали x-2=0

то диагональ пересекается со сторонами x + 2y + 2 = 0 и x + y–4= 0

Середина ВС — точка О

Так как О- середина AD, то координаты точки D легко найти из формул середины отрезка DA

[b]D(-6;6)[/b]

Найти четвертую вершину параллелограмма

Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?

В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.

Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.

Дано: ABCD — параллелограмм,

1) Найдём координаты точки O — середины диагонали AC.

2) По свойству диагоналей параллелограмма, точка O также является серединой BD:

Дано: ABCD — параллелограмм,

1) Ищем координаты точки O — середины отрезка BD:

2) Точка O также является серединой AC:

2 Comments

А как вы получили -14 в первом примере.

Можно применить основное свойство пропорции: 12+xD=2∙(-1), xD=-2-12=-14.

Уравнение стороны параллелограмма по координатам вершин

Даны уравнения двух сторон параллелограмма x + 2y + 1 = 0 (AB), 2x + y — 3 = 0 (AD) и точка пересечения его диагоналей N(1, 2). Найти уравнения двух других сторон этого параллелограмма.

При решении, замечая, что данные стороны параллелограмма не параллельны, будем следовать такому плану:

1) Найдем координаты точки A пересечения данных сторон.

2) Зная координаты точек A и N, найдем координаты точки C, что мы легко сможем сделать по формуле определения координат середины отрезка.

3) Через найденную точку C проведем сначала прямую, параллельную AD, а потом прямую, параллельную AB.

4) Определим координаты точки A, как точки пересечения прямых AB и AD, и получим, что

5) Формулы для определения координат середины отрезка в данном случае запишутся так:

По этим формулам получим

Итак, точка .

6) Через точку C проведем прямую, параллельную AD, и получим, что уравнение стороны BC будет таким:

2

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---

---

---

---

---

---

---

Решение типового варианта контрольной работы. Аналитическая геометрия.

Задача №1.

Даны три последовательные вершины параллелограмма А(2;-3), В(5;1),С(3;-4). Не находя координаты вершины D, найти:

1)  уравнение стороны AD;

2)  уравнение высоты BK, опущенной из вершины В на сторону AD;

3)  длину высоты BK;

4)  уравнение диагонали BD;

5)  тангенс угла между диагоналями параллелограмма.

Записать общие уравнения найденных прямых. Построить чертеж.

Решение.

Сначала построим чертеж. Построим в прямоугольной декартовой системе координат точки , , . Построим отрезки и .

Рис. 1

Достроим полученный рисунок до параллелограмма и нанесем на чертеж высоту BK.

Рис. 2

1)  Составим уравнение прямой AD.

А) Предварительно найдем уравнение прямой BС. Уравнение прямой, проходящей через точки и , имеет вид

(3.1)

По условию , . Подставим координаты точек и в уравнение (3.1): , т. е. .

Запишем полученное уравнение в общем виде, то есть в виде . Для этого в последнем уравнении избавимся от знаменателей и проведем преобразования, перенося все слагаемые в левую часть равенства: или .

Из этого уравнения выразим : ; . Получили уравнение вида – уравнение с угловым коэффициентом.

Б) Воспользуемся тем фактом, что противоположные стороны параллелограмма параллельны. Составим искомое уравнение прямой AD как уравнение прямой, проходящей через точку параллельно прямой .

Уравнение прямой, проходящей через данную точку в данном направлении, имеет вид

(3.2)

Где направление определяется угловым коэффициентом .

Условие параллельности двух прямых и имеет вид

(3.3)

По условию задачи , прямая . Подставим координаты точки в уравнение (3.2): . Так как прямая параллельна прямой , то в силу формулы (3.3) их угловые коэффициенты совпадают. Угловой коэффициент прямой равен , следовательно, уравнение прямой имеет вид .

Запишем уравнение прямой в общем виде. Для этого раскроем скобки и все слагаемые перенесем в левую часть равенства: . Умножим обе часть равенства на (-2) и получим общее уравнение прямой : .

Запишем уравнение прямой в виде с угловым коэффициентом. Для этого выразим из общего уравнения: .

2) Составим уравнение высоты , проведенной из вершины на сторону как уравнение прямой, проходящей через точку перпендикулярно прямой .

Условие перпендикулярности двух прямых и имеет вид

(3.4)

Подставим координаты точки в уравнение (3.2): . Так как высота перпендикулярна прямой , то их угловые коэффициенты связаны соотношением (3.4). Угловой коэффициент прямой равен , следовательно, угловой коэффициент высоты равен и уравнение прямой имеет вид . Запишем уравнение высоты в общем виде: . Запишем это же уравнение в виде с угловым коэффициентом: .

3) Найдем длину высоты как расстояние от точки до прямой .

Расстояние от точки до прямой представляет собой длину перпендикуляра, опущенного из точки на прямую и определяется формулой

(3.5)

Так как перпендикулярна , то длина может быть найдена с помощью формулы (3.5). По условию , прямая определяется уравнением . В силу формулы (3.5) длина высоты равна =.

4) Найдем уравнение диагонали как уравнение прямой, проходящей через точки И , где – середина отрезка .

А) Если и , то координаты точки – середины отрезка , определяются формулами

(3.6)

По условию , . В силу формул (3.6) имеем: , . Следовательно .

Б) Так как точка пересечения диагоналей является их серединой, то точка (середина отрезка ) является точкой пересечения диагоналей и диагональ проходит через точку .

Воспользуемся уравнением (3.1). По условию , . В силу формулы (3.1) уравнение прямой (диагонали ) имеет вид: или . Запишем это уравнение в общем виде: . Запишем это же уравнение в виде с угловым коэффициентом: .

5) Найдем тангенс угла между диагоналями и .

А) Найдем уравнение диагонали как уравнение прямой, проходящей через две данные точки.

Воспользуемся уравнением (3.1). По условию , . Следовательно, . Общее уравнение диагонали имеет вид , уравнение с угловым коэффициентом – вид , угловой коэффициент прямой равен .

Б) Уравнение диагонали имеет вид , ее угловой коэффициент .

В) Тангенс угла между прямыми и определяется формулой

Следовательно, . Отсюда .

Задача №2.

Условие задачи №2 несколько различается в зависимости от номера варианта контрольной работы. Приведем решения простейших задач, входящих в это задание.

1) Составить уравнение плоскости, проходящей через точки , , .

Решение.

Уравнение плоскости, проходящей через точки , , имеет вид:

(3.7)

Тогда уравнение плоскости в силу уравнения (3.7) имеет вид или .

Запишем полученное уравнение в общем виде, т. е. в виде . Для этого раскроем определитель по первой строке . После преобразований получим: .

2) Найти нормальный вектор плоскости .

Решение.

Нормальный вектор – это вектор, перпендикулярный плоскости. Если плоскость задана общим уравнением , то нормальный вектор имеет координаты .

Рис. 3

Для плоскости нормальным является вектор =.

Отметим, что любой вектор, коллинеарный вектору = так же является нормальным вектором плоскости . Таким образом, при каждом ненулевом вектор с координатами будет являться нормальным вектором рассматриваемой плоскости.

3) Найти косинус угла между плоскостями и .

Решение.

Угол между двумя плоскостями и представляет собой угол между их нормальными векторами и определяется равенством

Для плоскости координаты нормального вектора определяются равенствами , , . Для плоскости – равенствами , , . Следовательно, =.

4) Составить уравнение плоскости , проходящей через точку параллельно плоскости : .

Решение.

Уравнение плоскости, проходящей через точку , имеет вид

(3.8)

Подставим в уравнение (3.8) координаты точки : .

Условие параллельности плоскостей и имеет вид

(3.9)

Так как плоскости и параллельны, то в качестве нормального вектора Плоскости можно взять нормальный вектор плоскости , т. е. в формуле (3.9) отношение можно принять равным единице. Следовательно, уравнение плоскости примет вид . Запишем это уравнение в общем виде: .

5) Найти расстояние от точки до плоскости : .

Решение.

Расстояние от точки до плоскости представляет собой длину перпендикуляра, опущенного из точки на плоскость, и определяется формулой

(3.10)

Для плоскости координаты нормального вектора определяются равенствами , , . Следовательно, .

6) Составить канонические уравнения прямой, проходящей через точки и .

Решение.

Уравнения прямой, проходящей через точки и имеют вид

(3.11)

Так как , , то в силу (3.11) получим уравнения или .

7) Найти направляющий вектор прямой .

Решение.

Направляющий вектор – это вектор, параллельный прямой.

Если прямая задана каноническими уравнениями , то направляющий вектор имеет координаты .

Рис. 4

Для рассматриваемой прямой направляющим вектором является вектор .

Отметим, что любой вектор, коллинеарный вектору так же является направляющим вектором прямой . Таким образом, при каждом ненулевом вектор с координатами будет являться направляющим вектором рассматриваемой прямой.

8) Найти косинус угла между прямыми и .

Решение.

Угол между двумя прямыми и представляет собой угол между их направляющими векторами и определяется равенством

Для прямой координаты направляющего вектора определяются равенствами , , . Для прямой – равенствами , , . Значит, .

9) Составить канонические уравнения прямой , проходящей через точку параллельно прямой : .

Решение.

Канонические уравнения прямой имеют вид . Здесь – координаты точки, через которую проходит прямая.

В канонические уравнения прямой подставим координаты точки . Получим: .

Условие параллельности прямых и имеет вид

(3.12)

Так как прямые и параллельны, то в качестве направляющего вектора прямой можно взять направляющий вектор прямой , т. е. в формуле (3.12) отношение можно принять равным единице. Следовательно, уравнение прямой примет вид .

10) Найти угол между прямой : и плоскостью : .

Решение.

Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость. Угол между прямой и плоскостью равен , где – угол между направляющим вектором прямой и нормальным вектором плоскости.

Рис. 5

Угол между прямой и плоскостью определяется формулой

Для плоскости : координаты нормального вектора определяются равенствами , , . Для прямой : координаты направляющего вектора – равенствами , , . Синус угла между прямой и плоскостью равен =. Следовательно, .

11) Составить уравнение плоскости , проходящей через точку перпендикулярно прямой : .

Решение.

Уравнение плоскости, проходящей через данную точку, имеет вид .

Подставим в указанное уравнение координаты точки . Получим: .

Условие перпендикулярности плоскости и прямой имеет вид

(3.13)

Так как искомая плоскость перпендикулярна прямой , то в качестве нормального вектора плоскости можно взять направляющий вектор прямой , т. е. в формуле (3.13) отношение можно принять равным единице. Следовательно, уравнение плоскости примет вид . Запишем это уравнение в общем виде: .

12) Составить канонические уравнения прямой , проходящей через точку перпендикулярно плоскости : .

Решение.

Канонические уравнения прямой, проходящей через данную точку, имеют вид .

Подставим в эти уравнения координаты точки . Получим:

Условие перпендикулярности прямой и плоскости имеет вид .

Так как прямая перпендикулярна плоскости , то в качестве направляющего вектора прямой можно взять нормальный вектор плоскости , т. е. в формуле (3.13) отношение можно принять равным единице. Следовательно, уравнение прямой примет вид: .

13) Найти координаты точки пересечения прямой : и плоскости : .

Решение.

Координаты точки пересечения прямой и плоскости представляют собой решение системы

(3.14)

Запишем параметрические уравнения прямой : и подставим выражения для в уравнение плоскости : . Отсюда ; . Подставим найденное значение в параметрические уравнения прямой : . Следовательно, .

Задача №3.

К кривым второго порядка относятся эллипс (рис.6), гипербола (рис. 7 и 8), парабола (рис. 9-12). Приведем рисунки и канонические уравнения этих кривых.

Эллипс

Рис. 6

Гипербола Гипербола .

Рис. 7 Рис. 8

Парабола Парабола

Рис. 9

Рис. 10

Парабола Парабола

Рис. 11

Рис. 12

Приведем примеры решения задачи №3.

Пример 1. Привести уравнение кривой второго порядка к каноническому виду и построить кривую.

Решение.

Для приведения уравнения кривой второго порядка к каноническому виду применяют метод выделения полного квадрата.

Сгруппируем слагаемые, содержащие текущие координаты. Коэффициенты при и вынесем за скобки: .

Выделим полный квадрат: . Отсюда . Разделим обе части равенства на 25: . Запишем полученное уравнение в каноническом виде: .

Выполним параллельный перенос осей координат по формулам . При таком преобразовании начало координат переносится в точку , уравнение эллипса принимает канонический вид .

В нашем примере , , , .

Итак, рассматриваемое уравнение определяет эллипс с центром в точке и полуосями и .

Рис. 13

Пример 2. Привести уравнение кривой второго порядка к каноническому виду и построить кривую.

Решение.

Как и в предыдущем примере, сгруппируем слагаемые, содержащие текущие координаты: .

В скобках выделим полный квадрат: ; . Отсюда .

Выполним замену переменных . После этого преобразования уравнение параболы принимает канонический вид , вершина параболы в системе координат расположена в точке .

Рис. 14

Задача №4.

Кривая задана в полярной системе координат уравнением .

Требуется:

1)  найти точки, лежащие на кривой, давая значения через промежуток, равный , начиная от до ;

2)  построить полученные точки;

3)  построить кривую, соединив построенные точки (от руки или с помощью лекала);

4)  составить уравнение этой кривой в прямоугольной декартовой системе координат.

Решение.

Сначала построим таблицу значений и :

	0
	2,00	1,92	1,71	1,38	1,00	0,62	0,29	0,08	0,00	0,08	0,29	0,62	1,00	1,38	1,71	1,92

Построим эти точки в полярной системе координат. Полярная система координат состоит из начала координат (полюса) и полярной оси . Координаты точки в полярной системе координат определяются расстоянием от полюса (полярным радиусом) и углом между направлением полярной оси и полярным радиусом (полярным углом). Для того, чтобы построить точку , необходимо построить луч, выходящий из точки под углом к полярной оси; отложить на этом луче отрезок длиной .

Рис. 15

Построим все точки, определенные в таблице и соединим их плавной линией

Рис. 16

Запишем уравнение рассматриваемой кривой в прямоугольной декартовой системе координат. Для этого воспользуемся формулами перехода от декартовой к полярной системе координат.

Если полюс совпадает с началом координат прямоугольной декартовой системы координат, полярная ось – с осью абсцисс, то между прямоугольными декартовыми координатами и полярными координатами существует следующая связь:

,

Откуда

Рис. 17

Итак, в уравнении исходной кривой , . Поэтому уравнение принимает вид . После преобразований получим уравнение .

Задача №5.

Построить на плоскости геометрическое место точек, определяемое неравенствами

1)

2)

Решение.

Для того, чтобы решить неравенство на плоскости, надо построить график линии . Кривая разбивает плоскость на части, в каждой из которых выражение сохраняет свой знак. Выбирая пробную точку в каждой из этих частей, найдем часть плоскости, являющуюся искомым решением неравенства.

1) Построим прямые и , заштрихуем область, в которой . Затем построим параболу и заштрихуем область, содержащую ось симметрии параболы (расположенную внутри параболы); построим прямую и заштрихуем область, лежащую выше прямой. Пересечение всех заштрихованных областей и определит множество точек, представляющих решение рассматриваемой системы.

Рис. 18

2) Построим линию, определяемую уравнением . Эта линия представляет собой ту часть окружности или , на которой . Далее построим прямую (). Решением рассматриваемого двойного неравенства является часть плоскости, расположенная между нижней половиной окружности с центром в точке радиуса прямой .

Рис. 19

< Предыдущая		Следующая >

Диагонали параллелограмма в точке пересечения делятся пополам, значит точка пересечения является серединой отрезков АС и BD

Найдем координаты точки D (x; y; z) исходя из формулы нахождения координат середины отрезка^

(xA+xC) / 2 = (xB+xD) / 2; (yA+yC) / 2 = (yB+yD) / 2; (zA+zC) / 2 = (zB+zD) / 2

(3+3) / 2 = (1+х) / 2⇒1+x=6⇒x=5

(4+7) / 2 = (2+y) / 2⇒2+y=11⇒y=9

(-1-2) / 2 = (4+z) / 2⇒4+z=-3⇒z=-7

D (5; 9; -7)

Уравнение прямой, проходящей через 2 точки

(x-x1) / (x2-x1) = (y-y1) / (y2-y1) = (z-z1) / (z2-z1)

Уравнение АВ

(x-3) / (1-3) = (y-4) / (2-4) = (z+1) / (4+1)

(x-3) / (-2) = (y-4) / (-2) = (z+1) / 5

Уравнение ВС

(x-1) / (3-1) = (y-2) / (7-2) = (z-4) / (-2-4)

(x-1) / 2 = (y-2) / 5 = (z-4) / (-6)

Уравнение CD

(x-3) / (5-3) = (y-7) / (9-7) = (z+2) / (-7+2)

(x-3) / 2 = (y-7) / 2 = (z+2) / (-5)

Уравнение AD

(x-3) / (5-3) = (y-4) / (9-4) = (z+1) / (-7+1)

(x-3) / 2 = (y-4) / 5 = (z+1) / (-5)