Как найти уравнение стороны ас треугольника авс

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Составить уравнение стороны ab треугольника abc

Как составить уравнение сторон треугольника по координатам его вершин?

Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.

Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)

Составить уравнения сторон треугольника.

1) Составим уравнение прямой AB, проходящей через 2 точки A и B.

Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:

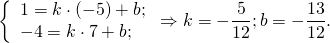
Таким образом, уравнение стороны AB

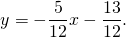
2) Прямая BC проходит через точки B(7;-4) и C(3;7):

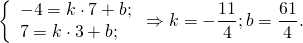
Отсюда уравнение стороны BC —

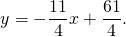
3) Прямая AC проходит через точки A(-5;1) и C(3;7):

УСЛОВИЕ:

Даны вершины треугольника ABC. Найти: а) уравнение стороны AB; б) уравнение высоты CH; в) уравнение медианы AM; г) точку персечения медианы AM и высоты CH; д) уравнение прямой, проходящей через вершину C параллельно стороне AB; е) расстояние от точки C до прямой AB
A(-3,8); B(-6;2); C(0,-5)

РЕШЕНИЕ ОТ u821511235 ✪ ЛУЧШЕЕ РЕШЕНИЕ

Добавил vk247797756 , просмотры: ☺ 17346 ⌚ 2018-11-27 17:51:50. математика 1k класс

Решения пользователей

Написать комментарий

Делим обе части равенства на π

и умножаем на 4

+pi k, k in Z
Можно правую часть записать в виде двух ответов:

x=1+8n in Z : это . [b] -15; -7; 1; 9; 17; ..[/b].

x=3+ 8n, n in Z : это[b] -13; -5; 3; 11; . [/b]

[b]x=-5 – наибольшее отрицательное [/b]

О т в е т. x=1+8n in Z или x=3+ 8n, n in Z

корни чередуются так:

. -15;-13;-7;-5; 1;3; 9;11; 17; 19; .

[b]x=-5 – наибольшее отрицательное [/b] (прикреплено изображение)

a=1 – старший коэффициент
b=1 – средний коэффициент
с=-2 – свободный член

4.
x^2=a-5
При a-5=0 ⇒ при а=5
уравнение имеет один корень х=0

5.
Δ Прямоугольный, так как верно равенство: b^2=a^2+c^2
5^2=3^2+4^2
25=9+16
Значит, ∠ B=90 градусов и ∠ А+ ∠ С=90 градусов.

∠ А- ∠ С=36 градусов.
∠ А+ ∠ С=90 градусов.

складываем оба равенства:

2* ∠ А=126 градусов.

По формулам приведения:

sin^2x+sinx-2=0
D=9
sinx=-2 или sinx=1

sinx=-2 уравнение не имеет корней, -1 ≤ sinx ≤ 1

sinx=1 ⇒ x=(π/2)+2πk, k ∈ Z или х=90 ° +360 ° *k, k ∈ Z

Найдем корни, принадлежащие указанному отрезку с помощью неравенства:

-286 ° ≤ 90 ° +360 ° *k ≤ 204 °

-286 °-90 ° ≤ 360 ° *k ≤ 204 ° -90 °

-376 ° ≤ 360 ° *k ≤ 114 °

Неравенство верно при k=[green]-1[/green] и k=[red]0[/red]

Значит, указанному отрезку принадлежат два корня:

x=90 ° +360 °* ([green]-1[/green])=-270 °

x=90 ° +360 °*[red]0[/red]=90 °

7. KT- средняя линия трапеции:

Cредняя линия трапеции делит высоту трапеции пополам ( см. рис)

Высоты треугольников АКО и СОК равны половине высоты трапеции

S_( Δ АКО)+S_( Δ COK)=44

S_( Δ АКО)+S_( Δ COK)=KO*(h/4) +OT*(h/4)=

О т в е т. [b]176[/b]

B=-2
[i]l[/i]=8 – количество ребер четырехугольной пирамиды

Что ты хочешь узнать?

Ответ

Проверено экспертом

а) Длина стороны АВ:

б) Уравнение сторон АВ и ВС и их угловые коэффициенты: АВ : Х-Ха = У-Уа
Хв-Ха Ув-Уа

Получаем уравнение в общем виде:
АВ: 4х – 8 = 3у – 6 или
АВ: 4х – 3у – 2 = 0
Это же уравнение в виде у = кх + в:
у = (4/3)х – (2/3).
Угловой коэффициент к = 4/3.

ВС: 2х + у – 16 = 0.
ВС: у = -2х + 16.
Угловой коэффициент к = -2.

в) Внутренний угол В:Можно определить по теореме косинусов.
Находим длину стороны ВС аналогично стороне АВ:
BC = √((Хc-Хв)²+(Ус-Ув)²) = 2.236067977
cos В= ( АВ²+ВС²-АС²) / ( 2*АВ*ВС) = 0.447214
Угол B = 1.107149 радиан = 63.43495 градусов.

Можно определить векторным способом:
Пусть координаты точек
A: (Xa, Ya) = (2; 2) .
B: (Xb, Yb) = (5; 6).
С: (Xc, Yc) = (6; 4).

Находим координаты векторов AB и BС:
AB= (Xb-Xa; Yb-Ya) = ((5 – 2); (6 – 2)) = (3; 4);
BС= (Xc-Xв; Yс-Yв) = ((6 – 5); (4 – 6)) = (1; -2).
Находим длины векторов:
|AB|=√((Xb-Xa)² + (Yb-Ya)^2) = 5 ( по пункту а)
|ВС|=√((Xс-Xв)²+(Yс – Yв) = √(1²+(-2)²) = √5 = 2.236067977 .
b=cos α=(AB*ВС)/(|AB|*|ВС|
AB*ВC = (Xв – Xa)*(Xc – Xв) + (Yв – Ya)*(Yc – Yв) =
= 3*1 + 4*(-2) = 3 – 8 = -5.
b = cosα = |-5| / (5*2.236067977) = 5 / 11.18034 = 0.4472136 20
Угол α=arccos(b) = arc cos 0.4472136 = 1.1071487 радиан = 63.434949°.

г) Уравнение медианы АЕ.
Находим координаты точки Е (это основание медианы АЕ), которые равны полусумме координат точек стороны ВС.

3x – 6 = 3,5y – 7
3x – 3,5y + 1 =0, переведя в целые коэффициенты:
6х – 7у + 2 = 0,
С коэффициентом:
у = (6/7)х + (2/7) или
у = 0.85714 х + 0.28571.

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik

http://4apple.org/sostavit-uravnenie-storony-ab-treugolnika-abc/

[/spoiler]

Пример 1:

Построить треугольник, вершины которого находятся в точках А (2; 4), В (-3; 2), С (-3; -4). Найти:

1) уравнения сторон треугольника АВС;

2) координаты точки пересечения медиан;

3) длину и уравнение высоты, опущенной из вершины А;

4) площадь треугольника.

Решение от преподавателя:

Уравнение, прямой проходящей через две точки
1) Уравнения сторон треугольника АВС

2) Координаты точки пересечения медиан

Медиана – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Координаты т. E как середины отрезка ВС.

Уравнение АЕ

Координаты т. К как середины отрезка АВ.

Уравнение СК

3) Длина и уравнение высоты, опущенной из вершины А

Расстояние от точки до прямой

Уравнение прямой, проходящей через точку перпендикулярно другой прямой

Уравнение AN

4) Площадь треугольника

Длина ВС

Пример 2:

Решение от преподавателя:

Пример 3:

По координатам вершин треугольника ABC найти:

• периметр треугольника;
• уравнения сторон AB и BC;
• уравнение высоты AD; угол ABC;
• площадь треугольника.

Сделать чертеж.

А(1; 2); В (–1; 2); С(3; 0).

Решение от преподавателя:

Пример 4:

Даны координаты вершин треугольникаА, В, С.

Требуется найти:

1) уравнение и длину стороны ВС;

2) уравнение и длину высоты, проведённой из вершиныА;

3) уравнение медианы, проведённой из вершиныА;

4) площадь треугольника.

Сделать чертёж.

А(4;-3), B(-2;-1), C(3;-2).

Решение от преподавателя:

Пример 5:

Решение от преподавателя:

1)

2)

3) Находим координаты точки М – середины стороны ВС:

       

Определяем длину медианы АМ:

4) Составляем уравнение медианы – прямой АМ:

5) Если ВН – высота, проведенная из вершины В к стороне АС, то, поскольку ВН проходит через точку В перпендикулярно вектору , то составляем уравнение высоты по формуле , где (a,b) – координаты вектора перпендикулярного искомой прямой,  – координаты точки, принадлежащей этой прямой. Находим координаты вектора АС:

и подставляем в формулу, ,

6) Длину высоты ВН находим как расстояние от точки В до прямой АС:

7) Площадь треугольника АВС:

8) Находим угол ВАС треугольника:

9) Составляем уравнение прямой, проходящей через т.А параллельно ВС:

Ответ:

Пример 6:

Решение от преподавателя:

1. Уравнение прямой 
   Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями: 
   
   Уравнение прямой AB 
   Каноническое уравнение прямой: 
   
   или 
   
   или 
   y = ^-3/₇x + ¹⁶/₇ или 7y + 3x – 16 = 0 
2. Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 
   
   
   M(3;1) 
   Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-8;2) и М(3;1), поэтому: 
   Каноническое уравнение прямой: 
   
   или 
   
   или 
   y = ^-1/₁₁x + ¹⁴/₁₁ или 11y + x – 14 = 0 
3. Уравнение высоты через вершину C 
   Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 
   
   Найдем уравнение высоты через вершину C 
   
   y = ⁷/₃x + ⁶²/₃ или 3y -7x – 62 = 0
4. уравнение параллельной прямой AB, проходящей через точку (-8,2)
   Уравнение прямой AB: y = ^-3/₇x + ¹⁶/₇
   Уравнение KN параллельно AB находится по формуле:
   y – y₀ = k(x – x₀)
   Подставляя x₀ = -8, k = ^-3/₇, y₀ = 2 получим:
   y-2 = ^-3/₇(x-(-8))
   или
   y = ^-3/₇x – ¹⁰/₇ или 7y + 3x +10 = 0

Пример 7:

Даны координаты вершин треугольника: A(1,1), B(4,13), C(10,5). 

Решение от преподавателя:

4) Уравнение высоты через вершину C 
Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 

Найдем уравнение высоты через вершину C 

y = ^-1/₄x + ¹⁵/₂ или 4y +x -30 = 0 
Данное уравнение можно найти и другим способом. Для этого найдем угловой коэффициент k₁ прямой AB. 
Уравнение AB: y = 4x -3, т.е. k₁ = 4 
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k₁*k = -1. 
Подставляя вместо k₁ угловой коэффициент данной прямой, получим: 
4k = -1, откуда k = ^-1/₄ 
Так как перпендикуляр проходит через точку C(10,5) и имеет k = ^-1/₄,то будем искать его уравнение в виде: y-y₀ = k(x-x₀). 
Подставляя x₀ = 10, k = ^-1/₄, y₀ = 5 получим: 
y-5 = ^-1/₄(x-10) 
или 
y = ^-1/₄x + ¹⁵/₂ или 4y + x – 30 = 0 
Найдем точку пересечения с прямой AB: 
Имеем систему из двух уравнений: 
y -4x +3 = 0 
4y + x – 30 = 0 
Из первого уравнения выражаем y и подставим во второе уравнение. 
Получаем: 
x = ⁴²/₁₇ 
y = ¹¹⁷/₁₇ 
D(⁴²/₁₇;¹¹⁷/₁₇) 
Длина высоты треугольника, проведенной из вершины C 
Расстояние d от точки M₁(x₁;y₁) до прямой Ax + By + С = 0 равно абсолютному значению величины: 

Найдем расстояние между точкой C(10;5) и прямой AB (y -4x +3 = 0) 

5,7) Уравнение медианы треугольника 
Обозначим середину стороны BC буквой Е. Тогда координаты точки Е найдем по формулам деления отрезка пополам. 


Е(7;9) 
Уравнение медианы AЕ найдем, используя формулу для уравнения прямой, проходящей через две заданные точки A(1;1) иЕ(7;9), поэтому: 
Каноническое уравнение прямой: 

или 

или 
y = ⁴/₃x ^-1/₃ или 3y -4x +1 = 0 
Найдем длину медианы. 
Расстояние между двумя точками выражается через координаты формулой: 

6) CD–диаметр окружности. Центр окружности точка О лежит в середине отрезка CD

Уравнение окружности  (x-x₀)²+(y-y₀)²=r²

(x-106/17)²+(y-101/17)²=256/17 

8) Уравнение прямой, параллельной CD, проходящей через точку A 

Пример 8:

Решение от преподавателя:

Точка D – середина стороны АВ , ее координаты равны полусумме координат А и В. Получим D(1, -1)

Пример 9:

Даны координаты вершин треугольника АВС: А (3,-2), В (-5,-4),  С (-1,6).

Найдите: 1) уравнения сторон треугольника АВ, ВС и АС;

2) периметр (сумму длин) треугольника;

3) уравнение высоты СН;

4) расстояние d от точки С до прямой АВ;

5) сделайте чертеж.

Решение от преподавателя:

Решение.

1) уравнения сторон треугольника АВ, ВС и АС

Уравнение, прямой проходящей через две точки

2) периметр (сумму длин) треугольника

Расстояние между двумя точками

3) уравнение высоты СН

Уравнение прямой, проходящей через точку перпендикулярно другой прямой

4) расстояние d от точки С до прямой АВ

Расстояние от точки до прямой

Пример 10:

Даны вершины A (x₁; y₁), B (x₂; y₂), C (x₃; y₃)    треугольника.

Найти: 1) уравнение стороны AB;

2) уравнение медианы, проведенной из вершины C;

3) уравнение высоты, проведенной из вершины C ;

4) уравнение прямой, проходящей через вершину C параллельно стороне AB .

A (6; 0), B (2; − 6), C (−3; −9).

Решение от преподавателя:

Пример 11:

Решение от преподавателя:

Пример 12:

Дан треугольник  с координатами вершин найти:

а) длину стороны AB;

б) косинус угла ABC;

в) площадь треугольника ABC (через векторное произведение);

Решение от преподавателя:

Пример 13:

Решение от преподавателя:

Даны координаты вершин треугольника: A(6,0), B(2,-6), C(-3,-9). 
1) Уравнение прямой 
Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями: 

Уравнение прямой AB 
Каноническое уравнение прямой: 

или 

или 
y = ³/₂x -9 или 2y -3x +18 = 0 

2) Уравнение медианы треугольника 
Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 


M(4;-3) 
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-3;-9) и М(4;-3), поэтому: 
Каноническое уравнение прямой: 

или 

или 
y = ⁶/₇x ^-45/₇ или 7y -6x +45 = 0 
3) Уравнение высоты через вершину C 
Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 

Найдем уравнение высоты через вершину C 

y = ^-2/₃x -11 или 3y +2x + 33 = 0 
4) Уравнение прямой, параллельной AB, проходящей через С(-3,-9) 
Уравнение прямой AB: 2y -3x +18 = 0 
Уравнение СN параллельно AB находится по формуле: 

Или     2y -3x +9 = 0 

Пример 14:

Даны вершины треугольника А(8,1), В(0,3), С(-2,-3). Напишите уравнения стороны AB, медианы AD, высоты BE.

Решение от преподавателя:

Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 


M(-1;0) 
Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(8;1) и М(-1;0), поэтому: 

или 

или 
y = ¹/₉x + ¹/₉ или 9y -x – 1 = 0 
3) Уравнение высоты через вершину B

Пример 15:

Дан треугольник АВС. Найти:

а) величину угла А;

б) уравнение стороны АС;

в) уравнение высоты и медианы, опущенных из вершины В.

Сделать чертеж.

А(-1,2); В(1,3); С(3,-4).

Решение от преподавателя:

Пример 16:

Треугольник задан вершинами А(-6; -2);  В(4; 8); С(2; -8). Найти:

а) уравнение прямой BN, параллельной  стороне АС;

б) уравнение медианы CD;

в) уравнение высоты АЕ;

Решение от преподавателя:

а) уравнение прямой BN, параллельной  стороне АС;

Уравнение прямой AC:

Каноническое уравнение прямой:

или

или
y = ^-3/₄x ^-13/₂ или 4y + 3x +26 = 0

Уравнение BN параллельно AC находится по формуле:
y – y₀ = k(x – x₀)
Подставляя x₀ = 4, k = ^-3/₄, y₀ = 8 получим:
y-8 = ^-3/₄(x-4)
или
y = ^-3/₄x + 11 или 4y + 3x – 44 = 0

б) уравнение медианы CD;

Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.


M(-1;3)
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(2;-8) и М(-1;3), поэтому:
Каноническое уравнение прямой:

или

или
y = ^-11/₃x ^-2/₃ или 3y + 11x +2 = 0

в) уравнение высоты АЕ;

Прямая, проходящая через точку Е₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:

Найдем уравнение высоты через вершину A

y = ^-1/₈x – ¹¹/₄ или 8y +x + 22 = 0

Пример 17:

A(1, 2), В(5, 8), С(11, 3).

Решение от преподавателя:

Пример 18:

В ∆ABC вершины имеют координаты точки А (-3;4), точки В (-4;-3), точки С (8;1).

Составить уравнения стороны (AB), высоты (ВК)  и медианы (CМ).

Решение от преподавателя:

Уравнение прямой AB
Каноническое уравнение прямой:

или

или
x +4 = 0 или x = -4
Уравнение прямой AC
Каноническое уравнение прямой:

или

или
y = ^-1/₄x + 3 или 4y + x – 12 = 0

Найдем уравнение высоты через вершину B

y = 4x + 13 или y -4x – 13 = 0

Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(8;1) и М(-4;¹/₂), поэтому:
Каноническое уравнение прямой:

или

или
y = ¹/₂₄x + ²/₃ или 24y -x – 16 = 0

Пример 19:

Дан треугольник ABC с координатами вершин A(-5;-3; 2), B(-2;-6;-3) и C(-2; 2;-1).
Найти:
а) длину стороны АВ;
б) косинус угла ABC;
в) площадь треугольника АВС (через векторное произведение).

Решение от преподавателя: