Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение показательных уравнений.
Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> –> Введите показательное уравнение
Решить уравнение
Немного теории.
Показательная функция, её свойства и график
Напомним основные свойства степени. Пусть а > 0, b > 0, n, m – любые действительные числа. Тогда
1) a n a m = a n+m
4) (ab) n = a n b n
7) a n > 1, если a > 1, n > 0
8) a n m , если a > 1, n n > a m , если 0 x , где a – заданное положительное число, x – переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, ( a neq 1)
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, ( a neq 1), не имеет корней, если ( b leqslant 0), и имеет корень при любом b > 0.
3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х
Показательные уравнения
Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, ( a neq 1), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, ( a neq 1) равны тогда и только тогда, когда равны их показатели.
Решить уравнение 2 3x • 3 x = 576
Так как 2 3x = (2 3 ) x = 8 x , 576 = 24 2 , то уравнение можно записать в виде 8 x • 3 x = 24 2 , или в виде 24 x = 24 2 , откуда х = 2.
Ответ х = 2
Решить уравнение 3 х + 1 – 2 • 3 x – 2 = 25
Вынося в левой части за скобки общий множитель 3 х – 2 , получаем 3 х – 2 (3 3 – 2) = 25, 3 х – 2 • 25 = 25,
откуда 3 х – 2 = 1, x – 2 = 0, x = 2
Ответ х = 2
Решить уравнение 3 х = 7 х
Так как ( 7^x neq 0 ) , то уравнение можно записать в виде ( frac<3^x> <7^x>= 1 ), откуда ( left( frac<3> <7>right) ^x = 1 ), х = 0
Ответ х = 0
Решить уравнение 9 х – 4 • 3 х – 45 = 0
Заменой 3 х = t данное уравнение сводится к квадратному уравнению t 2 – 4t – 45 = 0. Решая это уравнение, находим его корни: t1 = 9, t2 = -5, откуда 3 х = 9, 3 х = -5.
Уравнение 3 х = 9 имеет корень х = 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ х = 2
Решить уравнение 3 • 2 х + 1 + 2 • 5 x – 2 = 5 х + 2 х – 2
Запишем уравнение в виде
3 • 2 х + 1 – 2 x – 2 = 5 х – 2 • 5 х – 2 , откуда
2 х – 2 (3 • 2 3 – 1) = 5 х – 2 ( 5 2 – 2 )
2 х – 2 • 23 = 5 х – 2 • 23
( left( frac<2> <5>right) ^ = 1 )
x – 2 = 0
Ответ х = 2
Решить уравнение 3 |х – 1| = 3 |х + 3|
Так как 3 > 0, ( 3 neq 1), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х – 1) 2 = (х + 3) 2 , откуда
х 2 – 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1
Уравнения
Решение уравнений онлайн
Если вы это читаете, значит вас интересует вопрос решения уравнений.
Да, наши калькуляторы могут решить все уравнения, которые встречаются в школьном курсе и не только. Но нужно понимать, что большинство уравнений имеют несколько способов решения, а калькулятор выдает лишь только какое-то одно.
Бесспорно все способы решения хороши по-своему, но каждому методу отводится свое место в программе обучения.
Поэтому не стоит злоупотреблять калькуляторами, если ваш школьный учитель или личный репетитор требует решить уравнение одним способом, а вы предоставляете ему альтернативное решение.
Да, это может быть похвально, но опытный педагог сразу поймет, что решение уравнения не ваше.
Калькулятор решения уравнений
Калькулятор уравнений незаменимый помощник. Именно помощник, а не решатель проблем. Всегда старайтесь своими силами решать уравнения, а калькулятор используйте в качестве проверки вашего ответа.
Для грамотного учителя не столько важен конечный ответ, сколько сам ход решения уравнения.
Как вы могли заметить, при решении некоторых уравнений, например, квадратных, калькулятор может выполнить три разных способа решения. Это разложение уравнения на множители, выделение полного квадрата или найти корни уравнения через дискриминант.
Попытайтесь сначала самостоятельно решить заданное уравнение, вспомните чему вас учили на уроке.
Даже если вы ошибетесь в числах, то ничего страшного, ученик имеет право на ошибку, главное правильно мыслить.
С нашим калькулятором уравнений вы с легкостью исправите допущенную в вычислениях ошибку.
Хотите решить задачу онлайн? Получите ответ на любую задачу по математике с подробным решением за несколько секунд, например, как решить уравнение.
Pocket Teacher искусственный интеллект, который 30 лет разрабатывали в МГУ
Получите онлайн-помощника в решении множества математических дисциплин. Решить любую задачу, например решить уравнение очень просто!
- Иррациональные
- Рациональные
- Тригонометрические
- Логарифмические
- Экспоненциальные
- С произвольными параметрами
- Показательные произвольной сложности
- Определенные
- Неопределенные
- Геометрические задачи можно вводить в текстовом виде
- Подробное решение для дифференциальных уравнений
- Системы дифференциальных уравнений
- Матрицы – посчитать определитель
- Пределы – пока без подробного решения
- Текстовые математические задачи
Решайте задачи, заданные в текстовом виде
- Геометрии
- Физике скоро
- Химии скоро
Pocket Teacher всегда под рукой
- мобильная версия
Сервис будет полезен всем, кто сталкивается с математикой
- Проверит домашнее задание: решите задачи или уравнения и сравните результат
- Поможет разобраться в теме, которую вы пропустили или не поняли
- Поможет подготовиться к ЕГЭ
- Проверит решение ребенка
- Поможет решить задачу
- Сэкономит на репетиторе
- Поможет подготовиться к поступлению в ВУЗ и вспомнить пройденный материал
- Выручит на контрольной и экзамене
- Решит задачи из курсовой
- Сэкономит время на решении сложных задач на старших курсах
- Станет спасением для тех, у кого математика непрофильный предмет
Pocket Teacher пользуются человек
Поступил в этом году на «вышку». Ваш сайт использовал для решения вступительных примеров и тестов. Всё понравилось! Четко, быстро и правильно. Спасибо! Буду использовать ваш ресурс и дальше, но уже в работе.
Нас всё устраивает. Ошибок в решениях выявлено не было. Приятный интерфейс. Решить уравнение очень просто и быстро.
Всё отлично работает, спасибо за помощь в решении сложных заданий! Решить задачу реально очень просто!
Очень удобный и полезный сервис. Очень устраивает! Спасибо!
Я пишу студентам научные работы, и использую ваш сайт для решения задач. Своим детям также решаю задачи и сложные примеры при помощи вашего сайта. Пока все разделы и интерфейс меня полностью устраивают.
Пока испробовал не все разделы сайта, но на данный момент меня все устраивает: быстро, правильно, профессионально.
Я являюсь мамой старшеклассника, и мой сын свято верит в то, что я могу решить по математике практически всё. Поэтому ваш сайт в данном случае меня прекрасно выручает! Никаких косяков как таковых не было!
С уважением, Ольга.
Благодарю за помощь, всё работает прекрасно! Очень благодарен разработчикам за такой сервис!
[spoiler title=”источники:”]
http://math24.biz/equation
http://www.pocketteacher.ru/
[/spoiler]

Получите пошаговые объяснения
Узнайте, как решать задачи, и покажите свою работу, а также получите определения для математических понятий
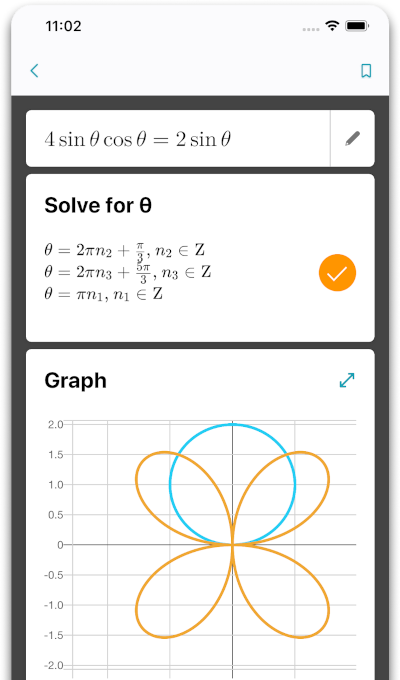
Создавайте графическое представление ваших математических задач
Мгновенно представьте любое уравнение в графическом виде, чтобы визуализировать вашу функцию и понять связь между переменными
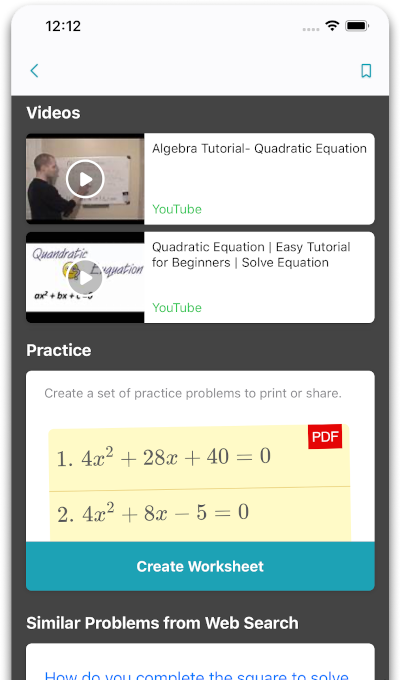
Практика, практика и ещё раз практика
Ищите дополнительные учебные материалы, такие как связанные журналы и видеоуроки
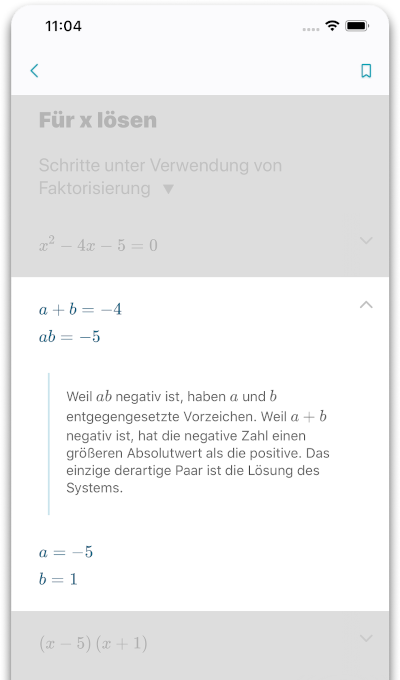
Получите справку по математике на своем языке
Работает на испанском, хинди, немецком и других языках
 Доброго времени!
Доброго времени!
Да… ребята! Мы сейчас входим в такую эру, когда типовые задачки, уже ранее решенные другими людьми — будут щелкаться искусственным интеллектом на раз-два… 👌
Например, возникли у вас трудности с решением мат. уравнения (с иксами, косинусами, логарифмами и прочими производными) — достаточно установить спец. приложение и сфотографировать данное уравнение.
Далее искусственный интеллект его проанализирует и выдаст вам правильное решение (да еще и построит график, если нужно)! Это просто мечта любого учащегося (и 10-20 лет назад это себе и представить нельзя было…).
Собственно, в этой заметке покажу вам как это все можно реализовать… ✌
*
Содержание статьи
- 1 Решение примеров/уравнений по математике, постройка графиков
- 1.1 ШАГ 1: приготовления или установка спец. приложения
- 1.2 ШАГ 2: вводим данные и получаем решение
- 1.2.1 Способ 1: с помощью фотографирования
- 1.2.2 Способ 2: вручную рисуем (пишем) формулу
- 1.3 Полевые условия: учебник математики
- 1.4 Дополнение (20.04.2021): в браузер Edge была встроена функция Math Solver

→ Задать вопрос | дополнить
Решение примеров/уравнений по математике, постройка графиков
ШАГ 1: приготовления или установка спец. приложения
Для работы в первую очередь нам понадобиться относительно современный смартфон и приложение Math Solver (от Microsoft!). Не перепутайте, схожих по названию приложений достаточно много!
👉 Math Solver (Ссылка на Google Play)
Это приложение от Microsoft, призванное помочь в решении математических уравнений. Важно сразу отметить: что оно рассчитано на новичков (и людей ничего не понимающих в математике).
Всё, что от вас потребуется — это сфотографировать на телефон непонятную для вас формулу. Дальше приложение рассчитает ее автоматически.
Впрочем, есть возможность ручного ввода уравнения…
Внешний вид окна Math Solver
Обратите внимание, что Math Solver может решать как самые простейшие арифметические действия, так и довольно сложные системы уравнений (с синусами, косинусами, логарифмами, производными, интегралами и т.д.). 👇
Какие уравнения может решать Math Solver
Примечание: для фотографирования формул у вас на смартфоне должна быть достаточно качественная камера (не менее 10 Мегапикселей!). Иначе, есть риск, что приложение просто не сможет разобрать, что у вас там на снимке…
*
ШАГ 2: вводим данные и получаем решение
Способ 1: с помощью фотографирования
И так, для первого теста я взял самое простое уравнение, написанное на клочке бумаге. После запуска программы — появился небольшой “прямоугольник”, в который нужно сфотографировать наш пример.

Фотографируем бумажку с уравнением
Далее приложение автоматически распознает с фотографии написанное и сразу же предлагает решение (см. пример ниже 👇).

Ответ найден
Кстати, что еще более подкупает — можно посмотреть не только ответ, а подробное пошаговое решение! 👇

Подробное решение
Добавлю, что такие простые задачки — Math Solver щелкает как орешки. Как правило, никаких проблем не возникает!
Способ 2: вручную рисуем (пишем) формулу
Решил я для теста несколько усложнить задачу и “нарисовал” на экране отличную от вышеприведенной формулу... (это Match Solver также допускает — т.е. приложение хорошо распознает даже рукописный текст!).

Нарисовал формулу пальцем! Math Solver
После, Math Solver представил вариант решения (действий уже несколько больше, но всё-таки…).
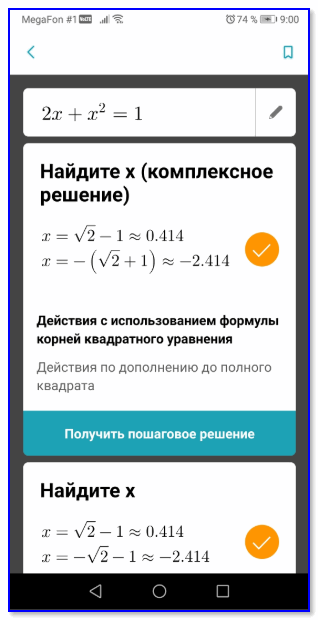
Комплексное решение найдено!

Подробное пошаговое решение уравнения
Кстати, график уравнения также представлен (строится автоматически).
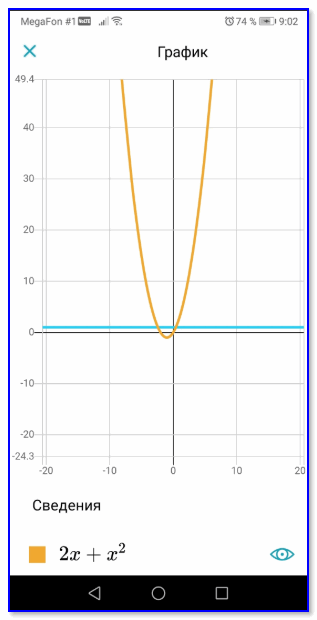
Построен автоматически график функции
*
Полевые условия: учебник математики
После всего вышеприведенного, решил я пробежаться по старым учебникам математики. Как приложение справится с ними…?
На удивление, больше 90% уравнение легко решаются практически в лёт! Достаточно выделить в прямоугольник нужную формулу и сфотографировать ее.

Пример из учебника
После в авто-режиме и решение и график.
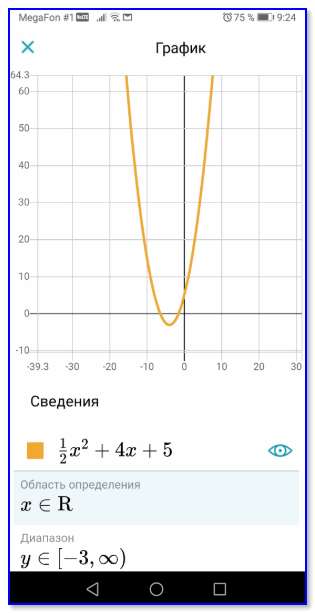
Ответ программы
Если сравнить с ответом в учебнике — как правило всё совпадает! 👌
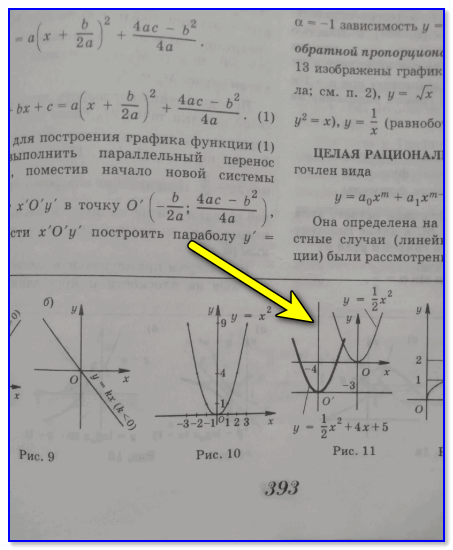
Ответ из учебника (для сравнения)
*
Единственное: иногда приложение неправильно читает дроби, знаки плюса, минуса, равно (прим.: когда бумага поистирается, некоторые символы становятся трудно-читаемыми). В этом случае уравнение нужно аккуратно переписать вручную на листок бумаги и уже с него фотографировать… 👌
*
Дополнение (20.04.2021): в браузер Edge была встроена функция Math Solver
Относительно недавно в браузер Edge (он встроен в Windows 10) была добавлена функция Math Solver! Теперь можно, не выходя из браузера, решать любые* уравнения, которые вам попадаются (в том числе и на картинках).
Покажу на примере, как ее включить, и как пользоваться…👇
*
1) Итак, сначала запускаем браузер Edge. У кого его нет – можно скачать отсюда (ссылка на офиц. сайт).

Windows 10 – Edge
2) Далее в адресной строке набираем edge://flags/ — с помощью поиска нужно найти функцию “Math Solver in…”, перевести ее в режим “Enabled” (т.е. включена) и перезагрузить браузер.
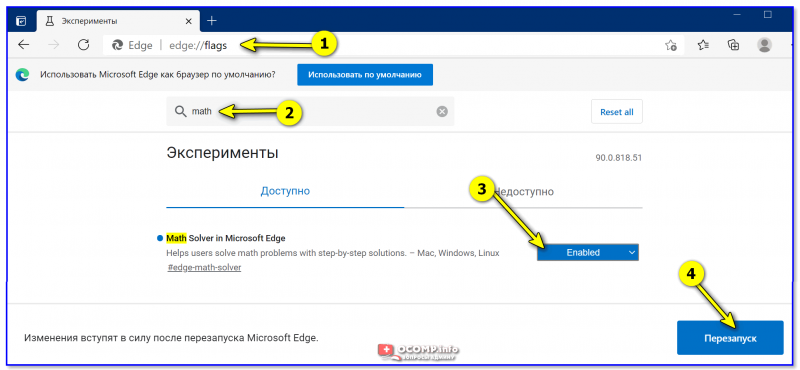
Включаем функцию для решения уравнений
3) После необходимо набрать в адресной строке edge://settings/appearance — и разрешить отображение кнопки для решения уравнений. 👇
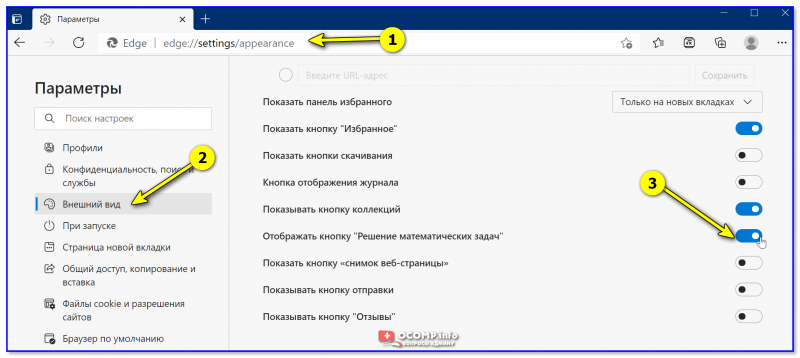
Отображать кнопку решения математических задач
4) Всё! Теперь находим уравнение, которое нужно решить, и:
- нажимаем по кнопке “Решение…” на панели задач браузера;
- выделяем нужное уравнение;
- нажимаем на кнопку “Решить”;
- Ждем… (5-10 сек. в среднем).
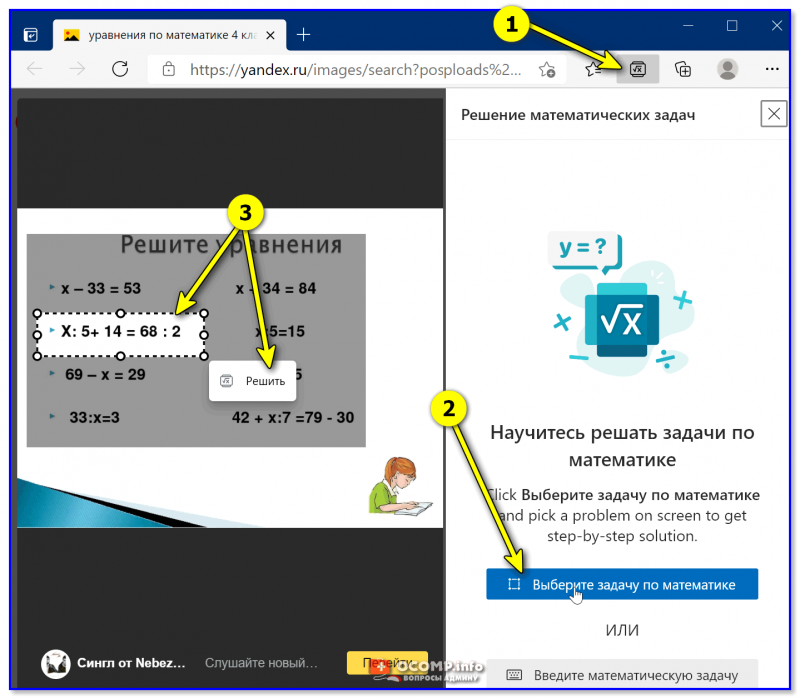
Выбираем задачку
5) На выходе получаем и ответ, и пошаговые действия (для его нахождения), и графики и пр. штуки. Удобно?! 😉
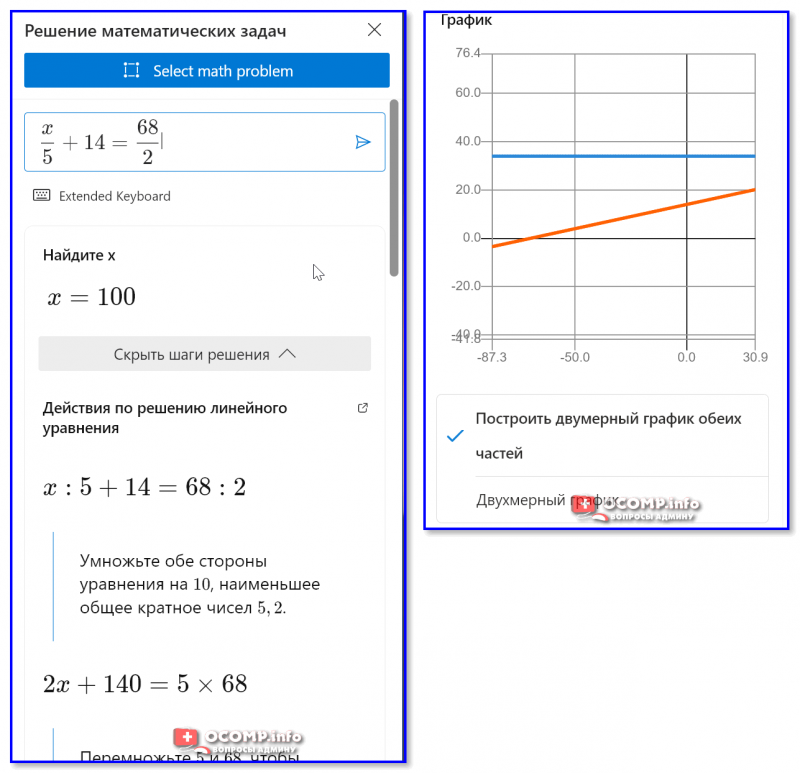
Решение (пример)
*
Дополнения по теме приветствуются…
Удачи!
👋
Первая публикация: 15.02.2020
Корректировка: 20.04.2021

Полезный софт:
-

- Видео-Монтаж
Отличное ПО для создания своих первых видеороликов (все действия идут по шагам!).
Видео сделает даже новичок!
-

- Ускоритель компьютера
Программа для очистки Windows от “мусора” (удаляет временные файлы, ускоряет систему, оптимизирует реестр).


Калькулятор онлайн.
Решение показательных уравнений.
Этот математический калькулятор онлайн поможет вам решить показательное уравнение.
Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное
решение с пояснениями, т.е. отображает процесс получения результата.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Вы можете посмотреть теорию о показательной функции и
общие методы решения показательных уравнений.
Примеры подробного решения >>
Введите показательное уравнение
Наши игры, головоломки, эмуляторы:
Немного теории.
Показательная функция, её свойства и график
Напомним основные свойства степени. Пусть а > 0, b > 0, n, m – любые действительные числа. Тогда
1) an am = an+m
2) ( frac{a^n}{a^m} = a^{n-m} )
3) (an)m = anm
4) (ab)n = an bn
5) ( left( frac{a}{b} right)^n = frac{a^n}{b^n} )
6) an > 0
7) an > 1, если a > 1, n > 0
8) an < am, если a > 1, n < m
9) an > am, если 0< a < 1, n < m
В практике часто используются функции вида y = ax, где a – заданное положительное число, x – переменная.
Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является
показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = ax, где а — заданное число, a > 0, ( a neq 1)
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень ax где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение ax = b, где а > 0, ( a neq 1), не имеет корней,
если ( b leqslant 0), и имеет корень при любом b > 0.
3) Показательная функция у = ax является возрастающей на множестве всех действительных чисел, если a > 1, и
убывающей, если 0 < a < 1.
Это следует из свойств степени (8) и (9)
Построим графики показательных функций у = ax при a > 0 и при 0 < a < 1.
Использовав рассмотренные свойства отметим, что график функции у = ax при a > 0 проходит через точку (0; 1) и
расположен выше оси Oх.
Если х < 0 и |х| увеличивается, то график быстро приближается к оси Oх (но не пересекает её).
Таким образом, ось Ох является горизонтальной асимптотой графика функции у = ax при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = ax при 0 < a < 1 также проходит через точку (0; 1) и расположен выше оси Ох.
Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является
горизонтальной асимптотой графика.
Если х < 0 и |х| увеличивается, то график быстро поднимается вверх.


Показательные уравнения
Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени.
Решение показательных уравнений часто сводится к решению уравнения ax = ab где а > 0, ( a neq 1),
х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, ( a neq 1) равны
тогда и только тогда, когда равны их показатели.
Решить уравнение 23x • 3x = 576
Так как 23x = (23)x = 8x, 576 = 242, то уравнение можно записать в виде
8x • 3x = 242, или в виде 24x = 242, откуда х = 2.
Ответ х = 2
Решить уравнение 3х + 1 – 2 • 3x – 2 = 25
Вынося в левой части за скобки общий множитель 3х – 2, получаем 3х – 2(33 – 2) = 25,
3х – 2 • 25 = 25,
откуда 3х – 2 = 1, x – 2 = 0, x = 2
Ответ х = 2
Решить уравнение 3х = 7х
Так как ( 7^x neq 0 ) , то уравнение можно записать в виде ( frac{3^x}{7^x} = 1 ), откуда ( left( frac{3}{7} right) ^x = 1 ), х = 0
Ответ х = 0
Решить уравнение 9х – 4 • 3х – 45 = 0
Заменой 3х = t данное уравнение сводится к квадратному уравнению t2 – 4t – 45 = 0. Решая это уравнение,
находим его корни: t1 = 9, t2 = -5, откуда 3х = 9, 3х = -5.
Уравнение 3х = 9 имеет корень х = 2, а уравнение 3х = -5 не имеет корней, так как показательная функция не
может принимать отрицательные значения.
Ответ х = 2
Решить уравнение 3 • 2х + 1 + 2 • 5x – 2 = 5х + 2х – 2
Запишем уравнение в виде
3 • 2х + 1 – 2x – 2 = 5х – 2 • 5х – 2, откуда
2х – 2 (3 • 23 – 1) = 5х – 2( 5 2 – 2 )
2х – 2 • 23 = 5х – 2• 23
( left( frac{2}{5} right) ^{x-2} = 1 )
x – 2 = 0
Ответ х = 2
Решить уравнение 3|х – 1| = 3|х + 3|
Так как 3 > 0, ( 3 neq 1), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х – 1)2 = (х + 3)2, откуда
х2 – 2х + 1 = х2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1
Обычные уравнения по-шагам

Примеры
- Линейные уравнения
-
-5*(3*x - 2)/7 + 4 = 7*x - 4 /9*(x - 3)
-
36/(x + 2) = 20/(x - 2)
-
(x - 14)/(x - 15) = 14/13
-
x^2 - x + 9 = (x + 2)^2
- Квадратные уравнения
-
x^2 - x + 5/3 = 0
-
10/(x - 4) + 4/(x - 10) = 2
- Тригонометрические уравнения
-
sin(2*x/5 + pi/3) = -1/2
-
cos(x) - sin(x) = 1
- уравнения с модулем
-
|x + 1| + |x^2 - 7| = 20
- Логарифмические уравнения
-
log(x^2 - 5) - log(x) = 7
- Показательные уравнения
-
7^(2*x + 1) + 4*7^(x - 1) = 347
- Уравнения с корнями
-
sqrt(x - 1) = x
-
(x - 1)^(1/3) = 4*x
- Кубические и высших степеней уравнения
-
x^3 + 5*x^2 = x - 1
-
x^4 - x^3 + 5*x^2 = 0
- уравнения с численным решением
-
(x - 1)^(1/3) = x^2/tan(x)
-
x - 1 = sin(x)
- Выразить x через y в уравнении
-
x-3y=7
-
2x+y=5
- Решить уравнение с параметром
-
(a^2-1)*x^2 = (8 + 9*a)*x + 1
- Решить уравнение с модулем
-
|x + 1| + |x – 5| = 20
- Решить квадратное уравнение
-
x^2 + 7*x + 12 = 0
- Решить уравнение с дробью
-
sqrt((1 - x) / (1 + x)) = 5
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
-
квадратные корни sqrt(x),
кубические корни cbrt(x) -
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
-
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x) -
натуральные логарифмы ln(x),
десятичные логарифмы log(x) -
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x) -
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) -
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x) -
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) -
знак числа:
sign(x) -
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x) -
Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
-
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- – умножение
- 3/x
- – деление
- x^2
- – возведение в квадрат
- x^3
- – возведение в куб
- x^5
- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
- Действительные числа
- вводить в виде 7.5, не 7,5
Постоянные
- pi
- – число Пи
- e
- – основание натурального логарифма
- i
- – комплексное число
- oo
- – символ бесконечности