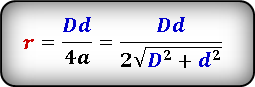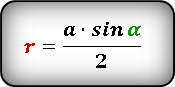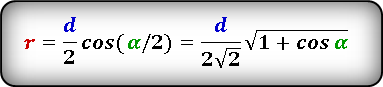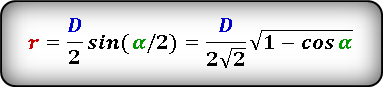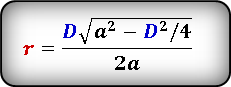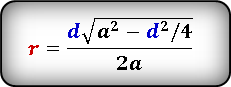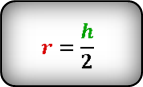Как найти уравнение вписанной окружности
Составить уравнение окружности, вписанной в треугольник, стороны которого лежат на прямых x = 0, y = 0 и 3x + 4y – 12 = 0.
найдем координаты вершин треугольника, решив следующие системы уравнений:
Этот треугольник прямоугольный, так как прямые x = 0 и y = 0 перпендикулярны. Пусть r – радиус вписанной окружности в треугольник, S – площадь треугольника, p – полупериметр треугольника. Тогда
и .
Так как окружность касается прямых x = 0 и y = 0, то координаты центра окружности – (r; r) или (1; 1).
Итак, искомое уравнение окружности (x – 1) 2 + (y – 1) 2 = 1.
Все формулы для радиуса вписанной окружности
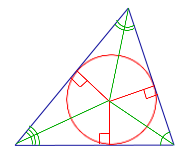
Радиус вписанной окружности в треугольник
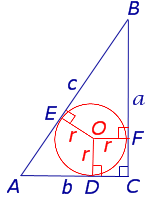
a , b , c – стороны треугольника
p – полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Радиус вписанной окружности в равносторонний треугольник
a – сторона треугольника
r – радиус вписанной окружности
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
a – равные стороны равнобедренного треугольника
b – сторона ( основание)
α – угол при основании
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a – равные стороны равнобедренного треугольника
b – сторона ( основание)
h – высота
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
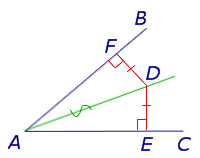
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
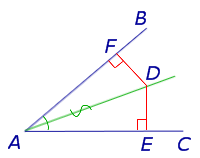
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно
что и требовалось доказать.
Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.
Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
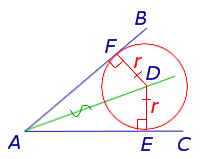
Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).
Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .
Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.
a, b, c – стороны треугольника,
S – площадь,
r – радиус вписанной окружности,
p – полупериметр
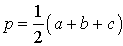
a – сторона равностороннего треугольника,
r – радиус вписанной окружности
| Фигура | Рисунок | Формула | Обозначения |
| Произвольный треугольник | 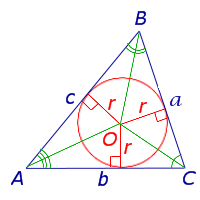 |
||
| Равнобедренный треугольник | 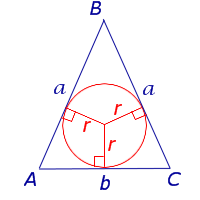 |
||
| Равносторонний треугольник | 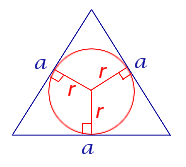 |
||
| Прямоугольный треугольник | 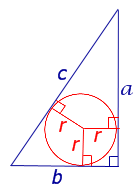 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр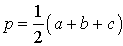
где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр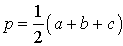
где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности
| Произвольный треугольник |
 |
| Равнобедренный треугольник |
 |
| Равносторонний треугольник |
 |
| Прямоугольный треугольник |
 |
| Произвольный треугольник |
 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр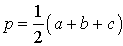
где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр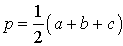
Равнобедренный треугольник
Равносторонний треугольник
где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности
Прямоугольный треугольник
Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, 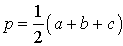
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
то, в случае равнобедренного треугольника, когда
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
то, в случае равностороннего треугольника, когда
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
Доказательство . Рассмотрим рисунок 9.
Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
[spoiler title=”источники:”]
http://www-formula.ru/2011-09-24-00-40-48
http://www.resolventa.ru/uslugi/uslugischoolrost.htm
[/spoiler]
Как найти точку пересечения биссектрис треугольника по координатам его вершин?
Как найти радиус вписанной в треугольник окружности по координатам его вершин?
Точка пересечения биссектрис треугольника является центром вписанной в этот треугольник окружности.
Эта точка равноудалена от сторон треугольника. Расстояние от точки пересечения биссектрис до сторон треугольника равно радиусу вписанной окружности.
Следовательно, все три задачи сводятся к нахождению точки пересечения биссектрис треугольника.
Для этого надо сначала составить уравнения биссектрис треугольника и найти точку их пересечения.
Пример.
Дан треугольник ABC с вершинами в точках A(0;-3), B(12;-12) и C(3,36;-0,48).
1) Найти точку пересечения биссектрис треугольника ABC.
2) Найти радиус вписанной в треугольник ABC окружности.
3) Составить уравнение вписанной в треугольник ABC окружности.
Решение:
1) Составим уравнения прямых, содержащих стороны треугольника.
Уравнение прямой, проходящей через две точки можно искать, например, в виде
Для прямой AB
Уравнение прямой AC:
Уравнение прямой BC:
Составим уравнение биссектрисы треугольника ABC, исходящей из угла B. Она образована прямыми AB и BC:
откуда уравнения биссектрис угла B: x-y-24=0 или x+y=0. Чтобы понять, которое из двух уравнений является биссектрисой внутреннего угла треугольника, следует подставить в уравнения координаты точек A и C. Поскольку они лежат по разные стороны от биссектрисы внутреннего угла B, то подстановка их координат в уравнение биссектрисы даёт числа разных знаков.
A(0;-3) и C(3,36;-0,48) в x-y-24=0: 0-(-3)-24<0; 3,36-(-0,48)-24<0. Получили числа одного знака, значит это уравнение не является биссектрисой внутреннего угла треугольника.
A(0;-3) и C(3,36;-0,48) в x+y=0: 0+(-3)<0, 3,36+(-0,48)>0. Получили числа разных знаков, x+y=0 — биссектриса угла B треугольника ABC.
Составим уравнение биссектрисы угла C. Угол C образован прямыми AC и BC, откуда
уравнения биссектрис угла C: 7x-y-24=0 и x+7y=0.
A(0;-3), B(12;-12) в 7x-y-24=0: 7·0-(-3)-24<0, 7·12-(-12)-24>0. Получили числа разных знаков, значит 7x-y-24=0 — уравнение биссектрисы внутреннего угла C.
Поскольку все три биссектрисы треугольника пересекаются в одной точке, третью биссектрису находить не требуется.
Точку пересечения биссектрис углов B и C найдём из системы уравнений
O(3;-3) — точка пересечения биссектрис треугольника ABC. Эта точка является центром вписанной в треугольник окружности.
2) Радиус вписанной в треугольник ABC окружности можно найти как расстояние от точки O до прямой AB, BC или AC. Найдем, например, расстояние от O до AB:
3) Чтобы найти уравнение вписанной в треугольник ABC окружности, в уравнение окружности подставляем координаты центра O(3;-3) и r=9/5:
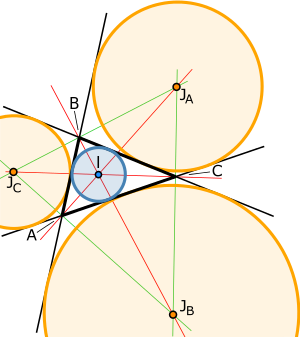
Треугольник (чёрный) с вписанной окружностью (синей), инцентр (I), вневписанными окружностями (оранжевые), эксцентры (JA,JB,JC), внутренние биссектрисы (красные) и внешние биссектрисы (зелёные)
Вписанная в треугольник окружность — окружность внутри треугольника, касающаяся всех его сторон; наибольшая окружность, которая может находиться внутри треугольника. Центр этой окружности является точкой пересечения биссектрис треугольника и называется инцентром треугольника.
Вневписанная окружность треугольника — окружность, лежащая вне треугольника и касающаяся одной стороны треугольника и продолжения двух других сторон[en]. Любой треугольник имеет три различные вневписанные окружности, каждая из которых касается своей стороны треугольника.
Центром вневписанной окружности является пересечение биссектрисы одного внутреннего угла[en] и биссектрис двух других внешних углов[en]. Поскольку биссектриса внутреннего угла перпендикулярна биссектрисе смежного внешнего угла, центр вписанной окружности вместе с тремя центрами вневписанных окружностей образуют ортоцентричную систему[en][1].
Не все многоугольники с числом сторон более трёх имеют вписанную окружность. Те, которые имеют, называются описанными.
Связь с площадью треугольника[править | править код]
Радиусы вписанных и вневписанных окружностей имеют тесную связь с площадью треугольника[2].
Вписанная окружность[править | править код]
Пусть 
Пусть a — длина BC, b — длина AC, а c — длина AB.
Пусть вписанная окружность касается AB в некоторой точке C′, тогда

Тогда радиус C’I будет высотой треугольника

Таким образом,
имеет основание длины c и высоту r, а следовательно, его площадь равна

Подобным же образом
имеет площадь
и
имеет площадь 
Поскольку эти три треугольника разбивают 
где 


Чтобы получить альтернативную формулу, рассмотрим 


Вневписанные окружности[править | править код]
Пусть вневписанная окружность, касающаяся стороны AB, касается продолжения стороны AC в точке G, и пусть радиус этой окружности равен 



так что 

имеет площадь

а
имеет площадь

Тогда
.
Таким образом, ввиду симметрии,
.
По теореме косинусов получаем
Комбинируя это с тождеством 
Но 
и это формула Герона вычисления площади треугольника по его сторонам.
Комбинируя формулу Герона с 
.
Аналогично, 
.
Из этих формул видно, что вневписанные окружности всегда больше вписанной и наибольшая окружность соответствует самой длинной стороне, а самая наименьшая из вневписанных окружностей соответствует самой маленькой стороне. Дальнейшее комбинирование формул приводит к:[3]
Отношение площади вписанной окружности к площади треугольника меньше или равно 
Связанные построения[править | править код]
Окружность девяти точек и точка Фейербаха[править | править код]
- Теорема Эйлера об окружности Эйлера. Середины отрезков высот от ортоцентра до вершин треугольника называются точками Эйлера. Основания медиан, основания высот и точки Эйлера лежат на одной окружности, называемой окружностью девяти точек[5].
- Теорема Фейербаха. Окружность девяти точек касается всех трёх вневписанных окружностей, а также вписанной окружности в четырёх разных точках. Одна из них – точка касания окружности Эйлера и вписанной окружности известна как точка Фейербаха.
Треугольник и точка Жергонна[править | править код]
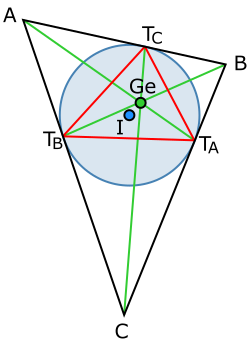
Треугольник ΔABC с вписанной окружностью (синяя), и её центр (синий, I), треугольник точек касания (красный, ΔTaTbTc) и точка Жергонна (зелёная, Ge)
Треугольник Жергонна (для треугольника ABC) определяется тремя точками касания вписанной окружности на трёх сторонах.
Эти вершины обозначим TA, и т. д..
Точка TA лежит напротив вершины A.
Этот треугольник Жергонна TATBTC известен также как треугольник касаний треугольника ABC.
Три прямые ATA, BTB и CTC пересекаются в одной точке — точке Жергонна и обозначается Ge — X(7). Точка Жергонна лежит внутри открытого ортоцентроидного круга[en] с выколотым центром[6].
Интересно, что точка Жергонна треугольника является точкой пересечения симедиан треугольника Жергонна. Полный набор свойств точки Жергонна можно найти в статье Декова[7].
Трилинейные координаты вершин треугольника касаний задаются формулами
- вершина
- вершина
- вершина
Трилинейные координаты точки Жергонна
,
или, эквивалентно, по теореме синусов,
.
Точка Жергонна является изотомическим сопряжением точки Нагеля.
Треугольник и точка Нагеля[править | править код]
Треугольник Нагеля (см. рис. выше) для треугольника ABC определяется вершинами TA, TB и TC, которые являются точками касания вневписанных окружностей треугольника ABC и точка XA противоположна стороне A, и т. д. Описанная вокруг треугольника TATBTC окружность называется окружностью Мандарта (частный случай эллипса Мандарта). Три прямые ATA, BTB и CTC делят периметр пополам и пересекаются в одной точке Нагеля Na — X(8).
Трилинейные координаты точек касания треугольника вневписанными окружностями задаются формулами
- вершина
- вершина
- вершина
Трилинейные координаты точки Нагеля задаются формулами
,
или, эквивалентно, по теореме синусов,
.
Точка Нагеля является изотомическим сопряжением точки Жергонна.
Трилинейные координаты вписанных треугольников[править | править код]
Трилинейные координаты вершин треугольника, образованного основаниями биссектрис, задаются формулами
- вершина
- вершина
- вершина
Трилинейные координаты треугольника, образованного точками касания сторон внеописанными окружностями, задаются формулами
- вершина
- вершина
- вершина
Уравнения окружностей[править | править код]
Пусть x : y : z — координаты точки в трилинейных координатах, и пусть u = cos2(A/2), v = cos2(B/2), w = cos2(C/2). Четыре окружности, описанные выше, можно задать любым из двух указанных способов[8]:
-
- Вписанная окружность:
-
- A-внешневписанная:
-
- B-внешневписанная:
-
- C-внешневписанная:
Другие свойства вписанной окружности[править | править код]
Некоторые формулы с радиусом вписанной окружности[править | править код]
- Радиус вписанной окружности не больше одной девятой суммы высот треугольника[9].
- Неравенство Эйлера: радиус вписанной окружности не превосходит половины радиуса описанной окружности и равенство имеет место лишь для равностороннего треугольника[10].
- Предположим, что точки касания вписанной окружности делят стороны на отрезки длиной x и y, y и z, z и x. Тогда вписанная окружность имеет радиус[11]
и площадь треугольника равна
- Если высоты, опущенные на стороны a, b и c есть ha, hb и hc, то радиус вписанной окружности r равен одной трети гармонического среднего этих высот, то есть
- Произведение радиуса вписанной окружности r и радиуса описанной окружности R треугольника со сторонами a, b и c равен[1]
- Некоторые связи сторон, радиусов вписанной окружности и описанной окружностей[12]:
- Любая прямая, проходящая через треугольник и делящая площадь треугольника и периметр пополам, проходит через центр вписанной окружности. Таких прямых может существовать три, две или одна[13].
- Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности[14].
Формулы для расстояний до центра вписанной или вневписанной окружностей[править | править код]
Теорема Эйлера[править | править код]
Теорема Эйлера утверждает, что в треугольнике[10]:
где R и rin являются радиусами описанной и вписанной окружностей соответственно, а d — расстояние между центрами этих окружностей.
Для вневписанных окружностей уравнение выглядит похоже:
где rex — радиус одной из вневписанных окружностей, а d — расстояние между центрами описанной и вневписанной окружностей[15][16][17]
- Возводя в квадрат и приводя подобные из первой формулы Эйлера выше имеем:
Квадрат расстояния от центра вписанной окружности I до центра описанной O задаётся уравнением[18]
Аналогично для второй формулы:
Другие формулы для расстояний до центра вписанной или вневписанной окружностей[править | править код]
- Расстояние от центра вписанной окружности до центра N окружности девяти точек равно[18]
- Расстояние от вершины до точек касания вписанной окружности на прилегающих сторонах равно полусумме длин прилегающих сторон минус половина противолежащей стороны[19]. Так, для вершины B и прилежащих точек касания TA и TC,
- Если обозначить центр вписанной окружности треугольника ABC буквой I, мы получим[20]
и[21]
- Теорема Мансиона (составная часть Теоремы о трезубце). Середины трёх отрезков, соединяющих центр вписанной окружности с центрами вневписанных окружностей лежат на описанной окружности[10].
- Теорема Харкорта. Пусть треугольник задан своими вершинами A, B и C, противоположные вершинам стороны имеют длины a, b и c, площадь равна K и прямая касается вписанной в треугольник окружности в произвольной точке. Обозначим расстояния от вершин треугольника до прямой через a ‘, b ‘ и c ‘, при этом, если вершина и центр окружности лежат по разные стороны от прямой, расстояние считается отрицательным. Тогда
.
Другие свойства вневписанных окружностей[править | править код]
- Следующее отношение выполняется для радиуса r вписанной окружности, радиуса R описанной окружности, полупериметра s и радиусов вневписанных окружностей ra, rb, rc[12]:
- Окружность, проходящая через центры вневписанных окружностей, имеет радиус 2R[12].
- Если H — ортоцентр треугольника ABC, то[12]
- Вершины A, B и C треугольника ABC являются основаниями высот треугольника JAJB,JC,
где JAJB,JC — центры вневписанных окружностей[10].
- Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности[14].
- Центр Шпикера треугольника является радикальным центром его вневписанных окружностей[22]. Если из центра Шпикера треугольника провести 6 касательных к 3 вневписанным окружностям треугольника, то все их длины будут равны между собой.
Окружность Аполлония[править | править код]
Определение окружности Аполлония[править | править код]
Точка Аполлония и окружность Аполлония
Пусть дан треугольник ABC. Пусть вневписанные окружности треугольника ABC, противоположные вершинам A, B и C, есть соответственно EA, EB, EC (см. рисунок). Тогда окружность Аполлония E (на рис. справа показана зеленым цветом) касается внутренним образом сразу трех вневписанных окружностей треугольника ABC в точках соответственно EA, EB и EC (см. рисунок)[23].
Радиус окружности Аполлония[править | править код]
Радиус окружности Аполлония равен 
Определение точки Аполлония Ap[править | править код]
- Точка Аполлония Ap в Энциклопедии центров треугольника у Кларка Кимберлинга (Encyclopedia of Triangle Centers (ETC)) именуется как центр треугольника под именем X(181).
- Точка Аполлония Ap или X(181) определяется следующим образом:
Пусть A’ , B’ и C’ есть точки касания окружности Аполлония E с соответствтвующими вневписанными окружностями. Тогда прямые AA’ , BB’ и CC’ пересекаются в одной точке Ap, которую называют точкой Аполлония треугольника ABC.
Изогональное сопряжение[править | править код]
Изогональное сопряжение имеет ровно четыре неподвижные точки (то есть точки, которые сопряжены самим себе): центр вписанной окружности и центры вневписанных окружностей треугольника[25].
Ортоцентр треугольника изогонально сопряжён центру описанной окружности этого треугольника[25].
Обобщение на другие многоугольники[править | править код]
- Некоторые (но не все) четырёхугольники имеют вписанную окружность. Они называются описанными четырёхугольниками. Среди свойств этих четырёхугольников наиболее важным является то, что суммы противоположных сторон равны. Это утверждение называется теоремой Пито.
- Некоторые (но не все) четырёхугольники имеют вневписанную окружность. Они называются внеописанными четырёхугольниками. Среди свойств этих четырёхугольников наиболее важное свойство отмечает теорема Уркхарта. Она утверждает:
- Если противоположные стороны выпуклого четырёхугольника ABCD пересекаются в точках E и F, то
См. также[править | править код]
- Вневписанная окружность
- Внеописанный четырёхугольник
- Вписанная окружность
- Вписанные и описанные фигуры для треугольника
- Вписанное коническое сечение[en]
- Вписанная сфера
- Высота треугольника
- Замечательные точки треугольника
- Инцентр или Центр вписанной окружности
- Окружность
- Описанная окружность
- Описанный четырёхугольник
- Ортоцентр
- Степень точки относительно окружности
- Теорема Мансиона
- Теорема о трезубце
- Теорема Тебо 2 и 3
- Теорема Харкорта
- Точки Аполлония
- Степень точки относительно окружности
- Центр Шпикера
- Центроид
- Центроид треугольника
- Эллипс Мандарта
- Эллипс Штейнера
Примечания[править | править код]
- ↑ 1 2 Roger A. Johnson. Advanced Euclidean Geometry. — Dover, 2007 (оригинал — 1929).. — С. 189, #298(d).
- ↑ H.S.M. Coxeter. Introduction to Geometry. — 2. — Wiley, 1961..
- ↑ Marcus Baker. A collection of formulae for the area of a plane triangle. — January 1885. — Т. part 1, vol. 1(6). — С. 134-138.. См. также часть 2 в томе. 2(1), Сентябрь 1885, 11-18.)
- ↑ D. Minda, S. Phelps. Triangles, ellipses, and cubic polynomials // American Mathematical Monthly. — October 2008. — Вып. 115. — С. 679-689: Theorem 4.1..
- ↑ С. И. Зетель. Новая геометрия треугольника. — Москва: УЧПЕДГИЗ, 1962. — С. 52-53 Глава III.
- ↑ Christopher J. Bradley, Geoff C. Smith. The locations of triangle centers // Forum Geometricorum. — 2006. — Вып. 6. — С. 57-70..
- ↑ Deko Dekov. Computer-generated Mathematics : The Gergonne Point // Journal of Computer-generated Euclidean Geometry. — 2009. — Т. 1. — С. 1–14.. Архивировано 5 ноября 2010 года.
- ↑ William Allen Whitworth. Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions. — 2012. — С. 210-215. — (Forgotten Books).
- ↑ Alfred S. Posamentier, Ingmar Lehmann. The Secrets of Triangles. — Prometheus Books, 2012. — С. 289.
- ↑ 1 2 3 4 А. Д. Куланин, С. Н. Федин. Геометрия треугольника в задачах. — М.: Книжный дом «ЛИБРОКОМ», 2009. — ISBN 978-5-397-00786-3.
- ↑ Thomas Chu. The Pentagon. — Spring, 2005. — С. 45, задача 584..
- ↑ 1 2 3 4 Amy Bell. Hansen’s right triangle theorem, its converse and a generalization // Forum Geometricorum. — 2006. — Вып. 6. — С. 335–342.
- ↑ Dimitrios Kodokostas. Triangle Equalizers // Mathematics Magazine. — 2010. — Вып. 83, April. — С. 141-146..
- ↑ 1 2 Мякишев, 2002, с. 11, п. 5.
- ↑ Roger Nelson. Euler’s triangle inequality via proof without words // Mathematics Magazine. — February 2008. — Вып. 81(1). — С. 58-61.
- ↑ R. A. Johnson. Modern Geometry. — Boston: Houghton Mifflin, 1929. — С. 187.
- ↑ Lev Emelyanov, Tatiana Emelyanova. Euler’s formula and Poncelet’s porism // Forum Geometricorum. — 2001. — Вып. 1. — С. 137–140..
- ↑ 1 2 3 William N. Franzsen. The distance from the incenter to the Euler line // Forum Geometricorum. — 2011. — Т. 11. — С. 231–236..
- ↑ Mathematical Gazette, July 2003, 323—324.
- ↑ Patricia R. Allaire, Junmin Zhou, Haishen Yao. Proving a nineteenth century ellipse identity // Mathematical Gazette. — 2012. — Вып. 96, March. — С. 161-165..
- ↑ Nathan Altshiller-Court. College Geometry. — Dover Publications, 1980. — С. 121,#84.
- ↑ Odenhal, 2010, с. 35—40.
- ↑ Darij Grinberg, Paul Yiu. The Apollonius Circle as a Tucker Circle // Forum Geometricorum. — 2002. — Вып. 2. — С. 175-182.
- ↑ Milorad R. Stevanovi´c. The Apollonius circle and related triangle centers // Forum Geometricorum. — 2003. — Вып. 3. — С. 187-195..
- ↑ 1 2 В. В. Прасолов. Точки Брокара и изогональное сопряжение. — М.: МЦНПО, 2000. — (Библиотека «Математическое просвещение»). — ISBN 5-900916-49-9.
Литература[править | править код]
- Мякишев А.Г. Элементы геометрии треугольника. — М.: МЦНМО, 2002.
- Clark Kimberling. Triangle Centers and Central Triangles // Congressus Numerantium. — 1998. — Вып. 129. — С. i-xxv, 1-295.
- Sándor Kiss. The Orthic-of-Intouch and Intouch-of-Orthic Triangles // Congressus Numerantium. — 2006. — Вып. 6. — С. 171—177.
- Boris Odenhal. Some triangle centers associated with the circles tangent to the excircles // Forum Geometricorum. — 2010. — Т. 10.
Ссылки[править | править код]
- Derivation of formula for radius of incircle of a triangle
- Weisstein, Eric W. Incircle (англ.) на сайте Wolfram MathWorld.
Сайты с интерактивным содержанием[править | править код]
- Triangle incenter Triangle incircle Incircle of a regular polygon With interactive animations
- Constructing a triangle’s incenter / incircle with compass and straightedge An interactive animated demonstration
- Equal Incircles Theorem at cut-the-knot
- Five Incircles Theorem at cut-the-knot
- Pairs of Incircles in a Quadrilateral at cut-the-knot
- An interactive Java applet for the incenter
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Уравнение вписанной в треугольник окружности
|
|||
|
Здравствуйте!!! Задача следующая: В этой задаче не могу найти только уравнение вписанной окружности, пожалуйста помогите))
|
||
| Вернуться к началу |
|
||
|
bober |
Заголовок сообщения: Re: Уравнение вписанной в треугольник окружности
|
|
Спасибо)) Но по этой ссылке не могу найти, то что мне нужно – это координаты центра окружности и её радиус.
|
|
| Вернуться к началу |
|
|
bober |
Заголовок сообщения: Re: Уравнение вписанной в треугольник окружности
|
|
Я знаю об этом)) Знаю, как найти медиану, она делит сторону пополам, а вот биссектриса, как найти координаты второй точки – не доходит и точки их пересечения.
|
|
| Вернуться к началу |
|
|
bober |
Заголовок сообщения: Re: Уравнение вписанной в треугольник окружности
|
| Вернуться к началу |
|
|
bober |
Заголовок сообщения: Re: Уравнение вписанной в треугольник окружности
|
|
Уравнения сторон у меня получились вот такие:
|
|
| Вернуться к началу |
|
|
bober |
Заголовок сообщения: Re: Уравнение вписанной в треугольник окружности
|
| Вернуться к началу |
|
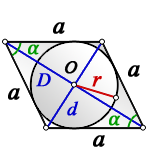
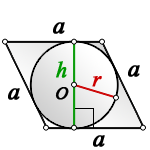
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
a – сторона ромба
D – большая диагональ
d – меньшая диагональ
α – острый угол
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в ромб через диагонали ( r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :
2. Радиус вписанной окружности ромба, равен половине его высоты
a – сторона ромба
h – высота
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в ромб ( r ) :
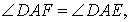
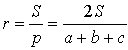
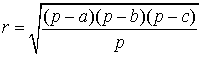
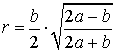
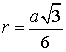
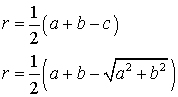
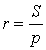
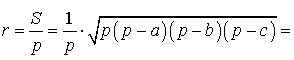
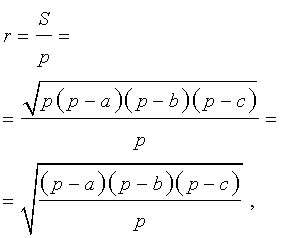
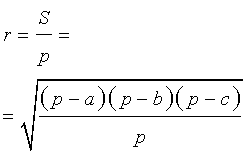
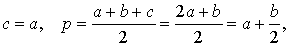
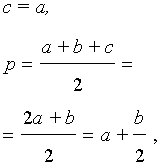
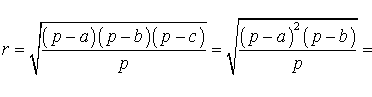
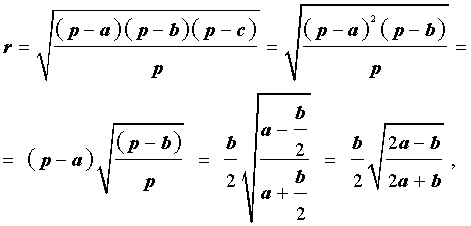
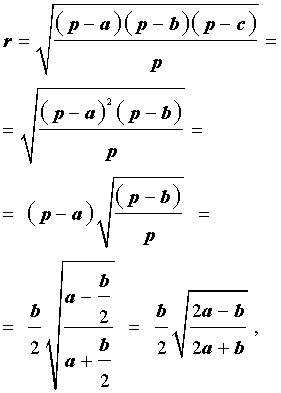
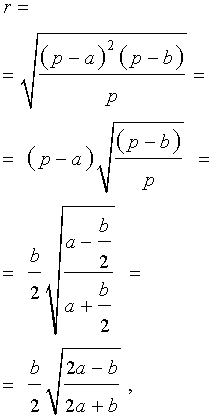
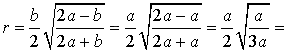
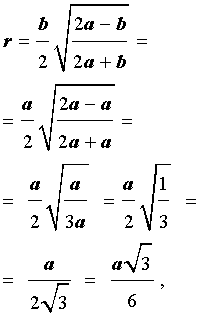
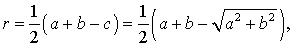
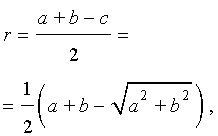
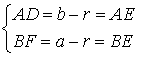
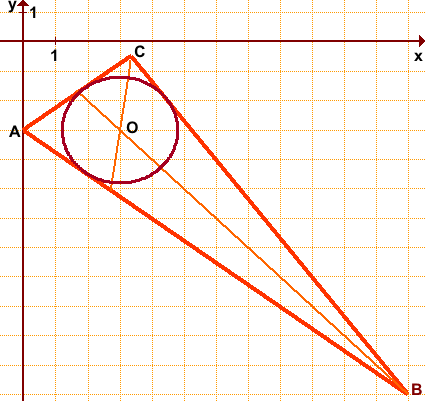

















































![{displaystyle OI^{2}={frac {abc,}{a+b+c}}left[{frac {abc,}{(a+b-c),(a-b+c),(-a+b+c)}}-1right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b69301d64b404e6d694db6fa821d53a2f3d65af9)